a general method of solving extremum problems

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Extremal problems, numerical methods

Methods of computational mathematics that are applied to find the extrema (maxima or minima) of functions and functionals.

The numerical solution of extremal problems considered in infinite-dimensional function spaces (for example, problems of optimal control by means of processes described by ordinary or partial differential equations) can be obtained by using appropriate generalizations of many methods of mathematical programming developed for problems of minimization or maximization of functions of finitely many variables. In this context it is very important to make the correct choice of a suitable function space in which a concrete problem should be considered. Such a space is usually chosen by taking into account physical considerations, properties of admissible controls, properties of the solutions of the corresponding initial-boundary value problems for a fixed control, etc.

For example, the problem of optimal control consisting of the minimization of the functional

$$ \tag{1 } J ( u) = \int\limits _ {t _ {0} } ^ { T } f ^ { 0 } ( x ( t) , u ( t) , t) d t + F ( x ( T) ) $$

under the conditions

$$ \tag{2 } \dot{x} = f ( x , u ( t) , t ),\ \ t _ {0} \leq t \leq T ; \ \ x ( t _ {0} ) = x _ {0} , $$

$$ \tag{3 } u = u ( t) \in V ( t) ,\ t _ {0} \leq t \leq T , $$

is usually considered in the function space $ L _ {2} ^ {r} [ t _ {0} , T ] $. Here $ x = ( x ^ {1} \dots x ^ {n} ) $, $ u = ( u ^ {1} \dots u ^ {r} ) $, $ f = ( f ^ {1} \dots f ^ { n } ) $, $ f ^ { i } ( x , u , t ) $, $ i = 1 \dots n $, and $ F ( x) $ are given functions, $ t _ {0} $ and $ T $ known moments in time, $ t _ {0} < T $, $ x _ {0} $ is a given initial point, $ V ( t) $ is a given set in the Euclidean space $ E ^ {r} $ for every $ t \in [ t _ {0} , T ] $, and $ L _ {2} ^ {r} [ t _ {0} , T ] $ is the Hilbert space of $ r $- dimensional vector functions $ u = u ( t) = ( u ^ {1} ( t) \dots u ^ {r} ( t) ) $, $ t _ {0} \leq t \leq T $, where each function $ u ^ {i} ( t) $ is, together with its square, Lebesgue integrable over $ [ t _ {0} , t] $ $ ( L _ {2} ^ {1} [ t _ {0} , T ] = L _ {2} [ t _ {0} , T ] ) $; the inner product of two functions $ u $ and $ v $ in this space is defined by

$$ \langle u , v \rangle _ {L _ {2} ^ {r} } = \int\limits _ {t _ {0} } ^ { T } \sum _ { i= } 1 ^ { r } u ^ {i} ( t) v ^ {i} ( t) d t , $$

and the norm by

$$ \| u \| _ {L _ {2} ^ {r} } = \left ( \int\limits _ {t _ {0} } ^ { T } \sum _ { i= } 1 ^ { r } | u ^ {i} ( t) | ^ {2} d t \right ) ^ {1/2} . $$

For a specific degree of smoothness of the functions $ f ^ { i } ( x , u , t ) $ and $ F ( x) $ the increment of the functional (1) can be represented in the form

$$ \tag{4 } J ( u + h ) - J ( u) = - \int\limits _ {t _ {0} } ^ { T } \sum _ { i= } 1 ^ { r } \frac{\partial H ( u) }{\partial u ^ {i} } h ^ {i} ( t) d t + R = $$

$$ = \ \langle - \frac{\partial H ( u) }{\partial u } , h \rangle _ {L _ {2} ^ {r} } + R ,\ R = o ( \| h \| _ {L _ {2} ^ {r} } ) , $$

$$ \tag{5 } H ( x , \psi , u , t ) = \sum _ { i= } 1 ^ { n } \psi _ {i} f ^ { i } ( x , u , t ) - f ^ { 0 } ( x , u , t ) , $$

$$ \frac{\partial H }{\partial u } = \left ( \frac{\partial H }{\partial u ^ {1} } \dots \frac{\partial H }{\partial u ^ {r} } \right ) ,\ \left . \frac{\partial H ( u) }{\partial u } = \frac{\partial H }{\partial u } \right | _ {\begin{array} {c} u = u ( t) \\ x = x ( t ; u ) \\ \psi = \psi ( t ; u ) \end{array} } , $$

$ x = x ( t ; u ) $ is the solution of the problem (2) for $ u = u ( t) $, and $ \psi = \psi ( t ; u ) $ is the solution of the adjoint problem

$$ \tag{6 } \left . \dot \psi _ {i} = - \frac{\partial H }{\partial x ^ {i} } \right | _ {\begin{array} {c} u = u ( y) \\ x = x ( t ; u ) \end{array} } ,\ \ t _ {0} \leq t \leq T ,\ \ i = 1 \dots n , $$

$$ \tag{7 } \left . \psi _ {i} ( T) = \frac{\partial F }{\partial x ^ {i} } \right | _ {x = x ( T ; u ) } . $$

Formula (4) implies that the functional (1) is differentiable in $ L _ {2} ^ {r} [ t _ {0} , T ] $ and that its gradient is the vector function

$$ \tag{8 } J ^ \prime ( u) = - \frac{\partial H ( u) }{\partial u } \in L _ {2} ^ {r} [ t _ {0} , T ] . $$

Hence, (1)–(3) can be solved by applying various methods that use the gradient of the functional. For $ V ( t) = E ^ {r} $ one may apply the gradient method

$$ u _ {k+} 1 ( t) = u _ {k} ( t) + \alpha _ {k} \frac{\partial H ( u _ {k} ) }{\partial u } ,\ \ k = 0 , 1 , . . . . $$

If $ V ( t) = \{ {u = ( u ^ {1} \dots u ^ {r} ) } : {\alpha _ {i} ( t) \leq u ^ {i} \leq \beta _ {i} ( t), i = 1 \dots r } \} $, where $ \alpha _ {i} ( t) $ and $ \beta _ {i} ( t) $ are given functions in $ L _ {2} [ t _ {0} , T ] $, then it is possible to apply the method of gradient projection:

$$ u _ {k+} 1 ( t) = P \left ( u _ {k} ( t) + \alpha _ {k} \frac{\partial H ( u _ {k} ) }{\partial u } \right ) ,\ \ k = 0 , 1 \dots $$

$$ P ( w) = ( w ^ {1} ( t) \dots w ^ {r} ( t) ) ,\ \ t _ {0} \leq t \leq T , $$

$$ w ^ {i} ( t) = \left \{ \begin{array}{ll} \alpha _ {i} ( t) &\textrm{ for } v ^ {i} ( t) \leq \alpha _ {i} ( t) , \\ v ^ {i} ( t) &\textrm{ for } \alpha _ {i} ( t) \leq v ^ {i} ( t) \leq \beta _ {i} ( t) , \\ \beta _ {i} ( t) &\textrm{ for } v ^ {i} ( t) > \beta _ {i} ( t) ,\ i = 1 \dots r . \\ \end{array} \right .$$

The parameter $ \alpha _ {k} > 0 $ can be chosen from the condition $ J ( u _ {k+} 1 ) < J ( u _ {k} ) $. The methods of the conditional gradient, dual gradients, etc. (see [4] – [6] and [11] ) can be adapted for the problem (1)–(3) analogously. If this problem is considered under the additional restrictions

$$ \tag{9 } x ( t ; u ) \in G ( t) ,\ \ t _ {0} \leq t \leq t , $$

where $ G ( t) $ is a given set in $ E ^ {n} $, then these restrictions can be taken into account by using the method of penalty functions (cf. Penalty functions, method of ). For example, if

$$ G ( t) = $$

$$ = \ \{ {x \in E ^ {n} } : {g _ {i} ( x , t ) \leq 0 ,\ i = 1 \dots m ; g _ {i} ( x , t ) = 0 , i = m + 1 \dots s } \} , $$

then as a penalty function one may take

$$ P ( u) = \int\limits _ {t _ {0} } ^ { T } \left ( \sum _ { i= } 1 ^ { m } ( \max \{ g _ {i} ( x ( t ; u ) , t ) ; 0 \} ) ^ {p\right} . + $$

$$ + \left . \sum _ { i= } m+ 1 ^ { s } | g _ {i} ( x ( t ; u ) , t ) | ^ {p} \right ) d t,\ p \geq 1 , $$

and (1)–(3), (9) is replaced by the problem of minimizing the functional $ \Phi _ {k} ( u) = J ( u) + A _ {k} P ( u) $ under the conditions (2) and (3), where $ A _ {k} $ is the penalty coefficient and $ \lim\limits _ {k \rightarrow \infty } A _ {k} = + \infty $.

Other methods for solving (1)–(3), (9) are based on Pontryagin's maximum principle and on dynamic programming (see Pontryagin maximum principle ; Dynamic programming and Variational calculus, numerical methods of ).

The problem of minimizing a quadratic functional subject to a system of linear ordinary differential equations or linear partial differential equations can be solved by applying the method of moments (see [3] and [8] ). This method is described below when applied to the problem of minimizing the functional

$$ \tag{10 } J ( u) = | x ( T ; u ) - y | _ {E ^ {n} } ^ {2} , $$

where $ x = x ( t ; u ) $ is the solution of the problem

$$ \tag{11 } \dot{x} = A ( t) x + B ( t) + f ( t) ,\ \ t _ {0} \leq t \leq T ,\ \ x ( t _ {0} ) = x _ {0} , $$

and the controls $ u = u ( t) \in L _ {2} ^ {r} [ t _ {0} , T ] $ are such that

$$ \tag{12 } \| u \| _ {L _ {2} ^ {r} } ^ {2} = \ \int\limits _ {t _ {0} } ^ { T } | u ( t) | _ {E ^ {r} } ^ {2} d t \leq R ^ {2} ; $$

here $ A ( t) $, $ B ( t) $ and $ f ( t) $ are given matrices of order $ n \times n $, $ n \times r $ and $ n \times 1 $, respectively, with piecewise-continuous entries on the interval $ t _ {0} \leq t \leq T $, $ 0 < R \leq \infty $, $ x , y \in E ^ {n} $ are given points, $ | x | _ {E ^ {m} } ^ {2} = \langle x , x \rangle _ {E ^ {m} } $, and $ \langle x , y \rangle _ {E ^ {m} } = \sum _ {i=} 1 ^ {m} x ^ {i} y ^ {i} $ is the inner product in $ E ^ {m} $. From the rule of Lagrange multipliers it follows that the control $ u = u ( t) $ is optimal in the problem (10)–(12) if and only if there is a number $ \gamma \geq 0 $( the Lagrange multiplier for the constraint (12)) such that

$$ \tag{13 } J ^ \prime ( u) + \gamma u = 0 , $$

$$ \tag{14 } \gamma ( \| u \| _ {L _ {2} ^ {r} } - R ) = \ 0 ,\ \| u \| _ {L _ {2} ^ {r} } \leq R ; $$

here $ \gamma = 0 $ for $ R = \infty $. Formulas (5)–(8) imply that the gradient $ J ^ \prime ( u) $ of the functional (10) in $ L _ {2} ^ {r} [ t _ {0} , T ] $ has the form

$$ J ^ \prime ( u) = B ^ {T} ( t) \psi ( t ; u ) ,\ \ t _ {0} \leq t \leq T , $$

where $ \psi = \psi ( t ; u ) $ is the solution of the problem

$$ \tag{15 } \dot \psi = - A ^ {T} ( t) \psi ,\ \ t _ {0} \leq t \leq T , $$

$$ \tag{16 } \psi ( T) = 2 ( x ( T ; u ) - y ) ; $$

here $ A ^ {T} $ and $ B ^ {T} $ are the transposed matrices of $ A $ and $ B $, respectively. Then condition (13) becomes

$$ \tag{17 } B ^ {T} ( t) \psi ( t ; u ) + \gamma u ( t) = 0 ,\ \ t _ {0} \leq t \leq T . $$

Condition (16) is equivalent to

$$ \tag{18 } \int\limits _ {t _ {0} } ^ { T } \langle u ( t), B ^ {T} ( t) p _ {k} ( t) \rangle _ {E ^ {r} } d t - \frac{1}{2} \langle \psi ( T) , p _ {k} ( T) \rangle _ {E ^ {n} } = a _ {k} , $$

for $ k = 1 \dots n $, where

$$ a _ {k} = \langle y , p _ {k} ( T) \rangle _ {E ^ {n} } - < x _ {0} ,\ p _ {k} ( t _ {0} ) > _ {E ^ {n} } - \int\limits _ {t _ {0} } ^ { T } \langle f ( t) , p _ {k} ( t) \rangle _ {E ^ {r} } d t , $$

and $ p _ {k} ( t) $ is the solution of the system (15) satisfying $ p _ {k} ( T) = e _ {k} = ( 0 \dots 0 , 1 , 0 \dots 0) $( a unit vector). Hence, the optimal control $ u = u ( t) $ in the problem (10)–(12) is determined by solving the system (14), (15), (17), (18) relative to the functions $ u ( t) $ and $ \psi ( t) $ and the number $ \gamma \geq 0 $. If $ R = \infty $, then $ \gamma = 0 $, $ \psi ( t) = 0 $ and (18) reduces to the problem of moments (see Moment problem ): To find a function $ u = u( t) $, knowing

$$ \int\limits _ {t _ {0} } ^ { T } \langle u ( t) , \phi _ {k} ( t) \rangle d t = a _ {k} $$

with respect to the system $ \phi _ {k} ( t) = B ^ {T} ( t) p _ {k} ( t) $, $ k = 1 \dots n $.

System (14), (15), (17), (18) is a generalized moment problem for (10)–(12) with $ 0 < R < \infty $( see [3] and [8] ).

Any solution $ \psi ( t) $ of (15) is uniquely representable in the form

$$ \tag{19 } \psi ( t) = \sum _ { k= } 1 ^ { n } \psi _ {k} p _ {k} ( t) ,\ \ t _ {0} \leq t \leq T . $$

System (15), (17), (18) has a solution $ \psi ( t ; \gamma ) $, $ u ( t ; \gamma ) $ for any fixed $ \gamma \geq 0 $, and among all its solutions there is a unique one such that $ u ( t ; \gamma ) $ has the form

$$ \tag{20 } u ( t ; \gamma ) = \sum _ { k= } 1 ^ { n } u _ {k} B ^ {T} ( t) p _ {k} ( t) ,\ \ t _ {0} \leq t \leq T . $$

To find $ \psi ( t ; \gamma ) $ and $ u ( t ; \gamma ) $ one substitutes (19) and (20) in (17) and (18) and obtains a system of linear algebraic equations with respect to $ \psi _ {1} \dots \psi _ {n} , u _ {1} \dots u _ {n} $, from which $ \psi _ {1} \dots \psi _ {n} $ are determined uniquely and $ u _ {1} \dots u _ {n} $ non-uniquely if the system $ \{ {B ^ {T} ( t) p _ {k} ( t) } : {k = 1 \dots n } \} $ is linearly dependent. In the practical solution of the problem (10)–(12) it is advisable to set $ \gamma = 0 $ and $ \psi ( t) = 0 $ from the beginning and to use (18) to determine $ u ( t ; 0 ) $ of the form (20). Next, it must be checked that $ \| u ( t ; 0 ) \| _ {L _ {2} ^ {r} } \leq R $. If this inequality holds, then $ u ( t ; 0 ) $ is the optimal control of (10)–(12) with minimal norm among all optimal controls; the set of all optimal controls in this case consists of controls of the form

$$ u ( t) = u ( t ; 0 ) + v ( t) ,\ \ t _ {0} \leq t \leq T , $$

where $ v ( t) $ belongs to the orthogonal complement in $ L _ {2} ^ {r} [ t _ {0} ; T ] $ of the linear span of the system of functions

$$ \{ {B ^ {T} ( t) p _ {k} ( t) } : {k = 1 \dots n } \} , $$

$$ \| v ( t) \| _ {L _ {2} ^ {r} } \leq R ^ {2} - \| u ( t ; 0 ) \| _ {L _ {2} ^ {r} } ^ {2} . $$

If $ \| u ( t ; 0 ) \| _ {L _ {2} ^ {r} } > R $, then for $ \gamma > 0 $ the solutions $ \psi ( t ; \gamma ) $ and $ u ( t ; \gamma ) $ of the form (19) and (20), respectively, are found from (17) and (18), and $ \gamma $ is found from the equation

$$ \tag{21 } \| u ( t ; \gamma ) \| _ {L _ {2} ^ {r} } = R ,\ \gamma > 0 . $$

The function $ \| u ( t ; \gamma ) \| _ {L _ {2} ^ {r} } $ of the variable $ \gamma $ is continuous and strictly decreasing for $ \gamma > 0 $, and $ \lim\limits _ {\gamma \rightarrow + \infty } \| u ( t ; 0 ) \| _ {L _ {2} ^ {r} } = 0 $; therefore, the desired $ \gamma = \gamma _ {*} $ is determined uniquely from (21). The control $ u ( t ; \gamma _ {*} ) $ is optimal for the problem (10)–(12); for $ \| u ( t ; 0 ) \| _ {L _ {2} ^ {r} } > R $ this problem has no other optimal controls.

The method of moments is also applicable for the solution of the high-speed problem for the system (11) and other linear systems (see [3] and [8] ).

The above methods are also widely used for the numerical solution of problems of optimal control by means of processes described by partial differential equations.

The numerical realizations of many methods for solving problems of optimal control are based on the use of some technique for the approximate solution of the intervening initial-boundary value problems (see Boundary value problem, numerical methods for partial differential equations ) and of approximate computations of integrals (see Integration, numerical ). As a result, the original problem of optimal control is replaced by a family of approximate problems depending on some parameters (for example, on the steps of the difference grid). About questions regarding the construction of approximate problems and the investigation of their convergence, see [5] .

Large classes of extremal problems are ill posed (see Ill-posed problems ) and their solution requires the use of a regularization method (see [5] and [3] ).

Constraints of the kind $ g _ {i} ( x, t) \leq 0 $ or $ g _ {i} ( x, t) = 0 $ are usually referred to as state constraints. Among the methods available for the numerical solution of optimal control problems, a distinction can be made between direct and indirect methods. With direct methods the optimal control problem is treated directly as a minimization problem, i.e. the method is started with an initial approximation of the solution, which is iteratively improved by minimizing the objective functional (cf. Objective function ) (augmented with a "penalty" term) along the direction of search. The direction of search is obtained via linearization of the problem. With indirect methods the optimality conditions, which must hold for a solution of the optimal control problem, are used to derive a multi-point boundary value problem. Solutions of the optimal control problem will also be solutions of this multi-point boundary value problem and hence the numerical solution of the multi-point boundary value problem yields a candidate for the solution of the optimal control problem.

Most direct methods are of the gradient type, i.e. they are function space analogues of the well-known gradient method for finite-dimensional non-linear programming problems [a1] . These methods can be extended to Newton-like methods [a1] , [a2] (cf. Newton method ). As indicated in the main article above, state constraints can be treated via a penalty-function approach. Numerical results, however, indicate that this approach yields an inefficient and inaccurate method for the solution of state-constrained optimal control problems [a3] . Another way to treat state constraints is via a slack-variable transformation technique, using quadratic slack variables [a4] .

A well-known indirect method is the one based on the numerical solution of the multi-point boundary value problem using multiple shooting [a3] , [a5] (cf. Shooting method ). For optimal control problems with state constraints, the right-hand side of the differential equation of the multi-point boundary value problem will, in general, be discontinuous at junction points, i.e. points where an inequality constraint changes from active to inactive or vice versa. These discontinuities require special attention [a1] .

In general, the properties of direct and indirect methods are somewhat complementary. Direct methods tend to have a relatively large region of convergence and tend to be relatively inaccurate, whereas indirect methods generally have a relatively small region of convergence and tend to be relatively accurate.

• This page was last edited on 5 June 2020, at 19:38.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

Forgot password? New user? Sign up

Existing user? Log in

Extremal Principle

Already have an account? Log in here.

• hemang sarkar
• Bradan Litzinger

The extremal principle is a technique that is useful for solving certain mathematical problems, by studying examples with extreme properties. This offers a useful starting point from which we can understand the simplified problem.

Most often the object or example we look at will have the smallest or largest value, in some sense. Recognizing when to use the extreme principle is often quite challenging. Some clues that can indicate that it would be helpful to use the extreme principle are:

• The values in a question are distinct.
• The possible set of values is bounded, either combinatorially (e.g. must choose a subset of a certain size) or absolutely (e.g. all numbers must be positive).
• You have a monovariant.

It is one of the most useful tools in a problem solver's repertoire, and can be used to solve a great variety of problems. It basically depends on the seemingly obvious, but useful fact that every non-empty finite ordered set has a smallest and a largest element.

The use of the extremal principle is best understood by working through examples and that's what we're going to do right now!

Additional Problems

Let's start with a simple example where the statement is proved by stating the obvious:

\(n\) students are standing in a field such that the distance between each pair is distinct. Each student is holding a ball, and when the teacher blows a whistle, each student throws their ball to the nearest student. Prove that there is a pair of students that throw their balls to each other. Consider the smallest distance between any pair of students. Since this is the smallest distance, the closest student to each of these is the other, so these students throw their ball to each other. \(_\square\) Note : It is certainly possible for other pairs of students to throw their balls to each other. By focusing on an extremal object, we were easily able to identify a scenario that must always work.

The interesting problem below effectively showcases the power of the extremal principle:

Say you have finitely many red and blue points on a plane with the following interesting property: every line segment that joins two points of the same color contains a point of another color. Prove that all the points lie on a single straight line. If you take out a pen and paper and start drawing points with this property, you might start to feel that if the points were not on a single line, then there can't be finitely many of them. You are right. But how do we prove this rigorously? By using the extremal principle of course! If the points were not a single straight line, you could draw different triangles with the points as vertices. Take the smallest such triangle, i.e. the triangle with the least area. At least two of the vertices of this triangle have the same color. So between them is a point of different color. Join this point with the third vertex and you end up with two triangles, each having less area than the 'triangle with the least area'. A contradiction! So all the points have to lie on a single line. \(_\square\)

See how easy that was! That's what looking at the extreme cases can do sometimes.

How do we know that there will always be a triangle with the least area? Not all ordered sets have a least element. For example, consider the interval \((2, 3]\).

The reason why there existed a triangle with the least area is that we had finitely many triangles, which was due to the fact that there were finitely many points to begin with.

So that's another thing to look out for when you want to use the extremal principle: make sure the extreme cases can exist, before you claim they do.

\(2n\) points are chosen in the plane such that no \(3\) are collinear. \(n\) are coloured blue and \(n\) are coloured red. Prove that there is a way to join the \(n\) red points to the \(n\) blue points by \(n\) line segments, such that no two line segments cross. Suppose we join the red points \(R\) to the blue points \(B\) in an arbitrary fashion. If this does not have the desired property, then we must have a segment \(S_1\) joining \(R_1\) to \(B_1\) and a segment \(S_2\) joining \(R_2\) to \(B_2\) such that these segments intersect. If we instead let \(S_1\) connect \(R_1\) to \(B_2\) and \(S_2\) connect \(R_1\) to \(B_2,\) then these segments will no longer intersect. However, it is possible that the new \(S_1\) and \(S_2\) now intersect some other segments. We notice that our swapping move decreases the total length of the segments (draw a figure and convince yourself this is the case). So, let us consider the configuration of segments \(S_1, S_2, \ldots, S_n\) that has minimal total length. Notice that such a minimum must exist, since there is a finite number of ways to pair the segments. If there was a pair of crossed segments in this configuration, then we could uncross them and get a smaller sum of lengths, contradicting our choice. Thus, this configuration has no pair of crossed segments. \(_\square\)

For \(n > 1,\) the integers from 1 to \(n^2\) are placed in the cells of an \(n \times n\) chessboard. Show that there is a pair of horizontally, vertically, or diagonally adjacent cells whose values differ by at least \(n+1.\) Consider the cells labelled \(1\) and \(n^2.\) There exists a sequence of at most \(k \leq n\) cells such that \(1 = c_1, c_2, \ldots, c_k =n^2\) and cells \(c_i\) and \(c_{i+1}\) are adjacent, for \(1 \leq i \leq k-1.\) If each pair of adjacent cells had value that differed by at most \(n,\) then the difference between \(c_1\) and \(c_k\) is at most \(n(n-1) = n^2 - n.\) However, the actual difference between them is \(n^2 - 1 > n^2 -n\) when \(n \geq 2.\) Thus, some pair along this chain have difference at least \(n+1.\) \(_\square\)

Consider an infinite chessboard, the squares of which have been filled with positive integers. Each of these integers is the arithmetic mean of four of its neighbors (above, below, left, right). Show that all the integers are equal to each other. Consider the smallest integer on this board. Let's call it \(k\). If \(k\) is the arithmetic mean of its neighbors \(a, b, c\) and \(d,\) then we have \[a+b+c+d=4k.\] Now since \(k\) is the smallest integer on the board, none of \(a, b, c, d\) can be greater than or less than \(k\). So they have to be equal to \(k\). In other words, \(a=b=c=d=k.\) It follows from this that all the integers are equal. \(_\square\)

In this example, how did we know that a smallest integer existed? Unlike the first one, we didn't have finitely many integers to deal with.

This actually follows from the well-ordering principle which states that every non-empty subset of non-negative integers always has a least element.

Another example:

In the coordinate plane, prove that the vertices of a regular pentagon cannot all be lattice points. Before we begin, remember that a lattice point is a point with integer coordinates. Now some of you are probably thinking something along the lines of trigonometry. Before we go into some (very messy) calculation, let's stop and think for a while. What if we had such a pentagon? What would happen? You might argue that if we had one such pentagon, we can make infinitely many such pentagons (how?). But that doesn't help us. Now among all these pentagons, take the one that has the least area. Consider the five vectors \(v_i=a_i \hat{i}+b_i \hat{j} \text{ for } i \in \{1, 2, 3, 4, 5\}\) that point from one vertex to the next. Note that \((a_i)^2+(b_i)^2=k^2,\) where \(k\) is the length of the side of the regular polygon. Since \(\displaystyle \sum_{i=1}^5 v_i=0\), we must have \(\displaystyle \sum_{i=1}^5 a_i=0\) and \(\displaystyle \sum_{i=1}^5 b_i=0\). Square the last two equations to get \(\displaystyle \sum_{i=1}^5 (a_i)^2+\displaystyle \sum_{i=1}^5 (b_i)^2+2\displaystyle \sum_{1\leq i< j\leq 5} (a_ia_j +b_ib_j)=0\). So we see that \( \displaystyle \sum_{i=1}^5 (a_i)^2+\displaystyle \sum_{i=1}^5 (b_i)^2\) has to be even. \(\displaystyle \sum_{i=1}^5 (a_i)^2+\displaystyle \sum_{i=1}^5 (b_i)^2\) is equal to \(5k^2\). This means \(k^2\) needs to be even and that implies that \(a_i\) and \(b_i\) have the same parity. If \(a_1\) and \(b_1\) are both odd, then \(k^2\) is not a multiple of a \(4\). This means all \(a_i\) and \(b_i\) are odd. But if that happens, \(\displaystyle \sum_{i=1}^5 a_i\) can't be equal to zero since you can't get an even number by adding \(5\) odd numbers. If \(a_1\) and \(b_1\) are both even, then \(4\) divides \(k^2\). This means that all \(a_i\) and \(b_i\) are even. Now we can scale our polygon by \(\frac{1}{2}\) to get another regular pentagon with lattice points as vertices but with a smaller area. That's a contradiction. So, there can't be such a pentagon. \(_\square\)

Note that this argument works for any regular \(n\)-gon, where \(n\) is odd.

1) Prove that a cube cannot be divided into a finite number of smaller cubes, each of different sizes. Also, show that a hypercube cannot be hypercubed.

2) A finite set of points in the plane has the property that the triangle formed by any \(3\) of them has area less than \(1\). Prove that there is a triangle of area \(4\) that contains all the points.

3) Every vertex of a graph \(G\) has degree \(3\). Prove that we can partition the vertices of \(G\) into \(2\) sets \(A\) and \(B\) such that each vertex in \(A\) has at least 2 neighbours in \(B\) and each vertex in \(B\) has at least \(2\) neighbors in \(A.\)

• Invariant Principle
• The Well-Ordering Principle
• Proof by Contradiction
• Fermat's Method of Infinite Descent

You are given the task of making a list of 10 distinct, positive integers which have an average of 20. What is the largest possible value of a single number in the list?

Problem Loading...

Note Loading...

Set Loading...

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Extremas

• Last updated
• Save as PDF
• Page ID 10302

This page is a draft and is under active development. 

Given a particular function, we are often interested in determining the largest and smallest values of the function. This information is important in creating accurate graphs. Finding the maximum and minimum values of a function also has practical significance because we can use this method to solve optimization problems, such as maximizing profit, minimizing the amount of material used in manufacturing an aluminum can, or finding the maximum height a rocket can reach. In this section, we look at how to use derivatives to find the largest and smallest values for a function.

Absolute Extrema

Consider the function \(f(x)=x^2+1\) over the interval \((−∞,∞)\). As \(x→±∞, f(x)→∞.\) Therefore, the function does not have a largest value. However, since \(x^2+1≥1\) for all real numbers \(x\) and \(x^2+1=1\) when \(x=0\), the function has a smallest value, 1, when \(x=0\). We say that 1 is the absolute minimum of \(f(x)=x^2+1\) and it occurs at \(x=0\). We say that \(f(x)=x^2+1\) does not have an absolute maximum (Figure \(\PageIndex{1}\)).

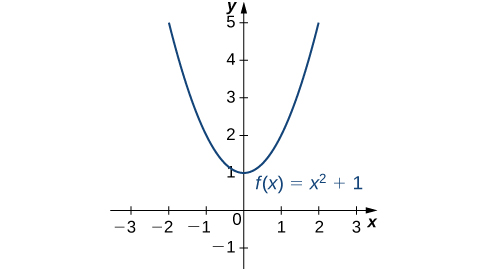
Definition: absolute extrema

Let \(f\) be a function defined over an interval \(I\) and let \(c∈I\). We say \(f\) has an absolute maximum on \(I\) at \(c\) if \(f(c)≥f(x)\) for all \(x∈I\). We say \(f\) has an absolute minimum on \(I\) at \(c\) if \(f(c)≤f(x)\) for all \(x∈I\). If \(f\) has an absolute maximum on \(I\) at \(c\) or an absolute minimum on \(I\) at \(c\), we say \(f\) has an absolute extremum on \(I\) at \(c\).

Before proceeding, let’s note two important issues regarding this definition. First, the term absolute here does not refer to absolute value. An absolute extremum may be positive, negative, or zero. Second, if a function \(f\) has an absolute extremum over an interval \(I\) at \(c\), the absolute extremum is \(f(c)\). The real number c is a point in the domain at which the absolute extremum occurs. For example, consider the function \(f(x)=1/(x^2+1)\) over the interval \((−∞,∞)\). Since

\[f(0)=1≥\frac{1}{x^2+1}=f(x)\]

for all real numbers \(x\), we say \(f\) has an absolute maximum over \((−∞,∞)\) at \(x=0\). The absolute maximum is \(f(0)=1\). It occurs at \(x=0\), as shown in Figure(b).

A function may have both an absolute maximum and an absolute minimum, just one extremum, or neither. Figure \(\PageIndex{2}\) shows several functions and some of the different possibilities regarding absolute extrema. However, the following theorem, called the Extreme Value Theorem , guarantees that a continuous function \(f\) over a closed, bounded interval \([a,b]\) has both an absolute maximum and an absolute minimum.

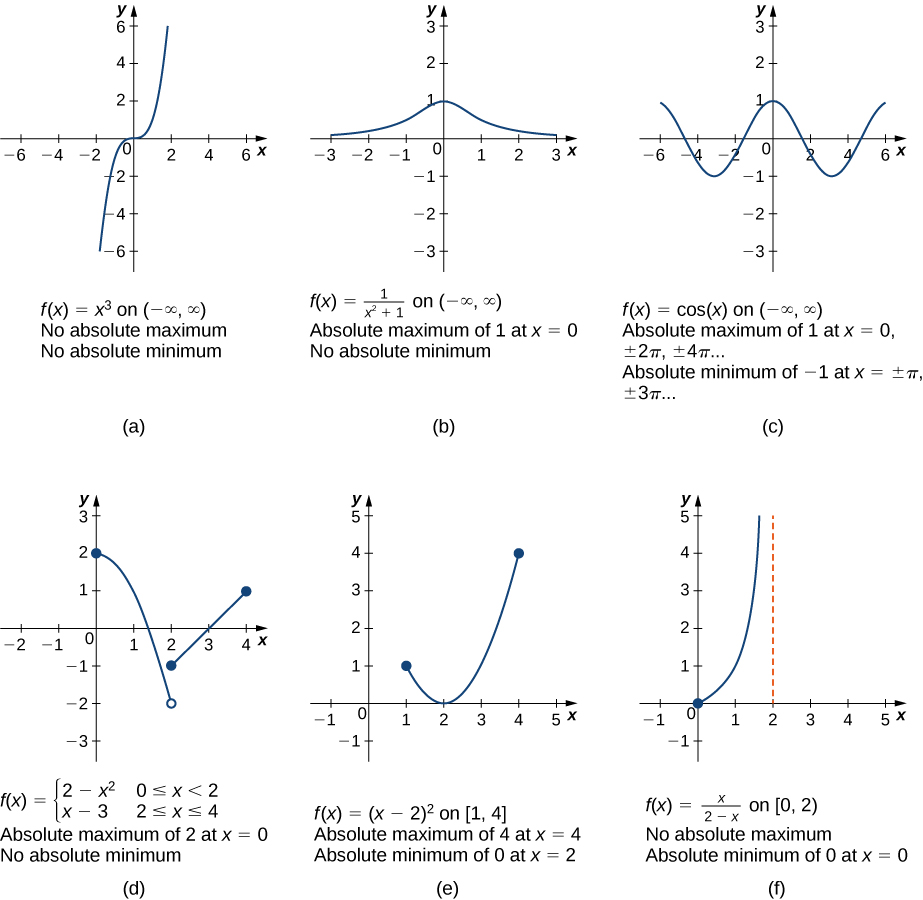
Extreme Value Theorem

If \(f\) is a continuous function over the closed, bounded interval \([a,b]\), then there is a point in \([a,b]\) at which \(f\) has an absolute maximum over \([a,b]\) and there is a point in \([a,b]\) at which \(f\) has an absolute minimum over \([a,b]\).

The proof of the extreme value theorem is beyond the scope of this text. Typically, it is proved in a course on real analysis. There are a couple of key points to note about the statement of this theorem. For the extreme value theorem to apply, the function must be continuous over a closed, bounded interval. If the interval \(I\) is open or the function has even one point of discontinuity, the function may not have an absolute maximum or absolute minimum over \(I\). For example, consider the functions shown in Figure(d), (e), and (f). All three of these functions are defined over bounded intervals. However, the function in graph (e) is the only one that has both an absolute maximum and an absolute minimum over its domain. The extreme value theorem cannot be applied to the functions in graphs (d) and (f) because neither of these functions is continuous over a closed, bounded interval. Although the function in graph (d) is defined over the closed interval \([0,4]\), the function is discontinuous at \(x=2\). The function has an absolute maximum over \([0,4]\) but does not have an absolute minimum. The function in graph (f) is continuous over the half-open interval \([0,2)\), but is not defined at \(x=2\), and therefore is not continuous over a closed, bounded interval. The function has an absolute minimum over \([0,2)\), but does not have an absolute maximum over \([0,2)\). These two graphs illustrate why a function over a bounded interval may fail to have an absolute maximum and/or absolute minimum.

Before looking at how to find absolute extrema, let’s examine the related concept of local extrema. This idea is useful in determining where absolute extrema occur.

Local Extrema and Critical Points

Consider the function \(f\) shown in Figure \(\PageIndex{3}\). The graph can be described as two mountains with a valley in the middle. The absolute maximum value of the function occurs at the higher peak, at \(x=2\). However, \(x=0\) is also a point of interest. Although \(f(0)\) is not the largest value of \(f\), the value \(f(0)\) is larger than \(f(x)\) for all \(x\) near 0. We say \(f\) has a local maximum at \(x=0\). Similarly, the function \(f\) does not have an absolute minimum, but it does have a local minimum at \(x=1\) because \(f(1)\) is less than \(f(x)\) for \(x\) near 1.

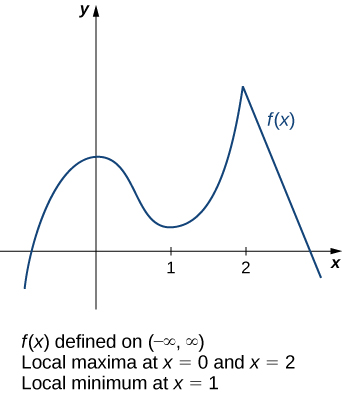
Definition: local extrema

A function \(f\) has a local maximum at \(c\) if there exists an open interval \(I\) containing \(c\) such that \(I\) is contained in the domain of \(f\) and \(f(c)≥f(x)\) for all \(x∈I\). A function \(f\) has a local minimum at \(c\) if there exists an open interval \(I\) containing \(c\) such that \(I\) is contained in the domain of \(f\) and \(f(c)≤f(x)\) for all \(x∈I\). A function \(f\) has a local extremum at \(c\) if \(f\) has a local maximum at \(c\) or \(f\) has a local minimum at \(c\).

Note that if \(f\) has an absolute extremum at \(c\) and \(f\) is defined over an interval containing \(c\), then \(f(c)\) is also considered a local extremum. If an absolute extremum for a function \(f\) occurs at an endpoint, we do not consider that to be a local extremum, but instead refer to that as an endpoint extremum.

Given the graph of a function \(f\), it is sometimes easy to see where a local maximum or local minimum occurs. However, it is not always easy to see, since the interesting features on the graph of a function may not be visible because they occur at a very small scale. Also, we may not have a graph of the function. In these cases, how can we use a formula for a function to determine where these extrema occur?

To answer this question, let’s look at Figure \(\PageIndex{3}\) again. The local extrema occur at \(x=0, x=1,\) and \(x=2.\) Notice that at \(x=0\) and \(x=1\), the derivative \(f'(x)=0\). At \(x=2\), the derivative \(f'(x)\) does not exist, since the function \(f\) has a corner there. In fact, if \(f\) has a local extremum at a point \(x=c\), the derivative \(f'(c)\) must satisfy one of the following conditions: either \(f'(c)=0\) or \(f'(c)\) is undefined. Such a value \(c\) is known as a critical point and it is important in finding extreme values for functions.

Definition: critical points

Let \(c\) be an interior point in the domain of \(f\). We say that \(c\) is a critical point of \(f\) if \(f'(c)=0\) or \(f'(c)\) is undefined.

As mentioned earlier, if \(f\) has a local extremum at a point \(x=c\), then \(c\) must be a critical point of \(f\). This fact is known as Fermat’s theorem.

Fermat’s Theorem

If \(f\) has a local extremum at \(c\) and \(f\) is differentiable at \(c\), then \(f'(c)=0.\)

Suppose \(f\) has a local extremum at \(c\) and \(f\) is differentiable at \(c\). We need to show that \(f'(c)=0\). To do this, we will show that \(f'(c)≥0\) and \(f'(c)≤0\), and therefore \(f'(c)=0\). Since \(f\) has a local extremum at \(c\), \(f\) has a local maximum or local minimum at \(c\). Suppose \(f\) has a local maximum at \(c\). The case in which \(f\) has a local minimum at \(c\) can be handled similarly. There then exists an open interval I such that \(f(c)≥f(x)\) for all \(x∈I\). Since \(f\) is differentiable at \(c\), from the definition of the derivative, we know that

\[f'(c)=\lim_{x→c}\frac{f(x)−f(c)}{x−c}.\]

Since this limit exists, both one-sided limits also exist and equal \(f'(c)\). Therefore,

\[f'(c)=\lim_{x→c^+}\frac{f(x)−f(c)}{x−c,}\]

\[f'(c)=\lim_{x→c^−}\frac{f(x)−f(c)}{x−c}.\]

Since \(f(c)\) is a local maximum, we see that \(f(x)−f(c)≤0\) for \(x\) near \(c\). Therefore, for \(x\) near \(c\), but \(x>c\), we have \(\frac{f(x)−f(c)}{x−c}≤0\). From Equation we conclude that \(f'(c)≤0\). Similarly, it can be shown that \(f'(c)≥0.\) Therefore, \(f'(c)=0.\) □

From Fermat’s theorem, we conclude that if \(f\) has a local extremum at \(c\), then either \(f'(c)=0\) or \(f'(c)\) is undefined. In other words, local extrema can only occur at critical points.

Note this theorem does not claim that a function \(f\) must have a local extremum at a critical point. Rather, it states that critical points are candidates for local extrema. For example, consider the function \(f(x)=x^3\). We have \(f'(x)=3x^2=0\) when \(x=0\). Therefore, \(x=0\) is a critical point. However, \(f(x)=x^3\) is increasing over \((−∞,∞)\), and thus \(f\) does not have a local extremum at \(x=0\). In Figure, we see several different possibilities for critical points. In some of these cases, the functions have local extrema at critical points, whereas in other cases the functions do not. Note that these graphs do not show all possibilities for the behavior of a function at a critical point.

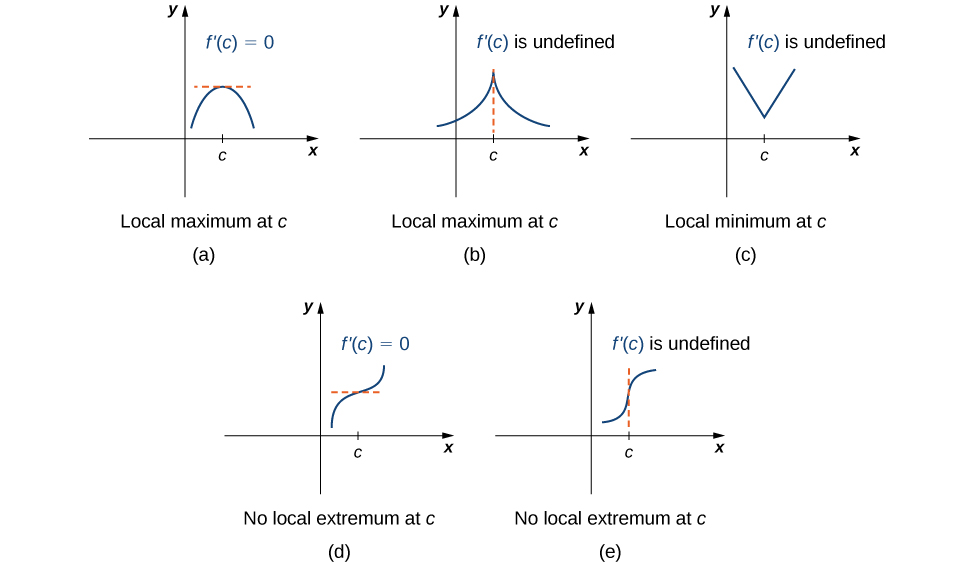
Later in this chapter we look at analytical methods for determining whether a function actually has a local extremum at a critical point. For now, let’s turn our attention to finding critical points. We will use graphical observations to determine whether a critical point is associated with a local extremum.

Example \(\PageIndex{1}\): Locating Critical Points

For each of the following functions, find all critical points. Use a graphing utility to determine whether the function has a local extremum at each of the critical points.

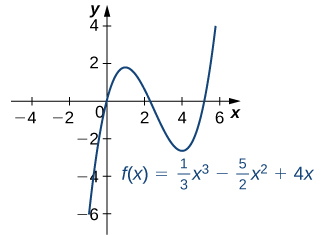
• \(f(x)=\frac{1}{3}x^3−\frac{5}{2}x^2+4x\)
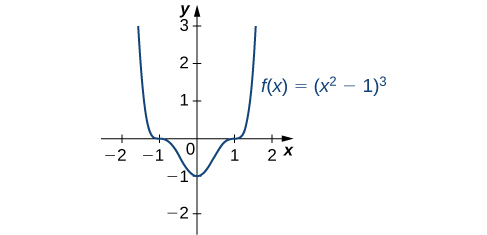
• \(f(x)=(x^2−1)^3\)
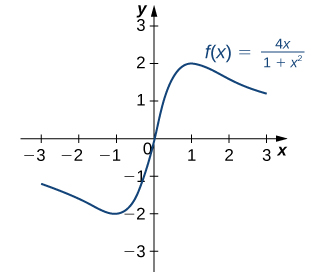
• \(f(x)=\frac{4x}{1+x^2}\)

a. The derivative \(f'(x)=x^2−5x+4\) is defined for all real numbers \(x\). Therefore, we only need to find the values for \(x\) where \(f'(x)=0\). Since \(f'(x)=x^2−5x+4=(x−4)(x−1)\), the critical points are \(x=1\) and \(x=4.\) From the graph of \(f\) in Figure, we see that \(f\) has a local maximum at \(x=1\) and a local minimum at \(x=4\).

b. Using the chain rule, we see the derivative is

\(f'(x)=3(x^2−1)^2(2x)=6x(x^2−1)^2.\)

Therefore, \(f\) has critical points when \(x=0\) and when \(x^2−1=0\). We conclude that the critical points are \(x=0,±1\). From the graph of \(f\) in Figure, we see that \(f\) has a local (and absolute) minimum at \(x=0\), but does not have a local extremum at \(x=1\) or \(x=−1\).

c. By the chain rule, we see that the derivative is

\(f'(x)=\frac{(1+x^24)−4x(2x)}{(1+x^2)^2}=\frac{4−4x^2}{(1+x^2)^2}\).

The derivative is defined everywhere. Therefore, we only need to find values for \(x\) where \(f'(x)=0\). Solving \(f'(x)=0\), we see that \(4−4x^2=0,\) which implies \(x=±1\). Therefore, the critical points are \(x=±1\). From the graph of \(f\) in Figure, we see that f has an absolute maximum at \(x=1\) and an absolute minimum at \(x=−1.\) Hence, \(f\) has a local maximum at \(x=1\) and a local minimum at \(x=−1\). (Note that if \(f\) has an absolute extremum over an interval \(I\) at a point \(c\) that is not an endpoint of \(I\), then \(f\) has a local extremum at \(c.)\)

Exercise \(\PageIndex{1}\)

Find all critical points for \(f(x)=x^3−\frac{1}{2}x^2−2x+1.\)

Calculate \(f'(x).\)

\(x=−23, x=1\)

Locating Absolute Extrema

The extreme value theorem states that a continuous function over a closed, bounded interval has an absolute maximum and an absolute minimum. As shown in Figure, one or both of these absolute extrema could occur at an endpoint. If an absolute extremum does not occur at an endpoint, however, it must occur at an interior point, in which case the absolute extremum is a local extremum. Therefore, by Note, the point \(c\) at which the local extremum occurs must be a critical point. We summarize this result in the following theorem.

Location of Absolute Extrema

Let \(f\) be a continuous function over a closed, bounded interval \(I\). The absolute maximum of \(f\) over \(I\) and the absolute minimum of \(f\) over \(I\) must occur at endpoints of \(I\) or at critical points of \(f\) in \(I\).

With this idea in mind, let’s examine a procedure for locating absolute extrema.

Problem-Solving Strategy: Locating Absolute Extrema over a Closed Interval

Consider a continuous function \(f\) defined over the closed interval \([a,b].\)

• Evaluate \(f\) at the endpoints \(x=a\) and \(x=b.\)
• Find all critical points of \(f\) that lie over the interval \((a,b)\) and evaluate \(f\) at those critical points.
• Compare all values found in (1) and (2). From Note, the absolute extrema must occur at endpoints or critical points. Therefore, the largest of these values is the absolute maximum of \(f\). The smallest of these values is the absolute minimum of \(f\).

Now let’s look at how to use this strategy to find the absolute maximum and absolute minimum values for continuous functions.

Example \(\PageIndex{2}\): Locating Absolute Extrema

For each of the following functions, find the absolute maximum and absolute minimum over the specified interval and state where those values occur.

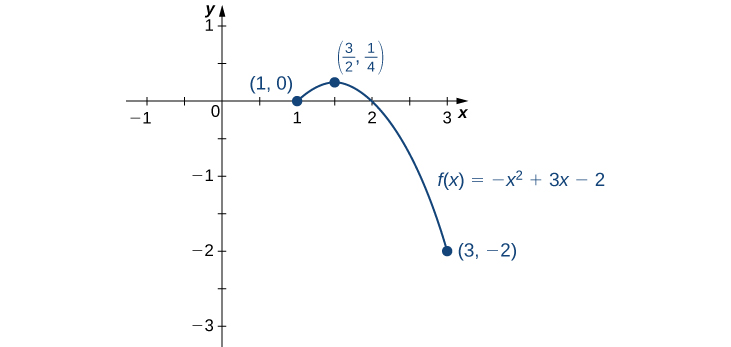
• \(f(x)=−x^2+3x−2\) over \([1,3].\)
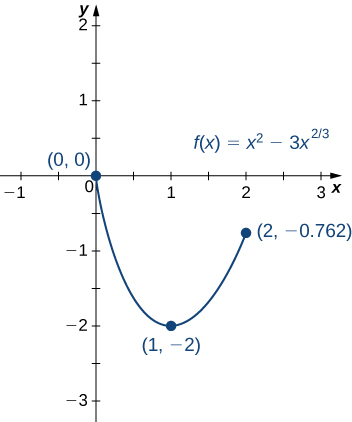
• \(f(x)=x^2−3x^{2/3}\) over \([0,2]\).

a. Step 1. Evaluate \(f\) at the endpoints \(x=1\) and \(x=3\).

\(f(1)=0\) and \(f(3)=−2\)

Step 2. Since \(f'(x)=−2x+3, f'\) is defined for all real numbers x. Therefore, there are no critical points where the derivative is undefined. It remains to check where \(f'(x)=0\). Since \(f'(x)=−2x+3=0 \)at \(x=\frac{3}{2}\) and \(\frac{3}{2}\) is in the interval \([1,3], f(\frac{3}{2})\) is a candidate for an absolute extremum of \(f\) over \([1,3]\). We evaluate \(f(\frac{3}{2})\) and find

\(f(\frac{3}{2})=\frac{1}{4}\).

Step 3. We set up the following table to compare the values found in steps 1 and 2.

From the table, we find that the absolute maximum of \(f\) over the interval [1, 3] is \(\frac{1}{4}\), and it occurs at \(x=\frac{3}{2}\). The absolute minimum of f over the interval [1, 3] is \(−2\), and it occurs at \(x=3\) as shown in Figure \(\PageIndex{8}\).

b. Step 1. Evaluate \(f\) at the endpoints \(x=0\) and \(x=2\).

\(f(0)=0\) and \(f(2)=4−3\frac[3]{4}≈−0.762\)

Step 2. The derivative of \(f\) is given by

\(f'(x)=2x−\frac{2}{x^{1/3}}=\frac{2x^{4/3}−2}{x^{1/3}}\)

for \(x≠0\). The derivative is zero when \(2x^{4/3}−2=0\), which implies \(x=±1\). The derivative is undefined at \(x=0\). Therefore, the critical points of \(f\) are \(x=0,1,−1\). The point \(x=0\) is an endpoint, so we already evaluated \(f(0)\) in step 1. The point \(x=−1\) is not in the interval of interest, so we need only evaluate \(f(1)\). We find that

\(f(1)=−2.\)

Step 3. We compare the values found in steps 1 and 2, in the following table.

We conclude that the absolute maximum of \(f\) over the interval [0, 2] is zero, and it occurs at \(x=0\). The absolute minimum is −2, and it occurs at \(x=1\) as shown in Figure \(\PageIndex{9}\).

Exercise \(\PageIndex{2}\)

Find the absolute maximum and absolute minimum of \((x)=x^2−4x+3\) over the interval \([1,4]\).

Look for critical points. Evaluate \(f\) at all critical points and at the endpoints.

The absolute maximum is \(3\) and it occurs at \(x=4\). The absolute minimum is \(−1\) and it occurs at \(x=2\).

Example \(\PageIndex{3}\):

Find the absolute maximum and absolute minimum values for the functions over the specified domain:

• \(f(x)= \dfrac{3x}{\sqrt{4x^2+1}}, x \in [-1,1]\).

1. Critical points:

Since \(f(x)= \dfrac{3x}{\sqrt{4x^2+1}}\), by using the quotient rule we have,

\(f'(x)= \dfrac{3\sqrt{4x^2+1}- \dfrac{(3x)(8x)}{\sqrt{4x^2+1}} }{4x^2+1}\)

\(=\dfrac{3(4x^2+1)- 24x^2 }{(4x^2+1)^{\frac{3}{2}}}\)

\(=\dfrac{12x^2+3- 24x^2}{(4x^2-1)^{\frac{3}{2}}}\)

\(=\dfrac{-12x^2+3}{(4x^2-1)^{\frac{3}{2}}}\).

The derivative is zero when \(-12x^2+3=-3(4x^2-1) =0, \) which implies \(x= \pm \dfrac{1}{2}\).

Therefore, the critical points of \(f\) are \(x= \dfrac{1}{2},− \dfrac{1}{2}\).

We compare the values in the following table:\(x\)

We conclude that the absolute maximum of \(f\) over the interval [-1, 1] is \( \dfrac{3}{\sqrt{5}}\), and it occurs at \(x=1\). The absolute minimum is \( \dfrac{-3}{\sqrt{8}}\), and it occurs at \(x=-\dfrac{1}{2}\).

2. Critical points:

At this point, we know how to locate absolute extrema for continuous functions over closed intervals. We have also defined local extrema and determined that if a function \(f\) has a local extremum at a point \(c\), then \(c\) must be a critical point of \(f\). However, \(c\) being a critical point is not a sufficient condition for \(f\) to have a local extremum at \(c\). Later in this chapter, we show how to determine whether a function actually has a local extremum at a critical point. First, however, we need to introduce the Mean Value Theorem, which will help as we analyze the behavior of the graph of a function.

Key Concepts

• A function may have both an absolute maximum and an absolute minimum, have just one absolute extremum, or have no absolute maximum or absolute minimum.
• If a function has a local extremum, the point at which it occurs must be a critical point. However, a function need not have a local extremum at a critical point.
• A continuous function over a closed, bounded interval has an absolute maximum and an absolute minimum. Each extremum occurs at a critical point or an endpoint.

Contributors and Attributions

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org .

Pamini Thangarajah  (Mount Royal University, Calgary, Alberta, Canada)

Formal Derivation of a Generic Algorithmic Program for Solving a Class of Extremum Problems

Ieee account.

• Change Username/Password
• Update Address

Purchase Details

• Payment Options
• Order History
• View Purchased Documents

Profile Information

• Communications Preferences
• Profession and Education
• Technical Interests
• US & Canada: +1 800 678 4333
• Worldwide: +1 732 981 0060
• Contact & Support
• About IEEE Xplore
• Accessibility
• Terms of Use
• Nondiscrimination Policy
• Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.

On the projected subgradient method for nonsmooth convex optimization in a Hilbert space

• Published: March 1998
• Volume 81 , pages 23–35, ( 1998 )

Cite this article

• Ya. I. Alber 1   nAff2 ,
• A. N. Iusem 1 &
• M. V. Solodov 1  

863 Accesses

119 Citations

Explore all metrics

We consider the method for constrained convex optimization in a Hilbert space, consisting of a step in the direction opposite to an ε k -subgradient of the objective at a current iterate, followed by an orthogonal projection onto the feasible set. The normalized stepsizes ε k are exogenously given, satisfying Σ ∞ k=0 α k = ∞, Σ ∞ k=0 α 2 k < ∞, and ε k is chosen so that ε k ⩽ μα k for some μ > 0. We prove that the sequence generated in this way is weakly convergent to a minimizer if the problem has solutions, and is unbounded otherwise. Among the features of our convergence analysis, we mention that it covers the nonsmooth case, in the sense that we make no assumption of differentiability of f , and much less of Lipschitz continuity of its gradient. Also, we prove weak convergence of the whole sequence, rather than just boundedness of the sequence and optimality of its weak accumulation points, thus improving over all previously known convergence results. We present also convergence rate results. © 1998 The Mathematical Programming Society, Inc. Published by Elsevier Science B.V.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Regularized gradient-projection methods for finding the minimum-norm solution of the constrained convex minimization problem

Ming Tian & Hui-Fang Zhang

Stochastic proximal gradient methods for nonconvex problems in Hilbert spaces

Caroline Geiersbach & Teresa Scarinci

Methods for solving constrained convex minimization problems and finding zeros of the sum of two operators in Hilbert spaces

Ming Tian, Si-Wen Jiao & Yeong-Cheng Liou

R. Correa, C. Lemaréchal, Convergence of some algorithms for convex minimization, Mathematical Programming 62 (1993) 261–275.

Google Scholar  

B.T. Polyak, Introduction to Optimization, Optimization Software, New York, 1987.

J.R. Giles, Convex analysis with applications in differentiation of convex functions, in: Research Notes in Mathematics, vol. 58, Pitman, Boston, MA, 1982.

R.T. Rockafellar, Local boundedness of nonlinear monotone operators, Michigan Mathematical Journal 16 (1969) 397–407.

A. Brønsted, R.T. Rockafellar, On the subdifferentiability of convex functions, Proceedings of the American Mathematical Society 16 (1965) 605–611.

B.T. Polyak, A general method of solving extremum problems, Soviet Mathematics Doklady 8 (1967) 593–597.

Yu.M. Ermoliev, Methods for solving nonlinear extremal problems, Cybernetics 2 (1966) 1–17.

Ya.I. Alber, On minimization of smooth functional by gradient methods, USSR Computational Mathematics and Mathematical Physics 11 (1971) 752–758.

Ya.I. Alber, Recurrence relations and variational inequalities, Soviet Mathematics Doklady 27 (1983) 511–517.

M.V. Solodov, S.K. Zavriev, Error stability properties of generalized gradient-type algorithms Journal of Optimization Theory and Applications 98 (1998), to appear.

E. Golstein, N. Tretyakov, Modified Lagrangian Functions, Nauka, Moscow, 1989.

Yu. Nesterov, Effective Methods in Nonlinear Programming, Nauka, Moscow, 1989.

M. Minoux, Mathematical Programming, Theory and Algorithms, Wiley, New York, 1986.

V.A. Bereznyev, V.G. Karmanov, A.A. Tretyakov, The stabilizing properties of the gradient method, USSR Computational Mathematics and Mathematical Physics 26 (1986) 84–85.

R. Burachik, L.M. Graña Drummond, A.N. Iusem, B.F. Svaiter, Full convergence of the steepest descent method with inexact line searches, Optimization 32 (1995) 137–146.

K. Kiwiel, K. Murty, Convergence of the steepest descent method for minimizing quasi convex functions, Journal of Optimization Theory and Applications 89 (1996) 221–226.

B.F. Svaiter, Steepest descent method in Hilbert spaces with Armijo search (to be published).

Yu.M. Ermoliev, On the method of generalized stochastic gradients and quasi-Fejér sequences, Cybernetics 5 (1969) 208–220.

A.N. Iusem, B.F. Svaiter, M. Teboulle, Entropy-like proximal methods in convex programming, Mathematics of Operations Research 19 (1994) 790–814.

K. Knopp, Theory and Application of Infinite Series, Dover, New York, 1990.

Ya.I. Alber, A.N. Iusem, M.V. Solodov, Minimization of nonsmooth convex functionals in Banach spaces, Journal of Convex Analysis; to appear.

Download references

Author information

Ya. I. Alber

Present address: Department of Mathematics, The Technion — Israel Institute of Technology, 32000, Haifa, Israel

Authors and Affiliations

Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, CEP 22460-320, Jardim Botânico, Rio de Janeiro, RJ, Brazil

Ya. I. Alber, A. N. Iusem & M. V. Solodov

You can also search for this author in PubMed   Google Scholar

Additional information

Research of this author was partially supported by CNPq grant nos. 301280/86 and 300734/95-6.

Rights and permissions

Reprints and permissions

About this article

Alber, Y.I., Iusem, A.N. & Solodov, M.V. On the projected subgradient method for nonsmooth convex optimization in a Hilbert space. Mathematical Programming 81 , 23–35 (1998). https://doi.org/10.1007/BF01584842

Download citation

Received : 18 January 1996

Revised : 01 January 1997

Issue Date : March 1998

DOI : https://doi.org/10.1007/BF01584842

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Convex optimization
• Nonsmooth optimization
• Projected gradient method
• Steepest descent method
• Weak convergence
• Convergence rate
• Find a journal
• Publish with us
• Track your research