- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- This Or That Game New
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics

How to Solve Systems of Algebraic Equations Containing Two Variables
Last Updated: July 30, 2023 Fact Checked
This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. There are 8 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,063,112 times.
In a "system of equations," you are asked to solve two or more equations at the same time. When these have two different variables in them, such as x and y, or a and b, it can be tricky at first glance to see how to solve them. [1] X Research source Fortunately, once you know what to do, all you need is basic algebra skills (and sometimes some knowledge of fractions) to solve the problem. If you are a visual learner or if your teacher requires it, learn how to graph the equations as well. Graphing can be useful to "see what's going on" or to check your work, but it can be slower than the other methods, and doesn't work well for all systems of equations.
Using the Substitution Method

- This method often uses fractions later on. You can try the elimination method below instead if you don't like fractions.

- 4x = 8 - 2y
- (4x)/4 = (8/4) - (2y/4)

- You know that x = 2 - ½y .
- Your second equation, that you haven't yet altered, is 5x + 3y = 9 .
- In the second equation, replace x with "2 - ½y": 5(2 - ½y) + 3y = 9 .

- 5(2 - ½y) + 3y = 9
- 10 – (5/2)y + 3y = 9
- 10 – (5/2)y + (6/2)y = 9 (If you don't understand this step, learn how to add fractions . This is often, but not always, necessary for this method.)
- 10 + ½y = 9

- You know that y = -2
- One of the original equations is 4x + 2y = 8 . (You can use either equation for this step.)
- Plug in -2 instead of y: 4x + 2(-2) = 8 .

- If you end up with an equation that has no variables and isn't true (for instance, 3 = 5), the problem has no solution . (If you graphed both of the equations, you'd see they were parallel and never intersect.)
- If you end up with an equation without variables that is true (such as 3 = 3), the problem has infinite solutions . The two equations are exactly equal to each other. (If you graphed the two equations, you'd see they were the same line.)
Using the Elimination Method

- You have the system of equations 3x - y = 3 and -x + 2y = 4 .
- Let's change the first equation so that the y variable will cancel out. (You can choose x instead, and you'll get the same answer in the end.)
- The - y on the first equation needs to cancel with the + 2y in the second equation. We can make this happen by multiplying - y by 2.
- Multiply both sides of the first equation by 2, like this: 2(3x - y)=2(3) , so 6x - 2y = 6 . Now the - 2y will cancel out with the +2y in the second equation.

- Your equations are 6x - 2y = 6 and -x + 2y = 4 .
- Combine the left sides: 6x - 2y - x + 2y = ?
- Combine the right sides: 6x - 2y - x + 2y = 6 + 4 .

- You have 6x - 2y - x + 2y = 6 + 4 .
- Group the x and y variables together: 6x - x - 2y + 2y = 6 + 4 .
- Simplify: 5x = 10
- Solve for x: (5x)/5 = 10/5 , so x = 2 .

- You know that x = 2 , and one of your original equations is 3x - y = 3 .
- Plug in 2 instead of x: 3(2) - y = 3 .
- Solve for y in the equation: 6 - y = 3
- 6 - y + y = 3 + y , so 6 = 3 + y

- If your combined equation has no variables and is not true (like 2 = 7), there is no solution that will work on both equations. (If you graph both equations, you'll see they're parallel and never cross.)
- If your combined equation has no variables and is true (like 0 = 0), there are infinite solutions . The two equations are actually identical. (If you graph them, you'll see that they're the same line.)
Graphing the Equations

- The basic idea is to graph both equations, and find the point where they intersect. The x and y values at this point will give us the value of x and the value of y in the system of equations.

- Your first equation is 2x + y = 5 . Change this to y = -2x + 5 .
- Your second equation is -3x + 6y = 0 . Change this to 6y = 3x + 0 , then simplify to y = ½x + 0 .
- If both equations are identical , the entire line will be an "intersection". Write infinite solutions .

- If you don't have graph paper, use a ruler to make sure the numbers are spaced precisely apart.
- If you are using large numbers or decimals, you may need to scale your graph differently. (For example, 10, 20, 30 or 0.1, 0.2, 0.3 instead of 1, 2, 3).

- In our examples from earlier, one line ( y = -2x + 5 ) intercepts the y-axis at 5 . The other ( y = ½x + 0 ) intercepts at 0 . (These are points (0,5) and (0,0) on the graph.)
- Use different colored pens or pencils if possible for the two lines.

- In our example, the line y = -2x + 5 has a slope of -2 . At x = 1, the line moves down 2 from the point at x = 0. Draw the line segment between (0,5) and (1,3).
- The line y = ½x + 0 has a slope of ½ . At x = 1, the line moves up ½ from the point at x=0. Draw the line segment between (0,0) and (1,½).
- If the lines have the same slope , the lines will never intersect, so there is no answer to the system of equations. Write no solution .

- If the lines are moving toward each other, keep plotting points in that direction.
- If the lines are moving away from each other, move back and plot points in the other direction, starting at x = -1.
- If the lines are nowhere near each other, try jumping ahead and plotting more distant points, such as at x = 10.

Practice Problems and Answers

Community Q&A
- You can check your work by plugging the answers back into the original equations. If the equations end up true (for instance, 3 = 3), your answer is correct. Thanks Helpful 3 Not Helpful 1
- In the elimination method, you will sometimes have to multiply one equation by a negative number in order to get a variable to cancel out. Thanks Helpful 1 Not Helpful 1

- These methods cannot be used if there is a variable raised to an exponent, such as x 2 . For more information on equations of this type, look up a guide to factoring quadratics with two variables. [11] X Research source Thanks Helpful 0 Not Helpful 0
You Might Also Like

- ↑ https://www.mathsisfun.com/definitions/system-of-equations.html
- ↑ https://calcworkshop.com/systems-equations/substitution-method/
- ↑ https://www.cuemath.com/algebra/substitution-method/
- ↑ https://tutorial.math.lamar.edu/Classes/Alg/SystemsTwoVrble.aspx
- ↑ http://www.purplemath.com/modules/systlin2.htm
- ↑ http://www.virtualnerd.com/algebra-2/linear-systems/graphing/solve-by-graphing/equations-solution-by-graphing
- ↑ https://www.khanacademy.org/math/algebra/multiplying-factoring-expression/factoring-quadratics-in-two-vari/v/factoring-quadratics-with-two-variables
About This Article

To solve systems of algebraic equations containing two variables, start by moving the variables to different sides of the equation. Then, divide both sides of the equation by one of the variables to solve for that variable. Next, take that number and plug it into the formula to solve for the other variable. Finally, take your answer and plug it into the original equation to solve for the other variable. To learn how to solve systems of algebraic equations using the elimination method, scroll down! Did this summary help you? Yes No
- Send fan mail to authors
Reader Success Stories
Jan 8, 2018
Did this article help you?

Jul 24, 2017
Kaurovandu Uozondo
Apr 19, 2018
Nahid Shafreen Shareef
Feb 12, 2018
May 15, 2017

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
wikiHow Tech Help Pro:
Develop the tech skills you need for work and life
Sciencing_Icons_Science SCIENCE
Sciencing_icons_biology biology, sciencing_icons_cells cells, sciencing_icons_molecular molecular, sciencing_icons_microorganisms microorganisms, sciencing_icons_genetics genetics, sciencing_icons_human body human body, sciencing_icons_ecology ecology, sciencing_icons_chemistry chemistry, sciencing_icons_atomic & molecular structure atomic & molecular structure, sciencing_icons_bonds bonds, sciencing_icons_reactions reactions, sciencing_icons_stoichiometry stoichiometry, sciencing_icons_solutions solutions, sciencing_icons_acids & bases acids & bases, sciencing_icons_thermodynamics thermodynamics, sciencing_icons_organic chemistry organic chemistry, sciencing_icons_physics physics, sciencing_icons_fundamentals-physics fundamentals, sciencing_icons_electronics electronics, sciencing_icons_waves waves, sciencing_icons_energy energy, sciencing_icons_fluid fluid, sciencing_icons_astronomy astronomy, sciencing_icons_geology geology, sciencing_icons_fundamentals-geology fundamentals, sciencing_icons_minerals & rocks minerals & rocks, sciencing_icons_earth scructure earth structure, sciencing_icons_fossils fossils, sciencing_icons_natural disasters natural disasters, sciencing_icons_nature nature, sciencing_icons_ecosystems ecosystems, sciencing_icons_environment environment, sciencing_icons_insects insects, sciencing_icons_plants & mushrooms plants & mushrooms, sciencing_icons_animals animals, sciencing_icons_math math, sciencing_icons_arithmetic arithmetic, sciencing_icons_addition & subtraction addition & subtraction, sciencing_icons_multiplication & division multiplication & division, sciencing_icons_decimals decimals, sciencing_icons_fractions fractions, sciencing_icons_conversions conversions, sciencing_icons_algebra algebra, sciencing_icons_working with units working with units, sciencing_icons_equations & expressions equations & expressions, sciencing_icons_ratios & proportions ratios & proportions, sciencing_icons_inequalities inequalities, sciencing_icons_exponents & logarithms exponents & logarithms, sciencing_icons_factorization factorization, sciencing_icons_functions functions, sciencing_icons_linear equations linear equations, sciencing_icons_graphs graphs, sciencing_icons_quadratics quadratics, sciencing_icons_polynomials polynomials, sciencing_icons_geometry geometry, sciencing_icons_fundamentals-geometry fundamentals, sciencing_icons_cartesian cartesian, sciencing_icons_circles circles, sciencing_icons_solids solids, sciencing_icons_trigonometry trigonometry, sciencing_icons_probability-statistics probability & statistics, sciencing_icons_mean-median-mode mean/median/mode, sciencing_icons_independent-dependent variables independent/dependent variables, sciencing_icons_deviation deviation, sciencing_icons_correlation correlation, sciencing_icons_sampling sampling, sciencing_icons_distributions distributions, sciencing_icons_probability probability, sciencing_icons_calculus calculus, sciencing_icons_differentiation-integration differentiation/integration, sciencing_icons_application application, sciencing_icons_projects projects, sciencing_icons_news news.
- Share Tweet Email Print
- Home ⋅
- Math ⋅
- Algebra ⋅
- Linear Equations
How to Solve for Both X & Y

How to Solve a System of Equations
Solving for two variables (normally denoted as "x" and "y") requires two sets of equations. Assuming you have two equations, the best way for solving for both variables is to use the substitution method, which involves solving for one variable as far as possible, then plugging it back in to the other equation. Knowing how to solve a system of equations with two variables is important for several areas, including trying to find the coordinate for points on a graph.
Write out the two equations that have the two variables you want to solve. For this example, we will find the value for "x" and "y" in the two equations "3x + y = 2" and "x + 5y = 20"
Solve for one of the variables in on one of the equations. For this example, let's solve for "y" in the first equation. Subtract 3x from each side to get "y = 2 - 3x"
Plug in the y value found from the first equation in to the second equation in order to find the x value. In the previous example, this means the second equation becomes "x + 5(2- 3x) = 20"
Solve for x . The example equation becomes "x + 10 - 15x = 20," which is then "-14 x + 10 = 20." Subtract 10 from each side, divide by 14 and you have end up with x = -10/14, which simplifies to x = -5/7.
Plug in the x value in to the first equation to find out the y value. y = 2 - 3(-5/7) becomes 2 + 15/7, which is 29/7.
Check your work by plugging in the x and y values in to both of the equations.
Related Articles
How do i define two step equations for algebra 2, how to solve linear systems algebraically, how to graph and find the solution on a calculator, how to create linear equations, how to solve a parabola, how to find equations of tangent lines, how to find the slope in a circle, to calculate arcsine, what buttons do you press on..., how to find the y-intercept of a circle, algebra 1 substitution method, how to use elimination to solve the linear equation, how to solve inequalities, how to find y value for the slope of a line, how to find quadratic equations from a table, how to add parentheses to make a statement true, how to find the x intercept of a function, how to get the value of a letter in algebra 1, how to find dimensions in geometric shapes, how to solve linear equations with 2 variables.
About the Author
Drew Lichtenstein started writing in 2008. His articles have appeared in the collegiate newspaper "The Red and Black." He holds a Master of Arts in comparative literature from the University of Georgia.
Photo Credits
BananaStock/BananaStock/Getty Images
Find Your Next Great Science Fair Project! GO
We Have More Great Sciencing Articles!
Solving Linear Equations
Solving linear equations means finding the value of the variable(s) given in the linear equations. A linear equation is a combination of an algebraic expression and an equal to (=) symbol. It has a degree of 1 or it can be called a first-degree equation. For example, x + y = 4 is a linear equation. Sometimes, we may have to find the values of variables involved in a linear equation. When we are given two or more such linear equations, we can find the values of each variable by solving linear equations. There are a few methods to solve linear equations. Let us discuss each of these methods in detail.
Solving Linear Equations in One Variable
A linear equation in one variable is an equation of degree one and has only one variable term. It is of the form 'ax+b = 0', where 'a' is a non zero number and 'x' is a variable. By solving linear equations in one variable, we get only one solution for the given variable. An example for this is 3x - 6 = 0. The variable 'x' has only one solution, which is calculated as 3x - 6 = 0 3x = 6 x = 6/3 x = 2
For solving linear equations with one variable, simplify the equation such that all the variable terms are brought to one side and the constant value is brought to the other side. If there are any fractional terms then find the LCM ( Least Common Multiple ) and simplify them such that the variable terms are on one side and the constant terms are on the other side. Let us work out a small example to understand this.
4x + 8 = 8x - 10. To find the value of 'x', let us simplify and bring the 'x' terms to one side and the constant terms to another side.
4x - 8x = -10 - 8 -4x = -18 4x = 18 x = 18/4 On simplifying, we get x = 9/2.
Solving Linear Equations by Substitution Method
The substitution method is one of the methods of solving linear equations. In the substitution method , we rearrange the equation such that one of the values is substituted in the second equation. Now that we are left with an equation that has only one variable, we can solve it and find the value of that variable. In the two given equations, any equation can be taken and the value of a variable can be found and substituted in another equation. For solving linear equations using the substitution method, follow the steps mentioned below. Let us understand this with an example of solving the following system of linear equations. x + y = 6 --------------(1) 2x + 4y = 20 -----------(2)
Step 1: Find the value of one of the variables using any one of the equations. In this case, let us find the value of 'x' from equation (1). x + y = 6 ---------(1) x = 6 - y Step 2: Substitute the value of the variable found in step 1 in the second linear equation. Now, let us substitute the value of 'x' in the second equation 2x + 4y = 20.
x = 6 - y Substituting the value of 'x' in 2x + 4y = 20, we get,
2(6 - y) + 4y = 20 12 - 2y + 4y = 20 12 + 2y = 20 2y = 20 - 12 2y = 8 y = 8/2 y = 4 Step 3: Now substitute the value of 'y' in either equation (1) or (2). Let us substitute the value of 'y' in equation (1).
x + y = 6 x + 4 = 6 x = 6 - 4 x = 2 Therefore, by substitution method, the linear equations are solved, and the value of x is 2 and y is 4.
Solving Linear Equations by Elimination Method
The elimination method is another way to solve a system of linear equations. Here we make an attempt to multiply either the 'x' variable term or the 'y' variable term with a constant value such that either the 'x' variable terms or the 'y' variable terms cancel out and gives us the value of the other variable. Let us understand the steps of solving linear equations by elimination method . Consider the given linear equations: 2x + y = 11 ----------- (1) x + 3y = 18 ---------- (2) Step 1: Check whether the terms are arranged in a way such that the 'x' term is followed by a 'y' term and an equal to sign and after the equal to sign the constant term should be present. The given set of linear equations are already arranged in the correct way which is ax+by=c or ax+by-c=0.
Step 2: The next step is to multiply either one or both the equations by a constant value such that it will make either the 'x' terms or the 'y' terms cancel out which would help us find the value of the other variable. Now in equation (2), let us multiply every term by the number 2 to make the coefficients of x the same in both the equations. x + 3y = 18 ---------- (2) Multiplying all the terms in equation (2) by 2, we get,
2(x) + 2(3y) = 2(18). Now equation (2) becomes, 2x + 6y = 36 -----------(2)
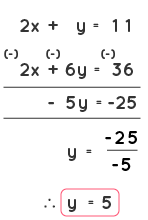
Therefore, y = 5. Step 4: Using the value obtained in step 3, find out the value of another variable by substituting the value in any of the equations. Let us substitute the value of 'y' in equation (1). We get, 2x + y = 11 2x + 5 = 11 2x = 11 - 5 2x = 6 x = 6/2 x = 3
Therefore, by solving linear equations, we get the value of x = 3 and y = 5.
Graphical Method of Solving Linear Equations
Another method for solving linear equations is by using the graph. When we are given a system of linear equations, we graph both the equations by finding values for 'y' for different values of 'x' in the coordinate system. Once it is done, we find the point of intersection of these two lines. The (x,y) values at the point of intersection give the solution for these linear equations. Let us take two linear equations and solve them using the graphical method.
x + y = 8 -------(1)
y = x + 2 --------(2)
Let us take some values for 'x' and find the values for 'y' for the equation x + y = 8. This can also be rewritten as y = 8 - x.
Let us take some values for 'x' and find the values for 'y' in the equation y = x + 2.
Plotting these points on the coordinate plane, we get a graph like this.
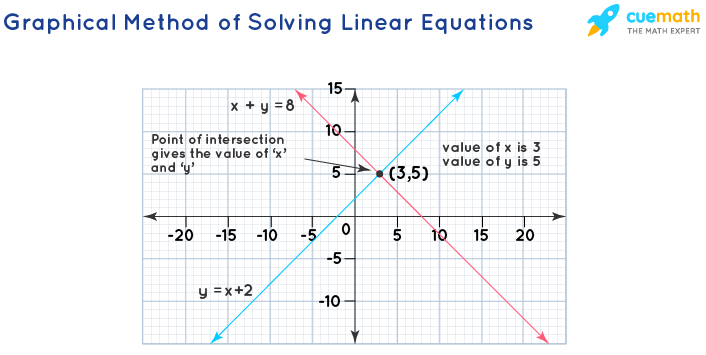
Now, we find the point of intersection of these lines to find the values of 'x' and 'y'. The two lines intersect at the point (3,5). Therefore, x = 3 and y = 5 by using the graphical method of solving linear equations .
This method is also used to find the optimal solution of linear programming problems. Let us look at one more method of solving linear equations, which is the cross multiplication method.
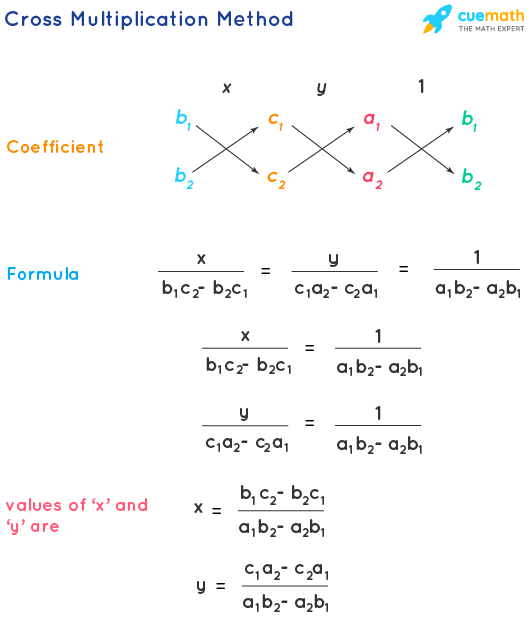
Cross Multiplication Method of Solving Linear Equations
The cross multiplication method enables us to solve linear equations by picking the coefficients of all the terms ('x' , 'y' and the constant terms) in the format shown below and apply the formula for finding the values of 'x' and 'y'.
Topics Related to Solving Linear Equations
Check the given articles related to solving linear equations.
- Linear Equations
- Application of Linear Equations
- Two-Variable Linear Equations
- Linear Equations and Half Planes
- One Variable Linear Equations and Inequations
Solving Linear Equations Examples
Example 1: Solve the following linear equations by the substitution method.
3x + y = 13 --------- (1) 2x + 3y = 18 -------- (2)
By using the substitution method of solving linear equations, let us take the first equation and find the value of 'y' and substitute it in the second equation.
From equation (1), y = 13-3x. Now, substituting the value of 'y' in equation (2), we get, 2x + 3 (13 - 3x) = 18 2x + 39 - 9x = 18 -7x + 39 = 18 -7x = 18 - 39 -7x = -21 x = -21/-7 x = 3 Now, let us substitute the value of 'x = 3' in equation (1) and find the value of 'y'. 3x + y = 13 ------- (1) 3(3) + y = 13 9 + y = 13 y = 13 - 9 y = 4
Therefore, by the substitution method, the value of x is 3 and y is 4.
Example 2: Using the elimination method of solving linear equations find the values of 'x' and 'y'.
3x + y = 21 ------ (1) 2x + 3y = 28 -------- (2)
By using the elimination method, let us make the 'y' variable to be the same in both the equations (1) and (2). To do this let us multiply all the terms of the first equation by 3. Therefore equation (1) becomes,
3(3x) + 3(y) = 63 9x + 3y = 63 ---------- (3) The second equation is, 2x + 3y = 28 Now let us cancel the 'y' terms and find the value of 'x' by subtracting equation (2) from equation (3). This is done by changing the signs of all the terms in equation (2).

Example 3: Using the cross multiplication method of solving linear equations, solve the following equations.
x + 2y - 16 = 0 --------- (1) 4x - y - 10 = 0 ---------- (2)
Compare the given equation with \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0, and \(a_{2}\)x+\(b_{2}\)y+\(c_{2}\) = 0. From the given equations,
\(a_{1}\) = 1, \(a_{2}\) = 4, \(b_{1}\) = 2, \(b_{2}\) = -1, \(c_{1}\) = -16, and \(c_{2}\) = -10.
By cross multiplication method,
x = \(b_{1}\)\(c_{2}\) - \(b_{2}\)\(c_{1}\)/\(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\) y = \(c_{1}\)\(a_{2}\) - \(c_{2}\)\(a_{1}\) / \(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\)
Substituting the values in the formula we get,
x = ((2)(-10)) - ((-1)(-16)) / ((1)(-1)) - ((4)(2)) x = (-20-16)/(-1-8) x = -36/-9 x = 36/9 x = 4 y = ((-16)(4)) - ((-10)(1)) / ((1)(-1)) - ((4)(2)) y = (-64 + 10) / (-1 - 8) y = -54 / -9 y = 54/9 y = 6 Therefore, by the cross multiplication method, the value of x is 4 and y is 6.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Solving Linear Equations
Faqs on solving linear equations, what does it mean by solving linear equations.
An equation that has a degree of 1 is called a linear equation. We can have one variable linear equations , two-variable linear equations , linear equations with three variables, and more depending on the number of variables in it. Solving linear equations means finding the values of all the variables present in the equation. This can be done by substitution method, elimination method, graphical method, and the cross multiplication method . All these methods are different ways of finding the values of the variables.
How to Use the Substitution Method for Solving Linear Equations?
The substitution method of solving equations states that for a given system of linear equations, find the value of either 'x' or 'y' from any of the given equations and then substitute the value found of 'x' or 'y' in another equation so that the other unknown value can be found.
How to Use the Elimination Method for Solving Linear Equations?
In the elimination method of solving linear equations, we multiply a constant or a number with one equation or both the equations such that either the 'x' terms or the 'y' terms are the same. Then we cancel out the same term in both the equations by either adding or subtracting them and find the value of one variable (either 'x' or 'y'). After finding one of the values, we substitute the value in one of the equations and find the other unknown value.
What is the Graphical Method of Solving Linear Equations?
In the graphical method of solving linear equations, we find the value of 'y' from the given equations by putting the values of x as 0, 1, 2, 3, and so on, and plot a graph in the coordinate system for the line for various values of 'x' for both the system of linear equations. We will see that these two lines intersect at a point. This point is the solution for the given system of linear equations. If there is no intersection point between two lines, then we consider them as parallel lines , and if we found that both the lines lie on each other, those are known as coincident lines and have infinitely many solutions.
What are the Steps of Solving Linear Equations that has One Variable?
A linear equation is an equation with degree 1. To solve a linear equation that has one variable we bring the variable to one side and the constant value to the other side. Then, a non-zero number may be added, subtracted, multiplied, or divided on both sides of the equation. For example, a linear equation with one variable will be of the form 'x - 4 = 2'. To find the value of 'x', we add the constant value '4' to both sides of the equation. Therefore, the value of 'x = 6'.
What are the Steps of Solving Linear Equations having Three Variables?
To solve a system of linear equations that has three variables, we take any two equations and variables. We then take another pair of linear equations and also solve for the same variable. Now that, we have two linear equations with two variables, we can use the substitution method or elimination method, or any other method to solve the values of two unknown variables. After finding these two variables, we substitute them in any of the three equations to find the third unknown variable.
What are the 4 Methods of Solving Linear Equations?
The methods for solving linear equations are given below:
- Substitution method
- Elimination method
- Cross multiplication method
- Graphical method
Solving Equations
What is an equation.
An equation says that two things are equal. It will have an equals sign "=" like this:
That equations says:
what is on the left (x − 2) equals what is on the right (4)
So an equation is like a statement " this equals that "
What is a Solution?
A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .
Example: x − 2 = 4
When we put 6 in place of x we get:
which is true
So x = 6 is a solution.
How about other values for x ?
- For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
- For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .
In this case x = 6 is the only solution.
You might like to practice solving some animated equations .
More Than One Solution
There can be more than one solution.
Example: (x−3)(x−2) = 0
When x is 3 we get:
(3−3)(3−2) = 0 × 1 = 0
And when x is 2 we get:
(2−3)(2−2) = (−1) × 0 = 0
which is also true
So the solutions are:
x = 3 , or x = 2
When we gather all solutions together it is called a Solution Set
The above solution set is: {2, 3}
Solutions Everywhere!
Some equations are true for all allowed values and are then called Identities
Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities
Let's try θ = 30°:
sin(−30°) = −0.5 and
−sin(30°) = −0.5
So it is true for θ = 30°
Let's try θ = 90°:
sin(−90°) = −1 and
−sin(90°) = −1
So it is also true for θ = 90°
Is it true for all values of θ ? Try some values for yourself!
How to Solve an Equation
There is no "one perfect way" to solve all equations.
A Useful Goal
But we often get success when our goal is to end up with:
x = something
In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.
Example: Solve 3x−6 = 9
Now we have x = something ,
and a short calculation reveals that x = 5
Like a Puzzle
In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.
Here are some things we can do:
- Add or Subtract the same value from both sides
- Clear out any fractions by Multiplying every term by the bottom parts
- Divide every term by the same nonzero value
- Combine Like Terms
- Expanding (the opposite of factoring) may also help
- Recognizing a pattern, such as the difference of squares
- Sometimes we can apply a function to both sides (e.g. square both sides)
Example: Solve √(x/2) = 3
And the more "tricks" and techniques you learn the better you will get.
Special Equations
There are special ways of solving some types of equations. Learn how to ...
- solve Quadratic Equations
- solve Radical Equations
- solve Equations with Sine, Cosine and Tangent
Check Your Solutions
You should always check that your "solution" really is a solution.
How To Check
Take the solution(s) and put them in the original equation to see if they really work.
Example: solve for x:
2x x − 3 + 3 = 6 x − 3 (x≠3)
We have said x≠3 to avoid a division by zero.
Let's multiply through by (x − 3) :
2x + 3(x−3) = 6
Bring the 6 to the left:
2x + 3(x−3) − 6 = 0
Expand and solve:
2x + 3x − 9 − 6 = 0
5x − 15 = 0
5(x − 3) = 0
Which can be solved by having x=3
Let us check x=3 using the original question:
2 × 3 3 − 3 + 3 = 6 3 − 3
Hang On: 3 − 3 = 0 That means dividing by Zero!
And anyway, we said at the top that x≠3 , so ...
x = 3 does not actually work, and so:
There is No Solution!
That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!
This gives us a moral lesson:
"Solving" only gives us possible solutions, they need to be checked!
- Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
- Show all the steps , so it can be checked later (by you or someone else)
4.1 Solve Systems of Linear Equations with Two Variables
Learning objectives.
By the end of this section, you will be able to:
- Determine whether an ordered pair is a solution of a system of equations
- Solve a system of linear equations by graphing
- Solve a system of equations by substitution
- Solve a system of equations by elimination
- Choose the most convenient method to solve a system of linear equations
Be Prepared 4.1
Before you get started, take this readiness quiz.
For the equation y = 2 3 x − 4 , y = 2 3 x − 4 , ⓐ Is ( 6 , 0 ) ( 6 , 0 ) a solution? ⓑ Is ( −3 , −2 ) ( −3 , −2 ) a solution? If you missed this problem, review Example 3.2 .
Be Prepared 4.2
Find the slope and y -intercept of the line 3 x − y = 12 . 3 x − y = 12 . If you missed this problem, review Example 3.16 .
Be Prepared 4.3
Find the x- and y -intercepts of the line 2 x − 3 y = 12 . 2 x − 3 y = 12 . If you missed this problem, review Example 3.8 .
Determine Whether an Ordered Pair is a Solution of a System of Equations
In Solving Linear Equations , we learned how to solve linear equations with one variable. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations .
System of Linear Equations
When two or more linear equations are grouped together, they form a system of linear equations .
In this section, we will focus our work on systems of two linear equations in two unknowns. We will solve larger systems of equations later in this chapter.
An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.
A linear equation in two variables, such as 2 x + y = 7 , 2 x + y = 7 , has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.
To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) ( x , y ) that make both equations true. These are called the solutions of a system of equations .
Solutions of a System of Equations
The solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ) . ( x , y ) .
To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.
Example 4.1
Determine whether the ordered pair is a solution to the system { x − y = −1 2 x − y = −5 . { x − y = −1 2 x − y = −5 .
ⓐ ( −2 , −1 ) ( −2 , −1 ) ⓑ ( −4 , −3 ) ( −4 , −3 )
Determine whether the ordered pair is a solution to the system { 3 x + y = 0 x + 2 y = −5 . { 3 x + y = 0 x + 2 y = −5 .
ⓐ ( 1 , −3 ) ( 1 , −3 ) ⓑ ( 0 , 0 ) ( 0 , 0 )
Determine whether the ordered pair is a solution to the system { x − 3 y = −8 − 3 x − y = 4 . { x − 3 y = −8 − 3 x − y = 4 .
ⓐ ( 2 , −2 ) ( 2 , −2 ) ⓑ ( −2 , 2 ) ( −2 , 2 )
Solve a System of Linear Equations by Graphing
In this section, we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.
The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.
Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.
Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.
Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end of the section you’ll decide which method was the most convenient way to solve this system.
Example 4.2
How to solve a system of equations by graphing.
Solve the system by graphing { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .
Solve the system by graphing: { x − 3 y = −3 x + y = 5 . { x − 3 y = −3 x + y = 5 .
Solve the system by graphing: { − x + y = 1 3 x + 2 y = 12 . { − x + y = 1 3 x + 2 y = 12 .
The steps to use to solve a system of linear equations by graphing are shown here.
Solve a system of linear equations by graphing.
- Step 1. Graph the first equation.
- Step 2. Graph the second equation on the same rectangular coordinate system.
- Step 3. Determine whether the lines intersect, are parallel, or are the same line.
- If the lines intersect, identify the point of intersection. This is the solution to the system.
- If the lines are parallel, the system has no solution.
- If the lines are the same, the system has an infinite number of solutions.
- Step 5. Check the solution in both equations.
In the next example, we’ll first re-write the equations into slope–intercept form as this will make it easy for us to quickly graph the lines.
Example 4.3
Solve the system by graphing: { 3 x + y = − 1 2 x + y = 0 . { 3 x + y = − 1 2 x + y = 0 .
We’ll solve both of these equations for y y so that we can easily graph them using their slopes and y -intercepts.
Solve the system by graphing: { − x + y = 1 2 x + y = 10 . { − x + y = 1 2 x + y = 10 .
Solve the system by graphing: { 2 x + y = 6 x + y = 1 . { 2 x + y = 6 x + y = 1 .
In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.
Example 4.4
Solve the system by graphing: { y = 1 2 x − 3 x − 2 y = 4 . { y = 1 2 x − 3 x − 2 y = 4 .
Solve the system by graphing: { y = − 1 4 x + 2 x + 4 y = − 8 . { y = − 1 4 x + 2 x + 4 y = − 8 .
Solve the system by graphing: { y = 3 x − 1 6 x − 2 y = 6 . { y = 3 x − 1 6 x − 2 y = 6 .
Sometimes the equations in a system represent the same line. Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. There are infinitely many solutions to the system.
Example 4.5
Solve the system by graphing: { y = 2 x − 3 − 6 x + 3 y = − 9 . { y = 2 x − 3 − 6 x + 3 y = − 9 .
If you write the second equation in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.
Solve the system by graphing: { y = − 3 x − 6 6 x + 2 y = − 12 . { y = − 3 x − 6 6 x + 2 y = − 12 .
Try It 4.10
Solve the system by graphing: { y = 1 2 x − 4 2 x − 4 y = 16 . { y = 1 2 x − 4 2 x − 4 y = 16 .
When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident . Coincident lines have the same slope and same y- intercept.
Coincident Lines
Coincident lines have the same slope and same y- intercept.
The systems of equations in Example 4.2 and Example 4.3 each had two intersecting lines. Each system had one solution.
In Example 4.5 , the equations gave coincident lines, and so the system had infinitely many solutions.
The systems in those three examples had at least one solution. A system of equations that has at least one solution is called a consistent system.
A system with parallel lines, like Example 4.4 , has no solution. We call a system of equations like this inconsistent. It has no solution.
Consistent and Inconsistent Systems
A consistent system of equations is a system of equations with at least one solution.
An inconsistent system of equations is a system of equations with no solution.
We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent, they each have their own set of solutions. Intersecting lines and parallel lines are independent.
If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines.
Let’s sum this up by looking at the graphs of the three types of systems. See below and Table 4.1 .
Example 4.6
Without graphing, determine the number of solutions and then classify the system of equations.
ⓐ { y = 3 x − 1 6 x − 2 y = 12 { y = 3 x − 1 6 x − 2 y = 12 ⓑ { 2 x + y = − 3 x − 5 y = 5 { 2 x + y = − 3 x − 5 y = 5
ⓐ We will compare the slopes and intercepts of the two lines.
A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.
ⓑ We will compare the slope and intercepts of the two lines.
A system of equations whose graphs are intersect has 1 solution and is consistent and independent.
Try It 4.11
ⓐ { y = −2 x − 4 4 x + 2 y = 9 { y = −2 x − 4 4 x + 2 y = 9 ⓑ { 3 x + 2 y = 2 2 x + y = 1 { 3 x + 2 y = 2 2 x + y = 1
Try It 4.12
ⓐ { y = 1 3 x − 5 x − 3 y = 6 { y = 1 3 x − 5 x − 3 y = 6 ⓑ { x + 4 y = 12 − x + y = 3 { x + 4 y = 12 − x + y = 3
Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.
Solve a System of Equations by Substitution
We will now solve systems of linear equations by the substitution method.
We will use the same system we used first for graphing.
We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.
Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!
After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.
Example 4.7
How to solve a system of equations by substitution.
Solve the system by substitution: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .
Try It 4.13
Solve the system by substitution: { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 .
Try It 4.14
Solve the system by substitution: { 2 x + y = −1 4 x + 3 y = 3 . { 2 x + y = −1 4 x + 3 y = 3 .
Solve a system of equations by substitution.
- Step 1. Solve one of the equations for either variable.
- Step 2. Substitute the expression from Step 1 into the other equation.
- Step 3. Solve the resulting equation.
- Step 4. Substitute the solution in Step 3 into either of the original equations to find the other variable.
- Step 5. Write the solution as an ordered pair.
- Step 6. Check that the ordered pair is a solution to both original equations.
Be very careful with the signs in the next example.
Example 4.8
Solve the system by substitution: { 4 x + 2 y = 4 6 x − y = 8 . { 4 x + 2 y = 4 6 x − y = 8 .
We need to solve one equation for one variable. We will solve the first equation for y .
Try It 4.15
Solve the system by substitution: { x − 4 y = −4 − 3 x + 4 y = 0 . { x − 4 y = −4 − 3 x + 4 y = 0 .
Try It 4.16
Solve the system by substitution: { 4 x − y = 0 2 x − 3 y = 5 . { 4 x − y = 0 2 x − 3 y = 5 .
Solve a System of Equations by Elimination
We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.
The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.
The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.
For any expressions a, b, c, and d .
To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.
Notice how that works when we add these two equations together:
The y ’s add to zero and we have one equation with one variable.
Let’s try another one:
This time we don’t see a variable that can be immediately eliminated if we add the equations.
But if we multiply the first equation by −2 , −2 , we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2 . −2 .
Then rewrite the system of equations.
Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.
Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.
Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.
Example 4.9
How to solve a system of equations by elimination.
Solve the system by elimination: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .
Try It 4.17
Solve the system by elimination: { 3 x + y = 5 2 x − 3 y = 7 . { 3 x + y = 5 2 x − 3 y = 7 .
Try It 4.18
Solve the system by elimination: { 4 x + y = − 5 − 2 x − 2 y = − 2 . { 4 x + y = − 5 − 2 x − 2 y = − 2 .
The steps are listed here for easy reference.
Solve a system of equations by elimination.
- Step 1. Write both equations in standard form. If any coefficients are fractions, clear them.
- Decide which variable you will eliminate.
- Multiply one or both equations so that the coefficients of that variable are opposites.
- Step 3. Add the equations resulting from Step 2 to eliminate one variable.
- Step 4. Solve for the remaining variable.
- Step 5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
- Step 6. Write the solution as an ordered pair.
- Step 7. Check that the ordered pair is a solution to both original equations.
Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.
Example 4.10
Solve the system by elimination: { 4 x − 3 y = 9 7 x + 2 y = −6 . { 4 x − 3 y = 9 7 x + 2 y = −6 .
In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by different constants to get the opposites.
Try It 4.19
Solve the system by elimination: { 3 x − 4 y = − 9 5 x + 3 y = 14 . { 3 x − 4 y = − 9 5 x + 3 y = 14 .
Try It 4.20
Solve each system by elimination: { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 .
When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by the LCD of all the fractions in the equation.
Example 4.11
Solve the system by elimination: { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 . { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 .
In this example, both equations have fractions. Our first step will be to multiply each equation by the LCD of all the fractions in the equation to clear the fractions.
Try It 4.21
Solve each system by elimination: { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 . { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 .
Try It 4.22
Solve each system by elimination: { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 . { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 .
When we solved the system by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.
The same is true using substitution or elimination. If the equation at the end of substitution or elimination is a true statement, we have a consistent but dependent system and the system of equations has infinitely many solutions. If the equation at the end of substitution or elimination is a false statement, we have an inconsistent system and the system of equations has no solution.

Example 4.12
Solve the system by elimination: { 3 x + 4 y = 12 y = 3 − 3 4 x . { 3 x + 4 y = 12 y = 3 − 3 4 x .
This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.
After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.
Try It 4.23
Solve the system by elimination: { 5 x − 3 y = 15 y = − 5 + 5 3 x . { 5 x − 3 y = 15 y = − 5 + 5 3 x .
Try It 4.24
Solve the system by elimination: { x + 2 y = 6 y = − 1 2 x + 3 . { x + 2 y = 6 y = − 1 2 x + 3 .
Choose the Most Convenient Method to Solve a System of Linear Equations
When you solve a system of linear equations in in an application, you will not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.
Example 4.13
For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
ⓐ { 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32 ⓑ { 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1
Since both equations are in standard form, using elimination will be most convenient.
Since one equation is already solved for y , using substitution will be most convenient.
Try It 4.25
For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
ⓐ { 4 x − 5 y = −32 3 x + 2 y = −1 { 4 x − 5 y = −32 3 x + 2 y = −1 ⓑ { x = 2 y − 1 3 x − 5 y = −7 { x = 2 y − 1 3 x − 5 y = −7
Try It 4.26
ⓐ { y = 2 x − 1 3 x − 4 y = − 6 { y = 2 x − 1 3 x − 4 y = − 6 ⓑ { 6 x − 2 y = 12 3 x + 7 y = −13 { 6 x − 2 y = 12 3 x + 7 y = −13
Section 4.1 Exercises
Practice makes perfect.
In the following exercises, determine if the following points are solutions to the given system of equations.
{ 2 x − 6 y = 0 3 x − 4 y = 5 { 2 x − 6 y = 0 3 x − 4 y = 5
ⓐ ( 3 , 1 ) ( 3 , 1 ) ⓑ ( −3 , 4 ) ( −3 , 4 )
{ − 3 x + y = 8 − x + 2 y = −9 { − 3 x + y = 8 − x + 2 y = −9
ⓐ ( −5 , −7 ) ( −5 , −7 ) ⓑ ( −5 , 7 ) ( −5 , 7 )
{ x + y = 2 y = 3 4 x { x + y = 2 y = 3 4 x
ⓐ ( 8 7 , 6 7 ) ( 8 7 , 6 7 ) ⓑ ( 1 , 3 4 ) ( 1 , 3 4 )
{ 2 x + 3 y = 6 y = 2 3 x + 2 { 2 x + 3 y = 6 y = 2 3 x + 2 ⓐ ( −6 , 2 ) ( −6 , 2 ) ⓑ ( −3 , 4 ) ( −3 , 4 )
In the following exercises, solve the following systems of equations by graphing.
{ 3 x + y = −3 2 x + 3 y = 5 { 3 x + y = −3 2 x + 3 y = 5
{ − x + y = 2 2 x + y = −4 { − x + y = 2 2 x + y = −4
{ y = x + 2 y = −2 x + 2 { y = x + 2 y = −2 x + 2
{ y = x − 2 y = −3 x + 2 { y = x − 2 y = −3 x + 2
{ y = 3 2 x + 1 y = − 1 2 x + 5 { y = 3 2 x + 1 y = − 1 2 x + 5
{ y = 2 3 x − 2 y = − 1 3 x − 5 { y = 2 3 x − 2 y = − 1 3 x − 5
{ x + y = −4 − x + 2 y = −2 { x + y = −4 − x + 2 y = −2
{ − x + 3 y = 3 x + 3 y = 3 { − x + 3 y = 3 x + 3 y = 3
{ − 2 x + 3 y = 3 x + 3 y = 12 { − 2 x + 3 y = 3 x + 3 y = 12
{ 2 x − y = 4 2 x + 3 y = 12 { 2 x − y = 4 2 x + 3 y = 12
{ x + 3 y = −6 y = − 4 3 x + 4 { x + 3 y = −6 y = − 4 3 x + 4
{ − x + 2 y = −6 y = − 1 2 x − 1 { − x + 2 y = −6 y = − 1 2 x − 1
{ − 2 x + 4 y = 4 y = 1 2 x { − 2 x + 4 y = 4 y = 1 2 x
{ 3 x + 5 y = 10 y = − 3 5 x + 1 { 3 x + 5 y = 10 y = − 3 5 x + 1
{ 4 x − 3 y = 8 8 x − 6 y = 14 { 4 x − 3 y = 8 8 x − 6 y = 14
{ x + 3 y = 4 − 2 x − 6 y = 3 { x + 3 y = 4 − 2 x − 6 y = 3
{ x = −3 y + 4 2 x + 6 y = 8 { x = −3 y + 4 2 x + 6 y = 8
{ 4 x = 3 y + 7 8 x − 6 y = 14 { 4 x = 3 y + 7 8 x − 6 y = 14
{ 2 x + y = 6 − 8 x − 4 y = −24 { 2 x + y = 6 − 8 x − 4 y = −24
{ 5 x + 2 y = 7 − 10 x − 4 y = −14 { 5 x + 2 y = 7 − 10 x − 4 y = −14
{ y = 2 3 x + 1 − 2 x + 3 y = 5 { y = 2 3 x + 1 − 2 x + 3 y = 5
{ y = 3 2 x + 1 2 x − 3 y = 7 { y = 3 2 x + 1 2 x − 3 y = 7
{ 5 x + 3 y = 4 2 x − 3 y = 5 { 5 x + 3 y = 4 2 x − 3 y = 5
{ y = − 1 2 x + 5 x + 2 y = 10 { y = − 1 2 x + 5 x + 2 y = 10
{ 5 x − 2 y = 10 y = 5 2 x − 5 { 5 x − 2 y = 10 y = 5 2 x − 5
In the following exercises, solve the systems of equations by substitution.
{ 2 x + y = −4 3 x − 2 y = −6 { 2 x + y = −4 3 x − 2 y = −6
{ 2 x + y = −2 3 x − y = 7 { 2 x + y = −2 3 x − y = 7
{ x − 2 y = −5 2 x − 3 y = −4 { x − 2 y = −5 2 x − 3 y = −4
{ x − 3 y = −9 2 x + 5 y = 4 { x − 3 y = −9 2 x + 5 y = 4
{ 5 x − 2 y = −6 y = 3 x + 3 { 5 x − 2 y = −6 y = 3 x + 3
{ − 2 x + 2 y = 6 y = −3 x + 1 { − 2 x + 2 y = 6 y = −3 x + 1
{ 2 x + 5 y = 1 y = 1 3 x − 2 { 2 x + 5 y = 1 y = 1 3 x − 2
{ 3 x + 4 y = 1 y = − 2 5 x + 2 { 3 x + 4 y = 1 y = − 2 5 x + 2
{ 2 x + y = 5 x − 2 y = −15 { 2 x + y = 5 x − 2 y = −15
{ 4 x + y = 10 x − 2 y = −20 { 4 x + y = 10 x − 2 y = −20
{ y = −2 x − 1 y = − 1 3 x + 4 { y = −2 x − 1 y = − 1 3 x + 4
{ y = x − 6 y = − 3 2 x + 4 { y = x − 6 y = − 3 2 x + 4
{ x = 2 y 4 x − 8 y = 0 { x = 2 y 4 x − 8 y = 0
{ 2 x − 16 y = 8 − x − 8 y = −4 { 2 x − 16 y = 8 − x − 8 y = −4
{ y = 7 8 x + 4 − 7 x + 8 y = 6 { y = 7 8 x + 4 − 7 x + 8 y = 6
{ y = − 2 3 x + 5 2 x + 3 y = 11 { y = − 2 3 x + 5 2 x + 3 y = 11
In the following exercises, solve the systems of equations by elimination.
{ 5 x + 2 y = 2 − 3 x − y = 0 { 5 x + 2 y = 2 − 3 x − y = 0
{ 6 x − 5 y = −1 2 x + y = 13 { 6 x − 5 y = −1 2 x + y = 13
{ 2 x − 5 y = 7 3 x − y = 17 { 2 x − 5 y = 7 3 x − y = 17
{ 5 x − 3 y = −1 2 x − y = 2 { 5 x − 3 y = −1 2 x − y = 2
{ 3 x − 5 y = −9 5 x + 2 y = 16 { 3 x − 5 y = −9 5 x + 2 y = 16
{ 4 x − 3 y = 3 2 x + 5 y = −31 { 4 x − 3 y = 3 2 x + 5 y = −31
{ 3 x + 8 y = −3 2 x + 5 y = −3 { 3 x + 8 y = −3 2 x + 5 y = −3
{ 11 x + 9 y = −5 7 x + 5 y = −1 { 11 x + 9 y = −5 7 x + 5 y = −1
{ 3 x + 8 y = 67 5 x + 3 y = 60 { 3 x + 8 y = 67 5 x + 3 y = 60
{ 2 x + 9 y = −4 3 x + 13 y = −7 { 2 x + 9 y = −4 3 x + 13 y = −7
{ 1 3 x − y = −3 x + 5 2 y = 2 { 1 3 x − y = −3 x + 5 2 y = 2
{ x + 1 2 y = 3 2 1 5 x − 1 5 y = 3 { x + 1 2 y = 3 2 1 5 x − 1 5 y = 3
{ x + 1 3 y = −1 1 3 x + 1 2 y = 1 { x + 1 3 y = −1 1 3 x + 1 2 y = 1
{ 1 3 x − y = −3 2 3 x + 5 2 y = 3 { 1 3 x − y = −3 2 3 x + 5 2 y = 3
{ 2 x + y = 3 6 x + 3 y = 9 { 2 x + y = 3 6 x + 3 y = 9
{ x − 4 y = −1 − 3 x + 12 y = 3 { x − 4 y = −1 − 3 x + 12 y = 3
{ − 3 x − y = 8 6 x + 2 y = −16 { − 3 x − y = 8 6 x + 2 y = −16
{ 4 x + 3 y = 2 20 x + 15 y = 10 { 4 x + 3 y = 2 20 x + 15 y = 10
In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.
ⓐ { 8 x − 15 y = −32 6 x + 3 y = −5 { 8 x − 15 y = −32 6 x + 3 y = −5 ⓑ { x = 4 y − 3 4 x − 2 y = −6 { x = 4 y − 3 4 x − 2 y = −6
ⓐ { y = 7 x − 5 3 x − 2 y = 16 { y = 7 x − 5 3 x − 2 y = 16 ⓑ { 12 x − 5 y = −42 3 x + 7 y = −15 { 12 x − 5 y = −42 3 x + 7 y = −15
ⓐ { y = 4 x + 9 5 x − 2 y = −21 { y = 4 x + 9 5 x − 2 y = −21 ⓑ { 9 x − 4 y = 24 3 x + 5 y = −14 { 9 x − 4 y = 24 3 x + 5 y = −14
ⓐ { 14 x − 15 y = −30 7 x + 2 y = 10 { 14 x − 15 y = −30 7 x + 2 y = 10 ⓑ { x = 9 y − 11 2 x − 7 y = −27 { x = 9 y − 11 2 x − 7 y = −27
Writing Exercises
In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.
Solve the system of equations by substitution and explain all your steps in words: { 3 x + y = 12 x = y − 8 . { 3 x + y = 12 x = y − 8 .
Solve the system of equations by elimination and explain all your steps in words: { 5 x + 4 y = 10 2 x = 3 y + 27 . { 5 x + 4 y = 10 2 x = 3 y + 27 .
Solve the system of equations { x + y = 10 x − y = 6 { x + y = 10 x − y = 6
ⓐ by graphing ⓑ by substitution ⓒ Which method do you prefer? Why?
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Intermediate Algebra 2e
- Publication date: May 6, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-1-solve-systems-of-linear-equations-with-two-variables
© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

4.2: Solve Systems of Linear Equations with Two Variables
- Last updated
- Save as PDF
- Page ID 114156

Learning Objectives
By the end of this section, you will be able to:
- Determine whether an ordered pair is a solution of a system of equations
- Solve a system of linear equations by graphing
- Solve a system of equations by substitution
- Solve a system of equations by elimination
- Choose the most convenient method to solve a system of linear equations
Be Prepared 4.1
Before you get started, take this readiness quiz.
For the equation y = 2 3 x − 4 , y = 2 3 x − 4 , ⓐ Is ( 6 , 0 ) ( 6 , 0 ) a solution? ⓑ Is ( −3 , −2 ) ( −3 , −2 ) a solution? If you missed this problem, review Example 3.2.
Be Prepared 4.2
Find the slope and y -intercept of the line 3 x − y = 12 . 3 x − y = 12 . If you missed this problem, review Example 3.16.
Be Prepared 4.3
Find the x- and y -intercepts of the line 2 x − 3 y = 12 . 2 x − 3 y = 12 . If you missed this problem, review Example 3.8.
Determine Whether an Ordered Pair is a Solution of a System of Equations
In Solving Linear Equations, we learned how to solve linear equations with one variable. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations .
System of Linear Equations
When two or more linear equations are grouped together, they form a system of linear equations .
In this section, we will focus our work on systems of two linear equations in two unknowns. We will solve larger systems of equations later in this chapter.
An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.
{ 2 x + y = 7 x − 2 y = 6 { 2 x + y = 7 x − 2 y = 6
A linear equation in two variables, such as 2 x + y = 7 , 2 x + y = 7 , has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.
To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) ( x , y ) that make both equations true. These are called the solutions of a system of equations .
Solutions of a System of Equations
The solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ) . ( x , y ) .
To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.
Example 4.1
Determine whether the ordered pair is a solution to the system { x − y = −1 2 x − y = −5 . { x − y = −1 2 x − y = −5 .
ⓐ ( −2 , −1 ) ( −2 , −1 ) ⓑ ( −4 , −3 ) ( −4 , −3 )
Determine whether the ordered pair is a solution to the system { 3 x + y = 0 x + 2 y = −5 . { 3 x + y = 0 x + 2 y = −5 .
ⓐ ( 1 , −3 ) ( 1 , −3 ) ⓑ ( 0 , 0 ) ( 0 , 0 )
Determine whether the ordered pair is a solution to the system { x − 3 y = −8 − 3 x − y = 4 . { x − 3 y = −8 − 3 x − y = 4 .
ⓐ ( 2 , −2 ) ( 2 , −2 ) ⓑ ( −2 , 2 ) ( −2 , 2 )
Solve a System of Linear Equations by Graphing
In this section, we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.
The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.
Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.
Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.
Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end of the section you’ll decide which method was the most convenient way to solve this system.
Example 4.2
How to solve a system of equations by graphing.
Solve the system by graphing { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .
Solve the system by graphing: { x − 3 y = −3 x + y = 5 . { x − 3 y = −3 x + y = 5 .
Solve the system by graphing: { − x + y = 1 3 x + 2 y = 12 . { − x + y = 1 3 x + 2 y = 12 .
The steps to use to solve a system of linear equations by graphing are shown here.
Solve a system of linear equations by graphing.
- Step 1. Graph the first equation.
- Step 2. Graph the second equation on the same rectangular coordinate system.
- Step 3. Determine whether the lines intersect, are parallel, or are the same line.
- If the lines intersect, identify the point of intersection. This is the solution to the system.
- If the lines are parallel, the system has no solution.
- If the lines are the same, the system has an infinite number of solutions.
- Step 5. Check the solution in both equations.
In the next example, we’ll first re-write the equations into slope–intercept form as this will make it easy for us to quickly graph the lines.
Example 4.3
Solve the system by graphing: { 3 x + y = − 1 2 x + y = 0 . { 3 x + y = − 1 2 x + y = 0 .
We’ll solve both of these equations for y y so that we can easily graph them using their slopes and y -intercepts.
Solve the system by graphing: { − x + y = 1 2 x + y = 10 . { − x + y = 1 2 x + y = 10 .
Solve the system by graphing: { 2 x + y = 6 x + y = 1 . { 2 x + y = 6 x + y = 1 .
In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.
Example 4.4
Solve the system by graphing: { y = 1 2 x − 3 x − 2 y = 4 . { y = 1 2 x − 3 x − 2 y = 4 .
Solve the system by graphing: { y = − 1 4 x + 2 x + 4 y = − 8 . { y = − 1 4 x + 2 x + 4 y = − 8 .
Solve the system by graphing: { y = 3 x − 1 6 x − 2 y = 6 . { y = 3 x − 1 6 x − 2 y = 6 .
Sometimes the equations in a system represent the same line. Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. There are infinitely many solutions to the system.
Example 4.5
Solve the system by graphing: { y = 2 x − 3 − 6 x + 3 y = − 9 . { y = 2 x − 3 − 6 x + 3 y = − 9 .
If you write the second equation in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.
Solve the system by graphing: { y = − 3 x − 6 6 x + 2 y = − 12 . { y = − 3 x − 6 6 x + 2 y = − 12 .
Try It 4.10
Solve the system by graphing: { y = 1 2 x − 4 2 x − 4 y = 16 . { y = 1 2 x − 4 2 x − 4 y = 16 .
When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident . Coincident lines have the same slope and same y- intercept.
Coincident Lines
Coincident lines have the same slope and same y- intercept.
The systems of equations in Example 4.2 and Example 4.3 each had two intersecting lines. Each system had one solution.
In Example 4.5, the equations gave coincident lines, and so the system had infinitely many solutions.
The systems in those three examples had at least one solution. A system of equations that has at least one solution is called a consistent system.
A system with parallel lines, like Example 4.4, has no solution. We call a system of equations like this inconsistent. It has no solution.
Consistent and Inconsistent Systems
A consistent system of equations is a system of equations with at least one solution.
An inconsistent system of equations is a system of equations with no solution.
We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent, they each have their own set of solutions. Intersecting lines and parallel lines are independent.
If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines.
Let’s sum this up by looking at the graphs of the three types of systems. See below and Table 4.1.
Example 4.6
Without graphing, determine the number of solutions and then classify the system of equations.
ⓐ { y = 3 x − 1 6 x − 2 y = 12 { y = 3 x − 1 6 x − 2 y = 12 ⓑ { 2 x + y = − 3 x − 5 y = 5 { 2 x + y = − 3 x − 5 y = 5
ⓐ We will compare the slopes and intercepts of the two lines.
A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.
ⓑ We will compare the slope and intercepts of the two lines.
A system of equations whose graphs are intersect has 1 solution and is consistent and independent.
Try It 4.11
ⓐ { y = −2 x − 4 4 x + 2 y = 9 { y = −2 x − 4 4 x + 2 y = 9 ⓑ { 3 x + 2 y = 2 2 x + y = 1 { 3 x + 2 y = 2 2 x + y = 1
Try It 4.12
ⓐ { y = 1 3 x − 5 x − 3 y = 6 { y = 1 3 x − 5 x − 3 y = 6 ⓑ { x + 4 y = 12 − x + y = 3 { x + 4 y = 12 − x + y = 3
Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.
Solve a System of Equations by Substitution
We will now solve systems of linear equations by the substitution method.
We will use the same system we used first for graphing.
We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.
Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!
After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.
Example 4.7
How to solve a system of equations by substitution.
Solve the system by substitution: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .
Try It 4.13
Solve the system by substitution: { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 .
Try It 4.14
Solve the system by substitution: { 2 x + y = −1 4 x + 3 y = 3 . { 2 x + y = −1 4 x + 3 y = 3 .
Solve a system of equations by substitution.
- Step 1. Solve one of the equations for either variable.
- Step 2. Substitute the expression from Step 1 into the other equation.
- Step 3. Solve the resulting equation.
- Step 4. Substitute the solution in Step 3 into either of the original equations to find the other variable.
- Step 5. Write the solution as an ordered pair.
- Step 6. Check that the ordered pair is a solution to both original equations.
Be very careful with the signs in the next example.
Example 4.8
Solve the system by substitution: { 4 x + 2 y = 4 6 x − y = 8 . { 4 x + 2 y = 4 6 x − y = 8 .
We need to solve one equation for one variable. We will solve the first equation for y .
Try It 4.15
Solve the system by substitution: { x − 4 y = −4 − 3 x + 4 y = 0 . { x − 4 y = −4 − 3 x + 4 y = 0 .
Try It 4.16
Solve the system by substitution: { 4 x − y = 0 2 x − 3 y = 5 . { 4 x − y = 0 2 x − 3 y = 5 .
Solve a System of Equations by Elimination
We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.
The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.
The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.
For any expressions a, b, c, and d .
if a = b and c = d then a + c = b + d . if a = b and c = d then a + c = b + d .
To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.
Notice how that works when we add these two equations together:
{ 3 x + y = 5 2 x − y = 0 ————— 5 x = 5 { 3 x + y = 5 2 x − y = 0 ————— 5 x = 5
The y ’s add to zero and we have one equation with one variable.
Let’s try another one:
{ x + 4 y = 2 2 x + 5 y = −2 { x + 4 y = 2 2 x + 5 y = −2
This time we don’t see a variable that can be immediately eliminated if we add the equations.
But if we multiply the first equation by −2 , −2 , we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2 . −2 .
Then rewrite the system of equations.
Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.
Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.
Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.
Example 4.9
How to solve a system of equations by elimination.
Solve the system by elimination: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .
Try It 4.17
Solve the system by elimination: { 3 x + y = 5 2 x − 3 y = 7 . { 3 x + y = 5 2 x − 3 y = 7 .
Try It 4.18
Solve the system by elimination: { 4 x + y = − 5 − 2 x − 2 y = − 2 . { 4 x + y = − 5 − 2 x − 2 y = − 2 .
The steps are listed here for easy reference.
Solve a system of equations by elimination.
- Step 1. Write both equations in standard form. If any coefficients are fractions, clear them.
- Decide which variable you will eliminate.
- Multiply one or both equations so that the coefficients of that variable are opposites.
- Step 3. Add the equations resulting from Step 2 to eliminate one variable.
- Step 4. Solve for the remaining variable.
- Step 5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
- Step 6. Write the solution as an ordered pair.
- Step 7. Check that the ordered pair is a solution to both original equations.
Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.
Example 4.10
Solve the system by elimination: { 4 x − 3 y = 9 7 x + 2 y = −6 . { 4 x − 3 y = 9 7 x + 2 y = −6 .
In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by different constants to get the opposites.
Try It 4.19
Solve the system by elimination: { 3 x − 4 y = − 9 5 x + 3 y = 14 . { 3 x − 4 y = − 9 5 x + 3 y = 14 .
Try It 4.20
Solve each system by elimination: { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 .
When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by the LCD of all the fractions in the equation.
Example 4.11
Solve the system by elimination: { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 . { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 .
In this example, both equations have fractions. Our first step will be to multiply each equation by the LCD of all the fractions in the equation to clear the fractions.
Try It 4.21
Solve each system by elimination: { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 . { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 .
Try It 4.22
Solve each system by elimination: { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 . { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 .
When we solved the system by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.
The same is true using substitution or elimination. If the equation at the end of substitution or elimination is a true statement, we have a consistent but dependent system and the system of equations has infinitely many solutions. If the equation at the end of substitution or elimination is a false statement, we have an inconsistent system and the system of equations has no solution.
Example 4.12
Solve the system by elimination: { 3 x + 4 y = 12 y = 3 − 3 4 x . { 3 x + 4 y = 12 y = 3 − 3 4 x .
This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.
After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.
Try It 4.23
Solve the system by elimination: { 5 x − 3 y = 15 y = − 5 + 5 3 x . { 5 x − 3 y = 15 y = − 5 + 5 3 x .
Try It 4.24
Solve the system by elimination: { x + 2 y = 6 y = − 1 2 x + 3 . { x + 2 y = 6 y = − 1 2 x + 3 .
Choose the Most Convenient Method to Solve a System of Linear Equations
When you solve a system of linear equations in in an application, you will not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.
Choose the Most Convenient Method to Solve a System of Linear Equations Graphing ———— Substitution ————— Elimination ————— Use when you need a Use when one equation is Use when the equations are picture of the situation. already solved or can be in standard form. easily solved for one variable. Choose the Most Convenient Method to Solve a System of Linear Equations Graphing ———— Substitution ————— Elimination ————— Use when you need a Use when one equation is Use when the equations are picture of the situation. already solved or can be in standard form. easily solved for one variable.
Example 4.13
For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
ⓐ { 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32 ⓑ { 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1
{ 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32
Since both equations are in standard form, using elimination will be most convenient.
{ 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1
Since one equation is already solved for y , using substitution will be most convenient.
Try It 4.25
For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
ⓐ { 4 x − 5 y = −32 3 x + 2 y = −1 { 4 x − 5 y = −32 3 x + 2 y = −1 ⓑ { x = 2 y − 1 3 x − 5 y = −7 { x = 2 y − 1 3 x − 5 y = −7
Try It 4.26
ⓐ { y = 2 x − 1 3 x − 4 y = − 6 { y = 2 x − 1 3 x − 4 y = − 6 ⓑ { 6 x − 2 y = 12 3 x + 7 y = −13 { 6 x − 2 y = 12 3 x + 7 y = −13
Section 4.1 Exercises
Practice makes perfect.
In the following exercises, determine if the following points are solutions to the given system of equations.
{ 2 x − 6 y = 0 3 x − 4 y = 5 { 2 x − 6 y = 0 3 x − 4 y = 5
ⓐ ( 3 , 1 ) ( 3 , 1 ) ⓑ ( −3 , 4 ) ( −3 , 4 )
{ − 3 x + y = 8 − x + 2 y = −9 { − 3 x + y = 8 − x + 2 y = −9
ⓐ ( −5 , −7 ) ( −5 , −7 ) ⓑ ( −5 , 7 ) ( −5 , 7 )
{ x + y = 2 y = 3 4 x { x + y = 2 y = 3 4 x
ⓐ ( 8 7 , 6 7 ) ( 8 7 , 6 7 ) ⓑ ( 1 , 3 4 ) ( 1 , 3 4 )
{ 2 x + 3 y = 6 y = 2 3 x + 2 { 2 x + 3 y = 6 y = 2 3 x + 2 ⓐ ( −6 , 2 ) ( −6 , 2 ) ⓑ ( −3 , 4 ) ( −3 , 4 )
In the following exercises, solve the following systems of equations by graphing.
{ 3 x + y = −3 2 x + 3 y = 5 { 3 x + y = −3 2 x + 3 y = 5
{ − x + y = 2 2 x + y = −4 { − x + y = 2 2 x + y = −4
{ y = x + 2 y = −2 x + 2 { y = x + 2 y = −2 x + 2
{ y = x − 2 y = −3 x + 2 { y = x − 2 y = −3 x + 2
{ y = 3 2 x + 1 y = − 1 2 x + 5 { y = 3 2 x + 1 y = − 1 2 x + 5
{ y = 2 3 x − 2 y = − 1 3 x − 5 { y = 2 3 x − 2 y = − 1 3 x − 5
{ x + y = −4 − x + 2 y = −2 { x + y = −4 − x + 2 y = −2
{ − x + 3 y = 3 x + 3 y = 3 { − x + 3 y = 3 x + 3 y = 3
{ − 2 x + 3 y = 3 x + 3 y = 12 { − 2 x + 3 y = 3 x + 3 y = 12
{ 2 x − y = 4 2 x + 3 y = 12 { 2 x − y = 4 2 x + 3 y = 12
{ x + 3 y = −6 y = − 4 3 x + 4 { x + 3 y = −6 y = − 4 3 x + 4
{ − x + 2 y = −6 y = − 1 2 x − 1 { − x + 2 y = −6 y = − 1 2 x − 1
{ − 2 x + 4 y = 4 y = 1 2 x { − 2 x + 4 y = 4 y = 1 2 x
{ 3 x + 5 y = 10 y = − 3 5 x + 1 { 3 x + 5 y = 10 y = − 3 5 x + 1
{ 4 x − 3 y = 8 8 x − 6 y = 14 { 4 x − 3 y = 8 8 x − 6 y = 14
{ x + 3 y = 4 − 2 x − 6 y = 3 { x + 3 y = 4 − 2 x − 6 y = 3
{ x = −3 y + 4 2 x + 6 y = 8 { x = −3 y + 4 2 x + 6 y = 8
{ 4 x = 3 y + 7 8 x − 6 y = 14 { 4 x = 3 y + 7 8 x − 6 y = 14
{ 2 x + y = 6 − 8 x − 4 y = −24 { 2 x + y = 6 − 8 x − 4 y = −24
{ 5 x + 2 y = 7 − 10 x − 4 y = −14 { 5 x + 2 y = 7 − 10 x − 4 y = −14
{ y = 2 3 x + 1 − 2 x + 3 y = 5 { y = 2 3 x + 1 − 2 x + 3 y = 5
{ y = 3 2 x + 1 2 x − 3 y = 7 { y = 3 2 x + 1 2 x − 3 y = 7
{ 5 x + 3 y = 4 2 x − 3 y = 5 { 5 x + 3 y = 4 2 x − 3 y = 5
{ y = − 1 2 x + 5 x + 2 y = 10 { y = − 1 2 x + 5 x + 2 y = 10
{ 5 x − 2 y = 10 y = 5 2 x − 5 { 5 x − 2 y = 10 y = 5 2 x − 5
In the following exercises, solve the systems of equations by substitution.
{ 2 x + y = −4 3 x − 2 y = −6 { 2 x + y = −4 3 x − 2 y = −6
{ 2 x + y = −2 3 x − y = 7 { 2 x + y = −2 3 x − y = 7
{ x − 2 y = −5 2 x − 3 y = −4 { x − 2 y = −5 2 x − 3 y = −4
{ x − 3 y = −9 2 x + 5 y = 4 { x − 3 y = −9 2 x + 5 y = 4
{ 5 x − 2 y = −6 y = 3 x + 3 { 5 x − 2 y = −6 y = 3 x + 3
{ − 2 x + 2 y = 6 y = −3 x + 1 { − 2 x + 2 y = 6 y = −3 x + 1
{ 2 x + 5 y = 1 y = 1 3 x − 2 { 2 x + 5 y = 1 y = 1 3 x − 2
{ 3 x + 4 y = 1 y = − 2 5 x + 2 { 3 x + 4 y = 1 y = − 2 5 x + 2
{ 2 x + y = 5 x − 2 y = −15 { 2 x + y = 5 x − 2 y = −15
{ 4 x + y = 10 x − 2 y = −20 { 4 x + y = 10 x − 2 y = −20
{ y = −2 x − 1 y = − 1 3 x + 4 { y = −2 x − 1 y = − 1 3 x + 4
{ y = x − 6 y = − 3 2 x + 4 { y = x − 6 y = − 3 2 x + 4
{ x = 2 y 4 x − 8 y = 0 { x = 2 y 4 x − 8 y = 0
{ 2 x − 16 y = 8 − x − 8 y = −4 { 2 x − 16 y = 8 − x − 8 y = −4
{ y = 7 8 x + 4 − 7 x + 8 y = 6 { y = 7 8 x + 4 − 7 x + 8 y = 6
{ y = − 2 3 x + 5 2 x + 3 y = 11 { y = − 2 3 x + 5 2 x + 3 y = 11
In the following exercises, solve the systems of equations by elimination.
{ 5 x + 2 y = 2 − 3 x − y = 0 { 5 x + 2 y = 2 − 3 x − y = 0
{ 6 x − 5 y = −1 2 x + y = 13 { 6 x − 5 y = −1 2 x + y = 13
{ 2 x − 5 y = 7 3 x − y = 17 { 2 x − 5 y = 7 3 x − y = 17
{ 5 x − 3 y = −1 2 x − y = 2 { 5 x − 3 y = −1 2 x − y = 2
{ 3 x − 5 y = −9 5 x + 2 y = 16 { 3 x − 5 y = −9 5 x + 2 y = 16
{ 4 x − 3 y = 3 2 x + 5 y = −31 { 4 x − 3 y = 3 2 x + 5 y = −31
{ 3 x + 8 y = −3 2 x + 5 y = −3 { 3 x + 8 y = −3 2 x + 5 y = −3
{ 11 x + 9 y = −5 7 x + 5 y = −1 { 11 x + 9 y = −5 7 x + 5 y = −1
{ 3 x + 8 y = 67 5 x + 3 y = 60 { 3 x + 8 y = 67 5 x + 3 y = 60
{ 2 x + 9 y = −4 3 x + 13 y = −7 { 2 x + 9 y = −4 3 x + 13 y = −7
{ 1 3 x − y = −3 x + 5 2 y = 2 { 1 3 x − y = −3 x + 5 2 y = 2
{ x + 1 2 y = 3 2 1 5 x − 1 5 y = 3 { x + 1 2 y = 3 2 1 5 x − 1 5 y = 3
{ x + 1 3 y = −1 1 3 x + 1 2 y = 1 { x + 1 3 y = −1 1 3 x + 1 2 y = 1
{ 1 3 x − y = −3 2 3 x + 5 2 y = 3 { 1 3 x − y = −3 2 3 x + 5 2 y = 3
{ 2 x + y = 3 6 x + 3 y = 9 { 2 x + y = 3 6 x + 3 y = 9
{ x − 4 y = −1 − 3 x + 12 y = 3 { x − 4 y = −1 − 3 x + 12 y = 3
{ − 3 x − y = 8 6 x + 2 y = −16 { − 3 x − y = 8 6 x + 2 y = −16
{ 4 x + 3 y = 2 20 x + 15 y = 10 { 4 x + 3 y = 2 20 x + 15 y = 10
In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.
ⓐ { 8 x − 15 y = −32 6 x + 3 y = −5 { 8 x − 15 y = −32 6 x + 3 y = −5 ⓑ { x = 4 y − 3 4 x − 2 y = −6 { x = 4 y − 3 4 x − 2 y = −6
ⓐ { y = 7 x − 5 3 x − 2 y = 16 { y = 7 x − 5 3 x − 2 y = 16 ⓑ { 12 x − 5 y = −42 3 x + 7 y = −15 { 12 x − 5 y = −42 3 x + 7 y = −15
ⓐ { y = 4 x + 9 5 x − 2 y = −21 { y = 4 x + 9 5 x − 2 y = −21 ⓑ { 9 x − 4 y = 24 3 x + 5 y = −14 { 9 x − 4 y = 24 3 x + 5 y = −14
ⓐ { 14 x − 15 y = −30 7 x + 2 y = 10 { 14 x − 15 y = −30 7 x + 2 y = 10 ⓑ { x = 9 y − 11 2 x − 7 y = −27 { x = 9 y − 11 2 x − 7 y = −27
Writing Exercises
In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.
Solve the system of equations by substitution and explain all your steps in words: { 3 x + y = 12 x = y − 8 . { 3 x + y = 12 x = y − 8 .
Solve the system of equations by elimination and explain all your steps in words: { 5 x + 4 y = 10 2 x = 3 y + 27 . { 5 x + 4 y = 10 2 x = 3 y + 27 .
Solve the system of equations { x + y = 10 x − y = 6 { x + y = 10 x − y = 6
ⓐ by graphing ⓑ by substitution ⓒ Which method do you prefer? Why?
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
- Math Articles
- Linear equations in two variables
Solving a system of two linear equations
Solving a system of linear equations by substitution.
The substitution method involves substituting an expression for one variable in terms of the other in another equation of a system. For example, to solve the system
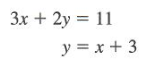
by substitution, replace y in the first equation
noticing that parentheses are required. Then solve this equation for x.
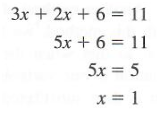
Replace x with 1 in y = x + 3 to find that y = 1 + 3 = 4. The solution set for this system is {(1, 4)}.
Solve the system
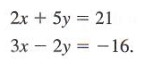
Begin by solving one equation for one of the variables in terms of the other. For example, solving the first equation for x gives :
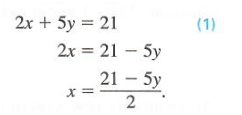
Now substitute this result for x into equation (2).
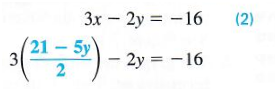
To eliminate the fraction on the left, multiply both sides of the equation by 2 and then solve for y.

Substitute y = 5 back into equation (3) to find x
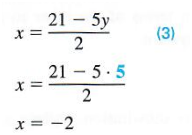
The solution set for the system is ((-2, 5)}. Check by substituting -2 for x and 5 for y in each of the equations of the system.
Solving a system of linear equations by addition
Another method of solving systems of two equations is the addition method. With this method, we first multiply the equations on both sides by suitable numbers, so that when they are added, one variable is eliminated. The result is an equation in one variable that can be solved by methods used for linear equations. The solution is then substituted into one of the original equations, making it possible to solve for the other variable. In this process the given system is replaced by new systems that have the same solution set as the original system. Systems that have the same solution set are called equivalent systems. The addition method is illustrated by the following examples.

eliminate x, multiply both sides of equation (4) by -2 and both sides of equation (S) by 3 to get equations (6) and (7).

Although this new system is not the same as the given system, it will have the same solution set.
Now add the two equations to eliminate x, and then solve the result for y.
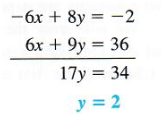
Substitute 2 for yin equation (4) or (5). Choosing equation (4) gives
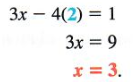
The solution set of the given system is { (3, 2)}, which can be checked by substituting 3 for x and 2 for y in equation (5).
Since the addition method of solution results in the elimination of one variable from the system, it is also called the elimination method.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions
[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Solving equations
Here you will learn about solving equations, including linear and quadratic algebraic equations, and how to solve them.
Students will first learn about solving equations in grade 8 as a part of expressions and equations, and again in high school as a part of reasoning with equations and inequalities.
What is solving an equation?
Solving equations is a step-by-step process to find the value of the variable. A variable is the unknown part of an equation, either on the left or right side of the equals sign. Sometimes, you need to solve multi-step equations which contain algebraic expressions.
To do this, you must use the order of operations, which is a systematic approach to equation solving. When you use the order of operations, you first solve any part of an equation located within parentheses. An equation is a mathematical expression that contains an equals sign.
For example,
\begin{aligned}y+6&=11\\\\ 3(x-3)&=12\\\\ \cfrac{2x+2}{4}&=\cfrac{x-3}{3}\\\\ 2x^{2}+3&x-2=0\end{aligned}
There are two sides to an equation, with the left side being equal to the right side. Equations will often involve algebra and contain unknowns, or variables, which you often represent with letters such as x or y.
You can solve simple equations and more complicated equations to work out the value of these unknowns. They could involve fractions, decimals or integers.

Common Core State Standards
How does this relate to 8 th grade and high school math?
- Grade 8 – Expressions and Equations (8.EE.C.7) Solve linear equations in one variable.
- High school – Reasoning with Equations and Inequalities (HSA.REI.B.3) Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
![how to solve 2 equations with x and y [FREE] Solving Equations Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/03/Solving-Equations-Worksheet-listing-image.png)
[FREE] Solving Equations Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of solving equations. 15 questions with answers to identify areas of strength and support!
How to solve equations
In order to solve equations, you need to work out the value of the unknown variable by adding, subtracting, multiplying or dividing both sides of the equation by the same value.
- Combine like terms .
- Simplify the equation by using the opposite operation to both sides.
- Isolate the variable on one side of the equation.
Solving equations examples
Example 1: solve equations involving like terms.
Solve for x.
Combine like terms.
Combine the q terms on the left side of the equation. To do this, subtract 4q from both sides.
The goal is to simplify the equation by combining like terms. Subtracting 4q from both sides helps achieve this.
After you combine like terms, you are left with q=9-4q.
2 Simplify the equation by using the opposite operation on both sides.
Add 4q to both sides to isolate q to one side of the equation.
The objective is to have all the q terms on one side. Adding 4q to both sides accomplishes this.
After you move the variable to one side of the equation, you are left with 5q=9.
3 Isolate the variable on one side of the equation.
Divide both sides of the equation by 5 to solve for q.
Dividing by 5 allows you to isolate q to one side of the equation in order to find the solution. After dividing both sides of the equation by 5, you are left with q=1 \cfrac{4}{5} \, .
Example 2: solve equations with variables on both sides
Combine the v terms on the same side of the equation. To do this, add 8v to both sides.
7v+8v=8-8v+8v
After combining like terms, you are left with the equation 15v=8.
Simplify the equation by using the opposite operation on both sides and isolate the variable to one side.
Divide both sides of the equation by 15 to solve for v. This step will isolate v to one side of the equation and allow you to solve.
15v \div 15=8 \div 15
The final solution to the equation 7v=8-8v is \cfrac{8}{15} \, .
Example 3: solve equations with the distributive property
Combine like terms by using the distributive property.
The 3 outside the parentheses needs to be multiplied by both terms inside the parentheses. This is called the distributive property.
\begin{aligned}& 3 \times c=3 c \\\\ & 3 \times(-5)=-15 \\\\ &3 c-15-4=2\end{aligned}
Once the 3 is distributed on the left side, rewrite the equation and combine like terms. In this case, the like terms are the constants on the left, –15 and –4. Subtract –4 from –15 to get –19.
Simplify the equation by using the opposite operation on both sides.
The goal is to isolate the variable, c, on one side of the equation. By adding 19 to both sides, you move the constant term to the other side.
\begin{aligned}& 3 c-19+19=2+19 \\\\ & 3 c=21\end{aligned}
Isolate the variable to one side of the equation.
To solve for c, you want to get c by itself.
Dividing both sides by 3 accomplishes this.
On the left side, \cfrac{3c}{3} simplifies to c, and on the right, \cfrac{21}{3} simplifies to 7.
The final solution is c=7.
As an additional step, you can plug 7 back into the original equation to check your work.
Example 4: solve linear equations
Combine like terms by simplifying.
Using steps to solve, you know that the goal is to isolate x to one side of the equation. In order to do this, you must begin by subtracting from both sides of the equation.
\begin{aligned} & 2x+5=15 \\\\ & 2x+5-5=15-5 \\\\ & 2x=10 \end{aligned}
Continue to simplify the equation by using the opposite operation on both sides.
Continuing with steps to solve, you must divide both sides of the equation by 2 to isolate x to one side.
\begin{aligned} & 2x \div 2=10 \div 2 \\\\ & x= 5 \end{aligned}
Isolate the variable to one side of the equation and check your work.
Plugging in 5 for x in the original equation and making sure both sides are equal is an easy way to check your work. If the equation is not equal, you must check your steps.
\begin{aligned}& 2(5)+5=15 \\\\ & 10+5=15 \\\\ & 15=15\end{aligned}
Example 5: solve equations by factoring
Solve the following equation by factoring.
Combine like terms by factoring the equation by grouping.
Multiply the coefficient of the quadratic term by the constant term.
2 x (-20) = -40
Look for two numbers that multiply to give you –40 and add up to the coefficient of 3. In this case, the numbers are 8 and –5 because 8 x -5=–40, and 8+–5=3.
Split the middle term using those two numbers, 8 and –5. Rewrite the middle term using the numbers 8 and –5.
2x^2+8x-5x-20=0
Group the terms in pairs and factor out the common factors.
2x^2+8x-5x-20=2x(x + 4)-5(x+4)=0
Now, you’ve factored the equation and are left with the following simpler equations 2x-5 and x+4.
This step relies on understanding the zero product property, which states that if two numbers multiply to give zero, then at least one of those numbers must equal zero.
Let’s relate this back to the factored equation (2x-5)(x+4)=0
Because of this property, either (2x-5)=0 or (x+4)=0
Isolate the variable for each equation and solve.
When solving these simpler equations, remember that you must apply each step to both sides of the equation to maintain balance.
\begin{aligned}& 2 x-5=0 \\\\ & 2 x-5+5=0+5 \\\\ & 2 x=5 \\\\ & 2 x \div 2=5 \div 2 \\\\ & x=\cfrac{5}{2} \end{aligned}
\begin{aligned}& x+4=0 \\\\ & x+4-4=0-4 \\\\ & x=-4\end{aligned}
The solution to this equation is x=\cfrac{5}{2} and x=-4.
Example 6: solve quadratic equations
Solve the following quadratic equation.
Combine like terms by factoring the quadratic equation when terms are isolated to one side.
To factorize a quadratic expression like this, you need to find two numbers that multiply to give -5 (the constant term) and add to give +2 (the coefficient of the x term).
The two numbers that satisfy this are -1 and +5.
So you can split the middle term 2x into -1x+5x: x^2-1x+5x-5-1x+5x
Now you can take out common factors x(x-1)+5(x-1).
And since you have a common factor of (x-1), you can simplify to (x+5)(x-1).
The numbers -1 and 5 allow you to split the middle term into two terms that give you common factors, allowing you to simplify into the form (x+5)(x-1).
Let’s relate this back to the factored equation (x+5)(x-1)=0.
Because of this property, either (x+5)=0 or (x-1)=0.
Now, you can solve the simple equations resulting from the zero product property.
\begin{aligned}& x+5=0 \\\\ & x+5-5=0-5 \\\\ & x=-5 \\\\\\ & x-1=0 \\\\ & x-1+1=0+1 \\\\ & x=1\end{aligned}
The solutions to this quadratic equation are x=1 and x=-5.
Teaching tips for solving equations
- Use physical manipulatives like balance scales as a visual aid. Show how you need to keep both sides of the equation balanced, like a scale. Add or subtract the same thing from both sides to keep it balanced when solving. Use this method to practice various types of equations.
- Emphasize the importance of undoing steps to isolate the variable. If you are solving for x and 3 is added to x, subtracting 3 undoes that step and isolates the variable x.
- Relate equations to real-world, relevant examples for students. For example, word problems about tickets for sports games, cell phone plans, pizza parties, etc. can make the concepts click better.
- Allow time for peer teaching and collaborative problem solving. Having students explain concepts to each other, work through examples on whiteboards, etc. reinforces the process and allows peers to ask clarifying questions. This type of scaffolding would be beneficial for all students, especially English-Language Learners. Provide supervision and feedback during the peer interactions.
Easy mistakes to make
- Forgetting to distribute or combine like terms One common mistake is neglecting to distribute a number across parentheses or combine like terms before isolating the variable. This error can lead to an incorrect simplified form of the equation.
- Misapplying the distributive property Incorrectly distributing a number across terms inside parentheses can result in errors. Students may forget to multiply each term within the parentheses by the distributing number, leading to an inaccurate equation.
- Failing to perform the same operation on both sides It’s crucial to perform the same operation on both sides of the equation to maintain balance. Forgetting this can result in an imbalanced equation and incorrect solutions.
- Making calculation errors Simple arithmetic mistakes, such as addition, subtraction, multiplication, or division errors, can occur during the solution process. Checking calculations is essential to avoid errors that may propagate through the steps.
- Ignoring fractions or misapplying operations When fractions are involved, students may forget to multiply or divide by the common denominator to eliminate them. Misapplying operations on fractions can lead to incorrect solutions or complications in the final answer.
Related math equations lessons
- Math equations
- Rearranging equations
- How to find the equation of a line
- Solve equations with fractions
- Linear equations
- Writing linear equations
- Substitution
- Identity math
- One step equation
Practice solving equations questions
1. Solve 4x-2=14.

Add 2 to both sides.
Divide both sides by 4.
2. Solve 3x-8=x+6.
Add 8 to both sides.
Subtract x from both sides.
Divide both sides by 2.
3. Solve 3(x+3)=2(x-2).
Expanding the parentheses.
Subtract 9 from both sides.
Subtract 2x from both sides.
4. Solve \cfrac{2 x+2}{3}=\cfrac{x-3}{2}.
Multiply by 6 (the lowest common denominator) and simplify.
Expand the parentheses.
Subtract 4 from both sides.
Subtract 3x from both sides.
5. Solve \cfrac{3 x^{2}}{2}=24.
Multiply both sides by 2.
Divide both sides by 3.
Square root both sides.
6. Solve by factoring:
Use factoring to find simpler equations.
Set each set of parentheses equal to zero and solve.
x=3 or x=10
Solving equations FAQs
The first step in solving a simple linear equation is to simplify both sides by combining like terms. This involves adding or subtracting terms to isolate the variable on one side of the equation.
Performing the same operation on both sides of the equation maintains the equality. This ensures that any change made to one side is also made to the other, keeping the equation balanced and preserving the solutions.
To handle variables on both sides of the equation, start by combining like terms on each side. Then, move all terms involving the variable to one side by adding or subtracting, and simplify to isolate the variable. Finally, perform any necessary operations to solve for the variable.
To deal with fractions in an equation, aim to eliminate them by multiplying both sides of the equation by the least common denominator. This helps simplify the equation and make it easier to isolate the variable. Afterward, proceed with the regular steps of solving the equation.
The next lessons are
- Inequalities
- Types of graph
- Coordinate plane
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview

Online Systems of Equations Solver
Solve equations and systems of equations with wolfram|alpha, a powerful tool for finding solutions to systems of equations and constraints.
Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.
Learn more about:
- Systems of equations
Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.
- solve y = 2x, y = x + 10
- solve system of equations {y = 2x, y = x + 10, 2x = 5y}
- y = x^2 - 2, y = 2 - x^2
- solve 4x - 3y + z = -10, 2x + y + 3z = 0, -x + 2y - 5z = 17
- solve system {x + 2y - z = 4, 2x + y + z = -2, z + 2y + z = 2}
- solve 4 = x^2 + y^2, 4 = (x - 2)^2 + (y - 2)^2
- x^2 + y^2 = 4, y = x
- View more examples
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
- Step-by-step solutions
- Wolfram Problem Generator
What are systems of equations?
A system of equations is a set of one or more equations involving a number of variables..
The solutions to systems of equations are the variable mappings such that all component equations are satisfied—in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.
Systems of linear equations are a common and applicable subset of systems of equations. In the case of two variables, these systems can be thought of as lines drawn in two-dimensional space. If all lines converge to a common point, the system is said to be consistent and has a solution at this point of intersection. The system is said to be inconsistent otherwise, having no solutions. Systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).
More general systems involving nonlinear functions are possible as well. These possess more complicated solution sets involving one, zero, infinite or any number of solutions, but work similarly to linear systems in that their solutions are the points satisfying all equations involved. Going further, more general systems of constraints are possible, such as ones that involve inequalities or have requirements that certain variables be integers.
Solving systems of equations is a very general and important idea, and one that is fundamental in many areas of mathematics, engineering and science.
Equation Solver
What do you want to calculate.
- Solve for Variable
- Practice Mode
- Step-By-Step
Solver Title
Generating PDF...
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- Pre Calculus
- Basic (Linear)
- Biquadratic
- Logarithmic
- Exponential
- Solve For x
- Scientific Calculator
- Scientific Notation Arithmetics
- Complex Numbers
- Cartesian to Polar
- Polar to Cartesian
- System of Inequalities
- Partial Fractions
- Periodicity
- Y Intercept
- X Intercepts
- Point Slope Form
- Step Functions
- Arithmetics
- Start Point
- Area & Perimeter
- Sides & Angles
- Law of Sines
- Law of Cosines
- Width & Length
- Volume & Surface
- Edges & Diagonal
- Volume & Radius
- Surface Area
- Radius & Diameter
- Volume & Height
- Circumference
- Eccentricity
- Trigonometric Equations
- Evaluate Functions
- Linear Algebra
- Trigonometry
- Conversions

Most Used Actions
Number line.
- x+y+z=25,\:5x+3y+2z=0,\:y-z=6
- x+2y=2x-5,\:x-y=3
- 5x+3y=7,\:3x-5y=-23
- x^2+y=5,\:x^2+y^2=7
- xy+x-4y=11,\:xy-x-4y=4
- 3-x^2=y,\:x+1=y
- xy=10,\:2x+y=1
- substitution\:x+2y=2x-5,\:x-y=3
- elimination\:x+2y=2x-5,\:x-y=3
- How to solve linear Simultaneous equations with two variables by graphing?
- To solve linear simultaneous equations with two variables by graphing, plot both equations on the same set of axes. The coordinates of the points at which the two lines intersect are the solutions to the system.
- What are Simultaneous Equations?
- Simultaneous equations are a set of equations that are solved at the same time. These equations are used to define the relationships between variables and can have multiple solutions, a single solution, or no solution.
- What are Simultaneous Equations used for?
- Simultaneous equations can be used to solve a wide range of problems in finance, science, engineering, and other fields. They are often used to find the values of variables that make multiple equations or expressions true at the same time.
- What are the methods for solving Simultaneous Equations?
- The common methods for solving simultaneous equations are Graphing, Substitution, and Elimination. The choice of method depends on the specific equations and the desired solution.
simultaneous-equations-calculator
- Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations. Symbolab math solutions...
Please add a message.
Message received. Thanks for the feedback.
- PRE-ALGEBRA
- MORE MATH FINANCE BUSINESS ENGINEERING FINANCE CHARTS MATH WORKSHEETS CURRENCY CONVERTER MULTIPLICATION TABLES DEPRECIATION SPORTS CALCULATORS HEALTH equations tricks history notes register login

- Engineering
Find the Value of X and Y Calculator
Find the value of X and Y calculator to find the 2 unknown variables X and Y in a set of 2 equations. Each equation has containing the unknown variables X and Y. This 2 equations 2 unknown solver computes the output value of the variables X and Y with respect to the input values of X and Y coefficients. In mathematic calculations, there are many situation arises where the usage of equation containing 2 unknown variables need to be solved prior to go further with the calculations. Therefore when it comes to online calculation, this Find the value of X and Y calculator is an essential tool to assist you to find out the variable values given in the equation.
- Quadratic Equation Calculator
- (A + B)^n and (A-B)^n Formulas
- Unknown Value of X, Y & Z Calculator
- Radical Equation Calculator
- Polynomial Equations Addition Calculator
- Vertex Calculator
- Adding Complex Numbers Calculator
- Complex Numbers Subtraction Calculator
- Complex Numbers Multiplication Calculator
- Complex Numbers Division Calculator
- Vectors Addition Calculator
- Vector Subtraction Calculator
Solve for x Calculator
Enter the Equation you want to solve into the editor.
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&

IMAGES
VIDEO
COMMENTS
2. Divide both sides of the equation to "solve for x." Once you have the x term (or whichever variable you are using) on one side of the equation, divide both sides of the equation to get the variable alone. [3] For example: 4x = 8 - 2y. (4x)/4 = (8/4) - (2y/4) x = 2 - ½y. 3. Plug this back into the other equation.
Algebra. Equation Solver. Step 1: Enter the Equation you want to solve into the editor. The equation calculator allows you to take a simple or complex equation and solve by best method possible. Step 2: Click the blue arrow to submit and see the result! The equation solver allows you to enter your problem and solve the equation to see the result.
To isolate y, first subtract 2x from both sides (4y = -2x + 100), then divide by 4 (y = -1/2 x + 25). This is the more common usage because this is a linear function in slope intercept form - y in terms of x or y dependent on x. To solve for x, subtract 4y from both sides (2x = - 4y + 100), then divide by 2 (x = - 2y + 50).
Subtract 3x from each side to get "y = 2 - 3x". Plug in the y value found from the first equation in to the second equation in order to find the x value. In the previous example, this means the second equation becomes "x + 5 (2- 3x) = 20". Solve for x. The example equation becomes "x + 10 - 15x = 20," which is then "-14 x + 10 = 20."
The (x,y) values at the point of intersection give the solution for these linear equations. Let us take two linear equations and solve them using the graphical method. x + y = 8 -----(1) y = x + 2 -----(2) Let us take some values for 'x' and find the values for 'y' for the equation x + y = 8. This can also be rewritten as y = 8 - x.
The reason both (-5,-8) and (5,8) are solutions to this equation is because they show up on the equation's line. Sal later says the (simplified) equation for the question is y=8x/5. To make this answer more clear, another equation, such as y=x-3, when x=-5, y is equal to -8, but when x equals 5, y equals 2. Hope this helps.
To solve a system of equations by elimination, write the system of equations in standard form: ax + by = c, and multiply one or both of the equations by a constant so that the coefficients of one of the variables are opposite. Then, add or subtract the two equations to eliminate one of the variables.
In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do. Here are some things we can do: Add or Subtract the same value from both sides; Clear out any fractions by Multiplying every term by the bottom parts; Divide every term by the same nonzero value; Combine Like Terms; Factoring
Try It 4.6. Solve the system by graphing: {2x + y = 6 x + y = 1. In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we'll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.
An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations. {2x + y = 7 x − 2y = 6. A linear equation in two variables, such as 2x + y = 7, has an infinite number of solutions. Its graph is a line.
For example, solving the first equation for x gives : Now substitute this result for x into equation (2). To eliminate the fraction on the left, multiply both sides of the equation by 2 and then solve for y. Substitute y = 5 back into equation (3) to find x. The solution set for the system is ( (-2, 5)}. Check by substituting -2 for x and 5 for ...
Free equations calculator - solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. Type in any equation to get the solution, steps and graph ... This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
Equation solving; Tips for entering queries. Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to formulate queries. find roots to quadratic x^2-7x+12; plot inequality x^2-7x+12<=0; solve {3x-5y==2,x+2y==-1} plot inequality 3x-5y>=2 and x+2y<=-1
Get the free "Two Equation System Solver" widget for your website, blog, Wordpress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha.
👉 Learn how to solve literal equations. A literal equation is an equation where the unknown values are represented by variables. To solve a literal equation...
Example 1: solve equations involving like terms. Solve for x. x. 5q-4q=9 5q −4q = 9. Combine like terms. Combine the q q terms on the left side of the equation. To do this, subtract 4q 4q from both sides. (5 q-4 q)=9-4 q (5q −4q) = 9− 4q. The goal is to simplify the equation by combining like terms.
Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.
To solve your equation using the Equation Solver, type in your equation like x+4=5. The solver will then show you the steps to help you learn how to solve it on your own. Solving Equations Video Lessons. Solving Simple Equations; Need more problem types? Try MathPapa Algebra Calculator. ...
The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require. The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
To solve linear simultaneous equations with two variables by graphing, plot both equations on the same set of axes. The coordinates of the points at which the two lines intersect are the solutions to the system.
Each equation has containing the unknown variables X and Y. This 2 equations 2 unknown solver computes the output value of the variables X and Y with respect to the input values of X and Y coefficients. In mathematic calculations, there are many situation arises where the usage of equation containing 2 unknown variables need to be solved prior ...
In this video we'll draw the graph for x + y = 2.First, we will use a table of values to plot points on the graph. Once we have two or three points, we can d...
Step 1: Enter the Equation you want to solve into the editor. The equation calculator allows you to take a simple or complex equation and solve by best method possible. Step 2: Click the blue arrow to submit and see the result! The solve for x calculator allows you to enter your problem and solve the equation to see the result.