how to solve a terminating decimal problem

Terminating Decimals

Terminating decimals are the numbers that have a fixed or a finite number of digits after the decimal point. Decimal numbers are used to represent the partial amount of whole, just like fractions. In this lesson, we will focus on the type of decimal numbers, that is, terminating decimal numbers. The word 'terminate' means to bring to an end. In terms of decimal, it is a number that ends. In this article, we will learn what are terminating decimals and the ways to recognize these numbers.

Terminating Decimal Definition

The number which has a finite number of digits after the decimal point is referred to as a terminating decimal. Decimals are used to express the whole number and fraction together that is separated from each other by inserting a "." i.e. a decimal point. For example, 10.4, 10 is the whole number and 4 is the decimal fraction. There are different categories of decimals depending on what type of digits occur after the decimal point, they are:

• Terminating decimal expansion
• Non-terminating recurring decimal expansion
• Non-terminating non-recurring decimal expansion

A number has a terminating decimal expansion if the digits after the decimal point terminate or are finite. The fraction 5/10 has the decimal expansion of 0.5, which is a terminating decimal expansion because digits after the decimal point end after one digit. A rational number has either a terminating decimal expansion or a non-terminating recurring decimal expansion. For example, 23.5 is a terminating decimal number because it has 1 digit after the decimal point.

How to Recognize a Terminating Decimal?

Here are a few points that will help you to recognize a terminating decimal number.

• A number that is not rational is never a terminating decimal number.
• If you can express the denominator of a simplified rational number in the form 2 p 5 q or 2 p or 5 q , where p, q ∈ N, then the number has a terminating decimal expansion.
• A terminating decimal number always has a finite number of digits after the decimal point.

Terminating Decimals Examples

To differentiate whether a given decimal is terminating or non-terminating decimal, it is necessary to understand their basic differences like:

• Terminating decimal has finite digits and non-terminating decimals do not have finite digits.
• It is easy to represent a terminating decimal in the form of p/q but it is difficult to express a non-terminating decimal (non-repeating) in p/q form, where q is not equal to 0.

The table given below shows examples which will help you in identifying terminating decimals better.

Tips to Remember

• Terminating decimal numbers has a finite number of digits after the decimal point.
• A number with a terminating decimal is always a rational number.
• If the denominator of a rational number can be expressed in form 2 p 5 q or 2 p or 5 q , where p,q∈N, then the decimal expansion of the rational number terminates.
• If the denominator of a rational number cannot be expressed in form 2 p 5 q or 2 p or 5 q , where p,q∈N, then the rational number has a non-terminating recurring decimal expansion.

Related Topics

Check these articles related to the concept of terminating decimal numbers.

• Decimal Representation of Rational Numbers
• Decimal Representation of Irrational Numbers
• A Rational Number as a Decimal
• How to convert decimal numbers to p by q form?

Terminating Decimal Examples

• Example 1: The length and breadth of a rectangle are 7.1 inches and 2.5 inches respectively. Determine whether the area of the rectangle is a terminating decimal or not. Solution: Given, the length of rectangle is 7.1 inches and the breadth of rectangle = 2.5 inches. Area of Rectangle = Length × Breadth = 7.1 inches × 2.5 inches =17.75 inches 2 As the number of digits is finite after the decimal point, the area of rectangle is a terminating decimal expansion.

Example 2: Look at the following pie charts. Which one of the pie charts represents a terminating decimal number?

Solution: From the above figures we understand: a)The shaded portion of the first pie chart represents the number 4/6. 4/6 can be simplified as 2/3. The decimal expansion of 2/3 is 0.66... which is non-terminating and repeating decimal expansion. b)The shaded portion of the second pie chart represents the number 2/8. 2/8 can be simplified as 1/4. The decimal expansion of 1/4 is 0.25 which is terminating decimal expansion. Therefore, b) pie chart represents the terminating decimal expansion.

Example 3: Mary's teacher wrote 4 fractions on board: 2/7, 8/20, 10/30, and 5/32. Help Mary to find which among them is a terminating decimal? Solution: The fractions can be expressed as: 2/7 = 0.285714.... 8/20 = 0.4 10/30 = 0.333... 5/32 = 0.15625

Therefore, the fractions which are terminating decimals are 8/20 and 5/32.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Terminating Decimals

go to slide go to slide

FAQs on Terminating Decimal

What does terminating decimal mean.

Terminating decimal numbers are decimals that have a finite number of decimal places. In other words, these numbers end after a fixed number of digits after the decimal point. For example, 0.87, 82.25, 9.527, 224.9803, etc.

What is an Example of Terminating Decimal?

A decimal number that has finite number of digits after the decimal point is known as a terminating decimal. One example of terminating decimal is 0.5.

How to Find Terminating Decimal Without Division?

If we have to find whether a number is a terminal decimal expansion or not, we can use prime factorization method. Here, we factorize the denominator and see if the prime factorization results in the form of either 2 p 5 q , 2 p, or 5 q . If this condition is satisfied it means that the decimal expansion of the given rational number would be terminating. This is how we can find terminating decimals without division .

How to know if a Fraction is a Terminating Decimal?

To identify whether a fraction is a terminating decimal or not, we can use the division operation and divide numerator by denominator. For example, 1/8 is a terminating decimal expansion as the quotient after dividing 1 by 8 is 0.125.

Is 7/8 a terminating decimal?

The decimal representation of 7/8 is 0.875. So, it is a terminating decimal.

Is 11/20 a terminating decimal?

The decimal representation 11/20 is 0.55. So, it is a terminating decimal.

Is 3.3 a terminating decimal?

Yes, 3.3 is a terminating decimal because the digits after the decimal point come to an end. The number of digits after the decimal point is finite which is counted as 1.

Is Pi a terminating decimal?

No, pi is not a terminating decimal as the value of pi is 3.141592653589793238... It does not terminate and is not repetitive either which makes it an irrational number .

Is 0.75 a terminating decimal?

Yes, 0.75 is a terminating decimal because the digits after the decimal point come to an end. The number of digits after the decimal point is 2.

Terminating decimal

A terminating decimal is a decimal that has a finite number of digits. All terminating decimals can be expressed in the form of a fraction, and all of the digits of the terminating decimal can be determined by carrying out the division problem. Technically, an infinite number of zeros can be added to the end of a decimal. However, since the value of the decimal does not change regardless of the number of zeros added, these decimals would still be considered terminating decimals. The following are all terminating decimals.

• ½ expressed as a decimal is 0.5.
• ¼ expressed as a decimal is 0.25.
• "0.250000000000000000..." is still equal to ¼ regardless of how many zeros are added.

Terminating, non-terminating, and repeating decimals

These three types of decimals are often discussed together because they are closely related. As discussed above, a terminating decimal is one that has a finite number of digits. All of the digits in a terminating decimal are known. A non-terminating decimal is a decimal that never ends. It has an infinite number of digits.

There are two types of non-terminating decimals, ones that repeat and ones that do not repeat. Non-terminating decimals that repeat are referred to as repeating decimals. Although they have an infinite number of digits, all of the digits in a repeating decimal are known. Also, to be considered a repeating decimal, the repeating digits cannot all be zero. For non-terminating decimals that do not repeat, not all of the digits are known. No matter how many digits are known, there will always be a digit following it that needs to be determined.

Note that ⅓ is both a non-terminating decimal as well as a repeating decimal. Understanding the differences between these types of decimals is important when trying to distinguish rational and irrational numbers. All terminating decimals are rational numbers. The same is true of repeating decimals. Both terminating and repeating decimals can be expresed in the form of a fraction. Together, they make up the rational numbers.

Irrational numbers on the other hand, must be both non-terminating and non-repeating decimals. Examples include π (3.14159...) and the square root of 2 (1.4142135...). Regardless of the number of digits we compute, neither π nor the square root of 2 will ever terminate or repeat.

Terminating Decimals Calculator

Decimal representations: what is a terminating decimal and a repeating decimal, how to calculate terminating decimals and repeating decimals, calculate from repeating decimals to fraction, another example of terminating decimals and repeating decimals calculations.

Our terminating decimal calculator will teach you how to find the decimal representation of a number, detect the possible presence of repeating decimals , and much more. Keep reading to find out:

• What is a terminating decimal;
• What are repeating decimals;
• How to calculate the decimal representation of a fraction;
• When you should stop calculating the repeating decimals in a representation;
• How to convert from repeating decimals to fractions; and more.

Additionally, we have prepared several examples of all the math explained in the text. We promise it will be interesting (and surprisingly easy!). What are you waiting for?

The number of numbers is quite big: even natural numbers are infinite, and they are actually the smallest infinite set in math! This number only grows when we deal with real numbers . Real numbers allow for infinitely small variations (compare them to integers, where the smallest variation is 1 1 1 : 1 → 2 1\rightarrow 2 1 → 2 ). Between two adjacent integers , we can find infinitely many real numbers : this is when we need to introduce the decimal representation of a number:

Before the decimal separator , we meet the integer part . After the separator, we meet the decimal part.

Among real numbers, we can identify two subsets:

• Rational numbers; and
• Irrational numbers.

The difference between the two types is that the format can be represented as a ratio between two integers , while the latter cannot. Let's see a couple of examples to make things clear:

are rational numbers . On the other hand, Pi and the square roots of 2 2 2 are irrational numbers :

These numbers have an infinite amount of digits. Is this the condition that numbers have to satisfy to be irrational? No! In fact, we can find rational numbers with infinitely many digits :

Without going too deep, we can see the difference immediately: in a rational number with an infinite number of digits, we are forced to find a repeating pattern . In the example above, the digit 3 3 3 repeats an infinite number of times.

🙋 To write (or store) the decimal representation of an irrational number, you need an infinite amount of information . Conversely, a rational number, even with infinite decimal representation, can be "transmitted" in the finite message, for example, "one point three repeated infinite times".

To calculate the terminating decimals and repeating decimals from a fraction, you must calculate the decimal representation of the result of the fraction . To do so, we will use the long division procedure . We talked in detail about it in our long division calculator !

Let's get started. Take a fraction — any fraction. Above the line, we find the numerator , below the denominator . These two quantities correspond to the dividend and divisor :

🙋 If you need the result of such division directly, you can visit our fraction to decimal converter : specify the number of decimal digits, and let us do the math; in the terminating decimals calculator, you will learn how to calculate all the decimals !

To compute the decimal representation, perform these steps:

Check if the first digit of the dividend contains the divisor .

If it does, write down the result of the integer division , and keep the remainder of the division in mind.

If not, write down 0 0 0 or keep an empty position at the beginning of the result. Note the remainder.

"Copy" the remainder in front of the next digit of the dividend: you will obtain a number with, possibly, multiple digits. Worry not!

Compute the integer division between the number obtained in the previous step and the divisor. Note the result, and save the remainder.

Repeat the last two steps until you find one of the following two situations:

• The dividend is 0 0 0 : you've found a terminating decimal ; or
• You've already met the dividend (after the decimal separator): you've found a repeating decimal.

Let's follow the steps of the long division with an example. Take 17 17 17 as dividend and 14 14 14 as divisor . Write them down like this:

Consider the first digit of the dividend :

And compute:

17 / 14 = 0 17/14=0 17/14 = 0 will become the first digit of our result, while we carry 1 1 1 to the next digit. If the operations are too tricky, you can use our remainder calculator . We then perform the division between the number obtained by carrying 1 1 1 and the divisor:

Update the result and append the decimal separator : 17 / 14 = 01 17/14=01 17/14 = 01 . Now carry over that 3 3 3 , and proceed with the divisions:

Update the result: 17 / 14 = 01.2 17/14=01.2 17/14 = 01.2 and proceed.

Wait a minute! We've already computed this division: the result is 1 1 1 , with remainder 6 6 6 . This would throw us in a repeating pattern with the following digits: 142857 142857 142857 . As you can see, the 2 2 2 we've found at the beginning of the decimal representation doesn't make it in the repeating pattern!

We can stop our calculations for the repeating decimal part here. The result of the division of 17 17 17 by 14 14 14 is:

We can write the same result in a more succinct way, highlighting the repeating sequence :

We calculated the non-periodic part as 2 2 2 , and we calculated the repeating decimals as 142857 142857 142857 . 1 1 1 is the result of the integer division .

🙋 Fun fact: the number of digits in the repeating pattern can't be greater than the divisor (after you make it an integer by multiplying by the appropriate power of 10 10 10 ).

Why? Because all the possible remainders are contained in the sequence going from 1 1 1 to the divisor, then repeating. In the limited case of meeting all those digits , you will necessarily find a remainder you've already met!

Now that you know how to calculate the terminating decimals and the repeating decimals from a fraction, we can teach you how to do the opposite and calculate from the repeating decimals to the fraction that generated that result. We can identify three cases :

• Result with terminating decimals (only non-periodic part);
• Result with only repeating decimals ; and
• Mixed result (both non-periodic and periodic parts).

The first case is the easiest to analyze. To find the generating fraction:

• Make the result integer by multiplying by the appropriate power of 10 10 10 . E.g., 0.23 × 100 = 23 0.23 × 100 =23 0.23 × 100 = 23 (We multiply by 100 100 100 because there are 2 2 2 decimal places). This will be the numerator of the fraction.
• The power of 10 10 10 that you used in the previous step ( 100 100 100 ) will be the denominator of the fraction.
• Find the greatest common divisor of the two results, and divide them both by this quantity.

The result is the most reduced fraction that gives you the original decimal representation.

The calculations become slightly more complex in the presence of repeating decimals . Consider the real number 3. 18 ‾ 3.\overline{18} 3. 18 . Divide the integer and the decimal part:

Consider only the decimal part, and call it x x x . Multiply it by the power of 10 10 10 with exponent equal to the length of the repeating decimal part :

Now subtract the first number from the second one:

Hence, we can write x x x as:

Now think again when we split the original number: 3. 18 ‾ = 3 + 0. 18 ‾ = 3 + x 3.\overline{18} = 3+0.\overline{18} = 3+x 3. 18 = 3 + 0. 18 = 3 + x . Substitute x x x with the last result we've found, and sum the integer part and the fraction. You can use our adding fractions calculator if you don't want to spend time with the math!

What happens if there is a non-periodic part preceding the repeating decimals? You can add a simple step and reduce the problem to a mixture of the ones we've already met. Consider the number 1.23 145 ‾ 1.23\overline{145} 1.23 145 . We want to separate a strictly periodic and a terminating part. To do so, copy backward (from right to left) the digits of the periodic part over the digits of the non-periodic part (in the same right-to-left fashion) and create a periodic decimal number with the same digits of the period of the original one, but (possibly) a different starting point.

🙋 Did you see how we replaced the non-periodic part? We started from the last digit of the period ( 5 5 5 ); we then copied the second-to-last digit ( 4 4 4 ). We changed the periodic part from 145 145 145 to 451 451 451 .

Notice how the digits of the periodic part are the same , even though we changed the starting point : 0. 451 ‾ 0.\overline{451} 0. 451 is the decimal we will use to compute the fraction. To find the terminating decimal , subtract the original number and the last result:

Let's find the fractions corresponding to both numbers. For the terminating decimal we have:

For the repeating decimals, we have:

We can write the original number as the sum of these two fractions:

Not the best-looking fraction, but the right one, nevertheless!

🙋 Use our decimal to fraction calculator to see all the passages we explained above!

Let's try again to find the repeating and terminating decimals in an example. Take 13.7 13.7 13.7 as numerator, and 42 42 42 as denominator. Set up the division, and begin.

We've already met the remainder 26 26 26 at the fourth step of our calculations: this means that starting from the fourth reaching up to the last step, we've found our set of repeating digits . We can stop computing divisions and write down our result as:

What are the repeating decimals in a number?

The repeating decimals (or recurring decimals) in a number are a set of digits that repeat cyclically in the decimal part of a real number. Real numbers with repeating decimals are always rational ; thus, we can express them with the ratio of two integers . For example:

• 10/3 = 3.333333... = 3. 3 ;
• 131/88 = 1.4863636363... = 1.48 63 ; and
• 4679/1665 = 2.8102102... = 2.8 1 0 2 .

How do I calculate the repeating decimals from a fraction?

To calculate the repeating decimals from a fraction , follow these easy steps:

Divide the first digit of the numerator by the denominator; note the quotient and memorize the remainder.

Prepend the remainder to the next digit , and perform the division by the denominator again.

Note the decimal separator when you meet it.

Repeat steps 1 and 2 until:

• The new divisor is a number you've already met in the previous divisions; or
• The remainder of the division is 0.

The digits between the first and second occurrence of the remainder repeat in the decimal part of the result.

Are numbers with repeating decimals infinite?

Not exactly. Numbers with repeating decimals are not infinite, but the length of their decimal representation is infinite: this means that their decimal part has infinitely many digits . However, we can represent them using a finite number of digits by specifying the periodicity of the repeating part. To do so, we can write a bar over the numbers or enclose them in brackets.

What is the decimal representation of 12/55?

0.218181818... . To calculate this result, follow these steps:

Write 12 as 12.00000 .

Divide 12 by 55 . The result is 0 with the remainder 12 .

Copy the decimal point in the result.

Prepend 12 to 0 and find 120 . Divide 120 by 55 : the result is 2 with the remainder 10 .

Prepend 10 to 0 , take the result 100 , and divide by 55 . The result is 1 with remainder 45 .

The next number we divide will be 450 . 450/55 = 8 with remainder 10 .

We've already met this remainder: the digits 1 and 8 repeat infinitely.

The result is: 12/55 = 0.2181818...

Cross multiplication

Grams to cups, ideal egg boiling, isosceles triangle area.

• Biology (99)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (508)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Numbers Worksheets

Practice and master numbers with our helpful walkthroughs and downloadable practice worksheets from our team of elite math educators.

Terminating Decimal

By Anisha Patel

A terminating decimal is a decimal number that has digits that eventually end. In other words, it doesn't go on forever.

Why is this concept useful?

Where does this concept fit into the curriculum?

Sample Math Problems

• Downloadable PDFs

Practice Math Problems

What is a terminating decimal?

• 0.15 is a terminating decimal because it does not go on forever. It stops after two decimal places
• 0.2345 is a terminating decimal because it does not go on forever. It stops after four decimal places.

In contrast, there are decimals that go on forever, or are recurring decimals. These numbers have digits that will go on forever.

• 0.33333… is a recurring decimal because it continues to repeat 3 forever.

A good way to think about terminating decimals is to think about the definition of terminate. When something is terminated or terminates, it ends.

How can we use the concept:

To solve for a terminating decimal, one must know how to convert a fraction to a decimal. To do this, follow the following steps:

5/8 (See below for the solution)

• Read the fraction from top to bottom like so: “five divided by 8.” This will indicate to you that the numerator needs to go in the house (the dividend) and the denominator will go on the outside (the divisor).
• Divide normally if possible. If it is not, add a decimal and a zero after. This does not change the value of the number, but allows you to have more place values to work with.
• Stop when there is nothing left (no remainders/the decimal terminates) or where the question asks you to round to.

Question 1: Convert the fraction 5/8 to a decimal.

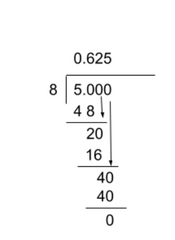
Question 2: Is 7/9 a terminating decimal?

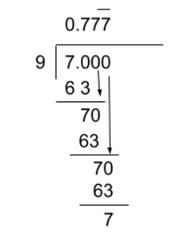
No, 7/9 is not a terminating decimal

Question 3: At which place value does 1/4 terminate?

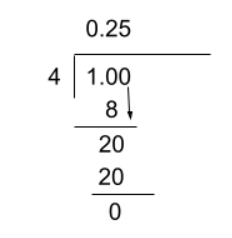
At the hundredths place

Question 4: What digit is in the thousandths place when 18is converted to a decimal?

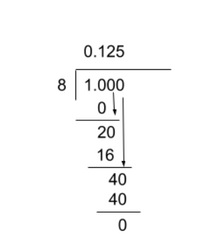
The 5 is in the thousandths place.

Download FREE Math Resources

Take advantage of our free downloadable resources and study materials for at-home learning.

8 Math Hacks and Tricks to Turn Your ‘Okay’ Math Student Into a Math Champion!

One thing we teach our students at Thinkster is that there are multiple ways to solve a math problem. This helps our students learn to think flexibly and non-linearly.

How to Make Sure Your Child is Highly Successful and Becomes a Millionaire

As a parent, you hope your child is extremely successful and likely become the next Gates, Zuckerberg, or Meg Whitman. To set your child on the right path, there are many skills and traits that you can start building and nurturing now. Doing so plants the seeds for future success.

Question 1: Convert the fraction 8/17 to a decimal

Question 2: Is 3/4 a terminating decimal?

Question 3: At which place value does 3/5 terminate?

Question 4 : What digit is in the thousandths place when 27/24 is converted to a decimal?

Kindergarten

Discover More at the Thinkster Blog

Parents like you are always looking for tips, suggestions, and activities to help their child become the best they can be! Learn more from our expert educators by visiting our blog.

Math Tutor and Coaching Program

With personalized attention from elite math tutors, help your child gain confidence in their math skills.

The Book of Secrets

Learn how to Make Your Child Math Fit for Life.

Related Topics

By Puja Varude

Normal Distribution

By Patricia Martin

Tossing a Coin

By Mandi Elam

Properties of Exponents

By Debi DalPezzo

Solve for x

Your child can improve their math scores by 90% within 3 months.

Our elite math tutors are ready to help make your child a math champion! Sign up for our zero $ free trial to get started today.

Talk to our experts

1800-120-456-456

• Terminating Decimal

What is a Decimal?

Before learning about terminating decimal meaning, let us learn about decimals. Decimals are an alternate way to write fractions. In a decimal number, the whole numbers are written on the left side of the decimal point ‘.’ and the remainders/ fractional part is written on its right. For example, 310/100 can be written as 0.31. 

Image: An example of a decimal number.

Decimals are of Three Types:

Terminating decimals

Non-Terminating Non-Repeating decimals

Non-Terminating Repeating decimals

In this article, we will learn about terminating decimals in detail.

What is Terminating Math Definition?

Terminating decimal definition is a decimal number with a finite number of digits after the decimal point. A terminating decimal like 5.65 can be represented as the repeating decimal 5.6500000000..., but when the repeating digit is zero , the number is usually labelled as terminating. Terminating decimals are rational numbers, which when converted into fractions have 0 as a remainder. Any terminating decimal representation can be written as a fraction with a power of ten in the denominator. 

Recognising a Terminating Decimal

For a number to have a terminating decimal expansion, you must check for the following points:

It should always have a finite number of digits after the decimal point.

It should be a rational number.

It shouldn’t have a bar over the finite digits occurring after the decimal point. 

When expressing the number in the reduced fractional form, its denominator should not contain any prime numbers other than two or five.

A terminating decimal number An example is given below. 

Image: Example of a terminating decimal.

In this, if we factorise 8, it’s 2 3 . This shows that 0.125 is terminating.

What is Non-Terminating Meaning?

Non-Repeating Decimal

A non-terminating, non-repeating decimal is a decimal number that lasts indefinitely with no repeating digits after the decimal point. In short, there is no uniform repetition of a number in non-repeating decimals. This sort of decimal can't be expressed as a fraction because it is an irrational number. Therefore, it can't be represented in the p/q format.

If the fraction form of this type of decimal expansion does not result in a remainder equal to zero, the decimal is referred to as a non-terminating in Maths. Examples of non-terminating non-repeating decimal numbers are: pi (π), √2, 157.8000619…, etc.

Repeating Decimals

A decimal representation of some periodic digits and an infinitely repeated number that is not zero is known as a repeating decimal. In certain cases of non-terminating decimals, a digit or a set of digits in the decimal portion repeats itself indefinitely, which are also called the pure repeated decimals.

Image: A non-terminating decimal expansion with recurring digits.

Contrary to the non-repeating decimals, repeating decimals are rational numbers and can be written in the form of p/q, where q ≠ 0. A bar is mounted on the shortest sequence of repeating digits to represent these decimal numbers. For example,

Image: A repeating decimal expansion with a bar.

Take another example, 68.5940000… with 0’s as repeating digits. In this, since the zeros can be omitted and the decimal terminates before these zeros, this decimal representation is considered a terminating decimal rather than a repeated decimal where the repeated number is a zero. 

Let x be a rational number with a decimal expansion that ends. Then prime factorization of q is of form 2 m 5 n , where n and m are non-negative integers, and x can be expressed in the form p/q,  q ≠ 0, where p and q are co-prime.

Let x = p/q, q ≠ 0 be a rational number with prime factorization 2 m 5 n , and non-negative integers n and m. As a consequence, x has a decimal extension that is terminating.

Let x =p/q, q ≠ 0 be a rational number with a q prime factorization that is not  2 m 5 n , and n and m be non-negative integers. Then x has a non-terminating and repeating decimal extension (recurring).

Therefore, terminating and non-terminating repeating decimals are rational, while only the non-terminating non-repeating decimals are irrational.

Also, these different decimal expansions of rational numbers make our daily lives quite convenient. We can use fractions or terminating/ repeating decimals in different ways depending on the context of a situation. 

For example, you will have to convert the weight of an item in terminating decimal form to check it on a digital scale, whereas while dividing a pizza among friends requires the knowledge of fractions.  

Solved Examples

1. Transform 8/11 to decimal.

Thus, 8/11 = 0.727272…

2. Identify 8/3 as terminating or non-terminating.

Ans: Method 1: We can write 8/3 in decimal form using the long division method.

Thus, 8/3 = 2.6666…. Which means it is a repeating decimal.

Method 2: We can factorise the denominator into the simplest form.

As, denominator 3 cannot be written in the form of 2 m 5 n , 8/3 is a non-terminating repeating decimal.

3. Convert 0.7777777... to fraction.

Ans: Let us start by equating 0.7777777… to x,

x = 0.777777...

10x = 7.777777

10x - x = 7.777777 - 0.7777777

Thus, x =7/9

4. State whether 798/500 will have a terminating or a non-terminating decimal form without performing division.

Ans: Factorising the denominator, 500 = 2 x 2 x 5 x 5 x 5

It can be written as 2 2 x 5 3 

Since it can be factorized in the form of 2 p 5 q , it is terminating decimal.

FAQs on Terminating Decimal

1. How to find if a fraction is terminating or non-terminating without long division?

If we have to find the decimal expansion of a number given in the fractional form, we can use the prime factorization method. For this, factorize the denominator and see if the prime factorization results in the form of either 2 p 5 q . If this condition is satisfied it means that the decimal expansion of the given rational number would be terminating. If not, then the number is non-terminating repeating.

2. What is the main difference between terminating decimals and repeating decimals?

A terminating decimal is defined by only a set number of digits after the decimal point, no matter they are different or repetitve. Whereas, in a repeating decimal, the digits after the decimal point are infinitely continuing in a repeated non-zero pattern.

GMAT Math: Terminating and Repeating Decimals

Rational Numbers

Integers are positive and negative whole numbers, including zero.  Here are the integers:

{ … -3, -2, -1, 0, 1, 2, 3, …}

When we take a ratio of two integers, we get a ratio nal number. 

• A rational number is any number of the form a/b, where a & b are integers, and b ≠ 0.
• Rational numbers are the set of all fractions made with integer ingredients.   Notice that all integers are included in the set of rational numbers, because, for example, 3/1 = 3.

Rational Numbers as Decimals

When we make a decimal out of a fraction, one of two things happens.  It either terminates (comes to an end) or repeats (goes on forever in a pattern).  Terminating rational numbers include:

• 1/8 = 0.125

3/20 = 0.15

9/160 = 0.05625

Repeating rational numbers include:

1/3 = 0.333333333333333333333333333333333333…

1/7 = 0.142857142857142857142857142857142857…

1/11 = 0.090909090909090909090909090909090909…

1/15 = 0.066666666666666666666666666666666666…

When Do Rational Numbers Terminate?

The GMAT won’t give you a complicated fraction like 9/160 and expect you to figure out what its decimal expression is.  BUT, the GMAT could give you a fraction like 9/160 and ask whether it terminates or not.  How do you know?

Well, first of all, any terminating decimal (like 0.0376) is, essentially, a fraction with a power of ten in the dominator ; for example, 0.0376 = 376/10000 = 47/1250.  Notice we simplified this fraction, by cancelling a factor of 8 in the numerator.  Ten has factors of 2 and 5, so any power of ten will have powers of 2 and powers of 5, and some might be canceled by factors in the numerator , but no other factors will be introduced into the denominator.  Thus, if the prime factorization of the denominator of a fraction has only factors of 2 and factors of 5, then it can be written as something over a power of ten, which means its decimal expression will terminate.

• If the prime factorization of the denominator of a fraction has only factors of 2 and factors of 5, the decimal expression terminates.  If there is any prime factor in the denominator other than 2 or 5, then the decimal expression repeats.

Here’s some examples of this concept at work:

• 1/24 repeats (there’s a factor of 3)
• 1/25 terminates (just powers of 5)
• 1/28 repeats (there’s a factor of 7)
• 1/32 terminates (just powers of 2)
• 1/40 terminates (just powers of 2 and 5)

Notice, as long as the fraction is in lowest terms, the numerator doesn’t matter at all. Since 1/40 terminates, then 7/40, 13/40, or any other integer over 40 also terminates. Since 1/28 repeats, then 5/28 and 15/28 and 25/28 all repeat; notice, though that 7/28 doesn’t repeat, because of the cancellation: 7/28 = 1/4 = 0.25.

Shortcut Decimals to Know

There are certain decimals that are good to know as shortcuts, both for fraction-to-decimal conversions and for fraction-to-percent conversions.  These are:

• 1/3 = 0.33333333333333333333333333…
• 2/3 = 0.66666666666666666666666666…
• 1/5 = 0.2 (and times 2, 3, and 4 for other easy decimals)
• 1/6 = 0.166666666666666666666666666….
• 5/6 = 0.833333333333333333333333333…
• 1/9 = 0.111111111111111111111111111… (and times other digits for other easy decimals)
• 1/11 = 0.09090909090909090909090909… (and times other digits for other easy decimals)

Irrational Numbers

There’s another category of decimals that don’t terminate (they go on forever) and they have no repeating pattern.   These numbers, the non-terminating non-repeating decimals, are called the irrational numbers . 

• It is impossible to write any irrational number as a ratio of two integers.

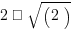
That’s the first 70 digits of pi, and the digits never repeat—they go on forever with no repeating pattern.  There are infinitely many irrational numbers: in fact, the infinity of irrational numbers is infinitely bigger than the infinity of the rational numbers, but that gets into some math that is much more advanced than what you need to know for the GMAT.

Terminating and Repeating Decimals: Practice Questions

Now here’s your chance to test your understanding! Try to answer these practice questions and then check the answer and explanation.

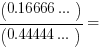
From our shortcuts, we know 0.166666666666… = 1/6, and 0.444444444444… = 4/9.  Therefore (1/6)*(9/4) = 3/8. 

And now for a sample question from our GMAT product :

2. Given that represents a decimal in which the digit k repeats without end, then what is the value of ?

0.1 1 4.5 6 18

Click here for the answer and video explanation!

If you’d like to practice more with decimals, check out our GMAT practice questions with fractions and decimals .

Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as “member of the month” for over two years at GMAT Club . Mike holds an A.B. in Physics (graduating magna cum laude ) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test .

View all posts

More from Magoosh

113 responses to “GMAT Math: Terminating and Repeating Decimals”

I have a question, 100/3=33.333…. and the division keeps on going , this means if we multiple 33.3333….with 3 result should be exactly equal to 100 but we get 99.99999…..why?? And only the calculators show 100 but practically doing we get 99.99999…..Please explain

Hi Sam! Great question. The answer here is simple but frustrating. We get 99.9999… instead of 100 because calculators are imperfect! Most calculators are simply not good at properly calculating multiplication with infinitely repeating decimals. You are correct that 33.33333…(repeating) should be 100 when it’s multiplied by 3. And on a sufficiently sophisticated calculator, it would be. However, most calculators are not properly programmed to do this operation correctly.

The good news is that you can still do this calculation correctly on any calculator that can multiply fractions. Simply convert 33.33333… to 33 and 1/3, or 100/3. From there, multiply 100/3 by 3, and you’ll get the 100 you’re looking for. This works anytime you can convert an infinitely repeating decimal to a fraction. 🙂

is 2/5 and – 2/3 a repeating or terminating decimal

2/5 is a terminating decimal, and -2/3 is a repeating one. 🙂

What is 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9 as a decimal please tell me is it is terminating or not terminating. THANKS!!!

1/9 = 0.11111111111… and it is a repeating decimal.

2/9 = 0.22222222222… 3/9 = 1/3 = 0.3333333…

And so on and so forth. 🙂 These are all non-terminating, repeating decimals.

To get the rest, you just multiply 0.11111… by your number of interest. 😀

Is 5/11 in a repeating or terminating decimal

It is a repeating decimal, because we have 0.454545… that never ends. Hope that helps!

Is 2/5 a repeating or termanting decimal?

It is terminating!

Is there any decimal expansion of rational number that repeated and terminate?

If I understand the question correctly, you’re wondering if there are any rational numbers where the decimal repeats, but repeats for a finite amount of time, and then terminates.

There definitely are. For example, the number 1.2525 is the same as the ratio 12,525/10,000 (or 501/400, in simplest terms). The “25” repeats twice and then terminates, and this is completely expressable as a fraction or ratio. There are plenty of other examples too, since any number that repeats for a time and then terminates will be rational.

When dividing to get a decimal and adding zero to the dividend to continue the quotient, how do you know when to stop? I always thought that once you see a number repeat three times with the same subtraction pattern that it was enough to show that it repeats. However, I noticed that pi has some digits that repeat up to nine times! Does this only happen with irrational numbers and what’s the max number of digits that will repeat? Thanks!

That’s a really good question, Angie. 🙂 In a strict mathematical sense, you could have a rational number that has a pattern of hundreds or thousands of digits that repeat. Or more. There really is no limit. However, in a GMAT mathematical sense, you only need to worry about repeating decimals for simple ratios such as 1/3, 1/7, 1/9, etc…. The longest strong of repeating decimals you’ll lkely have to deal with on the exam is 1/7 specifically. There you have a pattern of 6 decimals that repeats. You may have to deal with 1/13 (8 repeating decimals), but it won’t get more complex than that on the test.

If you’re curious, this web page indexes several PDFs that list the number of digits in a repeating pattern for a very large set of fractions. Type “ctrl-f” and enter the phrase “repeating digits” into the search to find the PDFs in question.

Can you help me is 4.65 eight terminate number or a repeated number And same with 0.68

Any number that ends is a terminating number. So 0.5 or 0.1276 or 0.11736 (and infinitely many others) are terminating. In contrast, repeating decimals are those that go forever. So 1/3 is 0.333… repeating infinitely. Or 1.851851851… if it does not end, it is a repeating decimal. 🙂

hey can u please help me with a question whether pie{22/7} is a rational number or not?

Hello! Pi is an irrational number. 🙂

Thank you this really helped me a lot in math thanks Mike. 🙂 😛 you told me what my math teacher did (but I actually got it this time).

Thanks/Cheers

hello, what are two examples of rational numbers, one taht can be wrtitten as a terminating decimal, and one that terminates? tank you

happy to help. But I think you meant you wanted two examples of rational numbers, one that can be written as a REPEATING decimal and one that terminates. (“One that can be written as a terminating decimal” and “one that terminates” mean the same thing, of course!)

In this article, under the heading Rational Numbers as Decimals , Mike gives several examples of rational numbers as repeating decimals, and several examples of rational numbers that terminate. Then, under the heading When Do Rational Numbers Terminate , Mike explains that rational numbers terminate if their denominators contain only factors of 2 or 5 (or factors of both 2 and 5). Otherwise, rational numbers will repeat.

Based on that rule, here are two additional examples each for rational numbers that repeat and terminate.

Repeating rational numbers: 1/66, 3/19 (Denominator 66 has a factor of 2, but also factors of 11 and 3; denominator 19 contains neither factors of 2 nor of 5.)

Terminating rational numbers: 26/25, 51/200 (Denominator 25 contains only factors of 5; denominator 200 contains only factors of 5 and 10.)

Is 64\455 is a terminating decimal

Nope, it is a repeating decimal. Check it out on Wolfram Alpha .

is 1/99 terminating?

1/99 is a repeating decimal.

1/99 = 0.0101010101….

Would thirty-three over forty be considered a terminating or repeating decimal? Thank you, love the site.

Hi Luciann,

33/40 is equal to 0.825 and as we have a finished expression that does not continue indefinitely, it is a terminating decimal. 🙂

is 7/10 a terminating decimal or an equivalent fraction

“7/10” is a terminating decimal. It can also be an equivalent fraction. For example, “7/10” and “14/20” are equivalent fractions.

Is a whole number considered being a terminating decimal? e.g: 1400

Yes, whole numbers are technically considered terminating decimals as the digits do not go on forever.

7/15=.46 with bar notation so is this terminating, non-terminating, repeating, or non repeating

3/5=.60 so is this terminating, non-terminating, repeating, or non repeating

9/16=.5625 so is this terminating, non-terminating, repeating, or non repeating

1/3=.33 with bar notation so is this terminating, non-terminating, repeating, or non repeating

7/15 and 1/3 equal repeating decimals. 3/5 and 9/16 are terminating decimals.

What is 9/20 in a terminating decimal form?

Hi Jessica,

9/20 creates a terminating decimal that is equal to .45 🙂

Hi can help me for this problems 10/12 7/72 15/75 9/14 35/40

10/12 actually creates a repeating decimal, 0.83 with 3 repeating. 7/72 is also a repeating decimal, 0.972 with 2 repeating. 15/75 is the non-repeating 0.2, or 1/5 (1/5 being what 15/75 simplifies to in fraction form).

9/14 is tricky. It amounts to a fairly complex repeating decimal: 0.642857142857… with 142857 repeating. (This is because 142857 is a repeating number in fractions that involve dividing by 7 or dividing by certain multiples of 7. See this for more info: https://www.douglastwitchell.com/142857calculator.php )

35/40 is the same as 7/8, which is the non-repeating decimal of 0.875 .

is 5/12 a repeating or terminating decimal is 7/8 a repeating or termination decimal

5/12 is 0.41666… repeating, so it is a repeating decimal. 7/8 is 0.875 and it ends, so it is a terminating decimal.

Hope that helps! 🙂

What does 1/11 turn into as a decimal?

1/11 becomes 0.090909… repeating the 09 forever!

What is repeating fraction for two fiftieths, eleven twentieths

These values are not repeating decimals. Check it out:

2/50 = 4/100 = 0.4 11/20 = 55/100 = 0.55

I hope that helps! 🙂

I helped me out thanks???

Why is it than when 1.4999999999… is converted to a fraction it is equal to 3/2 which would be the fraction of a different decimal as well (1.5)? What would be the explanation to this?

This can be hard to wrap your mind around. There is a similar and commonly-discussed argument that 0.999…. is equal to 1. This is an example of a discussion on that topic: https://www.math.hmc.edu/funfacts/ffiles/10012.5.shtml . The explanation can be extremely complicated depending on the mathematical level of the person trying to prove the point, so be careful not to fall too deeply down a math rabbit hole! 🙂

Wait… 22/7 and 3.1415… (π) are the same, but when you pry in closer they aren’t. To prove my point, 22/7 = 3.142857… Meanwhile, π is 3.14159265358979… How are they equivalent? Or are they just said to be equivalent

You’re right! 22/7 is an approximation of pi, and a pretty famously used one at that. It’s not the real thing because pi cannot be expressed as a ratio of integers, but it’s near enough for many purposes. This is because pi is irrational and so we have to make an approximation in order to be able to do any kind of easy notation. There are other approximations like that such as 333/106, and 355/113. Hope that helps. 🙂

Hi, thank you always for the wonderful articles.

I have a question, if

0.111… = 1/9 0.888… = 8/9

is 0.999…= 9/9? (Well, no, right?)

How does that logic work again?

Happy to help! 🙂

In mathematics, the repeating decimal 0.999… denotes a real number that can be shown to be the number one. In other words, the symbols “0.999…” and “1” represent the same number. There are tons of mathematical proofs that work through this (at varying levels of difficulty), but this page gives a brief explanation. You can also read about this on Wikipedia! I hope this helps get you started. 🙂

Is -54/19 irrational. When do you end or terminate a decimal,up to what place? Thanks

Good question! Wolfram Alpha is amazing for things like this. Y ou can see here that -54/19 is actually rational , but it has a repeating period of 18 digits. There is no standard place to terminate a decimal–in this example, the decimal needs to go 18 places to see the full extent of its period!

Hi is it possible to be terminating decimal even if denominators cannot be expressed as powers of 2 and 5 for ex-

is 39/128 a terminating decimal?

Hi Gayathri,

Happy to help! As mentioned in the post, “If the prime factorization of the denominator of a fraction has only factors of 2 and factors of 5, the decimal expression terminates. If there is any prime factor in the denominator other than 2 or 5, then the decimal expression repeats.” So, no, a denominator whose prime factorization includes other primes besides 2 and 5 will not terminate.

In terms of your question, 128 = 2^7 and thus can be expressed as a power of 2. Furthermore,

39/128 = 0.3045875

Because the decimal ends at some point, it is a terminating decimal. In this case, if we were to multiply the fraction by 10^7, we would see that the quotient would be an integer:

39/128 * 10^7 = 390,000,000/128 = 3,046,875

On the other hand, it is not possible to do this with repeating or irrational numbers to get an integer quotient.

Hope this helps! 🙂

hi which one is a terminating decimal? 1/3 7/9 2/5 or 5/6

Hi Sabrina,

Terminating decimals are decimals that eventually come to an end, while repeating decimals go on forever. In terms of the fractions you asked about:

1/3 = 0.3333… (where the 3 repeats) 7/9 = 0.7777… (where the 7 repeats) 2/5 = 0.4 (this decimal ends, so it is a terminating decimal) 5/6 = 0.8333… (where the 3 repeats)

As you can see, the only example above of a terminating decimal is 2/5 = 0.4

Hope this helps!

is 7/18 a terminating decimal?

Hi Kaitlynn,

No, 7/18 is not a terminating decimal. As a decimal

7/18 = 0.3888… (where the 8 repeats)

Hope this helps 🙂

Does the line mean it terminates or repeats

Hi Frankie,

A line over one or more digits in the decimal place indicates that the digit (or digits) repeat(s) 🙂

Hope this clears things up for you!

Can a number be rational in fraction form (22/7) and irrational in decimal form (3.141592653. . .)? As a middle school math teacher, we say any number that can be expressed as a fraction is rational, yet some fractions are not repeating or terminating in their decimal form. What’s the mathematician’s answer to this?

Yes! There are many examples of this! A classic one is pi, as you pointed out. In order to calculate pi, you divide the circumference of a circle by it’s diameter. Both the circumference and diameter are numbers that form a fraction (22/7) but when you divide 22/7 you get an irrational number, pi. In fact, there is no rule saying that a rational fraction must be rational in decimal form. This is why it is sometimes convenient to represent irrational numbers in their decimal form for a more precise answer.

I think 22/7 in decimal is still rational since you can see a repeated pattern with the numbers.

Hi Emerzen,

You’re right. 22/7 is an approximation of pi. It’s not the real thing because pi cannot be expressed as a ratio of integers, but it’s near enough for many purposes. This is because pi is irrational and so we have to make an approximation in order to be able to do any kind of easy notation. There are other approximation like that such as 333/106, and 355/113. Hope that helps. 🙂

in the decimal 0.15.why is there a line over the number 15

Happy to help! 🙂 The line means that the numbers occurring under the line repeat infinitely. I hope that clarifies!

is 1.765 a rational or irrational number and where would it fall o a number line????

Hi Ta’jhai!

In mathematics, an irrational number is a real number that cannot be expressed as a ratio of integers, i.e. as a fraction. Therefore, irrational numbers, when written as decimal numbers, do not terminate, nor do they repeat. A good example of an irrational number is pi.

The decimal 1.765 that you mention can be written as many fractions, including 353/200. Therefore, it is a rational number. It would fall between 1 and 2 on a number line of only whole numbers. It would be possible to give an infinite number of places it would fall depending on the specificity of your number line units. For example, it could also be between 1.764 and 1.766 if you had decimals that specific.

I hope this helps! 🙂

How do you decide by which power of 10 to multiply an equation when writing a decimal with repeating digits as a fraction?

Usually, we use this method only for terminating decimals. To determine which power of ten to use, you need to count the number of decimal places from the decimal point to the end of the terminating number. That will give you the power of 10 by which to multiply. For example, let’s say we have the decimal

To see what power of 10 we should multiply by to write this decimal as a fraction, we start at the decimal point and count the places until reaching the final digit, 7. There are 6 digits, so we will multiply this decimal by 10^6:

0.004137*10^6 = 4137

And to write the decimal as a fraction, we need to divide this integer 4137 by 10^6:

0.004137 = 4137/1,000,000

For repeating decimals, there’s no power of 10 by which we can multiply to be able to rewrite the decimal as a fraction. Rather, dealing with repeating rational numbers is a matter of recognizing familiar patterns and guess and check to determine the equivalent fraction.

I hope this helps, at least a little 🙂

Can I know where will I put the terminating and repeating decimals if I make a map about Real Numbers ?

If I understand correctly, you’re asking where repeating decimals would fit in a concept map of real numbers, such as this one: http://edtech2.boisestate.edu/dougwolfe/images/real_numbers2.jpg . In any concept map of different categories of real numbers, numbers with repeating decimals would fall under the category of rational numbers — numbers that can be expressed in fraction form. All repeating decimal numbers have a fraction expression. 1/3 is 0.333333333 repeating, 2/7 is 0.285714 repeating, and so on. Rational numbers also includes terminating decimals, such as 2.25 (9/4 in fraction form).

can you help me why 0 is included in even numbers

Hi Mohammad,

This is just a quirk of how numbers are classified. While 0 is neither negative nor positive, it is considered an even number. 🙂

how to convert 0.07 into fraction and 7 is repeating decimal… please sir help me

Happy to help! Firstly, let’s look at 0.07 or seven hundredths. As its name suggest, seven hundredths is 7 parts of 100. So, we can rewrite 0.07 as

0.07 = 7/100.

In terms of 0.777…, here’s a nice trick. For repeating decimals that have the same repeating digit, from 0.111.. to 0.888…, as fractions, they are that digit over 9:

0.111… = 1/9 0.888… = 8/9 etc.

So, 0.777… repeating is equivalent to 7/9.

Hey can u help me what’s the decimal expansion of the rational number 1/9 repeats.

1/9 = 0.111… where 1 repeats indefinitely in the decimal part of the number.

sir, please help me in mine situation as my exams are nearer. which least number must be divided to 2/5×7 to make it terminating decimal expansion plz sir reply me fast I m waiting for your reply

Let’s look at the two factors in the denominator:

5: 1/5 = 0.2 and is therefore a terminating decimal 7: 1/7 = 0.142857… The decimal does not terminate but rather repeats as 1428567.

So, if we want to create a terminating decimal from 2/(5*7), we must multiply by 7. By multiplying by 7, we can cancel the term of 7 in the denominator, leaving us with a factor of 5, which will give us a terminating decimal:

2/(5*7)*7 = 2/5 = 0.4

I hope that helps!

Pi is an irrational number. Pi is ratio of circumference to its diameter. But if we make a circle with rational diameter say x then we will get a circle with circumference of rational value i guess. Now if we take the ratio it should be rational. Then why pi is irrational

Pi is an irrational number because when written as a decimal number it does not terminate or repeat. The circumference of a circle, C, is defined as 2(pi)r, where r is the radius of the circle. Since 2r = d, then C = d(pi) and C/d = pi. With that in mind, you’ll find that we cannot write pi as a ratio of two rational numbers. Typically in GMAT questions, you’ll be given either the radius or diameter as a rational number. That means that the circumference will be pi multiplied by that rational number. Since pi is irrational, the circumference in that case will also be an irrational number.

That said, physically measuring the exact circumference of a circle with a rational radius is not possible and requires estimation, which can result in a very good approximation of the circumference. The precision of that approximation can be tested by comparing the experimental C/r ratio with pi.

And if you’re interested, you can read up about the proof that pi is an irrational number on Wikipedia .

Hi Samridhi,

Good question! 🙂 The popular approximation of 22/7 = 3.1428571428571… is close but not quite accurate for pi. In either case, pi is a famous irrational number! I hope that helps. 🙂

Why do calculators put a 7 as last decimal digit when dividing numbers like 2, 5, 20, 40, 80, 110, 140 and so on by 3? Calculating by hand the result has a never ending 6 as decimal. How do they get the 7?

Good question! 🙂

The calculator is forced to round up by the end of its display, and a repeating 6 decimal would warrant rounding up to 7. But you are right, it is actually a never-ending 6. I hope that makes sense!

Hii Can u plz help me I have a question Is root 6 + root 9 Rational??

Happy to help! The sum of a irrational number and rational number is irrational. In this case, we have

sqrt(6) + sqrt(9) = sqrt(6) + 3

Sqrt(6) is an irrational number and is 2.4494… w

So, the sum is

2.4494… + 3 = 5.4494…

The three dots represent the irrational decimal part of sqrt(6). Since the decimal does not terminate, the decimal in the sum will not terminate either. Therefore sqrt(6) + sqrt(9) results in a irrational number.

What if the number is 3.067 but only the 7 has a repeating line over the number. Is that rational or irrational?

A number can be a rational number and not have the first decimal place repeating. Consider some common repeating decimals:

1/6 = 0.1666… 5/6 = 0.8333… 1/12 = 0.08333… 5/12 = 0.41666…

I do not know off hand what the fraction representation of your suggested 3.0677… would be, but presumably we could find a ratio of two integers that would create that number, making it a rational number. 🙂

No. On a number line 1 is farther away from 0 than .75

Would .75 be bigger than 1?

No it would be smaller because 1 is a whole number and .75 is 3/4 of a whole so 1 is bigger

Great article Mike!!!

Dear Hamza, I’m glad you found this helpful! Best of luck to you! Mike 🙂

Hi Mike definitely great explanation about rationals and irrationals.

I have a question. Is there some sort of formula to determine when a decimal number is Irrational? so it can be implemented by code.

Matt, I’m happy to respond. 🙂 Everything about the relationship of rationals and irrationals defies all attempts to encapsulate it in a formula. For simple GMAT purposes, the GMAT will give you a decimal with, say, 10 or 12 places after the decimal showing. Either there will be a simple repeating pattern or not. If there’s a repeating pattern, the number is rational. For GMAT purposes, if the decimals shown contain no repeating pattern, then we can assume the decimal is irrational. Technically, the GMAT never asks about rational or irrational anyway: that’s already between the GMAT. Now, in the bigger picture, it’s certainly true that there are decimals that have repeating patterns that consist, say, of a string of some large number of decimals. For example, the decimal pattern of 1/29 repeats a pattern that is 28-decimal-places long: 1/29 = 0.03448275862068965517241379310344827586206896551724137931 03448275862068965517241379310344827586206896551724137931 03448275862068965517241379310344827586206896551724137931 . . . (courtesy of Wolfram Alpha ) As I am sure you appreciate, if you have only, say, the first 12 decimals places, there are an infinity of possible rational numbers and another, larger infinity of possible irrational numbers that start with those initial 12 decimals. Having 12 decimal places, while extremely precise, is known mathematically as a decimal approximation , a sharply curtailed approximation of the infinite decimal. From a mathematical point of view, if we have 12 decimal places, we have essentially nothing. Mathematician regularly examine decimals to millions and billions of decimal places. For example, in 2014, pi was calculated to 13,300,000,000,000 decimals. If we are looking at any number that can be printed on a single sheet of paper, on a single line of text, then, from a purely mathematical point of view, that’s kiddie pool stuff. Basically, there’s no code as efficient as the human mind on this. However many decimals we have, the question is simple: do we see a repeating pattern or not? The human brain is a better pattern-detecting and pattern-matching machine than any computer. Does all this answer your question? Mike 🙂

Example of 9/160 at top of the page is wrong. You forgot to add 0 after decimal point.

Dear “John”, Very perceptive! Thank you very much for pointing out that typo. I just corrected it. Best of luck to you, my friend. Mike 🙂

Can you please give an example of the division problem of 1/8 converted into a decimal and can you tell me if the answer is terminating or if it’s repeating?

If a denominator have prime factors of only 2 or only or both then the number terminates ( because any denominator will be in the form ten’s , so factors of 10 is 2* 5 )

If the denominator factors are other than 2 and 5 then the decimal repeats But taking an ex 1/14 ( factors are 2 and 7 ) it has a repeating decimal.

It’s very useful,thank you.Is my understanding is Right?

Dear Anusha, Your understanding is correct. For example, 1/35 has 5 & 7 in the denominator, so this would be a repeating non-terminating decimals. 1/35 = 0.0285714285714285714 … But, notice, if we put something divisible by 7 in the numerator, then the sevens would cancel, and the fraction would terminate: 21/35 = 3/5 = 0.6 Does all this make sense? Mike 🙂

If the number is itself 2 & 5. And if multiplies it with 5/2 and gives answers in which digit in ones place is 0 then that number will terminates always for example 3/4 it will terminates 4*5/2=10 ad we got 0 at ones digit we can easily identify it.

Dear “anonmoyous” or “anonymous”, Yes, I believe if I understand you correctly, we are saying very much the same thing. You seem to understand this issue well, which is great. Best of luck to you. Mike 🙂

Give me some reasons why 1/6 is irrational number?

Happy to help! 🙂 Can you tell me why you think 1/6 is an irrational number? 1/6 is actually not an irrational number because we can express it as a ratio of integers or a fraction! I hope that helps. 🙂

Hi Mike…

Thanks a ton for this explanation..I just gave a Practice Test from GMAC ( the new Exam pack) and got two questions to do with terminating decimals…Have my GMAT in 36 hours from now..I have absolutely loved the Magoosh product…Hope to get a good score on Monday and write a good testimonial for Magoosh 🙂

Dear Nishant, You are quite welcome. I am very glad you found this blog article helpful, and I’m glad you like the Magoosh product. Best of luck to you my friend! Mike 🙂

Found what i was looking for! Thanks this really helped! 🙂

Dear Saketh, I’m glad it helped you. Best of luck to you! Mike 🙂

I didn’t find what I was looking for, but it is very useful! 🙂 Thank You for spreading your knowledge with others. Sincerely, Sara

Well, thank you. I hope you find that for which you seek. Best of luck to you. Mike 🙂

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.4: Decimals

• Last updated
• Save as PDF
• Page ID 70335

• Julie Harland
• MiraCosta College

The meaning of decimals is best understood once one has a real understanding of place value and fractions. The decimal notation we commonly use is an extension of place value in base ten. The decimal point indicates that succeeding digits represent tenths, hundredths, thousandths, etc. So a person must understand what these fractions mean in order to understand and make the connection to decimals.

The key to understanding the relationship between decimals and fractions (or mixed numbers) begins with READING the decimal correctly. Most people read 5.3 as "five point three" which doesn't help one understand its meaning. It should be read "five and three tenths." In doing so, the connection between the decimal 5.3 and the mixed number \(5 \frac{3}{10}\) is clear. Similarly, 18.035 should be read "Eighteen and thirty-five thousandths" and corresponds to the mixed number \(18\frac{35}{1000}\). Here are a few more:

• 0.309 and \(\frac{309}{1000}\) are both correctly read "three hundred nine thousandths"
• 10.04 and \(10\frac{4}{100}\) are both correctly read "ten and four hundredths"

Note that the decimal point is read as "and". The decimal point (and the word "and") separates the whole part from the fractional part of a mixed number. This is the only correct use of the word "and" when reading numbers. 760 is read "seven hundred sixty." A common mistake is to read 760 as "seven hundred and sixty." If there is no decimal point, don't say the word "and".

People just learning about decimals (like elementary school children) should NOT read the number 5.4 as "five point four". This is a shortcut way of reading the number that is only appropriate to use once one really understands the connection between decimals and fractions. Remember that a number written in decimal form is really just a different way to write a mixed number where the denominator of the fractional part is a power of ten! The name of the fractional part (tenths, hundredths, thousandths, etc.) is the place value of the last digit of the number after the decimal point, which also happens to be the denominator of the number written in fractional form.

Look again at 0.309 and \(\frac{309}{1000}\). In the decimal, there are three digits (or place values) after the decimal point. In the fraction, there are three zeroes after the 1 (which is the number 1000 in the denominator). The same applies to 18.035 and \(18\frac{35}{1000}\). For 5.3 and \(5\frac{3}{10}\), the decimal has one digit after the decimal point, and the fraction has one zero after the 1. It's best if students are allowed to discover this fact for themselves. It's always more meaningful to discover relationships (that often become rules) on your own. Students who are regularly asked to read decimals, fractions and mixed numbers the correct way are more likely to make this particular discovery by themselves.

Mixed numbers like 5.3 and 18.035 can also be written immediately as improper fractions. The denominator of the fraction will still be the same as if it were written as a mixed number. The numerator is the number without a decimal point at all. For instance, 5.3 can be written as \(5\frac{3}{10}\) or \(\frac{53}{10}\); and 18.035 can be written as \(18\frac{35}{1000}\) or \(\frac{18035}{1000}\).

Note that when you first write a decimal as a fraction, it isn't necessarily in simplest (or reduced) form.

On the line, write in words how to read each of the following decimals. Do not use the word "point". Then, underneath, write each decimal as a fraction. If the number is greater than or equal to 1, first write the fraction as a mixed number and then write it as an improper fraction. Simplify any fraction that is not in simplest form. Show all steps (including original fractions before simplifying).

a. 0.4 _________________________________________________________________

b. 0.26 _________________________________________________________________

c. 3.08 _________________________________________________________________

d. 9.85 _________________________________________________________________

e. 17.305 _____________________________________________________________

Write each proper fraction as a decimal. Write each improper fraction first as a mixed number (don't reduce), and then also as a decimal. Do not use your calculator.

a. \(\frac{14}{100}\) = __________

b. \(\frac{8}{1000}\) = __________

c. \(\frac{435}{100}\) = _______________ = _______________

d. \(\frac{5638}{10}\) = _______________ = _______________

e. \(\frac{305}{100}\) = _______________ = _______________

The rule you may remember for multiplying fractions is to multiply the numbers together as if there were no decimal point, and then move the decimal point in from the right the total number of places it is in for both numbers. For instance, (8)(0.4) is done by multiplying 8 times 4 and then moving the decimal point in one place to get 3.2. Similarly, (0.06)(0.7) is done by multiplying 6 times 7 and moving the decimal point in three places (two for 0.06 and one more for 0.7 for a total of three) to get 0.042. Many people make this harder than it really is and don't realize they can easily multiply 0.3 and 0.4 in their head. It's as simple as 3 \(\cdot\) 4 and moving the decimal in two places to get 0.12. Now, how about 1.1 times 1.2? It's simply 11 times 12 with the decimal moved in two places: 1.32.

Let's observe why this rule for multiplying decimals works by rewriting the numbers as fractions first. The key here is to write numbers greater than or equal to one as improper fractions. Then multiply (without canceling or reducing) the fractions. Lastly, rewrite the fraction as a decimal.

Exercise Example 1

(8)(0.4) = \(\frac{8}{1} \cdot \frac{4}{10} = \frac{32}{10}\) = 3.2 (notice the decimal point is one place in for .4)

Exercise Example 2

(1.2)(1.01) = \(\frac{12}{10} \cdot \frac{101}{100} = \frac{1212}{1000}\) = 1.212

(notice the decimal point is three places in, one for 1.2 plus two more for 1.01)

Multiply the following decimals mentally, and write the answer on the blank. Then do it again by showing the same steps as shown in the previous two examples where each decimal is first written as a fraction, then multiply the numerators and denominators, and then convert that answer (don't simplify) to a decimal. Do not use your calculator.

a. (0.4)(.07) = ______________

(0.4)(.07) =

b. (1.6)(0.2) = ______________

(1.6)(0.2) =

c. (0.25)(0.3) = ______________

(0.25)(0.3) =

d. (2.2)(0.3) = ______________

(2.2)(0.3) =

Recognizing Equivalent Decimals and Comparing Decimals

Zeroes, which are behind a decimal's last non-zero digit, can be added or removed without changing the value of the decimal. If you look at some equivalent fraction, you'll see why this should be true. For example,

\[\dfrac{14}{10} = \dfrac{140}{1000} = \dfrac{1400}{10000} = \dfrac{14000}{100000}. \nonumber \]

These are all equivalent to \(\frac{14}{100}\) because the numerator and denominator was multiplied by some power of 10 (10, 100 or 1000) to get one of the other equivalent fractions. If we replace each of the four fractions above with their decimal equivalents, we get 0.14 = 0.140 = 0.1400 = 0.14000. Let's call any zeroes at the end of a decimal's last non-zero digit " trailing zeroes ". Then, we could conclude that any number starting with .14 that has trailing zeroes is also equivalent, like 0.1400000.

Two decimals are equal only if one can be made to look identical to the other by adding or removing trailing zeroes. You can also determine if they are equivalent by removing any excess trailing zeroes from each to see if they are identical.

For the first decimal given, circle any of the next four decimals that are equal to it.

To compare two or more decimals that are not equal, but have the same number of digits after the decimal point, you can write each as a fraction with the same denominator and then compare the numerator. For instance 0.14 is less than 0.21 since fourteen hundredths is less than twenty-one hundredths. Basically, in this case, it's just like comparing whole numbers. You'll be able to determine which is larger by comparing each number as if there was no decimal point. But, keep in mind this only makes sense if the numbers you are looking at have the same number of digits after the decimal point.

Compare each of the following decimals using <, = or >.

To compare two or more decimals that are not equal that do not all have the same number of digits after the decimal point, first write each decimal with the same number of digits after the decimal point (by adding trailing zeroes to one or more if necessary). By doing that, you are comparing tenths with tenths, or hundredths with hundredth, etc., as you did in exercise 5.

If a fraction is written with a power of ten in the denominator, it's basic to write the same number in decimal form. You did that in Exercise 2. Any fraction that is written with a power of 10 in the denominator can be written as a terminal decimal. This means that it's possible to write the number with trailing zeroes. But what if the fraction doesn't have a power of 10 (like 10, 100, 1000, etc.) in the denominator? Sometimes those can be tricky!

If a fraction WITHOUT a power of ten in the denominator CAN be written as an equivalent fraction WITH a power of ten in the denominator, then it can be written as a terminating decimal.

For instance, \(\frac{1}{2}\) can be written as \(\frac{5}{10}\) (by multiplying the numerator and denominator by 5)

Therefore, \(\frac{1}{2}\) = \(\frac{5}{10}\) = 0.5 (remember to read this as five-tenths)

Well, that one wasn't too hard, but what about \(\frac{7}{80}\)? The question is whether you can multiply the denominator, 80, by something to get 10, 100, 1000, 10000, etc. There is no whole number you can multiply 80 by to get 10, 100 or 1000. But, if you multiply 80 times 125, it equals 100000. So, by multiplying both 7 and 80 by 125, we get the equivalent fraction \(\frac{875}{10000}\) for \(\frac{7}{80}\) which can now be written as the decimal 0.0875.

How about writing \(\frac{5}{6}\) as a terminating decimal? Well, there is nothing you can multiply 6 by to get 10 or 100 or 1000 or 10000. Is there maybe some number we could multiply 6 by to get some higher power of ten? Well, that's a good question! Actually, there isn't, but how could you be sure? You certainly can't try every power of ten since there are an infinite number of them to try.

It would be nice if there was an easy way to determine if any given fraction could be written as a terminating decimal. The key is to consider the factors of the denominator of a fraction that can be written as a terminating decimal. If a fraction can be written as a terminating decimal, then there is some equivalent fraction where the denominator must be a power of ten: 10 or 100 or 1000, etc.

Write the prime factorization of each of the following:

a. 10 = _______________

b. 100 = _______________

c. 1000 = _______________

d. 10000 = _______________

e. 100000 = _______________

What are the only prime factors of powers of 10? ______________

If a power of ten has three factors of 5, how many factors of 2 does it have? ______

Exercise 10

If a power of ten has two factors of 2, how many factors of 5 does it have? _____

Powers of ten only have 2s and 5s as its prime factors and nothing else.

Let's go back to our three numbers , \(\frac{1}{2}\), \(\frac{7}{80}\), and \(\frac{5}{6}\), that we were trying to write as terminating decimals and analyze the situation.

\(\frac{1}{2}\) is simplified, and in its prime factored form, there is exactly one 2 in the denominator. To write as an equivalent fraction with a denominator that is a power of ten, it must have only 2s and 5s as prime factors in the denominator, and the same number of each! Therefore, multiplying by one more 5 in the numerator and denominator did the trick!

Prime factor the numerator and denominator of this reduced fraction: \(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5}\)

We must determine if it is possible to multiply the denominator by something so that the resulting denominator will be made up of only 2s and 5s and the same number of each. Well, there are four factors of 2 and one factor of 5. Since we need the same number of each factor, making an equivalent fraction by multiplying the numerator and denominator by three more factors of 5 will do the trick.

\(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5} \cdot \frac{5 \cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.0875\)

In both examples, note we either multiplied by extra factors of 2 or 5, but not both!

What about \(\frac{5}{6}\)? Well, it's reduced, and the prime factorization of the denominator is 2 \(\cdot\) 3. No matter what the denominator is multiplied by, we'll be stuck with a factor of 3 in the denominator. Since the only prime factors of powers of 10 are 2 and 5, there can't be a prime factor of 3 in the denominator if we want to end up with only a power of 10 in the denominator. Therefore, since it is impossible to write \(\frac{5}{6}\) as an equivalent fraction with a power of ten in the denominator, it cannot be written as a terminating decimal.

How about \(\frac{63}{72}\)? If we prime factor the denominator, we get 2 \(\cdot\) 2 \(\cdot\) 2 \(\cdot\) 3 \(\cdot\) 3.

Exercise 11

Well, what do you think? Can \(\frac{63}{72}\) be written as a terminating decimal? ________

Explain why or why not.

One way to check that you are obtaining the correct results is to use a calculator. For \(\frac{1}{2}\), we got 0.5, which you can check by doing the division 1 \(\div\) 2 on your calculator.

Exercise 12

Use your calculator to find the decimal equivalent for each of the following:

a. \(\frac{7}{80}\) = _____________

b. \(\frac{63}{72}\) = _____________

Exercise 13

Hmmm, did you get 0.0875 for part a? _________

If you did part b on your calculator, did you get a terminating decimal of 0.875?

Is that what you expected? Why or why not?

The reason \(\frac{63}{72}\) can be written as a terminating decimal is because in its simplified form, it only has 2’s and/or 5’s as its prime factors. Here is how to finish this problem by simplifying first, and then multiplying by any needed factors of 2 or 5 to get the same number of each:

\(\frac{63}{72} = \frac{3 \cdot 3 \cdot 7}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3} = \frac{7}{2 \cdot 2 \cdot 2} \cdot \frac{5\cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.875\)

Exercise 14

For each fraction, determine if it can be written as an equivalent fraction with a power of ten in the denominator. If a fraction cannot be written as a terminal decimal, explain why not. Otherwise, show ALL of the steps (as shown in the previous examples) to write it as a terminal decimal. The steps are listed below.

• Simplify if possible
• Prime factor the denominator
• Multiply the numerator and denominator by an appropriate number of factors of 2 or 5 so that the denominator will be a power of 10
• Simplify the numerator and denominator
• Write as a terminating decimal

Then, check your answer with a calculator by taking the original fraction and dividing the numerator by the denominator. You should get the same decimal obtained by doing the five steps outlined above.

a. \(\frac{3}{4}\)

b. \(\frac{9}{20}\)

c. \(\frac{9}{15}\)

d. \(\frac{18}{25}\)

e. \(\frac{5}{14}\)

Okay, now we have to deal with those fractions that cannot be written as terminating decimals. Any simplified fraction that has at least one prime factor that isn't a 2 or 5 is in this category. Let's look at \(\frac{5}{6}\) again. One way to write this as a decimal is to divide 5 by 6.

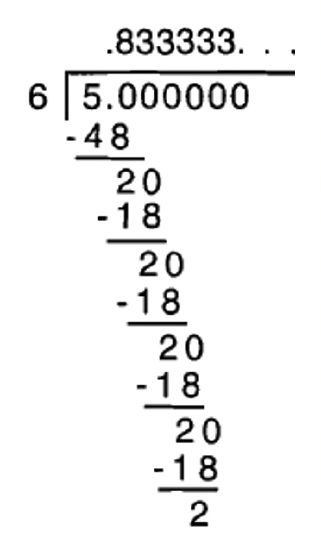
As you could see, I keep dividing 6 into 20, write 3, multiply to get 18, subtract from 20, get 2, bring down the 0, and start all over again. This can go on forever and ever. So, the 3’s at the end will trail on forever. This is NOT a terminating decimal since the number cannot be written with trailing zeroes. In this case, there are trailing 3s. The three dots at the end (called ellipses) of the number are to show that the 3s repeat forever. The answer can be written as 0.8333333... or \(0.8\bar{3}\). Remember to put the ellipses (three dots) at the end of the number! The bar over the 3 indicates that the 3 repeats forever and ever. Here are other ways to represent the same thing: \(0.8\overline{33}\) or \(0.8333\bar{3}\). In the first case, it says 33 repeats forever. In the second case, it says after the first three 3’s, the 3 repeats forever. In both cases, when you write it out in long form, it looks like 0.8333333... so it's the same number. Usually, we'll write 0.8333333... or \(0.8\bar{3}\).

Exercise 15

Write 0.8333333... or \(0.8\bar{3}\) in three more ways, different than \(0.8\overline{33}\) or \(0.8333\bar{3}\).

____________________ , ____________________, and ____________________

One thing to notice about what happened when we divided 5 by 6 is that I kept getting 2 after each subtraction in the division, this is like the remainder. Also remember that when you divide, each remainder must be less than or equal than what you are dividing by.

Exercise 16

Write the possible remainders for each number.

a. 6: _________________________________

b. 7: _________________________________

c. 9: _________________________________

d. 11: _________________________________

e. 3: _________________________________

Let's now look at what happens when you do long division compute \(\frac{4}{11}\) and \(\frac{2}{7}\).

In both of these cases, eventually, you get a remainder that you got previously, so the computation repeats itself. In the case of dividing 4 by 11, two remainders come up before there is some repetition 4 and 7. From 16d, you should have realized that the only possible remainders for 11 are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Now if you got a remainder of 0 when dividing, you'd have a terminating decimal. So, when dividing by 11, the most remainders you might get in a row before one repeats is 10 in a row. But in the case of \(\frac{4}{11}\), the remainders repeat after the 4 and 7. This means you keep dividing into 40 or 70 (since you bring the zero down) and that's why in the quotient the digits start repeating. Remember to put the ellipses (three dots) at the end of the number if there is a pattern of repeating digits.

Now in the case of dividing 2 by 7, the remainders you get as you go along are 6, then 4, then 5, then 1, then 3, and then 2. When you bring down the 0, you are dividing 7 into 20 again, and hence the remainders repeat. Notice that the sequence of remainders (6, 4, 5, 1, 3, and 2) is different than the sequence of digits that repeat in the quotient. The digits that repeat in the quotient are 285714, so \(\frac{2}{7}\) = 0.285714285714... or \(0.\overline{285714}\).

Since there are only six possible remainders other than zero when dividing by 7, only a sequence of 6 digits could possibly repeat. In this case, all six possible remainders of 7 appeared in the long division.

There are many ways to express the infinite or repeating decimal 0.285714285714... or \(0.\overline{285714}\). First of all, to establish what is repeating, you would want to see the sequence of digits repeating at least two times through. Therefore, 0.285714285714...is the shortest possible way of showing it when the ellipses (three dots) are used. If you simply wrote 0.285714..., it wouldn't be clear whether or not the 4 repeated or the 14 repeated, etc.

Here are a few other ways to write 0.285714285714... besides \(0.\overline{285714}\).

0.285714285714285714285714...

0.2857142857142857142...

(in this case, you see it as the 857142 repeating from this point on)

0.2857142857142857...

(in this case, you see it as the 142857 repeating from this point on)

\(0.28\overline{571428}\)

(in this case, you see it as the 571428 repeating from this point on)

Exercise 17

Write 0.285714285714... two more ways using ellipses (the three dots) and two more ways using a bar over a repeating sequence of digits.

Exercise 18

Determine which of the following is equivalent to 0.383432432432...

One way to do this is write the number out in long form by carefully continuing the pattern and then check the digits one place value at a time.

• 0.3834324324...
• 0.383432432...
• 0.3834323432...
• \(0.38343\overline{243}\)
• \(0.38\overline{34324}\)

Keep in mind that if you are finding a decimal equivalent for a fraction with 17 in the denominator that there may be up to sixteen digits in a row before you see any repetition. Now, obviously, there are only 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) in base ten. Note that the sequence of digits repeating in the quotient is totally different than the possible remainders you might get when you divide by 17 since a remainder may be more than a single-digit number.

Exercise 19

a. How many possible remainders could there be if you divide a number by 33?

b. Do long division to write \(\frac{31}{33}\) as a repeating decimal using ellipses and then using the bar over the repeating digits on this line: ______________________________

Show work here:

c. In the long division, how many digits repeat? ______

d. In the long division, what were the remainders you would keep getting if you continued the division forever and ever? _________________

Exercise 20

Use your calculator to write each as a repeating decimal. Write the answer two ways, first with a bar over the repeating digits, and then in long form, using ellipses . Note that your calculator may or may not round the last digit shown. It can't show digits repeating forever, so you have to be savvy enough to know whether the decimal showing on the display is terminal or if it is an approximation.

a. \(\frac{5}{9}\) = ________________ = _______________________________

b. \(\frac{5}{7}\) = ________________ = _______________________________

c. \(\frac{1}{6}\) = ________________ = _______________________________

d. \(\frac{2}{3}\) = ________________ = _______________________________

e. \(\frac{7}{11}\) = ________________ = _______________________________

f. \(\frac{5}{12}\) = ________________ = _______________________________

g. \(\frac{8}{15}\) = ________________ = _______________________________

h. \(\frac{16}{45}\) = ________________ = _______________________________

i. \(\frac{5}{66}\) = ________________ = _______________________________

Exercise 21

If you are changing a simplified fraction to a decimal where the denominator is x, how many digits at most can repeat in the quotient? _________

Well, you've learned how to write terminating decimals as fractions, and how to write fractions as decimals. You should be able to determine whether a fraction can be written as a terminating or repeating decimal before doing the actual division.

Rational Numbers are defined to be numbers which can be expressed as the ratio of two integers. Fractions as we usually refer to them (without decimal points or square roots, etc. in the numerator or denominator) are rational numbers. Since all fractions can be written as terminating or nonterminating (infinite, repeating) decimals, then all terminating and repeating decimals are also rational numbers. In Exercise 1, you wrote some terminating decimals as fractions. Since all nonterminating decimals came from a fraction, now we want to be able to go the other way around and write a repeating decimal as a fraction. We've got a nifty trick for doing just that!

Let's say we wanted to write \(0.\overline{72}\) or 0.727272727272... as a fraction.

First, notice this is a very different number from 0.72, since 0.72 is seventy-two hundredths, or \(\frac{72}{100}\). This simplifies to \(\frac{18}{25}\). So,0 .72 and \(\frac{18}{25}\) are the same number. You can check to make sure \(\frac{18}{25}\) is the correct fraction by using a calculator and dividing 18 by 25. The calculator should read 0.72, which is where we started.

Okay, so how do we write \(0.\overline{72}\) as a fraction? Since this is a repeating decimal that has infinitely many digits, there is no single power of ten we can put in the denominator. The trick is to use algebra to write a number in a way that eliminates the infinitely repeating part of the decimal. First, let's write out \(0.\overline{72}\) the long way:

\(0.\overline{72}\) = .727272727272... and call it the number x. So x = 0.727272727272...

Remember that if you multiply a decimal by 10, the decimal point moves one place to the right, and when you multiply a decimal by 100, the decimal point moves two places to the right, etc.

Exercise 22

If x = 0.727272727272..., then write out what 10x, 100x and 1000x equals. Write it out without using the bar over the repeating digits. Use the ellipses (three dots).

10x = _______________________________

100x = _______________________________

1000x = _______________________________

Exercise 23

Okay, let's work with x = 0.727272727272... and 100x = 72.727272727272...

a. In algebra, what is 100x - x? _________ (Hint: Subtract coefficients.)

b. Compute 100x - x another way: Line up the decimal points and subtract 0.727272727272... from 72.727272727272... Notice that if the decimals are lined up, the "tails" at the end of both repeating decimals are exactly the same so it should be easy to subtract. Show the work below.

c. Write an equation so that the answer to part a equals the answer to part b. Then use algebra to solve for x. Show work.

d. Simplify the fraction you got for x in part c. Show work.

e. Use a calculator to rewrite the fraction you got in part c as a decimal:

Is it equal to \(0.\overline{72}\)? __________

If so, you must have written \(0.\overline{72}\) as the correct fraction!

Here's the trick for changing repeating decimals to simplified fractions:

Call the number you are trying to write as a decimal a variable, like \(n\) or x.

If there is one repeating digit, compute 10x; if there are two repeating digits, compute 100x; if there are three repeating digits, compute 1000x, etc. This aligns the repeating decimals up with each other so that the tail of x and the other number (10x, 100x, 1000x, etc.) is the same.

Then subtract x from the other number (10x, 100x, 1000x, etc.) The tails of both numbers will come off and you should have an algebraic problem to solve at this point. Make sure you write your answer as a reduced fraction with only integers in the numerator and denominator.

Here are two examples. If you write the number in decimal form without the bar over the number, remember to put the ellipses (three dots) at the end!

Exercise 24

Rewrite each of the following decimals as simplified fractions. For repeating decimals, use the technique shown in the previous examples. Then, check your answer using a calculator by dividing the numerator by the denominator to see if the result matches the original problem.

b. \(0.\bar{4}\) Begin by letting x = \(0.\bar{4}\) or x = 0.44444...

d. \(0.\overline{06}\) Begin by letting x = \(0.\overline{06}\) or x = 0.060606...

f. \(0.\bar{9}\) Begin by letting x = \(0.\bar{9}\) or x = 0.9999... (this answer might surprise you)

h. \(0.\overline{45}\) Begin by letting x = \(0.\overline{45}\) or x = 0.454545...

j. \(0.\overline{084}\) Begin by letting x = \(0.\overline{084}\) or 0.084084084...

Sometimes, the arithmetic gets a little more challenging. Consider writing 0.14444... as a fraction. The 4 repeats starting two places after the decimal point. We plunge forward as before, but there's a little glitch at the end because one side of the equation will have a decimal point in it. If we were to divide by 9, the fraction will have a decimal point in the numerator so it isn't a reduced rational number; both the numerator and denominator have to be integers. Here are basic steps up until that point.

\(10n = 1.444444...\) and \(n = 0.144444\)

Subtracting, we get \(9n = 1.3\)

One way to remedy this situation is to multiply both sides of the equation by 10 (or 100 or 1000 as needed) to eliminate the decimal. This is like clearing fractions by multiplying both sides of an equation by the least common denominator.

So multiply both sides of \(9n = 1.3\) by 10 to get \(90n = 13\). Then divide by 90 to get \(\frac{13}{90}\).

Another way to remedy this situation is to write the right side of the equation as a fraction. Remember that 1.3 is \(\frac{13}{10}\). So the equation is \(9n=\frac{13}{10}\).

You can cross multiply to get \(90n = 13\) and then divide by 90 to get \(n = \frac{13}{90}\)

In any case, remember that a reduced fraction is the ratio of two integers that are relatively prime.

Exercise 25

Rewrite each repeating decimal, use the technique shown in the previous example, as a simplified fraction. Then, using your calculator, divide the numerator by the denominator and see if the result matches the original problem.

a. 0.02828...

b. 0.2888...

c. 0.00666...

d. 0.1011011...

e. 0.3999...

So, what did you think about the answer to 24f and 25e? Both of those are little mind-boggling. It's kind of hard to accept, but 0.999999... is really the same number as 1. It's not less than 1 it's exactly 1! For 24f, if you let \(10n = 9.999...\) and \(n =0 .999...\), then subtracting \(n\) from \(10n\) yields \(9n = 9\), so \(n = 1\). That's hard to swallow, but it's the truth! Another way to see this is to realize that 1/3 + 2/3 = 1. But 1/3 = 0.333333.... and 2/3 = 0.666666... Then, 1/3 + 2/3 = 0.33333... + 0.66666... = 0.99999.... We know 1/4 + 2/3 = 1, so 0.99999... must also equal 1, as well. Oh, this stuff is just too cool!

For 0.39999..., the result of repeating 9s after a decimal makes 0.39999...= 0.4 = \(\frac{4}{10} = \frac{2}{5}\).

So, basically, any number with a bunch of trailing 9s ends up being a terminating decimal.

All of the numbers we've been dealing with so far fractions, terminating decimals, and repeating decimals make up the rational numbers. Every rational number can be written as the ratio of two relatively prime integers, and can also be written as a terminating or repeating decimal. Conversely, every terminating and repeating decimal is a rational number.

Oh, but there's more...much more!

The rationals make up a very small part of the real numbers. To complete the real number system, we have to talk about the irrational numbers. Every real number is either rational or irrational. Those numbers which cannot be written as the ratio of two relatively prime integers is irrational. Those decimal numbers which neither terminate nor repeat are irrational. So, what do they look like?

One of the most commonly known irrational numbers is \(\pi\). It is the number that is the ratio of the circumference of a circle to its diameter. Sounds like it's a ratio of two integers, but it's not! \(\pi\) can only be approximated. The most common approximation is 3.14 or 22/7. Neither of these is equal to \(\pi\) because both of these are rational numbers, and \(\pi\) is not!

Other irrational numbers are square roots of numbers that are not perfect squares, or cube roots of numbers that are not perfect cubes, etc.

For instance, these numbers are irrational: \( \sqrt{5}, \sqrt{3}, \sqrt{12}, \sqrt{20}, \sqrt[3]{35}, \sqrt[4]{72}\)

Exercise 26

Write five irrational numbers not already listed above ________________________

Exercise 27

Is \(\sqrt{9}\) irrational? _____ Why or why not? ________________________________

Another way to express an irrational number in decimal form is to make up a decimal that perhaps has some pattern to it, but never terminates or repeats. Two examples of this type are 2.12112111211112... and 5.010203040506070809010011012...

Exercise 28

Write four irrational numbers in decimal form that shows a clear pattern.

Exercise 29

Write both a rational number and an irrational number in decimal form that is between 0.53 and 0.54.

Exercise 30

Write both a rational number and an irrational number in decimal form that is between 0.53333... and 0.54444...

Rational ______________________

Irrational ______________________

Exercise 31

Classify each of the following numbers as rational or irrational.

a. 0.428222... ___________________

b. 0.283848... ___________________

c. \(\frac{5}{13}\) ___________________

d. \(\sqrt{80}\) ___________________

e. \(\sqrt{100}\) ___________________

f. \(\pi\) ___________________

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 6: Decimals

About this unit, intro to decimals.

• Decimal place value (Opens a modal)
• Decimals as words (Opens a modal)
• Writing decimal numbers shown in grids (Opens a modal)
• Decimals in words 4 questions Practice
• Write decimals and fractions greater than 1 shown on grids 4 questions Practice

Decimal place value intro

• Place value names 7 questions Practice
• Value of a digit 7 questions Practice

Decimals on the number line

• Comparing decimal numbers on a number line (Opens a modal)
• Plotting decimal numbers on a number line (Opens a modal)
• Decimals on the number line: tenths 0-1 4 questions Practice
• Decimals on the number line: tenths 4 questions Practice
• Decimals on the number line: hundredths 0-0.1 4 questions Practice
• Decimals on the number line: hundredths 4 questions Practice

Rewriting decimals as fractions

• Writing a number as a fraction and decimal (Opens a modal)
• Rewriting decimals as fractions: 0.15 (Opens a modal)
• Rewriting decimals as fractions: 0.8 (Opens a modal)
• Rewriting decimals as fractions: 0.36 (Opens a modal)
• Rewriting tricky fractions to decimals (Opens a modal)
• Write fractions as decimals (denominators of 10 & 100) 4 questions Practice
• Write decimals and fractions shown on grids 4 questions Practice
• Write decimals as fractions 7 questions Practice

Adding decimals

• Adding decimals (Opens a modal)
• Adding decimals < 1 (tenths) 4 questions Practice
• Adding decimals and whole numbers (tenths) 4 questions Practice
• Adding decimals (tenths) 4 questions Practice
• Adding decimals < 1 (hundredths) 4 questions Practice
• Adding decimals and whole numbers (hundredths) 4 questions Practice
• Adding decimals (hundredths) 4 questions Practice

Adding decimals: standard algorithm

• Adding decimals: 9.087+15.31 (Opens a modal)
• Adding decimals: 0.822+5.65 (Opens a modal)
• Adding three decimals (Opens a modal)
• Adding decimals: tenths 7 questions Practice
• Adding decimals: hundredths 7 questions Practice
• Adding decimals: thousandths 7 questions Practice

Subtracting decimals

• Subtracting decimals: 9.57-8.09 (Opens a modal)
• Subtracting decimals: 10.1-3.93 (Opens a modal)
• Subtracting decimals (Opens a modal)
• Subtract decimals < 1 (tenths) 4 questions Practice
• Subtracting decimals (tenths) 4 questions Practice
• Subtracting decimals and whole numbers (tenths) 4 questions Practice
• Subtract decimals < 1 (hundredths) 4 questions Practice
• Subtract decimals (hundredths) 4 questions Practice
• Subtract decimals and whole numbers (hundredths) 4 questions Practice

Subtracting decimals: standard algorithm

• Subtracting decimals: 9.005 - 3.6 (Opens a modal)
• Subtracting decimals: 39.1 - 0.794 (Opens a modal)
• Subtracting decimals: tenths 7 questions Practice
• Subtracting decimals: hundredths 7 questions Practice
• Subtracting decimals: thousandths 7 questions Practice

Adding and subtracting decimals word problems

• Adding decimals word problem (Opens a modal)
• Adding & subtracting decimals word problem (Opens a modal)
• Adding & subtracting decimals word problems 4 questions Practice

Multiplying decimals

• Intro to multiplying decimals (Opens a modal)
• Multiplying decimals: place value (Opens a modal)
• Multiplying decimals (no standard algorithm) (Opens a modal)
• Multiply decimals tenths 7 questions Practice
• Multiply whole numbers and decimals less than 1 4 questions Practice
• Multiply decimals (1&2-digit factors) 4 questions Practice

Multiplying decimals: standard algorithm

• Multiplying challenging decimals (Opens a modal)
• Decimal multiplication place value 4 questions Practice
• Multiplying decimals like 0.847x3.54 (standard algorithm) 4 questions Practice

Dividing decimals

• Dividing whole numbers to get a decimal (Opens a modal)
• Dividing decimals (Opens a modal)
• Divide whole numbers to get a decimal (1-digit divisors) 4 questions Practice
• Divide whole numbers to get a decimal (2-digit divisors) 4 questions Practice
• Divide decimals by whole numbers 4 questions Practice
• Divide decimals like 16.8÷40 by factoring out a 10 4 questions Practice
• Divide whole numbers like 80÷200 to get a decimal 4 questions Practice
• Divide whole numbers by decimals 4 questions Practice
• Divide whole numbers by 0.1 or 0.01 7 questions Practice
• Divide decimals like 1.32÷0.12 4 questions Practice

Dividing decimals: standard algorithm

• Dividing decimals with hundredths (Opens a modal)
• Dividing decimals completely (Opens a modal)
• Long division with decimals (Opens a modal)
• Dividing by a multi-digit decimal (Opens a modal)
• Dividing decimals: hundredths 4 questions Practice
• Dividing decimals: thousandths 4 questions Practice

Significant figures

• Intro to significant figures (Opens a modal)
• Rules of significant figures (Opens a modal)
• Multiplying and dividing with significant figures (Opens a modal)
• Addition and subtraction with significant figures (Opens a modal)
• Significant figures 7 questions Practice

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Perform Operations of Decimals: Word Problems

Greetings, budding mathematicians! Today, we're going to jump into an adventure with decimals. Working with decimals is a fundamental math skill that you'll use in many aspects of life, from managing money to measuring distances.

Introduction to Decimal Operations

First things first, let’s talk about decimals. A decimal is a way of representing a number that’s less than one, or a number that’s a whole and a fraction together. When you work with decimals, the same rules apply as when you’re working with whole numbers, but the decimal point plays a crucial role.

There are four major operations that you can perform on decimals:

• Subtraction
• Multiplication

Now, let’s tackle some word problems involving decimal operations.

Step-By-Step Guide to Solving Word Problems with Decimal Operations

Step 1: understand the problem.

First and foremost, carefully read through the problem. Identify what you know and what you need to find out.

Step 2: Plan the Solution

Next, decide which operation (addition, subtraction, multiplication, or division) will help you solve the problem. This will depend on what the problem is asking.

Step 3: Carry Out the Operation

Perform the operation on the decimals. Remember to align the decimal points when you’re adding or subtracting, and apply the rules for multiplication and division of decimals correctly.

Step 4: Check the Answer

Finally, check if your answer makes sense in the context of the problem.

Consider this problem: Laura bought \(2.3\) kilograms of apples and \(1.5\) kilograms of grapes. How many kilograms of fruit did she buy in total?

Step 1: Understand that you know the weight of apples and grapes separately, and you need to find the total weight.

Step 2: Realize that to find the total, you need to add the weights together.

Step 3: Add the weights: \(2.3\ kg + 1.5\ kg = 3.8\ kg\).

Step 4: Check that the answer makes sense. Laura bought \(2.3\ kg\) of apples and \(1.5\ kg\) of grapes, so it makes sense that she bought \(3.8\ kg\) in total.

Keep practicing with different word problems, and you’ll get the hang of decimal operations in no time. Remember, the more you practice, the better you’ll get. Happy calculating!

by: Effortless Math Team about 9 months ago (category: Articles )

What people say about "How to Perform Operations of Decimals: Word Problems - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos
• Google Play
• Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Module 9: Multi-Step Linear Equations

Introduction to solving word problems that have decimals, what you’ll learn to do: solve word problems that have decimals by applying the problem-solving method.

Decimals often appear in problems dealing with money.

Emily is digging through her car to find change to put in the parking meter. She finds twice as many dimes as nickels, and one fewer quarter than dimes. Altogether, she comes up with $2.00–just enough to cover the amount of time she’ll have to park for her appointment! How can you figure out how many of each coin Emily put in the meter? You’ll need to think about the value of each coin, which is usually expressed as a decimal (quarters are worth $.25, dimes are $.10, and so on). In this section, you’ll practice solving word problems like this one involving coins, tickets, and stamps.

Before you get started in this module, try a few practice problems and review prior concepts.

readiness quiz

• Question ID 140282, 140288, 140292. Authored by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Ex: Solve a Basic Two Step Equation With Decimals (Clear Decimals). Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/Yc74lLdtPrU . License : CC BY: Attribution
• Using the Distributive Property to Multiply Quickly. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/VyDN3wUjYZs . License : CC BY: Attribution
• Examples 1: Multiplication of Decimals. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/4LcYhKMbGzk . License : CC BY: Attribution
• Coins. Authored by : chefranden. Located at : https://www.flickr.com/photos/chefranden/908539119/ . License : CC BY: Attribution
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

• Math Article
• Repeating Decimal To Fraction

Repeating Decimal to Fraction

In mathematics, a fraction is a value, which defines the part of a whole. In other words, the fraction is a ratio of two numbers. Whereas, the decimal is a number, whose whole number part and the fractional part is separated by a decimal point. The decimal number can be classified into different types, such as terminating and non-terminating decimals, repeating and non-repeating decimals. While solving many mathematical problems, the conversion of decimal to the fractional value is preferred, as we can easily simplify the fractional values. In this article, we are going to discuss how to convert repeating decimals to fractions in an easy way.

Terminating and Non-Terminating Decimals

A terminating decimal is a decimal, that has an end digit. It is a decimal, which has a finite number of digits(or terms).

Example: 0.15, 0.86, etc.

Non-terminating decimals are the one that does not have an end term. It has an infinite number of terms.

Example: 0.5444444….., 0.1111111….., etc.

Repeating and Non-Repeating Decimals

Repeating decimals are the one, which has a set of terms in decimal to be repeated uniformly.

Example: 0.666666…., 0.123123…., etc.

It is to be noted that the repeated term in decimal is represented by a bar on top of the repeated part. Such as \(\begin{array}{l}0.333333….. = 0.\bar{3}\end{array} \)

Non-repeating decimals are the one that does have repeated terms.

The square roots of all the terms (except perfect squares) are irrational numbers.

Non- Terminating and repeating decimals are Rational numbers and can be represented in the form of p/q, where q is not equal to 0.

Repeating Decimals to Fraction Conversion

Let us now learn the conversion of repeating decimals into the fractional form. Now, we are going to discuss the two different cases of the repeating fraction.

The formula to convert this type of repeating decimal to a fraction is given by:

Example 1: 

Here, the number of repeated term is 7 only. Thus the number of times 9 to be repeated in the denominator is only once.

Example 2: 

Convert 0.125125125… to the fractional form.

Here, 125 consists of three terms, and it is repeated in a continuous manner. Thus, the number of time 9 to be repeated in the denominator becomes three.

The formula to convert this type of repeating decimal to the fraction is given by:

In the given decimal number, 12 is a non-repeated decimal value, and 34 is in the repeating form. Thus denominator becomes 9900.

In the given decimal number, the number 00 is a non-repeated decimal value, and 69 is in the repeating form. Thus, the denominator becomes 9900.

It is all about the conversion of repeating decimals to the fraction form. To learn more interesting topics in Maths, download BYJU’S – The Learning App and learn with ease.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Very helpful

very good work of Byjus and I am also having your plan

Very useful and interesting fantastic 😁

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Non Terminating Decimal Examples (The Ultimate List)

Whether you realize it or not, non terminating decimal examples are everywhere in math. They can be quite scary when you happen to come across one! There is something unnerving about seeing a long string of seemingly random numbers to the right of the decimal point. 

But just what exactly are non terminating decimal numbers? And how do you recognize non terminating decimal examples when you see them? 

Let’s get into it so that you can  terminate  your confusion once and for all! See what I did there?

Non-Terminating Decimal Definition

Simply put, non terminating decimals are decimal numbers that do not have an end. An easy way to remember this definition is that the word “terminate” literally means “bring to an end.” So, it makes sense that  non -terminating means  does not  come to an end.

When you look to right of the decimal point in a non-terminating decimal number, you will see a series of decimal digits that does not end.

Pretty scary, right? No end!?

There are a few specific types of decimals that can be grouped to make it easier to understand non terminating decimal numbers. For example:

• Irrational Numbers: numbers that cannot be expressed as a fraction of two integers.
• Repeating decimal numbers: numbers that have repeating digits that form some sort of pattern.
• Non-repeating decimal numbers (or non-recurring decimal numbers): numbers that do not have a set of digits that repeat in some sort of pattern.

Let’s take a look at a few common non terminating decimal examples from each of these categories to simplify things!

Non Terminating Decimal Examples

When it comes to decimal numbers that do not have an end, there are an infinite number of such decimals. Some are quite famous, while others are more obscure and harder to come across. 

Non terminating decimal examples can take many forms. You may come across them when evaluating a square root, finding the decimal representation of a fraction, or calculating the area of a circle. 

This list of non terminating decimal examples will help you understand the possible cases where you could encounter a decimal number that does not have an end term to the right of the decimal point.

Pi: The Most Famous Non Terminating Decimal Example

Pi (written as π) is potentially one of the most famous numbers there is. It has been depicted in movies and TV shows, and it even has it’s own day named after it !

Even non-mathematicians know at least a few digits of pi, but few know its meaning or the reason it is an example of a non-terminating decimal number.

Pi is considered an irrational non-terminating decimal number because it cannot be written as the ratio of two integer numbers. To calculate an accurate estimation of pi, one must look at the ratio of the circumference of a circle to its diameter. The result is a value that is non terminating  and  non-repeating. 

This means that not only does pi not end, but it also has no group of digits to form any sort of repeated pattern. There are just an infinite number of digits to the right of the decimal point.

Because of this, it is common for mathematicians to  round  pi to 3.14. However, rounding pi in this way can be problematic as it can lead to inaccuracies in complex calculations.

Euler’s Number

While it isn’t as famous amongst non-mathematicians as Pi, Euler’s number has many applications that range from compound interest, to probability, to calculus.

Named after Swiss mathematician Leonhard Euler, Euler’s number is approximately equal to 2.71828 and is commonly known as  e.  Like Pi, Euler’s number is a non-terminating decimal number that is also a non-repeating decimal number. This means that  e  has no end term nor any single block of digits that is repeated to the right of the decimal point.

Also like Pi,  e  is an irrational number, meaning that it cannot be expressed as a fraction of two integer numbers. 

Square Root Examples

Another common place that you will see non terminating decimal examples is when calculating square roots. 

Not every square root will be non-terminating. Perfect roots will result in whole numbers when a square root is performed. For example, calculating the square root of 4 will result in 2 – a whole number. This is also the case for 9, 16, 25, and any other perfect square number. Since these numbers do not contain decimals that continue without end, they are considered examples of terminating decimal numbers .

By comparison, a number such as the square root of 2, or \(\sqrt{2}\), is a different story! The decimal equivalent of the square root of 2 turns out to be 1.4142135624… You will notice that \(\sqrt{2}\) has an infinite number of decimal places and does not have a repeating block of digits. 

This is also the case for square roots such as \(\sqrt{3}\), \(\sqrt{5}\), and many more!

These types of square root numbers are non-terminating, non-repeating,  and  irrational numbers.

Decimal numbers are often seen as a different form of a fraction. Because of this, it makes sense that there are some examples of fractions that will produce non-terminating decimal numbers as well!

There are many non terminating decimal examples that are fractions. For example, the fraction \(\frac{1}{3}\) can be written in decimal form as 0.3333…  Notice that the digit 3 forms a repeating pattern. Because of this, 0.3333… in fraction form is considered a repeating non-terminating decimal number. 

By contrast, the fraction \(\frac{2}{7}\) can be written as 0.285714285714…. This is an interesting example of a decimal number that has a repeating block of digits that forms a repeating pattern to the right of the decimal point. Notice that the block of “285714” is repeated without end. As such, \(\frac{2}{7}\) is considered a repeating non-terminating decimal number when it is written in decimal form.

There are also examples of improper fractions that are non terminating when written in decimal form. Consider the fraction \(\frac{12}{7}\) for example. In decimal form, this fraction is equal to 1.7142857142857 …

You will notice that when this improper fraction is written in decimal form, it also forms a repeating block of digits. As such, \(\frac{12}{7}\) is considered a repeating non-terminal decimal number.

Understanding Non Terminating Decimal Examples

In order to fully understand the concept of a non terminating decimal number, it is important to look at many different examples and types of decimals. As you saw with the non terminating decimal examples above, there are many different ways for a decimal number to “not end’.

Whether it is a repeating pattern, or no pattern at all, non terminating decimal numbers are a pretty bizarre idea! You may think to yourself “so, wait … the decimal keeps going forever? Without end?” But with some practice, this idea becomes a bit easier to process.

Did you find this guide to non terminating decimal examples helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

Linear Equations Word Problems Worksheet with Solutions

Free Linear Inequalities Word Problems Worksheet