how to solve convex optimization problems

• Create an account
• Analytic Solver Overview
• Analytic Solver Optimization
• Analytic Solver Simulation
• Analytic Solver Data Science
• Analytic Solver Academy
• RASON Decision Services
• Solver Engines
• Optimization and Simulation
• Forecasting and Data Mining
• Case Studies
• Data Mining Webinar
• Optimization Webinar
• Simulation Webinar
• Optimization Tutorials
• Simulation Tutorials
• Data Mining Tutorials
• Finance Examples
• Investment Examples
• Production Examples
• Distribution Examples
• Purchasing Examples
• Scheduling Examples
• Video Demos
• Technical Support
• Consulting Help
• Academy Courses
• Excel Solver Help
• Data Science Help
• Excel User Guides
• SDK User Guides
• Recommended Books
• Product Catalog
• Types of Licenses
• License Agreement
• Limited Warranty
• Standard vs Custom Terms
• Invoicing Payment

Optimization Problem Types - Convex Optimization

Optimization problem types, why convexity matters, convex optimization problems, convex functions, solving convex optimization problems.

• Other Problem Types

"...in fact, the great watershed in optimization isn't between linearity and nonlinearity, but convexity and nonconvexity."

- R. Tyrrell Rockafellar, in SIAM Review , 1993

Convex optimization problems are far more general than linear programming problems, but they share the desirable properties of LP problems:  They can be solved quickly and reliably up to very large size -- hundreds of thousands of variables and constraints. The issue has been that, unless your objective and constraints were linear, it was difficult to determine whether or not they were convex.  But Frontline System's Premium Solver Platform products includes an automated test for convexity of your problem functions.

A convex optimization problem is a problem where all of the constraints are convex functions , and the objective is a convex function if minimizing, or a concave function if maximizing.  Linear functions are convex , so linear programming problems are convex problems.  Conic optimization problems -- the natural extension of linear programming problems -- are also convex problems. In a convex optimization problem, the feasible region -- the intersection of convex constraint functions -- is a convex region, as pictured below.

With a convex objective and a convex feasible region, there can be only one optimal solution, which is globally optimal .  Several methods -- notably Interior Point methods -- will either find the globally optimal solution, or prove that there is no feasible solution to the problem.  Convex problems can be solved efficiently up to very large size.

A non-convex optimization problem is any problem where the objective or any of the constraints are non-convex, as pictured below.

Such a problem may have multiple feasible regions and multiple locally optimal points within each region.  It can take time exponential in the number of variables and constraints to determine that a non-convex problem is infeasible, that the objective function is unbounded, or that an optimal solution is the "global optimum" across all feasible regions.

Geometrically, a function is convex if a line segment drawn from any point (x, f(x)) to another point (y, f(y)) -- called the chord from x to y -- lies on or above the graph of f, as in the picture below:

Algebraically, f s convex if, for any x and y, and any t between 0 and 1, f( tx + (1-t)y ) <= t f(x) + (1-t) f(y).  A function is concave if -f is convex -- i.e. if the chord from x to y lies on or below the graph of f.  It is easy to see that every linear function -- whose graph is a straight line -- is both convex and concave.

A non-convex function "curves up and down" -- it is neither convex nor concave.  A familiar example is the sine function:

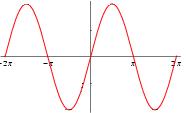
but note that this function is convex from -pi to 0, and concave from 0 to +pi.  If the bounds on the variables restrict the domain of the objective and constraints to a region where the functions are convex, then the overall problem is convex .

Because of their desirable properties, convex optimization problems can be solved with a variety of methods.  But Interior Point or Barrier methods are especially appropriate for convex problems, because they treat linear, quadratic, conic, and smooth nonlinear functions in essentially the same way -- they create and use a smooth convex nonlinear barrier function for the constraints, even for LP problems.

These methods make it practical to solve convex problems up to very large size, and they are especially effective on second order (quadratic and SOCP) problems , where the Hessians of the problem functions are constant. Both theoretical results and practical experience show that Interior Point methods require a relatively small number of iterations (typically less than 50) to reach an optimal solution, independent of the number of variables and constraints (though the computational effort per iteration rises with the number of variables and constraints).  Interior Point methods have also benefited, more than other methods, from hardware advances -- instruction caching, pipelining, and other changes in processor architecture.

Frontline Systems Solver Technology for Convex Problems

All Frontline Systems Solvers are effective on convex problems with the appropriate types of problem functions (linear, quadratic, conic, or nonlinear).  See Solver Technology for an overview of the available methods and Solver products. 

6.S098: Intro to Applied Convex Optimization

Course Syllabus

Convex optimization problems appear in a huge number of applications and can be solved very efficiently, even for problems with millions of variables. However, recognizing what can be transformed into a convex optimization problem can be challenging. This course will teach you how to recognize, formulate, and solve these problems. We will briefly survey theoretical results in convex analysis, but the majority of the course will focus on formulating and solving problems that come up in practice. Applications will include signal processing, statistics & machine learning, finance, circuit design, mechanical structure design, control, power systems, and other areas based on student interest. This course is designed for advanced undergraduates and beginning graduate students.

Prerequisites: multivariable calculus (18.02), linear algebra (18.06 or 18.061), basic probability, basic programming, mathematical maturity (e.g., 6.042)

Course Objectives

After this course, you should be able to...

recognize and formulate convex optimization problems that appear in various fields.

use open source software to solve these optimization problems.

decide which solver is best for your problem.

Textbook: Convex Optimization , by Stephen Boyd and Lieven Vandenberghe

Software: Convex.jl and convex optimization solvers.

Lectures are every Tuesday and Thursday from 1:00-2:30 PM, in 32-124. Most lectures will be taught by Theo Diamandis , but there may be a guest lecture or two.

Jan 10: Introduction to Optimization

Overview of optimization: least squares → \to → linear programs → \to → convex programs

Examples: portfolio optimization, mechanical design, machine learning, etc.

Convex sets & their properties

Jan 12: Convex Analysis & Optimization

Convex functions & their properties

Disciplined Convex Programming (DCP) & convex optimization software

Jan 17: Convex Optimization Problems and Applications

Problem classes: LPs, QPs, QCQPs, SOCPs, GPs

Multiobjective optimization ( e.g., regularized least squares, Markowitz portfolio optimization)

Case studies: model predictive control (how SpaceX lands rockets); circuit design

Jan 19: Applications: Approximation, Signal Processing

Regression problems (regularized, robust, quantile)

Case studies: minimax polynomial fitting (how does my computer compute sin , exp , etc.); image & audio denoising

Jan 24: Duality ( i.e. , understanding the output of your solver)

The Lagrange dual function and the dual problem

Case study: bounds for the two-way partitioning problem

Jan 27: Duality II

Optimality conditions & sensitivity analysis

Case studies: assigning power to communication channels ("water-filling"); FX arbitrage and no-arbitrage prices

Jan 31: Applications: Statistics & Machine Learning

Maximum likelihood & maximum a posteriori probability estimation (MLE & MAP)

Nonparametric distribution estimation

Case studies: Logistic regression, Support Vector Machine (SVM)

Feb 2: Advanced Topics

TBD based on class interest

Possible topics: more application areas, mixed integer programming, semidefinite programming, robust optimization

I will try to post course notes before the corresponding lectures. The notes are organized by topic instead of by lecture. Please let me know if you find any typos, either on Piazza or via email ([email protected]).

Optimization overview

Convex sets and functions

Convex optimization problem classes

Applications: approximation, signal processing, machine learning

Semidefinite programming and conic programs

Assignments

Problem sets.

Problem sets are assigned on Thursday and due the following Thursday at 11:59pm. Each problem set will ask you to model and solve convex optimization problems that come from various application areas. You'll need to use Julia and Convex.jl for the problem sets. See instructions here.

Most homework problems will be taken from the Convex Optimization additional exercises . Data files can be found here . It's easy to load these variables with include("filename.jl") .

HW 0: please sign up for Piazza and fill out the course survey. Also make sure you have Julia installed and Convex.jl working ( instructions ).

All homework will be submitted on Gradescope . Course code: 3JBNZX

There will be an optional course project during the last week of IAP that will allow you to apply convex optimization to a problem of interest. The final product will be a short mathematical description of this problem (akin to the descriptions you see on the problem sets) and a solution. Course grading is designed such that this project can take the place of the final problem set.

Project Information

Attendance is encouraged and will reflected in your final grade. You will received 1pt for each lecture attended, up to a maximum of 6pts.

Lecture attendance form

This course is offered for 6 units of credit, and the grading is P/D/F. To receive credit, you must get 14 or more points. The main goal of this course is to learn about optimization and solve some fun problems.

Office Hours

Tu/Th 2:30 - 3:30pm in 36-153, directly after class

Study night Wed 5pm - 7pm in [01/18: 32-144, 01/25: 32-141, 02/01: 32-144]

Room is booked 4pm - 8pm if you want to work there early/late

Acknowledgements

Much of the material for this course comes from the following courses:

Stephen Boyd's Convex Optimization I ( link )

Lieven Vandenberghe's Convex Optimization ( link )

Ryan Tibshirani's Convex Optimization ( link )

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Convex Optimization Problems

• Maximizing a convex function

Definition The optimization problem in standard form:

Note that these conditions are not always feasible, since the problem may not have any minimizer. This can happen for example when the optimal value is only attained in the limit; or, in constrained problems, when the feasible set is empty. Examples: – Minimization of a convex quadratic function. – Optimality condition for a convex, unconstrained problem. – Optimality condition for a convex, linearly constrained problem. The optimality conditions given above might be hard to solve. We will return to this issue later.

In the example mentioned above, where we seek to maximize the Euclidean norm of a point in a polyhedron, if we know the vertices of the polyhedron, that is, we can express the polyhedron as

Hyper-Textbook: Optimization Models and Applications Copyright © by L. El Ghaoui. All Rights Reserved.

Share This Book

• Convex Optimization

CSE 440: Introduction to Artificial Intelligence

Vishnu Boddeti

October 13, 2020

Content Credits: CMU AI, http://ai.berkeley.edu

Convex Optimization: Definition

• Convex Optimization Problem:
• A special class of optimization problem
• An optimization problem whose optimization objective $f$ is a convex function and feasible region $\mathcal{F}$ is a convex set.

Convex Combination

• A point between two points
• Given $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$, a convex combination of them is any point of the form $\mathbf{z}=\theta\mathbf{x}+(1-\theta)\mathbf{y}$ where $\theta \in [0,1]$.
• When $\theta \in [0,1]$, $\mathbf{z}$ is called a strict convex combination of $\mathbf{x}$, $\mathbf{y}$.

Convex Sets

• Conceptually : Any convex combination of two points in the set is also in the set
• Mathematically : A set $\mathcal{F}$ is convex if $\forall x,y\in \mathcal{F}, \forall \theta \in [0,1]$,

Quiz: Convex Set

• Which of the following sets are convex?
• $\mathcal{F} = \mathbb{R}^n$
• $\mathcal{F} = \emptyset$
• $\mathcal{F} = \{\mathbf{x}_0\}, \mathbf{x}_0 \in \mathbb{R}^n$
• $\mathcal{F} = \mathcal{F}_1 \bigcap \mathcal{F}_2$, where $\mathcal{F}_1$ and $\mathcal{F}_2$ are convex sets.
• $\mathcal{F} = \mathcal{F}_1 \bigcup \mathcal{F}_2$, where $\mathcal{F}_1$ and $\mathcal{F}_2$ are convex sets.

Convex Function

• Value in the middle point is lower than average value
• Let $\mathcal{F}$ be a convex set. A function $f:\mathcal{F}\rightarrow\mathbb{R}$ is convex in $\mathcal{F}$ if $\forall x,y \in \mathcal{F}, \forall \theta \in [0,1]$,
• If $\mathcal{F}=\mathbb{R}^n$, we simply say $f$ is convex.

How to determine if a functions is convex?

• Prove by definition
• Use properties of convex functions
• Sum of convex functions is convex
• Convexity is preserved under a linear transformation
• If $f$ is a twice differentiable function of one variable, $f$ is convex on an interval $[a,b]\subseteq \mathbb{R}$ iff (if and only if) its second derivative $f''(x) \geq 0$ in $[a,b]$
• If $f$ is a twice continuously differentiable function of $n$ variables, $f$ is convex on $\mathcal{F}$ iff its Hessian matrix of second partial derivatives is positive semidefinite on the interior of $\mathcal{F}$.
• $H$ is positive semidefinite in $S$ if $\forall \mathbf{x} \in S, \forall \mathbf{z}\in\mathbb{R}^n, \mathbf{z}^T H(\mathbf{x}) \mathbf{z} \geq 0$
• $H$ is positive semidefinite in $\mathbb{R}^n$ iff all eigenvalues of $H$ are non-negative.
• Alternatively, prove $\mathbf{z}^T H(\mathbf{x})\mathbf{z} = \sum_i g_i^2(x,z)$

Concavity and Convexity

• Concave function
• A function $f$ is concave if $-f$ is convex
• Let $\mathcal{F}$ be a convex set. A function $f:\mathcal{F}\rightarrow\mathbb{R}$ is concave in $\mathcal{F}$ if $\forall \mathbf{x},\mathbf{y}\in\mathcal{F}, \forall \theta\in[0,1]$,
• The following is a convex optimization problem if $f$ is a concave function and $\mathcal{F}$ is a convex set

Quiz 2: Convex Function

• Which of the following functions are convex?
• $f(x) = e^{ax}, a\in\mathbb{R}$
• $f(x) = \log x, x\in(0,+\infty)$
• $f(x) = \|\mathbf{x}\|_2=\sqrt{\sum_{i}^nx_i^2}$
• $f(\mathbf{x},\mathbf{y})=\mathbf{x}^T\mathbf{A}\mathbf{y}$, $\mathbf{A}\in\mathbb{R}^{m\times n}$, $\mathbf{x}\in\mathbb{R}^{m}$, $\mathbf{y}\in\mathbb{R}^{n}$
• $f(x)=x^3, x\in\mathbb{R}$

Convex Optimization: Local Optima=Global Optima

• Given an optimization problem, a point $\mathbf{x}\in\mathbb{R}^n$ is globally optimal if $\mathbf{x}\in\mathcal{F}$ and $\forall \mathbf{y}\in\mathcal{F}$, $f(\mathbf{x})\leq f(\mathbf{y})$
• Given an optimization problem, a point $\mathbf{x}\in\mathbb{R}^n$ is locally optimal if $\mathbf{x}\in\mathcal{F}$ and $\exists R>0$ such that $\forall \mathbf{y}:\mathbf{y}\in\mathcal{F}$ and $\|\mathbf{x}-\mathbf{y}\|_2\leq R$, $f(\mathbf{x})\leq f(\mathbf{y})$
• Theorem 1 : For a convex optimization problem, all locally optimal points are globally optimal

Convex Optimization: How to Solve?

• Recall discrete setting
• Local search
• Iteratively improving an assignment
• Continuous and differentiable setting
• Iteratively improving value of $\mathbf{x}$
• Based on gradient
• For $f:\mathbb{R}^n\rightarrow\mathbb{R}$, gradient is the vector of partial derivatives
• A multi-variable generalization of the derivative
• Point in the direction of steepest increase in $f$

Gradient Descent

• Gradient descent: iteratively update the value of $\mathbf{x}$
• A simple algorithm for unconstrained optimization $\min_{\mathbf{x}\in\mathbb{R}^n} f(\mathbf{x})$
• How to choose $\mathbf{x}_0$, e.g., $\mathbf{x}_0=\mathbf{0}$
• How to choose and update step-size $\alpha$, e.g., trial and error, line-search methods etc.
• How to define "convergence", e.g., $\|\mathbf{x}^{i+1}-\mathbf{x}^i\| \leq \epsilon$

Projected Gradient Descent

• Iteratively update the value of $\mathbf{x}$ while ensuring $\mathbf{x}\in\mathcal{F}$
• $P_{\mathcal{F}}$ projects a point to the constraint set.
• How to choose $P_{\mathcal{F}}$, e.g., $P_{\mathcal{F}}=\underset{\mathbf{x'} \in \mathcal{F}}{\operatorname{arg min}}\|\mathbf{x}-\mathbf{x'}\|_2^2$
• Unconstrained and differentiable
• Gradient descent
• Set derivative to be 0
• Closed form solution
• (Not covered) Newton's Method (if twice differentiable)
• Constrained and differentiable
• (Not covered) Projected gradient descent
• (Not covered) Interior Point Method
• (Not covered) Non-differentiable
• $\epsilon$-Subgradient Method
• Cutting Plane Method

Convex Optimization: Apply

• Model a problem as a convex optimization problem
• Define variable, feasible set, objective function
• Prove it is convex (convex function + convex set)
• Solve the convex optimization problem
• Build up the model
• Call a solver
• Examples: fmincon (MATLAB), cvxpy (Python), cvxopt (Python), cvx (MATLAB)
• Map the solution back to the original problem

Stanford University

Stanford engineering, s tanford e ngineering e verywhere, ee364a - convex optimization i, course details, course description.

Concentrates on recognizing and solving convex optimization problems that arise in engineering. Convex sets, functions, and optimization problems. Basics of convex analysis. Least-squares, linear and quadratic programs, semidefinite programming, minimax, extremal volume, and other problems. Optimality conditions, duality theory, theorems of alternative, and applications. Interiorpoint methods. Applications to signal processing, control, digital and analog circuit design, computational geometry, statistics, and mechanical engineering. Prerequisites: Good knowledge of linear algebra. Exposure to numerical computing, optimization, and application fields helpful but not required; the engineering applications will be kept basic and simple.

• DOWNLOAD All Course Materials

Boyd, Stephen

In addition to teaching large graduate courses on Linear Dynamical Systems, Nonlinear Feedback Systems, and Convex Optimization, Professor Boyd has regularly taught introductory undergraduate Electrical Engineering courses on Circuits, Signals and Systems, Digital Signal Processing, and Automatic Control. In 1994 he received the Perrin Award for Outstanding Undergraduate Teaching in the School of Engineering, and in 1991, an ASSU Graduate Teaching Award. In 2003, he received the AACC Ragazzini Education award, for contributions to control education, with citation: “For excellence in classroom teaching, textbook and monograph preparation, and undergraduate and graduate mentoring of students in the area of systems, control, and optimization.”

Lecture Notes

Additional lecture notes:, review session notes, assignments, reading assignments.

Unless otherwise noted, all reading assignments are from the textbook . Copyright in this book is held by Cambridge University Press.

Homework Assignments

All numbered exercises are from the textbook . Copyright in this book is held by Cambridge University Press.

You will sometimes need to download Matlab files, see Software below.

Matlab Files

Course sessions (19):, transcripts, stanford center for professional development.

• Stanford Home
• Maps & Directions
• Search Stanford
• Emergency Info
• Terms of Use
• Non-Discrimination
• Accessibility

© Stanford University, Stanford, California 94305

Help | Advanced Search

Computer Science > Data Structures and Algorithms

Title: improving the bit complexity of communication for distributed convex optimization.

Abstract: We consider the communication complexity of some fundamental convex optimization problems in the point-to-point (coordinator) and blackboard communication models. We strengthen known bounds for approximately solving linear regression, $p$-norm regression (for $1\leq p\leq 2$), linear programming, minimizing the sum of finitely many convex nonsmooth functions with varying supports, and low rank approximation; for a number of these fundamental problems our bounds are nearly optimal, as proven by our lower bounds. Among our techniques, we use the notion of block leverage scores, which have been relatively unexplored in this context, as well as dropping all but the ``middle" bits in Richardson-style algorithms. We also introduce a new communication problem for accurately approximating inner products and establish a lower bound using the spherical Radon transform. Our lower bound can be used to show the first separation of linear programming and linear systems in the distributed model when the number of constraints is polynomial, addressing an open question in prior work.

Submission history

Access paper:.

• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Imagery Overlap Block Compressive Sensing With Convex Optimization

Ieee account.

• Change Username/Password
• Update Address

Purchase Details

• Payment Options
• Order History
• View Purchased Documents

Profile Information

• Communications Preferences
• Profession and Education
• Technical Interests
• US & Canada: +1 800 678 4333
• Worldwide: +1 732 981 0060
• Contact & Support
• About IEEE Xplore
• Accessibility
• Terms of Use
• Nondiscrimination Policy
• Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.

MATLAB Answers

• Trial software

You are now following this question

• You will see updates in your followed content feed .
• You may receive emails, depending on your communication preferences .

How to implement a convex optimization problem in MATLAB using CVX

Direct link to this question

https://www.mathworks.com/matlabcentral/answers/1958444-how-to-implement-a-convex-optimization-problem-in-matlab-using-cvx

   1 Comment Show -1 older comments Hide -1 older comments

Direct link to this comment

https://www.mathworks.com/matlabcentral/answers/1958444-how-to-implement-a-convex-optimization-problem-in-matlab-using-cvx#comment_2734589

Sign in to comment.

Sign in to answer this question.

Accepted Answer

Direct link to this answer

https://www.mathworks.com/matlabcentral/answers/1958444-how-to-implement-a-convex-optimization-problem-in-matlab-using-cvx#answer_1241074

   0 Comments Show -2 older comments Hide -2 older comments

More answers (0).

• optimization

Community Treasure Hunt

Find the treasures in MATLAB Central and discover how the community can help you!

An Error Occurred

Unable to complete the action because of changes made to the page. Reload the page to see its updated state.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

You can also select a web site from the following list

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)
• 简体中文 Chinese
• 日本 Japanese (日本語)
• 한국 Korean (한국어)

Contact your local office

Enhanced Bilevel Optimization via Bregman Distance

Part of Advances in Neural Information Processing Systems 35 (NeurIPS 2022) Main Conference Track

Feihu Huang, Junyi Li, Shangqian Gao, Heng Huang

Bilevel optimization has been recently used in many machine learning problems such as hyperparameter optimization, policy optimization, and meta learning. Although many bilevel optimization methods have been proposed, they still suffer from the high computational complexities and do not consider the more general bilevel problems with nonsmooth regularization. In the paper, thus, we propose a class of enhanced bilevel optimization methods with using Bregman distance to solve bilevel optimization problems, where the outer subproblem is nonconvex and possibly nonsmooth, and the inner subproblem is strongly convex. Specifically, we propose a bilevel optimization method based on Bregman distance (BiO-BreD) to solve deterministic bilevel problems, which achieves a lower computational complexity than the best known results. Meanwhile, we also propose a stochastic bilevel optimization method (SBiO-BreD) to solve stochastic bilevel problems based on stochastic approximated gradients and Bregman distance. Moreover, we further propose an accelerated version of SBiO-BreD method (ASBiO-BreD) using the variance-reduced technique, which can achieve a lower computational complexity than the best known computational complexities with respect to condition number $\kappa$ and target accuracy $\epsilon$ for finding an $\epsilon$-stationary point. We conduct data hyper-cleaning task and hyper-representation learning task to demonstrate that our new algorithms outperform related bilevel optimization approaches.

Name Change Policy

Requests for name changes in the electronic proceedings will be accepted with no questions asked. However name changes may cause bibliographic tracking issues. Authors are asked to consider this carefully and discuss it with their co-authors prior to requesting a name change in the electronic proceedings.

Use the "Report an Issue" link to request a name change.