how to solve math probability questions

+ ACCUPLACER Mathematics
+ ACT Mathematics
+ AFOQT Mathematics
+ ALEKS Tests
+ ASVAB Mathematics
+ ATI TEAS Math Tests
+ Common Core Math
+ DAT Math Tests
+ FSA Tests
+ FTCE Math
+ GED Mathematics
+ Georgia Milestones Assessment
+ GRE Quantitative Reasoning
+ HiSET Math Exam
+ HSPT Math
+ ISEE Mathematics
+ PARCC Tests
+ Praxis Math
+ PSAT Math Tests
+ PSSA Tests
+ SAT Math Tests
+ SBAC Tests
+ SIFT Math
+ SSAT Math Tests
+ STAAR Tests
+ TABE Tests
+ TASC Math
+ TSI Mathematics
+ ACT Math Worksheets
+ Accuplacer Math Worksheets
+ AFOQT Math Worksheets
+ ALEKS Math Worksheets
+ ASVAB Math Worksheets
+ ATI TEAS 6 Math Worksheets
+ FTCE General Math Worksheets
+ GED Math Worksheets
+ 3rd Grade Mathematics Worksheets
+ 4th Grade Mathematics Worksheets
+ 5th Grade Mathematics Worksheets
+ 6th Grade Math Worksheets
+ 7th Grade Mathematics Worksheets
+ 8th Grade Mathematics Worksheets
+ 9th Grade Math Worksheets
+ HiSET Math Worksheets
+ HSPT Math Worksheets
+ ISEE Middle-Level Math Worksheets
+ PERT Math Worksheets
+ Praxis Math Worksheets
+ PSAT Math Worksheets
+ SAT Math Worksheets
+ SIFT Math Worksheets
+ SSAT Middle Level Math Worksheets
+ 7th Grade STAAR Math Worksheets
+ 8th Grade STAAR Math Worksheets
+ THEA Math Worksheets
+ TABE Math Worksheets
+ TASC Math Worksheets
+ TSI Math Worksheets
+ AFOQT Math Course
+ ALEKS Math Course
+ ASVAB Math Course
+ ATI TEAS 6 Math Course
+ CHSPE Math Course
+ FTCE General Knowledge Course
+ GED Math Course
+ HiSET Math Course
+ HSPT Math Course
+ ISEE Upper Level Math Course
+ SHSAT Math Course
+ SSAT Upper-Level Math Course
+ PERT Math Course
+ Praxis Core Math Course
+ SIFT Math Course
+ 8th Grade STAAR Math Course
+ TABE Math Course
+ TASC Math Course
+ TSI Math Course
+ Number Properties Puzzles
+ Algebra Puzzles
+ Geometry Puzzles
+ Intelligent Math Puzzles
+ Ratio, Proportion & Percentages Puzzles
+ Other Math Puzzles

How to Solve Probability Problems? (+FREE Worksheet!)

Do you want to know how to solve Probability Problems? Here you learn how to solve probability word problems.

Step by step guide to solve Probability Problems

Probability is the likelihood of something happening in the future. It is expressed as a number between zero (can never happen) to $1$ (will always happen).
Probability can be expressed as a fraction, a decimal, or a percent.
To solve a probability problem identify the event, find the number of outcomes of the event, then use probability law: $\frac{number\ of \ favorable \ outcome}{total \ number \ of \ possible \ outcomes}$

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Probability problems – example 1:.

If there are $8$ red balls and $12$ blue balls in a basket, what is the probability that John will pick out a red ball from the basket?

There are $8$ red balls and $20$ a total number of balls. Therefore, the probability that John will pick out a red ball from the basket is $8$ out of $20$ or $\frac{8}{8+12}=\frac{8}{20}=\frac{2}{5}$.

Probability Problems – Example 2:

A bag contains $18$ balls: two green, five black, eight blue, a brown, a red, and one white. If $17$ balls are removed from the bag at random, what is the probability that a brown ball has been removed?

If $17$ balls are removed from the bag at random, there will be one ball in the bag. The probability of choosing a brown ball is $1$ out of $18$. Therefore, the probability of not choosing a brown ball is $17$ out of $18$ and the probability of having not a brown ball after removing $17$ balls is the same.

Exercises for Solving Probability Problems

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

A number is chosen at random from $1$ to $10$. Find the probability of selecting a $4$ or smaller.
A number is chosen at random from $1$ to $50$. Find the probability of selecting multiples of $10$.
A number is chosen at random from $1$ to $10$. Find the probability of selecting of $4$ and factors of $6$.
A number is chosen at random from $1$ to $10$. Find the probability of selecting a multiple of $3$.
A number is chosen at random from $1$ to $50$. Find the probability of selecting prime numbers.
A number is chosen at random from $1$ to $25$. Find the probability of not selecting a composite number.

Download Probability Problems Worksheet

$\color{blue}{\frac{2}{5}}$
$\color{blue}{\frac{1}{10}}$
$\color{blue}{\frac{1}{2}}$
$\color{blue}{\frac{3}{10}}$
$\color{blue}{\frac{9}{25}}$

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

What people say about "How to Solve Probability Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

ATI TEAS 6 Math
ISEE Upper Level Math
SSAT Upper-Level Math
Praxis Core Math
8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

Math Worksheets
Math Courses
Math Topics
Math Puzzles
Math eBooks
GED Math Books
HiSET Math Books
ACT Math Books
ISEE Math Books
ACCUPLACER Books
Premium Membership
Youtube Videos
Google Play
Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

Bulk Orders
Refund Policy

Free Mathematics Tutorials

Probability questions with solutions.

Tutorial on finding the probability of an event. In what follows, S is the sample space of the experiment in question and E is the event of interest. n(S) is the number of elements in the sample space S and n(E) is the number of elements in the event E.

Questions and their Solutions

Answers to the above exercises, more references and links, popular pages.

Statistics and Probability Problems with Solutions - sample 3
File Not Found
Math Word Problems with Answers - Grade 8
Math Problems, Questions and Online Self Tests
High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers

Resource Links

Share with us.

Forgot password? New user? Sign up

Existing user? Log in

Probability - Problem Solving

Already have an account? Log in here.

Geoff Pilling
Sandeep Bhardwaj

To solve problems on this page, you should be familiar with

Uniform Probability
Probability - By Outcomes
Probability - Rule of Sum
Probability - Rule of Product
Probability - By Complement
Probability - Independent Events
Conditional Probability

Problem Solving - Basic

Problem solving - intermediate, problem solving - difficult.

If I throw 2 standard 5-sided dice, what is the probability that the sum of their top faces equals to 10? Assume both throws are independent to each other. Solution : The only way to obtain a sum of 10 from two 5-sided dice is that both die shows 5 face up. Therefore, the probability is simply $ \frac15 \times \frac15 = \frac1{25} = .04$

If from each of the three boxes containing $3$ white and $1$ black, $2$ white and $2$ black, $1$ white and $3$ black balls, one ball is drawn at random. Then the probability that $2$ white and $1$ black balls will be drawn is?

2 fair 6-sided dice are rolled. What is the probability that the sum of these dice is $10$? Solution : The event for which I obtain a sum of 10 is $\{(4,6),(6,4),(5,5) \}$. And there is a total of $6^2 = 36$ possible outcomes. Thus the probability is simply $ \frac3{36} = \frac1{12} \approx 0.0833$

If a fair 6-sided dice is rolled 3 times, what is the probability that we will get at least 1 even number and at least 1 odd number?

Three fair cubical dice are thrown. If the probability that the product of the scores on the three dice is $90$ is $\dfrac{a}{b}$, where $a,b$ are positive coprime integers, then find the value of $(b-a)$.

You can try my other Probability problems by clicking here

Suppose a jar contains 15 red marbles, 20 blue marbles, 5 green marbles, and 16 yellow marbles. If you randomly select one marble from the jar, what is the probability that you will have a red or green marble? First, we can solve this by thinking in terms of outcomes. You could draw a red, blue, green, or yellow marble. The probability that you will draw a green or a red marble is $\frac{5 + 15}{5+15+16+20}$. We can also solve this problem by thinking in terms of probability by complement. We know that the marble we draw must be blue, red, green, or yellow. In other words, there is a probability of 1 that we will draw a blue, red, green, or yellow marble. We want to know the probability that we will draw a green or red marble. The probability that the marble is blue or yellow is $\frac{16 + 20}{5+15+16+20}$. , Using the following formula $P(\text{red or green}) = 1 - P(\text{blue or yellow})$, we can determine that $P(\text{red or green}) = 1 - \frac{16 + 20}{5+15+16+20} = \frac{5 + 15}{5+15+16+20}$.

Two players, Nihar and I, are playing a game in which we alternate tossing a fair coin and the first player to get a head wins. Given that I toss first, the probability that Nihar wins the game is $\dfrac{\alpha}{\beta}$, where $\alpha$ and $\beta$ are coprime positive integers.

Find $\alpha + \beta$.

If I throw 3 fair 5-sided dice, what is the probability that the sum of their top faces equals 10? Solution : We want to find the total integer solution for which $a +b+c=10 $ with integers $1\leq a,b,c \leq5 $. Without loss of generality, let $a\leq b \leq c$. We list out the integer solutions: \[ (1,4,5),(2,3,5), (2,4,4), (3,3,4) \] When relaxing the constraint of $a\leq b \leq c$, we have a total of $3! + 3! + \frac{3!}{2!} + \frac{3!}{2!} = 18 $ solutions. Because there's a total of $5^3 = 125$ possible combinations, the probability is $ \frac{18}{125} = 14.4\%. \ \square$

Suppose you and 5 of your friends each brought a hat to a party. The hats are then put into a large box for a random-hat-draw. What is the probability that nobody selects his or her own hat?

How many ways are there to choose exactly two pets from a store with 8 dogs and 12 cats? Since we haven't specified what kind of pets we pick, we can choose any animal for our first pick, which gives us $ 8+12=20$ options. For our second choice, we have 19 animals left to choose from. Thus, by the rule of product, there are $ 20 \times 19 = 380 $ possible ways to choose exactly two pets. However, we have counted every pet combination twice. For example, (A,B) and (B,A) are counted as two different choices even when we have selected the same two pets. Therefore, the correct number of possible ways are $ {380 \over 2} = 190 $

A bag contains blue and green marbles. If 5 green marbles are removed from the bag, the probability of drawing a green marble from the remaining marbles would be 75/83 . If instead 7 blue marbles are added to the bag, the probability of drawing a blue marble would be 3/19 . What was the number of blue marbles in the bag before any changes were made?

Bob wants to keep a good-streak on Brilliant, so he logs in each day to Brilliant in the month of June. But he doesn't have much time, so he selects the first problem he sees, answers it randomly and logs out, despite whether it is correct or incorrect.

Assume that Bob answers all problems with $\frac{7}{13}$ probability of being correct. He gets only 10 problems correct, surprisingly in a row, out of the 30 he solves. If the probability that happens is $\frac{p}{q}$, where $p$ and $q$ are coprime positive integers, find the last $3$ digits of $p+q$.

Out of 10001 tickets numbered consecutively, 3 are drawn at random .

Find the chance that the numbers on them are in Arithmetic Progression .

The answer is of the form $ \frac{l}{k} $ .

Find $ k - l $ where $k$ and $l$ are co-prime integers.

HINT : You might consider solving for $2n + 1$ tickets .

You can try more of my Questions here .

A bag contains a blue ball, some red balls, and some green balls. You reach into the bag and pull out three balls at random. The probability you pull out one of each color is exactly 3%. How many balls were initially in the bag?

Photo credit: www.figurerealm.com

Amanda decides to practice shooting hoops from the free throw line. She decides to take 100 shots before dinner.

Her first shot has a 50% chance of going in.

But for Amanda, every time she makes a shot, it builds her confidence, so the probability of making the next shot goes up, But every time she misses, she gets discouraged so the probability of her making her next shot goes down.

In fact, after $n$ shots, the probability of her making her next shot is given by $P = \dfrac{b+1}{n+2}$, where $b$ is the number of shots she has made so far (as opposed to ones she has missed).

So, after she has completed 100 shots, if the probability she has made exactly 83 of them is $\dfrac ab$, where $a$ and $b$ are coprime positive integers, what is $a+b$?

Photo credit: http://polymathprogrammer.com/

Problem Loading...

Note Loading...

Set Loading...

Probability

How likely something is to happen.

Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability.

Tossing a Coin

When a coin is tossed, there are two possible outcomes:

Heads (H) or Tails (T)

the probability of the coin landing H is ½
the probability of the coin landing T is ½

Throwing Dice

When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6 .

The probability of any one of them is 1 6

In general:

Probability of an event happening = Number of ways it can happen Total number of outcomes

Example: the chances of rolling a "4" with a die

Number of ways it can happen: 1 (there is only 1 face with a "4" on it)

Total number of outcomes: 6 (there are 6 faces altogether)

So the probability = 1 6

Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked?

Number of ways it can happen: 4 (there are 4 blues)

Total number of outcomes: 5 (there are 5 marbles in total)

So the probability = 4 5 = 0.8

Probability Line

We can show probability on a Probability Line :

Probability is always between 0 and 1

Probability is Just a Guide

Probability does not tell us exactly what will happen, it is just a guide

Example: toss a coin 100 times, how many Heads will come up?

Probability says that heads have a ½ chance, so we can expect 50 Heads .

But when we actually try it we might get 48 heads, or 55 heads ... or anything really, but in most cases it will be a number near 50.

Learn more at Probability Index .

Some words have special meaning in Probability:

Experiment : a repeatable procedure with a set of possible results.

Example: Throwing dice

We can throw the dice again and again, so it is repeatable.

The set of possible results from any single throw is {1, 2, 3, 4, 5, 6}

Outcome: A possible result.

Example: "6" is one of the outcomes of a throw of a die.

Trial: A single performance of an experiment.

Example: I conducted a coin toss experiment. After 4 trials I got these results:

Three trials had the outcome "Head", and one trial had the outcome "Tail"

Sample Space: all the possible outcomes of an experiment.

Example: choosing a card from a deck

There are 52 cards in a deck (not including Jokers)

So the Sample Space is all 52 possible cards : {Ace of Hearts, 2 of Hearts, etc... }

The Sample Space is made up of Sample Points:

Sample Point: just one of the possible outcomes

Example: Deck of Cards

the 5 of Clubs is a sample point
the King of Hearts is a sample point

"King" is not a sample point. There are 4 Kings, so that is 4 different sample points.

There are 6 different sample points in that sample space.

Event: one or more outcomes of an experiment

Example Events:

An event can be just one outcome:

Getting a Tail when tossing a coin
Rolling a "5"

An event can include more than one outcome:

Choosing a "King" from a deck of cards (any of the 4 Kings)
Rolling an "even number" (2, 4 or 6)

Hey, let's use those words, so you get used to them:

Example: Alex wants to see how many times a "double" comes up when throwing 2 dice.

The Sample Space is all possible Outcomes (36 Sample Points):

{1,1} {1,2} {1,3} {1,4} ... ... ... {6,3} {6,4} {6,5} {6,6}

The Event Alex is looking for is a "double", where both dice have the same number. It is made up of these 6 Sample Points :

{1,1} {2,2} {3,3} {4,4} {5,5} and {6,6}

These are Alex's Results:

After 100 Trials , Alex has 19 "double" Events ... is that close to what you would expect?

Teach yourself statistics

How to Solve Probability Problems

You can solve many simple probability problems just by knowing two simple rules:

The probability of any sample point can range from 0 to 1.
The sum of probabilities of all sample points in a sample space is equal to 1.

The following sample problems show how to apply these rules to find (1) the probability of a sample point and (2) the probability of an event.

Probability of a Sample Point

The probability of a sample point is a measure of the likelihood that the sample point will occur.

Example 1 Suppose we conduct a simple statistical experiment . We flip a coin one time. The coin flip can have one of two equally-likely outcomes - heads or tails. Together, these outcomes represent the sample space of our experiment. Individually, each outcome represents a sample point in the sample space. What is the probability of each sample point?

Solution: The sum of probabilities of all the sample points must equal 1. And the probability of getting a head is equal to the probability of getting a tail. Therefore, the probability of each sample point (heads or tails) must be equal to 1/2.

Example 2 Let's repeat the experiment of Example 1, with a die instead of a coin. If we toss a fair die, what is the probability of each sample point?

Solution: For this experiment, the sample space consists of six sample points: {1, 2, 3, 4, 5, 6}. Each sample point has equal probability. And the sum of probabilities of all the sample points must equal 1. Therefore, the probability of each sample point must be equal to 1/6.

Probability of an Event

The probability of an event is a measure of the likelihood that the event will occur. By convention, statisticians have agreed on the following rules.

The probability of any event can range from 0 to 1.
The probability of event A is the sum of the probabilities of all the sample points in event A.
The probability of event A is denoted by P(A).

Thus, if event A were very unlikely to occur, then P(A) would be close to 0. And if event A were very likely to occur, then P(A) would be close to 1.

Example 1 Suppose we draw a card from a deck of playing cards. What is the probability that we draw a spade?

Solution: The sample space of this experiment consists of 52 cards, and the probability of each sample point is 1/52. Since there are 13 spades in the deck, the probability of drawing a spade is

P(Spade) = (13)(1/52) = 1/4

Example 2 Suppose a coin is flipped 3 times. What is the probability of getting two tails and one head?

Solution: For this experiment, the sample space consists of 8 sample points.

S = {TTT, TTH, THT, THH, HTT, HTH, HHT, HHH}

Each sample point is equally likely to occur, so the probability of getting any particular sample point is 1/8. The event "getting two tails and one head" consists of the following subset of the sample space.

A = {TTH, THT, HTT}

The probability of Event A is the sum of the probabilities of the sample points in A. Therefore,

P(A) = 1/8 + 1/8 + 1/8 = 3/8

PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
EDIT Edit this Article
EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
Browse Articles
Learn Something New
Quizzes Hot
This Or That Game New
Train Your Brain
Explore More
Support wikiHow
About wikiHow
Log in / Sign up
Education and Communications
Mathematics
Probability and Statistics

How to Calculate Probability

Last Updated: July 31, 2023 Fact Checked

This article was co-authored by Mario Banuelos, PhD . Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels. There are 8 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 3,432,023 times.

Chances are (pun intended) you've encountered probability by now, but what exactly is probability, and how do you calculate it? Probability is the likelihood of a specific event happening, like winning the lottery or rolling a 6 on a die. Finding probability is easy using the probability formula (the number of favorable outcomes divided by the total number of outcomes). In this article, we'll walk you through exactly how to use the probability formula step by step, plus show you some examples of the probability formula in action.

Finding the Probability of a Single Random Event

Step 1 Choose an event with mutually exclusive outcomes.

Example: It would be impossible to calculate the probability of an event phrased as: “Both a 5 and a 6 will come up on a single roll of a die.”

Step 2 Define all possible events and outcomes that can occur.

Example 1 : What is the likelihood of choosing a day that falls on the weekend when randomly picking a day of the week? "Choosing a day that falls on the weekend" is our event, and the number of outcomes is the total number of days in a week: 7.
Example 2 : A jar contains 4 blue marbles, 5 red marbles and 11 white marbles. If a marble is drawn from the jar at random, what is the probability that this marble is red? "Choosing a red marble" is our event, and the number of outcomes is the total number of marbles in the jar, 20.

Example 1 : What is the likelihood of choosing a day that falls on the weekend when randomly picking a day of the week? The number of events is 2 (since 2 days out of the week are weekends), and the number of outcomes is 7. The probability is 2 ÷ 7 = 2/7. You could also express this as 0.285 or 28.5%.
Example 2 : A jar contains 4 blue marbles, 5 red marbles and 11 white marbles. If a marble is drawn from the jar at random, what is the probability that this marble is red? The number of events is 5 (since there are 5 red marbles), and the number of outcomes is 20. The probability is 5 ÷ 20 = 1/4. You could also express this as 0.25 or 25%.

For example, the likelihood of rolling a 3 on a 6-sided die is 1/6. But the probability of rolling all five other numbers on a die is also 1/6. 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6 , which = 100%.

Note: If you had, for example, forgotten about the number 4 on the dice, adding up the probabilities would only reach 5/6 or 83%, indicating a problem.

Step 5 Represent the probability of an impossible outcome with a 0.

For example, if you were to calculate the probability of the Easter holiday falling on a Monday in the year 2020, the probability would be 0 because Easter is always on a Sunday.

Calculating the Probability of Multiple Random Events

Step 1 Deal with each probability separately to calculate independent events.

Note: The probability of the 5s being rolled are called independent events, because what you roll the first time does not affect what happens the second time.

Step 2 Consider the effect of prior events when calculating probability for dependent events.

Now, the likelihood that the second card is a club is 12/51, since 1 club will have already been removed. This is because what you do the first time affects the second. If you draw a 3 of clubs and don't put it back, there will be one less club and one less card in the deck (51 instead of 52).
The probability that the first marble is red is 5/20, or 1/4. The probability of the second marble being blue is 4/19, since we have 1 less marble, but not 1 less blue marble. And the probability that the third marble is white is 11/18, because we’ve already chosen 2 marbles.

Example 1 : Two cards are drawn randomly from a deck of cards. What is the likelihood that both cards are clubs? The probability of the first event happening is 13/52. The probability of the second event happening is 12/51. The probability is 13/52 x 12/51 = 12/204 = 1/17. You could also express this as 0.058 or 5.8%.
Example 2 : A jar contains 4 blue marbles, 5 red marbles and 11 white marbles. If three marbles are drawn from the jar at random, what is the probability that the first marble is red, the second marble is blue, and the third is white? The probability of the first event is 5/20. The probability of the second event is 4/19. And the probability of the third event is 11/18. The probability is 5/20 x 4/19 x 11/18 = 44/1368 = 0.032. You could also express this as 3.2%.

Converting Odds to Probabilities

Step 1 Set the odds as a ratio with the positive outcome as a numerator.

The number 11 represents the likelihood of choosing a white marble and the number 9 represents the likelihood of choosing a marble of a different color.
So, odds are that you will draw a white marble.

Step 2 Add the numbers together to convert the odds to probability.

The event that you’ll draw a white marble is 11; the event another color will be drawn is 9. The total number of outcomes is 11 + 9, or 20.

Step 3 Find the odds as if you were calculating the probability of a single event.

So, in our example, the probability of drawing a white marble is 11/20. Divide this out: 11 ÷ 20 = 0.55 or 55%.

Probability Cheat Sheets

Expert Q&A

Mathematicians typically use the term “relative probability” to refer to the chances of an event happening. They insert the word "relative" since no outcome is 100% guaranteed. For example, if you flip a coin 100 times, you probably won't get exactly 50 heads and 50 tails. Relative probability takes this caveat into account. [10] X Research source Thanks Helpful 0 Not Helpful 1
You may need to know that that in sports betting and bookmaking, odds are expressed as “odds against,” which means that the odds of an event happening are written first, and the odds of an event not happening come second. Although it can be confusing, it's important to know this if you’re planning to bet on a sporting event. Thanks Helpful 13 Not Helpful 4
The most common ways of writing down probabilities include putting them as fractions, as decimals, as percentages, or on a 1–10 scale. Thanks Helpful 8 Not Helpful 5

↑ https://www.theproblemsite.com/reference/mathematics/probability/mutually-exclusive-outcomes
↑ Mario Banuelos, PhD. Assistant Professor of Mathematics. Expert Interview. 11 December 2021.
↑ https://www.mathplanet.com/education/pre-algebra/probability-and-statistic/probability-of-events
↑ https://www.mathsisfun.com/probability_line.html
↑ https://www.probabilisticworld.com/not-all-zero-probabilities/
↑ https://www.khanacademy.org/math/ap-statistics/probability-ap/stats-conditional-probability/e/calculating-conditional-probability
↑ https://www.mathsisfun.com/data/probability.html
↑ https://www.mathsisfun.com/data/probability-events-types.html

About This Article

Probability is the likelihood that a specific event will occur. To calculate probability, first define the number of possible outcomes that can occur. For example, if someone asks, “What is the probability of choosing a day that falls on the weekend when randomly picking a day of the week,” the number of possible outcomes when choosing a random day of the week is 7, since there are 7 days of the week. Now define the number of events. In this example, the number of events is 2 since 2 days out of the week fall on the weekend. Finally, divide the number of events by the number of outcomes to get the probability. In our example, we would divide 2, the number of events, by 7, the number of outcomes, and get 2/7, or 0.28. You could also express the answer as a percentage, or 28.5%. Therefore, there’s a 28.5% probability that you would choose a day that falls on the weekend when randomly picking a day of the week. To learn how to calculate the probability of multiple events happening in a row, keep reading! Did this summary help you? Yes No

Send fan mail to authors

Reader Success Stories

Nathalie Ricardo

May 11, 2022

Did this article help you?

Jan 28, 2023

Jan 15, 2019

Victoria Dobson

May 24, 2017

Krishna Mitra

Nov 25, 2017

Featured Articles

Watch Articles

Terms of Use
Privacy Policy
Do Not Sell or Share My Info
Not Selling Info

Get all the best how-tos!

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

How To Calculate Probability

Here we will learn how to calculate probability, including basic probability, mutually exclusive events, independent events and conditional probability.

There are also calculating probability worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is probability?

Probability is the likelihood of an event occurring.

To find the probability of an event happening we use the formula

For example,

Let’s look at the probability of getting an even number when a die is rolled.

The desired outcome is getting an even number. There are 3 even numbers on a die.

The total number of possible outcomes is 6 since there are 6 numbers on a die.

Probabilities range from \bf{0} to \bf{1}.

If something has a probability of \bf{0} then it is impossible and if something has a probability of \bf{1} then it is certain .

We use the notation P(event) to represent the probability of an event happening.

If we wanted to write the probability of getting a 1 we could write P (1).

Calculating probabilities of combined events

Sometimes we want to find the probability of more than one event occurring. There are different probability rules that we can use.

Mutually exclusive events

Mutually exclusive events are two or more events that cannot occur at the same time. For example, getting heads and tails when tossing a coin or rolling a 2 and a 3 on a die.

For mutually exclusive events: P(A or B) = P(A) + P(B)

If we have an exhaustive list of outcomes, their probabilities sum to 1. For example, the probability of getting an even or an odd number on a die.

The probability of getting an even number is \frac{3}{6}

and the probability of getting an odd number is \frac{3}{6}.

The probability of getting an even or an odd number is \frac{3}{6}+\frac{3}{6}=\frac{6}{6}=1.

Since getting an even number or an odd number covers all the possible outcomes, it is an exhaustive list and the probabilities add up to 1.

Step-by-step guide: Mutually exclusive events (coming soon)

Independent events

Independent events are events which are not affected by the occurrence of other events. For example, if we roll a die twice, the outcome of the first roll and second roll have no effect on each other – they are independent events.

For independent events: P(A and B) = P(A) x P(B)

Step-by-step guide: Independent events (coming soon)

Conditional probability

Conditional probability is the probability of an event occurring based on the occurrence of another event.

For conditional probability the probabilities are calculated based on what has already occurred.

For example, there are 5 counters in a bag, 2 are black and the rest are white.

A counter is picked at random and not replaced. A second counter is picked at random. The probability that the second counter is black depends on what the colour of the first counter was.

Step-by-step guide: Conditional probability

How to calculate probability

In order to calculate probability:

Write out the basic probability
Solve the problem, using AND or OR rules as appropriate .

Explain how to calculate probability

How to calculate probability worksheet

Get your free how to calculate probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.

How to calculate probability examples

Example 1: basic probability.

Jamie has the following cards,

A card is chosen at random. Find the probability the card has a letter B on it.

Write out the basic probability .

We can write down the basic probability by using

\text{Probability}=\frac{\text{number of desired outcomes}}{\text{total number of outcomes}} .

The number of cards with B is 2, and the total number of cards is 11.

2 Solve the problem using AND or OR rules as appropriate .

Not needed as this is a basic probability question.

Example 2: mutually exclusive events

What is the probability of landing on a 2 or a 3 on the following spinner?

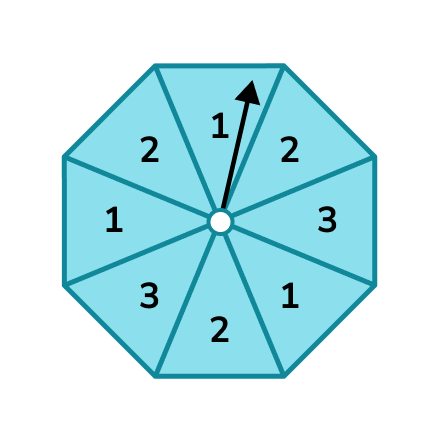
We can write down the probability of getting a 2 and the probability of getting a 3.

P(2)=\frac{3}{8}

P(3)=\frac{2}{8}

Solve the problem using AND or OR rules as appropriate .

The probability of landing on a 2 or a 3 is \frac{5}{8}.

Example 3: independent events

Olivia flips a coin and rolls a die. What is the probability that the coin lands on heads and the die lands on 1 ?

\text{P(1)}=\frac{1}{6}

The probability that the coin lands on heads and the die lands on 1 is \frac{1}{12}.

Example 4: using a tree diagram

The probability that Kate wins a game of tennis is 0.6. The probability that Billy wins a game of tennis is 0.7. Kate plays a match on Saturday and Billy plays a match on Sunday.

Find the probability that one of them wins and one of them loses.

We can work out the probabilities that the people do not win their tennis games.

\text{P(Kate NOT win)}=1-0.6=0.4

\text{P(Billy NOT win)}=1-0.7=0.3

For this question we are going to draw a tree diagram so we can clearly see the different outcomes.

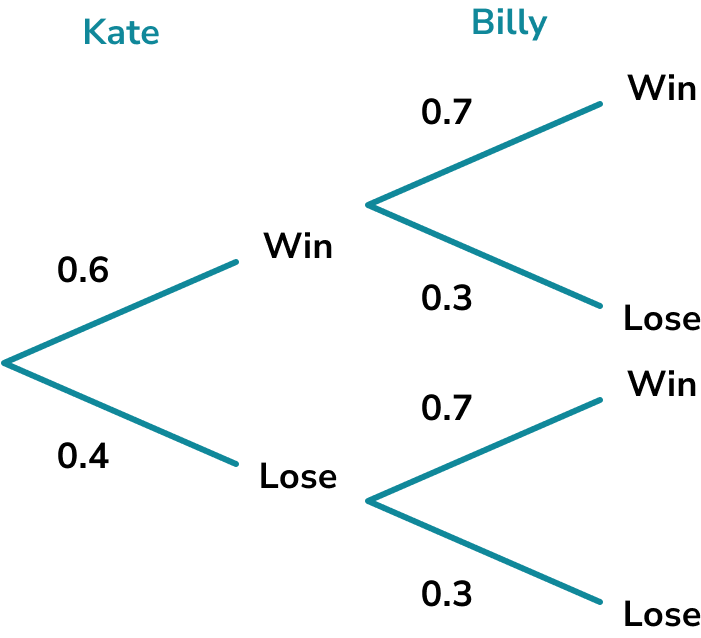
For the outcome that one of them wins and the other loses, we could have Kate wins and Billy loses or Kate loses and Billy wins.

\text{P(Kate wins and Billy loses)}=0.6 \times 0.3=0.18

\text{P(Kate loses and Billy wins)}=0.4 \times 0.7=0.28

\text{P(one wins and one loses)}=0.18+0.28=0.46

The probability that one of them wins and the other loses is 0.46.

Example 5: conditional probability

A bag contains 7 red marbles and 5 blue marbles. 1 marble is chosen at random.

The marble is red. A second marble is chosen. Find the probability the second marble is also red.

These are dependent events. The first event affects the probabilities for the second event.

\text{P(first marble is red)}=\frac{7}{12}

Given that one red marble has been chosen, there are now 6 red marbles and 11 marbles altogether. This is conditional probability.

\text{P(second marble is red)}=\frac{6}{11}

The probability that the second marble is red is \frac{6}{11}.

Example 6: using a Venn diagram

The Venn diagram below shows the number of students who pass their mock exams in English and Maths.

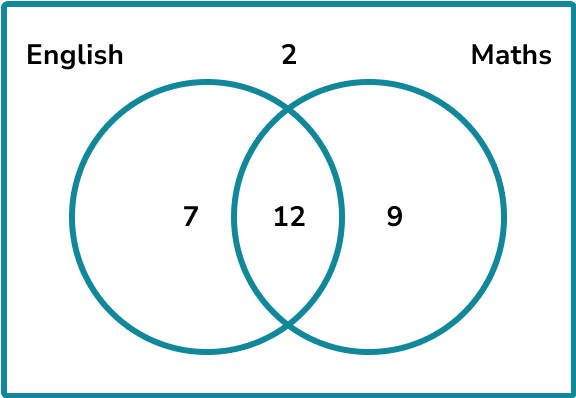
A student is chosen at random. Given that the chosen student passes Maths, find the probability that they did not pass English.

This is a more complex probability question to work out. However we can work out how many students pass Maths.

This is a conditional probability question.

The desired outcome is that the student passes Maths but not English. There are 9 students who pass Maths but not English. The condition is that they pass Maths so we need to consider all the students who pass Maths. We know that 21 students pass Maths.

Therefore the probability that the student did not pass English given that they pass Maths is \frac{9}{21}.

Example 7: using a two-way table

The two-way shows information about the gender and eye colour of the children in class 6.

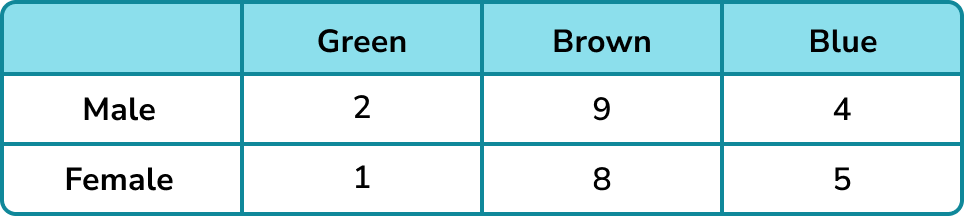
A child is chosen at random. What is the probability that the child has green eyes given that they are male?

This is a more complex probability question to work out. However we can work out how many children are male.

The desired outcome is that the child has green eyes but is male. There are 2 children who have green eyes and are male. The condition is that they are male, so we need to consider all the children who are male. We know that 15 children are male.

Therefore the probability that the child has green eyes given that they are male is \frac{2}{15}.

Common misconceptions

Adding probabilities instead of multiplying them

For independent events P(A \ and \ B) = P(A) \times (P(B). For mutually exclusive events P(A \ or \ B) = P(A) + P(B).

Multiplying or dividing fractions incorrectly

To multiply fractions, multiply the numerators and multiply the denominators. To divide fractions, turn the second one upside down and multiply.

Adding fractions incorrectly

Remember, fractions can only be added or subtracted if they have a common denominator.

Not changing the probability for the second pick when picking two objects (conditional probability)

For example, if you have a bag containing 3 blue balls and 7 yellow balls, the probability of picking a blue ball on the first pick is \frac{3}{10} and the probability of picking a yellow ball on the first pick is \frac{7}{10}. The probabilities of picking the second ball depend on whether the first ball is replaced into the bag or not.

Practice how to calculate probability questions

1. Luke has a deck of cards. Luke draws one card at random. Find the probability that Luke picks a King.

There are 4 Kings in a deck of cards. There are 52 cards in total.

2. The probability that Tom wears a certain colour t-shirt is shown below.

Find the probability that Tom wears a black or a grey t-shirt.

3. Evie takes the bus to work. The probability the bus is late on any given day is \frac{2}{5}, independent of whether it was late on the previous day. Find the probability the bus is late two days in a row.

4. Eddy has 10 red socks, 8 blue socks and 2 yellow socks.

Eddy picks a sock from the drawer. It is red.

Eddy picks a second sock. Find the probability it is also red.

Once Eddy has taken a red sock, there will be 9 red socks left and 19 socks left altogether. Therefore the probability is \frac{9}{19}.

5. The two-way table shows information about the height and hair colour of the children in class 3.

How to calculate probability practice question 5

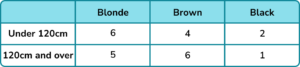
A student is chosen at random. Find the probability the student has blonde hair given that they are under 120cm.

The desired outcome is a student that has blonde hair and is under 120cm. There are 6 such students.

The condition is that the student is under 120cm. There are a total of 12 students under 120cm.

The probability is \frac{6}{12}=\frac{1}{2} .

6. Rachel has 9 balls in a bag. 4 of the balls are blue and the other 5 are red. Rachel picks one ball, notes its colour and replaces the ball. She then picks a second ball. Find the probability the two balls she picks are the same colour.

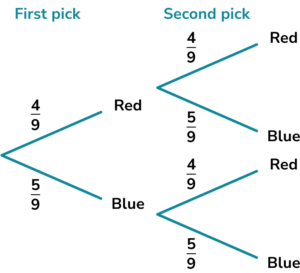
Rachel can pick two red balls or two blue balls.

The total probability is \frac{41}{81} .

How to calculate probability GCSE questions

1. Jason picks one of the following cards at random.

(a) Find the probability that Jason picks a H.

(b) Find the probability that Jason picks an M or an A.

(a) \frac{1}{11}

(b) \frac{2}{11}+\frac{2}{11}=\frac{4}{11}

2. (a) Yasmin designs a game where players must roll a dice and pick a card from a set of cards containing the numbers 1-10 once each. Players win if they roll a multiple of 3 and pick a card that is a multiple of 5.

Find the probability that a player wins the game.

(b) 150 people play the game.

Yasmin charges players £1 to play and winners receive a prize of £5. How much profit should Yasmin expect to make?

Number of winners = \frac{1}{15} \times 150=10

Profit = £150-£50=£100

3. Janet has a bag of sweets containing three strawberry sweets, four blackcurrant sweets and five orange sweets.

Janet picks two sweets at random. Find the probability that both sweets are strawberry.

Learning checklist

You have now learned how to:

Calculate basic probabilities
Calculate the probability of two events happening
Calculate the probability of mutually exclusive events
Calculate the probability of independent events
Deal with conditional probability
Solve probability problems

The next lessons are

Combined events probability
Probability distribution
Describing probability

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Solver Title

Generating PDF...

Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
Linear Algebra Matrices Vectors
Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
Physics Mechanics
Chemistry Chemical Reactions Chemical Properties
Finance Simple Interest Compound Interest Present Value Future Value
Economics Point of Diminishing Return
Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
Pre Algebra
One-Step Addition
One-Step Subtraction
One-Step Multiplication
One-Step Division
One-Step Decimals
Two-Step Integers
Two-Step Add/Subtract
Two-Step Multiply/Divide
Two-Step Fractions
Two-Step Decimals
Multi-Step Integers
Multi-Step with Parentheses
Multi-Step Rational
Multi-Step Fractions
Multi-Step Decimals
Solve by Factoring
Completing the Square
Quadratic Formula
Biquadratic
Logarithmic
Exponential
Rational Roots
Floor/Ceiling
Equation Given Roots
Newton Raphson
Substitution
Elimination
Cramer's Rule
Gaussian Elimination
System of Inequalities
Perfect Squares
Difference of Squares
Difference of Cubes
Sum of Cubes
Polynomials
Distributive Property
FOIL method
Perfect Cubes
Binomial Expansion
Negative Rule
Product Rule
Quotient Rule
Expand Power Rule
Fraction Exponent
Exponent Rules
Exponential Form
Logarithmic Form
Absolute Value
Rational Number
Powers of i
Partial Fractions
Is Polynomial
Leading Coefficient
Leading Term
Standard Form
Complete the Square
Synthetic Division
Linear Factors
Rationalize Denominator
Rationalize Numerator
Identify Type
Convergence
Interval Notation
Pi (Product) Notation
Boolean Algebra
Truth Table
Mutual Exclusive
Cardinality
Caretesian Product
Age Problems
Distance Problems
Cost Problems
Investment Problems
Number Problems
Percent Problems
Addition/Subtraction
Multiplication/Division
Dice Problems
Coin Problems
Card Problems
Pre Calculus
Linear Algebra
Trigonometry
Conversions

Most Used Actions

Number line.

A\:fair\:coin\:is\:tossed\:four\:times\:what\:is\:the\:probability\:of\:obtaining\:at\:least\:three\:heads
What\:is\:the\:probability\:of\:rolling\:2\:standard\:dice\:which\:sum\:to\:11
One\:card\:is\:selected\:at\:random\:from\:a\:deck\:of\:cards.\:Determine\:the\:probability\:that\:the\:card\:selected\:is\:a\:9?

probability-problems-calculator

Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations. Symbolab math solutions...

Please add a message.

Message received. Thanks for the feedback.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

5.3: Probability Rules- “And” and “Or”

Last updated
Save as PDF
Page ID 91507

Maxie Inigo, Jennifer Jameson, Kathryn Kozak, Maya Lanzetta, & Kim Sonier

Maxie Inigo, Jennifer Jameson, Kathryn Kozak, Maya Lanzetta, & Kim Sonier
Coconino Community College

Learning Objectives

Students will be able to:

Determine if two events are mutually exclusive and/or independent.
Apply the "Or" rule to calculate the probability that either of two events occurs.
Apply the "And" rule to calculate the probability that both of two events occurs.

Many probabilities in real life involve more than one event. If we draw a single card from a deck we might want to know the probability that it is either red or a jack. If we look at a group of students, we might want to know the probability that a single student has brown hair and blue eyes. When we combine two events we make a single event called a compound event . To create a compound event, we can use the word “and” or the word “or” to combine events. It is very important in probability to pay attention to the words “and” and “or” if they appear in a problem. The word “and” restricts the field of possible outcomes to only those outcomes that simultaneously describe all events. The word “or” broadens the field of possible outcomes to those that describe one or more events.

Example $\PageIndex{1}$: Counting Students

Suppose a teacher wants to know the probability that a single student in her class of 30 students is taking either Art or English. She asks the class to raise their hands if they are taking Art and counts 13 hands. Then she asks the class to raise their hands if they are taking English and counts 21 hands. The teacher then calculates

\[P(\text{Art or English}) = \dfrac{13+21}{30} = \dfrac{33}{30} \nonumber\]

The teacher knows that this is wrong because probabilities must be between zero and one, inclusive. After thinking about it she remembers that nine students are taking both Art and English. These students raised their hands each time she counted, so the teacher counted them twice. When we calculate probabilities we have to be careful to count each outcome only once.

$http://media.townhall.com/townhall/reu/ha/2013/190/b00cc532-24d8-4028-9beb-877e2c63baf7.jpg$

Mutually Exclusive Events

An experiment consists of drawing one card from a well shuffled deck of 52 cards. Consider the events E : the card is red, F : the card is a five, and G : the card is a spade. It is possible for a card to be both red and a five at the same time but it is not possible for a card to be both red and a spade at the same time. It would be easy to accidentally count a red five twice by mistake. It is not possible to count a red spade twice.

Definition: Mutually Exclusive

Two events are mutually exclusive if they have no outcomes in common.

Example $\PageIndex{2}$: Mutually Exclusive with Dice

Two fair dice are tossed and different events are recorded. Let the events E , F and G be as follows:

E = {the sum is five} = {(1, 4), (2, 3), (3, 2), (4, 1)}
F = {both numbers are even} = {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}
G = {both numbers are less than five} = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4,1), (4, 2), (4, 3), (4,4)}
Are events E and F mutually exclusive?

Yes. E and F are mutually exclusive because they have no outcomes in common. It is not possible to add two even numbers to get a sum of five.

Are events E and G mutually exclusive?

No. E and G are not mutually exclusive because they have some outcomes in common. The pairs (1, 4), (2, 3), (3, 2) and (4, 1) all have sums of 5 and both numbers are less than five.

Are events F and G mutually exclusive?

No. F and G are not mutually exclusive because they have some outcomes in common. The pairs (2, 2), (2, 4), (4, 2) and (4, 4) all have two even numbers that are less than five.

Addition Rule for “Or” Probabilities

The addition rule for probabilities is used when the events are connected by the word “or”. Remember our teacher in Example $\PageIndex{1}$ at the beginning of the section? She wanted to know the probability that her students were taking either art or English. Her problem was that she counted some students twice. She needed to add the number of students taking art to the number of students taking English and then subtract the number of students she counted twice. After dividing the result by the total number of students she will find the desired probability. The calculation is as follows:

\[ \begin{align*} P(\text{art or English}) &= \dfrac{\# \text{ taking art + } \# \text{ taking English - } \# \text{ taking both}}{\text{total number of students}} \\[4pt] &= \dfrac{13+21-9}{30} \\[4pt] &= \dfrac{25}{30} \approx {0.833} \end{align*}\]

The probability that a student is taking art or English is 0.833 or 83.3%.

When we calculate the probability for compound events connected by the word “or” we need to be careful not to count the same thing twice. If we want the probability of drawing a red card or a five we cannot count the red fives twice. If we want the probability a person is blonde-haired or blue-eyed we cannot count the blue-eyed blondes twice. The addition rule for probabilities adds the number of blonde-haired people to the number of blue-eyed people then subtracts the number of people we counted twice.

If A and B are any events then

\[P(A\, \text{or}\, B) = P(A) + P(B) – P(A \,\text{and}\, B).\]

If A and B are mutually exclusive events then $P(A \,\text{and}\, B) = 0$, so then

\[P(A \, \text{or}\, B) = P(A) + P(B).\]

Example $\PageIndex{3}$: Additional Rule for Drawing Cards

A single card is drawn from a well shuffled deck of 52 cards. Find the probability that the card is a club or a face card.

There are 13 cards that are clubs, 12 face cards (J, Q, K in each suit) and 3 face cards that are clubs.

\[ \begin{align*} P(\text{club or face card}) &= P(\text{club}) + P(\text{face card}) - P(\text{club and face card}) \\[4pt] &= \dfrac{13}{52} + \dfrac{12}{52} - \dfrac{3}{52} \\[4pt] &= \dfrac{22}{52} = \dfrac{11}{26} \approx {0.423} \end{align*}\]

The probability that the card is a club or a face card is approximately 0.423 or 42.3%.

A simple way to check this answer is to take the 52 card deck and count the number of physical cards that are either clubs or face cards. If you were to set aside all of the clubs and face cards in the deck, you would end up with the following:

{2 Clubs, 3 Clubs, 4 Clubs, 5 Clubs, 6 Clubs, 7 Clubs, 8 Clubs, 9 Clubs, 10 Clubs, J Clubs, Q Clubs, K Clubs, A Clubs, J Hearts, Q Hearts, K Hearts, J Spades, Q Spades, K Spades, J Diamonds, Q Diamonds, K Diamonds}

That is 22 cards out of the 52 card deck, which gives us a probably of: \[ \begin{align*} \dfrac{22}{52} = \dfrac{11}{26} \approx {0.423} \end{align*}\]

This confirms our earlier answer using the formal Addition Rule.

Example $\PageIndex{4}$: Addition Rule for Tossing a Coin and Rolling a Die

An experiment consists of tossing a coin then rolling a die. Find the probability that the coin lands heads up or the number is five.

Let H represent heads up and T represent tails up. The sample space for this experiment is S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}.

There are six ways the coin can land heads up, {H1, H2, H3, H4, H5, H6}.
There are two ways the die can land on five, {H5, T5}.
There is one way for the coin to land heads up and the die to land on five, {H5}.

\[ \begin{align*} P(\text{heads or five}) &= P(\text{heads}) + P(\text{five}) - P(\text{both heads and five}) \\[4pt] &= \dfrac{6}{12} + \dfrac{2}{12} - \dfrac{1}{12} \\[4pt] &= \dfrac{7}{12} = \approx {0.583} \end{align*}\]

The probability that the coin lands heads up or the number is five is approximately 0.583 or 58.3%.

Example $\PageIndex{5}$: Addition Rule for Satisfaction of Car Buyers

Two hundred fifty people who recently purchased a car were questioned and the results are summarized in the following table.

Find the probability that a person bought a new car or was not satisfied.

\[\begin{align*} P(\text{new car or not satisfied}) &= P(\text{new car}) + P(\text{not satisfied}) - P(\text{new car and not satisfied}) \\[4pt] &= \dfrac{120}{250} + \dfrac{75}{250} - \dfrac{28}{250} = \dfrac{167}{250} \approx 0.668 \end{align*}\]

The probability that a person bought a new car or was not satisfied is approximately 0.668 or 66.8%.

Independent Events

Sometimes we need to calculate probabilities for compound events that are connected by the word “and.” Tossing a coin multiple times or rolling dice are independent events. Each time you toss a fair coin the probability of getting heads is ½. It does not matter what happened the last time you tossed the coin. It’s similar for dice. If you rolled double sixes last time that does not change the probability that you will roll double sixes this time. Drawing two cards without replacement is not an independent event. When you draw the first card and set it aside, the probability for the second card is now out of 51 cards not 52 cards.

Definition: Independent Events

Two events are independent events if the occurrence of one event has no effect on the probability of the occurrence of the other event.

Example $\PageIndex{6}$: Determining When Events are Independent

Are these events independent?

a) A fair coin is tossed two times. The two events are (1) first toss is a head and (2) second toss is a head.

b) The two events (1) “It will rain tomorrow in Houston” and (2) “It will rain tomorrow in Galveston” (a city near Houston).

c) You draw a card from a deck, then draw a second card without replacing the first.

a) The probability that a head comes up on the second toss is $\frac{1}{2}$ regardless of whether or not a head came up on the first toss, so these events are independent .

b) These events are not independent because it is more likely that it will rain in Galveston on days it rains in Houston than on days it does not.

c) The probability of the second card being red depends on whether the first card is red or not, so these events are not independent .

Multiplication Rule for “And” Probabilities: Independent Events

If events A and B are independent events, then $ P(\text{A and B}) = P(A) \cdot P(B)$.

Example $\PageIndex{7}$: Independent Events for Tossing Coins

Suppose a fair coin is tossed four times. What is the probability that all four tosses land heads up?

The tosses of the coins are independent events. Knowing a head was tossed on the first trial does not change the probability of tossing a head on the second trial.

$P(\text{four heads in a row}) = P(\text{1st heads and 2nd heads and 3rd heads and 4th heads})$

$ = P(\text{1st heads}) \cdot P(\text{2nd heads}) \cdot P(\text{3rd heads}) \cdot P(\text{4th heads})$

$ = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2}$

$ = \dfrac{1}{16}$

The probability that all four tosses land heads up is $\dfrac{1}{16}$.

Example $\PageIndex{8}$: Independent Events for Drawing Marbles

A bag contains five red and four white marbles. A marble is drawn from the bag, its color recorded and the marble is returned to the bag. A second marble is then drawn. What is the probability that the first marble is red and the second marble is white?

Since the first marble is put back in the bag before the second marble is drawn these are independent events.

\[\begin{align*} P(\text{1st red and 2nd white}) &= P(\text{1st red}) \cdot P(\text{2nd white}) \\[4pt] &= \dfrac{5}{9} \cdot \dfrac{4}{9} = \dfrac{20}{81}\end{align*}\]

The probability that the first marble is red and the second marble is white is $\dfrac{20}{81}$.

Example $\PageIndex{9}$: Independent Events for Faulty Alarm Clocks

Abby has an important meeting in the morning. She sets three battery-powered alarm clocks just to be safe. If each alarm clock has a 0.03 probability of malfunctioning, what is the probability that all three alarm clocks fail at the same time?

Since the clocks are battery powered we can assume that one failing will have no effect on the operation of the other two clocks. The functioning of the clocks is independent.

\[\begin{align*} P(\text{all three fail}) &= P(\text{first fails}) \cdot P(\text{second fails})\cdot P(\text{third fails}) \\[4pt] &= (0.03)(0.03)(0.03) \\[4pt] &= 2.7 \times 10^{-5} \end{align*}\]

The probability that all three clocks will fail is approximately 0.000027 or 0.0027%. It is very unlikely that all three alarm clocks will fail.

At Least Once Rule for Independent Events

Many times we need to calculate the probability that an event will happen at least once in many trials. The calculation can get quite complicated if there are more than a couple of trials. Using the complement to calculate the probability can simplify the problem considerably. The following example will help you understand the formula.

Example $\PageIndex{10}$: At Least Once Rule

The probability that a child forgets her homework on a given day is 0.15. What is the probability that she will forget her homework at least once in the next five days?

Assume that whether she forgets or not one day has no effect on whether she forgets or not the second day.

If P (forgets) = 0.15, then P (not forgets) = 0.85.

\[\begin{align*} P(\text{forgets at least once in 5 tries}) &= P(\text{forgets 1, 2, 3, 4 or 5 times in 5 tries}) \\[4pt] & = 1 - P(\text{forgets 0 times in 5 tries}) \\[4pt] &= 1 - P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \cdot P(\text{not forget}) \\[4pt] &= 1 - (0.85)(0.85)(0.85)(0.85)(0.85) \\[4pt] & = 1 - (0.85)^{5} = 0.556 \end{align*}\]

The probability that the child will forget her homework at least one day in the next five days is 0.556 or 55.6%

The idea in Example $\PageIndex{9}$ can be generalized to get the At Least Once Rule.

Definition: At Least Once Rule

If an experiment is repeated n times, the n trials are independent and the probability of event A occurring one time is P(A) then the probability that A occurs at least one time is: $P(\text{A occurs at least once in n trials}) = 1 - P(\overline{A})^{n}$

Example $\PageIndex{11}$: At Least Once Rule for Bird Watching

The probability of seeing a falcon near the lake during a day of bird watching is 0.21. What is the probability that a birdwatcher will see a falcon at least once in eight trips to the lake?

Let A be the event that he sees a falcon so P(A) = 0.21. Then, $P(\overline{A}) = 1 - 0.21 = 0.79$.

$P(\text{at least once in eight tries}) = 1 - P(\overline{A})^{8}$

$ = 1 - (0.79)^{8}$

$ = 1 - (0.152) = 0.848$

The probability of seeing a falcon at least once in eight trips to the lake is approximately 0.848 or 84.8%.

Example $\PageIndex{12}$: At Least Once Rule for Guessing on Multiple Choice Tests

A multiple choice test consists of six questions. Each question has four choices for answers, only one of which is correct. A student guesses on all six questions. What is the probability that he gets at least one answer correct?

Let A be the event that the answer to a question is correct. Since each question has four choices and only one correct choice, $P(\text{correct}) = \dfrac{1}{4}$.

That means $P(\text{not correct}) =1 - \dfrac{1}{4} = \dfrac{3}{4}$.

\[ \begin{align*} P(\text{at least one correct in six trials}) &= 1 - P(\text{not correct})^{6} \\[4pt] &= 1 - \left(\dfrac{3}{4}\right)^{6} \\[4pt] &= 1 - (0.178) = 0.822 \end{align*}\]

The probability that he gets at least one answer correct is 0.822 or 82.2%.

Probabilities from Two-Way Tables

Two-way tables can be used to define events and find their probabilities using two different approaches: intuitively or using the probability rules. We can calculate “and” and "or" probabilities by combining the data in relevant cells.

Example $\PageIndex{13}$: Probabilities from a Two-Way Table

Continuation of Example $\PageIndex{5}$:

A person is chosen at random. Find the probability that the person:

bought a new car

\[\begin{align*} P(\text{new car}) &= \dfrac{\text{number of new car}}{\text{number of people}} \\[4pt] &= \dfrac{120}{250} = 0.480 = 48.0 \% \end{align*} \]

was satisfied

\[\begin{align*} P(\text{satisfied}) &= \dfrac{\text{number of satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{175}{250} = 0.700 = 70.0 \% \end{align*} \]

bought a new car and was satisfied

\[\begin{align*} P(\text{new car and satisfied}) &= \dfrac{\text{number of new car and satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{92}{250} = 0.368 = 36.8 \% \end{align*} \]

bought a new car or was satisfied

\[\begin{align*} P(\text{new car or satisfied}) &= \dfrac{\text{number of new car + number of satisfied - number of new car and satisfied}}{\text{number of people}} \\[4pt] &= \dfrac{120 + 175 - 92}{250} = \dfrac{203}{250} = 0.812 = 81.2 \% \end{align*} \]

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Praxis Core Math

Course: praxis core math > unit 1.

Data representations | Lesson
Data representations | Worked example
Center and spread | Lesson
Center and spread | Worked example
Random sampling | Lesson
Random sampling | Worked example
Scatterplots | Lesson
Scatterplots | Worked example
Interpreting linear models | Lesson
Interpreting linear models | Worked example
Correlation and Causation | Lesson
Correlation and causation | Worked example
Probability | Lesson

Probability | Worked example

Want to join the conversation.

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

Math Article

Probability Questions

The probability questions , with answers, are provided here for students to make them understand the concept in an easy way. The chapter Probability has been included in Class 9, 10, 11 and 12. Therefore, it is a very important chapter. The questions here will be provided, as per NCERT guidelines. Get Probability For Class 10 at BYJU’S.

The application of probability can be seen in Maths as well as in day to day life. It is necessary to learn the basics of this concept. The questions here will cover the basics as well as the hard level problems for all levels of students. Thus, students will be confident in solving problems based on it. Also, solving these probability problems will help them to participate in competitive exams, going further.

Definition: Probability is nothing but the possibility of an event occurring. For example, when a test is conducted, then the student can either get a pass or fail. It is a state of probability.

Probability Questions & Answers

1. Two coins are tossed 500 times, and we get:

Two heads: 105 times

One head: 275 times

No head: 120 times

Find the probability of each event to occur.

Solution: Let us say the events of getting two heads, one head and no head by E 1 , E 2 and E 3 , respectively.

P(E 1 ) = 105/500 = 0.21

P(E 2 ) = 275/500 = 0.55

P(E 3 ) = 120/500 = 0.24

The Sum of probabilities of all elementary events of a random experiment is 1.

P(E 1 )+P(E 2 )+P(E 3 ) = 0.21+0.55+0.24 = 1

2. A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced. The table shows the results of 1000 cases.

If a tyre is bought from this company, what is the probability that :

(i) it has to be substituted before 4000 km is covered?

(ii) it will last more than 9000 km?

(iii) it has to be replaced after 4000 km and 14000 km is covered by it?

Solution: (i) Total number of trials = 1000.

The frequency of a tyre required to be replaced before covering 4000 km = 20

So, P(E 1 ) = 20/1000 = 0.02

(ii) The frequency that tyre will last more than 9000 km = 325 + 445 = 770

So, P(E 2 ) = 770/1000 = 0.77

(iii) The frequency that tyre requires replacement between 4000 km and 14000 km = 210 + 325 = 535.

So, P(E 3 ) = 535/1000 = 0.535

3. The percentage of marks obtained by a student in the monthly tests are given below:

Based on the above table, find the probability of students getting more than 70% marks in a test.

Solution: The total number of tests conducted is 5.

The number of tests when students obtained more than 70% marks = 3.

So, P(scoring more than 70% marks) = ⅗ = 0.6

4. One card is drawn from a deck of 52 cards, well-shuffled. Calculate the probability that the card will

(i) be an ace,

(ii) not be an ace.

Solution: Well-shuffling ensures equally likely outcomes.

(i) There are 4 aces in a deck.

Let E be the event the card drawn is ace.

The number of favourable outcomes to the event E = 4

The number of possible outcomes = 52

Therefore, P(E) = 4/52 = 1/13

(ii) Let F is the event of ‘card is not an ace’

The number of favourable outcomes to F = 52 – 4 = 48

Therefore, P(F) = 48/52 = 12/13

5. Two players, Sangeet and Rashmi, play a tennis match. The probability of Sangeet winning the match is 0.62. What is the probability that Rashmi will win the match?

Solution: Let S and R denote the events that Sangeeta wins the match and Reshma wins the match, respectively.

The probability of Sangeet to win = P(S) = 0.62

The probability of Rashmi to win = P(R) = 1 – P(S)

= 1 – 0.62 = 0.38

6. Two coins (a one rupee coin and a two rupee coin) are tossed once. Find a sample space.

Solution: Either Head(H) or Tail(T) can be the outcomes.

Heads on both coins = (H,H) = HH

Head on 1st coin and Tail on the 2nd coin = (H,T) = HT

Tail on 1st coin and Head on the 2nd coin = (T,H) = TH

Tail on both coins = (T,T) = TT

Therefore, the sample space is S = {HH, HT, TH, TT}

7. Consider the experiment in which a coin is tossed repeatedly until a head comes up. Describe the sample space.

Solution: In the random experiment where the head can appear on the 1st toss, or the 2nd toss, or the 3rd toss and so on till we get the head of the coin. Hence, the required sample space is :

S= {H, TH, TTH, TTTH, TTTTH,…}

8. Consider the experiment of rolling a die. Let A be the event ‘getting a prime number’, B be the event ‘getting an odd number’. Write the sets representing the events

(ii) A and B

(iii) A but not B

(iv) ‘not A’.

Solution: S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} and B = {1, 3, 5}

(i) A or B = A ∪ B = {1, 2, 3, 5}

(ii) A and B = A ∩ B = {3,5}

(iii) A but not B = A – B = {2}

(iv) not A = A′ = {1,4,6}

9. A coin is tossed three times, consider the following events.

P: ‘No head appears’,

Q: ‘Exactly one head appears’ and

R: ‘At Least two heads appear’.

Check whether they form a set of mutually exclusive and exhaustive events.

Solution: The sample space of the experiment is:

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and

Q = {HTT, THT, TTH},

R = {HHT, HTH, THH, HHH}

P ∪ Q ∪ R = {TTT, HTT, THT, TTH, HHT, HTH, THH, HHH} = S

Therefore, P, Q and R are exhaustive events.

P ∩ R = φ and

Therefore, the events are mutually exclusive.

Hence, P, Q and R form a set of mutually exclusive and exhaustive events.

10. If P(A) = 7/13, P(B) = 9/13 and P(A∩B) = 4/13, evaluate P(A|B).

Solution: P(A|B) = P(A∩B)/P(B) = (4/13)/(9/13) = 4/9.

Video Lesson

Probability important topics.

Probability Important Questions

Practice Questions

Solve the following probability questions.

Write the sample space for rolling two dice.
If two coins are tossed simultaneously, what is the probability of getting exactly two heads?
From a well-shuffled deck of 52 cards, what is the probability of getting a king?
In a bag, there are 5 red balls and 7 black balls. What is the probability of getting a black ball?
If the probability of an event happening is 0.7, then what is the probability of an event that will not happen?

Stay tuned with BYJU’S – The Learning App and learn all Maths-related concepts easily by exploring more videos.

Register with BYJU'S & Download Free PDFs

Choose Your Test

Sat / act prep online guides and tips, probability questions on act math: strategies and practice.

What is the probability that you’ll toss a coin and get heads? What about twice in a row? Three times? Probability questions ask you determine the likelihood that an event or any number of events is to occur, and the more you practice, the better your odds will be at mastering these types of questions on the ACT (see what we did there?).

This will be your complete guide to probability on the ACT —how probability works, the different types of probability questions you’ll see on the test, and the steps you’ll need to take to solve them.

What Does Probability Mean?

$\Probability = {\desired \outcome}/{\all \possible \outcomes}$

On the ACT, probability questions can be framed in several different ways. You may be asked to find the “probability” that an event will occur, the “chances,” the “odds,” or the “likelihood.” But no matter how you see it written on the test, these are all ways of asking for the same thing.

The way we represent the probability of an event (or events) is to express, as a fraction, how often that event occurs over the total number of possible outcomes.

So if we use our example from above—”What are the odds that you’ll flip a coin and get heads?”—the odds will be:

${\desired \outcome}/{\all \possible \outcomes}$

In this one throw, there is one possible chance of getting heads. This means our numerator is 1.

There are also two possible outcomes total (heads or tails), which means that our denominator will be 2.

Now let’s take a look at another example:

Mara is stringing a necklace and she selects each bead at random from a basket of beads. If there are currently 5, yellow beads, 10 red beads, 15 green beads, and 20 blue beads in the basket, what are the chances that she will select a red bead next?

There are 10 red beads, which is our desired outcome. This means 10 is our numerator.

There are also a total of $5 \yellow \beads + 10 \red \beads + 15 \green \beads + 20 \blue \beads = 50 \total \beads$ in the basket. This is our denominator, as it represents all the outcomes possible.

When we put these together, our probability is:

The chances that Mara will select a red bead are 1 in 5 or $1/5$.

Now what if we framed our desired outcome as a negative?

What are the odds that Mara will NOT select a green bead?

In order to find a negative probability, we must subtract out the chances that Mara will draw a green bead. (We could also think of this as finding the desired outcome of her selecting a yellow bead, a red bead or a blue bead, which we will cover in more detail in the next section.)

There are only yellow, red, green, and blue beads, so we can add up our odds of yellow, red and blue beads, excluding the green. There are 5 yellow beads, 10 red beads and 20 blue beads, so we can put those together to get our numerator.

$5 + 10 + 20 = 35$

And there are still $5 + 10 + 15 + 20 = 50$ beads total for our denominator.

So what are the odds that Mara will NOT select a green bead?

The odds are 7 in 10 ($7/10$) that Mara will draw any color bead except green.

Expressing Probabilities

As you can see, probabilities are expressed as fractions. This means that an event that will always and absolutely occur will have a probability of $1/1$ or 1.

On the other hand, an impossible event will have a probability of $0/x$ or 0.

You can also think about probabilities as percentages. If the odds are $4/52$ that you’ll draw an ace from a deck of cards, it’s the same as saying that there is a 7.69% chance that you will draw an ace.

Why? Because $4 ÷ 52 = 0.0769$, and $0.0769 * 100 = 7.69%$.

Either/Or Probability

${\probability \of \either \event = [{\outcome A}/{\total \number \of \outcomes}] + [{\outcome B}/{\total \number \of \outcomes}]$

(Special note: this is called a “non-overlapping” probability. In this case, it is impossible for the two (or more) events to both happen at the same time. There is such a thing as an either/or probability for overlapping events, but you will never be asked to do this on the ACT, so we have not included it in this guide.)

An either/or probability increases the odds that our desired outcome will happen because we do not care which of the two events happen, only that one of them does.

To solve this kind of problem, we must therefore add the probability of each individual event. Their sum will become the probability of either event happening.

So let’s look again at our earlier example with Mara and her beads.

Instead of asking the odds of Mara selecting only a red bead, what are the odds that Mara will select either a red bead or a green bead if she has 5 yellow beads, 10 red beads, 15 green beads, and 20 blue beads in the basket?

We have increased our odds, since it doesn’t matter whether or not the bead is green or red, so long as the bead we select is NOT blue or yellow (essentially, we are doing another version of our earlier negative problem—”what are the odds that a particular event will NOT happen?”)

This means we can add the probabilities of our individual events together in order to find their combined probability.

So let us find the probability of her drawing a red bead:

$10/(5 + 10 + 15 + 20)$

And let us find the probability of her drawing a green bead:

$15/(5 + 10 + 15 + 25)$

So, if we put the two probabilities together, we’ll have:

$10/50 + 15/50$

Because this problem involves the odds of two events with the same total number of outcomes (there are 50 total possible beads to choose from each time), we could also simply add our two desired outcomes together over the total number of outcomes. So:

$(10 + 15)/(5 + 10 + 15 + 20)$

Either way, the odds of Mara drawing either a red bead or a green bead are 1 in 2, or $1/2$ (50%).

What are the odds that we go this way or that way ?

Combined Probability

$\Combined \probability = [{\outcome A}/{\total \number \of \outcomes}] * [{\outcome B}/{\total \number \of \outcomes}]$

"What are the odds of two or more events both/all happening?" This kind of probability question is called a combined probability and there is a good chance you’ll see a question of this type in the later half of the ACT math section.

Note that a combined probability question is distinctly different from an either/or probability question. An “either/or” question asks whether or not one of the multiple events occurs (no matter which event is was). A “both/and” question requires that multiple events all occur.

To find the probability of an “either/or” question, we must add our probabilities. To find the probability of a combined probability question, we must multiply our probabilities.

A good way to remember this is to remember that a combined probability question will ultimately have a lower probability than the that of just one (or either) event occurring. The more events you need to happen, the less likely it will be that they all will. How likely is it that your first AND second coin tosses will BOTH be heads? Lower than the odds of just flipping heads once.

On the other hand, an either/or probability question will have higher odds than the probability of just one of its events happening. You are combining forces to increase your odds of getting a desirable outcome. How likely is it that you’ll flip either heads or tails for each toss? 100%!

What are the odds that Jenny will roll a pair of dice and get six on both?

A die has six faces, so the odds of rolling any particular number is $1/6$. Because the question is asking us to find the odds of rolling two sixes (and nothing else), we must use our combined probability. So:

$1/6 * 1/6 = 1/36$

There is a 1 in 36 chance that Jenny will roll a pair of dice and get two sixes.

Combined probability questions mean that events cannot be separated.

Typical ACT Probability Questions

There are many different kinds of probabilities and probability questions (including overlapping, and conditional probabilities), but ACT probability questions use only the basic probabilities we have covered above.

For most ACT probability questions, you will be asked to find either a straight probability or a probability ratio. You may also be asked to find or alter a new probability from an existing one.

Now let us look at each type of problem.

Simple Probability

These kind of questions will always be word problems in which you are told a story and asked to find the probability of one or more events. This may be a straight probability, an either/or probability, or a combined probability.

Simply use the understandings we learned above and you’ll be able to solve these kinds of questions without issue.

We know that probability is ${\desired \outcome}/{\all \possible \outcomes}$.

Our desired outcome is to get one of the five extra pieces, so our numerator will be 5.

There are 750 puzzle pieces PLUS the extra five pieces in the box total, so our denominator will be: $750 + 5 = 755$

When we put them together, our final probability will be:

Our final answer is D.

Probability Ratio

One way the ACT likes to spin probabilities and make them more complex is to present them as ratios or to ask you for your answer in a ratio. For a refresher on ratios, check out our guide to ACT fractions and ratios .

For these types of questions, pay close attention to what the ratio represents so that you don’t end up solving the wrong question entirely.

We are told that we must find the odds of an event as a ratio of $\in \the 25 - 35 \age \range: \not \in \the 25-35 \age \range$ (in other words, $\desired \outcome: \remaining \outcomes$).

We are given the number of voters in terms of percentages, so we can translate the 42% of voters in the 25-35 age range as $42/100$.

And if the 25-35 age category has a probability of $42/100$, then the remaining voters will have a probability of:

${100 - 42}/100$

Now, we can represent our ratio of $25-35 \voters: \all \other \voters$ as:

Both numbers are divisible by 2, so we can reduce the ratio to:

Altering a Probability

Finally, it is quite common for the ACT to ask you to alter a probability. Usually, they will present you with an existing probability and then ask you to find the number to which you must increase the desired outcome(s) and the total number of outcomes in order to achieve a specific new probability.

For example:

Now, there are two ways to solve this kind of problem—using proportions or using the strategy of plugging in answers. Let’s look at both methods.

Method 1—Proportions

We are asked to find an additional number of red marbles that we must add to the total number of marbles in order to find a new probability. The current probability of selecting a red marble is:

Now, we are adding a certain number of red marbles and only red marbles. This means that the number of red marbles increases by exactly the same amount that the total increases. We can therefore represent the new probability as:

${12 + x}/{32 + x}$

Now, we want this new probability to be equal to $3/5$, so let us set them up as a proportion.

${12 + x}/{32 + x} = 3/5$

And because this is a proportion, we can cross multiply.

$(32 + x)(3) = (12 + x)(5)$

$96 + 3x = 60 + 5x$

Now solve for $x$.

So we must add 18 red marbles in order to get a new probability of:

${12 + 18}/{32 + 18$

Our final answer is G, 18.

Method 2—Plugging in answers

The alternative to using proportions is to use PIA . We can simply add the answer options to the 12 red marbles in our numerator and the 32 marbles in our denominator and see which answer choice gives us a final ratio of $3/5$.

Let us begin, as always, with the answer choice in the middle.

Answer option H gives us 28, so let us try adding 28 to both the red marbles and the total number of marbles.

${12 + 28}/{32 + 28}$

This answer is a little bit too large. We can also see that the larger the number we add to both the numerator and the denominator, the larger our probability will be (you can test this by plugging in answer choice J or K—for K, if you add 40 to both 12 and 32, your final probability fraction will be $52/72$ => $13/18$, which is even larger than $2/3$.)

This means that we can eliminate answer choices H, J, and K.

Now let us try answer choice G.

${12 + 18}/{32 + 18}$

We have found our desired ratio.

As you can see, no matter which method you use, you can find the right solution.

How to Solve a Probability Question

There are several ACT math strategies you must keep in mind when solving a probability question. First of all, you will know if you are being asked for a probability question on the ACT because, somewhere in the problem, it will ask you for the "probability of," the "chances of," or the "odds of" one or more events happening.

Almost always, the ACT will use the word “probability,” but make sure to note that these words are all interchangeable. When you see those phrases, make sure to follow these steps:

#1: Make sure you look carefully at exactly what the question is asking.

It can be easy to make a mistake with probability ratios, or to mix up an either/or probability question with a both/and question. Make sure you always carefully examine the problem before you waste precious time trying to answer the wrong question.

Kyle has been tossing a coin and recording the number of heads and tails results. So far, he has tossed the coin 5 times and gotten heads each time. What are the odds that he will get tails on his next coin toss?

You may be tempted to think that our desired outcome (our numerator) is influenced by the number of times Kyle has already tossed the coin and the outcomes so far, but in all actuality, the probability that Kyle will get tails on his next toss is $1/2$.

Why? Because each coin toss is independent of another coin toss. This means that this is a simple matter of determining our desired outcome over the number of total outcomes. There is one possibility of getting tails—numerator 1—and two possible options—heads or tails, denominator 2.

So Kyle’s chances of getting tails on the next toss are 1 in 2 .

Now let’s look at a slightly different question.

Kyle tossed the coin 5 times and got heads each time. What were the odds of this happening?

Now we are being asked to find the probability of a both/and question, since we are being asked to identify the probability of multiple events all happening. (If it helps to picture, you can rephrase the question as: “What are the odds that BOTH his first coin tosses were heads? And What were the odds that BOTH his next tosses were heads?”, etc.)

So if we use what we know about combined probabilities, we would be able to say:

$1/2 * 1/2 * 1/2 * 1/2 * 1/2$

The odds are 1 in 32 (3.125%) that Kyle would have tossed heads five times in a row.

#2: Think logically about when your odds will increase or decrease

The odds of either two or more events occurring will be greater than the odds of one of the events alone. The odds of both (or multiple events) all occurring will be less than the odds of the odds of one of those events alone.

Always take a moment to think about probability questions logically so that you don’t multiply when you should add, or vice versa.

#3: Simplify the idea of a probability

Once you get used to working with probabilities, you’ll find that probability questions are often just fancy ways of working with fractions and percentages.

A probability ratio is the exact same thing as a question that simply asks you for a ratio. Just brush up on your fractions and ratios if you find yourself intimidated for any reason.

And always feel free to fall back on your PIA or PIN , as needed. These methods will sometimes take a little extra time, but they will always lead you to the right answer.

Test Your Knowledge

Now it’s time to test what you’ve learned, using real ACT practice problems:

Answers: F, E, D, B

Answer Explanations:

1. This is another example of an altering probability question and, again, we have two choices when it comes to solving it. Let’s go through both the algebra/proportion method and PIA.

Method 1—proportions.

We know that we must increase the number of red marbles and only red marbles, so the amount of new marbles added to the set of red marbles and to the overall total of marbles will be the same.

Our starting probability of red marbles is:

So now we must increase each part of our fraction by the same amount and set it equal to the desired probability of $⅗$.

${6 + x}/{18 + x} = 3/5$

$(18 + x)(3) = (6 + x)(5)$

$54 + 3x = 30 + 5x$

So we must increase our red marbles (and, consequently, the total number of marbles) by 12 in order to get a probability of $⅗$ of selecting a red marble.

To double-check this, we can plug the number back into our probability.

${6 + 12}/{18 + 12}$

We have successfully found our answer!

Our final answer is F, 12.

Method 2—PIA

The alternative method is to use plugging in answers. We will simply plug in our answer choices to increase our red marbles (and our total number of marbles) and see which answer choice results in a probability of $3/5$.

Let us start with answer choice H, 18.

${6 + 18}/{18 + 18}$

This probability is too large and any larger numbers will only get us larger probabilities. This means we can eliminate answer choices H, J, and K.

Now, let us try answer choice G, 16.

${6 + 16}/{18 + 16}$

This probability is still slightly too large. By process of elimination, our answer must be F, but let us test it to be sure.

Success! We have found our right answer.

Our final answer is, again, F , 12.

2. Because Elliott must answer all the questions correctly, this means that this is a combination probability question. We are told that he answers each question at random, and all the questions have 3 answer options, which means that answering one question correctly has a probability of:

And, since this is a combination problem, answering ALL 4 questions correctly will be:

$1/3 * 1/3 * 1/3 * 1/3$

Our final answer is E, $1/81$

3. We have a total of 150 people and 67 of them have type A blood, while 6 of them have type AB. This means that type A blood has a probability of:

And type AB blood has a probability of:

Now we can add these probabilities together.

$67/150 + 6/150 = 73/150$

Our final answer is D, $73/150$

4. Here, we have another probability question made more complicated by the use of ratios. Again, if you need a refresher on ratios, check out our guide to ACT fractions and ratios .

First, we must find the actual number of 10th and 11th graders.

We are told that the 10th graders have a ratio of 86:255 to the school population and the 11th graders have a ratio of 18:51 to the total student population. We must first set these ratios to an equal number of total students in order to determine the number of students in each class.

We can see that the 11th graders have a reduced ratio, so we must multiply each side of the ratio by the same amount in order to equal the total number of students as the 10th graders’ ratio (255).

Luckily for us, $255/51 = 5$. This is a nice, round number to work with.

Now, we must multiply the 11th grade ratio by 5 on each side to even out the playing field.

$18(5):51(5)$

We are assuming for now that there are 255 students total (there may be $255 *2$ or $255 * 3$, and so forth, but this will not affect our final outcome; all that matters is that we choose a total number of students that is equal for all grades/ratios.)

So there are 86 10th graders, 90 11th graders, and the remaining students are 12th graders. Knowing that there are 255 students total, we can find the number of 12th graders by saying:

$255 - 86 - 90 = 79$

There are 79 12th graders.

This means that the probability of selecting a 10th, 11th, or 12th grader at random is:

$86/255$, $90/255$, $79/255$, respectively.

The odds are higher that the lottery will select an 11th grader, as the numerator for 11th graders is larger than that of the others.

Our final answer is B, 11th graders.

The Take Aways

The more you practice working with probabilities, the easier they will become. Although it can take some time to learn how to properly differentiate between the different types of probability questions, most ACT probability questions are fairly straightforward.

Understand that probabilities are simply fractional relationships of desired outcomes over all potential outcomes, and you’ll be able to tackle these kinds of ACT math questions in no time.

What’s Next?

Now that you've stacked the odds in your favor on your probability questions, it's time to make sure you're caught up with the rest of your ACT math topics . We've got guides on all your individual math needs , from trigonometry to slopes and more.

Wondering how your score stacks up? See what makes a "good" score and how you can get the most out of your studying time to reach your target goal.

Running out of time on the ACT? Look to our guide on how to maximize your time and your score in the hour allotted.

Want to get a perfect score? Check out how to get a perfect score on the ACT math , written by a 36-scorer.

Want to improve your ACT score by 4 points?

Check out our best-in-class online ACT prep program . We guarantee your money back if you don't improve your ACT score by 4 points or more.

Our program is entirely online, and it customizes what you study to your strengths and weaknesses . If you liked this Math lesson, you'll love our program. Along with more detailed lessons, you'll get thousands of practice problems organized by individual skills so you learn most effectively. We'll also give you a step-by-step program to follow so you'll never be confused about what to study next.

Check out our 5-day free trial:

Get 4 More Points on Your ACT, GUARANTEED

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Student and Parent Forum

Our new student and parent forum, at ExpertHub.PrepScholar.com , allow you to interact with your peers and the PrepScholar staff. See how other students and parents are navigating high school, college, and the college admissions process. Ask questions; get answers.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

Search IntMath
Math interactives
About (site info)
Uses of Trignometry
ASCIIMath input, KaTeX output
ASCIIMath input, LaTeX and KaTeX output
Send Math in emails
Syntax for ASCIIMathML
Math Display Experiments
Scientific Notebook
Math Problem Solver

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Probability Problem Solver

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of artificial intelligence large language models to parse and generate natural language answers. This creates a math problem solver that's more accurate than ChatGPT, more flexible than a math calculator, and provides answers faster than a human tutor.

Problem Solver Subjects

Our math problem solver that lets you input a wide variety of probability math problems and it will provide a step by step answer. This math solver excels at math word problems as well as a wide range of math subjects.

Math Word Problems
Pre-Algebra
Geometry Graphing
Trigonometry
Precalculus
Finite Math
Linear Algebra

Here are example math problems within each subject that can be input into the calculator and solved. This list is constanstly growing as functionality is added to the calculator.

Basic Math Solutions

Below are examples of basic math problems that can be solved.

Long Arithmetic
Rational Numbers
Operations with Fractions
Ratios, Proportions, Percents
Measurement, Area, and Volume
Factors, Fractions, and Exponents
Unit Conversions
Data Measurement and Statistics
Points and Line Segments

Math Word Problem Solutions

Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.

Word Problem: Rachel has 17 apples. She gives some to Sarah. Sarah now has 8 apples. How many apples did Rachel give her?

Simplified Equation: 17 - x = 8

Word Problem: Rhonda has 12 marbles more than Douglas. Douglas has 6 marbles more than Bertha. Rhonda has twice as many marbles as Bertha has. How many marbles does Douglas have?

Variables: Rhonda's marbles is represented by (r), Douglas' marbles is represented by (d) and Bertha's marbles is represented by (b)

Simplified Equation: {r = d + 12, d = b + 6, r = 2 �� b}

Word Problem: if there are 40 cookies all together and Angela takes 10 and Brett takes 5 how many are left?

Simplified: 40 - 10 - 5

Pre-Algebra Solutions

Below are examples of Pre-Algebra math problems that can be solved.

Variables, Expressions, and Integers
Simplifying and Evaluating Expressions
Solving Equations
Multi-Step Equations and Inequalities
Ratios, Proportions, and Percents
Linear Equations and Inequalities

Algebra Solutions

Below are examples of Algebra math problems that can be solved.

Algebra Concepts and Expressions
Points, Lines, and Line Segments
Simplifying Polynomials
Factoring Polynomials
Linear Equations
Absolute Value Expressions and Equations
Radical Expressions and Equations
Systems of Equations
Quadratic Equations
Inequalities
Complex Numbers and Vector Analysis
Logarithmic Expressions and Equations
Exponential Expressions and Equations
Conic Sections
Vector Spaces
3d Coordinate System
Eigenvalues and Eigenvectors
Linear Transformations
Number Sets
Analytic Geometry

Trigonometry Solutions

Below are examples of Trigonometry math problems that can be solved.

Algebra Concepts and Expressions Review
Right Triangle Trigonometry
Radian Measure and Circular Functions
Graphing Trigonometric Functions
Simplifying Trigonometric Expressions
Verifying Trigonometric Identities
Solving Trigonometric Equations
Complex Numbers
Analytic Geometry in Polar Coordinates
Exponential and Logarithmic Functions
Vector Arithmetic

Precalculus Solutions

Below are examples of Precalculus math problems that can be solved.

Operations on Functions
Rational Expressions and Equations
Polynomial and Rational Functions
Analytic Trigonometry
Sequences and Series
Analytic Geometry in Rectangular Coordinates
Limits and an Introduction to Calculus

Calculus Solutions

Below are examples of Calculus math problems that can be solved.

Evaluating Limits
Derivatives
Applications of Differentiation
Applications of Integration
Techniques of Integration
Parametric Equations and Polar Coordinates
Differential Equations

Statistics Solutions

Below are examples of Statistics problems that can be solved.

Algebra Review
Average Descriptive Statistics
Dispersion Statistics
Probability
Probability Distributions
Frequency Distribution
Normal Distributions
t-Distributions
Hypothesis Testing
Estimation and Sample Size
Correlation and Regression

Finite Math Solutions

Below are examples of Finite Math problems that can be solved.

Polynomials and Expressions
Equations and Inequalities
Linear Functions and Points
Systems of Linear Equations
Mathematics of Finance
Statistical Distributions

Linear Algebra Solutions

Below are examples of Linear Algebra math problems that can be solved.

Introduction to Matrices
Linear Independence and Combinations

Chemistry Solutions

Below are examples of Chemistry problems that can be solved.

Unit Conversion
Atomic Structure
Molecules and Compounds
Chemical Equations and Reactions
Behavior of Gases
Solutions and Concentrations

Physics Solutions

Below are examples of Physics math problems that can be solved.

Static Equilibrium
Dynamic Equilibrium
Kinematics Equations
Electricity
Thermodymanics

Geometry Graphing Solutions

Below are examples of Geometry and graphing math problems that can be solved.

Step By Step Graphing
Linear Equations and Functions
Polar Equations

Looking for the old Mathway Calculator? We've moved it to here .

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

Netflix's hit sci-fi series '3 Body Problem' is based on a real math problem that is so complex it's impossible to solve

The three-body problem is a centuries-old physics question that puzzled Isaac Newton .
It describes the orbits of three bodies, like planets or stars, trapped in each other's gravity.
The problem is unsolvable and led to the development of chaos theory.

While Netflix's "3 Body Problem" is a science-fiction show, its name comes from a real math problem that's puzzled scientists since the late 1600s.

In physics, the three-body problem refers to the motion of three bodies trapped in each other's gravitational grip — like a three-star system.

It might sound simple enough, but once you dig into the mathematics, the orbital paths of each object get complicated very quickly.

Two-body vs. three- and multi-body systems

A simpler version is a two-body system like binary stars. Two-body systems have periodic orbits, meaning they are mathematically predictable because they follow the same trajectory over and over. So, if you have the stars' initial positions and velocities, you can calculate where they've been or will be in space far into the past and future.

However, "throwing in a third body that's close enough to interact leads to chaos," Shane Ross, an aerospace and ocean engineering professor at Virginia Tech, told Business Insider. In fact, it's nearly impossible to precisely predict the orbital paths of any system with three bodies or more.

While two orbiting planets might look like a ven diagram with ovular paths overlapping, the paths of three bodies interacting often resemble tangled spaghetti. Their trajectories usually aren't as stable as systems with only two bodies.

All that uncertainty makes what's known as the three-body problem largely unsolvable, Ross said. But there are certain exceptions.

The three-body problem is over 300 years old

The three-body problem dates back to Isaac Newton , who published his "Principia" in 1687.

In the book, the mathematician noted that the planets move in elliptical orbits around the sun. Yet the gravitational pull from Jupiter seemed to affect Saturn's orbital path.

Can you solve the three-body problem?

Cracking the three-body problem would help scientists chart the movements of meteors and planets, including Earth, into the extremely far future. Even comparatively small movements of our planet could have large impacts on our climate, Ross said.

Though the three-body problem is considered mathematically unsolvable, there are solutions to specific scenarios. In fact, there are a few that mathematicians have found.

For example, three bodies could stably orbit in a figure eight or equally spaced around a ring. Both are possible depending on the initial positions and velocities of the bodies.

One way researchers look for solutions is with " restricted " three-body problems, where two main bodies (like the sun and Earth) interact and a third object with much smaller mass (like the moon) offers less gravitational interference. In this case, the three-body problem looks a lot like a two-body problem since the sun and Earth comprise the majority of mass in the system.

However, if you're looking at a three-star system, like the one in Netflix's show "3 Body Problem," that's a lot more complicated.

Computers can also run simulations far more efficiently than humans, though due to the inherent uncertainties, the results are typically approximate orbits instead of exact.

Finding solutions to three-body problems is also essential to space travel, Ross said. For his work, he inputs data about the Earth, moon, and spacecraft into a computer. "We can build up a whole library of possible trajectories," he said, "and that gives us an idea of the types of motion that are possible."

Main content

Help | Advanced Search

Computer Science > Computation and Language

Title: large language models are unconscious of unreasonability in math problems.

Abstract: Large language models (LLMs) demonstrate substantial capabilities in solving math problems. However, they tend to produce hallucinations when given questions containing unreasonable errors. In this paper, we study the behavior of LLMs when faced with unreasonable math problems and further explore their potential to address these problems. First, we construct the Unreasonable Math Problem (UMP) benchmark to examine the error detection ability of LLMs. Experiments show that LLMs are able to detect unreasonable errors, but still fail in generating non-hallucinatory content. In order to improve their ability of error detection and correction, we further design a strategic prompt template called Critical Calculation and Conclusion(CCC). With CCC, LLMs can better self-evaluate and detect unreasonable errors in math questions, making them more reliable and safe in practical application scenarios.

Submission history

Access paper:.

HTML (experimental)
Other Formats

References & Citations

Google Scholar
Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

COMMENTS

How to Solve Probability Problems? (+FREE Worksheet!)
To solve a probability problem identify the event, find the number of outcomes of the event, then use probability law: $\frac{number\ of \ favorable \ outcome}{total \ number \ of \ possible \ outcomes}$ Probability Problems . The Absolute Best Books to Ace Pre-Algebra to Algebra II
Probability
About this unit. Probability tells us how often some event will happen after many repeated trials. You've experienced probability when you've flipped a coin, rolled some dice, or looked at a weather forecast. Go deeper with your understanding of probability as you learn about theoretical, experimental, and compound probability, and investigate ...
15 Probability Questions And Practice Problems
8th grade probability questions. 5. Alice has some red balls and some black balls in a bag. Altogether she has 25 balls. Alice picks one ball from the bag. The probability that Alice picks a red ball is x and the probability that Alice picks a black ball is 4x. Work out how many black balls are in the bag. 66. 100100.
Probability Questions with Solutions
a) A die is rolled, find the probability that the number obtained is greater than 4. b) Two coins are tossed, find the probability that one head only is obtained. c) Two dice are rolled, find the probability that the sum is equal to 5. d) A card is drawn at random from a deck of cards.
Probability: the basics (article)
2 months ago. Classical Probability (Equally Likely Outcomes): To find the probability of an event happening, you divide the number of ways the event can happen by the total number of possible outcomes. Probability of an Event Not Occurring: If you want to find the probability of an event not happening, you subtract the probability of the event ...
Probability
The probability that you will draw a green or a red marble is \frac {5 + 15} {5+15+16+20} 5+15+16+205+15. We can also solve this problem by thinking in terms of probability by complement. We know that the marble we draw must be blue, red, green, or yellow. In other words, there is a probability of 1 that we will draw a blue, red, green, or ...
Probability
Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability. Tossing a Coin. When a coin is tossed, there are two possible outcomes: Heads (H) or Tails (T) Also: the probability of the coin landing H is ½; the probability of the coin landing T is ½ . Throwing Dice
How to Solve Probability Problems
Solution: The sum of probabilities of all the sample points must equal 1. And the probability of getting a head is equal to the probability of getting a tail. Therefore, the probability of each sample point (heads or tails) must be equal to 1/2. Example 2 Let's repeat the experiment of Example 1, with a die instead of a coin.
Probability
If you're curious about the mathematical ins and outs of probability, you've come to the right unit! Here, we'll take a deep dive into the many ways we can calculate the likelihood of different outcomes. From using simulations to the addition and multiplication rules, we'll build a solid foundation that will help us tackle statistical questions down the line.
4 Ways to Calculate Probability
2. Add the numbers together to convert the odds to probability. Converting odds is pretty simple. First ,break the odds into 2 separate events: the odds of drawing a white marble (11) and the odds of drawing a marble of a different color (9). Add the numbers together to calculate the number of total outcomes.
How To Calculate Probability
For mutually exclusive events: P (A or B) = P (A) + P (B) If we have an exhaustive list of outcomes, their probabilities sum to 1. 1. For example, the probability of getting an even or an odd number on a die. The probability of getting an even number is \frac {3} {6} 63. and the probability of getting an odd number is \frac {3} {6}.
Probability
In the language of measure theory, probability is formally defined as a triple known as a probability space, denoted . Here is a set called the sample space, and is a class of events given by certain subsets of . must satisfy certain properties (it must be a -algebra) to qualify as a class of events.
Probability Problems Calculator
High School Math Solutions - Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables. In this blog post,...
Probability Problems: Solve them the easy way!
Finding the probability of a simple event happening is fairly straightforward: add the probabilities together. For example, if you have a 10% chance of winning $10 and a 25% chance of winning $20 then your overall odds of winning something is 10% + 25% = 35%. This only works for mutually exclusive events (events that cannot happen at the same ...
5.3: Probability Rules- "And" and "Or"
To create a compound event, we can use the word "and" or the word "or" to combine events. It is very important in probability to pay attention to the words "and" and "or" if they appear in a problem. The word "and" restricts the field of possible outcomes to only those outcomes that simultaneously describe all events.
Complete Guide to Probability on SAT Math + Practice Questions
1. or 1. There is no higher chance of it happening—this particular event will happen every single time, without fail. A probability of an absolutely impossible event, however, will be 0 because. 0. x. = 0. You can also think of probabilities as percentages. If I select a red marble from a bag at a probability of.
Probability
And you divide the denominator by six, you get five. So anything you do to the numerator of a fraction, as long as you do it to the denominator as well, it doesn't change the value of the fraction. So we just divided the numerator and the denominator by six to get to 1/5. And we do see that choice right over there.
Probability Questions
Solution: The total number of tests conducted is 5. The number of tests when students obtained more than 70% marks = 3. So, P (scoring more than 70% marks) = ⅗ = 0.6. 4. One card is drawn from a deck of 52 cards, well-shuffled. Calculate the probability that the card will. (i) be an ace, (ii) not be an ace.
Probability Questions on ACT Math: Strategies and Practice
5. ( 18 + x) ( 3) = ( 6 + x) ( 5) 54 + 3 x = 30 + 5 x. 24 = 2 x. 12 = x. So we must increase our red marbles (and, consequently, the total number of marbles) by 12 in order to get a probability of ⅗ of selecting a red marble. To double-check this, we can plug the number back into our probability. 6 + 12.
Probability Problem Solver
Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms. Word Problem: Rachel has 17 apples ...
Probability Practice Questions
Practice Questions. Previous: Direct and Inverse Proportion Practice Questions. Next: Reverse Percentages Practice Questions. The Corbettmaths Practice Questions on Probability.
Probability Involving AND and OR
The rule for OR must take into account values that may get counted more than once where the sets overlap. In the first version, this overlap is dealt with when finding n(A or B). In the second version, this overlap is dealt with in the subtraction of the intersection, P(A and B). If sets A and B are mutually exclusive (no elements in common), P(A and B) = 0,
How to solve Probability questions?
The probability is the number of outcomes favourable to the question, divided by the total number of possible outcomes. In your question: there are 18 marbles, so there are 18 possible outcomes. For (a) Favourable outcomes are black or red. There are 7 such outcomes, so probability is 7/18 For (b) Favourable outcomes are yellow or green.
Why the Three-Body Problem in Physics Is Unsolvable
While Netflix's "3 Body Problem" is a science-fiction show, its name comes from a real math problem that's puzzled scientists since the late 1600s. In physics, the three-body problem refers to the ...
Large Language Models Are Unconscious of Unreasonability in Math Problems
Large language models (LLMs) demonstrate substantial capabilities in solving math problems. However, they tend to produce hallucinations when given questions containing unreasonable errors. In this paper, we study the behavior of LLMs when faced with unreasonable math problems and further explore their potential to address these problems. First, we construct the Unreasonable Math Problem (UMP ...