how to solve surface area and volume problems easily class 10

NCERT Solutions for Class 10 Maths Chapter 12 Surface areas and volumes

Revised NCERT Solutions for class 10 Maths Chapter 12 Surface areas and volumes in Hindi and English Medium updated for CBSE Board exams 2024. As per the new syllabus and NCERT Books published for academic year 2023-24, there are only two exercises in chapter 12 of 10th mathematics.

NCERT Solutions of Class 10 Maths Chapter 12 for CBSE Board

Class 10 Maths Exercise 12.1 in English Class 10 Maths Exercise 12.2 in English Class 10 Maths Exercise 12.1 in Hindi Class 10 Maths Exercise 12.2 in Hindi

Class 10 Maths Chapter 12 Solutions for State Boards Class 10 Maths Exercise 12.1 Class 10 Maths Exercise 12.2 Class 10 Maths Exercise 12.3

Class 10 Maths Chapter 12 all exercises (Ex. 12.1 and Ex. 12.2) for all boards. We have updated all the contents for new academic session 2023-24. UP Board students are now using NCERT Textbooks for their course and exams, so they can download UP Board Solutions for Class 10 Maths Chapter 12 all exercises from the links given below. Contents are applicable for UP Board 2023-24 and CBSE Board in Hindi and English medium. Contents are free in PDF format to download without any login or registration. Download NCERT Solutions Online and Offline App for session 2023-24 based on updated NCERT Solutions and latest NCERT Books 2023-24. Previous year CBSE Exam question, important questions for practice are also given below. Download and practice to score good marks and solve your doubts easily.

CBSE NCERT Solutions for class 10 Maths Chapter 12 Surface areas and volumes exercises 12.1 and 12.2 are given here to free download in PDF or view online without downloading. All the solutions are updated for new academic session 2023-24 for UP Board, MP Board, Gujrat, CBSE board, etc., who are using latest NCERT Books for course.

ONE MARK QUESTIONS 1. Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere? [CBSE 2017] THREE MARKS QUESTIONS 1. A metallic solid sphere of radius 10.5 cm is melted and recast into smaller solid cones, each of radius 3.5 cm and height 3 cm. How many cones will be made? [CBSE 2017] FOUR MARKS QUESTIONS 1. In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If the tank is filled completely then what will be the height of standing water used for irrigation the park. Write your views on recycling of water. [CBSE 2017] 2. The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is 1/27 of the given cone, then at what height it is cut from its base? [CBSE 2017] 3. The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts. [CBSE 2017]

1. To identify situations where there is a need of finding surface area and where there is a need of finding volume of a solid figure and to find the surface areas & volumes of cuboids, cubes, cylinders, cones spheres and hemispheres, using their respective formulae. To solve some problems related to daily life situations involving surface areas and volumes of above solid figures. 2. In this chapter, we will deal with problems such as finding the area of sheet to covers a solid body, area of an object which is combination of two objects, finding the number of one object, required for creating another different object, finding the cost of ploughing a given field at a given rate, finding the cost of constructing a water tank with a particular capacity, finding area & volume of frustum (Frustum is a Latin word meaning ‘piece cut off’ and its plural form is ‘Frusta’) and the conversion of one solid into another solid on the basis of volume and so on. For solving above type of problems, we need to find the perimeters and areas of simple closed plane figures (figure which lie in a plane) and surface areas and volumes of solid figures (figures which do not lie wholly in a plane). You are already familiar with the concepts of perimeters, areas, surface areas and volumes. In this chapter, we will study these in details.

Archimedes of Syracuse, Sicily, is remembered as the greatest Greek mathematician of the ancient era. He contributed significantly in geometry regarding the areas of plane figures and the areas and volumes of solid figures. He proved that the volume of a sphere is equal to two-third the volume of a circumscribed cylinder.

What are the topics to study in chapter 12 Surface Areas and Volumes of 10th Maths?

In chapter 12, Surface Areas and Volumes of class 10 math, students will study

• Surface Area of a Combination of Solids.
• Volume of a Combination of Solids.
• Conversion of Solid from one shape to another.

Which topics students should revise before starting chapter 12 of class 10 Maths?

Before starting chapter 12 of class 10 Maths, Students should revise all the formulas mentioned in chapter 12 (surface areas and volumes) of class 9th Maths.

Is there any optional exercise in chapter 12 of class 10th Maths?

Yes, there are no optional exercise in chapter 12 of class 10th Maths. Exercise 13.2 is challenging because this exercise contains logical questions which require higher-order thinking skills. Students find this exercise a little complex as compared to other exercises of this chapter.

Is chapter 12 of class 10th math difficult to solve?

Chapter 12 of class 10th Maths is not easy and not difficult. It lies in the middle of easy and difficult because some examples and questions of this chapter are easy, and some are difficult. However, the difficulty level of anything varies from student to student. So, Chapter 12 of class 10th Maths is easy or not depends on students also. Some students find it difficult, some find it easy, and some find it in the middle of easy and difficult.

« Chapter 11: Area Related to Circles

Chapter 13: statistics ».

Copyright 2024 by Tiwari Academy | A step towards Free Education

Surface Area and Volume Class 10 Formulas

Surface Area and Volume class 10 formulas help students to study various dimensions of different solid shapes like cube, cone, cylinder, cuboid, etc. As these concepts are a part of our everyday life, students need to efficiently memorize these surface area and volume class 10 formulas along with formulas of solid figures studied in previous grades.

List of Surface Area and Volume Class 10 Formulas

Here is a list of the Surface Area and Volume formulas for class 10.

• Surface Area of a cuboid of length (l), breadth (b), and height (h) = 2 (lb + bh + lh)
• Lateral Surface Area of cuboid = 2 (l + b)h
• Surface Area of a cube = 6 ✕ l2 where l is the length
• Lateral Surface Area of cube = 4 ✕ l 2 , where l is the length
• Volume of cube = l 3
• Lateral Surface Area of a Cylinder = 2πrh
• Total Surface Area of a Cylinder = 2πr (h+r)
• Volume of Cylinder = πr 2 h
• Lateral Surface Area of Cone = πrL
• Total surface area of cone = πr ( L+ r)
• Volume of Cone = ⅓ (πr 2 h)
• Surface Area of Sphere= 4 πr 2
• Volume of Sphere = 4/3 (πr 3 )
• Volume of a frustum of a cone = 1/3 πh(r ₁ 2 + r ₂ 2 + r ₁ r ₂ )

Applications of Surface Area and Volume Class 10 Formulas

Here are some of the applications of surface area and volume class 10 formulas:

• Surface area and volume class 10 formulas are used for finding out things that are proportional to the surface area and volume. For example, to determine the quantity of paint that would be needed to cover the object or the amount of wallpaper that would be required to cover a wall.
• Surface area and volume formulas are utilized in cooking to measure the ingredients in the various recipes.
• These formulas are applied in many routine calculations like determining the amount of fuel to fill a car's tank or for adding detergent to the washing machine.
• Surface area formulas are often used in electronics to design circuit boards.
• These formulas are also applied to calculate the cost of an apartment/house based on the price per square feet.
• Construction and architectural works, material estimating, pattern layout, programming, budgeting, site design, code analyses, etc. are some of the other fields where Surface area and volume formulas are widely applied.

Tips to Memorize Surface Area and Volume Class 10 Formulas

Here are some tips that could be helpful for kids to memorize Surface area and volume formulas for class 10.

• The students must make sure to understand the concepts first before moving ahead to memorize the formulas. They should also clear their doubts and seek help from their teachers to form a clear understanding of each concept.
• They can also go through the derivation of these formulas to develop a rock-solid foundation as well as understand the underlying concepts.
• It is necessary that the students must practice a variety of questions based on surface area and volume formulas to ensure a thorough conceptual understanding of all important formulas.

Surface Area and Volume Class 10 Formulas Examples

Example: Two cubes with volume 27 cm 3 are joined back-to-back with each other. Determine the surface area of the cuboid formed.

Solution: Let’s determine the length of the edge of each cube by applying the volume of the cube formula. The volume of a cube = a 3 , where the length of the edge is 'a'.

Using the formula for the surface area of a cuboid = 2(lb + bh + lh), where l, b, and h are length, breadth, and height respectively.

Let the length of the edge of each cube be 'a'

Therefore, volume of the cube = a 3

Volume of the cube, a 3 = 27 cm 3

a 3 = 27 cm 3

a = ∛(27 cm 3 )

Length of the resulting cuboid, l = a = 3 cm

Breadth of the resulting cuboid, b = a = 3 cm

Height of the resulting cuboid, h = 2a = 2 × 3 cm = 6 cm

Surface area of the resulting cuboid = 2 (lb + bh + lh)

= 2 (3 cm × 3 cm + 3 cm × 6 cm + 3 cm × 6 cm)

= 2 (9 cm 2 + 18 cm 2 + 18 cm 2 )

= 2 × 45 cm 2

Thus, the surface area of the resulting cuboid is 90 cm 2 .

Students can download the printable Maths Formulas Class 10  sheet from the link provided below:

FAQs on Surface Area and Volume Class 10 Formulas

What are the Important Surface Area and Volume class 10 formulas?

Here are important Surface Area and Volume Class 10 formulas that students need to remember in order to solve the questions related to the topic.

• Lateral Surface Area of cuboid = 2 ( l+ b) h
• Surface Area of a cube = 6 x l2 where l is the length
• Lateral Surface Area of cube = 4 x l 2 , where l is the length

How Many Formulas are There in Surface Area and Volume Class 10?

There is a long list of important formulas based on surface area and volume of different shapes like cube, cuboid, cylinder, hemisphere, cone, etc. Most of the questions covered in this chapter are based on formulas; therefore, it is necessary to memorize them. Besides, students should also learn to derive each of these formulas. It will benefit them to understand the solutions to all the questions with ease.

Why Should Students Practice Questions Based on Surface Area and Volume Class 10 Formulas?

Maths is all about practice and students must practice maximum questions based on Surface Area and Volume Class 10 Formulas. Solving all types of problems based on these formulas will help students understand key concepts and explore their applications. Getting well-versed with the concepts will enable students to identify and derive different formulas which are to be applied in the questions.

How to Memorize Surface Area and Volume Class 10 Formulas?

One of the most effective ways to learn and memorize surface area and volume class 10 formulas is to apply them in solving various types of problems. While applying these formulas students will be able to understand and derive them. It will be helpful for them to quickly revise them during exams.

How to Download Surface Area and Volume Formulas Class 10 pdf?

Students can easily download the surface area and volume formulas class 10 pdf by clicking on the download option provided on the page. On clicking the option, a popup will appear. Students need to provide a valid phone number to receive an OTP. Once the OTP is entered the pdf file will automatically download on the device.

ilatemaths.com

Chapter 12 of the Class 10 Maths NCERT book focuses on the surface areas and volumes of various objects and shapes. We will explore the surface area and volume of solid shapes like cubes, cuboids, cones, cylinders, and more. The surface area is divided into three categories: Lateral Surface Area (LSA), Total Surface Area (TSA), and Curved Surface Area (CSA). Let’s delve into the formulas for calculating surface area and volume for different three-dimensional shapes. This chapter also covers the study of combining different solid shapes and provides a detailed procedure for finding their volume and surface area. To begin your preparation, simply click on the link below:

Surface Area & Volume

Chapter 12 – Surface Areas and Volumes

Chapter 12 on Surface Areas and Volumes is an intriguing and important chapter when it comes to exams. It covers the computation of surface areas and volumes for various solids such as frustums, cones, cylinders, spheres, cubes, and more. Moreover, this chapter also provides practical applications for real-world objects. For instance, students can utilize the formula for finding the volume of a cylinder to determine the capacity of a cylindrical water tank. By thoroughly understanding the sums in the NCERT Solutions, students will be well-prepared to solve any type of question related to this chapter in the CBSE Maths examination.

Exercises in Chapter 12:

In Class 10 Maths Chapter 12 “Surface, Areas and Volumes”, you will find two exercises. Let me give you a brief explanation of each exercise:

Exercise 12.1: This exercise focuses on questions that require finding the surface areas and volumes of cuboids and cubes. It consists of nine questions that aim to test your understanding of the formulas and concepts related to these figures. The solutions for each question provide step-by-step instructions on how to calculate the surface area and volume accurately.

Exercise 12.2: This exercise deals with questions that involve finding the surface areas and volumes of right circular cylinders and cones. It includes eight questions that assess your comprehension of the concepts associated with the surface area and volume of cylinders and cones. The solutions for each question offer detailed explanations and diagrams to assist you in grasping the concept more effectively.

Importance of Ncert Solutions:

The Ncert solutions have been meticulously prepared in accordance with the latest syllabus and Ncert guidelines, ensuring that students can comprehensively cover the entire syllabus. These solutions for respective classes effectively elucidate the concepts covered in each chapter. Not only do the Ncert solutions adequately prepare students for their final exams, but they also enhance their understanding of the subject matter. 

Moreover, the Ncert solution serves as a highly reliable and accurate source of information. The study materials provide explanations for all Ncert questions, and each question is accompanied by detailed answers and the formula used to solve it. Ultimately, these resources enable students to establish a strong foundation in Mathematics and boost their confidence for the board examination.

Ncert solutions have been designed in such a way that they are easily comprehensible for every student. The Ncert book itself is self-explanatory and aids students in acquiring knowledge in mathematics. By solving Ncert problems, you can establish a solid foundation in Mathematics and enhance your confidence to tackle board examinations. 

Through the process of solving Ncert problems, you can also learn the steps to resolve complex solutions. The Ncert solutions serve as an additional reference and study material for students. Moreover, while solving textbook problems, students can cross-check their answers and gain insights into alternative methods of answering the questions. This platform is highly recommended for students to complete their assignments promptly.

Are you a CBSE student looking for reliable study materials to ace your exams? Look no further! Ilate Maths is here to help. Our educational website offers a wide range of study materials for subjects like English , Social , and Mathematics . Best of all, it’s completely free!.

You cannot copy content of this page

NCERT Solutions for Class 10 Maths Chapter 13- Surface Areas and Volumes:

Ncert solutions for class 10 maths chapter 13- surface areas and volumes.

The solutions to the NCERT -based questions of Chapter 13 for Class 10 Maths, Surface Area and Volumes , is an essential study resource for Class 10 students. These assist students in comprehending or solving the sorts of problems that a paper setter asked in the first term examinations of CBSE Class 10 Maths . Furthermore, offering solutions to all areas relating to circles assists students in effectively preparing for the CBSE 2023 examinations.

The subject matter experts make sure that the errors in the NCERT textbooks are resolved according to the NCERT rules and syllabus.

MUST BUY (New Arrival):  CBSE Question Bank Class 10 2023-24 (For New Academic Session)

BUY NOW FOR CLASS 10 BOARD EXAMS:  CBSE QUESTION BANK CLASS 10 MATHS, SCIENCE, ENGLISH & SOCIAL SCIENCE (SET OF 4 BOOKS) FOR THE 2024 BOARD EXAMS 

CBSE SAMPLE PAPER CLASS 10 FOR 2023-24 BOARD EXAMS  | FREE PDF DOWNLOAD

The solutions to the NCERT -based questions of Chapter 13 for Class 10 Maths are accessible at our website . These solutions will assist students in acing their CBSE 2023 examinations by preparing for the examinations ahead of time. Students may clarify all of their conceptual questions or doubts with the assistance of the notes of Maths NCERT Solutions for Class 10 of this chapter which we provide. Experts have created these NCERT Solutions based on the most recent update to the CBSE syllabus for 2022-23 to help students in Class 10 prepare well for their CBSE 2023 examinations.

NCERT Solutions for Class 10 Maths Chapter 13- Surface Areas and Volumes | Free PDF Download

The Class 10 Maths Chapter 13 of NCERT Solutions includes topics related to surface area and volume of shapes like cylinder, sphere, cube, cone, cuboid, etc. It has formulas and theories related to area and volume of these shapes.

Chapter 13 Surface Area and Volumes is one of the parts of the Mensuration , and it has a total weightage of 10 points in the first term examinations. One question from this chapter is frequently asked in the first term test.

Parts of circles, their measurements, and the areas of planar figures are covered in Chapter 13 of Maths NCERT Solutions for Class 10 . Our  subject matter specialists have created solutions for each question based on the CBSE syllabus for 2023-24.

The following are some of the concepts covered in Chapter 13, Surface Area and Volumes are:

Surface Area : Surface area is a measurement of the entire area occupied by the object's surface.

Volume:  Volume in math refers to the quantity of space in a 3D object. In this chapter we will learn how to calculate the volume of shapes like cylinder, sphere, cube, cone, cuboid, etc. with the help of some formulas. A fish tank, for example, is 3 feet long, 1 foot wide, and 2 feet tall. To calculate the volume, multiply the length by the breadth by the height, which is 3x1x2, six. As a result, the fish tank has six cubic feet.

NCERT Solutions Class 10 Maths  All Chapters:

NCERT Solution Class 10 Maths Chapter 13 Surface Area and Volumes include major subjects as:

Exercise 13.1 Introduction

Exercise 13.2 Surface Area of a Combination of Solids

Exercise 13.3 Volume of a Combination of Solids

Exercise 13.4 Conversion of Solid from One Shape to Another

Exercise 13.5 Frustum of a Cone

Exercise 13.6 Summary

Practicing the NCERT Solutions for Class 10 might be highly important for the CBSE  2023 examinations.

Class 10 Maths NCERT Solutions of Chapter 13 Surface Area and Volumes Highlights:  

NCERT Solutions assist students in solidifying their knowledge in circle-related areas.

Diagrams are used to answer questions, making learning more dynamic and thorough.

The language used in NCERT Solutions is simple and easy to grasp.

Students benefit from a step-by-step approach to problem-solving.

Allows learners to work through challenging problems in their own time.

Trending & Recommended:    CBSE Question Bank Class 10 for 2023-2024 Board Exams 

Don't Miss:    CBSE Previous Last 6 Years Question Papers Class 10 Maths Science Social & All Subjects ,  CBSE Class 10 LMP (Last Minute Preparation System)

Latest:  CBSE Class 10 RMT Flashcards for 2023-24 Board Exams

CBSE CLASS 10 SAMPLE PAPERS FOR 2022-23 BOARDS EXAMS

NCERT Solutions for various courses and disciplines are also available for students to use. Our  well-experienced professors create these answers to offer clarity on essential ideas and problem-solving abilities.

Students can also obtain a firm grasp of critical topics by referring to additional study resources available in our CBSE Books Class 10.

Along with the  NCERT  Solutions, college students also can exercise the alternative textbook answers to apprehend the ideas in a miles higher way.

Frequently Asked Questions for NCERT Solution Class 10 Maths Chapter 13:

What are the benefits of studying NCERT Solutions for Class 10 Maths Chapter 13?

Answer: NCERT Class 10 Maths Chapter 13 solutions assist students in obtaining a summary of the question paper format, which includes a range of questions, such as usually repeated questions, brief and long response type questions, multiple-choice questions, marks, and so on. The more problems you solve, the more confident you will be in your achievement.

Mention exam-relevant concepts in NCERT Solutions for Class 10 Maths Chapter 13?

Answer:  The most important exam topics in NCERT Solutions for Class 10 Maths Chapter 13 are Introduction, Surface Area of a Combination of Solids, Volume of a Combination of Solids, Conversion of Solid from One Shape to Another, Frustum of a Cone and finally the Summary.

What number of exercises in NCERT Solutions for Class 10 Maths Chapter 13?

Answer:  It includes five exercises. The first exercise has eight questions. The second contains 8 questions. The third exercise contains 9. The fourth exercise contains 5 questions. The fifth exercise contains 7 questions based on introduction, Surface Area of a Combination of Solids, Volume of a Combination of Solids, Conversion of Solid from One Shape to Another and Frustum of a Cone respectively.

Free Study Materials Class 10 | For 2024 Board Exams

Shop now | for 2024 board exams.

Free CBSE Question Banks for 2022-23

Medical, Engineering & Law Entrance Exams

CISCE Board

Free Sample Question Papers CBSE Board

Free Sample Question Papers CISCE Board

Karnataka SSLC

Karnataka PUC

Olympiad Books

One For All Worksheets

Safe Shopping

Quick Shipping

Inclusive Pricing

Trusted Products

Compare Products

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Surface areas and volumes

Combination of solids.

• Area of combination of solids (Opens a modal)
• Problem types: surface area of combination of solids (Opens a modal)
• Volume of combination of solids (Opens a modal)
• Problem types: volume of combination of solids (Opens a modal)
• Combination of solids (basic) Get 3 of 4 questions to level up!
• Area of combination of solids (intermediate) Get 3 of 4 questions to level up!
• Area of combination of solids (advanced) Get 3 of 4 questions to level up!

Conversion of solids

• Volume word problem: gold ring (Opens a modal)
• Volume of rectangles inside rectangles (Opens a modal)
• Conversion of solids Get 3 of 4 questions to level up!
• Conversion of solids (advanced) Get 3 of 4 questions to level up!

Frustum of a cone

• Curved surface area of a frustum (Opens a modal)
• Volume of a frustum (Opens a modal)
• Finding dimensions of a frustum Get 3 of 4 questions to level up!
• Finding dimensions of a frustum using similar triangles Get 3 of 4 questions to level up!
• Area of frustum Get 3 of 4 questions to level up!
• Volume of frustum Get 3 of 4 questions to level up!
• Frustum (advanced) Get 3 of 4 questions to level up!

Register here

In case you want to be notified about school in your locality then please register here.

• Are you a Parent or Student?
• Are you a Teacher?
• Are you a School Supplier?

• Our other Domains Olympiad Preparation Math Square Science Square English Square Cyber Square School Square Scholar Square Global Olympiads NCERT Solutions CBSE Sample Papers
• Join WhatsApp Channel
• Apply for CREST Olympiads

Surface Area and Volumes

We all know about the solids and various kinds and combinations of solids which can be formed. Now in our earlier classes, we have learnt about finding the areas of all the 2D bodies like the square, rectangle, circles. But here we are going to extend our vision to determine the areas of the solid bodies or in simple words 3D bodies.

• Solids are the 3D objects are called as solids. It means that any object which has length, breadth and width is termed as a solid.
• The surface area of a solid object is a measure of the total area that the surface of the object occupies .
• The concept of surface area if taken to the molecular level leads us to the concept of integration of very small 2D areas which finally constitutes the whole area of the solid body.
• And the most common example of this is the surface area of a sphere which is an overall integration of the small circle elements together leading to the area of the circle.
• Volume is the quantity of three-dimensional space enclosed by a closed surface or a solid, for example, the space that a substance or shape occupies or contains.
• In simple words the amount of liquid up to the saturation point of the solid object.

Formulae for the Surface area and Volume of Solids

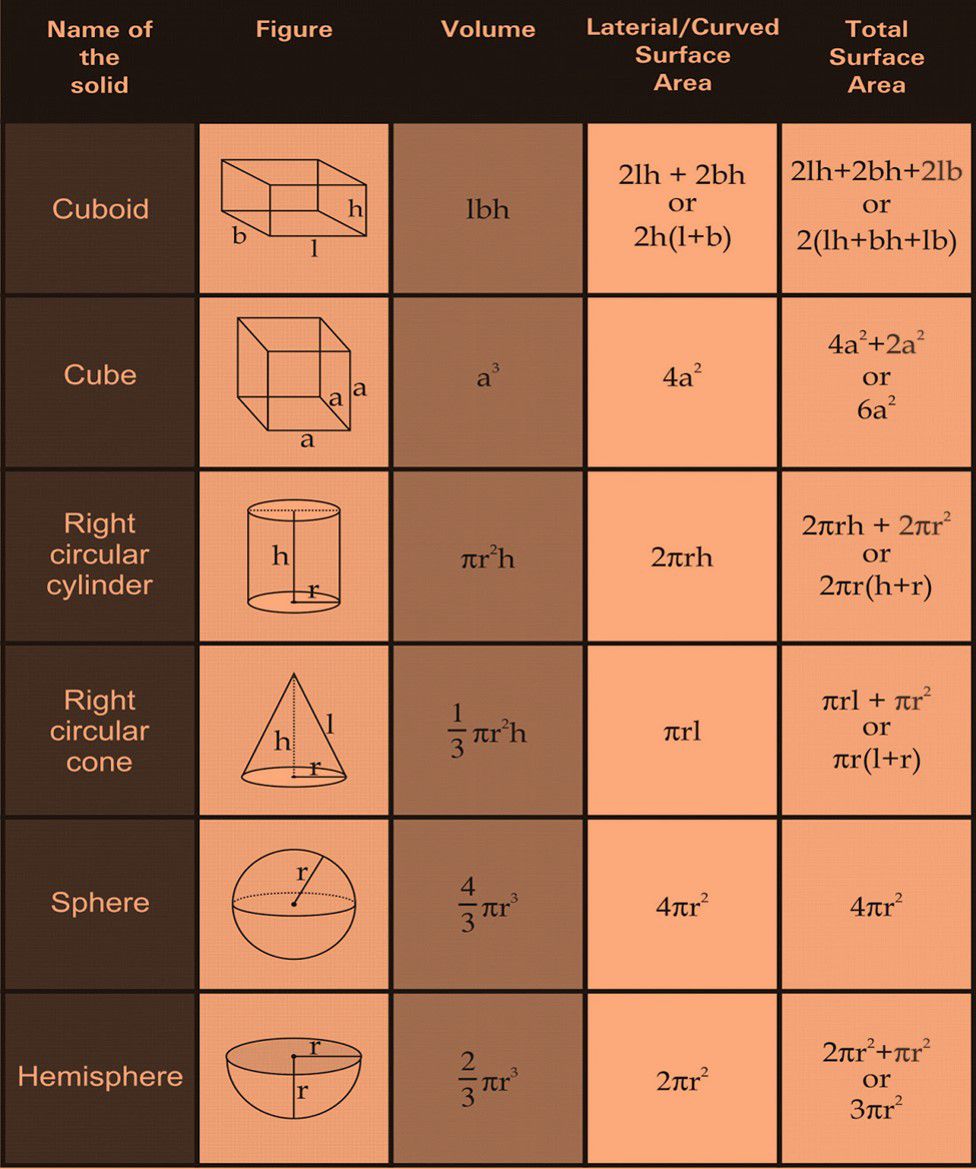
Combination of solids

When two same or different kinds of solids combine they form a completely new solid whose surface area depends accordingly on the constituent solids.

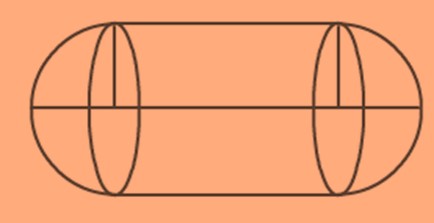
For example, the given solid is a combination of two hemispheres and a cylinder, and hence the total surface area of the solids will depend on the surface areas of the constituent solids which means

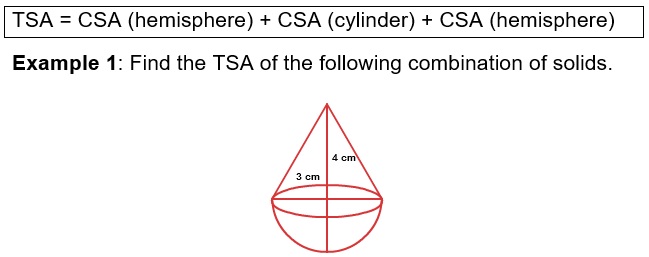
Solution: The solid is the combination of cone and a hemisphere

TSA = CSA of hemisphere + CSA of cone

TSA = 2πr 2 + πrl

TSA = 2 x 3.14 x 9 + 3.14 x 3 x 4

TSA = 56.52 cm 2 + 37.68 cm 2 = 94.2cm 2

Example 2: Find the volume of the following combination of solids.

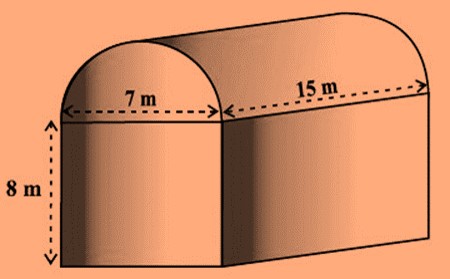
Solution: The above combination is of a cuboid and a half cylinder and hence the total volume of the solid will be:

Total Volume = Volume of cuboid + Volume of half cylinder

Total Volume = lbh + ½ πr 2 h

= [15 x 7 x 8 m 3 + ½ x 3.14 x 3.5 x 3.5 x 15 m 3 ]

= 840m 3 + 288.45m 3 = 1128.45m 3

Change of shape of solid

A solid can be changed to different shapes and sizes by melting it and then casting it to any other form. This process is known as casting of solids.

Here an important point is to be remembered that by doing the above process the volume of the solid before and after melting will always remain the same.

Example 3: A metallic sphere of diameter 8.4 cm is melted and recast into a shape of cylinder of diameter 12 cm. Find the height of the cylinder.

Solution : As we know that the volume will be constant

Therefore Volume of sphere = Volume of sphere

4/3πr 3 = πr 2 h

4/3 x 3.14 x 4.2 x 4.2 x 4.2 cm 3 = 3.14 x 6 x 6 x h cm 3

h = 2.744 cm.

When a cone is cut in such a manner that the cutting axis is parallel to the axis of the cone, then the solid obtained is called as a frustum.

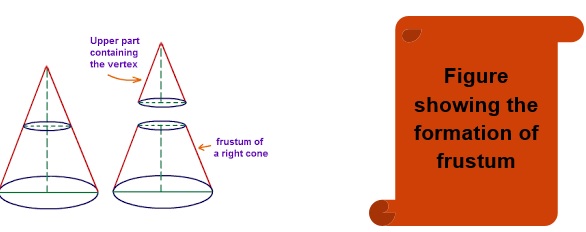
Example 4 : Find the TSA and CSA of the frustum of height 14 cm, the radius of the two circular surfaces are 2cm and 4cm.

Solution : TSA = π(r+R)√[(R+r) 2 + h 2 ] + πr 2 + πR 2

TSA = 3.14 x 6 x √232 cm 2 + 3.14 x 4 cm 2 + 3.14 x 16 cm 2

TSA = 286.96 cm 2 + 12.56 cm 2 + 50.24 cm 2 = 349.76 cm 2

CSA = π(r+R) )√[(R+r) 2 + h 2 ]

CSA = 286.96 cm 2 .

Areas Related to Circles

A circle is a 2D shape having the radius as one parameter of measurement.

Circumference = 2πr

Area = πr 2

We all know about the tangent, secant, major and minor sector as well as segment.

Here we are going to learn about the areas of these parts whioch they occupy in a circle.

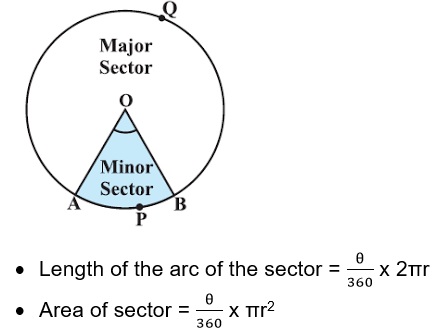
• Area of segment = Area of the corresponding sector – Area of the corresponding triangle.

Example 5: Find the area of the sector and the length of the arc if the substituted angle is 90° and the radius of the circle is 10cm.

Solution: Here we have been given that  = 90° and r = 10cm

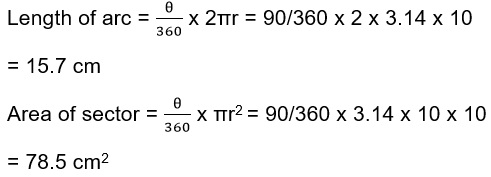
Practice Questions

Q2) Find the area and circumference of the circle having radius 15 cm.

Q3) A drinking glass is in the shape of a frustum of a cone of height 18 cm. The diameters of its two circular ends are 3 cm and 6 cm. Find the capacity of the glass.

Q4) Find the TSA and Volume of the following solid.

• Given a right circular cone, which is sliced through by a plane parallel to its base, when the smaller conical portion is removed, the resulting solid is called a Frustum of a Right Circular Cone.

Quiz for Surface Area and Volumes

Your Score: 0 /10

Other Chapters of Class 10

Quick Links

SchoolPlus Program

Yearlong program for Olympiads preparation & to build necessary skills for future.

Olympiad Exam Dates

Time to mark your calendar with the upcoming Olympiads exam schedule.

LIVE Classes for Olympiads

Take your Olympiad preparation to next-level by taking LIVE Classes.

Olympiad Test Series

Assess your performance by taking topic-wise and full length mock tests.

India’s First Summer Olympiads

Know your true potential by participating in Unicus Olympiads for classes 1-11.

Asia’s Biggest Winter Olympiads

Give wings to your innovation by appearing in CREST Olympiads for Prep/KG to classes 1-10.

Talk to our experts

1800-120-456-456

• CBSE Maths Chapter 13 Surface Area and Volume Class 10 MCQ

Solve CBSE Class 10 Maths Chapter 13 Surface Area and Volume MCQs

We have studied 2D and 3D objects in the previous chapters. We have learned how to calculate the area of many 2D geometric figures by deriving and using formulas. In Class 10 Maths Chapter 13, we will proceed to learn what 3D objects are and how we can calculate their volume and surface area. To understand these concepts well, download and solve Surface Area and Volume Class 10 MCQ.

The questions have been formulated by the top Maths experts of Vedantu. They have focused on the topics included in CBSE Class 10 Maths Chapter 13 and given a consolidated platform to test your skills. Solving these MCQs will help you learn more about the problems and sharpen your answering skills.

Topics Covered in CBSE Class 10 Maths Chapter 13 Surface Area and Volume

Before checking out the MCQs, we need to recall the topics covered in this chapter. By using the previous concepts of 2D geometry and calculation of area, we will progress to understand what 3D geometry is. We will learn a lot about regular 3D objects and find out the formulas to calculate their surface areas and volumes.

The basic and advanced concepts of this chapter will help you find out how the formulas are derived. You will also learn to use these formulas to find the right answers. Let us check the topics covered in this chapter.

Basics of 3D geometry and regular shapes

The combination of solids and finding their surface area and volume

Converting shapes of solids and finding their volume and surface area

We can clearly understand how this chapter introduces the students to the basics of 3D shapes and then to the advanced methods of calculating surface areas and volumes. Study these topics well and complete preparing this chapter. Once done, download and solve the Class 10 Chapter 13 Maths MCQs.

Class 10 Maths Chapter 13 Surface Area and Volume MCQs with Answers 

1. What is the total surface area of a cube with an edge of 5 cm?

Answer : d) 150 cm²

2. The diameter of a sphere is 10 cm. What is its volume?

a) 314.16 cm³

b) 523.6 cm³

c) 1000 cm³

d) 1256.64 cm³

Answer : b) 523.6 cm³

3. A cylinder with a radius of 7 cm and a height of 10 cm has a total surface area of:

Answer : d) 494 cm²

4. A cone has a radius of 8 cm and a slant height of 10 cm. What is its volume?

Answer : b) 267 cm³

5. The lateral surface area of a cylinder with radius 4 cm and height 6 cm is:

Answer : b) 96 cm²

6. What is the total surface area of a hemisphere with a diameter of 8 cm?

a) $128\pi$ cm²

b) $64\pi$ cm²

c) $32\pi$ cm²

d) $16\pi$ cm²

Answer : b) $64\pi$ cm²

7. The height of a cone is 12 cm and the radius of its base is 5 cm. What is its slant height?

Answer : a) 13 cm

8. The volume of a cuboid is 288 cm³ and its dimensions are in the ratio of 2:3:4. What is its surface area?

Answer : d) 240 cm²

9. A hemisphere has a radius of 7 cm. What is its curved surface area?

a) $77\pi$ cm²

b) $98\pi$ cm²

c) $154\pi$ cm²

d) $308\pi$ cm²

Answer : d) $308\pi$ cm²

10. What is the volume of a right circular cone with radius 6 cm and height 8 cm?

a) $96\pi$ cm³

b) $192\pi$ cm³

c) $288\pi$ cm³

d) $384\pi$ cm³

Answer : a) $96\pi$ cm³

11. The base of a prism is a right triangle with legs of length 3 cm and 4 cm. If the height of the prism is 6 cm, what is its volume?

Answer : b) 18 cm³

12. What is the volume of a sphere with a radius of 9 cm?

a) 3051 cm³

b) 3052 cm³

c) 4070 cm³

d) 4071 cm³

Answer : a) 3051 cm³

13. A cube has a volume of 729 cm³. What is the length of its diagonal?

Answer : b) 27 cm

14. A cylinder with a radius of 6 cm and a height of 10 cm has a volume of:

c) 1080 cm³

d) 2160 cm³

Answer : c) 1080 cm³

15. The base of a pyramid is a square with sides of 8 cm. If the height of the pyramid is 12 cm, what is its volume?

Answer : b) 256 cm³

How to Solve Class 10 Maths Chapter 13 Surface Area and Volume MCQs?

Solving MCQs is quite easy. It all depends on the perspective you have developed by studying the basic and advanced mathematical principles related to the surface area and volume of 3D regular objects. Let us find out the steps to follow and solve the MCQs.

Complete Studying the Topics

The first step is to complete studying one topic after the other in this chapter. Start from the first topic and don’t jump the steps. Remember, the method of concept building is elaborate and defined. Hence, recall what you have studied in the previous years. Focus on the basics explained in the first topic and then take a step ahead to understand solids.

Understand the Terms

Understand the crucial terminology of this chapter such as surface area, volume, cylinder, cone, right circular cone, cube, etc. These terms will be used in the problems in the textbook exercises. Unless you understand the meaning of these terms, you will not be able to depict the meaning of the problem. Try to visualize the terms by drawing them on your rough copies and understanding their features.

Derive the Formulas

This chapter will have a list of formulas used to calculate the surface area and volume of the solids. You will start deriving the formulas from scratch to understand how they are formed. By doing so, your concept related to using the formulas in the right place will be clarified.

Solve Exercise Questions

The next step is to solve the exercise questions for every topic. Make sure you complete all the exercise problems. You can seek assistance from NCERT exercise solutions for Class 10 Maths Chapter 13 and develop your concepts.

Resolve Doubts and Solve MCQs

When you are done with the exercise problems, resolve your doubts with the online tutors of Vedantu. Make sure you have no questions unanswered. When you are pretty confident, download the Surface Area and Volume Class 10 MCQ with answers and solve them at home. Check your answers and compare them with the given solutions.

Practice Class 10 Maths Chapter 13 Surface Area and Volume MCQs PDF

Get the free version of the Surface Area and Volume Class 10 MCQ PDF here and start solving the problems at home. Learn how to solve the problems by checking the stepwise methods explained in the solutions. Figure out how to use the formulas and save your time while solving these problems. Develop your concepts related to the surface area and volume of solids and excel in class.

FAQs on CBSE Maths Chapter 13 Surface Area and Volume Class 10 MCQ

1. Do I have to understand the difference between a cone and a cylinder?

It is a crucial step for you to identify the difference between the solid shapes taught in this chapter. It is then you can recognise the difference between the formulas used to calculate their surface areas and volumes.

2. How can we combine two solid objects in Class 10 Maths Chapter 13?

If you observe the problems of the combination of solids, you will find out that the solid shapes are either placed inside or above each other. Focus on the outcome of a combination by using your imagination and applying the formulas to calculate their surface area and volumes.

3. How can I improve in solving questions related to Class 10 Maths Chapter 13 Surface Area and Volume?

Understand the derivation of formulas by sketching the solids. Understand every step used in solving the exercise problems to use the same.

• IIT JEE Study Material
• Examples on Surface Area and Volume

Surface Area and Volume Examples

The world we live in is three dimensional in nature. Every object can be measured in terms of length, breadth and height. For example, the house that we live in has dimensions. The surface area is the outer part of the figure, whereas volume is the inner part. This article contains solved examples on surface area and volume.

Surface Area and Volume Definitions

The complete area of the surface of a three dimensional solid can be termed as surface area. It is denoted by “S” and measured in square units.

The quantity of a three dimensional solid or the space taken by it is called volume. Volume is denoted by “V” and measured in cubic units.

Surface Area and Volume Formulae

To find the surface area and volume of the solids individually or combined together, the following table can be used for reference.

Example 1: The radius and height of a cone are in the ratio 4 : 3. The area of the base is 154cm 2 . What is its curved surface area?

Example 2: The percentage decrease in the surface area of the cube, when each side decreased to 0.5 times the original length is ____________.

The surface area of the cube = 6a 2

Example 3: A circus tent is bent in the form of a cone over a cylinder. The diameter of the base is 9 m, the height of the cylindrical part is 4.8 m, and the total height of the tent is 10.8 m. What is the amount of canvas required for the tent?

The surface area of the conical part

Example 4: A toy is in the shape of a cone over a hemisphere. The radius of the hemisphere is 3.5 cm, and the total height of the toy is 15.5 cm. Find the total area of the toy.

The top is made up of two shapes, one is a hemisphere of radius r = 3.5 cm and the other cone of height h = 15.5 – 3.5 = 12 cm.

The total area of the top \(\begin{array}{l} = 2\pi\times (3.5)^2+[\pi]3.5\times \sqrt{3.5^2+12^2}=214.5 \ sq\ cm\end{array} \) .

Example 5: The dimensions of the cuboid are in the ratio of 1 : 2 : 3, and its total surface area is 88 cm 2 . What is the lateral surface area?

Let the length, breadth and height of the cuboid be l, 2l and 3l, respectively.

Total surface area = 2{(l * 2l) + (2l * 3l) + (3l * l)} = 88 cm 2

Hence l = 2 cm, 2l = 4 cm, 3l = 6 cm

Lateral surface area = 2(l * 3l) + (2l * 3l) = 18l 2 = 72 cm 2

Example 6: A sphere, a cylinder and a cone are of the same height and same radius, then the ratio of their curved surfaces is ______.

Let the radius of the sphere be r

Height of the sphere = 2r

Height of the cylinder = 2r

Height of the cone = 2r

Hence, the ratio of the curved surface area is

\(\begin{array}{l}=4 \pi r^{2}:2 \pi r (2r):\pi r\sqrt{r^{2}+(2r)^{2}}\\ =4 \pi r^{2}:4 \pi r^{2}:\pi r^{2}\sqrt{5}\\ =4:4:\sqrt{5}\end{array} \)

Example 7: Each side of a cube increases by 50%. Then, the surface area of the cube increases by ______.

Let each side of the cube be a.

After increment, each sides of the cube \(\begin{array}{l} = a+\frac{50a}{500}\end{array} \)

The surface area of the cube = a 2

Surface area, after increment \(\begin{array}{l}=6(\frac{a\times 3}{2})^{2}\\ =6a^{2}\times \frac{9}{4}\\\end{array} \)

\(\begin{array}{l}\text{Increment in surface area} =[\frac{\text{Increment} -\text{Original}}{\text{Original}}\times 100] \%\\ =[\frac{6a^{2}\times \frac{9}{4}-6a^{2}}{6a^{2}}\times 100] \% \\ =[\frac{5}{4}\times 100] \%\\ =125 \%\\\end{array} \)

Example 8: The level of water of a swimming pool is rectangular, of which length is 32 metres and width is 9.5 metres, and the depth of water at one end is 1 ½ metres which increases to 4 ½ metres at the other end. Find the volume of water in the swimming pool.

The cross-section of the swimming pool is like a trapezium, of which parallel sides are 4 ½ metres and 1 ½ metres, and the vertical perpendicular is 32 metres.

Therefore, the area of cross-section \(\begin{array}{l}=\frac{1}{2}\times 16\times \left( 4\frac{1}{2}+1\frac{1}{2} \right)\end{array} \) = 48 sq.m.

Hence, the volume of water in the swimming pool = area of the cross-section × length

= 456 cubic metres.

Example 9: The length of a cold storage is double its breadth. The height is 3 metres, and the area of its four walls (including doors) is 108 metre ​​2 . Find its volume.

Let the length, breadth and height of the cold storage be l metres, b metres and h metres, respectively.

Then, l = 2b (given) and h = 3 metres.

Now, the area of the four walls = 108

⇒ 2 (l + b) h = 108

⇒ 2 (2b + b) × 3 = 108

⇒ 18b = 108

⇒ b = 6 metres

⇒ l = 12 metres

Hence, the volume of the cold storage = (lbh) m 3 = (12 × 6 × 3) m 3 = 216 m 3 .   

Example 10: A cone and a cylinder have the same curved surface area and base area. If the height of the cylinder is 3 m, find the slant height of the cone.

Solution:  

The cone and cylinder have the same base area. It implies that they have the same radius.

The curved surface area of cone = Curved surface area of the cylinder

Frequently Asked Questions

What do you mean by the surface area of a solid.

Surface area is the complete area of the surface of a three dimensional solid.

What is the total surface area of a sphere?

The total surface area of a sphere = 4πr 2 , where r is the radius of the sphere.

What is the volume of a cylinder?

The volume of a cylinder = πr 2 h, where r is the radius, and h is the height of the cylinder.

What is the volume of a sphere?

The volume of a sphere = (4/3)πr 3 , where r is the radius of the sphere.

What is the volume of a cone?

The volume of a cone = (⅓)πr 2 h.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.