quadratic equation solving by factoring

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 14

Solving quadratics by factoring.

• Quadratics by factoring (intro)
• Solving quadratics by factoring: leading coefficient ≠ 1
• Quadratics by factoring
• Solving quadratics using structure
• Solve equations using structure
• Quadratic equations word problem: triangle dimensions
• Quadratic equations word problem: box dimensions
• Solving quadratics by factoring review

What you should be familiar with before taking this lesson

• Factoring using the Sum-Product pattern
• Factoring by grouping
• Factoring special products

What you will learn in this lesson

• how to solve factored equations like ( x − 1 ) ( x + 3 ) = 0 ‍   and
• how to use factorization methods in order to bring other equations ( ‍   like x 2 − 3 x − 10 = 0 ) ‍   to a factored form and solve them.

Solving factored quadratic equations

• (Choice A)   x = 5 ‍   and x = 7 ‍   A x = 5 ‍   and x = 7 ‍  
• (Choice B)   x = 5 ‍   and x = − 7 ‍   B x = 5 ‍   and x = − 7 ‍  
• (Choice C)   x = − 5 ‍   and x = 7 ‍   C x = − 5 ‍   and x = 7 ‍  
• (Choice D)   x = − 5 ‍   and x = − 7 ‍   D x = − 5 ‍   and x = − 7 ‍  

( x + 5 ) ( x + 7 ) = 0 ‍  

↙ ↘ x + 5 = 0 x + 7 = 0 x = − 5 x = − 7 ‍  

• (Choice A)   x = 1 ‍   and x = 3 ‍   A x = 1 ‍   and x = 3 ‍  
• (Choice B)   x = 1 2 ‍   and x = 3 4 ‍   B x = 1 2 ‍   and x = 3 4 ‍  
• (Choice C)   x = 2 ‍   and x = 4 3 ‍   C x = 2 ‍   and x = 4 3 ‍  
• (Choice D)   x = − 1 ‍   and x = − 3 ‍   D x = − 1 ‍   and x = − 3 ‍  

( 2 x − 1 ) ( 4 x − 3 ) = 0 ‍  

↙ ↘ 2 x − 1 = 0 4 x − 3 = 0 2 x = 1 4 x = 3 x = 1 2 x = 3 4 ‍  

Reflection question

• (Choice A)   Yes, of course. A Yes, of course.
• (Choice B)   No, the product must be equal to zero. B No, the product must be equal to zero.
• if one of the factors is 1 ‍   , the other is 6 ‍   ;
• if one of the factors is 2 ‍   , the other is 3 ‍   ; or
• if one of the factors is 1 2 ‍   , the other is 12 ‍   .

A note about the zero-product property

If the product of two quantities is equal to zero, then at least one of the quantities must be equal to zero. Why is this true? We already know that the product of any number and zero is equal to zero, but this principle tells us that if the product is zero, then it's certain that one of the factors is zero. Think about the case where both factors are not zero. In this case, the product wouldn't be zero either. For example, there's nothing you can multiply by 2 ‍   to get zero, except zero. Therefore, in order for a product to be zero, one of the factors must be zero.

Solving by factoring

x 2 − 3 x − 10 = 0 ( x + 2 ) ( x − 5 ) = 0 Factor. ‍  

↙ ↘ x + 2 = 0 x − 5 = 0 x = − 2 x = 5 ‍  

Solve x 2 + 5 x = 0 ‍   .

x 2 + 5 x = x ( x + 5 ) ‍  

• (Choice A)   x = 5 ‍   and x = − 5 ‍   A x = 5 ‍   and x = − 5 ‍  
• (Choice B)   x = 0 ‍   and x = 5 ‍   B x = 0 ‍   and x = 5 ‍  
• (Choice C)   x = 5 ‍   and x = − 5 ‍   C x = 5 ‍   and x = − 5 ‍  
• (Choice D)   x = 0 ‍   and x = − 5 ‍   D x = 0 ‍   and x = − 5 ‍  

x 2 + 5 x = 0 x ( x + 5 ) = 0 Factor. ‍  

↙ ↘ x = 0 x + 5 = 0 x = − 5 ‍  

Solve x 2 − 11 x + 28 = 0 ‍   .

• (Choice A)   x = 2 ‍   and x = 14 ‍   A x = 2 ‍   and x = 14 ‍  
• (Choice B)   x = 4 ‍   and x = 7 ‍   B x = 4 ‍   and x = 7 ‍  
• (Choice C)   x = − 2 ‍   and x = − 14 ‍   C x = − 2 ‍   and x = − 14 ‍  
• (Choice D)   x = − 4 ‍   and x = − 7 ‍   D x = − 4 ‍   and x = − 7 ‍  

x 2 − 11 x + 28 = 0 ( x − 4 ) ( x − 7 ) = 0 Factor. ‍  

↙ ↘ x − 4 = 0 x − 7 = 0 x = 4 x = 7 ‍  

Solve 4 x 2 + 4 x + 1 = 0 ‍   .

4 x 2 + 4 x + 1 = ( 2 x ) 2 + 2 ( 2 x ) ( 1 ) + ( 1 ) 2 ‍  

• (Choice A)   x = − 1 2 ‍   A x = − 1 2 ‍  
• (Choice B)   x = 1 2 ‍   and x = − 1 2 ‍   B x = 1 2 ‍   and x = − 1 2 ‍  
• (Choice C)   x = 1 2 ‍   C x = 1 2 ‍  
• (Choice D)   x = 2 ‍   and x = − 2 ‍   D x = 2 ‍   and x = − 2 ‍  

4 x 2 + 4 x + 1 = 0 ( 2 x + 1 ) 2 = 0 Factor. ‍  

2 x + 1 = 0 2 x = − 1 x = − 1 2 ‍  

Solve 3 x 2 + 11 x − 4 = 0 ‍   .

= 3 x 2 + 11 x − 4 = 3 x 2 + 12 x − x − 4 = 3 x ( x + 4 ) − 1 ( x + 4 ) = ( 3 x − 1 ) ( x + 4 ) ‍  

• (Choice A)   x = 1 4 ‍   and x = − 3 ‍   A x = 1 4 ‍   and x = − 3 ‍  
• (Choice B)   x = − 1 ‍   and x = 12 ‍   B x = − 1 ‍   and x = 12 ‍  
• (Choice C)   x = 1 3 ‍   and x = − 4 ‍   C x = 1 3 ‍   and x = − 4 ‍  
• (Choice D)   x = 1 ‍   and x = − 12 ‍   D x = 1 ‍   and x = − 12 ‍  

3 x 2 + 11 x − 4 = 0 ( 3 x − 1 ) ( x + 4 ) = 0 Factor. ‍  

↙ ↘ 3 x − 1 = 0 x + 4 = 0 3 x = 1 x = − 4 x = 1 3 ‍  

Arranging the equation before factoring

One of the sides must be zero..

x 2 + 2 x = 40 − x x 2 + 2 x − 40 + x = 0 Subtract 40 and add  x . x 2 + 3 x − 40 = 0 Combine like terms. ( x + 8 ) ( x − 5 ) = 0 Factor. ‍  

Removing common factors

2 x 2 − 12 x + 18 = 0 x 2 − 6 x + 9 = 0 Divide by 2. ( x − 3 ) 2 = 0 Factor. ↓ x − 3 = 0 x = 3 ‍  

2 x 2 − 3 x − 20 = x 2 + 34 ‍  

• (Choice A)   x = − 6 ‍   A x = − 6 ‍  
• (Choice B)   x = − 5 ‍   B x = − 5 ‍  
• (Choice C)   x = 8 ‍   C x = 8 ‍  
• (Choice D)   x = 9 ‍   D x = 9 ‍  

↙ ↘ x + 6 = 0 x − 9 = 0 x = − 6 x = 9 ‍  

3 x 2 + 33 x + 30 = 0 ‍  

• (Choice A)   x = − 10 ‍   A x = − 10 ‍  
• (Choice B)   x = − 1 ‍   B x = − 1 ‍  
• (Choice C)   x = 1 ‍   C x = 1 ‍  
• (Choice D)   x = 11 ‍   D x = 11 ‍  

3 x 2 + 33 x + 30 = 0 x 2 + 11 x + 10 = 0 Divide by 3. ( x + 1 ) ( x + 10 ) = 0 Factor . ‍  

↙ ↘ x + 1 = 0 x + 10 = 0 x = − 1 x = − 10 ‍  

3 x 2 − 9 x − 20 = x 2 + 5 x + 16 ‍  

• (Choice A)   x = − 2 ‍   A x = − 2 ‍  
• (Choice B)   x = 1 ‍   B x = 1 ‍  
• (Choice C)   x = 5 ‍   C x = 5 ‍  

↙ ↘ x + 2 = 0 x − 9 = 0 x = − 2 x = 9 ‍  

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Factoring Quadratics

"Factoring" (or "Factorising" in the UK) a Quadratic is:

finding what to multiply to get the Quadratic

It is called "Factoring" because we find the factors (a factor is something we multiply by)

Example: (x+4) and (x−1) are factors of x 2 + 3x − 4

Let us "expand" (x+4) and (x−1) to be sure:

Yes, (x+4) and (x−1) are definitely factors of x 2 + 3x − 4

Did you see that Expanding and Factoring are opposites?

Expanding is usually easy, but Factoring can often be tricky .

OK, let's try an example where we don't know the factors yet:

Common Factor

First we can check for any common factors .

Example: what are the factors of 6x 2 − 2x = 0 ?

6 and 2 have a common factor of 2 :

2(3x 2 − x) = 0

And x 2 and x have a common factor of x :

2x(3x − 1) = 0

And we have done it! The factors are 2x and 3x − 1 ,

We can now also find the roots (where it equals zero):

• 2x is 0 when x = 0
• 3x − 1 is zero when x = 1 3

And this is the graph (see how it is zero at x=0 and x= 1 3 ):

But it is not always that easy ...

Guess and Check

Example: what are the factors of 2x 2 + 7x + 3 .

No common factors.

Maybe we can guess an answer? Then check if we are right ... we may get lucky!

Let's guess (2x+3)(x+1):

(2x+3)(x+1) = 2x 2 + 2x + 3x + 3 = 2x 2 + 5x + 3 (Close but WRONG )

How about (2x+7)(x−1):

(2x+7)(x−1) = 2x 2 − 2x + 7x − 7 = 2x 2 + 5x − 7 (WRONG AGAIN)

OK, how about (2x+9)(x−1):

(2x+9)(x−1) = 2x 2 − 2x + 9x − 9 = 2x 2 + 7x − 9 (WRONG AGAIN!)

We could be guessing for a long time before we get lucky.

That is not a very good method. So let us try something else.

A Method For Simple Cases

There is a method for simple cases.

With the quadratic equation in this form:

Step 1 : Find two numbers that multiply to give ac (in other words a times c), and add to give b .

Example: 2x 2 + 7x + 3

ac is 2×3 = 6 and b is 7

So we want two numbers that multiply together to make 6, and add up to 7

In fact 6 and 1 do that (6×1=6, and 6+1=7)

How do we find 6 and 1?

It helps to list the factors of ac= 6 , and then try adding some to get b= 7 .

Factors of 6 include 1, 2, 3 and 6.

Aha! 1 and 6 add to 7, and 6×1=6.

Step 2 : Rewrite the middle with those numbers:

Rewrite 7x with 6 x and 1 x:

2x 2 + 6x + x + 3

Step 3 : Factor the first two and last two terms separately:

The first two terms 2x 2 + 6x factor into 2x(x+3)

The last two terms x+3 don't actually change in this case

2x(x+3) + (x+3)

Step 4 : If we've done this correctly, our two new terms should have a clearly visible common factor.

In this case we can see that (x+3) is common to both terms, so we can go:

Check: (2x+1)(x+3) = 2x 2 + 6x + x + 3 = 2x 2 + 7x + 3 (Yes)

Let's see Steps 1 to 4 again, in one go :

OK, let us try another example:

Example: 6x 2 + 5x − 6.

Step 1 : ac is 6×(−6) = −36 , and b is 5

List the positive factors of ac = −36 : 1, 2, 3, 4, 6, 9, 12, 18, 36

One of the numbers has to be negative to make −36, so by playing with a few different numbers I find that −4 and 9 work nicely:

−4×9 = −36 and −4+9 = 5

Step 2 : Rewrite 5x with −4x and 9x:

6x 2 − 4x + 9x − 6

Step 3 : Factor first two and last two:

2x(3x − 2) + 3(3x − 2)

Step 4 : Common Factor is (3x − 2):

(2x+3)(3x − 2)

Check: (2x+3)(3x − 2) = 6x 2 − 4x + 9x − 6 = 6x 2 + 5x − 6 (Yes)

Finding Those Numbers

The hardest part is finding two numbers that multiply to give ac , and add to give b .

It is partly guesswork, and it helps to list out all the factors .

Here is another example to help you:

Example: ac = −120 and b = 7

What two numbers multiply to −120 and add to 7 ?

The factors of 120 are (plus and minus):

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120

We can try pairs of factors (start near the middle!) and see if they add to 7:

• −10 x 12 = −120, and −10+12 = 2 (no)
• −8 x 15 = −120 and −8+15 = 7 (YES!)

Get Some Practice

You can practice simple quadratic factoring .

Why Factor?

Well, one of the big benefits of factoring is that we can find the roots of the quadratic equation (where the equation is zero).

All we need to do (after factoring) is find where each of the two factors becomes zero

Example: what are the roots (zeros) of 6x 2 + 5x − 6 ?

We already know (from above) the factors are

(2x + 3)(3x − 2)

And we can figure out that

(2x + 3) is zero when x = −3/2

(3x − 2) is zero when x = 2/3

So the roots of 6x 2 + 5x − 6 are:

−3/2 and 2/3

Here is a plot of 6x 2 + 5x − 6 , can you see where it equals zero?

We can also check it using a bit of arithmetic:

At x = −3 2 : 6( −3 2 ) 2 + 5( −3 2 ) − 6 = 6×( 9 4 ) − 15 2 − 6 = 54 4 − 15 2 - 6 = 0

At x = 2 3 : 6( 2 3 ) 2 + 5( 2 3 ) − 6 = 6×( 4 9 ) + 10 3 − 6 = 24 9 + 10 3 - 6 = 0

We can also try graphing the quadratic equation . Seeing where it equals zero can give us clues.

Example: (continued)

Starting with 6x 2 + 5x − 6 and just this plot:

The roots are around x = −1.5 and x = +0.67, so we can guess the roots are:

Which can help us work out the factors 2x + 3 and 3x − 2

Always check though! The graph value of +0.67 might not really be 2/3

General Solution

Quadratic equations have symmetry, the left and right are like mirror images:

The midline is at −b/2 , and we can calculate the value w with these steps:

• First, "a" must be 1, if not then divide b and c by a:
• b = b/a, c = c/a
• w = √(mid 2 − c)
• roots are at mid−w and mid+w

Example: x 2 + 3x − 4

a = 1, b = 3 and c = −4

• a= 1, so we can go to next step
• mid = − 3 2
• w = √[( 3 2 ) 2 − (−4)] = √( 9 4 + 4) = √ 25 4 = 5 2
• roots are at  − 3 2 − 5 2 = −4 and − 3 2 + 5 2 = 1  

So we can factor x 2 + 3x − 4 into (x + 4)(x − 1) 

Quadratic formula

We can also use the quadratic formula :

We get two answers x + and x − (one is for the "+" case, and the other is for the "−" case in the "±") that gets us this factoring:

a(x − x + )(x − x − )

Example: what are the roots of 6x 2 + 5x − 6 ?

Substitute a=6, b=5 and c=−6 into the formula:

x = −b ± √(b 2 − 4ac) 2a

= −5 ± √(5 2 − 4×6×(−6)) 2×6

= −5 ± √(25 + 144) 12

= −5 ± √169 12

= −5 ± 13 12

So the two roots are:

x + = (−5 + 13) / 12 = 8/12 = 2/3,

x − = (−5 − 13) / 12 = −18/12 = −3/2

(Notice that we get the same answer as when we did the factoring earlier.)

Now put those values into a(x − x + )(x − x − ) :

6(x − 2/3)(x + 3/2)

We can rearrange that a little to simplify it:

3(x − 2/3) × 2(x + 3/2) = (3x − 2)(2x + 3)

Before you go, check this out!

We have lots more on the site to show you. You've only seen one page. Check out this post which is one of the most popular of all time.

A Step-by-Step Guide to Solving Quadratic Equations by Factoring

I believe that solving quadratic equations is an important skill that every high school student must master. While there are several methods to solve quadratic equations, factoring is perhaps the most elegant and straightforward method of all.

Not only does the factoring method allow students to understand the problem better, but it is also a versatile tool that can be applied to many other areas of math.

Read on to explore the process of solving quadratic equations by factoring its importance and some examples to help you understand it better.

If you are interested in learning how to solve quadratic equations by completing the square , I wrote a whole article detailing everything you need to know.

Table of Contents

What Are Quadratic Equations?

Quadratic equations are second-order polynomial equations in a single variable x raised to the power of 2. For example, ax 2 + bx + c = 0, where a,b, and c are constants. Since quadratic equations are second-order polynomial equations, the fundamental theorem of algebra guarantees that they have at least one solution.

There are generally four ways to solve a quadratic equation, including:

• Completing the square
• Using the quadratic formula

What are quadratic equations used for? Quadratic equations are helpful in various real-life situations, including calculating the speed of an object, the areas of an enclosed space, maximizing or minimizing, or graphing a piece of equipment for designing.

If you want to learn more about quadratics equations, I encourage you to check out Khan Academy or watch the video below.

Solving Quadratic Equations by Factoring

Solving quadratic equations by factoring is an essential skill as it provides the basis for working with other complex mathematical concepts, such as graphing quadratic equations.

Here are the steps to solve quadratic equations by factoring:

Step 1 : Rewrite The Quadratic Equation in Standard Form

The first step in solving quadratic equations by factoring is to rearrange the equation so that one side equals zero. From the equation, a quadratic factor is formed by identifying two factors that multiply together to give the constant c and add together to give the coefficient b .

The standard form of a quadratic equation is ax 2 + bx + c = 0, where a, b, and c are coefficients . The first step to solve any quadratic equation by factoring is to rearrange it in standard form.

Let’s take the example equation x 2 + 5x = -6. To rearrange it in standard form, we simply move the constant term to the left side of the equation: x 2 + 5x + 6 = 0

Step 2 : Factor The Quadratic Expression

The next step is to factor the quadratic expression on the left-hand side of the equation. Factorization is the process of finding two numbers that multiply to give you the quadratic expression .

In our example, the quadratic expression is x 2 + 5x + 6. To factor this expression, we need to find two numbers whose sum is 5 and whose product is 6. The two numbers are 2 and 3. Thus, we can factor the quadratic expression as (x + 2)(x + 3).

Step 3 : Apply The Zero Product Property

The zero product property states that if the product of two numbers is zero, then at least one of the numbers must be zero.

In our example, the product of (x + 2)(x + 3) is zero, which means that either x + 2 = 0 or x + 3 = 0. So, we have two possible solutions: x = -2 and x = -3.

Step 4 : Check Your Answers

The last step is to check your answers by substituting them into the original equation and verify that they make the equation true.

In our example, if we substitute x = -2 and x = -3 into the equation x^2 + 5x + 6 = 0, we get: (-2) 2 + 5(-2) + 6 = 0 and (-3) 2 + 5(-3) + 6 = 0. Both of these equations are true, which means that our answer is correct.

Watch the video below to learn how to solve quadratic equations by factoring.

What to read next:

• Understanding the Properties of Quadratic Functions .
• 17 Maths Websites for High School Students to Get Ahead .
• Different Types of Transformation in Math .

Wrapping Up

Factoring quadratic equations is an essential skill that every math student should master because it is a powerful technique that allows students to solve many quadratic equations faster and helps them understand the nature and behavior of quadratic equations better.

By following the steps outlined in this article, you can confidently solve any quadratic equation by factoring.

I am Altiné. I am the guy behind mathodics.com. When I am not teaching math, you can find me reading, running, biking, or doing anything that allows me to enjoy nature's beauty. I hope you find what you are looking for while visiting mathodics.com.

Recent Posts

How to Find the Y-Value of Stationary Points with TI-84 Plus CE

TI-84 Plus CE Calculator If you’re studying calculus or any advanced math course, you will certainly come across the concept of stationary points. So, what is a stationary point? A...

IB Maths Vs. A-Level Maths - Which One is Harder?

Maths is a subject that can be demanding for many students. It not only requires strong analytical skills but also an ability to handle complex concepts with ease. Students looking to further their...

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Quadratic Equations

1. Solving Quadratic Equations by Factoring

• 2. Completing the Square
• 3. The Quadratic Formula
• Sum and product of the roots of a quadratic equation
• 4. The Graph of the Quadratic Function
• Interactive Quadratic Function Graph
• 5. Equations in Quadratic Form

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Online Algebra Solver

Solve your algebra problem step by step!

IntMath Forum

Get help with your math queries:

The general form of a quadratic equation is

ax 2 + bx + c = 0

where x is the variable and a , b & c are constants

Examples of Quadratic Equations

(a) 5 x 2 − 3 x − 1 = 0 is a quadratic equation in quadratic form where

`a = 5`, `b = -3`, `c = -1`

(b) 5 + 3 t − 4.9 t 2 = 0 is a quadratic equation in quadratic form.

Here, `a = -4.9`, `b = 3`, `c = 5` [This equation arose from finding the time when a projectile, being acted on by gravity, hits the ground.]

(c) ( x + 1) 2 = 4 is a quadratic equation but not in quadratic form.

It has to be expanded and simplified to:

x 2 + 2 x − 3 = 0

In general, a quadratic equation:

• must contain an x 2 term
• must NOT contain terms with degrees higher than x 2 eg. x 3 , x 4 etc

Examples of NON-quadratic Equations

• bx − 6 = 0 is NOT a quadratic equation because there is no x 2 term.
• x 3 − x 2 − 5 = 0 is NOT a quadratic equation because there is an x 3 term (not allowed in quadratic equations).

Solutions of a Quadratic Equation

The solution of an equation consists of all numbers (roots) which make the equation true .

All quadratic equations have 2 solutions (ie. 2 roots). They can be:

• real and distinct
• real and equal
• imaginary (complex)

The quadratic equation x 2 − 7 x + 10 = 0 has roots of

`x = 2` and `x = 5`. (We'll show below how to find these roots.)

This can be seen by substituting in the equation:

When x = 2,

x 2 − 7 x + 10

= (2) 2 − 7(2) + 10 = 4 − 14 + 10 = 0

(This can be shown similarly for x = 5). In this example, the roots are real and distinct .

The quadratic equation x 2 − 6 x + 9 = 0 has double roots of x = 3 (both roots are the same)

This can be seen by substituting x = 3 in the equation:

x 2 − 6 x + 9

= (3) 2 − 6(3) + 9 = 9 − 18 + 9 = 0

The quadratic equation

x 2 + 9 = 0

has imaginary roots of

`x=sqrt(-9)` or `-sqrt(-9)`

Learn more about imaginary numbers .

Solving a Quadratic Equation by Factoring

For the time being, we shall deal only with quadratic equations that can be factored (factorised).

If you need a reminder on how to factor, go back to the section on:

Factoring Trinomials .

Using the fact that a product is zero if any of its factors is zero we follow these steps:

(i) Bring all terms to the left and simplify, leaving zero on the right side.

(ii) Factorise the quadratic expression

(iii) Set each factor equal to zero

(iv) Solve the resulting linear equations

(v) Check the solutions in the original equation

Solve x 2 − 2 x − 15 = 0

x 2 − 2 x − 15 = 0

Factoring gives:

( x − 5)( x + 3) = 0

Now, if either of the terms ( x − 5) or ( x + 3) is 0, the product is zero. So we conclude:

( x − 5) = 0 , therefore x = 5

( x + 3) = 0 , therefore x = − 3

Hence the roots are x = 5 and x = − 3 .

Are we correct?

We check the roots in the original equation by substitution.

When x = 5 :

x 2 − 2 x − 15

= (5) 2 − 10 − 15 = 25 − 10 − 15 = 0

(Similarly, when we substitute `x = -3`, we also get `0`.)

Alternate method (Po-Shen Loh's approach)

We could have proceded as follows to solve this quadratic equation. The following approach takes the guesswork out of the factoring step, and is similar to what we'll be doing next, in Completing the Square .

Step 1: Take −1/2 times the x coefficient. In this case, `-1/2 × (−2) = 1`

Step 2: Expand `(1 − u)(1 + u) = 1 − u^2`

Step 3: Set that expansion equal to the constant term: `1 - u^2 = -15`

Step 4: Solve for `u`:

`1 - u^2 = -15` `u^2 = 16` `u= +-4`

Step 5: Substitute either value (we'll use `+4`) into the `u` bracket expressions, giving us the same roots of the quadratic equation that we found above:

`x=(1-u)=1-4 = -3,` or

`x=(1+u)=1+4 = 5`

For more on this approach, see: A Different Way to Solve Quadratic Equations (video by Po-Shen Loh).

`9x^2+ 6x + 1 = 0`

9 x 2 + 6 x + 1 = 0

(3 x + 1)(3 x + 1) = 0

So we conclude:

(3 x + 1) = 0 ,

We say there is a double root of `x = -1/3`.

We first need to re-express the quadratic with a `1` as the coefficient of `x^2.`

`x^2+ 2/3x + 1/9 = 0`

Step 1: Take −1/2 times the x coefficient. In this case, `-1/2 × 2/3 = -1/3`

Step 2: Expand `(-1/3 − u)(-1/3 + u) = 1/9 − u^2`

Step 3: Set that expansion equal to the constant term: `1/9 - u^2 = 1/9`

`1/9 - u^2 = 1/9` `u^2 = 0` `u= 0`

Step 5: Substitute `u=0` into the `u` bracket expressions, giving us the same (repeated) root for the quadratic equation that we found above:

`x=-1/3-0 = -1/3,` or `x=-1/3+0 = -1/3`

Example 6 (involving fractions)

`2-1/x=3/(x+2)`

Multiply throughout by `x(x+2)` to remove the denominators (bottoms) of the fractions:

`2x(x+2)-(x(x+2))/x=(3(x)(x+2))/(x+2)`

Cancelling gives:

`2x(x+2)-(x+2)=3x`

Expanding the brackets:

`2x^2+4x-x-2=3x`

`(x+1)(x-1)=0`

So `x = -1` or `x = 1`.

CHECK: Substituting `x = -1` into both the left hand side and right hand side of the question gives:

`"LHS"=2-1/x=2-1/-1=3`

`"RHS"=3/(x+2)=3/(-1+2)=3="LHS" `

Likewise, for `x = +1`,

LHS `= 2 - 1 = 1` RHS `= 3/3 = 1 =` LHS

• Determine if the following are quadratic equations. If so, determine a , b , and c.

a. 5 x 2 = 9 − x b. (3 x − 2) 2 = 2

Q1a    `5x^2= 9 − x`

`5x^2+ x − 9 = 0`

So, yes, it is a quadratic equation with

`a = 5`, `b = 1`, `c = -9`

Q1b    `(3x − 2)^2= 2`

`9x^2− 12x + 4 = 2` `9x^2− 12x + 2 = 0`

`a = 9`, `b = -12`, `c = 2`

• Solve for x :

2 x 2 − 7 x + 6 = 3

2 x 2 − 7 x + 3 = 0 (2 x − 1)( x − 3) = 0

`x=1/2` or `x=3`.

Once again, we first need to re-express the quadratic with a `1` as the coefficient of `x^2.`

`x^2- 7/2x + 3/2 = 0`

Step 1: Take −1/2 times the x coefficient. In this case, `-1/2 × (-7/2) = 7/4`

Step 2: Expand `(7/4 − u)(7/4 + u) = 49/16 − u^2`

Step 3: Set that expansion equal to the constant term: `49/16 - u^2 = 3/2`

`49/16 - u^2 = 3/2` `u^2 = 49/16 - 24/16 = 25/16` `u= +-5/4`

Step 5: Substitute either value (we'll use `+5/4`) into the `u` bracket expressions, giving us the same roots of the quadratic equation that we found above:

`x=7/4-5/4 = 1/2,` or `x=7/4+5/4 = 3`

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

• Alphabetically
• In Study Order
• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• COMPASS Math
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Quadratic Equations by Factoring

Factoring Roots Completing the Square Formula Graphing Examples

This lesson covers many ways to solve quadratics, such as taking square roots, completing the square, and using the Quadratic Formula . But we'll start with solving by factoring.

(Before reaching the topic of solving quadratic equations, you should already know how to factor quadratic expressions. If not, first review how to factor quadratics .)

You've already factored quadratic expressions. The new thing here is that the quadratic expression is part of an equation, and you're told to solve for the values of the variable that make the equation true. Here's how it works:

Content Continues Below

MathHelp.com

Solve ( x – 3)( x – 4) = 0 by factoring..

Okay, this quadratic is already factored for me. But how do I use this factorisation to solve the equation?

To solve quadratics by factoring, we use something called "the Zero-Product Property". This property says something that seems fairly obvious, but only after it's been pointed out to us; namely:

Zero-Product Property : If we multiply two (or more) things together and the result is equal to zero, then we know that at least one of those things that we multiplied must also have been equal to zero. Put another way, the only way for us to get zero when we multiply two (or more) factors together is for one of the factors to have been zero.

So, if we multiply two (or more) factors and get a zero result, then we know that at least one of the factors was itself equal to zero. In particular, we can set each of the factors equal to zero, and solve the resulting equation for one solution of the original equation.

We can only draw the helpful conclusion about the factors (namely, that one of those factors must have been equal to zero, so we can set the factors equal to zero) if the product itself equals zero. If the product of factors is equal to anything non-zero, then we can not make any claim about the values of the factors.

Therefore, when solving quadratic equations by factoring, we must always have the equation in the form "(quadratic expression) equals (zero)" before we make any attempt to solve the quadratic equation by factoring.

Returning to the exercise:

The Zero Factor Principle tells me that at least one of the factors must be equal to zero. Since at least one of the factors must be zero, then I can set each of the factors equal to zero:

x – 3 = 0   or   x – 4 = 0

This gives me simple linear equations, and they're easy to solve :

x = 3   or   x = 4

And these two values are the solution they're looking for:

Note that " x = 3, 4 " means the same thing as " x  = 3 or x  = 4 "; the only difference is the formatting. The " x  = 3, 4 " format is more common.

Solve x 2  + 5 x  + 6 = 0 , and check.

This equation is already in the form "(quadratic) equals (zero)" but, unlike the previous example, this isn't yet factored. I MUST factor the quadratic first, because it is only when I MULTIPLY and get zero that I can say anything about the factors and solutions. I can't conclude anything about the individual terms of the unfactored quadratic (like the 5 x or the 6 ), because I can add lots of stuff that totals to zero.

So the first thing I have to do is factor:

x 2 + 5 x + 6 = ( x + 2)( x + 3)

Now I can restate the original equation in terms of a product of factors, with this product being equal to zero:

( x + 2)( x + 3) = 0

Now I can solve each factor by setting each one equal to zero and solving the resulting linear equations:

x + 2 = 0   or   x + 3 = 0

x = –2   or   x = – 3

These two values are the solution to the original quadratic equation. So my answer is:

x = –3, –2

I'm not done, though, because the original exercise told me to "check", which means that I need to plug my answers back into the original equation, and make sure it comes out right. In this case, I'll be plugging into the expression on the left-hand side of the original equation, and verifying that I end up with the right-hand side; namely, with 0 :

checking x = –3 :

[–3] 2 + 5[–3] + 6

9 – 15 + 6

9 + 6 – 15

15 – 15

checking x = –2 :

[–2] 2 + 5[–2] + 6

4 – 10 + 6

4 + 6 – 10

10 – 10

When an exercise specifies that you should solve "and check", the above plug-n-chug, they're looking for you to show that you plugged your answer into the original exercise and got something that worked out right. The above, where I showed my checks, is all they're wanting. But do your work neatly!

By the way, you can use this "checking" technique to verify your answers to any "solving" exercise. So, for instance, if you're not sure of your answer to a "factor and solve" question on the next test, try plugging your answers into the original equation, and confirming that your solutions lead to true statements.

Solve x 2 – 3 = 2 x .

This equation is not in "(quadratic) equals (zero)" form, so I can't try to solve it yet. The first thing I need to do is get all the terms over on one side, with zero on the other side. Only then can I factor and solve:

x 2 – 3 = 2 x

x 2 – 2 x – 3 = 0

( x – 3)( x + 1) = 0

x – 3 = 0, x + 1 = 0

x = 3, x = –1

Then my solution is:

x = –1, 3

Solve ( x + 2)( x + 3) = 12 .

It is very common for students to see this type of equation, and say:

"Cool! It's already factored! So I'll set the factors equal to 12 and solve to get x = 10 and x = 9. That was easy!"

Yeah, that was easy; it was also wrong. Very, very wrong.

Besides the fact that neither (10 + 2)(10 + 3) nor (9 + 2)(9 + 3) equals 12 , we should never forget that we must have "(quadratic) equals (zero)" before we can solve by factoring.

Tempting though it may be, I cannot set each of the factors on the left-hand side of the equation equal to the other side of the equation and solve. Doing so would give me an entirely-wrong mess.

Instead, I first have to multiply out and simplify the left-hand side, then subtract the 12 over to the left-hand side, and re-factor. Only then can I solve.

( x + 2)( x + 3) = 12

x 2 + 5 x + 6 = 12

x 2 + 5 x – 6 = 0

( x + 6)( x – 1) = 0

x + 6 = 0, x – 1 = 0

x = –6, x = 1

x = –6, 1

Solve x 2 + 5 x = 0 .

This two-term quadratic is easier to factor than were the previous quadratics: I see immediately that I can factor an x out of both terms, taking the x out front. This gives me:

x ( x + 5) = 0

A very common mistake that students make at this stage is to "solve" the equation for " x  + 5 = 0 " by dividing through by the x . But that's an invalid step. Why? Because we can't divide by zero. How does that come into play here?

Advertisement

Dividing through by the factor x makes the implicit assumption that x was not equal to zero. There is absolutely no justification for making that assumption! And making that assumption would cause us to lose half of our solution to this equation.

I need to remember that it's okay for a factor to contain only a variable, without being added to other terms; in particular, " x " is a perfectly valid factor. I need to set both of the factors equal to zero, and then solve the two resulting linear equations:

x = 0, x + 5 = 0

x = 0, x = –5

x = 0, –5

The previous example had two terms and was easy to factor. There is one other case of two-term quadratics that we can factor to solve. It's only a bit more complicated:

Solve x 2 – 4 = 0 .

This equation is in "(quadratic) equals (zero)" form, so it's ready for me to solve by factoring. But how do I factor this? By noticing that this is a difference of squares . I'll apply the difference-of-squares formula that I've memorized:

x 2 – 4 = 0

( x – 2)( x + 2) = 0

x – 2 = 0, x + 2 = 0

x = 2, x = –2

x = –2, 2

Note: The solution above can also be formatted as " x = ± 2" . This is pronounced as " x is equal to plus or minus 2 ".

The last example above leads us into how to solve by taking square roots, on the next page.

You can use the Mathway widget below to practice solving quadratic equations by factoring. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve by factoring" to compare your answer to Mathway's. (Or skip ahead to the next page.)

(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)

URL: http://www.purplemath.com/modules/solvquad.htm

Page 1 Page 2 Page 3 Page 4 Page 5 Page 6

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Factoring Calculator

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

How to factor expressions.

• Add up to 5
• Multiply together to get 4

Current calculator limitations

• Doesn't support multivariable expressions
• If you have an expression that you want the calculator to support in the future, please contact us

Factoring Expressions Video Lesson

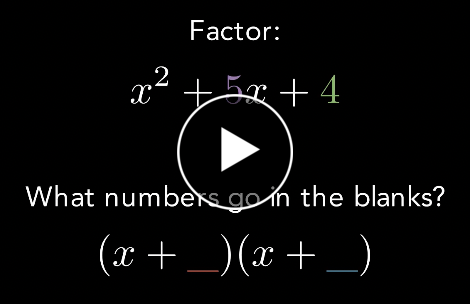
Need more problem types? Try MathPapa Algebra Calculator

Clear Factoring Calculator »

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.6: Quadratic Equations

• Last updated
• Save as PDF
• Page ID 114984

Learning Objectives

In this section, you will:

• Solve quadratic equations by factoring.
• Solve quadratic equations by the square root property.
• Solve quadratic equations by completing the square.
• Solve quadratic equations by using the quadratic formula.

The computer monitor on the left in Figure 1 is a 23.6-inch model and the one on the right is a 27-inch model. Proportionally, the monitors appear very similar. If there is a limited amount of space and we desire the largest monitor possible, how do we decide which one to choose? In this section, we will learn how to solve problems such as this using four different methods.

• Solving Quadratic Equations by Factoring

An equation containing a second-degree polynomial is called a quadratic equation . For example, equations such as 2 x 2 + 3 x − 1 = 0 2 x 2 + 3 x − 1 = 0 and x 2 − 4 = 0 x 2 − 4 = 0 are quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics.

Often the easiest method of solving a quadratic equation is factoring . Factoring means finding expressions that can be multiplied together to give the expression on one side of the equation.

If a quadratic equation can be factored, it is written as a product of linear terms. Solving by factoring depends on the zero-product property, which states that if a ⋅ b = 0 , a ⋅ b = 0 , then a = 0 a = 0 or b = 0 , b = 0 , where a and b are real numbers or algebraic expressions. In other words, if the product of two numbers or two expressions equals zero, then one of the numbers or one of the expressions must equal zero because zero multiplied by anything equals zero.

Multiplying the factors expands the equation to a string of terms separated by plus or minus signs. So, in that sense, the operation of multiplication undoes the operation of factoring. For example, expand the factored expression ( x − 2 ) ( x + 3 ) ( x − 2 ) ( x + 3 ) by multiplying the two factors together.

( x − 2 ) ( x + 3 ) = x 2 + 3 x − 2 x − 6 = x 2 + x − 6 ( x − 2 ) ( x + 3 ) = x 2 + 3 x − 2 x − 6 = x 2 + x − 6

The product is a quadratic expression. Set equal to zero, x 2 + x − 6 = 0 x 2 + x − 6 = 0 is a quadratic equation. If we were to factor the equation, we would get back the factors we multiplied.

The process of factoring a quadratic equation depends on the leading coefficient, whether it is 1 or another integer. We will look at both situations; but first, we want to confirm that the equation is written in standard form, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , where a , b , and c are real numbers, and a ≠ 0. a ≠ 0. The equation x 2 + x − 6 = 0 x 2 + x − 6 = 0 is in standard form.

We can use the zero-product property to solve quadratic equations in which we first have to factor out the greatest common factor (GCF), and for equations that have special factoring formulas as well, such as the difference of squares, both of which we will see later in this section.

The Zero-Product Property and Quadratic Equations

The zero-product property states

If  a ⋅ b = 0 , then  a = 0 or  b = 0 , If  a ⋅ b = 0 , then  a = 0 or  b = 0 ,

where a and b are real numbers or algebraic expressions.

A quadratic equation is an equation containing a second-degree polynomial; for example

a x 2 + b x + c = 0 a x 2 + b x + c = 0

where a , b , and c are real numbers, and if a ≠ 0 , a ≠ 0 , it is in standard form.

Solving Quadratics with a Leading Coefficient of 1

In the quadratic equation x 2 + x − 6 = 0 , x 2 + x − 6 = 0 , the leading coefficient, or the coefficient of x 2 , x 2 , is 1. We have one method of factoring quadratic equations in this form.

Given a quadratic equation with the leading coefficient of 1, factor it.

• Find two numbers whose product equals c and whose sum equals b .
• Use those numbers to write two factors of the form ( x + k ) or  ( x − k ) , ( x + k ) or  ( x − k ) , where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and −2 , −2 , the factors are ( x + 1 ) ( x − 2 ) . ( x + 1 ) ( x − 2 ) .
• Solve using the zero-product property by setting each factor equal to zero and solving for the variable.

Factoring and Solving a Quadratic with Leading Coefficient of 1

Factor and solve the equation: x 2 + x − 6 = 0. x 2 + x − 6 = 0.

To factor x 2 + x − 6 = 0 , x 2 + x − 6 = 0 , we look for two numbers whose product equals −6 −6 and whose sum equals 1. Begin by looking at the possible factors of −6. −6.

1 ⋅ ( −6 ) ( −6 ) ⋅ 1 2 ⋅ ( −3 ) 3 ⋅ ( −2 ) 1 ⋅ ( −6 ) ( −6 ) ⋅ 1 2 ⋅ ( −3 ) 3 ⋅ ( −2 )

The last pair, 3 ⋅ ( −2 ) 3 ⋅ ( −2 ) sums to 1, so these are the numbers. Note that only one pair of numbers will work. Then, write the factors.

( x − 2 ) ( x + 3 ) = 0 ( x − 2 ) ( x + 3 ) = 0

To solve this equation, we use the zero-product property. Set each factor equal to zero and solve.

( x − 2 ) ( x + 3 ) = 0 ( x − 2 ) = 0 x = 2 ( x + 3 ) = 0 x = −3 ( x − 2 ) ( x + 3 ) = 0 ( x − 2 ) = 0 x = 2 ( x + 3 ) = 0 x = −3

The two solutions are 2 2 and −3. −3. We can see how the solutions relate to the graph in Figure 2 . The solutions are the x- intercepts of y = x 2 + x − 6 = 0. y = x 2 + x − 6 = 0.

Factor and solve the quadratic equation: x 2 − 5 x − 6 = 0. x 2 − 5 x − 6 = 0.

Solve the Quadratic Equation by Factoring

Solve the quadratic equation by factoring: x 2 + 8 x + 15 = 0. x 2 + 8 x + 15 = 0.

Find two numbers whose product equals 15 15 and whose sum equals 8. 8. List the factors of 15. 15.

1 ⋅ 15 3 ⋅ 5 ( −1 ) ⋅ ( −15 ) ( −3 ) ⋅ ( −5 ) 1 ⋅ 15 3 ⋅ 5 ( −1 ) ⋅ ( −15 ) ( −3 ) ⋅ ( −5 )

The numbers that add to 8 are 3 and 5. Then, write the factors, set each factor equal to zero, and solve.

( x + 3 ) ( x + 5 ) = 0 ( x + 3 ) = 0 x = −3 ( x + 5 ) = 0 x = −5 ( x + 3 ) ( x + 5 ) = 0 ( x + 3 ) = 0 x = −3 ( x + 5 ) = 0 x = −5

The solutions are −3 −3 and −5. −5.

Solve the quadratic equation by factoring: x 2 − 4 x − 21 = 0. x 2 − 4 x − 21 = 0.

Using the Zero-Product Property to Solve a Quadratic Equation Written as the Difference of Squares

Solve the difference of squares equation using the zero-product property: x 2 − 9 = 0. x 2 − 9 = 0.

Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property.

x 2 − 9 = 0 ( x − 3 ) ( x + 3 ) = 0 ( x − 3 ) = 0 x = 3 ( x + 3 ) = 0 x = −3 x 2 − 9 = 0 ( x − 3 ) ( x + 3 ) = 0 ( x − 3 ) = 0 x = 3 ( x + 3 ) = 0 x = −3

The solutions are 3 3 and −3. −3.

Solve by factoring: x 2 − 25 = 0. x 2 − 25 = 0.

Solving a Quadratic Equation by Factoring when the Leading Coefficient is not 1

When the leading coefficient is not 1, we factor a quadratic equation using the method called grouping, which requires four terms. With the equation in standard form, let’s review the grouping procedures:

• With the quadratic in standard form, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , multiply a ⋅ c . a ⋅ c .
• Find two numbers whose product equals a c a c and whose sum equals b . b .
• Rewrite the equation replacing the b x b x term with two terms using the numbers found in step 1 as coefficients of x.
• Factor the first two terms and then factor the last two terms. The expressions in parentheses must be exactly the same to use grouping.
• Factor out the expression in parentheses.
• Set the expressions equal to zero and solve for the variable.

Solving a Quadratic Equation Using Grouping

Use grouping to factor and solve the quadratic equation: 4 x 2 + 15 x + 9 = 0. 4 x 2 + 15 x + 9 = 0.

First, multiply a c : 4 ( 9 ) = 36. a c : 4 ( 9 ) = 36. Then list the factors of 36. 36.

1 ⋅ 36 2 ⋅ 18 3 ⋅ 12 4 ⋅ 9 6 ⋅ 6 1 ⋅ 36 2 ⋅ 18 3 ⋅ 12 4 ⋅ 9 6 ⋅ 6

The only pair of factors that sums to 15 15 is 3 + 12. 3 + 12. Rewrite the equation replacing the b term, 15 x , 15 x , with two terms using 3 and 12 as coefficients of x . Factor the first two terms, and then factor the last two terms.

4 x 2 + 3 x + 12 x + 9 = 0 x ( 4 x + 3 ) + 3 ( 4 x + 3 ) = 0 ( 4 x + 3 ) ( x + 3 ) = 0 4 x 2 + 3 x + 12 x + 9 = 0 x ( 4 x + 3 ) + 3 ( 4 x + 3 ) = 0 ( 4 x + 3 ) ( x + 3 ) = 0

Solve using the zero-product property.

( 4 x + 3 ) ( x + 3 ) = 0 ( 4 x + 3 ) = 0 x = − 3 4 ( x + 3 ) = 0 x = − 3 ( 4 x + 3 ) ( x + 3 ) = 0 ( 4 x + 3 ) = 0 x = − 3 4 ( x + 3 ) = 0 x = − 3

The solutions are − 3 4 , − 3 4 , and −3. −3. See Figure 3 .

Solve using factoring by grouping: 12 x 2 + 11 x + 2 = 0. 12 x 2 + 11 x + 2 = 0.

Solving a Polynomial of Higher Degree by Factoring

Solve the equation by factoring: −3 x 3 − 5 x 2 − 2 x = 0. −3 x 3 − 5 x 2 − 2 x = 0.

This equation does not look like a quadratic, as the highest power is 3, not 2. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out − x − x from all of the terms and then proceed with grouping.

−3 x 3 − 5 x 2 − 2 x = 0 − x ( 3 x 2 + 5 x + 2 ) = 0 −3 x 3 − 5 x 2 − 2 x = 0 − x ( 3 x 2 + 5 x + 2 ) = 0

Use grouping on the expression in parentheses.

− x ( 3 x 2 + 3 x + 2 x + 2 ) = 0 − x [ 3 x ( x + 1 ) + 2 ( x + 1 ) ] = 0 − x ( 3 x + 2 ) ( x + 1 ) = 0 − x ( 3 x 2 + 3 x + 2 x + 2 ) = 0 − x [ 3 x ( x + 1 ) + 2 ( x + 1 ) ] = 0 − x ( 3 x + 2 ) ( x + 1 ) = 0

Now, we use the zero-product property. Notice that we have three factors.

− x = 0 x = 0 3 x + 2 = 0 x = − 2 3 x + 1 = 0 x = −1 − x = 0 x = 0 3 x + 2 = 0 x = − 2 3 x + 1 = 0 x = −1

The solutions are 0 , 0 , − 2 3 , − 2 3 , and −1. −1.

Solve by factoring: x 3 + 11 x 2 + 10 x = 0. x 3 + 11 x 2 + 10 x = 0.

Using the Square Root Property

When there is no linear term in the equation, another method of solving a quadratic equation is by using the square root property , in which we isolate the x 2 x 2 term and take the square root of the number on the other side of the equals sign. Keep in mind that sometimes we may have to manipulate the equation to isolate the x 2 x 2 term so that the square root property can be used.

The Square Root Property

With the x 2 x 2 term isolated, the square root property states that:

if x 2 = k , then x = ± k if x 2 = k , then x = ± k

where k is a nonzero real number.

Given a quadratic equation with an x 2 x 2 term but no x x term, use the square root property to solve it.

• Isolate the x 2 x 2 term on one side of the equal sign.
• Take the square root of both sides of the equation, putting a ± ± sign before the expression on the side opposite the squared term.
• Simplify the numbers on the side with the ± ± sign.

Solving a Simple Quadratic Equation Using the Square Root Property

Solve the quadratic using the square root property: x 2 = 8. x 2 = 8.

Take the square root of both sides, and then simplify the radical. Remember to use a ± ± sign before the radical symbol.

x 2 = 8 x = ± 8 = ± 2 2 x 2 = 8 x = ± 8 = ± 2 2

The solutions are 2 2 , 2 2 , −2 2 . −2 2 .

Solving a Quadratic Equation Using the Square Root Property

Solve the quadratic equation: 4 x 2 + 1 = 7. 4 x 2 + 1 = 7.

First, isolate the x 2 x 2 term. Then take the square root of both sides.

4 x 2 + 1 = 7 4 x 2 = 6 x 2 = 6 4 x = ± 6 2 4 x 2 + 1 = 7 4 x 2 = 6 x 2 = 6 4 x = ± 6 2

The solutions are 6 2 , 6 2 , and − 6 2 . − 6 2 .

Solve the quadratic equation using the square root property: 3 ( x − 4 ) 2 = 15. 3 ( x − 4 ) 2 = 15.

• Completing the Square

Not all quadratic equations can be factored or can be solved in their original form using the square root property. In these cases, we may use a method for solving a quadratic equation known as completing the square . Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. We then apply the square root property. To complete the square, the leading coefficient, a , must equal 1. If it does not, then divide the entire equation by a . Then, we can use the following procedures to solve a quadratic equation by completing the square.

We will use the example x 2 + 4 x + 1 = 0 x 2 + 4 x + 1 = 0 to illustrate each step.

Given a quadratic equation that cannot be factored, and with a = 1 , a = 1 , first add or subtract the constant term to the right side of the equal sign.

x 2 + 4 x = −1 x 2 + 4 x = −1

Multiply the b term by 1 2 1 2 and square it.

1 2 ( 4 ) = 2 2 2 = 4 1 2 ( 4 ) = 2 2 2 = 4

Add ( 1 2 b ) 2 ( 1 2 b ) 2 to both sides of the equal sign and simplify the right side. We have

x 2 + 4 x + 4 = − 1 + 4 x 2 + 4 x + 4 = 3 x 2 + 4 x + 4 = − 1 + 4 x 2 + 4 x + 4 = 3

The left side of the equation can now be factored as a perfect square.

x 2 + 4 x + 4 = 3 ( x + 2 ) 2 = 3 x 2 + 4 x + 4 = 3 ( x + 2 ) 2 = 3

Use the square root property and solve.

( x + 2 ) 2 = ± 3 x + 2 = ± 3 x = −2 ± 3 ( x + 2 ) 2 = ± 3 x + 2 = ± 3 x = −2 ± 3

The solutions are −2 + 3 , −2 + 3 , and −2 − 3 . −2 − 3 .

Solving a Quadratic by Completing the Square

Solve the quadratic equation by completing the square: x 2 − 3 x − 5 = 0. x 2 − 3 x − 5 = 0.

First, move the constant term to the right side of the equal sign.

x 2 − 3 x = 5 x 2 − 3 x = 5

Then, take 1 2 1 2 of the b term and square it.

1 2 ( −3 ) = − 3 2 ( − 3 2 ) 2 = 9 4 1 2 ( −3 ) = − 3 2 ( − 3 2 ) 2 = 9 4

Add the result to both sides of the equal sign.

x 2 − 3 x + ( − 3 2 ) 2 = 5 + ( − 3 2 ) 2 x 2 − 3 x + 9 4 = 5 + 9 4 x 2 − 3 x + ( − 3 2 ) 2 = 5 + ( − 3 2 ) 2 x 2 − 3 x + 9 4 = 5 + 9 4

Factor the left side as a perfect square and simplify the right side.

( x − 3 2 ) 2 = 29 4 ( x − 3 2 ) 2 = 29 4

( x − 3 2 ) 2 = ± 29 4 ( x − 3 2 ) = ± 29 2 x = 3 2 ± 29 2 ( x − 3 2 ) 2 = ± 29 4 ( x − 3 2 ) = ± 29 2 x = 3 2 ± 29 2

The solutions are 3 + 29 2 3 + 29 2 and 3 - 29 2 3 - 29 2 .

Solve by completing the square: x 2 − 6 x = 13. x 2 − 6 x = 13.

Using the Quadratic Formula

The fourth method of solving a quadratic equation is by using the quadratic formula , a formula that will solve all quadratic equations. Although the quadratic formula works on any quadratic equation in standard form, it is easy to make errors in substituting the values into the formula. Pay close attention when substituting, and use parentheses when inserting a negative number.

We can derive the quadratic formula by completing the square . We will assume that the leading coefficient is positive; if it is negative, we can multiply the equation by −1 −1 and obtain a positive a . Given a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , a ≠ 0 , a ≠ 0 , we will complete the square as follows:

First, move the constant term to the right side of the equal sign:

a x 2 + b x = − c a x 2 + b x = − c

As we want the leading coefficient to equal 1, divide through by a :

x 2 + b a x = − c a x 2 + b a x = − c a

Then, find 1 2 1 2 of the middle term, and add ( 1 2 b a ) 2 = b 2 4 a 2 ( 1 2 b a ) 2 = b 2 4 a 2 to both sides of the equal sign:

x 2 + b a x + b 2 4 a 2 = b 2 4 a 2 − c a x 2 + b a x + b 2 4 a 2 = b 2 4 a 2 − c a

Next, write the left side as a perfect square. Find the common denominator of the right side and write it as a single fraction:

( x + b 2 a ) 2 = b 2 − 4 a c 4 a 2 ( x + b 2 a ) 2 = b 2 − 4 a c 4 a 2

Now, use the square root property, which gives

x + b 2 a = ± b 2 − 4 a c 4 a 2 x + b 2 a = ± b 2 − 4 a c 2 a x + b 2 a = ± b 2 − 4 a c 4 a 2 x + b 2 a = ± b 2 − 4 a c 2 a

Finally, add − b 2 a − b 2 a to both sides of the equation and combine the terms on the right side. Thus,

x = − b ± b 2 − 4 a c 2 a x = − b ± b 2 − 4 a c 2 a

The Quadratic Formula

Written in standard form, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , any quadratic equation can be solved using the quadratic formula :

where a , b , and c are real numbers and a ≠ 0. a ≠ 0.

Given a quadratic equation, solve it using the quadratic formula

• Make sure the equation is in standard form: a x 2 + b x + c = 0. a x 2 + b x + c = 0.
• Make note of the values of the coefficients and constant term, a , b , a , b , and c . c .
• Carefully substitute the values noted in step 2 into the equation. To avoid needless errors, use parentheses around each number input into the formula.
• Calculate and solve.

Solve the Quadratic Equation Using the Quadratic Formula

Solve the quadratic equation: x 2 + 5 x + 1 = 0. x 2 + 5 x + 1 = 0.

Identify the coefficients: a = 1 , b = 5 , c = 1. a = 1 , b = 5 , c = 1. Then use the quadratic formula.

x = − ( 5 ) ± ( 5 ) 2 − 4 ( 1 ) ( 1 ) 2 ( 1 ) = − 5 ± 25 − 4 2 = − 5 ± 21 2 x = − ( 5 ) ± ( 5 ) 2 − 4 ( 1 ) ( 1 ) 2 ( 1 ) = − 5 ± 25 − 4 2 = − 5 ± 21 2

Solving a Quadratic Equation with the Quadratic Formula

Use the quadratic formula to solve x 2 + x + 2 = 0. x 2 + x + 2 = 0.

First, we identify the coefficients: a = 1 , b = 1 , a = 1 , b = 1 , and c = 2. c = 2.

Substitute these values into the quadratic formula.

x = − b ± b 2 − 4 a c 2 a = − ( 1 ) ± ( 1 ) 2 − ( 4 ) ⋅ ( 1 ) ⋅ ( 2 ) 2 ⋅ 1 = − 1 ± 1 − 8 2 = − 1 ± − 7 2 = − 1 ± i 7 2 x = − b ± b 2 − 4 a c 2 a = − ( 1 ) ± ( 1 ) 2 − ( 4 ) ⋅ ( 1 ) ⋅ ( 2 ) 2 ⋅ 1 = − 1 ± 1 − 8 2 = − 1 ± − 7 2 = − 1 ± i 7 2

The solutions to the equation are − 1 + i 7 2 − 1 + i 7 2 and − 1 − i 7 2 − 1 − i 7 2

Solve the quadratic equation using the quadratic formula: 9 x 2 + 3 x − 2 = 0. 9 x 2 + 3 x − 2 = 0.

The Discriminant

The quadratic formula not only generates the solutions to a quadratic equation, it tells us about the nature of the solutions when we consider the discriminant , or the expression under the radical, b 2 − 4 a c . b 2 − 4 a c . The discriminant tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type to expect. Table 1 relates the value of the discriminant to the solutions of a quadratic equation.

For a x 2 + b x + c = 0 a x 2 + b x + c = 0 , where a a , b b , and c c are real numbers, the discriminant is the expression under the radical in the quadratic formula: b 2 − 4 a c . b 2 − 4 a c . It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.

Using the Discriminant to Find the Nature of the Solutions to a Quadratic Equation

Use the discriminant to find the nature of the solutions to the following quadratic equations:

• ⓐ x 2 + 4 x + 4 = 0 x 2 + 4 x + 4 = 0
• ⓑ 8 x 2 + 14 x + 3 = 0 8 x 2 + 14 x + 3 = 0
• ⓒ 3 x 2 − 5 x − 2 = 0 3 x 2 − 5 x − 2 = 0
• ⓓ 3 x 2 − 10 x + 15 = 0 3 x 2 − 10 x + 15 = 0

Calculate the discriminant b 2 − 4 a c b 2 − 4 a c for each equation and state the expected type of solutions.

x 2 + 4 x + 4 = 0 x 2 + 4 x + 4 = 0

b 2 − 4 a c = ( 4 ) 2 − 4 ( 1 ) ( 4 ) = 0. b 2 − 4 a c = ( 4 ) 2 − 4 ( 1 ) ( 4 ) = 0. There will be one rational double solution.

8 x 2 + 14 x + 3 = 0 8 x 2 + 14 x + 3 = 0

b 2 − 4 a c = ( 14 ) 2 − 4 ( 8 ) ( 3 ) = 100. b 2 − 4 a c = ( 14 ) 2 − 4 ( 8 ) ( 3 ) = 100. As 100 100 is a perfect square, there will be two rational solutions.

3 x 2 − 5 x − 2 = 0 3 x 2 − 5 x − 2 = 0

b 2 − 4 a c = ( −5 ) 2 − 4 ( 3 ) ( −2 ) = 49. b 2 − 4 a c = ( −5 ) 2 − 4 ( 3 ) ( −2 ) = 49. As 49 49 is a perfect square, there will be two rational solutions.

3 x 2 −10 x + 15 = 0 3 x 2 −10 x + 15 = 0

b 2 − 4 a c = ( −10 ) 2 − 4 ( 3 ) ( 15 ) = −80. b 2 − 4 a c = ( −10 ) 2 − 4 ( 3 ) ( 15 ) = −80. There will be two complex solutions.

Using the Pythagorean Theorem

One of the most famous formulas in mathematics is the Pythagorean Theorem . It is based on a right triangle, and states the relationship among the lengths of the sides as a 2 + b 2 = c 2 , a 2 + b 2 = c 2 , where a a and b b refer to the legs of a right triangle adjacent to the 90° 90° angle, and c c refers to the hypotenuse. It has immeasurable uses in architecture, engineering, the sciences, geometry, trigonometry, and algebra, and in everyday applications.

We use the Pythagorean Theorem to solve for the length of one side of a triangle when we have the lengths of the other two. Because each of the terms is squared in the theorem, when we are solving for a side of a triangle, we have a quadratic equation. We can use the methods for solving quadratic equations that we learned in this section to solve for the missing side.

The Pythagorean Theorem is given as

a 2 + b 2 = c 2 a 2 + b 2 = c 2

where a a and b b refer to the legs of a right triangle adjacent to the 90 ∘ 90 ∘ angle, and c c refers to the hypotenuse, as shown in Figure 4 .

Finding the Length of the Missing Side of a Right Triangle

Find the length of the missing side of the right triangle in Figure 5 .

As we have measurements for side b and the hypotenuse, the missing side is a.

a 2 + b 2 = c 2 a 2 + ( 4 ) 2 = ( 12 ) 2 a 2 + 16 = 144 a 2 = 128 a = 128 = 8 2 a 2 + b 2 = c 2 a 2 + ( 4 ) 2 = ( 12 ) 2 a 2 + 16 = 144 a 2 = 128 a = 128 = 8 2

Use the Pythagorean Theorem to solve the right triangle problem: Leg a measures 4 units, leg b measures 3 units. Find the length of the hypotenuse.

Access these online resources for additional instruction and practice with quadratic equations.

• The Zero-Product Property
• Quadratic Formula with Two Rational Solutions
• Length of a leg of a right triangle

2.5 Section Exercises

How do we recognize when an equation is quadratic?

When we solve a quadratic equation, how many solutions should we always start out seeking? Explain why when solving a quadratic equation in the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 we may graph the equation y = a x 2 + b x + c y = a x 2 + b x + c and have no zeroes ( x -intercepts).

When we solve a quadratic equation by factoring, why do we move all terms to one side, having zero on the other side?

In the quadratic formula, what is the name of the expression under the radical sign b 2 − 4 a c , b 2 − 4 a c , and how does it determine the number of and nature of our solutions?

Describe two scenarios where using the square root property to solve a quadratic equation would be the most efficient method.

For the following exercises, solve the quadratic equation by factoring.

x 2 + 4 x − 21 = 0 x 2 + 4 x − 21 = 0

x 2 − 9 x + 18 = 0 x 2 − 9 x + 18 = 0

2 x 2 + 9 x − 5 = 0 2 x 2 + 9 x − 5 = 0

6 x 2 + 17 x + 5 = 0 6 x 2 + 17 x + 5 = 0

4 x 2 − 12 x + 8 = 0 4 x 2 − 12 x + 8 = 0

3 x 2 − 75 = 0 3 x 2 − 75 = 0

8 x 2 + 6 x − 9 = 0 8 x 2 + 6 x − 9 = 0

4 x 2 = 9 4 x 2 = 9

2 x 2 + 14 x = 36 2 x 2 + 14 x = 36

5 x 2 = 5 x + 30 5 x 2 = 5 x + 30

4 x 2 = 5 x 4 x 2 = 5 x

7 x 2 + 3 x = 0 7 x 2 + 3 x = 0

x 3 − 9 x = 2 x 3 − 9 x = 2

For the following exercises, solve the quadratic equation by using the square root property.

x 2 = 36 x 2 = 36

x 2 = 49 x 2 = 49

( x − 1 ) 2 = 25 ( x − 1 ) 2 = 25

( x − 3 ) 2 = 7 ( x − 3 ) 2 = 7

( 2 x + 1 ) 2 = 9 ( 2 x + 1 ) 2 = 9

( x − 5 ) 2 = 4 ( x − 5 ) 2 = 4

For the following exercises, solve the quadratic equation by completing the square. Show each step.

x 2 − 9 x − 22 = 0 x 2 − 9 x − 22 = 0

2 x 2 − 8 x − 5 = 0 2 x 2 − 8 x − 5 = 0

x 2 − 6 x = 13 x 2 − 6 x = 13

x 2 + 2 3 x − 1 3 = 0 x 2 + 2 3 x − 1 3 = 0

2 + z = 6 z 2 2 + z = 6 z 2

6 p 2 + 7 p − 20 = 0 6 p 2 + 7 p − 20 = 0

2 x 2 − 3 x − 1 = 0 2 x 2 − 3 x − 1 = 0

For the following exercises, determine the discriminant, and then state how many solutions there are and the nature of the solutions. Do not solve.

2 x 2 − 6 x + 7 = 0 2 x 2 − 6 x + 7 = 0

x 2 + 4 x + 7 = 0 x 2 + 4 x + 7 = 0

3 x 2 + 5 x − 8 = 0 3 x 2 + 5 x − 8 = 0

9 x 2 − 30 x + 25 = 0 9 x 2 − 30 x + 25 = 0

2 x 2 − 3 x − 7 = 0 2 x 2 − 3 x − 7 = 0

6 x 2 − x − 2 = 0 6 x 2 − x − 2 = 0

For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No Real Solution .

2 x 2 + 5 x + 3 = 0 2 x 2 + 5 x + 3 = 0

x 2 + x = 4 x 2 + x = 4

3 x 2 − 5 x + 1 = 0 3 x 2 − 5 x + 1 = 0

x 2 + 4 x + 2 = 0 x 2 + 4 x + 2 = 0

4 + 1 x − 1 x 2 = 0 4 + 1 x − 1 x 2 = 0

For the following exercises, enter the expressions into your graphing utility and find the zeroes to the equation (the x -intercepts) by using 2 nd CALC 2:zero . Recall finding zeroes will ask left bound (move your cursor to the left of the zero,enter), then right bound (move your cursor to the right of the zero,enter), then guess (move your cursor between the bounds near the zero, enter). Round your answers to the nearest thousandth.

Y 1 = 4 x 2 + 3 x − 2 Y 1 = 4 x 2 + 3 x − 2

Y 1 = −3 x 2 + 8 x − 1 Y 1 = −3 x 2 + 8 x − 1

Y 1 = 0.5 x 2 + x − 7 Y 1 = 0.5 x 2 + x − 7

To solve the quadratic equation x 2 + 5 x − 7 = 4 , x 2 + 5 x − 7 = 4 , we can graph these two equations

Y 1 = x 2 + 5 x − 7 Y 2 = 4 Y 1 = x 2 + 5 x − 7 Y 2 = 4

and find the points of intersection. Recall 2 nd CALC 5:intersection. Do this and find the solutions to the nearest tenth.

To solve the quadratic equation 0.3 x 2 + 2 x − 4 = 2 , 0.3 x 2 + 2 x − 4 = 2 , we can graph these two equations

Y 1 = 0.3 x 2 + 2 x − 4 Y 2 = 2 Y 1 = 0.3 x 2 + 2 x − 4 Y 2 = 2

Beginning with the general form of a quadratic equation, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , solve for x by using the completing the square method, thus deriving the quadratic formula.

Show that the sum of the two solutions to the quadratic equation is − b a − b a .

A person has a garden that has a length 10 feet longer than the width. Set up a quadratic equation to find the dimensions of the garden if its area is 119 ft. 2 . Solve the quadratic equation to find the length and width.

Abercrombie and Fitch stock had a price given as P = 0.2 t 2 − 5.6 t + 50.2 , P = 0.2 t 2 − 5.6 t + 50.2 , where t t is the time in months from 1999 to 2001. ( t = 1 t = 1 is January 1999). Find the two months in which the price of the stock was $30.

Suppose that an equation is given p = −2 x 2 + 280 x − 1000 , p = −2 x 2 + 280 x − 1000 , where x x represents the number of items sold at an auction and p p is the profit made by the business that ran the auction. How many items sold would make this profit a maximum? Solve this by graphing the expression in your graphing utility and finding the maximum using 2 nd CALC maximum. To obtain a good window for the curve, set x x [0,200] and y y [0,10000].

Real-World Applications

A formula for the normal systolic blood pressure for a man age A , A , measured in mmHg, is given as P = 0.006 A 2 − 0.02 A + 120. P = 0.006 A 2 − 0.02 A + 120. Find the age to the nearest year of a man whose normal blood pressure measures 125 mmHg.

The cost function for a certain company is C = 60 x + 300 C = 60 x + 300 and the revenue is given by R = 100 x − 0.5 x 2 . R = 100 x − 0.5 x 2 . Recall that profit is revenue minus cost. Set up a quadratic equation and find two values of x (production level) that will create a profit of $300.

A falling object travels a distance given by the formula d = 5 t + 16 t 2 d = 5 t + 16 t 2 ft, where t t is measured in seconds. How long will it take for the object to travel 74 ft?

A vacant lot is being converted into a community garden. The garden and the walkway around its perimeter have an area of 378 ft 2 . Find the width of the walkway if the garden is 12 ft. wide by 15 ft. long.

An epidemiological study of the spread of a certain influenza strain that hit a small school population found that the total number of students, P P , who contracted the flu t t days after it broke out is given by the model P = − t 2 + 13 t + 130 , P = − t 2 + 13 t + 130 , where 1 ≤ t ≤ 6. 1 ≤ t ≤ 6. Find the day that 160 students had the flu. Recall that the restriction on t t is at most 6.