rational inequality problem solving

7.6 Solve Rational Inequalities

Learning objectives.

By the end of this section, you will be able to:

• Solve rational inequalities
• Solve an inequality with rational functions

Be Prepared 7.16

Before you get started, take this readiness quiz.

Find the value of x − 5 x − 5 when ⓐ x = 6 x = 6 ⓑ x = −3 x = −3 ⓒ x = 5 . x = 5 . If you missed this problem, review Example 1.6 .

Be Prepared 7.17

Solve: 8 − 2 x < 12 . 8 − 2 x < 12 . If you missed this problem, review Example 2.52 .

Be Prepared 7.18

Write in interval notation: −3 ≤ x < 5 . −3 ≤ x < 5 . If you missed this problem, review Example 2.49 .

Solve Rational Inequalities

We learned to solve linear inequalities after learning to solve linear equations. The techniques were very much the same with one major exception. When we multiplied or divided by a negative number, the inequality sign reversed.

Having just learned to solve rational equations we are now ready to solve rational inequalities. A rational inequality is an inequality that contains a rational expression.

Rational Inequality

A rational inequality is an inequality that contains a rational expression.

Inequalities such as 3 2 x > 1 , 2 x x − 3 < 4 , 2 x − 3 x − 6 ≥ x , 3 2 x > 1 , 2 x x − 3 < 4 , 2 x − 3 x − 6 ≥ x , and 1 4 − 2 x 2 ≤ 3 x 1 4 − 2 x 2 ≤ 3 x are rational inequalities as they each contain a rational expression.

When we solve a rational inequality, we will use many of the techniques we used solving linear inequalities. We especially must remember that when we multiply or divide by a negative number, the inequality sign must reverse.

Another difference is that we must carefully consider what value might make the rational expression undefined and so must be excluded.

When we solve an equation and the result is x = 3 , x = 3 , we know there is one solution, which is 3.

When we solve an inequality and the result is x > 3 , x > 3 , we know there are many solutions. We graph the result to better help show all the solutions, and we start with 3. Three becomes a critical point and then we decide whether to shade to the left or right of it. The numbers to the right of 3 are larger than 3, so we shade to the right.

To solve a rational inequality, we first must write the inequality with only one quotient on the left and 0 on the right.

Next we determine the critical points to use to divide the number line into intervals. A critical point is a number which make the rational expression zero or undefined.

We then will evaluate the factors of the numerator and denominator, and find the quotient in each interval. This will identify the interval, or intervals, that contains all the solutions of the rational inequality.

We write the solution in interval notation being careful to determine whether the endpoints are included.

Example 7.54

Solve and write the solution in interval notation: x − 1 x + 3 ≥ 0 . x − 1 x + 3 ≥ 0 .

• Step 1. Write the inequality as one quotient on the left and zero on the right.

Our inequality is in this form. x − 1 x + 3 ≥ 0 x − 1 x + 3 ≥ 0

Step 2. Determine the critical points—the points where the rational expression will be zero or undefined.

The rational expression will be zero when the numerator is zero. Since x − 1 = 0 x − 1 = 0 when x = 1 , x = 1 , then 1 1 is a critical point.

The rational expression will be undefined when the denominator is zero. Since x + 3 = 0 x + 3 = 0 when x = −3 , x = −3 , then −3 −3 is a critical point.

The critical points are 1 and −3 . −3 .

• Step 3. Use the critical points to divide the number line into intervals.

The number line is divided into three intervals:

( − ∞ , −3 ) ( −3 , 1 ) ( 1 , ∞ ) ( − ∞ , −3 ) ( −3 , 1 ) ( 1 , ∞ )

Step 4. Test a value in each interval. Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.

To find the sign of each factor in an interval, we choose any point in that interval and use it as a test point. Any point in the interval will give the expression the same sign, so we can choose any point in the interval.

The number −4 −4 is in the interval ( − ∞ , −3 ) . ( − ∞ , −3 ) . Test x = −4 x = −4 in the expression in the numerator and the denominator.

Above the number line, mark the factor x − 1 x − 1 negative and mark the factor x + 3 x + 3 negative.

Since a negative divided by a negative is positive, mark the quotient positive in the interval ( − ∞ , −3 ) . ( − ∞ , −3 ) .

The number 0 is in the interval ( −3 , 1 ) . ( −3 , 1 ) . Test x = 0 . x = 0 .

Above the number line, mark the factor x − 1 x − 1 negative and mark x + 3 x + 3 positive.

Since a negative divided by a positive is negative, the quotient is marked negative in the interval ( −3 , 1 ) . ( −3 , 1 ) .

The number 2 is in the interval ( 1 , ∞ ) . ( 1 , ∞ ) . Test x = 2 . x = 2 .

Above the number line, mark the factor x − 1 x − 1 positive and mark x + 3 x + 3 positive.

Since a positive divided by a positive is positive, mark the quotient positive in the interval ( 1 , ∞ ) . ( 1 , ∞ ) .

• Step 5. Determine the intervals where the inequality is correct. Write the solution in interval notation.

We want the quotient to be greater than or equal to zero, so the numbers in the intervals ( − ∞ , −3 ) ( − ∞ , −3 ) and ( 1 , ∞ ) ( 1 , ∞ ) are solutions.

But what about the critical points?

The critical point x = −3 x = −3 makes the denominator 0, so it must be excluded from the solution and we mark it with a parenthesis.

The critical point x = 1 x = 1 makes the whole rational expression 0. The inequality requires that the rational expression be greater than or equal to 0. So, 1 is part of the solution and we will mark it with a bracket.

Recall that when we have a solution made up of more than one interval we use the union symbol, ∪ , ∪ , to connect the two intervals. The solution in interval notation is ( − ∞ , −3 ) ∪ [ 1 , ∞ ) . ( − ∞ , −3 ) ∪ [ 1 , ∞ ) .

Try It 7.107

Solve and write the solution in interval notation: x − 2 x + 4 ≥ 0 . x − 2 x + 4 ≥ 0 .

Try It 7.108

Solve and write the solution in interval notation: x + 2 x − 4 ≥ 0 . x + 2 x − 4 ≥ 0 .

We summarize the steps for easy reference.

Solve a rational inequality.

• Step 2. Determine the critical points–the points where the rational expression will be zero or undefined.
• Step 4. Test a value in each interval. Above the number line show the sign of each factor of the numerator and denominator in each interval. Below the number line show the sign of the quotient.

The next example requires that we first get the rational inequality into the correct form.

Example 7.55

Solve and write the solution in interval notation: 4 x x − 6 < 1 . 4 x x − 6 < 1 .

Try It 7.109

Solve and write the solution in interval notation: 3 x x − 3 < 1 . 3 x x − 3 < 1 .

Try It 7.110

Solve and write the solution in interval notation: 3 x x − 4 < 2 . 3 x x − 4 < 2 .

In the next example, the numerator is always positive, so the sign of the rational expression depends on the sign of the denominator.

Example 7.56

Solve and write the solution in interval notation: 5 x 2 − 2 x − 15 > 0 . 5 x 2 − 2 x − 15 > 0 .

Try It 7.111

Solve and write the solution in interval notation: 1 x 2 + 2 x − 8 > 0 . 1 x 2 + 2 x − 8 > 0 .

Try It 7.112

Solve and write the solution in interval notation: 3 x 2 + x − 12 > 0 . 3 x 2 + x − 12 > 0 .

The next example requires some work to get it into the needed form.

Example 7.57

Solve and write the solution in interval notation: 1 3 − 2 x 2 < 5 3 x . 1 3 − 2 x 2 < 5 3 x .

Try It 7.113

Solve and write the solution in interval notation: 1 2 + 4 x 2 < 3 x . 1 2 + 4 x 2 < 3 x .

Try It 7.114

Solve and write the solution in interval notation: 1 3 + 6 x 2 < 3 x . 1 3 + 6 x 2 < 3 x .

Solve an Inequality with Rational Functions

When working with rational functions, it is sometimes useful to know when the function is greater than or less than a particular value. This leads to a rational inequality.

Example 7.58

Given the function R ( x ) = x + 3 x − 5 , R ( x ) = x + 3 x − 5 , find the values of x that make the function less than or equal to 0.

We want the function to be less than or equal to 0.

Try It 7.115

Given the function R ( x ) = x − 2 x + 4 , R ( x ) = x − 2 x + 4 , find the values of x that make the function less than or equal to 0.

Try It 7.116

Given the function R ( x ) = x + 1 x − 4 , R ( x ) = x + 1 x − 4 , find the values of x that make the function less than or equal to 0.

In economics, the function C ( x ) C ( x ) is used to represent the cost of producing x units of a commodity. The average cost per unit can be found by dividing C ( x ) C ( x ) by the number of items x . x . Then, the average cost per unit is c ( x ) = C ( x ) x . c ( x ) = C ( x ) x .

Example 7.59

The function C ( x ) = 10 x + 3000 C ( x ) = 10 x + 3000 represents the cost to produce x , x , number of items. Find ⓐ the average cost function, c ( x ) c ( x ) ⓑ how many items should be produced so that the average cost is less than $40.

More than 100 items must be produced to keep the average cost below $40 per item.

Try It 7.117

The function C ( x ) = 20 x + 6000 C ( x ) = 20 x + 6000 represents the cost to produce x , x , number of items. Find ⓐ the average cost function, c ( x ) c ( x ) ⓑ how many items should be produced so that the average cost is less than $60?

Try It 7.118

The function C ( x ) = 5 x + 900 C ( x ) = 5 x + 900 represents the cost to produce x , x , number of items. Find ⓐ the average cost function, c ( x ) c ( x ) ⓑ how many items should be produced so that the average cost is less than $20?

Section 7.6 Exercises

Practice makes perfect.

In the following exercises, solve each rational inequality and write the solution in interval notation.

x − 3 x + 4 ≥ 0 x − 3 x + 4 ≥ 0

x + 6 x − 5 ≥ 0 x + 6 x − 5 ≥ 0

x + 1 x − 3 ≤ 0 x + 1 x − 3 ≤ 0

x − 4 x + 2 ≤ 0 x − 4 x + 2 ≤ 0

x − 7 x − 1 > 0 x − 7 x − 1 > 0

x + 8 x + 3 > 0 x + 8 x + 3 > 0

x − 6 x + 5 < 0 x − 6 x + 5 < 0

x + 5 x − 2 < 0 x + 5 x − 2 < 0

3 x x − 5 < 1 3 x x − 5 < 1

5 x x − 2 < 1 5 x x − 2 < 1

6 x x − 6 > 2 6 x x − 6 > 2

3 x x − 4 > 2 3 x x − 4 > 2

2 x + 3 x − 6 ≤ 1 2 x + 3 x − 6 ≤ 1

4 x − 1 x − 4 ≤ 1 4 x − 1 x − 4 ≤ 1

3 x − 2 x − 4 ≥ 2 3 x − 2 x − 4 ≥ 2

4 x − 3 x − 3 ≥ 2 4 x − 3 x − 3 ≥ 2

1 x 2 + 7 x + 12 > 0 1 x 2 + 7 x + 12 > 0

1 x 2 − 4 x − 12 > 0 1 x 2 − 4 x − 12 > 0

3 x 2 − 5 x + 4 < 0 3 x 2 − 5 x + 4 < 0

4 x 2 + 7 x + 12 < 0 4 x 2 + 7 x + 12 < 0

2 2 x 2 + x − 15 ≥ 0 2 2 x 2 + x − 15 ≥ 0

6 3 x 2 − 2 x − 5 ≥ 0 6 3 x 2 − 2 x − 5 ≥ 0

−2 6 x 2 − 13 x + 6 ≤ 0 −2 6 x 2 − 13 x + 6 ≤ 0

−1 10 x 2 + 11 x − 6 ≤ 0 −1 10 x 2 + 11 x − 6 ≤ 0

1 2 + 12 x 2 > 5 x 1 2 + 12 x 2 > 5 x

1 3 + 1 x 2 > 4 3 x 1 3 + 1 x 2 > 4 3 x

1 2 − 4 x 2 ≤ 1 x 1 2 − 4 x 2 ≤ 1 x

1 2 − 3 2 x 2 ≥ 1 x 1 2 − 3 2 x 2 ≥ 1 x

1 x 2 − 16 < 0 1 x 2 − 16 < 0

4 x 2 − 25 > 0 4 x 2 − 25 > 0

4 x − 2 ≥ 3 x + 1 4 x − 2 ≥ 3 x + 1

5 x − 1 ≤ 4 x + 2 5 x − 1 ≤ 4 x + 2

In the following exercises, solve each rational function inequality and write the solution in interval notation.

Given the function R ( x ) = x − 5 x − 2 , R ( x ) = x − 5 x − 2 , find the values of x x that make the function less than or equal to 0.

Given the function R ( x ) = x + 1 x + 3 , R ( x ) = x + 1 x + 3 , find the values of x x that make the function greater than or equal to 0.

Given the function R ( x ) = x − 6 x + 2 R ( x ) = x − 6 x + 2 , find the values of x that make the function less than or equal to 0.

Writing Exercises

Write the steps you would use to explain solving rational inequalities to your little brother.

Create a rational inequality whose solution is ( − ∞ , −2 ] ∪ [ 4 , ∞ ) . ( − ∞ , −2 ] ∪ [ 4 , ∞ ) .

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/7-6-solve-rational-inequalities

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Solving Rational Inequalities

A Rational Expression looks like:

Inequalities

Sometimes we need to solve rational inequalities like these:

Solving inequalities is very like solving equations ... you do most of the same things.

These are the steps:

• the "=0" points (roots), and
• "vertical asymptotes" (where the function is undefined)
• in between the "points of interest", the function is either greater than zero (>0) or less than zero (<0)
• then pick a test value to find out which it is (>0 or <0)

Here is an example:

Example: 3x−10 x−4 > 2

First , let us simplify!

But You Cannot Multiply By (x−4)

Because "x−4" could be positive or negative ... we don't know if we should change the direction of the inequality or not. This is all explained on Solving Inequalities .

Instead, bring "2" to the left:

3x−10 x−4 − 2 > 0

Then multiply the 2 by (x−4)/(x−4):

3x−10 x−4 − 2 x−4 x−4 > 0

Now we have a common denominator, let's bring it all together:

3x−10 − 2(x−4) x−4 > 0

x−2 x−4 > 0

Second , let us find "points of interest".

At x=2 we have: (0)/(x−4) > 0 , which is a "=0" point, or root

At x=4 we have: (x−2)/(0) > 0 , which is undefined

Third , do test points to see what it does in between:

• x−2 = −2, which is negative
• x−4 = −4, which is also negative
• So (x−2)/(x−4) must be positive

We can do the same for x=3 and x=5 , and end up with these results:

That gives us a complete picture!

And where is it > 0 ?

• Less than 2
• Greater than 4

So, after rearranging and analysing 3x−10 x−4 > 2 we get the result for x:

(−∞, 2) U (4, +∞)

We did all that without drawing a plot!

But here is the plot of (x−2)/(x−4) so you can see:

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Algebra (all content)

Course: algebra (all content)   >   unit 13.

• Rational inequalities: one side is zero

Rational inequalities: both sides are not zero

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Rational Inequalities

Explanation Examples

Solving rational inequalities is very similar to solving polynomial inequalities .

But because rational expressions have denominators (and therefore may have places where they're not defined), you have to be a little more careful in finding your solutions.

Content Continues Below

MathHelp.com

How do you solve rational inequalities?

To solve a rational inequality, use these steps:

Advertisement

• If needed, move all the terms to one side of the inequality symbol, with zero on the other side.
• If needed, combine all rational expressions into one polynomial fraction.
• Factor the numerator and denominator completely.
• Solve the factors for their zeroes; keep in mind that the denominator's zeroes would cause division by zero, so they cannot be included in your solution.
• Use the zeroes to divide the number line into intervals.
• Make a table of factors, showing where each factor is less than and greater than zero.
• Multiply the factors' signs on each interval (that is, down the table's columns) to find the sign of the rational expression on that interval.
• Select the intervals that match the inequality they gave you; remember to discard any endpoints that would cause division by zero.

Let's see how these instructions work in practice:

They've already put this inequality into (one rational expression) with (zero) on the other side. So I can start with factoring everything:

This polynomial fraction will be zero wherever the numerator is zero, so I'll set the numerator equal to zero and solve:

( x + 2)( x + 1) = 0

x + 2 = 0   or   x + 1 = 0

x = −2   or   x = −1

The fraction will be undefined wherever the denominator is zero, so I'll set the denominator equal to zero and solve:

( x + 4)( x − 4) = 0

x + 4 = 0   or   x − 4 = 0

x = −4   or   x = 4

These four values, −4, −2, −1, and +4 , divide the number line into five intervals, namely:

(−∞, −4)

(−4, −2)

(−2, −1)

(−1, 4)

(4, +∞)

I could use "test points" to find the solution to the inequality, by picking an x -value in each interval, plugging it into the original rational expression, simplifying to get a numerical answer, and then checking the sign, but that process gets long and annoying (and is prone to errors), so I'll use the easier and faster factor-table method instead.

My factor table looks like this:

My table has one row for each factor, a row for the number line, and a row for the rational expression. Each row is split into columns, with each column corresponding to one of the intervals on the number line.

The sign of the overall rational expression is a result of the signs of its various factors, so I need to find where each factor is positive:

x + 4 > 0   for   x > −4 x + 2 > 0   for   x > −2 x + 1 > 0   for   x > −1 x − 4 > 0   for   x > 4

Now I can put "plus" signs on the intervals in each row where that row's factor is positive:

Wherever a factor isn't positive, it's negative, so I'll put "minus" signs in the remaining entries of each row:

I know that the product of an even number of "minus" signs is a plus; the product of an odd number of "minus" signs is a minus. So, by multiplying the signs down the columns (or just counting up the minusses), I get the overall sign of the rational expression on each interval:

Then the rational is positive on the intervals (−∞, −4), (−2, −1), and (4, +∞) .

Looking back at the original exercise, this is an "or equal to" inequality, so I need to consider the interval endpoints, too.

If this were a polynomial inequality, I could just throw all the interval endpoints into the solution, and I'd be done. For rational expressions, though, I have to be careful not to include any x -values that would cause division by zero.

The intervals' endpoints are −4, −2, −1, and 4 . I can include −2 and −1 in the solution, because they just make the expression equal to zero by making the numerator zero. But plugging −4 or 4 into the rational expression would cause division by zero, making the rational expression undefined, so I can't include these values in the solution.

Then my full solution is:

I wrote my solution above in "interval" notation. If you have to write your solution in "inequality" notation, it would look like this:

x < −4, −2 ≤  x  ≤ −1 , and x  > 4

Don't forget: "Infinity" is not a "number" in the way that, say, " 2 " is. "Infinity" cannot be "included" in your solution, so never draw a square bracket next to an "infinity" "endpoint".

URL: https://www.purplemath.com/modules/ineqrtnl.htm

You can use the Mathway widget below to practice solving rational inequalities. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve the Inequality for x" (or just "Solve for x") to compare your answer to Mathway's. (Or skip the widget,and continue with the lesson.

Please accept "preferences" cookies in order to enable this widget.

(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)

Page 1 Page 2

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Rational Expressions and Functions

Solve Rational Inequalities

Learning Objectives

By the end of this section, you will be able to:

• Solve rational inequalities
• Solve an inequality with rational functions

Before you get started, take this readiness quiz.

We learned to solve linear inequalities after learning to solve linear equations. The techniques were very much the same with one major exception. When we multiplied or divided by a negative number, the inequality sign reversed.

Having just learned to solve rational equations we are now ready to solve rational inequalities. A rational inequality is an inequality that contains a rational expression.

A rational inequality is an inequality that contains a rational expression.

When we solve a rational inequality, we will use many of the techniques we used solving linear inequalities. We especially must remember that when we multiply or divide by a negative number, the inequality sign must reverse.

Another difference is that we must carefully consider what value might make the rational expression undefined and so must be excluded.

To solve a rational inequality, we first must write the inequality with only one quotient on the left and 0 on the right.

Next we determine the critical points to use to divide the number line into intervals. A critical point is a number which make the rational expression zero or undefined.

We then will evaluate the factors of the numerator and denominator, and find the quotient in each interval. This will identify the interval, or intervals, that contains all the solutions of the rational inequality.

We write the solution in interval notation being careful to determine whether the endpoints are included.

Step 1. Write the inequality as one quotient on the left and zero on the right.

Step 2. Determine the critical points—the points where the rational expression will be zero or undefined.

Step 3. Use the critical points to divide the number line into intervals.

The number line is divided into three intervals:

Step 4. Test a value in each interval. Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.

To find the sign of each factor in an interval, we choose any point in that interval and use it as a test point. Any point in the interval will give the expression the same sign, so we can choose any point in the interval.

Step 5. Determine the intervals where the inequality is correct. Write the solution in interval notation.

But what about the critical points?

We summarize the steps for easy reference.

• Write the inequality as one quotient on the left and zero on the right.
• Determine the critical points–the points where the rational expression will be zero or undefined.
• Use the critical points to divide the number line into intervals.
• Test a value in each interval. Above the number line show the sign of each factor of the numerator and denominator in each interval. Below the number line show the sign of the quotient.
• Determine the intervals where the inequality is correct. Write the solution in interval notation.

The next example requires that we first get the rational inequality into the correct form.

In the next example, the numerator is always positive, so the sign of the rational expression depends on the sign of the denominator.

The next example requires some work to get it into the needed form.

Solve an Inequality with Rational Functions

When working with rational functions, it is sometimes useful to know when the function is greater than or less than a particular value. This leads to a rational inequality.

We want the function to be less than or equal to 0.

More than 100 items must be produced to keep the average cost below ?40 per item.

Key Concepts

• Test a value in each interval. Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.

Section Exercises

Practice makes perfect.

In the following exercises, solve each rational inequality and write the solution in interval notation.

In the following exercises, solve each rational function inequality and write the solution in interval notation.

Writing Exercises

Write the steps you would use to explain solving rational inequalities to your little brother.

Answers will vary.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Chapter Review Exercises

Simplify, multiply, and divide rational expressions.

Determine the Values for Which a Rational Expression is Undefined

In the following exercises, determine the values for which the rational expression is undefined.

Simplify Rational Expressions

In the following exercises, simplify.

Multiply Rational Expressions

In the following exercises, multiply.

Divide Rational Expressions

In the following exercises, divide.

Multiply and Divide Rational Functions

Add and Subtract Rational Expressions

Add and Subtract Rational Expressions with a Common Denominator

In the following exercises, perform the indicated operations.

Add and Subtract Rational Expressions Whose Denominators Are Opposites

In the following exercises, add and subtract.

Find the Least Common Denominator of Rational Expressions

In the following exercises, find the LCD.

Add and Subtract Rational Expressions with Unlike Denominators

Add and Subtract Rational Functions

Simplify Complex Rational Expressions

Simplify a Complex Rational Expression by Writing It as Division

Simplify a Complex Rational Expression by Using the LCD

7.4 Solve Rational Equations

Solve Rational Equations

In the following exercises, solve.

no solution

Solve Rational Equations that Involve Functions

Solve a Rational Equation for a Specific Variable

In the following exercises, solve for the indicated variable.

Solve Applications with Rational Equations

Solve Proportions

Solve Using Proportions

Rachael had a 21-ounce strawberry shake that has 739 calories. How many calories are there in a 32-ounce shake?

Leo went to Mexico over Christmas break and changed ?525 dollars into Mexican pesos. At that time, the exchange rate had ?1 US is equal to 16.25 Mexican pesos. How many Mexican pesos did he get for his trip?

Solve Similar Figure Applications

On a map of Europe, Paris, Rome, and Vienna form a triangle whose sides are shown in the figure below. If the actual distance from Rome to Vienna is 700 miles, find the distance from

ⓐ Paris to Rome

ⓑ Paris to Vienna

Francesca is 5.75 feet tall. Late one afternoon, her shadow was 8 feet long. At the same time, the shadow of a nearby tree was 32 feet long. Find the height of the tree.

The height of a lighthouse in Pensacola, Florida is 150 feet. Standing next to the statue, 5.5-foot-tall Natasha cast a 1.1-foot shadow. How long would the shadow of the lighthouse be?

Solve Uniform Motion Applications

When making the 5-hour drive home from visiting her parents, Lolo ran into bad weather. She was able to drive 176 miles while the weather was good, but then driving 10 mph slower, went 81 miles when it turned bad. How fast did she drive when the weather was bad?

Mark is riding on a plane that can fly 490 miles with a tailwind of 20 mph in the same time that it can fly 350 miles against a tailwind of 20 mph. What is the speed of the plane?

Josue can ride his bicycle 8 mph faster than Arjun can ride his bike. It takes Luke 3 hours longer than Josue to ride 48 miles. How fast can John ride his bike?

Curtis was training for a triathlon. He ran 8 kilometers and biked 32 kilometers in a total of 3 hours. His running speed was 8 kilometers per hour less than his biking speed. What was his running speed?

Solve Work Applications

Brandy can frame a room in 1 hour, while Jake takes 4 hours. How long could they frame a room working together?

Prem takes 3 hours to mow the lawn while her cousin, Barb, takes 2 hours. How long will it take them working together?

Jeffrey can paint a house in 6 days, but if he gets a helper he can do it in 4 days. How long would it take the helper to paint the house alone?

Marta and Deb work together writing a book that takes them 90 days. If Sue worked alone it would take her 120 days. How long would it take Deb to write the book alone?

Solve Direct Variation Problems

If the cost of a pizza varies directly with its diameter, and if an 8” diameter pizza costs ?12, how much would a 6” diameter pizza cost?

The distance to stop a car varies directly with the square of its speed. It takes 200 feet to stop a car going 50 mph. How many feet would it take to stop a car going 60 mph?

Solve Inverse Variation Problems

The number of tickets for a music fundraiser varies inversely with the price of the tickets. If Madelyn has just enough money to purchase 12 tickets for ?6, how many tickets can Madelyn afford to buy if the price increased to ?8?

On a string instrument, the length of a string varies inversely with the frequency of its vibrations. If an 11-inch string on a violin has a frequency of 360 cycles per second, what frequency does a 12-inch string have?

In the following exercises, solve each rational function inequality and write the solution in interval notation

The function

Practice Test

In the following exercises, perform the indicated operation and simplify.

In the following exercises, solve each equation.

Given the function,

Matheus can ride his bike for 30 miles with the wind in the same amount of time that he can go 21 miles against the wind. If the wind’s speed is 6 mph, what is Matheus’ speed on his bike?

Oliver can split a truckload of logs in 8 hours, but working with his dad they can get it done in 3 hours. How long would it take Oliver’s dad working alone to split the logs?

The volume of a gas in a container varies inversely with the pressure on the gas. If a container of nitrogen has a volume of 29.5 liters with 2000 psi, what is the volume if the tank has a 14.7 psi rating? Round to the nearest whole number.

The cities of Dayton, Columbus, and Cincinnati form a triangle in southern Ohio. The diagram gives the map distances between these cities in inches.

The actual distance from Dayton to Cincinnati is 48 miles. What is the actual distance between Dayton and Columbus?

The distance between Dayton and Columbus is 64 miles.

Intermediate Algebra Copyright © 2017 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Module 1: Equations and Inequalities

▪ solving rational inequalities, learning outcomes.

• Solve rational inequalities using boundary value method.

Solving Rational Inequalities using Boundary Value Method

Any inequality that can be put into one of the following forms

[latex]f(x)>0, f(x) \geq 0, f(x)<0, or f(x) \leq 0[/latex], where [latex]f[/latex] is a rational function

is called rational inequality .

How To: Solve Rational Inequalities

• Find restriction(s) of the given rational expression(s) in the inequality. The restriction(s) is(are) the boundary point(s) .
• Rewrite the given rational inequality as an equation by replacing the inequality symbol with the equal sign.
• Solve the rational equation. The real solution(s) of the equation is(are) the boundary point(s) .
• Plot the boundary point(s) from Step 1 & 3 on a number line. [latex] \Rightarrow [/latex] Use an open circle ALL restrictions. [latex] \Rightarrow [/latex] Use an open circle when the given inequality has [latex]<[/latex] or [latex]>[/latex] [latex]\Rightarrow[/latex] Use a closed circle when the given inequality has [latex]\leq[/latex] or [latex]\geq[/latex].
• Choose one number, which is called a test value , from each interval and test the intervals by evaluating the given inequality at that number. [latex]\Rightarrow[/latex] If the inequality is TRUE, then the interval is a solution of the inequality. [latex]\Rightarrow[/latex] If the inequality is FALSE, then the interval is not a solution of the inequality.
• Write the solution set (usually in interval notation), selecting the interval(s) from Step 5.

Example: Solving Rational Inequality using Boundary Value Method

Solve the rational inequality using boundary value method. Graph the solution set and write the solution in interval notation.

[latex]\frac{2x-1}{x+2} > 1[/latex]

First, find restriction(s):

[latex]x+2 \ne 0[/latex]

[latex]x \ne -2[/latex]

Second, let’s rewrite the inequality as an equation and then solve it:

[latex]\frac{2x-1}{x+2} = 1[/latex]

[latex]\frac{2x-1}{x+2} = \frac{1}{1}[/latex]

[latex]2x-1=x+2[/latex]

[latex]x=3[/latex]

Third, plot the restriction and the solution on the number line. All restrictions should be an  open circle. Since the inequality has “[latex]>[/latex]” (greater than), which doesn’t have “[latex]=[/latex]” (equal sign), the solution should be an  open circle as well:

Note that now there are three intervals on the number line: [latex](-\infty, -2), (-2, 3),[/latex] and [latex](3, \infty)[/latex].

Fourth, choose your choice of test value from each interval:

I chose [latex]-3, 0,[/latex] and [latex]4[/latex] from those three intervals.

fifth, test each interval using the test value:

When [latex]x=-3[/latex], [latex]\frac{2(-3)-1}{(-3)+2} > 1 \rightarrow \frac{-7}{-1}>1 \rightarrow 7>1[/latex]  (True)   [latex]\therefore[/latex] solution

When [latex]x=-3[/latex], [latex]\frac{2(0)-1}{(0)+2} > 1 \rightarrow \frac{-1}{2}>1 \rightarrow -\frac{1}{2}>1[/latex]  (False)   [latex]\therefore[/latex] not a solution

When [latex]x=4[/latex], [latex]\frac{2(4)-1}{(4)+2} > 1 \rightarrow \frac{7}{6}>1[/latex]  (True)   [latex]\therefore[/latex] solution

Actually, we can check the results of test values from the graph of [latex]f(x)=\frac{2x-1}{x+2}-1[/latex] below:

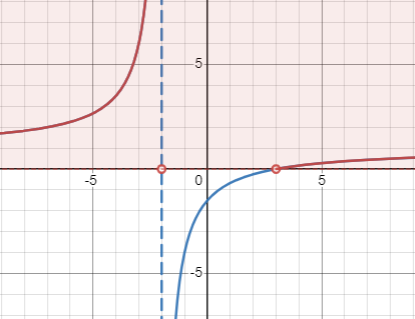
Therefore, the solution of the rational inequality [latex]\frac{2x-1}{x+2} > 1[/latex] is [latex](-\infty, -2) \cup (3, \infty)[/latex].

[latex]\frac{5x}{x-3} \leq 2[/latex]

[latex]x-3 \ne 0[/latex]

[latex]x \ne 3[/latex]

[latex]\frac{5x}{x-3}=2[/latex]

[latex]\frac{5x}{x-3} = \frac{2}{1}[/latex]

[latex]5x=2(x-3)[/latex]

[latex]5x=2x-6[/latex]

[latex]3x=-6[/latex]

[latex]x=-2[/latex]

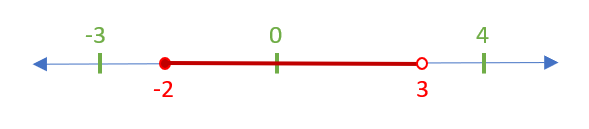
Third, plot the restriction and the solution on the number line. All restrictions should be an  open circle. Since the inequality has “[latex]\leq[/latex]” (less than or equal to), which has “[latex]=[/latex]” (equal sign), the solution should be a  closed circle:

Note that now there are three intervals on the number line: [latex](-\infty, -2], [-2, 3),[/latex] and [latex](3, \infty)[/latex].

When [latex]x=-3[/latex], [latex]\frac{5(-3)}{(-3)-3} \leq 2 \rightarrow \frac{-15}{-6} \leq 2 \rightarrow 2.5 \leq 2[/latex]  (False)   [latex]\therefore[/latex] not a solution

When [latex]x=0[/latex], [latex]\frac{5(0)}{(0)-3} \leq 2 \rightarrow \frac{0}{-3} \leq 2 \rightarrow 0 \leq 2[/latex]  (True)   [latex]\therefore[/latex] solution

When [latex]x=4[/latex], [latex]\frac{5(4)}{(4)-3} \leq 2 \rightarrow \frac{20}{1} \leq 2 \rightarrow 20 \leq 2[/latex]  (False)   [latex]\therefore[/latex] not a solution

Actually, we can check the results of test values from the graph of [latex]f(x)=\frac{5x}{x-3}-2[/latex] below:

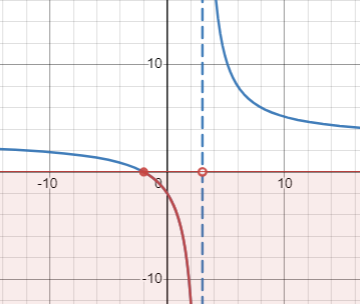
Therefore, the solution of the rational inequality [latex]\frac{5x}{x-3} \leq 2[/latex] is [latex][-2, 3)[/latex].

[latex]\frac{4x-5}{x+1} \geq 0[/latex]

[latex]x+1 \ne 0[/latex]

[latex]x \ne -1[/latex]

[latex]\frac{4x-5}{x+1}=0[/latex]

[latex]\frac{4x-5}{x+1} = \frac{0}{1}[/latex]

[latex]4x-5=0[/latex]

[latex]4x=5[/latex]

[latex]x=\frac{5}{4}[/latex]

Third, plot the restriction and the solution on the number line. All restrictions should be an  open circle. Since the inequality has “[latex]\geq[/latex]” (greater than or equal to), which has “[latex]=[/latex]” (equal sign), the solution should be a  closed circle:

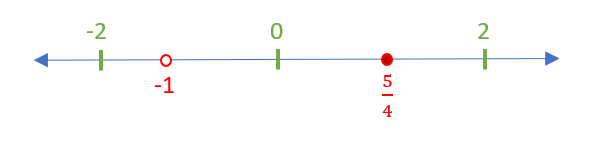
Note that now there are three intervals on the number line: [latex](-\infty, -1), (-1, \frac{5}{4}],[/latex] and [latex][\frac{5}{4}, \infty)[/latex].

I chose [latex]-2, 0,[/latex] and [latex]2[/latex] from those three intervals.

When [latex]x=-2[/latex], [latex]\frac{4(-2)-5}{(-2)+1} \geq 0 \rightarrow \frac{-13}{-1} \geq 0 \rightarrow 13 \geq 0[/latex]  (True)   [latex]\therefore[/latex] solution

When [latex]x=0[/latex], [latex]\frac{4(0)-5}{(0)+1} \geq 0 \rightarrow \frac{-5}{1} \geq 0 \rightarrow -5 \geq 0[/latex]  (False)   [latex]\therefore[/latex] not a solution

When [latex]x=2[/latex], [latex]\frac{4(2)-5}{(2)+1} \geq 0 \rightarrow \frac{3}{3} \geq 0 \rightarrow 1 \geq 0[/latex]  (True)   [latex]\therefore[/latex] solution

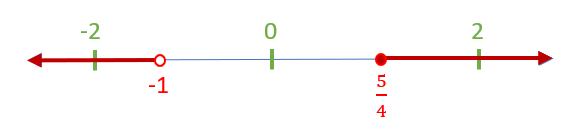
Actually, we can check the results of test values from the graph of [latex]f(x)=\frac{4x-5}{x+1}[/latex] below:

Therefore, the solution of the rational inequality [latex]\frac{4x-5}{x+1} \geq 0[/latex] is [latex](-\infty, -1) \cup [\frac{5}{4}, \infty)[/latex].

• Solving Rational Inequalities. Authored by : Michelle Eunhee Chung. Provided by : Georgia State University. License : CC BY: Attribution

Privacy Policy

Free Mathematics Tutorials

Solve Rational Inequalities Examples With Solutions

Rational Inequalities are solved in the examples below. Knowing that the sign of an algebraic expression changes at its zeros of odd multiplicity, solving an inequality may be reduced to finding the sign of an algebraic expression within intervals defined by the zeros of the expression in question.

Solve the following inequalities

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}

step-by-step

rational inequalities

• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.3: Rational Inequalities and Applications

• Last updated
• Save as PDF
• Page ID 80779

• Carl Stitz & Jeff Zeager
• Lakeland Community College & Lorain County Community College

In this section, we solve equations and inequalities involving rational functions and explore associated application problems. Our first example showcases the critical difference in procedure between solving a rational equation and a rational inequality.

Example 4.3.1

• Solve \(\dfrac{x^3-2x+1}{x-1} = \dfrac{1}{2}x-1\).
• Solve \(\dfrac{x^3-2x+1}{x-1} \geq \dfrac{1}{2}x-1\).
• Use your calculator to graphically check your answers to 1 and 2.

\[\begin{array}{rclr} \dfrac{x^3-2x+1}{x-1} & = & \dfrac{1}{2}x-1 & \\[4pt] \left(\dfrac{x^3-2x+1}{x-1}\right) \cdot 2(x-1) & = & \left( \dfrac{1}{2}x-1 \right) \cdot 2(x-1) & \\[4pt] 2x^3 - 4x + 2 & = & x^2-3x+2 & \mbox{expand} \\ 2x^3 -x^2 - x & = & 0 & \\ x(2x+1)(x-1) & = & 0 & \mbox{factor}\\ x & = & -\frac{1}{2}, \, 0, \, 1 & \\ \end{array}\nonumber\]

Since we cleared denominators, we need to check for extraneous solutions. Sure enough, we see that \(x=1\) does not satisfy the original equation and must be discarded. Our solutions are \(x=-\frac{1}{2}\) and \(x=0\).

\[\begin{array}{rclr} \dfrac{x^3-2x+1}{x-1} & \geq & \dfrac{1}{2}x-1 & \\[4pt] \dfrac{x^3-2x+1}{x-1} - \dfrac{1}{2} x + 1& \geq & 0& \\[4pt] \dfrac{2\left(x^3-2x+1\right)-x(x-1)+1(2(x-1))}{2(x-1)} & \geq & 0 & \mbox{get a common denominator} \\[4pt] \dfrac{2x^3-x^2-x}{2x-2} & \geq & 0 & \mbox{expand} \\ \end{array}\nonumber\]

Viewing the left hand side as a rational function \(r(x)\) we make a sign diagram. The only value excluded from the domain of \(r\) is \(x=1\) which is the solution to \(2x-2=0\). The zeros of \(r\) are the solutions to \(2x^3-x^2-x=0\), which we have already found to be \(x=0\), \(x=-\frac{1}{2}\) and \(x=1\), the latter was discounted as a zero because it is not in the domain. Choosing test values in each test interval, we construct the sign diagram below.

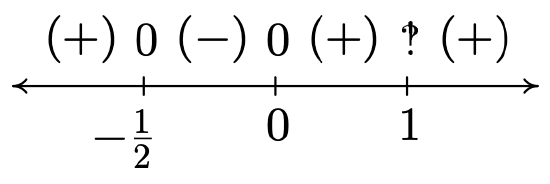
We are interested in where \(r(x) \geq 0\). We find \(r(x) > 0\), or \((+)\), on the intervals \(\left(-\infty, -\frac{1}{2}\right)\), \((0,1)\) and \((1, \infty)\). We add to these intervals the zeros of \(r\), \(-\frac{1}{2}\) and \(0\), to get our final solution: \(\left( - \infty, -\frac{1}{2} \right] \cup [0,1) \cup (1, \infty)\).

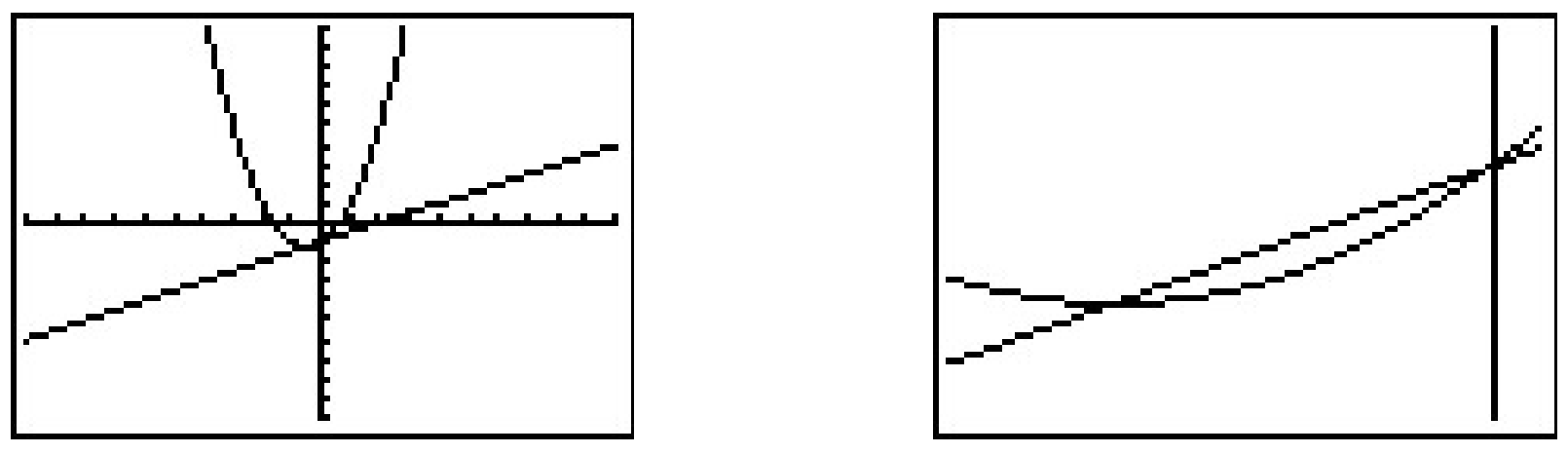
The ‘Intersect’ command confirms that the graphs cross when \(x=-\frac{1}{2}\) and \(x=0\). It is clear from the calculator that the graph of \(y=f(x)\) is above the graph of \(y=g(x)\) on \(\left(-\infty, -\frac{1}{2}\right)\) as well as on \((0,\infty)\). According to the calculator, our solution is then \(\left(-\infty, -\frac{1}{2}\right] \cup [0, \infty)\) which almost matches the answer we found analytically. We have to remember that \(f\) is not defined at \(x=1\), and, even though it isn’t shown on the calculator, there is a hole 1 in the graph of \(y=f(x)\) when \(x=1\) which is why \(x=1\) is not part of our final answer.

Next, we explore how rational equations can be used to solve some classic problems involving rates.

Example 4.3.2

Carl decides to explore the Meander River, the location of several recent Sasquatch sightings. From camp, he canoes downstream five miles to check out a purported Sasquatch nest. Finding nothing, he immediately turns around, retraces his route (this time traveling upstream), and returns to camp 3 hours after he left. If Carl canoes at a rate of 6 miles per hour in still water, how fast was the Meander River flowing on that day?

We are given information about distances, rates (speeds) and times. The basic principle relating these quantities is: \[\text{distance} = \text{rate} \cdot \text{time}\nonumber\] The first observation to make, however, is that the distance, rate and time given to us aren’t ‘compatible’: the distance given is the distance for only part of the trip, the rate given is the speed Carl can canoe in still water, not in a flowing river, and the time given is the duration of the entire trip. Ultimately, we are after the speed of the river, so let’s call that \(R\) measured in miles per hour to be consistent with the other rate given to us. To get started, let’s divide the trip into its two parts: the initial trip downstream and the return trip upstream. For the downstream trip, all we know is that the distance traveled is \(5\) miles.

\[\begin{array}{rcl} \text{distance downstream} & = & \text{rate traveling downstream} \cdot \text{time traveling downstream} \\ 5 \, \text{miles} & = & \text{rate traveling downstream} \cdot \text{time traveling downstream} \\ \end{array}\nonumber\]

Since the return trip upstream followed the same route as the trip downstream, we know that the distance traveled upstream is also 5 miles.

\[\begin{array}{rcl} \text{distance upstream} & = & \text{rate traveling upstream} \cdot \text{time traveling upstream} \\ 5 \, \text{miles} & = & \text{rate traveling upstream} \cdot \text{time traveling upstream} \\ \end{array}\nonumber\]

We are told Carl can canoe at a rate of \(6\) miles per hour in still water. How does this figure into the rates traveling upstream and downstream? The speed the canoe travels in the river is a combination of the speed at which Carl can propel the canoe in still water, 6 miles per hour, and the speed of the river, which we’re calling \(R\). When traveling downstream, the river is helping Carl along, so we add these two speeds:

\[\begin{array}{rcl} \text{rate traveling downstream} & = & \text{rate Carl propels the canoe} + \text{speed of the river} \\ & = & 6 \frac{\text{miles}}{\text{hour}} + R \frac{\text{miles}}{\text{hour}} \\ \end{array}\nonumber\]

So our downstream speed is \((6+R) \frac{\text{miles}}{\text{hour}}\). Substituting this into our ‘distance-rate-time’ equation for the downstream part of the trip, we get:

\[\begin{array}{rcl} 5 \, \text{miles} & = & \text{rate traveling downstream} \cdot \text{time traveling downstream} \\ 5 \, \text{miles} & = & (6+R) \frac{\text{miles}}{\text{hour}} \cdot \text{time traveling downstream} \\ \end{array}\nonumber\]

When traveling upstream, Carl works against the current. Since the canoe manages to travel upstream, the speed Carl can canoe in still water is greater than the river’s speed, so we subtract the river’s speed from Carl’s canoing speed to get:

\[\begin{array}{rcl} \text{rate traveling upstream} & = & \text{rate Carl propels the canoe} - \text{river speed} \\ & = & 6 \frac{\text{miles}}{\text{hour}} - R \frac{\text{miles}}{\text{hour}} \\ \end{array}\nonumber\]

Proceeding as before, we get

\[\begin{array}{rcl} 5 \, \text{miles} & = & \text{rate traveling upstream} \cdot \text{time traveling upstream} \\ 5 \, \text{miles} & = & (6 - R) \frac{\text{miles}}{\text{hour}} \cdot \text{time traveling upstream} \\ \end{array}\nonumber\]

The last piece of information given to us is that the total trip lasted \(3\) hours. If we let \(t_{\text{down}}\) denote the time of the downstream trip and \(t_{\text{up}}\) the time of the upstream trip, we have: \(t_{\text{down}} + t_{\text{up}} = 3 \, \text{hours}\). Substituting \(t_{\text{down}}\) and \(t_{\text{up}}\) into the ‘distance-rate-time’ equations, we get (suppressing the units) three equations in three unknowns: 2 \[\left\{\begin{array}{lrcl} E1 & (6+R) \, t_{\text{down}} & = & 5 \\ E2 & (6-R) \, t_{\text{up}} & = & 5 \\ E3 & t_{\text{down}} + t_{\text{up}} & = & 3 \end{array} \right.\nonumber\]

Since we are ultimately after \(R\), we need to use these three equations to get at least one equation involving only \(R\). To that end, we solve \(E1\) for \(t_{\text{down}}\) by dividing both sides 3 by the quantity \((6+R)\) to get \(t_{\text{down}} = \frac{5}{6+R}\). Similarly, we solve \(E2\) for \(t_{\text{up}}\) and get \(t_{\text{up}} = \frac{5}{6-R}\). Substituting these into \(E3\), we get: 4 \[\dfrac{5}{6+R} + \dfrac{5}{6 - R} = 3.\nonumber\] Clearing denominators, we get \(5(6-R) + 5(6+R) = 3(6+R)(6-R)\) which reduces to \(R^2 = 16\). We find \(R = \pm 4\), and since \(R\) represents the speed of the river, we choose \(R = 4\). On the day in question, the Meander River is flowing at a rate of \(4\) miles per hour.

One of the important lessons to learn from Example 4.3.2 is that speeds, and more generally, rates, are additive. As we see in our next example, the concept of rate and its associated principles can be applied to a wide variety of problems - not just ‘distance-rate-time’ scenarios.

Example 4.3.3

Working alone, Taylor can weed the garden in 4 hours. If Carl helps, they can weed the garden in 3 hours. How long would it take for Carl to weed the garden on his own?

The key relationship between work and time which we use in this problem is: \[\text{amount of work done} = \text{rate of work} \cdot \text{time spent working}\nonumber\]

We are told that, working alone, Taylor can weed the garden in 4 hours. In Taylor’s case then: \[\begin{array}{rcl} \text{amount of work Taylor does} & = & \text{rate of Taylor working} \cdot \text{time Taylor spent working} \\ 1 \, \text{garden} & = & (\text{rate of Taylor working}) \cdot (4 \, \text{hours}) \\ \end{array}\nonumber\]

So we have that the rate Taylor works is \(\frac{1 \, \text{garden}}{ 4 \, \text{hours}} = \frac{1}{4} \frac{\text{garden}}{\text{hour}}\). We are also told that when working together, Taylor and Carl can weed the garden in just 3 hours. We have:

\[\begin{array}{rcl} \text{amount of work done together} & = & \text{rate of working together} \cdot \text{time spent working together} \\ 1 \, \text{garden} & = & (\text{rate of working together}) \cdot (3 \, \text{hours}) \\ \end{array}\nonumber\]

From this, we find that the rate of Taylor and Carl working together is \(\frac{1 \, \text{garden}}{3 \, \text{hours}} = \frac{1}{3} \frac{\text{garden}}{\text{hour}}\). We are asked to find out how long it would take for Carl to weed the garden on his own. Let us call this unknown \(t\), measured in hours to be consistent with the other times given to us in the problem. Then:

\[\begin{array}{rcl} \text{amount of work Carl does} & = & \text{rate of Carl working} \cdot \text{time Carl spent working} \\ 1 \, \text{garden} & = & (\text{rate of Carl working}) \cdot (t \, \text{hours}) \\ \end{array}\nonumber\]

In order to find \(t\), we need to find the rate of Carl working, so let’s call this quantity \(R\), with units \(\frac{\text{garden}}{\text{hour}}\). Using the fact that rates are additive, we have:

\[\begin{array}{rcl} \text{rate working together} & = & \text{rate of Taylor working} + \text{rate of Carl working} \\[4pt] \frac{1}{3} \frac{\text{garden}}{\text{hour}} & = & \frac{1}{4} \frac{\text{garden}}{\text{hour}} + R \frac{\text{garden}}{\text{hour}} \\ \end{array}\nonumber\]

so that \(R = \frac{1}{12} \frac{\text{garden}}{\text{hour}}\). Substituting this into our ‘work-rate-time’ equation for Carl, we get:

\[\begin{array}{rcl} 1 \, \text{garden} & = & (\text{rate of Carl working}) \cdot (t \, \text{hours}) \\[4pt] 1 \, \text{garden} & = & \left(\frac{1}{12} \frac{\text{garden}}{\text{hour}} \right) \cdot (t \, \text{hours}) \\ \end{array}\nonumber\]

Solving \(1 = \frac{1}{12} t\), we get \(t = 12\), so it takes Carl 12 hours to weed the garden on his own. 5

As is common with ‘word problems’ like Examples 4.3.2 and 4.3.3 , there is no short-cut to the answer. We encourage the reader to carefully think through and apply the basic principles of rate to each (potentially different!) situation. It is time well spent. We also encourage the tracking of units, especially in the early stages of the problem. Not only does this promote uniformity in the units, it also serves as a quick means to check if an equation makes sense. 6

Our next example deals with the average cost function, first introduced on page 82, as applied to PortaBoy Game systems from Example 2.1.5 in Section 2.1 .

Example 4.3.4

Given a cost function \(C(x)\), which returns the total cost of producing \(x\) items, recall that the average cost function, \(\overline{C}(x) = \frac{C(x)}{x}\) computes the cost per item when \(x\) items are produced. Suppose the cost \(C\), in dollars, to produce \(x\) PortaBoy game systems for a local retailer is \(C(x) = 80x + 150\), \(x \geq 0\).

• Find an expression for the average cost function \(\overline{C}(x)\).
• Solve \(\overline{C}(x) < 100\) and interpret.
• Determine the behavior of \(\overline{C}(x)\) as \(x \rightarrow \infty\) and interpret.
• From \(\overline{C}(x) = \frac{C(x)}{x}\), we obtain \(\overline{C}(x) = \frac{80x+150}{x}\). The domain of \(C\) is \(x \geq 0\), but since \(x=0\) causes problems for \(\overline{C}(x)\), we get our domain to be \(x>0\), or \((0, \infty)\).

\[\begin{array}{rclr} \dfrac{80x+150}{x} & < & 100 & \\[4pt] \dfrac{80x+150}{x} - 100 & < & 0 & \\[4pt] \dfrac{80x + 150 - 100x}{x} & < & 0 & \mbox{common denominator} \\[4pt] \dfrac{150 - 20x}{x} & < & 0 & \\ \end{array}\nonumber\]

If we take the left hand side to be a rational function \(r(x)\), we need to keep in mind that the applied domain of the problem is \(x > 0\). This means we consider only the positive half of the number line for our sign diagram. On \((0, \infty)\), \(r\) is defined everywhere so we need only look for zeros of \(r\). Setting \(r(x)=0\) gives \(150-20x =0\), so that \(x = \frac{15}{2}= 7.5\). The test intervals on our domain are \((0, 7.5)\) and \((7.5, \infty)\). We find \(r(x) < 0\) on \((7.5, \infty)\).

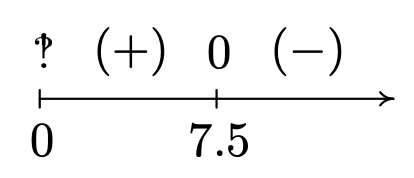
In the context of the problem, \(x\) represents the number of PortaBoy games systems produced and \(\overline{C}(x)\) is the average cost to produce each system. Solving \(\overline{C}(x) < 100\) means we are trying to find how many systems we need to produce so that the average cost is less than \(\$100\) per system. Our solution, \((7.5, \infty)\) tells us that we need to produce more than \(7.5\) systems to achieve this. Since it doesn’t make sense to produce half a system, our final answer is \([8, \infty)\).

• When we apply Theorem 4.2 to \(\overline{C}(x)\) we find that \(y=80\) is a horizontal asymptote to the graph of \(y=\overline{C}(x)\). To more precisely determine the behavior of \(\overline{C}(x)\) as \(x \rightarrow \infty\), we first use long division 7 and rewrite \(\overline{C}(x) = 80+\frac{150}{x}\). As \(x \rightarrow \infty\), \(\frac{150}{x} \rightarrow 0^{+}\), which means \(\overline{C}(x) \approx 80+\text { very small }(+)\). Thus the average cost per system is getting closer to \(\$ 80\) per system. If we set \(\overline{C}(x) = 80\), we get \(\frac{150}{x} = 0\), which is impossible, so we conclude that \(\overline{C}(x) > 80\) for all \(x > 0\). This means that the average cost per system is always greater than \(\$ 80\) per system, but the average cost is approaching this amount as more and more systems are produced. Looking back at Example 2.1.5 , we realize \(\$ 80\) is the variable cost per system \(-\) the cost per system above and beyond the fixed initial cost of \(\$150\). Another way to interpret our answer is that ‘infinitely’ many systems would need to be produced to effectively ‘zero out’ the fixed cost.

Our next example is another classic ‘box with no top’ problem.

Example 4.3.5

A box with a square base and no top is to be constructed so that it has a volume of \(1000\) cubic centimeters. Let \(x\) denote the width of the box, in centimeters as seen below.

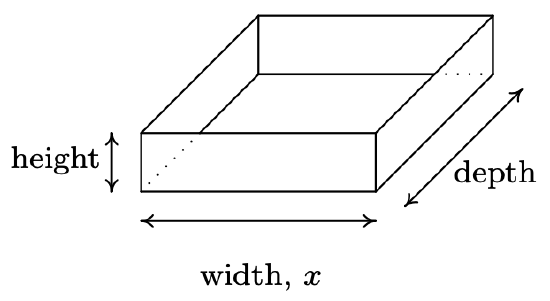
• Express the height \(h\) in centimeters as a function of the width \(x\) and state the applied domain.
• Solve \(h(x) \geq x\) and interpret.
• Find and interpret the behavior of \(h(x)\) as \(x \rightarrow 0^{+}\) and as \(x \rightarrow \infty\).
• Express the surface area \(S\) of the box as a function of \(x\) and state the applied domain.
• Use a calculator to approximate (to two decimal places) the dimensions of the box which minimize the surface area.
• We are told that the volume of the box is \(1000\) cubic centimeters and that \(x\) represents the width, in centimeters. From geometry, we know \(\mbox{Volume} = \mbox{width} \times \mbox{height} \times \mbox{depth}\). Since the base of the box is a square, the width and the depth are both \(x\) centimeters. Using \(h\) for the height, we have \(1000 = x^2h\), so that \(h = \frac{1000}{x^2}\). Using function notation, 8 \(h(x) = \frac{1000}{x^2}\) As for the applied domain, in order for there to be a box at all, \(x > 0\), and since every such choice of \(x\) will return a positive number for the height \(h\) we have no other restrictions and conclude our domain is \((0, \infty)\).

\[\begin{array}{rclr} h(x) & \geq & x & \\[4pt] \dfrac{1000}{x^2} & \geq & x & \\[4pt] \dfrac{1000}{x^2} - x & \geq & 0 \\[4pt] \dfrac{1000-x^3}{x^2} & \geq & 0 & \mbox{common denominator} \\[10pt] \end{array}\nonumber\]

We consider the left hand side of the inequality as our rational function \(r(x)\). We see \(r\) is undefined at \(x=0\), but, as in the previous example, the applied domain of the problem is \(x > 0\), so we are considering only the behavior of \(r\) on \((0, \infty)\). The sole zero of \(r\) comes when \(1000-x^3 = 0\), which is \(x=10\). Choosing test values in the intervals \((0,10)\) and \((10, \infty)\) gives the following diagram.

We see \(r(x) > 0\) on \((0,10)\), and since \(r(x) = 0\) at \(x=10\), our solution is \((0,10]\). In the context of the problem, \(h\) represents the height of the box while \(x\) represents the width (and depth) of the box. Solving \(h(x) \geq x\) is tantamount to finding the values of \(x\) which result in a box where the height is at least as big as the width (and, in this case, depth.) Our answer tells us the width of the box can be at most \(10\) centimeters for this to happen.

• As \(x \rightarrow 0^{+}\), \(h(x) = \frac{1000}{x^2} \rightarrow \infty\). This means that the smaller the width \(x\) (and, in this case, depth), the larger the height \(h\) has to be in order to maintain a volume of \(1000\) cubic centimeters. As \(x \rightarrow \infty\), we find \(h(x) \rightarrow 0^{+}\), which means that in order to maintain a volume of \(1000\) cubic centimeters, the width and depth must get bigger as the height becomes smaller.
• Since the box has no top, the surface area can be found by adding the area of each of the sides to the area of the base. The base is a square of dimensions \(x\) by \(x\), and each side has dimensions \(x\) by \(h\). We get the surface area, \(S = x^2+4xh\). To get \(S\) as a function of \(x\), we substitute \(h = \frac{1000}{x^2}\) to obtain \(S = x^2+4x \left( \frac{1000}{x^2}\right)\). Hence, as a function of \(x\), \(S(x) = x^2 + \frac{4000}{x}\). The domain of \(S\) is the same as \(h\), namely \((0, \infty)\), for the same reasons as above.
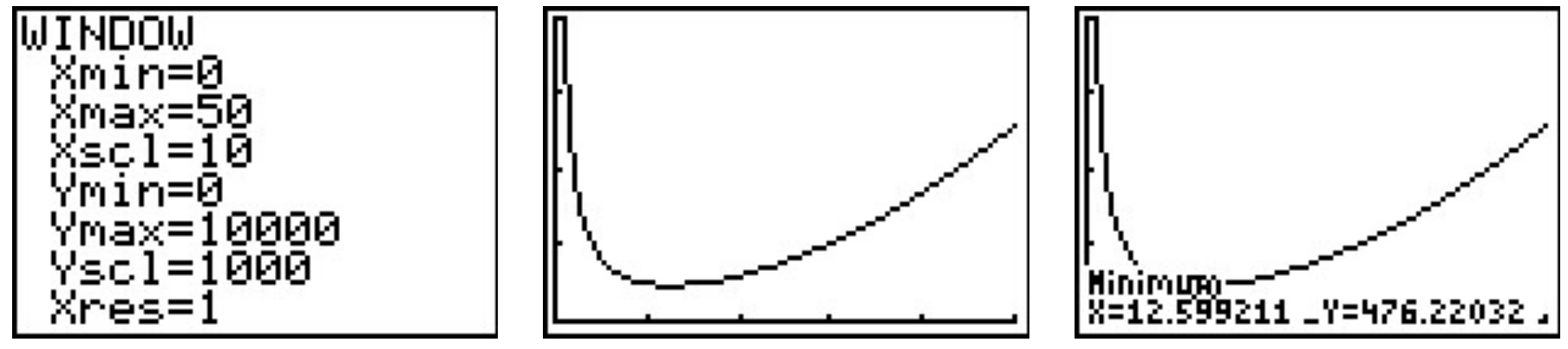
• A first attempt at the graph of \(y=S(x)\) on the calculator may lead to frustration. Chances are good that the first window chosen to view the graph will suggest \(y=S(x)\) has the \(x\)-axis as a horizontal asymptote. From the formula \(S(x) = x^2 + \frac{4000}{x}\), however, we get \(S(x) \approx x^2\) as \(x \rightarrow \infty\), so \(S(x) \rightarrow \infty\). Readjusting the window, we find \(S\) does possess a relative minimum at \(x \approx 12.60\). As far as we can tell, 9 this is the only relative extremum, so it is the absolute minimum as well. This means that the width and depth of the box should each measure approximately \(12.60\) centimeters. To determine the height, we find \(h(12.60) \approx 6.30\), so the height of the box should be approximately \(6.30\) centimeters.

4.3.1 Variation

In many instances in the sciences, rational functions are encountered as a result of fundamental natural laws which are typically a result of assuming certain basic relationships between variables. These basic relationships are summarized in the definition below.

Definition 4.5

Suppose \(x\), \(y\) and \(z\) are variable quantities. We say

• \(y\) varies directly with (or is directly proportional to ) \(x\) if there is a constant \(k\) such that \(y=kx\).
• \(y\) varies inversely with (or is inversely proportional to ) \(x\) if there is a constant \(k\) such that \(y=\frac{k}{x}\).
• \(z\) varies jointly with (or is jointly proportional to ) \(x\) and \(y\) if there is a constant \(k\) such that \(z = kxy\).

The constant \(k\) in the above definitions is called the constant of proportionality .

Example 4.3.6

Translate the following into mathematical equations using Definition 4.5 .

• Hooke’s Law : The force \(F\) exerted on a spring is directly proportional the extension \(x\) of the spring.
• Boyle’s Law : At a constant temperature, the pressure \(P\) of an ideal gas is inversely proportional to its volume \(V\).
• The volume \(V\) of a right circular cone varies jointly with the height \(h\) of the cone and the square of the radius \(r\) of the base.
• Ohm’s Law : The current \(I\) through a conductor between two points is directly proportional to the voltage \(V\) between the two points and inversely proportional to the resistance \(R\) between the two points.
• Newton’s Law of Universal Gravitation : Suppose two objects, one of mass \(m\) and one of mass \(M\), are positioned so that the distance between their centers of mass is \(r\). The gravitational force \(F\) exerted on the two objects varies directly with the product of the two masses and inversely with the square of the distance between their centers of mass.
• Applying the definition of direct variation, we get \(F = k x\) for some constant \(k\).
• Since \(P\) and \(V\) are inversely proportional, we write \(P = \frac{k}{V}\).
• There is a bit of ambiguity here. It’s clear that the volume and the height of the cone are represented by the quantities \(V\) and \(h\), respectively, but does \(r\) represent the radius of the base or the square of the radius of the base? It is the former. Usually, if an algebraic operation is specified (like squaring), it is meant to be expressed in the formula. We apply Definition 4.5 to get \(V = k h r^{2}\).
• Even though the problem doesn’t use the phrase ‘varies jointly’, it is implied by the fact that the current \(I\) is related to two different quantities. Since \(I\) varies directly with \(V\) but inversely with \(R\), we write \(I = \frac{k V}{R}\).
• We write the product of the masses \(mM\) and the square of the distance as \(r^2\). We have that \(F\) varies directly with \(mM\) and inversely with \(r^2\), so \(F = \frac{kmM}{r^2}\).

In many of the formulas in the previous example, more than two varying quantities are related. In practice, however, usually all but two quantities are held constant in an experiment and the data collected is used to relate just two of the variables. Comparing just two varying quantities allows us to view the relationship between them as functional, as the next example illustrates.

Example 4.3.7

According to this website the actual data relating the volume \(V\) of a gas and its pressure \(P\) used by Boyle and his assistant in 1662 to verify the gas law that bears his name is given below.

\[\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline V & 48 & 46 & 44 & 42 & 40 & 38 & 36 & 34 & 32 & 30 & 28 & 26 & 24 \\ \hline P & 29.13 & 30.56 & 31.94 & 33.5 & 35.31 & 37 & 39.31 & 41.63 & 44.19 & 47.06 & 50.31 & 54.31 & 58.81 \\ \hline \end{array}\nonumber\]

\[\begin{array}{|c||c||c|c|c|c|c|c|c|c|c|c|c|c|} \hline V & 23 & 22 & 21 & 20 & 19 & 18 & 17 & 16 & 15 & 14 & 13 & 12 \\ \hline P & 61.31 & 64.06 & 67.06 & 70.69 & 74.13 & 77.88 & 82.75 & 87.88 & 93.06 & 100.44 & 107.81 & 117.56 \\ \hline \end{array}\nonumber\]

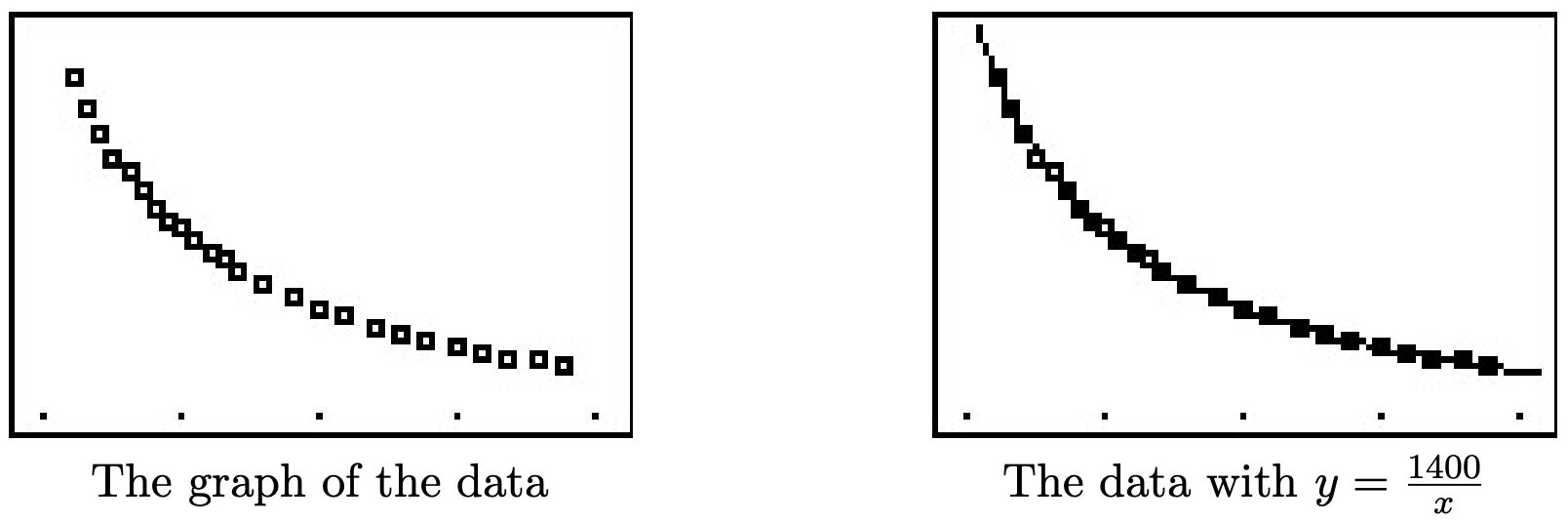
• Use your calculator to generate a scatter diagram for these data using \(V\) as the independent variable and \(P\) as the dependent variable. Does it appear from the graph that \(P\) is inversely proportional to \(V\)? Explain.
• Assuming that \(P\) and \(V\) do vary inversely, use the data to approximate the constant of proportionality.
• Use your calculator to determine a ‘Power Regression’ for this data 10 and use it verify your results in 1 and 2.
• If \(P\) really does vary inversely with \(V\), then \(P = \frac{k}{V}\) for some constant \(k\). From the data plot, the points do seem to lie along a curve like \(y = \frac{k}{x}\).

4.3.2 Exercises

In Exercises 1 - 6, solve the rational equation. Be sure to check for extraneous solutions.

• \(\dfrac{x}{5x + 4} = 3\)
• \(\dfrac{3x - 1}{x^{2} + 1} = 1\)
• \(\dfrac{1}{x + 3} + \dfrac{1}{x - 3} = \dfrac{x^{2} - 3}{x^{2} - 9}\)
• \(\dfrac{2x + 17}{x + 1} = x + 5\)
• \(\dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x} = 1\)
• \(\dfrac{-x^{3} + 4x}{x^{2} - 9} = 4x\)

In Exercises 7 - 20, solve the rational inequality. Express your answer using interval notation.

• \(\dfrac{1}{x + 2} \geq 0\)
• \(\dfrac{x - 3}{x + 2} \leq 0\)
• \(\dfrac{x}{x^{2} - 1} > 0\)
• \(\dfrac{4x}{x^2+4} \geq 0\)
• \(\dfrac{x^2-x-12}{x^2+x-6} > 0\)
• \(\dfrac{3x^2-5x-2}{x^2-9} < 0\)
• \(\dfrac{x^3+2x^2+x}{x^2-x-2} \geq 0\)
• \(\dfrac{x^{2} + 5x + 6}{x^{2} - 1} > 0\)
• \(\dfrac{3x - 1}{x^{2} + 1} \leq 1\)
• \(\dfrac{2x + 17}{x + 1} > x + 5\)
• \(\dfrac{-x^{3} + 4x}{x^{2} - 9} \geq 4x\)
• \(\dfrac{1}{x^{2} + 1} < 0\)
• \(\dfrac{x^4-4x^3+x^2-2x-15}{x^3-4x^2} \geq x\)
• \(\dfrac{5x^3-12x^2+9x+10}{x^2-1}\geq 3x-1\)
• Carl and Mike start a 3 mile race at the same time. If Mike ran the race at 6 miles per hour and finishes the race 10 minutes before Carl, how fast does Carl run?
• One day, Donnie observes that the wind is blowing at 6 miles per hour. A unladen swallow nesting near Donnie’s house flies three quarters of a mile down the road (in the direction of the wind), turns around, and returns exactly 4 minutes later. What is the airspeed of the unladen swallow? (Here, ‘airspeed’ is the speed that the swallow can fly in still air.)
• In order to remove water from a flooded basement, two pumps, each rated at 40 gallons per minute, are used. After half an hour, the one pump burns out, and the second pump finishes removing the water half an hour later. How many gallons of water were removed from the basement?
• A faucet can fill a sink in 5 minutes while a drain will empty the same sink in 8 minutes. If the faucet is turned on and the drain is left open, how long will it take to fill the sink?
• Working together, Daniel and Donnie can clean the llama pen in 45 minutes. On his own, Daniel can clean the pen in an hour. How long does it take Donnie to clean the llama pen on his own?
• In Exercise 32, the function \(C(x) = .03x^{3} - 4.5x^{2} + 225x + 250\), for \(x \geq 0\) was used to model the cost (in dollars) to produce \(x\) PortaBoy game systems. Using this cost function, find the number of PortaBoys which should be produced to minimize the average cost \(\overline{C}\). Round your answer to the nearest number of systems.
• Suppose we are in the same situation as Example 4.3.5 . If the volume of the box is to be \(500\) cubic centimeters, use your calculator to find the dimensions of the box which minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
• The box for the new Sasquatch-themed cereal, ‘Crypt-Os’, is to have a volume of \(140\) cubic inches. For aesthetic reasons, the height of the box needs to be \(1.62\) times the width of the base of the box. 13 Find the dimensions of the box which will minimize the surface area of the box. What is the minimum surface area? Round your answers to two decimal places.
• Sally is Skippy’s neighbor from Exercise 19 in Section 2.3 . Sally also wants to plant a vegetable garden along the side of her home. She doesn’t have any fencing, but wants to keep the size of the garden to 100 square feet. What are the dimensions of the garden which will minimize the amount of fencing she needs to buy? What is the minimum amount of fencing she needs to buy? Round your answers to the nearest foot. (Note: Since one side of the garden will border the house, Sally doesn’t need fencing along that side.)
• Find an expression for the volume \(V\) of the can in terms of the height \(h\) and the base radius \(r\).
• Find an expression for the surface area \(S\) of the can in terms of the height \(h\) and the base radius \(r\). (Hint: The top and bottom of the can are circles of radius \(r\) and the side of the can is really just a rectangle that has been bent into a cylinder.)
• Using the fact that \(V = 33.6\), write \(S\) as a function of \(r\) and state its applied domain.
• Use your graphing calculator to find the dimensions of the can which has minimal surface area.
• A right cylindrical drum is to hold 7.35 cubic feet of liquid. Find the dimensions (radius of the base and height) of the drum which would minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
• In Exercise 71 in Section 1.4 , the population of Sasquatch in Portage County was modeled by the function \(P(t) = \frac{150t}{t + 15}\), where \(t = 0\) represents the year 1803. When were there fewer than 100 Sasquatch in Portage County?

In Exercises 33 - 38, translate the following into mathematical equations.

• At a constant pressure, the temperature \(T\) of an ideal gas is directly proportional to its volume \(V\). (This is Charles’s Law )
• The frequency of a wave \(f\) is inversely proportional to the wavelength of the wave \(\lambda\).
• The density \(d\) of a material is directly proportional to the mass of the object \(m\) and inversely proportional to its volume \(V\).
• The square of the orbital period of a planet \(P\) is directly proportional to the cube of the semi-major axis of its orbit \(a\). (This is Kepler’s Third Law of Planetary Motion )
• The drag of an object traveling through a fluid \(D\) varies jointly with the density of the fluid \(\rho\) and the square of the velocity of the object \(\nu\).
• Suppose two electric point charges, one with charge \(q\) and one with charge \(Q\), are positioned \(r\) units apart. The electrostatic force \(F\) exerted on the charges varies directly with the product of the two charges and inversely with the square of the distance between the charges. (This is Coulomb’s Law )
• According to this webpage , the frequency \(f\) of a vibrating string is given by \(f = \dfrac{1}{2L} \sqrt{\dfrac{T}{\mu}}\) where \(T\) is the tension, \(\mu\) is the linear mass 15 of the string and \(L\) is the length of the vibrating part of the string. Express this relationship using the language of variation.
• Express this relationship as a mathematical equation.
• If a person who was \(5\) feet, \(10\) inches tall weighed 235 pounds had a Body Mass Index of 33.7, what is the value of the constant of proportionality?
• Rewrite the mathematical equation found in part 40a to include the value of the constant found in part 40b and then find your Body Mass Index.
• We know that the circumference of a circle varies directly with its radius with \(2\pi\) as the constant of proportionality. (That is, we know \(C = 2\pi r.\)) With the help of your classmates, compile a list of other basic geometric relationships which can be seen as variations.

4.3.3 Answers

• \(x = -\frac{6}{7}\)
• \(x = 1, \; x = 2\)
• \(x = -6, \; x = 2\)
• No solution
• \(x = 0, \; x = \pm 2\sqrt{2}\)
• \((-2, \infty)\)
• \((-2, 3]\)
• \((-1, 0) \cup (1, \infty)\)
• \([0, \infty)\)
• \((-\infty, -3) \cup (-3,2) \cup (4, \infty)\)
• \(\left(-3, -\frac{1}{3} \right) \cup (2,3)\)
• \((-1,0] \cup (2, \infty)\)
• \((-\infty, -3) \cup (-2, -1) \cup (1, \infty)\)
• \((-\infty, 1] \cup [2, \infty)\)
• \((-\infty, -6) \cup (-1, 2)\)
• \((-\infty, -3) \cup \left[-2\sqrt{2}, 0\right] \cup \left[2\sqrt{2}, 3\right)\)
• \([-3,0) \cup (0,4) \cup [5, \infty)\)
• \(\left(-1,-\frac{1}{2}\right] \cup (1, \infty)\)
• 4.5 miles per hour
• 24 miles per hour
• 3600 gallons
• \(\frac{40}{3} \approx 13.33\) minutes
• The absolute minimum of \(y=\overline{C}(x)\) occurs at \(\approx (75.73, 59.57)\). Since \(x\) represents the number of game systems, we check \(\overline{C}(75) \approx 59.58\) and \(\overline{C}(76) \approx 59.57\). Hence, to minimize the average cost, \(76\) systems should be produced at an average cost of \(\$59.57\) per system.
• The width (and depth) should be \(10.00\) centimeters, the height should be \(5.00\) centimeters. The minimum surface area is \(300.00\) square centimeters.
• The width of the base of the box should be \(\approx 4.12\) inches, the height of the box should be \(\approx 6.67\) inches, and the depth of the base of the box should be \(\approx 5.09\) inches; minimum surface area \(\approx 164.91\) square inches.
• The dimensions are \(\approx 7\) feet by \(\approx 14\) feet; minimum amount of fencing required \(\approx 28\) feet.
• \(V = \pi r^{2}h\)
• \(S = 2 \pi r^{2} + 2\pi r h\)
• \(S(r) = 2\pi r^{2} + \frac{67.2}{r}, \;\) Domain \(r > 0\)
• \(r \approx 1.749\,\)in. and \(h \approx 3.498\,\)in.
• The radius of the drum should be \(\approx 1.05\) feet and the height of the drum should be \(\approx 2.12\) feet. The minimum surface area of the drum is \(\approx 20.93\) cubic feet.
• \(P(t) < 100\) on \((-15, 30)\), and the portion of this which lies in the applied domain is \([0,30)\). Since \(t=0\) corresponds to the year 1803, from 1803 through the end of 1832, there were fewer than 100 Sasquatch in Portage County.
• \(T = k V\)
• 16 \(f = \dfrac{k}{\lambda}\)
• \(d = \dfrac{k m}{V}\)
• \(P^2 = k a^3\)
• 17 \(D = k \rho \nu^2\)
• 18 \(F = \dfrac{kqQ}{r^2}\)
• Rewriting \(f = \dfrac{1}{2L} \sqrt{\dfrac{T}{\mu}}\) as \(f = \dfrac{\frac{1}{2} \sqrt{T}}{L \sqrt{\mu}}\) we see that the frequency \(f\) varies directly with the square root of the tension and varies inversely with the length and the square root of the linear mass.
• \(B = \dfrac{kW}{h^{2}}\)
• 19 \(k = 702.68\)
• \(B = \dfrac{702.68W}{h^{2}}\)

1 There is no asymptote at \(x = 1\) since the graph is well behaved near \(x = 1\). According to Theorem 4.1 , there must be a hole there.

2 This is called a system of equations. No doubt, you’ve had experience with these things before, and we will study systems in greater detail in Chapter 8 .

3 While we usually discourage dividing both sides of an equation by a variable expression, we know \((6+R) \neq 0\) since otherwise we couldn’t possibly multiply it by \(t_{\text {down }}\) and get 5.

4 The reader is encouraged to verify that the units in this equation are the same on both sides. To get you started, the units on the ‘3’ is ‘hours.’

5 Carl would much rather spend his time writing open-source Mathematics texts than gardening anyway.

6 In other words, make sure you don’t try to add apples to oranges!

7 In this case, long division amounts to term-by-term division.

8 That is, \(h(x)\) means ‘\(h\) of \(x\)’, not ‘\(h\) times \(x\)’ here.

9 without Calculus, that is...

10 We will talk more about this in the coming chapters.

11 You can use tell the calculator to do this arithmetic on the lists and save yourself some time.

12 We will revisit this example once we have developed logarithms in Chapter 6 to see how we can actually ‘linearize’ this data and do a linear regression to obtain the same result.

13 1.62 is a crude approximation of the so-called ‘Golden Ratio’ \(\phi=\frac{1+\sqrt{5}}{2}\).

14 According to www.dictionary.com , there are different values given for this conversion. We will stick with 33.6in 3 for this problem.

15 Also known as the linear density. It is simply a measure of mass per unit length.

16 The character λ is the lower case Greek letter ‘lambda.’

17 The characters \(\rho\) and \(\nu\) are the lower case Greek letters ‘rho’ and ‘nu,’ respectively.

18 Note the similarity to this formula and Newton’s Law of Universal Gravitation as discussed in Example 5.

19 The CDC uses 703.