summarise the steps to solve kinematics problems using path coordinates

Path Coordinates

Here, we work on solving dynamics problems using path coordinates. Sometimes path coordinates are called normal & tangential coordinates because we choose basis vectors normal and tangential to the path.

Table of Links

• Theory Video: Express Acceleration in Path Coordinates
• Theory Video: The Mythical Centrifugal Force
• Problem: The “Wall of Death”
• Problem: Skate Park Loop Dynamics
• Problem: Dynamics of the Snowboard Halfpipe

Video: Expressing Acceleration in Path Coordinates

Video: The Mythical Centrifugal Force

The “Wall of Death”

Check out the video below and then work through the problem that follows:

Skate Park Loop Dynamics

Consider the following problem:

Here’s the solution:

FYI: Here is a link to a dreadful explanation of how a roller coaster loop works. If you click on the link to the author’s bio, you see why.  He has a B.A. in English, with no apparent training in physics, mathematics, or engineering.

Dynamics of the Snowboard Halfpipe

I invite you to watch a related video from the 2014 Winter Olympics coverage is which you can find HERE .

Conceptual Dynamics - Independent Learning

«Previous               Next »

Plane Curvilinear Motion: Polar Coordinates - Example Problem 3.4-5

A robotic arm extends along a path r = (1 + 0.5 cos θ ) m. At θ = π /4 rad, (dθ/dt) = 0.5 rad/s and (d 2 θ/dt 2 ) = 0.7 rad/s 2 , find the velocity and acceleration of point A .

• r = (1 + 0.5 cos θ ) m
• θ = π /4 rad
• (dθ/dt) = 0.5 rad/s
• (d 2 θ/dt 2 ) = 0.7 rad/s 2

The following video walks you through the solution to this problem. It is suggested that you try solving the problem first and then, if you have difficulties with the solution, watch the video for help.

We will use polar coordinates in this problem.

v = (dr/dt) e r + r(dθ/dt) e θ

a = ((d 2 r/dt 2 ) - r(dθ/dt) 2 ) e r + (r(d 2 θ/dt 2 ) + 2(dr/dt)(dθ/dt)) e θ

On the figure in your book, draw the x-y and r-θ axes. Click on the figure to see the results.

Notice that to calculate the velocity and acceleration of point A , we need to calculate the first and second time derivative of r .

Which of the following is the equation for (dr/dt) ?

Forgot password? New user? Sign up

Existing user? Log in

One Dimensional Kinematics

Already have an account? Log in here.

The First Step: Choosing Coordinates

Before beginning a problem in kinematics, you must set up your coordinate system. In one-dimensional kinematics, this is simply an x-axis and the direction of the motion is usually the positive-x direction. Though displacement, velocity, and acceleration are all vector quantities, in the one-dimensional case they can all be treated as scalar quantities with positive or negative values to indicate their direction.

The positive and negative values of these quantities are determined by the choice of how you align the coordinate system.

Velocity represents the rate of change of displacement over a given amount of time. The displacement in one-dimension is generally represented in regards to a starting point of \(x_1\) and \(x_2\). The time that the object in question is at each point is denoted as \(t_1\) and \(t_2\) (always assuming that \(t_2\) is later than \(t_1\), since time only proceeds one way). The change in a quantity from one point to another is generally indicated with the Greek letter delta, \(\Delta\).

Using these notations, it is possible to determine the average velocity (vav) in the following manner:

\(v_{av} = \dfrac{(x_2 - x_1)}{(t2 - t1)} = \dfrac{\Delta x}{\Delta t}\). If you apply a limit as \(\Delta t\) approaches 0, you obtain an instantaneous velocity at a specific point in the path. Such a limit in calculus is the derivative of x with respect to t, or \(\dfrac{dx}{dt}\). Acceleration

Acceleration represents the rate of change in velocity over time. Using the terminology introduced earlier, we see that the average acceleration (\(a_{av}\)) is: \(a_{av} = \dfrac{(v_2 - v_1)}{(t_2 - t_1)} = \dfrac{\Delta x}{\Delta t}\)

Again, we can apply a limit as \(\Delta t\) approaches 0 to obtain an instantaneous acceleration at a specific point in the path. The calculus representation is the derivative of v with respect to t, or \(\dfrac{dv}{dt}\). Similarly, since v is the derivative of x, the instantaneous acceleration is the second derivative of x with respect to t, or d2x/dt2. Constant Acceleration

In several cases, such as the Earth's gravitational field, the acceleration may be constant - in other words the velocity changes at the same rate throughout the motion. Using our earlier work, set the time at 0 and the end time as t (picture starting a stopwatch at 0 and ending it at the time of interest). The velocity at time 0 is \(v_0\) and at time t is v, yielding the following two equations:

\(a = \dfrac{(v - v_0)}{(t - 0)};\\ v = v_0 + at\)

Applying the earlier equations for \(v_{av}\) for \(x_0\) at time 0 and x at time t, and applying some manipulations (which I will not prove here), we get: \(x = x_0 + v_0t + 0.5at_2 v_2 = v_02 + 2a(x - x_0)\)

\(x - x_0 = \dfrac{(v_0 + v)t}2\)

The above equations of motion with constant acceleration can be used to solve any kinematic problem involving motion of a particle on a straight line with constant acceleration.

Problem Loading...

Note Loading...

Set Loading...

Introduction to One-Dimensional Kinematics

Chapter outline.

• Define position, displacement, distance, and distance traveled.
• Explain the relationship between position and displacement.
• Distinguish between displacement and distance traveled.
• Calculate displacement and distance given initial position, final position, and the path between the two.
• Define and distinguish between scalar and vector quantities.
• Assign a coordinate system for a scenario involving one-dimensional motion.
• Explain the relationships between instantaneous velocity, average velocity, instantaneous speed, average speed, displacement, and time.
• Calculate velocity and speed given initial position, initial time, final position, and final time.
• Derive a graph of velocity vs. time given a graph of position vs. time.
• Interpret a graph of velocity vs. time.
• Define and distinguish between instantaneous acceleration, average acceleration, and deceleration.
• Calculate acceleration given initial time, initial velocity, final time, and final velocity.
• Calculate displacement of an object that is not accelerating, given initial position and velocity.
• Calculate final velocity of an accelerating object, given initial velocity, acceleration, and time.
• Calculate displacement and final position of an accelerating object, given initial position, initial velocity, time, and acceleration.
• Apply problem-solving steps and strategies to solve problems of one-dimensional kinematics.
• Apply strategies to determine whether or not the result of a problem is reasonable, and if not, determine the cause.
• Describe the effects of gravity on objects in motion.
• Describe the motion of objects that are in free fall.
• Calculate the position and velocity of objects in free fall.
• Describe a straight-line graph in terms of its slope and y -intercept.
• Determine average velocity or instantaneous velocity from a graph of position vs. time.
• Determine average or instantaneous acceleration from a graph of velocity vs. time.
• Derive a graph of velocity vs. time from a graph of position vs. time.
• Derive a graph of acceleration vs. time from a graph of velocity vs. time.

Objects are in motion everywhere we look. Everything from a tennis game to a space-probe flyby of the planet Neptune involves motion. When you are resting, your heart moves blood through your veins. And even in inanimate objects, there is continuous motion in the vibrations of atoms and molecules. Questions about motion are interesting in and of themselves: How long will it take for a space probe to get to Mars? Where will a football land if it is thrown at a certain angle? But an understanding of motion is also key to understanding other concepts in physics. An understanding of acceleration, for example, is crucial to the study of force.

Our formal study of physics begins with kinematics which is defined as the study of motion without considering its causes . The word “kinematics” comes from a Greek term meaning motion and is related to other English words such as “cinema” (movies) and “kinesiology” (the study of human motion). In one-dimensional kinematics and Two-Dimensional Kinematics we will study only the motion of a football, for example, without worrying about what forces cause or change its motion. Such considerations come in other chapters. In this chapter, we examine the simplest type of motion—namely, motion along a straight line, or one-dimensional motion. In Two-Dimensional Kinematics , we apply concepts developed here to study motion along curved paths (two- and three-dimensional motion); for example, that of a car rounding a curve.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics
• Publication date: Jun 21, 2012
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics/pages/2-introduction-to-one-dimensional-kinematics

© Mar 3, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Problem-Solving Basics for One-Dimensional Kinematics

Learning objectives.

By the end of this section, you will be able to:

• Apply problem-solving steps and strategies to solve problems of one-dimensional kinematics.
• Apply strategies to determine whether or not the result of a problem is reasonable, and if not, determine the cause.

Figure 1. Problem-solving skills are essential to your success in Physics. (credit: scui3asteveo, Flickr)

Problem-solving skills are obviously essential to success in a quantitative course in physics. More importantly, the ability to apply broad physical principles, usually represented by equations, to specific situations is a very powerful form of knowledge. It is much more powerful than memorizing a list of facts. Analytical skills and problem-solving abilities can be applied to new situations, whereas a list of facts cannot be made long enough to contain every possible circumstance. Such analytical skills are useful both for solving problems in this text and for applying physics in everyday and professional life.

Problem-Solving Steps

While there is no simple step-by-step method that works for every problem, the following general procedures facilitate problem solving and make it more meaningful. A certain amount of creativity and insight is required as well.

Examine the situation to determine which physical principles are involved . It often helps to draw a simple sketch at the outset. You will also need to decide which direction is positive and note that on your sketch. Once you have identified the physical principles, it is much easier to find and apply the equations representing those principles. Although finding the correct equation is essential, keep in mind that equations represent physical principles, laws of nature, and relationships among physical quantities. Without a conceptual understanding of a problem, a numerical solution is meaningless.

Make a list of what is given or can be inferred from the problem as stated (identify the knowns) . Many problems are stated very succinctly and require some inspection to determine what is known. A sketch can also be very useful at this point. Formally identifying the knowns is of particular importance in applying physics to real-world situations. Remember, “stopped” means velocity is zero, and we often can take initial time and position as zero.

Identify exactly what needs to be determined in the problem (identify the unknowns) . In complex problems, especially, it is not always obvious what needs to be found or in what sequence. Making a list can help.

Find an equation or set of equations that can help you solve the problem . Your list of knowns and unknowns can help here. It is easiest if you can find equations that contain only one unknown—that is, all of the other variables are known, so you can easily solve for the unknown. If the equation contains more than one unknown, then an additional equation is needed to solve the problem. In some problems, several unknowns must be determined to get at the one needed most. In such problems it is especially important to keep physical principles in mind to avoid going astray in a sea of equations. You may have to use two (or more) different equations to get the final answer.

Substitute the knowns along with their units into the appropriate equation, and obtain numerical solutions complete with units . This step produces the numerical answer; it also provides a check on units that can help you find errors. If the units of the answer are incorrect, then an error has been made. However, be warned that correct units do not guarantee that the numerical part of the answer is also correct.

Check the answer to see if it is reasonable: Does it make sense? This final step is extremely important—the goal of physics is to accurately describe nature. To see if the answer is reasonable, check both its magnitude and its sign, in addition to its units. Your judgment will improve as you solve more and more physics problems, and it will become possible for you to make finer and finer judgments regarding whether nature is adequately described by the answer to a problem. This step brings the problem back to its conceptual meaning. If you can judge whether the answer is reasonable, you have a deeper understanding of physics than just being able to mechanically solve a problem.

When solving problems, we often perform these steps in different order, and we also tend to do several steps simultaneously. There is no rigid procedure that will work every time. Creativity and insight grow with experience, and the basics of problem solving become almost automatic. One way to get practice is to work out the text’s examples for yourself as you read. Another is to work as many end-of-section problems as possible, starting with the easiest to build confidence and progressing to the more difficult. Once you become involved in physics, you will see it all around you, and you can begin to apply it to situations you encounter outside the classroom, just as is done in many of the applications in this text.

Unreasonable Results

Physics must describe nature accurately. Some problems have results that are unreasonable because one premise is unreasonable or because certain premises are inconsistent with one another. The physical principle applied correctly then produces an unreasonable result. For example, if a person starting a foot race accelerates at 0.40 m/s 2 for 100 s, his final speed will be 40 m/s (about 150 km/h)—clearly unreasonable because the time of 100 s is an unreasonable premise. The physics is correct in a sense, but there is more to describing nature than just manipulating equations correctly. Checking the result of a problem to see if it is reasonable does more than help uncover errors in problem solving—it also builds intuition in judging whether nature is being accurately described.

Use the following strategies to determine whether an answer is reasonable and, if it is not, to determine what is the cause.

Solve the problem using strategies as outlined and in the format followed in the worked examples in the text . In the example given in the preceding paragraph, you would identify the givens as the acceleration and time and use the equation below to find the unknown final velocity. That is,

Check to see if the answer is reasonable . Is it too large or too small, or does it have the wrong sign, improper units, …? In this case, you may need to convert meters per second into a more familiar unit, such as miles per hour.

This velocity is about four times greater than a person can run—so it is too large.

If the answer is unreasonable, look for what specifically could cause the identified difficulty . In the example of the runner, there are only two assumptions that are suspect. The acceleration could be too great or the time too long. First look at the acceleration and think about what the number means. If someone accelerates at 0.40 m/s 2 , their velocity is increasing by 0.4 m/s each second. Does this seem reasonable? If so, the time must be too long. It is not possible for someone to accelerate at a constant rate of 0.40 m/s 2 for 100 s (almost two minutes).

Section Summary

The six basic problem solving steps for physics are:

• Step 1 . Examine the situation to determine which physical principles are involved.
• Step 2 . Make a list of what is given or can be inferred from the problem as stated (identify the knowns).
• Step 3 . Identify exactly what needs to be determined in the problem (identify the unknowns).
• Step 4 . Find an equation or set of equations that can help you solve the problem.
• Step 5 . Substitute the knowns along with their units into the appropriate equation, and obtain numerical solutions complete with units.
• Step 6 . Check the answer to see if it is reasonable: Does it make sense?

Conceptual Questions

1. What information do you need in order to choose which equation or equations to use to solve a problem? Explain. 2. What is the last thing you should do when solving a problem? Explain.

• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/[email protected]:aNsXe6tc@2/Problem-Solving-Basics-for-One . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected].

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

12 2.6 Problem-Solving Basics for One-Dimensional Kinematics

• Apply problem-solving steps and strategies to solve problems of one-dimensional kinematics.
• Apply strategies to determine whether or not the result of a problem is reasonable, and if not, determine the cause.

Problem-solving skills are obviously essential to success in a quantitative course in physics. More importantly, the ability to apply broad physical principles, usually represented by equations, to specific situations is a very powerful form of knowledge. It is much more powerful than memorizing a list of facts. Analytical skills and problem-solving abilities can be applied to new situations, whereas a list of facts cannot be made long enough to contain every possible circumstance. Such analytical skills are useful both for solving problems in this text and for applying physics in everyday and professional life.

Problem-Solving Steps

While there is no simple step-by-step method that works for every problem, the following general procedures facilitate problem solving and make it more meaningful. A certain amount of creativity and insight is required as well.

Examine the situation to determine which physical principles are involved . It often helps to draw a simple sketch at the outset. You will also need to decide which direction is positive and note that on your sketch. Once you have identified the physical principles, it is much easier to find and apply the equations representing those principles. Although finding the correct equation is essential, keep in mind that equations represent physical principles, laws of nature, and relationships among physical quantities. Without a conceptual understanding of a problem, a numerical solution is meaningless.

Make a list of what is given or can be inferred from the problem as stated (identify the knowns) . Many problems are stated very succinctly and require some inspection to determine what is known. A sketch can also be very useful at this point. Formally identifying the knowns is of particular importance in applying physics to real-world situations. Remember, “stopped” means velocity is zero, and we often can take initial time and position as zero.

Identify exactly what needs to be determined in the problem (identify the unknowns) . In complex problems, especially, it is not always obvious what needs to be found or in what sequence. Making a list can help.

Find an equation or set of equations that can help you solve the problem . Your list of knowns and unknowns can help here. It is easiest if you can find equations that contain only one unknown—that is, all of the other variables are known, so you can easily solve for the unknown. If the equation contains more than one unknown, then an additional equation is needed to solve the problem. In some problems, several unknowns must be determined to get at the one needed most. In such problems it is especially important to keep physical principles in mind to avoid going astray in a sea of equations. You may have to use two (or more) different equations to get the final answer.

Substitute the knowns along with their units into the appropriate equation, and obtain numerical solutions complete with units . This step produces the numerical answer; it also provides a check on units that can help you find errors. If the units of the answer are incorrect, then an error has been made. However, be warned that correct units do not guarantee that the numerical part of the answer is also correct.

Check the answer to see if it is reasonable: Does it make sense? This final step is extremely important—the goal of physics is to accurately describe nature. To see if the answer is reasonable, check both its magnitude and its sign, in addition to its units. Your judgment will improve as you solve more and more physics problems, and it will become possible for you to make finer and finer judgments regarding whether nature is adequately described by the answer to a problem. This step brings the problem back to its conceptual meaning. If you can judge whether the answer is reasonable, you have a deeper understanding of physics than just being able to mechanically solve a problem.

When solving problems, we often perform these steps in different order, and we also tend to do several steps simultaneously. There is no rigid procedure that will work every time. Creativity and insight grow with experience, and the basics of problem solving become almost automatic. One way to get practice is to work out the text’s examples for yourself as you read. Another is to work as many end-of-section problems as possible, starting with the easiest to build confidence and progressing to the more difficult. Once you become involved in physics, you will see it all around you, and you can begin to apply it to situations you encounter outside the classroom, just as is done in many of the applications in this text.

Unreasonable Results

Use the following strategies to determine whether an answer is reasonable and, if it is not, to determine what is the cause.

Solve the problem using strategies as outlined and in the format followed in the worked examples in the text . In the example given in the preceding paragraph, you would identify the givens as the acceleration and time and use the equation below to find the unknown final velocity. That is,

Check to see if the answer is reasonable . Is it too large or too small, or does it have the wrong sign, improper units, …? In this case, you may need to convert meters per second into a more familiar unit, such as miles per hour.

This velocity is about four times greater than a person can run—so it is too large.

Section Summary

Step 1 . Examine the situation to determine which physical principles are involved.

Step 2 . Make a list of what is given or can be inferred from the problem as stated (identify the knowns).

Step 3 . Identify exactly what needs to be determined in the problem (identify the unknowns).

Step 4 . Find an equation or set of equations that can help you solve the problem.

Step 5 . Substitute the knowns along with their units into the appropriate equation, and obtain numerical solutions complete with units.

Step 6 . Check the answer to see if it is reasonable: Does it make sense?

Conceptual Questions

1: What information do you need in order to choose which equation or equations to use to solve a problem? Explain.

2: What is the last thing you should do when solving a problem? Explain.

College Physics Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.4: Problem-Solving for Basic Kinematics

• Last updated
• Save as PDF
• Page ID 16931

Applications

There are four kinematic equations that describe the motion of objects without consideration of its causes.

learning objectives

• Choose which kinematics equation to use in problems in which the initial starting position is equal to zero

Kinematics is the branch of classical mechanics that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without consideration of the causes of motion. There are four kinematic equations when the initial starting position is the origin, and the acceleration is constant:

• \(\mathrm{v=v_0+at}\)
• \(\mathrm{d=\frac{1}{2}(v_0+v)t}\) or alternatively \(\mathrm{v_{average}=\frac{d}{t}}\)
• \(\mathrm{d=v_0t+(\frac{at^2}{2})}\)
• \(\mathrm{v^2=v^2_0+2ad}\)

Notice that the four kinematic equations involve five kinematic variables: \(\mathrm{d,v,v_0,a}\) and \(\mathrm{t}\). Each of these equations contains only four of the five variables and has a different one missing. This tells us that we need the values of three variables to obtain the value of the fourth and we need to choose the equation that contains the three known variables and one unknown variable for each specific situation.

Here the basic problem solving steps to use these equations:

Step one – Identify exactly what needs to be determined in the problem (identify the unknowns).

Step two – Find an equation or set of equations that can help you solve the problem.

Step three – Substitute the knowns along with their units into the appropriate equation, and obtain numerical solutions complete with units.

Step four – Check the answer to see if it is reasonable: Does it make sense?

Problem-solving skills are obviously essential to success in a quantitative course in physics. More importantly, the ability to apply broad physical principles, usually represented by equations, to specific situations is a very powerful form of knowledge. It is much more powerful than memorizing a list of facts. Analytical skills and problem-solving abilities can be applied to new situations, whereas a list of facts cannot be made long enough to contain every possible circumstance. Such analytical skills are useful both for solving problems in a physics class and for applying physics in everyday and professional life.

Motion Diagrams

A motion diagram is a pictorial description of an object’s motion and represents the position of an object at equally spaced time intervals.

• Construct a motion diagram

A motion diagram is a pictorial description of the motion of an object. It displays the object’s location at various equally spaced times on the same diagram; shows an object’s initial position and velocity; and presents several spots in the center of the diagram. These spots reveal whether or not the object has accelerated or decelerated. For simplicity, the object is represented by a simple shape, such as a filled circle, which contains information about an object’s position at particular time instances. For this reason, a motion diagram is more information than a path diagram. It may also display the forces acting on the object at each time instance.

is a motion diagram of a simple trajectory. Imagine the object as a hockey puck sliding on ice. Notice that the puck covers the same distance per unit interval along the trajectory. We can conclude that the puck is moving at a constant velocity and, therefore, there is no acceleration or deceleration during the motion.

Puck Sliding on Ice : Motion diagram of a puck sliding on ice. The puck is moving at a constant velocity.

One major use of motion diagrams is the presentation of film through a series of frames taken by a camera; this is sometimes called stroboscopic technique (as seen in ). Viewing an object on a motion diagram allows one to determine whether an object is speeding up or slowing down, or if it is at constant rest. As the frames are taken, we can assume that an object is at a constant rest if it occupies the same position over time. We can assume that an object is speeding up if there is a visible increase in the space between objects as time passes, and that it is slowing down if there is a visible decrease in the space between objects as time passes. The objects on the frame come very close together.

Bouncing Ball : A bouncing ball captured with a stroboscopic flash at 25 images per second.

• The four kinematic equations involve five kinematic variables: \(\mathrm{d,v,v_0,a}\) and \(\mathrm{t}\).
• Each equation contains only four of the five variables and has a different one missing.
• It is important to choose the equation that contains the three known variables and one unknown variable for each specific situation.
• Motion diagrams represent the motion of an object by displaying its location at various equally spaced times on the same diagram.
• Motion diagrams show an object’s initial position and velocity and presents several spots in the center of the diagram. These spots reveal the object’s state of motion.
• Motion diagrams contain information about an object’s position at particular time instances and is therefore more informative than a path diagram.
• kinematics : The branch of physics concerned with objects in motion.
• stroboscopic : Relating to an instrument used to make a cyclically moving object appear to be slow-moving, or stationary.
• diagram : A graph or chart.
• motion : A change of position with respect to time.

LICENSES AND ATTRIBUTIONS

CC LICENSED CONTENT, SHARED PREVIOUSLY

• Curation and Revision. Provided by : Boundless.com. License : CC BY-SA: Attribution-ShareAlike

CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

• OpenStax College, College Physics. September 17, 2013. Provided by : OpenStax CNX. Located at : http://cnx.org/content/m42125/latest/?collection=col11406/1.7 . License : CC BY: Attribution
• kinematics. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/kinematics . License : CC BY-SA: Attribution-ShareAlike
• Motion diagram. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/Motion_diagram . License : CC BY-SA: Attribution-ShareAlike
• motion. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/motion . License : CC BY-SA: Attribution-ShareAlike
• diagram. Provided by : Wiktionary. Located at : en.wiktionary.org/wiki/diagram . License : CC BY-SA: Attribution-ShareAlike
• stroboscopic. Provided by : Wikipedia. Located at : en.Wikipedia.org/wiki/stroboscopic . License : CC BY-SA: Attribution-ShareAlike
• Boundless. Provided by : Amazon Web Services. Located at : s3.amazonaws.com/figures.boundless.com/51129b2ee4b0c14bf464ce1b/1.jpg . License : CC BY: Attribution
• Provided by : Wikimedia. Located at : http://upload.wikimedia.org/Wikipedia/commons/3/3c/Bouncing_ball_strobe_edit.jpg . License : CC BY: Attribution

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.2: Equations of Motion in Rectangular Coordinates

• Last updated
• Save as PDF
• Page ID 50603

• Jacob Moore & Contributors
• Pennsylvania State University Mont Alto via Mechanics Map

To start our discussion of kinetics in two dimensions, we will examine Newton's Second Law as applied to a fixed coordinate system. In its basic form, Newton's Second Law states that the sum of the forces on a body will be equal to the mass of that body times its rate of acceleration. For bodies in motion, we can write this relationship out as the equation of motion.

\[ \sum \vec{F} = m * \vec{a} \]

With rectangular coordinates in two dimensions, we will break this single vector equation into two separate scalar equations. To solve the equations, we simply break any given forces and accelerations down into \(x\) and \(y\) components using sines and cosines and plug those known values in. With two equations, we should be able to solve for up to two unknown force or acceleration terms.

\begin{align} \sum F_x &= m * a_x = m * \ddot{x} \\[5pt] \sum F_y &= m * a_y = m * \ddot{y} \end{align}

Just as with a single dimension, the equations of motion are often used in conjunction with the kinematics equations that relate positions, velocities and accelerations as discussed in the previous chapter. Depending on the problem being examined, the kinematics equations may need to be examined either before or after the kinetics equations.

Rectangular coordinates can be used in any kinetics problem; however, they work best with problems where the forces do not change direction over time. Projectile motion is a good example of this, because the gravity force will maintain a constant direction, as opposed to the thrust force on a turning plane, where the thrust force changes direction with the plane.

Example \(\PageIndex{1}\)

You are controlling a satellite with a mass of 300 kg. The main and lateral thrusters can exert the forces shown. How long do you need to run each of the thrusters to achieve the final velocity as shown in the diagram? Assume the satellite has zero initial velocity.

Example \(\PageIndex{2}\)

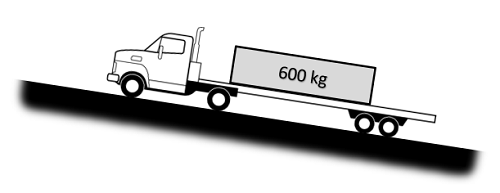
A man in a flatbed truck that starts at rest moves up a hill at an angle of 10 degrees. If he is carrying a 600-kg crate in the back and the static coefficient of friction is 0.3, what is the maximum rate of acceleration before the crate slides off of the back of the truck? How long will it take the truck to reach a speed of 25 m/s?