travelling salesman problem optimal solution

Explained: What is Traveling Salesman Problem (TSP)

• Last Updated: January 24, 2023

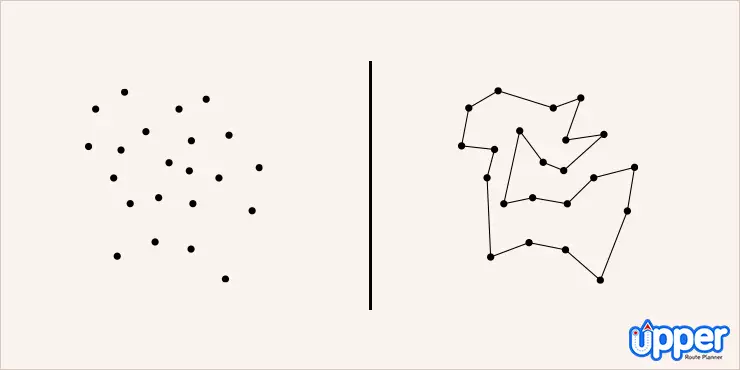
• A well-known mathematical problem called the Traveling Salesman Problem (TSP) aims to determine the shortest path between a number of places.
• Logistics, transportation, and manufacturing are just a few of the industries where the TSP is useful.
• The number of points, the form of the point set, and the algorithm employed can all have an impact on how the TSP is solved.
• Technology advancements like cloud computing and parallel processing have made it possible to solve the Traveling Salesman Problem effectively for larger and more complicated situations.

Traveling salesman problem is not new for delivery-based businesses. Its recent expansion has insisted that industry experts find optimal solutions in order to facilitate delivery operations.

The major challenge is to find the most efficient routes for performing multi-stop deliveries. Without the shortest routes, your delivery agent will take more time to reach the final destination. Sometimes problems may arise if you have multiple route options but fail to recognize the efficient one.

Eventually, traveling salesman problem would cost you time and result in late deliveries . So, before it becomes an irreparable issue for your delivery company, let us understand the traveling salesman problem and find optimal solutions in this blog.

Table of Content

• What is the Traveling Salesman Problem (TSP)?
• Commom challenges of Traveling Salesman Problem (TSP)

What are Some Popular Solutions to Traveling Salesman Problem?

What are other optimal solutions to the traveling salesman problem, what are some real-life applications of traveling salesman problem.

• How TSP and VRP Combinedly Pile up Challenges?
• Can a route planner resolve Traveling Salesman Problem (TSP)?

What is Traveling Salesman Problem (TSP)?

The traveling Salesman Problem (TSP) is a combinatorial problem that deals with finding the shortest and most efficient route to follow for reaching a list of specific destinations.

It is a common algorithmic problem in the field of delivery operations that might hamper the multiple delivery process and result in financial loss. TSP turns out when you have multiple routes available but choosing a minimum cost path is really hard for you or a traveling person.

How difficult is it to solve?

It is quite difficult to solve TSP as it is known as NP-hard, which means there is no polynomial time algorithm to solve it for more numbers of addresses. So, with an increasing amount of addresses, the complexity of solving TSP increases exponentially.

So, it is impossible to find TSP solutions manually. Also, many mathematical algorithms and the fastest computers fail to solve TSP.

However, TSP can be eliminated by determining the optimized and efficient path using approximation algorithms or automated processes.

Common Challenges of Traveling Salesman Problem (TSP)

Being a salesman is not easy, as you need to face various unavoidable challenges in your everyday schedules.

• Firstly, every day, salespeople have to carry out a number of deliveries in a very limited time, so there are a lot of time constraints. To overcome this, you need to plan your routes in a way that you make the most out of them.
• Secondly, there are chances of last-minute changes. Sometimes you get extra and urgent visits to make, while sometimes, some visits are postponed or canceled due to the customer’s unavailability.
• Lastly, a math problem, a combinatorial optimization problem, arises. A combinatorial optimization problem is a problem that is mathematically complex to solve as you have to deal with many variables.

These are major challenges in the Traveling Salesman Problem (TSP) as you are required to create a route with the shortest distances using hundreds and thousands of permutations and combinations that asks for less fuel, fulfill on-time delivery to customers, and are ready to modify routes considering last minute changes.

These are some of the near-optimal solutions to find the shortest route to a combinatorial optimization problem.

1. Nearest Neighbor (NN)

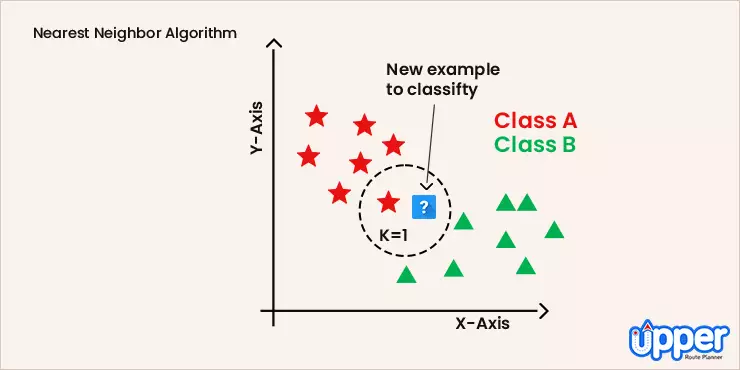
The Nearest Neighbor Method is probably the most basic TSP heuristic. The method followed by this algorithm states that the driver must start by visiting the nearest destination or closest city. Once all the cities in the loop are covered, the driver can head back to the starting point.

Solving TSP using this efficient method, requires the user to choose a city at random and then move on to the closest unvisited city and so on. Once all the cities on the map are covered, you must return to the city you started from.

2. The Branch and Bound Algorithm

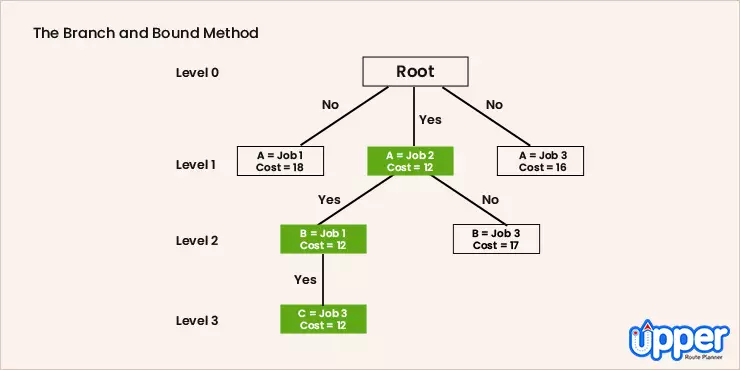
The Branch & Bound method follows the technique of breaking one problem into several little chunks of problems. So it solves a series of problems. Each of these sub-problems may have multiple solutions. The solution you choose for one problem may have an effect on the solutions of subsequent sub-problems.

3. The Brute Force Algorithm

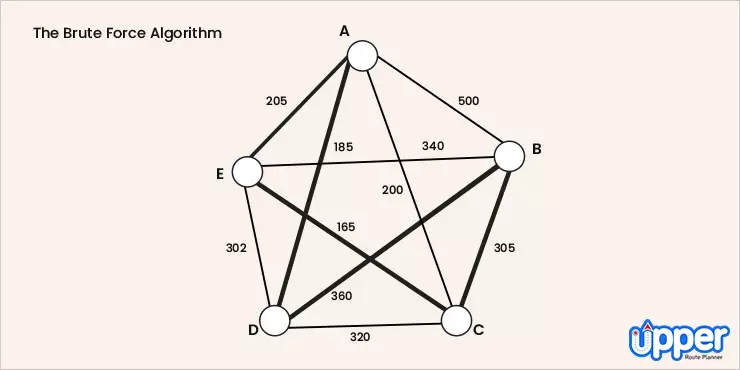
The Brute Force Approach takes into consideration all possible minimum cost permutation of routes using a dynamic programming approach. First, calculate the total number of routes. Draw and list all the possible routes that you get from the calculation. The distance of each route must be calculated and the shortest route will be the most optimal solution.

• Multi-Agent System : Involves distributing the pair of cities into groups. Then assign a single agent to discover the shortest path, covering all the cities in the assigned group.
• Zero Suffix Method : This method solves the classical symmetric TSP and was introduced by Indian researchers.
• Multi-Objective Evolutionary Algorithm : This method solves the TSP using NSGA-II
• Biogeography-based Optimization Algorithm : This method is based on the migration strategy of animals for solving optimization issues.
• Meta-Heuristic Multi Restart Iterated Local Search : This method states that the technique is more efficient compared to genetic algorithms.

Blow Away TSP using Upper

Need a permanent solution for recurring TSP? Sign up with Upper to keep your tradesmen updated all the time. Lay off your manual calculation and adopt an automated process now!

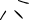
Most businesses see a rise in the Traveling Salesman Problem (TSP) due to the last mile delivery challenges . The last mile delivery is the process of delivering goods from the warehouse (or a depot) to the customer’s preferred location. Considering the supply chain management, it is the last mile deliveries that cost you a wholesome amount.

At the same time, you need to sacrifice financial loss in order to maintain your current position in the market. Suppose last mile delivery costs you $11, the customer will pay $8 and you would suffer a loss. This is because of pre-defined norms which may favor the customer to pay less amount.

This hefty last mile delivery cost is the result of a lack of Vehicle routing problem(VRP) software. VRP finds you the most efficient routes so that operational costs will not get increase. So, by using the right VRP software, you would not have to bother about TSP.

Such delivery management software uses an automated process that doesn’t need manual intervention or calculations to pick the best routes. Hence, it is the easiest way to get rid of the traveling Salesman Problem (TSP).

How TSP and VRP Combinedly Pile Up Challenges?

The traveling Salesman Problem is an optimization problem studied in graph theory and the field of operations research. In this optimization problem, the nodes or cities on the graph are all connected using direct edges or routes. The weight of each edge indicates the distance covered on the route between the two cities.

The problem is about finding an optimal route that visits each city once and returns to the starting and ending point after covering all cities once.

The TSP is often studied in a generalized version which is the Vehicle Routing Problem . It is one of the most broadly worked on problems in mathematical optimization. VRP deals with finding or creating a set of routes for reducing time, fuel, and delivery costs.

Is there any real world solution to TSP and VRP?

Many solutions for TSP and VRP are based on academics which means they are not so practical in everyday life. The reason is that many of them are just limited to perfection, but need a dynamic programming-based solution. So, if businesses really want to get rid of them, they need a TSP solver integrated with route optimization software.

The right TSP solver will help you disperse such modern challenges. It offers in-built route planning and optimization solutions in such a way that your tradesman doesn’t get stranded while delivering the parcel. Also, it is equipped with an efficient algorithm that provides true solutions to the TSP. As a result, the delivery manager can create a route plan hassle-free in a few minutes.

Can a Route Planner Resolve the Traveling Salesman Problem (TSP)?

In the general case, the Traveling Salesman Problem (TSP) involves finding the shortest optimized and possible route that includes a set of stops and returns to the starting point. The number of possible routes increases exponentially as the number of locations increases. Finding the best solution becomes difficult computationally, even for moderately sized problems.

But, Upper Route Planner, a route optimization software , is built differently. Upper has all the solutions you need when talking about TSP.

For example, if you are in charge of planning delivery routes with more than 500 stops in them, all you need to do is import an Excel or CSV file with multiple addresses into Upper, review, allot delivery drivers, optimize, and dispatch with a single click. This delivery route planning solution saves you hours of time spent on planning delivery routes and optimizing them.

Also, once the delivery is completed, Upper lets you collect proof of delivery. This is how the Upper Route Planner is a simple solution to the Traveling Salesman Problem.

Upper Route Planner

A simple-to-use route planner that every one is talking about

TSP stands for traveling Salesman Problem, while VRP is an abbreviation form of vehicle routing problem (VRP). In the delivery industry, both of them are widely known by their abbreviation form.

Yes, you can prevent TSP by using the right route planner. The online route planner helps you get the optimized path so that your delivery agents don’t have to deal with such challenges. In addition, they don’t struggle with multiple routes. Instead, they can progress on the shortest route.

The new method has made it possible to find solutions that are almost as good. This was done by the Christofides algorithm, the popular algorithm in theoretical computer science. This algorithm plugs into an alternate version of the problem that finds a combination of paths as per permutations of cities. It made the round trip route much longer. The round trip produced by the new method, while still not being efficient enough is better than the old one.

The vehicle routing problem (VRP) reduces the transportation costs as well as drivers’ expenses. It helps you serve more customers with fewer fleets and drivers. Thus, you don’t have any variation in the time taken to travel.

Create Optimized Routes Using Upper and Bid Goodbye to Traveling Salesman Problem

As a business owner, If you are dealing with TSP and want to get rid of them, we recommend using a TSP solver like Upper Route Planner. The online route planner is capable of plucking out the most efficient routes no matter how big your TSP is. It has an in-built sophisticated algorithm that helps you get the optimized path in a matter of seconds.

Therefore, you won’t fall prey to such real-world problems and perform deliveries in minimum time. Upper’s delivery route planner offers a dedicated driver app that makes sure your tradesman doesn’t go wrongfooted and quickly wraps up pending deliveries. Don’t just agree with our words, book a demo on Upper and disperse TSP once and for all.

Rakesh Patel, author of two defining books on reverse geotagging, is a trusted authority in routing and logistics. His innovative solutions at Upper Route Planner have simplified logistics for businesses across the board. A thought leader in the field, Rakesh's insights are shaping the future of modern-day logistics, making him your go-to expert for all things route optimization. Read more.

Sign Up Now!

Get weekly updates from Upper Route Planner.

Tired of Manual Routing?

Related Posts

Sales Route Planning Guide: Know How to Plan the Best Sales Routes

Sign Up with Upper Route Planner and automate your daily business process route planning, scheduling, and optimizing!

https://www.google.com/

https://www.upperinc.com/guides/travelling-salesman-problem/

www.google.com

Grab a FREE Trial of Upper

• Plan routes with hundreds of stops in a minute
• Schedule routes months in advance
• Collect reliable proof of delivery
• Track drivers live for real-time updates
• Experience unparalleled customer support

Grab a FREE Trial of Upper TODAY!

• Schedule routes in advance for weeks
• Collect proof of delivery to maintain accountability
• Experience 24/7 customer support
• Smart reporting to get real-time insights

Traveling salesman problem

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems

Author: Jessica Yu (ChE 345 Spring 2014)

Steward: Dajun Yue, Fengqi You

The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1

• 2.1 Graph Theory
• 2.2 Classifications of the TSP
• 2.3 Variations of the TSP
• 3.1 aTSP ILP Formulation
• 3.2 sTSP ILP Formulation
• 4.1 Exact algorithms
• 4.2.1 Tour construction procedures
• 4.2.2 Tour improvement procedures
• 5 Applications
• 7 References

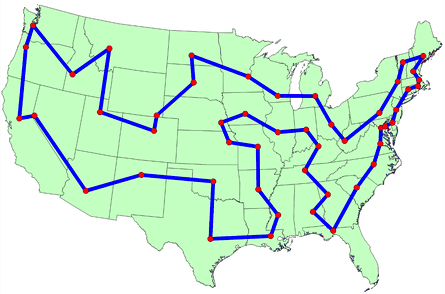
The origins of the traveling salesman problem are obscure; it is mentioned in an 1832 manual for traveling salesman, which included example tours of 45 German cities but gave no mathematical consideration. 2 W. R. Hamilton and Thomas Kirkman devised mathematical formulations of the problem in the 1800s. 2

It is believed that the general form was first studied by Karl Menger in Vienna and Harvard in the 1930s. 2,3

Hassler Whitney, who was working on his Ph.D. research at Harvard when Menger was a visiting lecturer, is believed to have posed the problem of finding the shortest route between the 48 states of the United States during either his 1931-1932 or 1934 seminar talks. 2 There is also uncertainty surrounding the individual who coined the name “traveling salesman problem” for Whitney’s problem. 2

The problem became increasingly popular in the 1950s and 1960s. Notably, George Dantzig, Delber R. Fulkerson, and Selmer M. Johnson at the RAND Corporation in Santa Monica, California solved the 48 state problem by formulating it as a linear programming problem. 2 The methods described in the paper set the foundation for future work in combinatorial optimization, especially highlighting the importance of cutting planes. 2,4

In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community. In 1972, Richard Karp demonstrated that the Hamiltonian cycle problem was NP-complete, implying that the traveling salesman problem was NP-hard. 4

Increasingly sophisticated codes led to rapid increases in the sizes of the traveling salesman problems solved. Dantzig, Fulkerson, and Johnson had solved a 48 city instance of the problem in 1954. 5 Martin Grötechel more than doubled this 23 years later, solving a 120 city instance in 1977. 5 Enoch Crowder and Manfred W. Padberg again more than doubled this in just 3 years, with a 318 city solution. 5

In 1987, rapid improvements were made, culminating in a 2,392 city solution by Padberg and Giovanni Rinaldi. In the following two decades, David L. Appelgate, Robert E. Bixby, Vasek Chvátal, & William J. Cook led the cutting edge, solving a 7,397 city instance in 1994 up to the current largest solved problem of 24,978 cities in 2004. 5

Description

Graph theory.

In the context of the traveling salesman problem, the verticies correspond to cities and the edges correspond to the path between those cities. When modeled as a complete graph, paths that do not exist between cities can be modeled as edges of very large cost without loss of generality. 6 Minimizing the sum of the costs for Hamiltonian cycle is equivalent to identifying the shortest path in which each city is visiting only once.

Classifications of the TSP

The TRP can be divided into two classes depending on the nature of the cost matrix. 3,6

• Applies when the distance between cities is the same in both directions

• Applies when there are differences in distances (e.g. one-way streets)

An ATSP can be formulated as an STSP by doubling the number of nodes. 6

Variations of the TSP

Formulation

The objective function is then given by

To ensure that the result is a valid tour, several contraints must be added. 1,3

There are several other formulations for the subtour elimnation contraint, including circuit packing contraints, MTZ constraints, and network flow constraints.

aTSP ILP Formulation

The integer linear programming formulation for an aTSP is given by

sTSP ILP Formulation

The symmetric case is a special case of the asymmetric case and the above formulation is valid. 3, 6 The integer linear programming formulation for an sTSP is given by

Exact algorithms

Branch-and-bound algorithms are commonly used to find solutions for TSPs. 7 The ILP is first relaxed and solved as an LP using the Simplex method, then feasibility is regained by enumeration of the integer variables. 7

Other exact solution methods include the cutting plane method and branch-and-cut. 8

Heuristic algorithms

Given that the TSP is an NP-hard problem, heuristic algorithms are commonly used to give a approximate solutions that are good, though not necessarily optimal. The algorithms do not guarantee an optimal solution, but gives near-optimal solutions in reasonable computational time. 3 The Held-Karp lower bound can be calculated and used to judge the performance of a heuristic algorithm. 3

There are two general heuristic classifications 7 :

• Tour construction procedures where a solution is gradually built by adding a new vertex at each step
• Tour improvement procedures where a feasbile solution is improved upon by performing various exchanges

The best methods tend to be composite algorithms that combine these features. 7

Tour construction procedures

Tour improvement procedures

Applications

The importance of the traveling salesman problem is two fold. First its ubiquity as a platform for the study of general methods than can then be applied to a variety of other discrete optimization problems. 5 Second is its diverse range of applications, in fields including mathematics, computer science, genetics, and engineering. 5,6

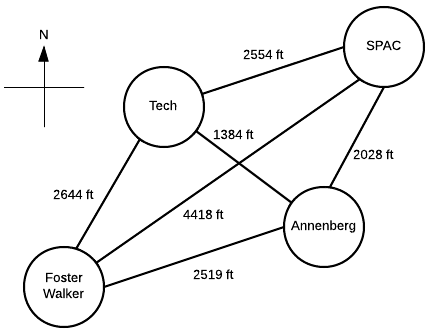
Suppose a Northwestern student, who lives in Foster-Walker , has to accomplish the following tasks:

• Drop off a homework set at Tech
• Work out a SPAC
• Complete a group project at Annenberg

Distances between buildings can be found using Google Maps. Note that there is particularly strong western wind and walking east takes 1.5 times as long.

It is the middle of winter and the student wants to spend the least possible time walking. Determine the path the student should take in order to minimize walking time, starting and ending at Foster-Walker.

Start with the cost matrix (with altered distances taken into account):

Method 1: Complete Enumeration

All possible paths are considered and the path of least cost is the optimal solution. Note that this method is only feasible given the small size of the problem.

From inspection, we see that Path 4 is the shortest. So, the student should walk 2.28 miles in the following order: Foster-Walker → Annenberg → SPAC → Tech → Foster-Walker

Method 2: Nearest neighbor

Starting from Foster-Walker, the next building is simply the closest building that has not yet been visited. With only four nodes, this can be done by inspection:

• Smallest distance is from Foster-Walker is to Annenberg
• Smallest distance from Annenberg is to Tech
• Smallest distance from Tech is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to Foster-Walker ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to SPAC
• Smallest distance from SPAC is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Tech ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Foster-Walker

So, the student would walk 2.54 miles in the following order: Foster-Walker → Annenberg → Tech → SPAC → Foster-Walker

Method 3: Greedy

With this method, the shortest paths that do not create a subtour are selected until a complete tour is created.

• Smallest distance is Annenberg → Tech
• Next smallest is SPAC → Annenberg
• Next smallest is Tech → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Anneberg → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is SPAC → Tech ( creates a subtour, therefore skip )
• Next smallest is Tech → Foster-Walker
• Next smallest is Annenberg → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Tech → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Tech ( creates a subtour, therefore skip )
• Next smallest is SPAC → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → SPAC

So, the student would walk 2.40 miles in the following order: Foster-Walker → SPAC → Annenberg → Tech → Foster-Walker

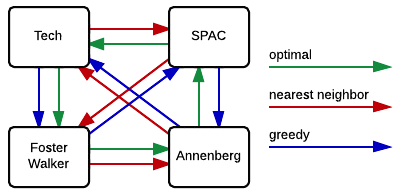
As we can see in the figure to the right, the heuristic methods did not give the optimal solution. That is not to say that heuristics can never give the optimal solution, just that it is not guaranteed.

Both the optimal and the nearest neighbor algorithms suggest that Annenberg is the optimal first building to visit. However, the optimal solution then goes to SPAC, while both heuristic methods suggest Tech. This is in part due to the large cost of SPAC → Foster-Walker. The heuristic algorithms cannot take this future cost into account, and therefore fall into that local optimum.

We note that the nearest neighbor and greedy algorithms give solutions that are 11.4% and 5.3%, respectively, above the optimal solution. In the scale of this problem, this corresponds to fractions of a mile. We also note that neither heuristic gave the worst case result, Foster-Walker → SPAC → Tech → Annenberg → Foster-Walker.

Only tour building heuristics were used. Combined with a tour improvement algorithm (such as 2-opt or simulated annealing), we imagine that we may be able to locate solutions that are closer to the optimum.

The exact algorithm used was complete enumeration, but we note that this is impractical even for 7 nodes (6! or 720 different possibilities). Commonly, the problem would be formulated and solved as an ILP to obtain exact solutions.

• Vanderbei, R. J. (2001). Linear programming: Foundations and extensions (2nd ed.). Boston: Kluwer Academic.
• Schrijver, A. (n.d.). On the history of combinatorial optimization (till 1960).
• Matai, R., Singh, S., & Lal, M. (2010). Traveling salesman problem: An overview of applications, formulations, and solution approaches. In D. Davendra (Ed.), Traveling Salesman Problem, Theory and Applications . InTech.
• Junger, M., Liebling, T., Naddef, D., Nemhauser, G., Pulleyblank, W., Reinelt, G., Rinaldi, G., & Wolsey, L. (Eds.). (2009). 50 years of integer programming, 1958-2008: The early years and state-of-the-art surveys . Heidelberg: Springer.
• Cook, W. (2007). History of the TSP. The Traveling Salesman Problem . Retrieved from http://www.math.uwaterloo.ca/tsp/history/index.htm
• Punnen, A. P. (2002). The traveling salesman problem: Applications, formulations and variations. In G. Gutin & A. P. Punnen (Eds.), The Traveling Salesman Problem and its Variations . Netherlands: Kluwer Academic Publishers.
• Laporte, G. (1992). The traveling salesman problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59 (2), 231–247.
• Goyal, S. (n.d.). A suvey on travlling salesman problem.

Navigation menu

Forgot password? New user? Sign up

Existing user? Log in

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

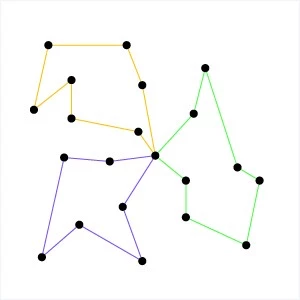
The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with \(n\) cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are \(4!\), or 24, paths. However, if the size of this map is increased to 20 cities, there will be \(1.22 \cdot 10^{17}\) paths!

The greedy approach to TSP would go like this:

• Find all possible paths.
• Find the cost of every paths.
• Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of \(O(n!)\). However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at \(O(n^2 2^n)\). Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a \(3/2\) approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then \(P = NP\). As it stands, most scientists believe that \(P \ne NP\).

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

Algorithms for the Travelling Salesman Problem

The Traveling Salesman Problem (TSP) is the challenge of finding the shortest path or shortest route for a salesperson to take, given a starting point, a number of cities (nodes), and optionally an ending point. It is a well-known algorithmic problem in the fields of computer science and operations research, with important real-world applications for logistics and delivery businesses.

There are obviously a lot of different routes to choose from, but finding the best one—the one that will require the least distance or cost—is what mathematicians and computer scientists have spent decades trying to solve.

It’s much more than just an academic problem. Finding more efficient routes using route optimization algorithms increases profitability for delivery businesses, and reduces greenhouse gas emissions because it means less distance traveled.

In theoretical computer science, the TSP has commanded so much attention because it’s so easy to describe yet so difficult to solve. The TSP is known to be a combinatorial optimization problem that’s an NP-hard problem, which means that the number of possible solution sequences grows exponential with the number of cities. Computer scientists have not found any algorithm that can solve this problem in polynomial time, and therefore rely on approximation algorithms to try numerous permutations and select the shortest route with the minimum cost.

The main problem can be solved by calculating every permutation using a brute force approach and selecting the optimal solution. However, as the number of destinations increases, the corresponding number of roundtrips grows exponentially and surpasses the capabilities of even the fastest computers. With 10 destinations, there can be more than 300,000 roundtrip permutations. With 15 destinations, the number of possible routes could exceed 87 billion.

For larger real-world travelling salesman problems, when manual methods such as Google Maps Route Planner or Excel route planner no longer suffice, businesses rely on approximate solutions that are sufficiently optimized by using fast tsp algorithms that rely on heuristics. Finding the exact optimal solution using dynamic programming is usually not practical for large problems.

Three popular Travelling Salesman Problem Algorithms

Here are some of the most popular solutions to the Travelling Salesman Problem:

1. The brute-force approach

The Brute Force approach, also known as the Naive Approach, calculates and compares all possible permutations of routes or paths to determine the shortest unique solution. To solve the TSP using the Brute-Force approach, you must calculate the total number of routes and then draw and list all the possible routes. Calculate the distance of each route and then choose the shortest one—this is the optimal solution. 

This is only feasible for small problems, rarely useful beyond theoretical computer science tutorials.

2. The branch and bound method

The branch and bound algorithm starts by creating an initial route, typically from the starting point to the first node in a set of cities. Then, it systematically explores different permutations to extend the route one node at a time. Each time a new node is added, the algorithm calculates the current path's length and compares it to the optimal route found so far. If the current path is already longer than the optimal route, it "bounds" or prunes that branch of the exploration, as it would not lead to a more optimal solution.

This pruning is the key to making the algorithm efficient. By discarding unpromising paths, the search space is narrowed down, and the algorithm can focus on exploring only the most promising paths. The process continues until all possible routes are explored, and the shortest one is identified as the optimal solution to the traveling salesman problem. Branch and bound is an effective greedy approach for tackling NP-hard optimization problems like the travelling salesman problem.

3. The nearest neighbor method

To implement the Nearest Neighbor algorithm, we begin at a randomly selected starting point. From there, we find the closest unvisited node and add it to the sequencing. Then, we move to the next node and repeat the process of finding the nearest unvisited node until all nodes are included in the tour. Finally, we return to the starting city to complete the cycle.

While the Nearest Neighbor approach is relatively easy to understand and quick to execute, it rarely finds the optimal solution for the traveling salesperson problem. It can be significantly longer than the optimal route, especially for large and complex instances. Nonetheless, the Nearest Neighbor algorithm serves as a good starting point for tackling the travelling salesman problem and can be useful when a quick and reasonably good solution is needed.

This greedy algorithm can be used effectively as a way to generate an initial feasible solution quickly, to then feed into a more sophisticated local search algorithm, which then tweaks the solution until a given stopping condition.  ‍

How route optimization algorithms work to solve the Travelling Salesman Problem.

Academic tsp solutions.

Academics have spent years trying to find the best solution to the Travelling Salesman Problem The following solutions were published in recent years:

• Machine learning speeds up vehicle routing : MIT researchers apply Machine Learning methods to solve large np-complete problems by solving sub-problems.
• Zero Suffix Method : Developed by Indian researchers, this method solves the classical symmetric TSP. 
• Biogeography‐based Optimization Algorithm : This method is designed based on the animals’ migration strategy to solve the problem of optimization. 
• Meta-Heuristic Multi Restart Iterated Local Search (MRSILS): The proponents of this research asserted that the meta-heuristic MRSILS is more efficient than the Genetic Algorithms when clusters are used. 
• Multi-Objective Evolutionary Algorithm : This method is designed for solving multiple TSP based on NSGA-II. 
• Multi-Agent System : This system is designed to solve the TSP of N cities with fixed resource. 

Real-world TSP applications

Despite the complexity of solving the Travelling Salesman Problem, it still finds applications in all verticals. 

For example, TSP solutions can help the logistics sector improve efficiency in the last mile. Last mile delivery is the final link in a supply chain, when goods move from a transportation hub, like a depot or a warehouse, to the end customer. Last mile delivery is also the leading cost driver in the supply chain. It costs an average of $10.1, but the customer only pays an average of $8.08 because companies absorb some of the cost to stay competitive. So bringing that cost down has a direct effect on business profitability.  

Minimizing costs in last mile delivery is essentially in last mile delivery is essentially a Vehicle Routing Problem (VRP). VRP, a generalized version of the travelling salesman problem, is one of the most widely studied problems in mathematical optimization. Instead of one best path, it deals with finding the most efficient set of routes or paths. The problem may involve multiple depots, hundreds of delivery locations, and several vehicles. As with the travelling salesman problem, determining the best solution to VRP is NP-complete.

Real-life TSP and VRP solvers

While academic solutions to TSP and VRP aim to provide the optimal solution to these NP-hard problems, many of them aren’t practical when solving real world problems, especially when it comes to solving last mile logistical challenges.

That’s because academic solvers strive for perfection and thus take a long time to compute the optimal solutions – hours, days, and sometimes years. If a delivery business needs to plan daily routes, they need a route solution within a matter of minutes. Their business depends on delivery route planning software so they can get their drivers and their goods out the door as soon as possible. Another popular alternative is to use Google maps route planner .

Real-life TSP and VRP solvers use route optimization algorithms that find a near-optimal solutions in a fraction of the time, giving delivery businesses the ability to plan routes quickly and efficiently.

If you want to know more about real-life TSP and VRP solvers, check out the resources below 👇

Route Optimization API - TSP Solver

Route Optimization API - VRP Solver

Frequently Asked Questions

Related articles.

Liked this article? See below for more recommended reading!

Solving the Vehicle Routing Problem (2024)

What Is Route Optimization?

How To Optimize Multi-Stop Routes With Google Maps (2024)

Try RoadWarrior free for 7 days

Solving the Traveling Salesman Problem

Get home early with RoadWarrior.

Enter your stops, optimize your routes, manage your team – quickly and efficiently.

Imagine a salesman who needs to visit multiple cities, but he wants to minimize the distance traveled and return to the starting point. This classic problem, known as the Traveling Salesman Problem (TSP), has been a subject of study for over a century. The applications of TSP are widespread, from logistics and agriculture to astronomy and computer-generated art. In this blog post, we will delve into the world of the Traveling Salesman Problem, exploring its history, algorithms, and real-world applications.

Short Summary

• The Traveling Salesman Problem is a complex problem of finding an optimal route for a round trip.
• Solutions to the TSP include NP-hard classification, brute force approach, dynamic programming and Christofides’ Algorithm.
• Route planning software such as OptimoRoute provide businesses with efficient tools for tackling the TSP, thereby improving their operations and saving resources.

Understanding the Traveling Salesman Problem

The Traveling Salesman Problem (TSP) is a problem of determining the most efficient route for a round trip, with the objective of maintaining the minimum cost and distance traveled. It serves as a foundational problem to test the limits of efficient computation in theoretical computer science.

The salesman’s objective in the TSP is to find a minimum weight Hamiltonian cycle, which maintains both the travel costs and the distance traveled at a minimum.

Theoretical Background

The TSP is classified as an NP-hard problem. This shows that the number of solution sequences grows rapidly with the number of cities. The brute force approach to resolving the TSP involves examining each round-trip route to ascertain the shortest one. However, as the number of cities increases, the number of round-trips to check can quickly surpass the capability of the most powerful computers. This limitation has led to the development of more sophisticated algorithms to tackle the TSP, such as dynamic programming and approximation algorithms.

The Hamiltonian Cycle Problem, also known as the Hamiltonian cycle problem, inquires whether there exists a closed walk in a graph that visits each vertex precisely once and is closely related to the TSP. Both problems have been studied extensively by computer scientists due to their implications in complexity theory and the P versus NP problem.

Optimal vs. Approximate Solutions

In solving the TSP, there is a distinction between optimal solutions and approximate solutions. Optimal solutions are the most advantageous route, while approximate solutions are round-trip routes whose lengths approach that of the most advantageous route. The brute force approach involves determining every potential solution and subsequently selecting the most advantageous one. However, this method is computationally intractable for large TSP instances.

One notable approximate solution is Christofides’ algorithm, which begins by determining the shortest spanning tree and subsequently converting it into a round-trip route. This algorithm guarantees a response that is, at most, 1.5 times the optimal solution. While not always yielding the optimal solution, approximate algorithms like Christofides’ algorithm provide a more feasible approach to solving the TSP.

Evolution of TSP Algorithms

TSP algorithms have been in existence since the 1950s, when the initial brute force approach was formulated. Subsequently, more sophisticated techniques such as dynamic programming and Christofides’ algorithm have been developed. These advanced algorithms have enabled researchers and practitioners to find near-optimal solutions to the TSP more quickly and efficiently.

By leveraging these algorithms, it is possible to solve the TSP in a fraction of the time.

Brute Force Approach

The brute force approach to TSP involves attempting all potential solutions, making it the most time-consuming and expensive method. As the number of destinations increases, the number of roundtrips likewise increases exponentially, rendering it computationally intractable even for the most powerful computers. Therefore, the brute force approach is not considered to be a viable solution for large TSP instances.

Despite its limitations, the brute force approach serves an important role in the history of TSP algorithms. It represents the initial attempt to solve the TSP and laid the groundwork for the development of more advanced and efficient algorithms.

Dynamic Programming

Dynamic programming is a technique employed to address intricate issues by segmenting them into more manageable subproblems and resolving them one at a time. It is regularly utilized to resolve the Traveling Salesman Problem due to its ability to avoid redundant calculations and identify the shortest route that visits all cities exactly once. The dynamic programming approach is more scalable than the brute force approach, as it can be employed to solve problems of any size.

However, dynamic programming is not without its limitations. It can be computationally expensive and time-consuming, as it necessitates solving a substantial number of subproblems. Despite these drawbacks, dynamic programming remains a popular and effective method for solving the TSP.

Christofides’ Algorithm

Christofides’ algorithm is an algorithm for obtaining approximate solutions to the Traveling Salesman Problem. It involves constructing a minimum spanning tree and then discovering a minimum-weight perfect matching on the odd-degree vertices of the tree. This algorithm, developed in the 1970s, utilizes a combination of graph theory and heuristics to address the TSP.

The significance of Christofides’ algorithm lies in its ability to yield routes that are guaranteed to be no more than 50 percent longer than the shortest route. While it may not always provide the optimal solution, its development marked a substantial improvement in the pursuit of efficient TSP algorithms.

Recent Advances in TSP Algorithms

In recent years, computer scientists have made significant advancements in TSP algorithms. These breakthroughs include:

• Approximation algorithms
• Metaheuristic approaches
• Local search operators
• Anytime Automatic Algorithm Selection

These cutting-edge algorithms have enabled researchers to find even more efficient solutions to the TSP, further demonstrating the importance of continued research and development in this area.

Geometry of Polynomials

Oveis Gharan and Nathan Klein used the geometry of polynomials approach to solve the TSP by representing the problem as a polynomial with variables corresponding to the edges between all the cities. This approach permits the utilization of geometric techniques and algorithms to discover an optimal or approximate solution to the problem, including determining the starting and ending point of the route.

This innovative method showcases the potential for leveraging mathematical techniques and geometrical properties in solving the TSP. As research progresses, it is expected that even more efficient algorithms and approaches will be developed, further pushing the boundaries of our understanding of the TSP.

Fractional Solutions and Rounding Techniques

Amin Saberi and Arash Asadpour developed a general rounding technique that employs randomness in an attempt to select a whole-number solution that preserves as many characteristics of the fractional solution as possible. The use of fractional solutions and rounding techniques can be utilized to construct effective approximation algorithms for the TSP.

Saberi, Gharan, and Singh implemented this general rounding technique to formulate a new approximation algorithm for the TSP. As computer scientists continue to explore new approaches and techniques, it is likely that even more powerful and efficient algorithms will be developed to tackle the complex TSP.

Practical Applications of TSP Solutions

TSP solutions are employed in a variety of industries, including logistics, astronomy, agriculture, and vehicle routing. Its applications range from planning efficient delivery routes and optimizing telescope trajectories to designing microchips and creating computer-generated art.

The widespread use of TSP solutions underscores the importance of continued research and development in this area, as advancements in TSP algorithms have the potential to positively impact numerous sectors.

Route Optimization

Route optimization is the process of determining the most efficient routes for various applications. In logistics, for example, TSP solutions can assist in enhancing efficiency in the last mile. By employing optimization techniques, businesses can reduce the number of stops, minimize total distance traveled, and ultimately save on fuel and labor costs.

The Vehicle Routing Problem (VRP), a generalized form of the TSP, focuses on discovering the most efficient set of routes or paths for multiple vehicles and hundreds of delivery locations. By utilizing TSP solutions and optimization techniques, companies can greatly improve their overall efficiency and productivity, leading to significant cost savings and improved customer service.

Last-Mile Delivery Challenges

The last-mile delivery problem refers to the final stage of a supply chain. It involves transporting goods from a transportation hub, such as a depot or warehouse, to the ultimate recipient. TSP solutions play a crucial role in addressing this challenge by optimizing delivery routes, reducing the number of stops, and minimizing total distance traveled.

For example, the Traveling Salesman Problem with Time Windows (TSPTW) approach considers specific time constraints for each delivery location, ensuring that deliveries are made within a specified time frame. By employing TSP algorithms and optimization techniques, businesses can:

• Overcome last-mile delivery challenges
• Improve overall efficiency
• Achieve cost savings
• Enhance customer satisfaction

TSP Solvers for Real-World Problems

Modern TSP solvers use advanced algorithms to provide near-optimal solutions quickly. These solvers include the routingpy library, real-life TSP and VRP solvers, and state-of-the-art TSP solvers based on local search.

By leveraging these powerful algorithms, businesses and researchers can tackle real-world TSP problems with greater efficiency and accuracy.

Branch and Bound Method

The branch and bound method is an algorithm utilized to address optimization problems, such as the TSP. It functions by exhaustively examining all potential solutions and identifying the most advantageous one. By dividing the problem into smaller subproblems and determining the optimal solution for each subproblem, the branch and bound method permits a more efficient and precise resolution to the problem.

Although the branch and bound method is computationally expensive, it has several advantages, such as being relatively straightforward to implement and capable of addressing large-scale problems. Its application in solving real-life TSP instances showcases its potential in effectively optimizing routes and minimizing costs.

Nearest Neighbor Method

The Nearest Neighbor algorithm is a greedy algorithm that finds the closest unvisited node and adds it to the sequencing until all nodes are included in the tour. While it rarely yields the optimal solution, particularly for large and intricate instances, it can be utilized effectively as a means to generate an initial feasible solution quickly.

This initial solution can then be supplied into a more sophisticated local search algorithm for further optimization. The Nearest Neighbor algorithm demonstrates that even relatively simple algorithms can play a valuable role in providing quick and feasible solutions to real-world TSP problems.

Route Planning Software for TSP

Utilizing route planning software to solve TSP problems in various industries offers numerous benefits. These software solutions, such as Route4Me, leverage advanced algorithms like Dijkstra’s Algorithm to quickly identify the most efficient route for a team.

By implementing route planning software, businesses can improve efficiency, reduce costs, and enhance customer satisfaction.

Advantages of Route Planning Software

Route planning software can help businesses in the following ways:

• Optimize routes
• Decrease the number of stops
• Minimize the total distance traveled
• Increase efficiency and productivity
• Reduce fuel and labor costs by optimizing routes and minimizing the time spent on route planning and decision-making.

Improved customer service is another benefit of route planning software. By optimizing routes and ensuring timely deliveries, businesses can enhance their reputation and build customer loyalty. In an increasingly competitive market, utilizing route planning software can give businesses a critical edge in delivering exceptional service and maintaining customer satisfaction.

Examples of Route Planning Solutions

There are numerous route planning solutions available for addressing the TSP, including vehicle routing software, optimization algorithms, and Excel sheets with order details and addresses. These solutions offer businesses a variety of options to choose from, depending on their specific needs and requirements.

Some examples of popular route planning software include OptimoRoute and Straightaway. These software solutions can help businesses tackle TSP problems efficiently, saving time and resources while improving overall operations. By leveraging advanced algorithms and powerful tools, route planning software provides a valuable solution for businesses looking to optimize their logistics and delivery processes.

Throughout this blog post, we have explored the fascinating world of the Traveling Salesman Problem, delving into its history, algorithms, and practical applications. From the early brute force approach to modern approximation algorithms and route planning software, the TSP continues to challenge and inspire researchers, computer scientists, and businesses alike. As we continue to push the boundaries of our understanding of the TSP, the potential for new and innovative solutions to real-world problems remains vast and exciting.

Frequently Asked Questions

Has anyone solved the traveling salesman problem.

No one has successfully come up with an algorithm to efficiently solve every traveling salesman problem, despite notable progress being made over the years.

What is the Traveling Salesman Problem (TSP)?

The Traveling Salesman Problem is an optimization problem that seeks to determine the most efficient route for a round trip, with the aim of minimizing cost and distance traveled.

What are some examples of industries that benefit from TSP solutions?

TSP solutions are widely used in industries such as logistics, astronomy, agriculture, and vehicle routing, providing a range of benefits.

What is the difference between optimal and approximate solutions in TSP?

Optimal solutions in TSP provide the most advantageous route, while approximate solutions offer a similar route whose length is close to that of the optimal solution.

These solutions can be used to solve a variety of problems, such as finding the shortest route between two cities or the most efficient way to deliver goods. They can also be used to optimize the use of resources, such as time and money.

What is an example of a modern TSP solver?

Routingpy is an example of a modern TSP solver, providing comprehensive tools to address the Traveling Salesman Problem and Vehicle Routing Problem.

It offers a range of features, including an intuitive user interface, fast computation times, and a wide range of optimization algorithms. It also provides a comprehensive set of tools for analyzing and visualizing the results of the optimization process.

Related Articles

Circuit route planner: an unbiased review for 2024.

8 minute read

Ranking the Best Food Delivery Services That Pay the Most in 2024

11 minute read

Badger Maps: A Comprehensive Review

5 minute read