problem solving examples for geometric sequence

Geometric Sequences Problems with Solutions

Geometric sequences are used in several branches of applied mathematics to engineering, sciences, computer sciences, biology, finance... Problems and exercises involving geometric sequences, along with answers are presented.

Review OF Geometric Sequences

The sequence shown below

Problems with Solutions

Problem 1 Find the terms a 2 , a 3 , a 4 and a 5 of a geometric sequence if a 1 = 10 and the common ratio r = - 1. Solution to Problem 1: Use the definition of a geometric sequence \( a_2 = a_1 \times r = 10 (-1) = - 10 \\ a_3 = a_2 \times r = - 10 (-1) = 10 \\ a_4 = a_3 \times r = 10 (-1) = - 10 \\ a_5 = a_4 \times r = - 10 (-1) = 10 \)

Find the 10 th term of a geometric sequence if a 1 = 45 and the common ration r = 0.2. Solution to Problem 2: Use the formula \[ a_n = a_1 \times r^{n-1} \] that gives the n th term to find a 10 as follows \( a_{10} = 45 \times 0.2^{10-1} = 2.304 \times 10^{-5} \)

Find a 20 of a geometric sequence if the first few terms of the sequence are given by

Given the terms a 10 = 3 / 512 and a 15 = 3 / 16384 of a geometric sequence, find the exact value of the term a 30 of the sequence. Solution to Problem 4: We first use the formula for the n th term to write a 10 and a 15 as follows \( a_{10} = a_1 \times r^{10-1} = a_1 r^9 = 3 / 512 \\ \\ a_{15} = a_1 \times r^{15-1} = a_1 r^{14} = 3 / 16384 \) We now divide the terms a 10 and a 15 to write \( a_{15} / a_{10} = a_1 \times r^{14} / (a_1 \times r^9) = (3 / 16384) / (3 / 512) \) Simplify expressions in the above equation to obtain. r 5 = 1 / 32 which gives r = 1/2 We now use a 10 to find a 1 as follows. \( a_{10} = 3 / 512 = a_1 (1/2)^9 \) Solve for a 1 to obtain. \( a_1 = 3 \) We now use the formula for the n th term to find a 30 as follows. \( a_{30} = 3(1/2)^{29} = 3 / 536870912 \)

Find the sum \[ S = \sum_{k=1}^{6} 3^{k - 1} \] Solution to Problem 5: We first rewrite the sum S as follows S = 1 + 3 + 9 + 27 + 81 + 243 = 364 Another method is to first note that the terms making the sum are those of a geometric sequence with a 1 = 1 and r = 3 using the formula s n = a 1 (1 - r n ) / (1 - r) with n = 6. s 6 = 1 (1 - 3 6 ) / (1 - 3) = 364

Find the sum \[ S = \sum_{i=1}^{10} 8 \times (1/4)^{i - 1} \] Solution to Problem 6: An examination of the terms included in the sum are 8 , 8× ((1/4) 1 , 8×((1/4) 2 , ... , 8×((1/4) 9 These are the terms of a geometric sequence with a 1 = 8 and r = 1/4 and therefore we can use the formula for the sum of the terms of a geometric sequence s 10 = a 1 (1 - r n ) / (1 - r) = 8 × (1 - (1/4) 10 ) / (1 - 1/4) = 10.67 (rounded to 2 decimal places)

Write the rational number 5.31313131... as the ratio of two integers. Solution to Problem 7: We first write the given rational number as an infinite sum as follows 5.313131... = 5 + 0.31 + 0.0031 + 0.000031 + .... The terms making 0.31 + 0.0031 + 0.000031 ... are those of a geometric sequence with a 1 = 0.31 and r = 0.01. Hence the use of the formula for an infinite sum of a geometric sequence S = a 1 / (1 - r) = 0.31 / (1 - 0.01) = 0.31 / 0.99 = 31 / 99 We now write 5.313131... as follows 5.313131... = 5 + 31/99 = 526 / 99

Exercises with Answers

Answer the following questions related to geometric sequences: a) Find a 20 given that a 3 = 1/2 and a 5 = 8 b) Find a 30 given that the first few terms of a geometric sequence are given by -2 , 1 , -1/2 , 1/4 ... c) Find r given that a 1 = 10 and a 20 = 10 -18 d) write the rational number 0.9717171... as a ratio of two positive integers.

a) a 20 = 2 18 b) a 30 = 1 / 2 28 c) r = 0.1 d) 0.9717171... = 481/495

More References and links

• Arithmetic Sequences Problems with Solutions
• math problems with detailed solutions
• Math Tutorials and Problems

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Geometric Sequences

Here we will learn what a geometric sequence is, how to continue a geometric sequence, how to find missing terms in a geometric sequence, and how to generate a geometric sequence.

At the end, you’ll find geometric sequence worksheets based on Edexcel, AQA, and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a geometric sequence?

A geometric sequence (geometric progression) is an ordered set of numbers that progresses by multiplying or dividing each term by a common ratio.

If we multiply or divide by the same number each time to make the sequence, it is a geometric sequence .

The common ratio is the same for any two consecutive terms in the same sequence.

Here are a few examples,

What are geometric sequences?

Geometric sequence formula

The geometric sequence formula is,

Where, 

\pmb{ a_{n} } is the n^{th} term (general term),

\pmb{ a_{1} } is the first term,

\pmb{ n } is the term position,

and \pmb{ r } is the common ratio.

We get the geometric sequence formula by looking at the following example,

We can see the common ratio (r) is 2 , so r = 2 .

a_{1} is the first term which is 5 ,

a_{2} is the second term which is 10 ,

and a_{3} is the third term which is 20 etc.

However we can write this using the common difference of 2 ,

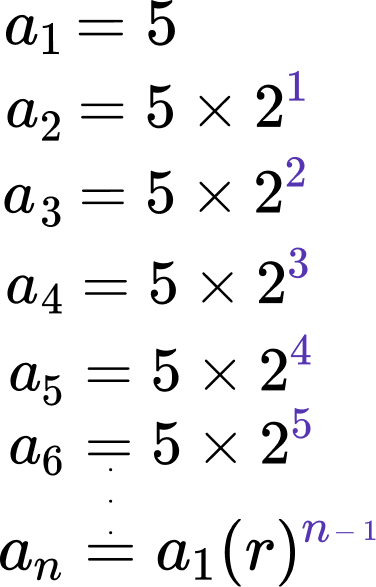
Related lessons on sequences

Geometric sequences  is part of our series of lessons to support revision on  sequences . You may find it helpful to start with the main sequences lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Quadratic sequences
• Arithmetic sequence
• Nth term of a sequence
• Recurrence relation
• Quadratic nth term

How to continue a geometric sequence

To continue a geometric sequence, you need to calculate the common ratio. This is the factor that is used to multiply one term to get the next term. To calculate the common ratio and continue a geometric sequence you need to:

Take two consecutive terms from the sequence.

• Divide the second term by the first term to find the common ratio r .

Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.

Explain how to continue a geometric sequence

Geometric sequences worksheet

Get your free geometric sequences worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Continuing a geometric sequence examples

Example 1: continuing a geometric sequence.

Calculate the next three terms for the geometric progression 1, 2, 4, 8, 16, …

Here we will take the numbers 4 and 8 .

2 Divide the second term by the first term to find the value of the common ratio, r .

3 Multiply the last term in the sequence by the common ratio to find the next term. Repeat for each new term.

The next three terms in the sequence are 32, 64, and 128 .

Example 2: continuing a geometric sequence with negative numbers

Calculate the next three terms for the sequence -2, -10, -50, -250, -1250, …

Here we will take the numbers -10 and -50 .

Divide the second term by the first term to find the common ratio, r.

The next three terms are -6250, -31250, and -156250.

Example 3: continuing a geometric sequence with decimals

Calculate the next three terms for the sequence 100, 10, 1, 0.1, 0.01, …

Here we will take the numbers 0.1 and 0.01 .

Divide the second term by the first term to find the common ratio, r .

The next three terms in the sequence are 0.001, 0.0001, and 0.00001.

Example 4: continuing a geometric sequence involving fractions

Calculate the next three terms for the sequence

Here we will take the numbers 5 and 2\frac{1}{2} .

The next three terms are

\frac{5}{16}, \frac{5}{32}, and \frac{5}{64} .

 Geometric sequence practice questions – continue the sequence

1. Write the next three terms of the sequence 0.5, 5, 50, 500, …

Choose two consecutive terms. For example, 5 and 50 .

Common ratio,

2. Write the next three terms of the sequence 0.04, 0.2, 1, 5, 25, …

Choose two consecutive terms. For example, 5 and 25 .

3. Calculate the next 3 terms of the sequence -1, -3, -9, -27, -81, …

Choose two consecutive terms. For example, -27 and -9 .

4. By finding the common ratio, state the next 3 terms of the sequence 640, 160, 40, 10, 2.5 .

Choose two consecutive terms. For example, 40 and 10 .

5. Work out the common ratio and therefore the next three terms in the sequence 36, 12, 4, \frac{4}{3}, \frac{4}{9}, …

Choose two consecutive terms. For example, 12 and 4 .

6. Find the common ratio and hence calculate the next three terms of the sequence 1, -1, 1, -1, 1, …

Choose two consecutive terms. For example, -1 and 1 .

How to find missing numbers in a geometric sequence

The common ratio can be used to find missing numbers in a geometric sequence. To find missing numbers in a geometric sequence you need to:

Calculate the common ratio between two consecutive terms.

• Multiply the term before any missing value by the common ratio.

Divide the term after any missing value by the common ratio.

Repeat Steps 2 and 3 until all missing values are calculated. You may only need to use Step 2 or 3 depending on what terms you have been given.

Explain how to find missing numbers in a geometric sequence

Finding missing numbers in a geometric sequence examples

Example 5: find the missing numbers in the geometric sequence.

Fill in the missing terms in the sequence 7, 14, …, …,112 .

  Multiply the term before any missing value by the common ratio.

The missing terms are 28 and 56 .

Note: Here, you could repeat Step 2 by using 28 \times 2 = 56.

Example 6: find the missing numbers in a geometric sequence including decimals

Find the missing values in the sequence 0.4, …, ..., 137.2, 960.4.

  Divide the term after any missing value by the common ratio.

The missing terms are 2.8 and 19.6 .

Example 7: find the missing numbers in a geometric sequence when there are multiple consecutive terms missing

Find the missing values in the sequence, -4, ..., …, -108,...

First, we need to find the factor between the two terms, -108 \div -4 = 27 .

To get from -108 to -4 , we jump 3 terms.

This means that -4 has been multiplied by the common ratio three times or -4 \times r \times r \times r = -4r^3 .

\begin{aligned} r^{3}&=27\\\\ r&=3 \end{aligned}

Note: Term -108 is already given.

The missing terms are -12, -36, and -324.

We don’t need to complete this step.

Example 8: find the missing numbers in a geometric sequence including mixed numbers

Find the missing values in the sequence

  Calculate the common ratio between two consecutive terms.

Repeat this step to find the next term.

40 \frac{1}{2} \times 3=121 \frac{1}{2}

The missing terms in the sequence are

1 \frac{1}{2}, 40 \frac{1}{2}, and 121 \frac{1}{2} .

 Geometric sequence practice questions – find missing numbers

1. Find the missing numbers in the geometric sequence 4, 2, …, 0.5, …

Choose two consecutive terms. For example, 4 and 2 .

2. Find the missing numbers in the sequence -7, -35, …, …, -4375

Choose two consecutive terms. For example, -7 and -35 .

3. Find the missing terms in the sequence 0.6, …, …, 0.075, 0.0375

Choose two consecutive terms. For example, 0.075 and 0.0375 .

4. Calculate the missing terms in the arithmetic sequence 2 \frac{1}{5}, \frac{11}{20}, \frac{11}{80}, \ldots, \ldots

Choose two consecutive terms. For example, \frac{11}{20} and \frac{11}{80} .

5. Work out the missing terms in the sequence 3, …, …, 24 .

3 has been multiplied by the common ratio, r, three times to get 24.

3 \times r \times r \times r=24 \text{ or } 3r^{3}=24 .

Solving the equation,

6. Work out the missing terms in the sequence 90, …, …, \frac{10}{3} .

90 has been multiplied by the common ratio, r, three times to get \frac{10}{3}.

90 \times r \times r \times r=\frac{10}{3} \text{ or } 90r^{3}=\frac{10}{3} .

How to generate a geometric sequence

In order to generate a geometric sequence, we need to know the n^{th} term. Using a as the first term of the sequence, r as the common ratio and n to represent the position of the term, the n^{th} term of a geometric sequence is written as ar^{n-1}.

Once we know the first term and the common ratio, we can work out any number of terms in the sequence.

The first term is found when n=1 , the second term when n=2 , the third term when n=3 and so on.

To generate a geometric sequence you need to:

• Substitute n=1 into the n^{th} term to calculate the first term.
• Substitute n=2 into the n^{th} term to calculate the second term.

Continue to substitute values for n until all the required terms of the sequence are calculated.

Explain how to generate a geometric sequence

Generating a geometric sequence examples

Example 9: generate a geometric sequence using the n th term.

Generate the first 5 terms of the sequence 4^{n-1} .

Substitute n = 1 into the n^{th} term to calculate the first term.

When n = 1,\quad 4^{1-1} = 4^{0} = 1 .

  Substitute n = 2 into the n^{th} term to calculate the second term.

When n = 2,\quad 4^{2-1 }= 4^{1} = 4 .

When n=3, \quad 4^{3-1}=4^{2}=16 .

When n=4, \quad 4^{4-1}=4^{3}=64 .

When n=5, \quad 4^{5-1}=4^{4}=256 .

The first 5 terms of the sequence are 1, 4, 16, 64, 256.

Example 10: generate a geometric sequence using a table

Complete the table for the first 5 terms of the arithmetic sequence 6 \times 2^{n-1}.

Example 11: generate larger terms in a geometric sequence

A geometric sequence has the n^{th} term \left(\frac{1}{2}\right)^{n} .

Calculate the 1^{st}, 2^{nd}, 10^{th} and 12^{th} terms in the sequence. Express your answers as fractions. 

When n=1,\quad \left(\frac{1}{2}\right)^{1}=\frac{1}{2} .

Substitute n = 2 into the n^{th} term to calculate the second term.

When n=2, \quad \left(\frac{1}{2}\right)^{2}=\frac{1}{4} .

When n=10,\quad \left(\frac{1}{2}\right)^{10}=\frac{1}{1024} .

When n=12,\quad \left(\frac{1}{2}\right)^{12}=\frac{1}{4096} .

The unknown terms are

1, \frac{1}{4}, \frac{1}{1024}, and \frac{1}{4096} .

Example 12: generate a geometric sequence with a negative common ratio

Generate the first 5 terms of the geometric sequence 2(- 3)^{n-1} .

When n=1, \quad 2(-3)^{n-1}=2(-3)^{1-1}=2(-3)^{0}=2 \times 1=2 .

When n=2,\quad 2(-3)^{n-1}=2(-3)^{2-1}=2(-3)^{1}=2 \times-3=-6 .

When n=3, \quad 2(-3)^{n-1}=2(-3)^{3-1}=2(-3)^{2}=2 \times 9=18 .

When n=4, \quad 2(-3)^{n-1}=2(-3)^{4-1}=2(-3)^{3}=2 \times-27=-54 .

When n=5, \quad 2(-3)^{n-1}=2(-3)^{5-1}=2(-3)^{4}=2 \times 81=162 .

The first 5 terms of the sequence are 2, -6, 18, -54, and 162 .

 Geometric sequence practice questions – generate a sequence

1. Generate the first 5 terms of the sequence 10^{n} .

When  n=1, 10^{1}=10 .

When n=2, 10^{2}=100 .

When n=3, 10^{3}=1000 .

When n=4, 10^{4}=10000 .

When n=5, 10^{5}=100000 .

2. Generate the first 5 terms of the sequence 5^{n-1} .

When n=1, 5^{1-1}=5^{0}=1 .

When n=2, 5^{2-1}=5^{1}=5 .

When n=3, 5^{3-1}=5^{2}=25 .

When n=4, 5^{4-1}=5^{3}=125 .

When n=5, 5^{5-1}=5^{4}=625  .

3. Generate the first 5 terms of the sequence 4 \times 3^{n-1} .

When n=1, 4 \times 3^{1-1}=4 \times 3^{0}=4 .

When n=2, 4 \times 3^{2-1}=4 \times 3^{1}=12 .

When n=3, 4 \times 3^{3-1}=4 \times 3^{2}=36 .

When n=4, 4 \times 3^{4-1}=4 \times 3^{3}=108 .

When n=5, 4 \times 3^{5-1}=4 \times 3^{4}=324  .

4. Generate the first 5 terms of the sequence \frac{3^{n}}{6} .

When n=1, \frac{3^1}{6}= \frac{1}{2} .

When n=2, \frac{3^2}{6}= \frac{9}{6} = 1 \frac{1}{2} .

When n=3, \frac{3^3}{6}= \frac{27}{6} = 4 \frac{1}{2} .

When n=4, \frac{3^4}{6}= \frac{81}{6} = 13 \frac{1}{2} .

When n=5, \frac{3^5}{6}= \frac{243}{6} = 40 \frac{1}{2}  .

5. Calculate the 1st, 3rd, 10th and 15th term of the sequence 2^{n} .

When n=1, 2^{1}= 2 .

When n=3, 2^{3}= 8 .

When n=10, 2^{10}= 1024 .

When n=15, 2^{15}= 32768 .

6. Calculate the first 5 terms of the sequence 3 \times (-5)^{n-1} .

When n=1, 3 \times (-5)^{1-1} = 3 \times (-5)^{0} = 3 .

When n=2, 3 \times (-5)^{2-1} = 3 \times (-5)^{1} = -15 .

When n=3, 3 \times (-5)^{3-1} = 3 \times (-5)^{2} = 75 .

When n=4, 3 \times (-5)^{4-1} = 3 \times (-5)^{3} = -375 .

When n=5, 3 \times (-5)^{5-1} = 3 \times (-5)^{4} = 1875 .

Geometric sequences GCSE exam questions

1. Which sequence is a geometric progression?

1, 3, 5, 7, 9,…. \quad \quad \quad 1, 3, 9, 27, 81, …..

1, 3, 6, 10, 15, …. \quad \quad 1, 0.6, 0.2, -0.2, -0.6,….

1, 3, 9, 27, 81, …..

2.  Here is a geometric progression,

1, -5, 25, …., 625, …

(a) Find the common ratio.

(b) Work out the fourth term of the sequence.

25 \div -5 = – 5

Common ratio = -5

25 \times -5

3.  A scientist is studying a type of bacteria. The number of bacteria over the first four days is shown below.

How many bacteria will there be on day 7?

180 \div 60 = 3

1620 \times 3 \times 3 \times 3

Common misconceptions

• Mixing up the common ratio with the common difference for arithmetic sequences

Although these two phrases are similar, each successive term in a geometric sequence of numbers is calculated by multiplying the previous term by a common ratio and not by adding a common difference.

• A negative value for r means that all terms in the sequence are negative

This is not always the case as when r is raised to an even power, the solution is always positive.

• The first term in a geometric sequence

The first term is a . With ar^{n-1} , the first term would occur when n = 1 and so the power of r would be equal to 0 . Anything to the power of 0 is equal to 1 , leaving a as the first term in the sequence. This is usually mistaken when a = 1 as it is not clearly noted in the question for example, 2^{n-1} is the same as 1 \times 2^{n-1} .

• Incorrect simplifying of the n th term

For example, 6 \times 3^{n-1} is incorrectly simplified to 18^{n-1} as 6 \times 3 = 18 .

• The difference between an arithmetic and a geometric sequence

Arithmetic sequences are formed by adding or subtracting the same number. Geometric sequences are formed by multiplying or dividing the same number.

Learning checklist

You have now learned how to:

• Recognise geometric sequences

The next lessons are

• Inequalities
• Functions in algebra
• Laws of indices

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

9.3 Geometric Sequences

Learning objectives.

In this section, you will:

• Find the common ratio for a geometric sequence.
• List the terms of a geometric sequence.
• Use a recursive formula for a geometric sequence.
• Use an explicit formula for a geometric sequence.

Many jobs offer an annual cost-of-living increase to keep salaries consistent with inflation. Suppose, for example, a recent college graduate finds a position as a sales manager earning an annual salary of $26,000. He is promised a 2% cost of living increase each year. His annual salary in any given year can be found by multiplying his salary from the previous year by 102%. His salary will be $26,520 after one year; $27,050.40 after two years; $27,591.41 after three years; and so on. When a salary increases by a constant rate each year, the salary grows by a constant factor. In this section, we will review sequences that grow in this way.

Finding Common Ratios

The yearly salary values described form a geometric sequence because they change by a constant factor each year. Each term of a geometric sequence increases or decreases by a constant factor called the common ratio . The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term.

Definition of a Geometric Sequence

A geometric sequence is one in which any term divided by the previous term is a constant. This constant is called the common ratio of the sequence. The common ratio can be found by dividing any term in the sequence by the previous term. If a 1 a 1 is the initial term of a geometric sequence and r r is the common ratio, the sequence will be

Given a set of numbers, determine if they represent a geometric sequence.

• Divide each term by the previous term.
• Compare the quotients. If they are the same, a common ratio exists and the sequence is geometric.

Is the sequence geometric? If so, find the common ratio.

• ⓐ 1 , 2 , 4 , 8 , 16 , ... 1 , 2 , 4 , 8 , 16 , ...
• ⓑ 48 , 12 , 4 ,  2 , ... 48 , 12 , 4 ,  2 , ...

Divide each term by the previous term to determine whether a common ratio exists.

The sequence is geometric because there is a common ratio. The common ratio is 2.

The sequence is not geometric because there is not a common ratio.

The graph of each sequence is shown in Figure 1 . It seems from the graphs that both (a) and (b) appear have the form of the graph of an exponential function in this viewing window. However, we know that (a) is geometric and so this interpretation holds, but (b) is not.

If you are told that a sequence is geometric, do you have to divide every term by the previous term to find the common ratio?

No. If you know that the sequence is geometric, you can choose any one term in the sequence and divide it by the previous term to find the common ratio.

Writing Terms of Geometric Sequences

Now that we can identify a geometric sequence, we will learn how to find the terms of a geometric sequence if we are given the first term and the common ratio. The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. For instance, if the first term of a geometric sequence is a 1 = − 2 a 1 = − 2 and the common ratio is r = 4, r = 4, we can find subsequent terms by multiplying − 2 ⋅ 4 − 2 ⋅ 4 to get − 8 − 8 then multiplying the result − 8 ⋅ 4 − 8 ⋅ 4 to get − 32 − 32 and so on.

The first four terms are { –2 ,  –8 ,  –32 ,  –128 } . { –2 ,  –8 ,  –32 ,  –128 } .

Given the first term and the common factor, find the first four terms of a geometric sequence.

• Multiply the initial term, a 1 , a 1 , by the common ratio to find the next term, a 2 . a 2 .
• Repeat the process, using a n = a 2 a n = a 2 to find a 3 a 3 and then a 3 a 3 to find a 4, a 4, until all four terms have been identified.
• Write the terms separated by commons within brackets.

Writing the Terms of a Geometric Sequence

List the first four terms of the geometric sequence with a 1 = 5 a 1 = 5 and r = –2. r = –2.

Multiply a 1 a 1 by − 2 − 2 to find a 2 . a 2 . Repeat the process, using a 2 a 2 to find a 3 , a 3 , and so on.

The first four terms are { 5 , –10 , 20 , –40 } . { 5 , –10 , 20 , –40 } .

List the first five terms of the geometric sequence with a 1 = 18 a 1 = 18 and r = 1 3 . r = 1 3 .

Using Recursive Formulas for Geometric Sequences

A recursive formula allows us to find any term of a geometric sequence by using the previous term. Each term is the product of the common ratio and the previous term. For example, suppose the common ratio is 9. Then each term is nine times the previous term. As with any recursive formula, the initial term must be given.

Recursive Formula for a Geometric Sequence

The recursive formula for a geometric sequence with common ratio r r and first term a 1 a 1 is

Given the first several terms of a geometric sequence, write its recursive formula.

• State the initial term.
• Find the common ratio by dividing any term by the preceding term.
• Substitute the common ratio into the recursive formula for a geometric sequence.

Write a recursive formula for the following geometric sequence.

The first term is given as 6. The common ratio can be found by dividing the second term by the first term.

Substitute the common ratio into the recursive formula for geometric sequences and define a 1 . a 1 .

The sequence of data points follows an exponential pattern. The common ratio is also the base of an exponential function as shown in Figure 2

Do we have to divide the second term by the first term to find the common ratio?

No. We can divide any term in the sequence by the previous term. It is, however, most common to divide the second term by the first term because it is often the easiest method of finding the common ratio.

Using Explicit Formulas for Geometric Sequences

Because a geometric sequence is an exponential function whose domain is the set of positive integers, and the common ratio is the base of the function, we can write explicit formulas that allow us to find particular terms.

Let’s take a look at the sequence { 18 ,  36 ,  72 ,  144 ,  288 ,  ... } . { 18 ,  36 ,  72 ,  144 ,  288 ,  ... } . This is a geometric sequence with a common ratio of 2 and an exponential function with a base of 2. An explicit formula for this sequence is

The graph of the sequence is shown in Figure 3 .

Explicit Formula for a Geometric Sequence

The n n th term of a geometric sequence is given by the explicit formula :

Writing Terms of Geometric Sequences Using the Explicit Formula

Given a geometric sequence with a 1 = 3 a 1 = 3 and a 4 = 24 , a 4 = 24 , find a 2 . a 2 .

The sequence can be written in terms of the initial term and the common ratio r . r .

Find the common ratio using the given fourth term.

Find the second term by multiplying the first term by the common ratio.

The common ratio is multiplied by the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by multiplying the first term by the common ratio nine times or by multiplying by the common ratio raised to the ninth power.

Given a geometric sequence with a 2 = 4 a 2 = 4 and a 3 = 32 a 3 = 32 , find a 6 . a 6 .

Writing an Explicit Formula for the n n th Term of a Geometric Sequence

Write an explicit formula for the n th n th term of the following geometric sequence.

The first term is 2. The common ratio can be found by dividing the second term by the first term.

The common ratio is 5. Substitute the common ratio and the first term of the sequence into the formula.

The graph of this sequence in Figure 4 shows an exponential pattern.

Write an explicit formula for the following geometric sequence.

Solving Application Problems with Geometric Sequences

In real-world scenarios involving geometric sequences, we may need to use an initial term of a 0 a 0 instead of a 1 . a 1 . In these problems, we can alter the explicit formula slightly by using the following formula:

In 2013, the number of students in a small school is 284. It is estimated that the student population will increase by 4% each year.

• ⓐ Write a formula for the student population.
• ⓑ Estimate the student population in 2020.

The situation can be modeled by a geometric sequence with an initial term of 284. The student population will be 104% of the prior year, so the common ratio is 1.04.

Let P P be the student population and n n be the number of years after 2013. Using the explicit formula for a geometric sequence we get

We can find the number of years since 2013 by subtracting.

We are looking for the population after 7 years. We can substitute 7 for n n to estimate the population in 2020.

The student population will be about 374 in 2020.

A business starts a new website. Initially the number of hits is 293 due to the curiosity factor. The business estimates the number of hits will increase by 2.6% per week.

• ⓐ Write a formula for the number of hits.
• ⓑ Estimate the number of hits in 5 weeks.

Access these online resources for additional instruction and practice with geometric sequences.

• Geometric Sequences
• Determine the Type of Sequence
• Find the Formula for a Sequence

9.3 Section Exercises

What is a geometric sequence?

How is the common ratio of a geometric sequence found?

What is the procedure for determining whether a sequence is geometric?

What is the difference between an arithmetic sequence and a geometric sequence?

Describe how exponential functions and geometric sequences are similar. How are they different?

For the following exercises, find the common ratio for the geometric sequence.

1 , 3 , 9 , 27 , 81 , ... 1 , 3 , 9 , 27 , 81 , ...

− 0.125 , 0.25 , − 0.5 , 1 , − 2 , ... − 0.125 , 0.25 , − 0.5 , 1 , − 2 , ...

− 2 , − 1 2 , − 1 8 , − 1 32 , − 1 128 , ... − 2 , − 1 2 , − 1 8 , − 1 32 , − 1 128 , ...

For the following exercises, determine whether the sequence is geometric. If so, find the common ratio.

− 6 , − 12 , − 24 , − 48 , − 96 , ... − 6 , − 12 , − 24 , − 48 , − 96 , ...

5 , 5.2 , 5.4 , 5.6 , 5.8 , ... 5 , 5.2 , 5.4 , 5.6 , 5.8 , ...

− 1 , 1 2 , − 1 4 , 1 8 , − 1 16 , ... − 1 , 1 2 , − 1 4 , 1 8 , − 1 16 , ...

6 , 8 , 11 , 15 , 20 , ... 6 , 8 , 11 , 15 , 20 , ...

0.8 , 4 , 20 , 100 , 500 , ... 0.8 , 4 , 20 , 100 , 500 , ...

For the following exercises, write the first five terms of the geometric sequence, given the first term and common ratio.

a 1 = 8 , r = 0.3 a 1 = 8 , r = 0.3

a 1 = 5 , r = 1 5 a 1 = 5 , r = 1 5

For the following exercises, write the first five terms of the geometric sequence, given any two terms.

a 7 = 64 , a 10 = 512 a 7 = 64 , a 10 = 512

a 6 = 25 , a 8 = 6.25 a 6 = 25 , a 8 = 6.25

For the following exercises, find the specified term for the geometric sequence, given the first term and common ratio.

The first term is 2, 2, and the common ratio is 3. 3. Find the 5 th term.

The first term is 16 and the common ratio is − 1 3 . − 1 3 . Find the 4 th term.

For the following exercises, find the specified term for the geometric sequence, given the first four terms.

a n = { − 1 , 2 , − 4 , 8 , ... } . a n = { − 1 , 2 , − 4 , 8 , ... } . Find a 12 . a 12 .

a n = { − 2 , 2 3 , − 2 9 , 2 27 , ... } . a n = { − 2 , 2 3 , − 2 9 , 2 27 , ... } . Find a 7 . a 7 .

For the following exercises, write the first five terms of the geometric sequence.

a 1 = − 486 , a n = − 1 3 a n − 1 a 1 = − 486 , a n = − 1 3 a n − 1

a 1 = 7 , a n = 0.2 a n − 1 a 1 = 7 , a n = 0.2 a n − 1

For the following exercises, write a recursive formula for each geometric sequence.

a n = { − 1 , 5 , − 25 , 125 , ... } a n = { − 1 , 5 , − 25 , 125 , ... }

a n = { − 32 , − 16 , − 8 , − 4 , ... } a n = { − 32 , − 16 , − 8 , − 4 , ... }

a n = { 14 , 56 , 224 , 896 , ... } a n = { 14 , 56 , 224 , 896 , ... }

a n = { 10 , − 3 , 0.9 , − 0.27 , ... } a n = { 10 , − 3 , 0.9 , − 0.27 , ... }

a n = { 0.61 , 1.83 , 5.49 , 16.47 , ... } a n = { 0.61 , 1.83 , 5.49 , 16.47 , ... }

a n = { 3 5 , 1 10 , 1 60 , 1 360 , ... } a n = { 3 5 , 1 10 , 1 60 , 1 360 , ... }

a n = { − 2 , 4 3 , − 8 9 , 16 27 , ... } a n = { − 2 , 4 3 , − 8 9 , 16 27 , ... }

a n = { 1 512 , − 1 128 , 1 32 , − 1 8 , ... } a n = { 1 512 , − 1 128 , 1 32 , − 1 8 , ... }

a n = − 4 ⋅ 5 n − 1 a n = − 4 ⋅ 5 n − 1

a n = 12 ⋅ ( − 1 2 ) n − 1 a n = 12 ⋅ ( − 1 2 ) n − 1

For the following exercises, write an explicit formula for each geometric sequence.

a n = { − 2 , − 4 , − 8 , − 16 , ... } a n = { − 2 , − 4 , − 8 , − 16 , ... }

a n = { 1 , 3 , 9 , 27 , ... } a n = { 1 , 3 , 9 , 27 , ... }

a n = { − 4 , − 12 , − 36 , − 108 , ... } a n = { − 4 , − 12 , − 36 , − 108 , ... }

a n = { 0.8 , − 4 , 20 , − 100 , ... } a n = { 0.8 , − 4 , 20 , − 100 , ... }

a n = { − 1.25 , − 5 , − 20 , − 80 , ... } a n = { − 1.25 , − 5 , − 20 , − 80 , ... }

a n = { − 1 , − 4 5 , − 16 25 , − 64 125 , ... } a n = { − 1 , − 4 5 , − 16 25 , − 64 125 , ... }

a n = { 2 , 1 3 , 1 18 , 1 108 , ... } a n = { 2 , 1 3 , 1 18 , 1 108 , ... }

a n = { 3 , − 1 , 1 3 , − 1 9 , ... } a n = { 3 , − 1 , 1 3 , − 1 9 , ... }

For the following exercises, find the specified term for the geometric sequence given.

Let a 1 = 4 , a 1 = 4 , a n = − 3 a n − 1 . a n = − 3 a n − 1 . Find a 8 . a 8 .

Let a n = − ( − 1 3 ) n − 1 . a n = − ( − 1 3 ) n − 1 . Find a 12 . a 12 .

For the following exercises, find the number of terms in the given finite geometric sequence.

a n = { − 1 , 3 , − 9 , ... , 2187 } a n = { − 1 , 3 , − 9 , ... , 2187 }

a n = { 2 , 1 , 1 2 , ... , 1 1024 } a n = { 2 , 1 , 1 2 , ... , 1 1024 }

For the following exercises, determine whether the graph shown represents a geometric sequence.

For the following exercises, use the information provided to graph the first five terms of the geometric sequence.

a 1 = 1 , r = 1 2 a 1 = 1 , r = 1 2

a 1 = 3 , a n = 2 a n − 1 a 1 = 3 , a n = 2 a n − 1

a n = 27 ⋅ 0.3 n − 1 a n = 27 ⋅ 0.3 n − 1

Use recursive formulas to give two examples of geometric sequences whose 3 rd terms are 200. 200.

Use explicit formulas to give two examples of geometric sequences whose 7 th terms are 1024. 1024.

Find the 5 th term of the geometric sequence { b , 4 b , 16 b , ... } . { b , 4 b , 16 b , ... } .

Find the 7 th term of the geometric sequence { 64 a ( − b ) , 32 a ( − 3 b ) , 16 a ( − 9 b ) , ... } . { 64 a ( − b ) , 32 a ( − 3 b ) , 16 a ( − 9 b ) , ... } .

At which term does the sequence { 10 , 12 , 14.4 , 17.28 , ... } { 10 , 12 , 14.4 , 17.28 , ... } exceed 100 ? 100 ?

At which term does the sequence { 1 2187 , 1 729 , 1 243 , 1 81 ... } { 1 2187 , 1 729 , 1 243 , 1 81 ... } begin to have integer values?

For which term does the geometric sequence a n = − 36 ( 2 3 ) n − 1 a n = − 36 ( 2 3 ) n − 1 first have a non-integer value?

Use the recursive formula to write a geometric sequence whose common ratio is an integer. Show the first four terms, and then find the 10 th term.

Use the explicit formula to write a geometric sequence whose common ratio is a decimal number between 0 and 1. Show the first 4 terms, and then find the 8 th term.

Is it possible for a sequence to be both arithmetic and geometric? If so, give an example.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra/pages/9-3-geometric-sequences

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Geometric Sequences? (+FREE Worksheet!)

Learn how to solve Geometric Sequence problems using the following step-by-step guide with detailed solutions.

Related Topics

• How to Solve Finite Geometric Series
• How to Solve Infinite Geometric Series
• How to Solve Arithmetic Sequences

Step by step guide to solve Geometric Sequence Problems

• It is a sequence of numbers where each term after the first is found by multiplying the previous item by the common ratio, a fixed, non-zero number. For example, the sequence \(2, 4, 8, 16, 32\), … is a geometric sequence with a common ratio of \(2\).
• To find any term in a geometric sequence use this formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\)
• \(a =\) the first term , \(r =\) the common ratio , \(n =\) number of items

Geometric Sequences – Example 1:

Given the first term and the common ratio of a geometric sequence find the first five terms of the sequence. \(a_1=3,r=-2\)

Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→x_{n}=0.8 .(-5)^{n-1}\) If \(n=1\) then: \(x_{1}=3 .(-2)^{1-1}=3 (1)=3\), First Five Terms: \(3,-6,12,-24,48\)

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Geometric sequences – example 2:.

Given two terms in a geometric sequence find the 8th term. \(a_{3}=10\) and \(a_{5}=40\)

Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_{3}=ar^{(3 – 1)}=ar^2=10\) \(x_{n}=ar^{(n – 1)}→a_5=ar^{(5 – 1)}=ar^4=40\) Now divide \(a_{5}\) by \(a_{3}\). Then: \(\frac{a_{5}}{a_{3}} =\frac{ar^4}{ar^2 }=\frac{40}{10}\), Now simplify: \(\frac{ar^4}{ar^2 }=\frac{40}{10}→r^2=4→r=2\) We can find a now: \(ar^2=12→a(2^2 )=10→a=2.5\) Use the formula to find the 8th term: \(x_{n}=ar^{(n – 1)}→a_8=(2.5) (2)^8=2.5(256)=640\)

Geometric Sequences – Example 3:

Given the first term and the common ratio of a geometric sequence find the first five terms of the sequence. \(a_{1}=0.8,r=-5\)

Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→x_{n}=0.8 .(-5)^{n-1}\) If \(n=1\) then: \(x_{1}=0.8 .(-5)^{1-1}=0.8 (1)=0.8\), First Five Terms: \(0.8,-4,20,-100,500\)

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

Geometric sequences – example 4:.

Given two terms in a geometric sequence find the 8th term. \(a_3=12\) and \(a_5=48\)

Use geometric sequence formula: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_3=ar^{(3 – 1)}=ar^2=12\) \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_5=ar^{(5 – 1)}=ar^4=48\) Now divide \(a_{5}\) by \(a_{3}\). Then: \(\frac{a_{5}}{a_{3} }=\frac{ar^4}{ar^2}=\frac{48}{12}\), Now simplify: \(\frac{ar^4}{ar^2}=\frac{48}{12}→r^2=4→r=2\) We can find a now: \(ar^2=12→a(2^2 )=12→a=3\) Use the formula to find the \(8^{th}\) term: \(\color{blue}{x_{n}=ar^{(n – 1)}}\) \(→a_{8}=(3) (2)^8=3(256)=768\)

Exercises for Solving Geometric Sequences

Determine if the sequence is geometric. if it is, find the common ratio..

• \(\color{blue}{1, – 5, 25, – 125, …}\)
• \(\color{blue}{– 2, – 4, – 8, – 16, …}\)
• \(\color{blue}{4, 16, 36, 64, …}\)
• \(\color{blue}{– 3, – 15, – 75, – 375, …}\)

Download Geometric Sequences Worksheet

• \(\color{blue}{r=-5}\)
• \(\color{blue}{r=2}\)
• \(\color{blue}{not \ geometric}\)
• \(\color{blue}{r=5}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• Top 10 GED Math Practice Questions
• Identify 3–Dimensional Figures
• 6th Grade Wisconsin Forward Math Worksheets: FREE & Printable
• The Ultimate SSAT Upper-Level Math Course (+FREE Worksheets)
• Objects on a Coordinate Plane
• How to Understand the Concept of Scale Changes: Area and Perimeter
• 8th Grade K-PREP Math Worksheets: FREE & Printable
• 10 Most Common ATI TEAS 7 Math Questions
• Top 10 Tips to Overcome SSAT Math Anxiety
• How to Decode Data Types

What people say about "How to Solve Geometric Sequences? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos
• Google Play
• Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Geometric Sequence

A geometric sequence is a special type of sequence. It is a sequence in which every term (except the first term) is multiplied by a constant number to get its next term. i.e., To get the next term in the geometric sequence, we have to multiply with a fixed term (known as the common ratio), and to find the preceding term in the sequence, we just have to divide the term by the same common ratio. Here is an example of a geometric sequence is 3, 6, 12, 24, 48, ...... with a common ratio of 2. The common ratio of a geometric sequence can be either negative or positive but it cannot be 0. Here, we learn the following geometric sequence formulas:

• The n th term of a geometric sequence
• The recursive formula of a geometric sequence
• The sum of a finite geometric sequence
• The sum of an infinite geometric sequence

The geometric sequences can be finite or infinite. Here we shall learn more about each of the above-mentioned geometric sequence formulas along with their proofs and examples.

What is a Geometric Sequence?

A geometric sequence is a special type of sequence where the ratio of every two successive terms is a constant. This ratio is known as a common ratio of the geometric sequence. In other words, in a geometric sequence, every term is multiplied by a constant which results in its next term. So a geometric sequence is in form a, ar, ar 2 ... where 'a' is the first term and 'r' is the common ratio of the sequence. The common ratio can be either a positive or a negative number.

Geometric Sequence Examples

• 1/4, 1/8, .... is a geometric sequence where a = 1/4 and r = 1/2
• -4, 2, -1, 1/2, -1/4, ... is a geometric sequence where a = -4 and r = -1/2
• π, 2π, 4π, 8π,.... is a geometric sequence where a = π and r = 2
• √2, -√2, √2, -√2, ... is a geometric sequence where a = √2 and r = -1

There are two types of geometric sequences based on the number of terms in them. They are

• Finite geometric sequences
• Infinite geometric sequences

Finite geometric sequence

A finite geometric sequence is a geometric sequence that contains a finite number of terms. i.e., its last term is defined. For example 2, 6, 18, 54, ....13122 is a finite geometric sequence where the last term is 13122.

Infinite geometric sequence

An infinite geometric sequence is a geometric sequence that contains an infinite number of terms. i.e., its last term is not defined. For example, 2, −4, 8, −16, ... is an infinite sequence where the last term is not defined.

Geometric Sequence Formulas

Here is the list of all geometric sequence formulas . For any geometric sequence a, ar, ar 2 , ar 3 , ...

• n th term , a n = ar n - 1 (or) a n = r a n - 1
• Sum of the first n terms , S n = a(r n - 1) / (r - 1) when r ≠ 1 and S n = na when r = 1.
• Sum of infinite terms , S ∞ = a / (1 - r) when |r| < 1 and S ∞ diverges when |r| ≥ 1.

Let us study each and every formula one by one here.

n^th Term of Geometric Sequence Formula

We have already seen that a geometric sequence is of the form a, ar, ar 2 , ar 3 , ...., where 'a' is the first term and 'r' is the common ratio . Here,

• The 1 st term, a 1 = a = a r 1-1
• The 2 nd term, a 2 = a r = a r 2-1
• The 3 rd term, a 3 = a r 2 = a r 3-1

So in general, the n th term of a geometric sequence is,

• a n = ar n-1
• a = first term of the geometric sequence
• r = common ratio of the geometric sequence
• a n = n th term

There is another formula used to find the n th term of a geometric sequence given its previous term and the common ratio which is called the recursive formula of the geometric sequence.

Recursive Formula of Geometric Sequence

We know that in a geometric sequence, a term (a n ) is obtained by multiplying its previous term (a n - 1 ) by the common ratio (r). So by the recursive formula of a geometric sequence, the n th term of a geometric sequence is,

• a n = r a n - 1
• a n - 1 = (n - 1) th term
• r = common ratio

Example: Find a 15 of a geometric sequence if a 1 3 = -8 and r = 1/3.

By the recursive formula of geometric sequence,

a 14 = r a 1 3 = (1/3) (-8) = -8/3

Applying the same formula again,

a 15 = r a 14 = (1/3) (-8/3) = -8/9.

Therefore, a 15 = -8/9.

Sum of Finite Geometric Sequence Formula

The sum of a finite geometric sequence formula is used to find the sum of the first n terms of a geometric sequence. Consider a geometric sequence with n terms whose first term is 'a' and common ratio is 'r'. i.e., a, ar, ar 2 , ar 3 , ... , ar n-1 . Then its sum is denoted by S n and is given by the formula:

• S n = a(r n - 1) / (r - 1) when r ≠ 1 and S n = na when r = 1.

Let us derive the formula now.

Sum of Finite Geometric Sequence Proof

We have S n = a + ar + ar 2 + ar 3 + ... + ar n-1 ... (1)

Multiply both sides by r,

rS n = ar + ar 2 + ar 3 + ... + ar n ... (2)

Subtracting (1) from (2),

rS n - S n = ar n - a

S n (r - 1) = a (r n - 1)

S n = a(r n - 1) / (r - 1)

Since (r - 1) is in its denominator, it is defined only when r ≠ 1. If r = 1, the sequence looks like a, a, a, ... and the sum of the first n terms, in this case, = a + a + a + ... (n times) = na.

Thus, we have derived the formula of the sum of a finite geometric sequence.

Sum of Infinite Geometric Sequence Formula

The sum of an infinite geometric sequence formula gives the sum of all its terms and this formula is applicable only when the absolute value of the common ratio of the geometric sequence is less than 1 (because if the common ratio is greater than or equal to 1, the sum diverges to infinity). i.e., An infinite geometric sequence

• converges (to finite sum) only when |r| < 1
• diverges (to infinity) when |r| ≥ 1

Consider an infinite geometric sequence a, ar, ar 2 , ar 3 , ... The sum of its infinite terms is denoted by S ∞ . Then

• S ∞ = a / (1 - r), when |r| < 1 and S ∞ diverges when |r| ≥ 1.

Sum of Infinite Geometric Sequence Proof

We have S ∞ = a + ar + ar 2 + ar 3 + ... ...(1)

Multiplying both sides by r,

rS ∞ = ar + ar 2 + ar 3 + ... ... (2)

Subtracting (2) from (1),

S ∞ - rS ∞ = a

S ∞ (1 - r) = a

S ∞ = a / (1 - r)

Hence we have derived the formula of the sum of an infinite geometric sequence.

Geometric Sequence vs Arithmetic Sequence

Here are a few differences between geometric sequence and arithmetic sequence shown in the table below:

Important Notes on Geometric Sequence:

• In a geometric sequence, every term is obtained by multiplying its previous term by a constant (r, which is called the common ratio).
• If r > 1, then the terms are in ascending order .
• When r = 1, and the first term of a geometric sequence is 'a' then its sum is a · n.
• When r ≥ 1, the infinite geometric sequence diverges.

☛ Related Topics:

• Sequence Calculator
• Series Calculator
• Arithmetic Sequence Calculator
• Geometric Sequence Calculator

Geometric Sequence Examples​​​​​​

Example 1: Find the 25 th term of the geometric sequence 1, 1/5, 1/25, 1/125, ...

Here, the first term is, a = 1 and

the common ratio is, r = (1/5) / 1 = (1/25) / (1/5) = ... = 1/5.

The n th term of a geometric sequence is calculated using,

• a n = ar n - 1

Substituting n = 25 here,

a 25 = (1) (1/5) 25-1 = 1/5 24

Answer: The 25 th term of the given geometric sequence is 1/5 24 .

Example 2: Find the sum of the first 18 terms of the geometric sequence 2, 6, 18, 54, .....

Here, the first term is, a = 2.

The common ratio, r = 6/2 = 18/6 = 54/18 = ... = 3.

Number of terms is, n = 18.

The sum of finite geometric sequence formula is,

S 1 ₈ = 2 (3 18 - 1) / (3 - 1) = 3 18 - 1.

Answer: The sum of the first 18 terms of the given geometric sequence is 3 18 - 1.

Example 3: Find the following sum of the terms of this infinite geometric sequence: 1/2, 1/4, 1/8... ∞

Here, the first term is, a = 1/2

Common ratio is, r = (1/4) / (1/2) = (1/8) / (1/4) = ... = 1/2

We have |r| = |1/2| = 1/2 < 1. So the geometric sequence converges.

So the sum of infinite geometric sequence is,

S ∞ = a/(1-r)

S ∞ = (1/2)(1 - 1/2) = (1/2) / (1/2) = 1

Answer: The sum of the given infinite geometric sequence is 1.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Geometric Sequence

go to slide go to slide

FAQs on Geometric Sequence

What is the definition of geometric sequence.

A geometric sequence is a sequence of numbers in which the ratio of every two successive terms is the constant . This constant is called the common ratio of the geometric sequence.

How to Find the n th Term of Geometric Sequence?

If 'a' is the first term and 'r' is the common ratio of a geometric sequence, then its n th term is calculated using the formula, a n = a · r n - 1 . For example, a 34 = a · r 33 .

What is r in Geometric Sequence Formula?

'r' in any geometric sequence formula represents the common ratio. It is the ratio of any term of the geometric sequence to its previous term. For example, the common ratio of the geometric sequence -1, 2, -4, 8, ... is -2.

When Does a Geometric Sequence Diverge?

A geometric sequence with the common ratio 'r' diverges when |r| ≥ 1. It converges only when |r| < 1. Here |r| is the absolute value of 'r'.

What is the Meaning of Common Ratio of Geometric Sequence?

In a geometric sequence, every term is obtained by multiplying its previous term by a fixed number. That fixed number is called the common ratio of the geometric sequence.

How to Find the Sum of a Finite Geometric Sequence?

The sum of the first n terms of a geometric sequence with first term 'a' and common ratio 'r' is calculated using the formula S n = a(r n - 1) / (r - 1) when r ≠ 1 and S n = na when r = 1.

What Are Geometric Sequence Formulas?

Here are the geometric sequence formulas where 'a' is the first term and 'r' is the common ratio.

• S n = a(r n - 1) / (r - 1), when r ≠ 1
• S ∞ = a / (1 - r) when |r| < 1

How to Find the Sum of an Infinite Geometric Sequence?

The sum of an infinite geometric sequence with the first term 'a' and common ratio 'r' is calculated using the formula S = a / (1 - r) when |r| < 1. If |r| ≥ 1, then the sum diverges (to infinity).

When Does a Geometric Sequence Converge?

A geometric sequence with a common ratio 'r' converges when |r| is less than 1. It diverges only when |r| ≥ 1, where |r| is the absolute value of 'r'.

Geometric Sequences and Sums

A Sequence is a set of things (usually numbers) that are in order.

Geometric Sequences

In a Geometric Sequence each term is found by multiplying the previous term by a constant .

Example: 1, 2, 4, 8, 16, 32, 64, 128, 256, ...

This sequence has a factor of 2 between each number.

Each term (except the first term) is found by multiplying the previous term by 2 .

In General we write a Geometric Sequence like this:

{a, ar, ar 2 , ar 3 , ... }

• a is the first term, and
• r is the factor between the terms (called the "common ratio" )

Example: {1,2,4,8,...}

The sequence starts at 1 and doubles each time, so

• a=1 (the first term)
• r=2 (the "common ratio" between terms is a doubling)

And we get:

= {1, 1×2, 1×2 2 , 1×2 3 , ... }

= {1, 2, 4, 8, ... }

But be careful, r should not be 0:

• When r=0 , we get the sequence {a,0,0,...} which is not geometric

We can also calculate any term using the Rule:

x n = ar (n-1)

(We use "n-1" because ar 0 is for the 1st term)

Example: 10, 30, 90, 270, 810, 2430, ...

This sequence has a factor of 3 between each number.

The values of a and r are:

• a = 10 (the first term)
• r = 3 (the "common ratio")

The Rule for any term is:

x n = 10 × 3 (n-1)

So, the 4th term is:

x 4 = 10 × 3 (4-1) = 10 × 3 3 = 10 × 27 = 270

And the 10th term is:

x 10 = 10 × 3 (10-1) = 10 × 3 9 = 10 × 19683 = 196830

A Geometric Sequence can also have smaller and smaller values:

Example: 4, 2, 1, 0.5, 0.25, ...

This sequence has a factor of 0.5 (a half) between each number.

Its Rule is x n = 4 × (0.5) n-1

Why "Geometric" Sequence?

Because it is like increasing the dimensions in geometry :

Geometric Sequences are sometimes called Geometric Progressions (G.P.’s)

Summing a Geometric Series

To sum these:

a + ar + ar 2 + ... + ar (n-1)

(Each term is ar k , where k starts at 0 and goes up to n-1)

We can use this handy formula:

What is that funny Σ symbol? It is called Sigma Notation

And below and above it are shown the starting and ending values:

It says "Sum up n where n goes from 1 to 4. Answer= 10

The formula is easy to use ... just "plug in" the values of a , r and n

Example: Sum the first 4 terms of 10, 30, 90, 270, 810, 2430, ...

The values of a , r and n are:

• n = 4 (we want to sum the first 4 terms)

You can check it yourself:

10 + 30 + 90 + 270 = 400

And, yes, it is easier to just add them in this example , as there are only 4 terms.

But imagine adding 50 terms ... then the formula is much easier.

Using the Formula

Let's see the formula in action:

Example: Grains of Rice on a Chess Board

On the page Binary Digits we give an example of grains of rice on a chess board. The question is asked:

When we place rice on a chess board:

• 1 grain on the first square,
• 2 grains on the second square,
• 4 grains on the third and so on,

... doubling the grains of rice on each square ...

... how many grains of rice in total?

So we have:

• a = 1 (the first term)
• r = 2 (doubles each time)
• n = 64 (64 squares on a chess board)

= 1−2 64 −1 = 2 64 − 1

= 18,446,744,073,709,551,615

Which was exactly the result we got on the Binary Digits page (thank goodness!)

And another example, this time with r less than 1:

Example: Add up the first 10 terms of the Geometric Sequence that halves each time:

{ 1/2, 1/4, 1/8, 1/16, ... }.

• a = ½ (the first term)
• r = ½ (halves each time)
• n = 10 (10 terms to add)

Very close to 1.

(Question: if we continue to increase n , what happens?)

Why Does the Formula Work?

Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.

Notice that S and S·r are similar?

Now subtract them!

Wow! All the terms in the middle neatly cancel out. (Which is a neat trick)

By subtracting S·r from S we get a simple result:

S − S·r = a − ar n

Let's rearrange it to find S :

Which is our formula (ta-da!):

Infinite Geometric Series

So what happens when n goes to infinity ?

We can use this formula:

But be careful :

r must be between (but not including) −1 and 1

and r should not be 0 because the sequence {a,0,0,...} is not geometric

So our infnite geometric series has a finite sum when the ratio is less than 1 (and greater than −1)

Let's bring back our previous example, and see what happens:

Example: Add up ALL the terms of the Geometric Sequence that halves each time:

{ 1 2 , 1 4 , 1 8 , 1 16 , ... }.

= ½×1 ½ = 1

Yes, adding 1 2 + 1 4 + 1 8 + ... etc equals exactly 1 .

Recurring Decimal

On another page we asked "Does 0.999... equal 1?" , well, let us see if we can calculate it:

Example: Calculate 0.999...

We can write a recurring decimal as a sum like this:

And now we can use the formula:

Yes! 0.999... does equal 1.

So there we have it ... Geometric Sequences (and their sums) can do all sorts of amazing and powerful things.

Geometric Sequences

A series of free, online lessons for Intermediate Algebra (Algebra II) with videos, examples and solutions.

Related Pages Number Sequences Arithmetic Sequences Quadratic and Cubic Sequences More Lessons for Algebra II

In these lessons, we will learn

• about geometric sequences
• how to find the common ratio of a geometric sequence
• how to find the formula for the nth term of an geometric sequence
• how to find the sum of an geometric series

The following figure gives the formula for the nth term of a geometric sequence. Scroll down the page for more examples and solutions.

A geometric sequence is a sequence that has a pattern of multiplying by a constant to determine consecutive terms.

We say geometric sequences have a common ratio. The formula is a n = a n-1 r

A sequence is a function. What is the domain and range of the following sequence? What is r? -12, 6, -3, 3/2, -3/4

Given the formula for the geometric sequence, determine the first 2 terms and then the 5th term. Also state the common ratio.

Given the geometric sequence, determine the formula. Then determine the 6th term. 1/3, 2/9, 4/27, 8/81, …

A Quick Introduction To Geometric Sequences

This video gives the definition of a geometric sequence and go through 4 examples, determining if each qualifies as a geometric sequence or not.

A geometric sequence is a sequence of numbers where each term after the first term is found by multiplying the previous one by a fixed non-zero number, called the common ratio.

Example: Determine which of the following sequences are geometric. If so, give the value of the common ratio, r.

3,6,12,24,48,96, …

3,3/2,3/4,3/8,3/16,3/32,3/62, …

10,15,20,25,30, …

-1,.1,-.01,-.001,-.0001, …

A list of numbers that follows a rule is called a sequence. Sequences whose rule is the multiplication of a constant are called geometric sequences, similar to arithmetic sequences that follow a rule of addition. Homework problems on geometric sequences often ask us to find the nth term of a sequence using a formula. Geometric sequences are important to understanding geometric series.

How To Find The General Term Of A Geometric Sequence?

Example: Find the formula for the general term or nth term of a geometric sequence.

Geometric Sequences And Series

A short introduction to geometric sequences and series.

Math Skills & Equations: Solving Math Sequences

There are two kinds of math sequences that can be solved: arithmetic sequences and geometric sequences. An arithmetic sequence is solved by adding or subtracting the same number, while geometric sequences use division and multiplication. Learn more about solving math sequences.

Example: Find the 9th term of 3,12,48,192, …

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.4: Geometric Sequences

• Last updated
• Save as PDF
• Page ID 114117

Learning Objectives

In this section, you will:

• Find the common ratio for a geometric sequence.
• List the terms of a geometric sequence.
• Use a recursive formula for a geometric sequence.
• Use an explicit formula for a geometric sequence.

Many jobs offer an annual cost-of-living increase to keep salaries consistent with inflation. Suppose, for example, a recent college graduate finds a position as a sales manager earning an annual salary of $26,000. He is promised a 2% cost of living increase each year. His annual salary in any given year can be found by multiplying his salary from the previous year by 102%. His salary will be $26,520 after one year; $27,050.40 after two years; $27,591.41 after three years; and so on. When a salary increases by a constant rate each year, the salary grows by a constant factor. In this section, we will review sequences that grow in this way.

Finding Common Ratios

The yearly salary values described form a geometric sequence because they change by a constant factor each year. Each term of a geometric sequence increases or decreases by a constant factor called the common ratio . The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term.

Definition of a Geometric Sequence

A geometric sequence is one in which any term divided by the previous term is a constant. This constant is called the common ratio of the sequence. The common ratio can be found by dividing any term in the sequence by the previous term. If a 1 a 1 is the initial term of a geometric sequence and r r is the common ratio, the sequence will be

{ a 1 , a 1 r , a 1 r 2 , a 1 r 3 , ... } . { a 1 , a 1 r , a 1 r 2 , a 1 r 3 , ... } .

Given a set of numbers, determine if they represent a geometric sequence.

• Divide each term by the previous term.
• Compare the quotients. If they are the same, a common ratio exists and the sequence is geometric.

Is the sequence geometric? If so, find the common ratio.

• ⓐ 1 , 2 , 4 , 8 , 16 , ... 1 , 2 , 4 , 8 , 16 , ...
• ⓑ 48 , 12 , 4 , 2 , ... 48 , 12 , 4 , 2 , ...

Divide each term by the previous term to determine whether a common ratio exists.

• The sequence is geometric because there is a common ratio. The common ratio is 2.
• The sequence is not geometric because there is not a common ratio.

The graph of each sequence is shown in Figure 1 . It seems from the graphs that both (a) and (b) appear have the form of the graph of an exponential function in this viewing window. However, we know that (a) is geometric and so this interpretation holds, but (b) is not.

If you are told that a sequence is geometric, do you have to divide every term by the previous term to find the common ratio?

No. If you know that the sequence is geometric, you can choose any one term in the sequence and divide it by the previous term to find the common ratio.

5 , 10 , 15 , 20 , ... 5 , 10 , 15 , 20 , ...

Writing Terms of Geometric Sequences

Now that we can identify a geometric sequence, we will learn how to find the terms of a geometric sequence if we are given the first term and the common ratio. The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. For instance, if the first term of a geometric sequence is a 1 = − 2 a 1 = − 2 and the common ratio is r = 4, r = 4, we can find subsequent terms by multiplying − 2 ⋅ 4 − 2 ⋅ 4 to get − 8 − 8 then multiplying the result − 8 ⋅ 4 − 8 ⋅ 4 to get − 32 − 32 and so on.

The first four terms are { –2 , –8 , –32 , –128 } . { –2 , –8 , –32 , –128 } .

Given the first term and the common factor, find the first four terms of a geometric sequence.

• Multiply the initial term, a 1 , a 1 , by the common ratio to find the next term, a 2 . a 2 .
• Repeat the process, using a n = a 2 a n = a 2 to find a 3 a 3 and then a 3 a 3 to find a 4, a 4, until all four terms have been identified.
• Write the terms separated by commons within brackets.

Writing the Terms of a Geometric Sequence

List the first four terms of the geometric sequence with a 1 = 5 a 1 = 5 and r = –2. r = –2.

Multiply a 1 a 1 by − 2 − 2 to find a 2 . a 2 . Repeat the process, using a 2 a 2 to find a 3 , a 3 , and so on.

a 1 = 5 a 2 = − 2 a 1 = − 10 a 3 = − 2 a 2 = 20 a 4 = − 2 a 3 = − 40 a 1 = 5 a 2 = − 2 a 1 = − 10 a 3 = − 2 a 2 = 20 a 4 = − 2 a 3 = − 40

The first four terms are { 5 , –10 , 20 , –40 } . { 5 , –10 , 20 , –40 } .

List the first five terms of the geometric sequence with a 1 = 18 a 1 = 18 and r = 1 3 . r = 1 3 .

Using Recursive Formulas for Geometric Sequences

A recursive formula allows us to find any term of a geometric sequence by using the previous term. Each term is the product of the common ratio and the previous term. For example, suppose the common ratio is 9. Then each term is nine times the previous term. As with any recursive formula, the initial term must be given.

Recursive Formula for a Geometric Sequence

The recursive formula for a geometric sequence with common ratio r r and first term a 1 a 1 is

a n = r a n − 1 , n ≥ 2 a n = r a n − 1 , n ≥ 2

Given the first several terms of a geometric sequence, write its recursive formula.

• State the initial term.
• Find the common ratio by dividing any term by the preceding term.
• Substitute the common ratio into the recursive formula for a geometric sequence.

Write a recursive formula for the following geometric sequence.

{ 6 , 9 , 13.5 , 20.25 , ... } { 6 , 9 , 13.5 , 20.25 , ... }

The first term is given as 6. The common ratio can be found by dividing the second term by the first term.

Substitute the common ratio into the recursive formula for geometric sequences and define a 1 . a 1 .

a n = r a n − 1 a n = 1.5 a n − 1 for n ≥ 2 a 1 = 6 a n = r a n − 1 a n = 1.5 a n − 1 for n ≥ 2 a 1 = 6

The sequence of data points follows an exponential pattern. The common ratio is also the base of an exponential function as shown in Figure 2

Do we have to divide the second term by the first term to find the common ratio?

No. We can divide any term in the sequence by the previous term. It is, however, most common to divide the second term by the first term because it is often the easiest method of finding the common ratio.

{ 2 , 4 3 , 8 9 , 16 27 , ... } { 2 , 4 3 , 8 9 , 16 27 , ... }

Using Explicit Formulas for Geometric Sequences

Because a geometric sequence is an exponential function whose domain is the set of positive integers, and the common ratio is the base of the function, we can write explicit formulas that allow us to find particular terms.

Let’s take a look at the sequence { 18 , 36 , 72 , 144 , 288 , ... } . { 18 , 36 , 72 , 144 , 288 , ... } . This is a geometric sequence with a common ratio of 2 and an exponential function with a base of 2. An explicit formula for this sequence is

a n = 18 · 2 n − 1 a n = 18 · 2 n − 1

The graph of the sequence is shown in Figure 3 .

Explicit Formula for a Geometric Sequence

The n n th term of a geometric sequence is given by the explicit formula :

a n = a 1 r n − 1 a n = a 1 r n − 1

Writing Terms of Geometric Sequences Using the Explicit Formula

Given a geometric sequence with a 1 = 3 a 1 = 3 and a 4 = 24 , a 4 = 24 , find a 2 . a 2 .

The sequence can be written in terms of the initial term and the common ratio r . r .

3 , 3 r , 3 r 2 , 3 r 3 , ... 3 , 3 r , 3 r 2 , 3 r 3 , ...

Find the common ratio using the given fourth term.

a n = a 1 r n − 1 a 4 = 3 r 3 Write the fourth term of sequence in terms of α 1 and r 24 = 3 r 3 Substitute 24 for a 4 8 = r 3 Divide r = 2 Solve for the common ratio a n = a 1 r n − 1 a 4 = 3 r 3 Write the fourth term of sequence in terms of α 1 and r 24 = 3 r 3 Substitute 24 for a 4 8 = r 3 Divide r = 2 Solve for the common ratio

Find the second term by multiplying the first term by the common ratio.

a 2 = 2 a 1 = 2 ( 3 ) = 6 a 2 = 2 a 1 = 2 ( 3 ) = 6

The common ratio is multiplied by the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by multiplying the first term by the common ratio nine times or by multiplying by the common ratio raised to the ninth power.

Given a geometric sequence with a 2 = 4 a 2 = 4 and a 3 = 32 a 3 = 32 , find a 6 . a 6 .

Writing an Explicit Formula for the n n th Term of a Geometric Sequence

Write an explicit formula for the n th n th term of the following geometric sequence.

{ 2 , 10 , 50 , 250 , ... } { 2 , 10 , 50 , 250 , ... }

The first term is 2. The common ratio can be found by dividing the second term by the first term.

The common ratio is 5. Substitute the common ratio and the first term of the sequence into the formula.

a n = a 1 r ( n − 1 ) a n = 2 ⋅ 5 n − 1 a n = a 1 r ( n − 1 ) a n = 2 ⋅ 5 n − 1

The graph of this sequence in Figure 4 shows an exponential pattern.

Write an explicit formula for the following geometric sequence.

{ –1 , 3 , –9 , 27 , ... } { –1 , 3 , –9 , 27 , ... }

Solving Application Problems with Geometric Sequences

In real-world scenarios involving geometric sequences, we may need to use an initial term of a 0 a 0 instead of a 1 . a 1 . In these problems, we can alter the explicit formula slightly by using the following formula:

In 2013, the number of students in a small school is 284. It is estimated that the student population will increase by 4% each year.

• ⓐ Write a formula for the student population.
• ⓑ Estimate the student population in 2020.

Let P P be the student population and n n be the number of years after 2013. Using the explicit formula for a geometric sequence we get

P n = 284 ⋅ 1.04 n P n = 284 ⋅ 1.04 n

2020 − 2013 = 7 2020 − 2013 = 7

We are looking for the population after 7 years. We can substitute 7 for n n to estimate the population in 2020.

P 7 = 284 ⋅ 1.04 7 ≈ 374 P 7 = 284 ⋅ 1.04 7 ≈ 374

The student population will be about 374 in 2020.

A business starts a new website. Initially the number of hits is 293 due to the curiosity factor. The business estimates the number of hits will increase by 2.6% per week.

• ⓐ Write a formula for the number of hits.
• ⓑ Estimate the number of hits in 5 weeks.

Access these online resources for additional instruction and practice with geometric sequences.

• Geometric Sequences
• Determine the Type of Sequence
• Find the Formula for a Sequence

11.3 Section Exercises

What is a geometric sequence?

How is the common ratio of a geometric sequence found?

What is the procedure for determining whether a sequence is geometric?

What is the difference between an arithmetic sequence and a geometric sequence?

Describe how exponential functions and geometric sequences are similar. How are they different?

For the following exercises, find the common ratio for the geometric sequence.

1 , 3 , 9 , 27 , 81 , ... 1 , 3 , 9 , 27 , 81 , ...

− 0.125 , 0.25 , − 0.5 , 1 , − 2 , ... − 0.125 , 0.25 , − 0.5 , 1 , − 2 , ...

− 2 , − 1 2 , − 1 8 , − 1 32 , − 1 128 , ... − 2 , − 1 2 , − 1 8 , − 1 32 , − 1 128 , ...

For the following exercises, determine whether the sequence is geometric. If so, find the common ratio.

− 6 , − 12 , − 24 , − 48 , − 96 , ... − 6 , − 12 , − 24 , − 48 , − 96 , ...

5 , 5.2 , 5.4 , 5.6 , 5.8 , ... 5 , 5.2 , 5.4 , 5.6 , 5.8 , ...

− 1 , 1 2 , − 1 4 , 1 8 , − 1 16 , ... − 1 , 1 2 , − 1 4 , 1 8 , − 1 16 , ...

6 , 8 , 11 , 15 , 20 , ... 6 , 8 , 11 , 15 , 20 , ...

0.8 , 4 , 20 , 100 , 500 , ... 0.8 , 4 , 20 , 100 , 500 , ...

For the following exercises, write the first five terms of the geometric sequence, given the first term and common ratio.

a 1 = 8 , r = 0.3 a 1 = 8 , r = 0.3

a 1 = 5 , r = 1 5 a 1 = 5 , r = 1 5

For the following exercises, write the first five terms of the geometric sequence, given any two terms.

a 7 = 64 , a 10 = 512 a 7 = 64 , a 10 = 512

a 6 = 25 , a 8 = 6.25 a 6 = 25 , a 8 = 6.25

For the following exercises, find the specified term for the geometric sequence, given the first term and common ratio.

The first term is 2, 2, and the common ratio is 3. 3. Find the 5 th term.

The first term is 16 and the common ratio is − 1 3 . − 1 3 . Find the 4 th term.

For the following exercises, find the specified term for the geometric sequence, given the first four terms.

a n = { − 1 , 2 , − 4 , 8 , ... } . a n = { − 1 , 2 , − 4 , 8 , ... } . Find a 12 . a 12 .

a n = { − 2 , 2 3 , − 2 9 , 2 27 , ... } . a n = { − 2 , 2 3 , − 2 9 , 2 27 , ... } . Find a 7 . a 7 .

For the following exercises, write the first five terms of the geometric sequence.

a 1 = − 486 , a n = − 1 3 a n − 1 a 1 = − 486 , a n = − 1 3 a n − 1

a 1 = 7 , a n = 0.2 a n − 1 a 1 = 7 , a n = 0.2 a n − 1

For the following exercises, write a recursive formula for each geometric sequence.

a n = { − 1 , 5 , − 25 , 125 , ... } a n = { − 1 , 5 , − 25 , 125 , ... }

a n = { − 32 , − 16 , − 8 , − 4 , ... } a n = { − 32 , − 16 , − 8 , − 4 , ... }

a n = { 14 , 56 , 224 , 896 , ... } a n = { 14 , 56 , 224 , 896 , ... }

a n = { 10 , − 3 , 0.9 , − 0.27 , ... } a n = { 10 , − 3 , 0.9 , − 0.27 , ... }

a n = { 0.61 , 1.83 , 5.49 , 16.47 , ... } a n = { 0.61 , 1.83 , 5.49 , 16.47 , ... }

a n = { 3 5 , 1 10 , 1 60 , 1 360 , ... } a n = { 3 5 , 1 10 , 1 60 , 1 360 , ... }

a n = { − 2 , 4 3 , − 8 9 , 16 27 , ... } a n = { − 2 , 4 3 , − 8 9 , 16 27 , ... }

a n = { 1 512 , − 1 128 , 1 32 , − 1 8 , ... } a n = { 1 512 , − 1 128 , 1 32 , − 1 8 , ... }

a n = − 4 ⋅ 5 n − 1 a n = − 4 ⋅ 5 n − 1

a n = 12 ⋅ ( − 1 2 ) n − 1 a n = 12 ⋅ ( − 1 2 ) n − 1

For the following exercises, write an explicit formula for each geometric sequence.

a n = { − 2 , − 4 , − 8 , − 16 , ... } a n = { − 2 , − 4 , − 8 , − 16 , ... }

a n = { 1 , 3 , 9 , 27 , ... } a n = { 1 , 3 , 9 , 27 , ... }

a n = { − 4 , − 12 , − 36 , − 108 , ... } a n = { − 4 , − 12 , − 36 , − 108 , ... }

a n = { 0.8 , − 4 , 20 , − 100 , ... } a n = { 0.8 , − 4 , 20 , − 100 , ... }

a n = { − 1.25 , − 5 , − 20 , − 80 , ... } a n = { − 1.25 , − 5 , − 20 , − 80 , ... }

a n = { − 1 , − 4 5 , − 16 25 , − 64 125 , ... } a n = { − 1 , − 4 5 , − 16 25 , − 64 125 , ... }

a n = { 2 , 1 3 , 1 18 , 1 108 , ... } a n = { 2 , 1 3 , 1 18 , 1 108 , ... }

a n = { 3 , − 1 , 1 3 , − 1 9 , ... } a n = { 3 , − 1 , 1 3 , − 1 9 , ... }

For the following exercises, find the specified term for the geometric sequence given.

Let a 1 = 4 , a 1 = 4 , a n = − 3 a n − 1 . a n = − 3 a n − 1 . Find a 8 . a 8 .

Let a n = − ( − 1 3 ) n − 1 . a n = − ( − 1 3 ) n − 1 . Find a 12 . a 12 .

For the following exercises, find the number of terms in the given finite geometric sequence.

a n = { − 1 , 3 , − 9 , ... , 2187 } a n = { − 1 , 3 , − 9 , ... , 2187 }

a n = { 2 , 1 , 1 2 , ... , 1 1024 } a n = { 2 , 1 , 1 2 , ... , 1 1024 }

For the following exercises, determine whether the graph shown represents a geometric sequence.

For the following exercises, use the information provided to graph the first five terms of the geometric sequence.

a 1 = 1 , r = 1 2 a 1 = 1 , r = 1 2

a 1 = 3 , a n = 2 a n − 1 a 1 = 3 , a n = 2 a n − 1

a n = 27 ⋅ 0.3 n − 1 a n = 27 ⋅ 0.3 n − 1

Use recursive formulas to give two examples of geometric sequences whose 3 rd terms are 200. 200.

Use explicit formulas to give two examples of geometric sequences whose 7 th terms are 1024. 1024.

Find the 5 th term of the geometric sequence { b , 4 b , 16 b , ... } . { b , 4 b , 16 b , ... } .

Find the 7 th term of the geometric sequence { 64 a ( − b ) , 32 a ( − 3 b ) , 16 a ( − 9 b ) , ... } . { 64 a ( − b ) , 32 a ( − 3 b ) , 16 a ( − 9 b ) , ... } .

At which term does the sequence { 10 , 12 , 14.4 , 17.28 , ... } { 10 , 12 , 14.4 , 17.28 , ... } exceed 100 ? 100 ?

At which term does the sequence { 1 2187 , 1 729 , 1 243 , 1 81 ... } { 1 2187 , 1 729 , 1 243 , 1 81 ... } begin to have integer values?

For which term does the geometric sequence a n = − 36 ( 2 3 ) n − 1 a n = − 36 ( 2 3 ) n − 1 first have a non-integer value?

Use the recursive formula to write a geometric sequence whose common ratio is an integer. Show the first four terms, and then find the 10 th term.

Use the explicit formula to write a geometric sequence whose common ratio is a decimal number between 0 and 1. Show the first 4 terms, and then find the 8 th term.

Is it possible for a sequence to be both arithmetic and geometric? If so, give an example.