solve the initial value problem differential equations

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• First Derivative
• Product Rule
• Quotient Rule
• Sum/Diff Rule
• Second Derivative
• Third Derivative
• Higher Order Derivatives
• Derivative at a point
• Partial Derivative
• Implicit Derivative
• Second Implicit Derivative
• Derivative using Definition
• Slope of Tangent
• Curved Line Slope
• Extreme Points
• Tangent to Conic
• Linear Approximation
• Difference Quotient
• Horizontal Tangent
• One Variable
• Multi Variable Limit
• At Infinity
• L'Hopital's Rule
• Squeeze Theorem
• Substitution
• Sandwich Theorem
• Indefinite Integrals
• Definite Integrals
• Partial Fractions
• U-Substitution
• Trigonometric Substitution
• Weierstrass Substitution
• Long Division
• Improper Integrals
• Antiderivatives
• Double Integrals
• Triple Integrals
• Multiple Integrals
• Limit of Sum
• Area under curve
• Area between curves
• Area under polar curve
• Volume of solid of revolution
• Function Average
• Riemann Sum
• Trapezoidal
• Simpson's Rule
• Midpoint Rule
• Geometric Series Test
• Telescoping Series Test
• Alternating Series Test
• P Series Test
• Divergence Test
• Comparison Test
• Limit Comparison Test
• Integral Test
• Absolute Convergence
• Radius of Convergence
• Interval of Convergence
• Linear First Order
• Linear w/constant coefficients
• Second Order
• Non Homogenous
• System of ODEs
• IVP using Laplace
• Series Solutions
• Method of Frobenius
• Gamma Function
• Taylor Series
• Maclaurin Series
• Fourier Series
• Fourier Transform
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• 2y'-y=4\sin(3t)
• ty'+2y=t^2-t+1
• y'=e^{-y}(2x-4)
• \frac{dr}{d\theta}=\frac{r^2}{\theta}
• y'+\frac{4}{x}y=x^3y^2
• y'+\frac{4}{x}y=x^3y^2, y(2)=-1
• laplace\:y^{\prime}+2y=12\sin(2t),y(0)=5
• bernoulli\:\frac{dr}{dθ}=\frac{r^2}{θ}
• How do you calculate ordinary differential equations?
• To solve ordinary differential equations (ODEs), use methods such as separation of variables, linear equations, exact equations, homogeneous equations, or numerical methods.
• Which methods are used to solve ordinary differential equations?
• There are several methods that can be used to solve ordinary differential equations (ODEs) to include analytical methods, numerical methods, the Laplace transform method, series solutions, and qualitative methods.
• Is there an app to solve differential equations?
• To solve ordinary differential equations (ODEs) use the Symbolab calculator. It can solve ordinary linear first order differential equations, linear differential equations with constant coefficients, separable differential equations, Bernoulli differential equations, exact differential equations, second order differential equations, homogenous and non homogenous ODEs equations, system of ODEs, ODE IVP's with Laplace Transforms, series solutions to differential equations, and more.
• What is the difference between ODE and PDE?
• An ordinary differential equation (ODE) is a mathematical equation involving a single independent variable and one or more derivatives, while a partial differential equation (PDE) involves multiple independent variables and partial derivatives. ODEs describe the evolution of a system over time, while PDEs describe the evolution of a system over space and time.
• What is the importance of studying ordinary differential equations?
• Ordinary differential equations (ODEs) help us understand and predict the behavior of complex systems, and for that, it is a fundamental tool in mathematics and physics.
• What is the numerical method?
• Numerical methods are techniques for solving problems using numerical approximation and computation. These methods are used to find approximate solutions to problems that cannot be solved exactly, or for which an exact solution would be difficult to obtain.

ordinary-differential-equation-calculator

• Advanced Math Solutions – Ordinary Differential Equations Calculator, Separable ODE Last post, we talked about linear first order differential equations. In this post, we will talk about separable...

Please add a message.

Message received. Thanks for the feedback.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Differential Equations : Initial-Value Problems

Study concepts, example questions & explanations for differential equations, all differential equations resources, example questions, example question #1 : initial value problems.

First identify what is known.

The general function is,

The initial value is six in mathematical terms is,

So this is a separable differential equation, but it is also subject to an initial condition. This means that you have enough information so that there should not be a constant in the final answer.

You start off by getting all of the like terms on their respective sides, and then taking the anti-derivative. Your pre anti-derivative equation will look like:

Then taking the anti-derivative, you include a C value:

Then, using the initial condition given, we can solve for the value of C:

Solving for C, we get 

So this is a separable differential equation with a given initial value.

To start off, gather all of the like variables on separate sides.

Then integrate, and make sure to add a constant at the end

Plug in the initial condition to get:

Solve the separable differential equation

none of these answers

To start off, gather all of the like variables on separate sides. 

Notice that when you divide sec(y) to the other side, it will just be cos(y),

and the csc(x) on the bottom is equal to sin(x) on the top. 

In order to solve for y, we just need to take the arcsin of both sides:

Solve the differential equation

Then, after the anti-derivative, make sure to add the constant C:

Solve for y

None of these answers

Taking the anti-derivative once, we get:

we get the final answer of:

Example Question #8 : Initial Value Problems

Solve the differential equation for y

subject to the initial condition:

Solving for C:

Then taking the square root to solve for y, we get:

Example Question #10 : Initial Value Problems

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Module 7: Second-Order Differential Equations

Initial-value problems and boundary-value problems, learning objectives.

• Solve initial-value and boundary-value problems involving linear differential equations.

So far, we have been finding general solutions to differential equations. However, differential equations are often used to describe physical systems, and the person studying that physical system usually knows something about the state of that system at one or more points in time. For example, if a constant-coefficient differential equation is representing how far a motorcycle shock absorber is compressed, we might know that the rider is sitting still on his motorcycle at the start of a race, time [latex]t=t_0[/latex]. This means the system is at equilibrium, so [latex]y(t_0)=0[/latex], and the compression of the shock absorber is not changing, so [latex]y'(t_0)=0[/latex]. With these two initial conditions and the general solution to the differential equation, we can find the  specific  solution to the differential equation that satisfies both initial conditions. This process is known as  solving an initial-value problem . (Recall that we discussed  initial-value problems  in  Introduction to Differential Equations .) Note that second-order equations have two arbitrary constants in the general solution, and therefore we require two initial conditions to find the solution to the initial-value problem.

Sometimes we know the condition of the system at two different times. For example, we might know [latex]y(t_0)=y_0[/latex] and [latex]y(t_1)=y_1[/latex]. These conditions are called  boundary conditions , and finding the solution to the differential equation that satisfies the boundary conditions is called solving a  boundary-value problem .

Mathematicians, scientists, and engineers are interested in understanding the conditions under which an initial-value problem or a boundary-value problem has a unique solution. Although a complete treatment of this topic is beyond the scope of this text, it is useful to know that, within the context of constant-coefficient, second-order equations, initial-value problems are guaranteed to have a unique solution as long as two initial conditions are provided. Boundary-value problems, however, are not as well behaved. Even when two boundary conditions are known, we may encounter boundary-value problems with unique solutions, many solutions, or no solution at all.

Example: solving an initial-value problem

Solve the following initial-value problem: [latex]y''+3y'-4y=0[/latex], [latex]y(0)=1[/latex], [latex]y'(0)=-9[/latex].

We already solved this differential equation in Example “Solving Second-Order Equations with Constant Coefficients” part a. and found the general solution to be

[latex]y(x)=c_1e^{-4x}+c_2e^x[/latex].

[latex]y^\prime=-4c_1e^{-4x}+c_2e^x[/latex].

When [latex]x=0[/latex], we have [latex]y(0)=c_1+c_2[/latex] and [latex]y^\prime(0)=-4c_1+c_2[/latex]. Applying the initial conditions, we have

[latex]\begin{aligned} c_1+c_2&=1 \\ -4c_1+c_2&=-9 \end{aligned}[/latex].

Then [latex]c_1=1-c_2[/latex]. Substituting this expression into the second equation, we see that

[latex]\begin{aligned} -4(1-c_2)+c_2&=-9 \\ -4+4c_2+c_2&=-9 \\ 5c_2&=-5 \\ c_2&=-1 \end{aligned}[/latex].

So, [latex]c_1=2[/latex] and the solution to the initial-value problem is

[latex]y(x)=2e^{-4x}-e^x[/latex].

Solve the initial-value problem [latex]y''-3y'-10y=0[/latex], [latex]y(0)=0[/latex], [latex]y'(0)=7[/latex].

[latex]y(x)=-e^{-2x}+e^{-5x}[/latex].

Watch the following video to see the worked solution to the above Try It

Example: solving an initial-value problem and graphing the solution

Solve the following initial-value problem and graph the solution:

[latex]y^{\prime\prime}+6y^\prime+13y=0, \ y(0)=0, \ y^\prime(0)=2[/latex].

We already solved this differential equation in Example “Solving Second-Order Equations with Constant Coefficients” part b. and found the general solution to be

[latex]y(x)=e^{-3x}(c_1\cos2x+c_2\sin2x)[/latex].

[latex]y^\prime(x)=e^{-3x}(-2c_1\sin2x+2c_2\cos2x)-3e^{-3x}(c_1\cos2x+c_2\sin2x)[/latex].

When [latex]x=0[/latex], we have [latex]y(0)=c_1[/latex] and [latex]y^\prime(0)=2c_2-3c_1[/latex]. Applying the initial conditions, we obtain

[latex]\begin{aligned} c_1&=0 \\ -3c_1+2c_2&= 2 \end{aligned}[/latex].

Therefore, [latex]c_1=0[/latex], [latex]c_2=1[/latex], and the solution to the initial value problem is shown in the following graph.

[latex]y=e^{-3x}\sin2x[/latex]

Solve the following initial-value problem and graph the solution: [latex]y''-2y'+10y=10=0[/latex], [latex]y(0)=2[/latex], [latex]y'(0)=-1[/latex].

[latex]y(x)=e^{x}(2\cos3x-\sin3x)[/latex]

Figure 2. Graph of [latex]y(x)=e^{x}(2\cos3x-\sin3x)[/latex].

Example: initial-value problem representing a spring-mass system

The following initial-value problem models the position of an object with mass attached to a spring. Spring-mass systems are examined in detail in  Applications . The solution to the differential equation gives the position of the mass with respect to a neutral (equilibrium) position (in meters) at any given time. (Note that for spring-mass systems of this type, it is customary to define the downward direction as positive.)

[latex]y^{\prime\prime}+2y^\prime+y=0, \ y(0)=1, \ y^\prime(0)=0[/latex]

Solve the initial-value problem and graph the solution. What is the position of the mass at time [latex]t=2[/latex] sec? How fast is the mass moving at time [latex]t=1[/latex] sec? In what direction?

In Example “Solving Second-Order Equations with Constant Coefficients” part c. we found the general solution to this differential equation to be

[latex]y(t)=c_1e^{-t}+c_2te^{-t}[/latex].

[latex]y^\prime(t)=-c_1e^{-t}+c_2(-te^{-t}+e^{-t})[/latex].

When [latex]t=0[/latex], we have [latex]y(0)=c_1[/latex] and [latex]y'(0)=-c_1+c_2[/latex]. Applying the initial conditions, we obtain

[latex]\begin{aligned} c_1&=1 \\ -c_1+c_2&= 0 \end{aligned}[/latex].

Thus, [latex]c_1=1[/latex], [latex]c_2=1[/latex], and the solution to the initial value problem is

[latex]y(t)=e^{-t}+te^{-t}[/latex].

This solution is represented in the following graph. At time [latex]t=2[/latex], the mass is at position [latex]y(2)=e^{-2}+2e^{-2}=3e^{-2}\approx0.406[/latex] [latex]m[/latex] below equilibrium.

To calculate the velocity at time [latex]t=1[/latex], we need to find the derivative. We have [latex]y(t)=e^{-t}+te^{-t}[/latex], so

[latex]y^\prime(t)=-e^{-t}+e^{-t}-te^{-t}=-te^{-t}[/latex].

Then [latex]y^\prime(1)=e^{-1}\approx-0.3679[/latex]. At time [latex]t=1[/latex], the mass is moving upward at [latex]0.3679[/latex] m/sec.

Suppose the following initial-value problem models the position (in feet) of a mass in a spring-mass system at any given time. Solve the initial-value problem and graph the solution. What is the position of the mass at time [latex]t=0.3[/latex] sec? How fast is it moving at time [latex]t=0.1[/latex] sec? In what direction?

[latex]y^{\prime\prime}+14y^\prime+49y=0, \ y(0)=0, \ y^\prime(0)=1[/latex]

[latex]y(t)=te^{-7t}[/latex]

At time [latex]t=0.3[/latex], [latex]y(0.3)=0.3^{(-7*0.3)}=0.3e^{-2.1}\approx0.0367[/latex]. The mass is [latex]0.0367[/latex] ft below equilibrium. At time [latex]t=0.1[/latex], [latex]y^\prime(0.1)=0.3e^{-0.7}\approx0.1490[/latex]. The mass is moving downward at a speed of [latex]0.1490[/latex] ft/sec.

Example: solving a boundary-value problem

In Example “Solving Second-Order Equations with Constant Coefficients” part f. we solved the differential equation [latex]y''+16y=0[/latex] and found the general solution to be [latex]y(t)=c_1\cos4t+c_2\sin4t[/latex]. If possible, solve the boundary-value problem if the boundary conditions are the following:

• [latex]y(0)=0[/latex], [latex]y\left(\frac{\pi}4\right)=0[/latex]
• [latex]y(0)=1[/latex], [latex]y\left(\frac{\pi}8\right)=0[/latex]
• [latex]y\left(\frac{\pi}8\right)=0[/latex], [latex]y\left(\frac{3\pi}8\right)=0[/latex]

[latex]y(x)=c_1\cos{4t}+c_2\sin{4t}[/latex]

• Applying the first boundary condition given here, we get [latex]y(0)=c_1=0[/latex]. So the solution is of the form [latex]y(t)=c_2\sin4t[/latex]. When we apply the second boundary condition, though, we get [latex]y\left(\frac{\pi}4\right)=c_2\sin\left(4\left(\frac{\pi}4\right)\right)=c_2\sin\pi=0[/latex] for all values of [latex]c_2[/latex]. The boundary conditions are not sufficient to determine a value for [latex]c_2[/latex], so this boundary-value problem has infinitely many solutions. Thus, [latex]y(t)=c_2\sin4t[/latex] is a solution for any value of [latex]c_2[/latex].
• Applying the first boundary condition given here, we get [latex]y(0)=c_1=1[/latex]. Applying the second boundary condition gives[latex]y(\frac{\pi}{8})=c_2=0[/latex], so [latex]c_2=0[/latex]. In this case, we have a unique solution: [latex]y(t)=\cos 4t[/latex].
• Applying the first boundary condition given here, we get [latex]y\left(\frac{\pi}8\right)=c_2=0[/latex]. However, applying the second boundary condition gives [latex]y\left(\frac{3\pi}8\right)=-c_2=2[/latex], so [latex]c_2=-2[/latex]. We cannot have [latex]c_2=0=-2[/latex] so this boundary value problem has no solution.
• CP 7.7. Authored by : Ryan Melton. License : CC BY: Attribution
• Calculus Volume 3. Authored by : Gilbert Strang, Edwin (Jed) Herman. Provided by : OpenStax. Located at : https://openstax.org/books/calculus-volume-3/pages/1-introduction . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike . License Terms : Access for free at https://openstax.org/books/calculus-volume-3/pages/1-introduction

Privacy Policy

Python Numerical Methods

This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists , the content is also available at Berkeley Python Numerical Methods .

The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license . If you find this content useful, please consider supporting the work on Elsevier or Amazon !

< 21.6 Summary and Problems | Contents | 22.1 ODE Initial Value Problem Statement >

Chapter 22. Ordinary Differential Equation - Initial Value Problems ¶

Chapter outline ¶.

22.1 ODE Initial Value Problem Statement

22.2 Reduction of Order

22.3 The Euler Method

22.4 Numerical Error and Instability

22.5 Predictor-Corrector Methods

22.6 Python ODE Solvers

22.7 Advanced Topics

22.8 Summary and Problems

Motivation ¶

Differential equations are relationships between a function and its derivatives, and they are used to model systems in every engineering and science field. For example, a simple differential equation relates the acceleration of a car with its position. Unlike differentiation where analytic solutions can usually be computed, in general finding exact solutions to differential equations is very hard. Therefore, numerical solutions are critical to making these equations useful for designing and understanding engineering and science systems.

Because differential equations are so common in engineering, physics, and mathematics, the study of them is a vast and rich field that cannot be covered in this introductory text. This chapter covers ordinary differential equations with specified initial values, a subclass of differential equations problems called initial value problems. To reflect the importance of this class of problem, Python has a whole suite of functions to solve this kind of problem. By the end of this chapter, you should understand what ordinary differential equation initial value problems are, how to pose these problems to Python, and how these Python solvers work.

You are about to erase your work on this activity. Are you sure you want to do this?

Updated Version Available

There is an updated version of this activity. If you update to the most recent version of this activity, then your current progress on this activity will be erased. Regardless, your record of completion will remain. How would you like to proceed?

Mathematical Expression Editor

The general constant coefficient system of differential equations has the form

In Section ??, we plotted the phase space picture of the planar system of differential equations

Thus, using matrix multiplication, we are able to prove analytically that there are solutions to (??) of exactly the type suggested by our MATLAB experiments. However, even more is true and this extension is based on the principle of superposition that was introduced for algebraic equations in Section ??.

Superposition in Linear Differential Equations

Consider a general linear differential equation of the form

Initial Value Problems

Thus we can solve our prescribed initial value problem, if we can solve the system of linear equations

Eigenvectors and Eigenvalues

Note that scalar multiples of eigenvectors are also eigenvectors. More precisely:

We have proved the following theorem.

An Example of a Matrix with No Real Eigenvalues

In Exercises ?? – ?? use map to find an (approximate) eigenvector for the given matrix. Hint: Choose a vector in map and repeatedly click on the button Map until the vector maps to a multiple of itself. You may wish to use the Rescale feature in the MAP Options. Then the length of the vector is rescaled to one after each use of the command Map. In this way, you can avoid overflows in the computations while still being able to see the directions where the vectors are moved by the matrix mapping. The coordinates of the new vector obtained by applying map can be viewed in the Vector input window.

• Compare the results of the two plots.

Subscribe to the PwC Newsletter

Join the community, edit social preview.

Add a new code entry for this paper

Remove a code repository from this paper, mark the official implementation from paper authors, add a new evaluation result row, remove a task, add a method, remove a method, edit datasets, a piecewise neural network method for solving large interval solution to initial value problem of ordinary differential equations.

28 Mar 2024  ·  Dongpeng Han , Chaolu Temuer · Edit social preview

Various traditional numerical methods for solving initial value problems of differential equations often produce local solutions near the initial value point, despite the problems having larger interval solutions. Even current popular neural network algorithms or deep learning methods cannot guarantee yielding large interval solutions for these problems. In this paper, we propose a piecewise neural network approach to obtain a large interval numerical solution for initial value problems of differential equations. In this method, we first divide the solution interval, on which the initial problem is to be solved, into several smaller intervals. Neural networks with a unified structure are then employed on each sub-interval to solve the related sub-problems. By assembling these neural network solutions, a piecewise expression of the large interval solution to the problem is constructed, referred to as the piecewise neural network solution. The continuous differentiability of the solution over the entire interval, except for finite points, is proven through theoretical analysis and employing a parameter transfer technique. Additionally, a parameter transfer and multiple rounds of pre-training technique are utilized to enhance the accuracy of the approximation solution. Compared with existing neural network algorithms, this method does not increase the network size and training data scale for training the network on each sub-domain. Finally, several numerical experiments are presented to demonstrate the efficiency of the proposed algorithm.

Code Edit Add Remove Mark official

Generalized fuzzy difference method for solving fuzzy initial value problem

• Open access
• Published: 27 March 2024
• Volume 43 , article number  129 , ( 2024 )

Cite this article

You have full access to this open access article

• S. Soroush 1 ,
• T. Allahviranloo   ORCID: orcid.org/0000-0002-6673-3560 1 , 2 ,
• H. Azari 3 &
• M. Rostamy-Malkhalifeh 3  

36 Accesses

Explore all metrics

We are going to explain the fuzzy Adams–Bashforth methods for solving fuzzy differential equations focusing on the concept of g -differentiability. Considering the analysis of normal, convex, upper semicontinuous, compactly supported fuzzy sets in \(R^n\) and also convergence of the methods, the general expression of solutions is obtained. Finally, we demonstrate the importance of our method with some illustrative examples. These examples are provided aiming to solve the fuzzy differential equations.

Similar content being viewed by others

Asymptotical stabilization of fuzzy semilinear dynamic systems involving the generalized Caputo fractional derivative for $$q \in (1,2)$$

Truong Vinh An, Vasile Lupulescu & Ngo Van Hoa

Numerical scheme for singularly perturbed Fredholm integro-differential equations with non-local boundary conditions

Lolugu Govindarao, Higinio Ramos & Sekar Elango

Numerical approach for time-fractional Burgers’ equation via a combination of Adams–Moulton and linearized technique

Yonghyeon Jeon & Sunyoung Bu

Avoid common mistakes on your manuscript.

1 Introduction

According to the most recent published papers, the fuzzy differential equation was introduced in 1978. Moreover, Kandel ( 1980 ) and Byatt and Kandel ( 1978 ) present the fuzzy differential equation and have rapidly expanded literature. First-order linear fuzzy differential equations emerge in modeling the uncertainty of dynamical systems. The solutions of first-order linear fuzzy differential equations have been widely considered (e. g., see Chalco-Cano and Roman-Flores 2008 ; Buckley and Feuring 2000 ; Seikkala 1987 ; Diamond 2002 ; Song and Wu 2000 ; Allahviranloo et al. 2009 ; Zabihi et al. 2023 ; Allahviranloo and Pedrycz 2020 ).

The most famous numerical solutions of order fuzzy differential equations are investigated and analyzed under the Hukuhara and gH -differentiability (Safikhani et al. 2023 ). It is widely believed that the common Hukuhara difference and so Hukuhara derivative between two fuzzy numbers are accessible under special circumstances (Kaleva 1987 ; Diamond 1999 , 2000 ). The gH -derivative, however, is available in less restrictive conditions, even though this is not always the case (Dubois et al. 2008 ). To overcome these serious defects of the concepts mentioned above, Bede and Stefanini (Dubois et al. 2008 ) describe g -derivative. In 2007, Allahviranloo used the predictor–corrector under the Seikkala-derivative method to propose a numerical solution of fuzzy differential equations (Allahviranloo et al. 2007 ).

Here, we investigate the Adams–Bashforth method to solve fuzzy differential equations focusing on g -differentiability. We restrict our study on normal, convex, upper semicontinuous, and compactly supported fuzzy sets in \(\mathbb {R}^n\) .

This paper has been arranged as mentioned below: firstly, in Sect.  2 , we recall the necessary definitions to be used in the rest of the article, after a preliminary section in Sect.  3 , which is dedicated to the description of the Adams–Bashforth method to fix the purposed equation. The convergence theorem is formulated and proved in Sect.  4 . For checking the accuracy of the method, three examples are presented. In Sect.  5 , their solutions are compared with the exact solutions. In the last section, some conclusions are given.

2 Preliminaries

Definition 2.1.

(Mehrkanoon et al. 2009 ) A fuzzy subset of the real line with a normal, convex, and upper semicontinuous membership function of bounded support is a fuzzy number \(\tilde{w}\) . The family of fuzzy numbers is indicated by F .

We show an arbitrary fuzzy number with an ordered pair of functions \((\underline{w}(\gamma ),\overline{w}(\gamma ))\) , \(0\le \gamma \le 1\) which provides the following:

\(\underline{w}(\gamma )\) is a bounded left continuous non-decreasing function over [0, 1], corresponding to any \(\gamma \) .

\(\overline{w}(\gamma )\) is a bounded left continuous non-decreasing function over [0, 1], corresponding to any \(\gamma \) .

Then, the \(\gamma \) -level set

is a closed bounded interval, which is denoted by:

Definition 2.2

(Bede and Stefanini 2013 ) The g -difference is defined as follows:

In Bede and Stefanini ( 2013 ), the difference between g -derivative and q -derivative has been fully investigated.

Definition 2.3

(Bede and Stefanini 2013 ; Diamond 1999 , The Hausdorff distance ) The Hausdorff distance is defined as follows:

where \(|| \cdot ||=D(\cdot , \cdot )\) and the gH -difference \(\circleddash _{gH}\) is with interval operands \([u]^\gamma \) and \([v]^\gamma \)

By definition, D is a metric in \(R_F\) which has the subsequent properties:

\(D(w+t, z+t)=D(w,z ) \qquad \forall w, z, t \in R_F\) ,

\(D(rw,rz)=|r|D(w,z)\qquad \forall w, z\in \ R_F, r\in R\) ,

\(D(w+t,z+d)\le D(w,z)+ D(t, d)\qquad \forall w, z, t, d \in R_F\) .

Then, \((D, R_F)\) is called a complete metric space.

Definition 2.4

(Bede and Stefanini 2013 ) Neumann’s integral of \(k{:}\, [m, n] \rightarrow R_F\) is defined level-wise by the fuzzy

Definition 2.5

(Bede and Stefanini 2013 ) Suppose \(k{:}\, [m,n] \rightarrow R_F\) is a function with \([k(y)]^{\gamma }=[\underline{k}_{\gamma }(y), \overline{k}_{\gamma }(y)]\) . If \(\underline{k}_{\gamma }(y)\) and \(\overline{k}_{\gamma }(y)\) are differentiable real-valued functions with respect to y , uniformly for \(\gamma \in [0, 1]\) , then k ( y ) is g -differentiable and we have

Definition 2.6

(Bede and Stefanini 2013 ) Let \(y_0 \in [m, n]\) and t be such that \(y_0+t \in ]m, n[\) , then the g -derivative of a function \(k{:}\, ]m, n[ \rightarrow R_F\) at \(y_0\) is defined as

If there exists \(k'_g(y_0)\in R_F\) satisfying ( 7 ), we call it generalized differentiable ( g -differentiable for short) at \(y_0\) . This relation depends on the existence of \(\circleddash _g\) , and there exists no such guarantee for this desire.

Theorem 2.7

Suppose \(k{:}\,[m,n]\rightarrow R_F\) is a continuous function with \([k(y)]^{\gamma }=[k^{-}_{\gamma }(y), k^{+}_{\gamma }(y)]\) and g -differentiable in [ m ,  n ]. In this case, we obtain

To show the assertion, it is enough to show their equality in level-wise form, suppose k is g -differentiable, so we have

\(\square \)

Definition 2.8

(Kaleva 1990 , fuzzy Cauchy problem ) Suppose \(x'_g(s)=k(s,x(s))\) is the first-order fuzzy differential equation, where y is a fuzzy function of s , k ( s ,  x ( s )) is a fuzzy function of the crisp variable s , and the fuzzy variable x and \(x'\) is the g -fuzzy derivative of x . By the initial value \(x(s_0)=\gamma _0\) , we define the first-order fuzzy Cauchy problem:

Proposition 2.9

Suppose \(\textit{k, h}{:}\, [\textit{a}, \textit{b}] {\rightarrow } R_F\) are two bounded functions, then

Since \(k(y)\le \textrm{sup}_A k\) and \(k(y)\le \textrm{sup}_A k\) for every \(y \in [m,n]\) , one can obtain \(k(y)+h(y)\le \textrm{sup}_A k+\textrm{sup}_A h\) . Thus, \(k+h\) is bounded from above by \(\textrm{sup}_A k+\textrm{sup}_A h\) , so \(\textrm{sup}_A( k+h) \le \textrm{sup}_A k+ \textrm{sup}_A h\) . The proof for the infimum is similar. \(\square \)

Definition 2.10

Let \(\{\widetilde{q}_m\}^\infty _{m=0}\) be a fuzzy sequence. Then, we define the backward g -difference \(\nabla _g \widetilde{q}_m\) as follows

So, we have

Consequently,

Proposition 2.11

For a given fuzzy sequence \({\left\{ {\widetilde{q}}_m\right\} }^{\infty }_{m=0}\) , by supposing backward g -difference, we have

We prove proposition by induction that, for all \(n \in \mathbb {Z}^+\) ,

Using Definition 2.10 , for base case, \(n = 1\) , we have

Induction step : Let \( k \in \mathbb {Z}^+\) be given and suppose ( 14 ) is true for \(n=k\) . Then,

Conclusion : For all \(m\in \mathbb {Z}^+\) , ( 14 ) is correct, by the principle of induction. \(\square \)

Definition 2.12

( Switching Point ) The concept of switching point refers to an interval where fuzzy differentiability of type-(i) turns into type-(ii) and also vice versa.

3 Fuzzy Adams–Bashforth method

To derivative of a fuzzy multistep method, we consider the solution of the initial-value problem:

To obtain the approximation \(t_{j+1}\) at the mesh point \(s_{j+1}\) , where initial values

are assumed.

If integrated over the interval \([s_j,s_{j+1}]\) , we get

but, without knowing \(\widetilde{x}(s)\) , we cannot integrate \(\widetilde{k}(s,\widetilde{x}(s))\) , one can apply an interpolating polynomial \(\widetilde{q}(s)\) to \(\widetilde{k}(s, \widetilde{x}(s))\) , which is computed by the data points \(\left( s_0, {\widetilde{t}}_0\right) , \left( s_1,{\widetilde{t}}_1\right) ,\ldots \left( s_j,{\widetilde{t}}_j\right) \) . These data were obtained in Sect.  2 .

Indeed, by supposing that \(\widetilde{x}\left( s_j\right) \approx \ {\widetilde{t}}_j\ \) , Eq. ( 17 ) is rewritten as

To take a fuzzy Adams–Bashforth explicit m -step method under the notion of g -difference, we construct the backward difference polynomial \({\widetilde{q}}_{n-1}(s)\) ,

We assume that the n th derivatives of the fuzzy function k exist. This means that all derivatives are g -differentiable. As \({\widetilde{q}}_{n-1}(s)\) is an interpolation polynomial of degree \(n-1\) , some number \({\xi }_j\) in \(\left( s_{j+1-n}, s_j\right) \) exists with

where the corresponding notation \({\widetilde{k}}^{(n)}_g (s, \widetilde{x}(s)),n\in \mathbb {N},\) exists. Moreover, it can be mentioned that the existence of this corresponding formula based on the existence of \({\circleddash }_g\) , and while \({\circleddash }_g\) exist this relation always exists.

We introduce the \(s=s_j+\beta h\) , with \(\textrm{d}s=h \textrm{d}\beta \) , substituting these variable into \({\widetilde{q}}_{n-1}(s)\) and the error term indicates

So, we will get

Obviously, the product of \(\beta \ \left( \beta +1\right) \cdots \left( \beta +n-1\right) \) does not change sign on [0, 1], so the Weighted Mean Value Theorem for some number \({\mu }_j\) , where \(s_{j+1-n}< {\mu }_j< s_{j+1}\) , can be applied to the last term in Eq. ( 22 ), hence it becomes

So, it simplifies to

So, Eq. ( 20 ) is written as

It is also worth mentioning that the notions \(\Delta _{g}\) and \(\oplus \) are extensively utilized solving the problems of sup and inf existence.

To illustrate this method, we discuss solving the fuzzy initial value problem \({\widetilde{x}}'\left( s\right) =\widetilde{k}(s,\widetilde{x}\left( s\right) )\) by Adams–Bashforth’s three-step method. To derive the three-step Adams–Bashforth technique, with \(n= 3\) , We have

For \(m=2, 3,\ldots , N-1.\) So

Here, we also describe our model as introduced models \(\Delta _{g}\) and \(\oplus \) .

By considering

As a consequence

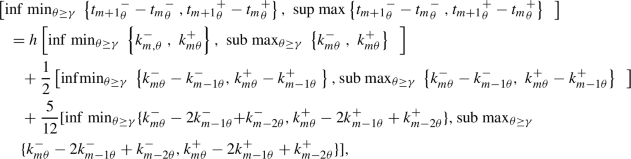
from which we obtain

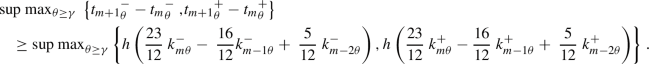
From ( 24 ) and ( 29 ), we get

if we suppose that

Then, we have

Similarly, we have

Then, we can say

4 Convergence

We begin our dissection with definitions of the convergence of multistep difference equation and consistency before discussing methods to solve the differential equation.

Definition 4.1

The differential fuzzy equation with initial condition

and similarly, the other models can be derived as

is the \(\left( j+1\right) \) st step in a multistep method. At this step, it has a fuzzy local truncation error as follows

Exists N that for all \(j= n-1, n, \ldots N-1\) , and \(h=\frac{b-a}{N}\) , where

And \(\widetilde{x}\left( s_j\right) \) indicates the exact value of the solution of the differential equation. The approximation \({\widetilde{t}}_j\) is taken from the different methods at the j th step.

Definition 4.2

A multistep method with local truncation error \({\widetilde{\nu }}_{j+1}\left( h\right) \) at the \((j+1)\) th step is called consistent with the differential equation approximation if

Theorem 4.3

Let the initial-value problem

be approximated by a multistep difference method:

Let a number \(h_0>0\) exist, and \(\phi \left( s_j,\widetilde{t}\left( s_j\right) \right) \) be continuous, with meets the constant Lipschitz T

Then, the difference method is convergent if and only if it is consistent. It is equal to

We are aware of the concept of convergence for the multistep method. As the step size approaches zero, the solution of the difference equation approaches the solution to the differential equation. In other words

For the multistep fuzzy Adams–Bashforth method, we have seen that

using Proposition 2.11 , \(\nabla ^l_g{\widetilde{k}}_m=h^l\widetilde{k}^{(l)}_{m_g}\) , and substituting it in Eq. ( 66 ), we have

under the hypotheses of paper, \(\widetilde{k}({(s}_j,\widetilde{x}(s_j))\in R_F\) , and by definition g -differentiability \(\widetilde{k}^{(n)}({(s}_j,\widetilde{x}(s_j))\in R_F\) so by Definition 2.1 \(\ {\widetilde{k}}^{(n)}\left( {(s}_j,\widetilde{x}\left( s_j\right) \right) \in R_F\) for \(j\ge 0\) are bounded, thus exists M such that

When \(h\rightarrow 0\) , we will have \(Z\rightarrow 0\) so

So, we see that it satisfied the first condition of Definition 4.2 . The concept of the second part is that if the one-step method generating the starting values is also consistent, then the multistep method is consistent. So our method is consistent; therefore according to Theorem 4.3 , this difference method is convergent.

Example 5.1

Consider the initial-value problem

Obviously, one can check the exact solution as follows:

Indeed, the solution is a triangular number

So, the exact solution in mesh point \(s=0.01\) is

On the other hand with the proposed method, the approximated solution in \(s=0.01\) is as follows:

where \(\tilde{t}^\gamma \) is a approximated of \(\tilde{x}\) .

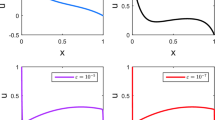
The maximum error in \(s=0.1\) , \(s=0.2, \ldots , s=1\) , also shows the errors (Table 1 ).

Thus, we have

where ( 90 ) are real values. Suppose

By ( 85 ), ( 86 ), ( 92 ), we obtain

According to the previous sections, this example has been solved by the two-step Adams–Bashforth method with \(t=0.1\) and \(N=10\) . We use the following relations to solve it.

Example 5.2

First, we solve the problem with the gH -differentiability. The initial-value problem on [0, 1] is \([(i)-gH]\) -differentiable and \([(i)-gH]\) -differentiable on (1, 2]. By solving the following system, the \([(i)-gH]\) -differentiable solution will be achieved

By solving the following system, the \([(ii)-gH]\) -differentiable solution will be achieved

If we apply the Euler method to the approximate solution of the initial-value problem by

The results are presented in Table  2 .

In the calculations of this method, we need to consider the \(i-gh\) -differentiability and \(ii-gH\) -differentiability. But when we use g -differentiability, we do not need to check the different states of the differentiability. To solve using the method mentioned in the article, we have:

Or we have \(x^\gamma (0)-[\gamma , 2-\gamma ]\) . The exact solution is as follows:

The results of the solution using the Adams–Bashforth two-step method for \(h = 1\) and calculating the approximate value of the solution and the error of the method can be seen in the Table  3 .

Consider the initial-value problem \(\tilde{x'}=(s\ominus 1)\odot \tilde{x}^2\) , where \(s\in [-1,1]\)

the exact solution is

6 Conclusion

In the present paper, the proposed method, which is based on the concept of g-differentiability, provides a fuzzy solution. This solution is related to a set of equations from the family of Adams-Bashforth differential equations, which coincide with the solutions derived by fuzzy differential equations.

The gH -difference is a powerful and versatile fuzzy differential operator that is more flexible, robust, and computationally efficient, making it a good choice for solving a wide range of fuzzy differential equations. It does not need i and ii -differentiability. In Examples, we compare g -differentiability and gH -differentiability.

G-differentiability allows for capturing gradual changes in a fuzzy-valued function. G-differentiable functions exhibit certain degrees of smoothness and continuity, which can be useful in modeling and analyzing fuzzy systems. The choice of the parameter g in g -differentiability is crucial and depends on the specific problem. Determining an appropriate value for g requires careful consideration and analysis. H -differentiability combines the gradual reduction of fuzziness (via the parameter g ) with the Hukuhara difference ( H -difference). It provides a more refined analysis of fuzzy-valued functions. gH -differentiability offers enhanced modeling capabilities by considering both the gradual reduction of fuzziness and the separation between fuzzy numbers or fuzzy sets. But gH -differentiability introduces an additional level of complexity compared to g -differentiability or H -differentiability alone. The combination of gradual reduction and H -difference requires careful understanding and analysis to ensure proper application.

Data availability

There is no data available for this research.

Allahviranloo T, Pedrycz W (2020) Soft numerical computing in uncertain dynamic systems. Academic Press, New York

Google Scholar  

Allahviranloo T, Ahmady N, Ahmady E (2007) Numerical solution of fuzzy differential equations by predictor-corrector method. Inf Sci 177(7):1633–1647

Article   MathSciNet   Google Scholar  

Allahviranloo T, Kiani NA, Motamedi N (2009) Solving fuzzy differential equations by differential transformation method. Inf Sci 179(7):956–966

Bede B, Stefanini L (2013) Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst 230:119–141. https://doi.org/10.1016/j.fss.2012.10.003

Buckley JJ, Feuring T (2000) Fuzzy differential equations. Fuzzy Sets Syst 110(1):43–54

Byatt W, Kandel A (1978) Fuzzy differential equations. In: Proceedings of the international conference on Cybernetics and Society, Tokyo, Japan, vol 1

Chalco-Cano Y, Roman-Flores H (2008) On new solutions of fuzzy differential equations. Chaos Solitons Fractals 38(1):112–119

Diamond P (1999) Time-dependent differential inclusions, cocycle attractors and fuzzy differential equations. IEEE Trans Fuzzy Syst 7(6):734–740

Article   Google Scholar  

Diamond P (2000) Stability and periodicity in fuzzy differential equations. IEEE Trans Fuzzy Syst 8(5):583–590

Diamond P (2002) Brief note on the variation of constants formula for fuzzy differential equations. Fuzzy Sets Syst 129(1):65–71

Dubois D, Lubiano MA, Prade H, Gil MA, Grzegorzewski P, Hryniewicz O (2008) Soft methods for handling variability and imprecision, vol 48. Springer, Berlin

Book   Google Scholar  

Kaleva O (1987) Fuzzy differential equations. Fuzzy Sets Syst 24(3):301–317

Kaleva O (1990) The Cauchy problem for fuzzy differential equations. Fuzzy Sets Syst 35(3):389–396. https://doi.org/10.1016/0165-0114(90)90010-4

Kandel A (1980) Fuzzy dynamical systems and the nature of their solutions. In: Fuzzy sets. Springer, Berlin, pp 93–121

Mehrkanoon S, Suleiman M, Majid Z (2009) Block method for numerical solution of fuzzy differential equations. In: International mathematical forum, vol 4, Citeseer, pp 2269–2280

Safikhani L, Vahidi A, Allahviranloo T, Afshar Kermani M (2023) Multi-step gh-difference-based methods for fuzzy differential equations. Comput Appl Math 42(1):27

Seikkala S (1987) On the fuzzy initial value problem. Fuzzy Sets Syst 24(3):319–330

Song S, Wu C (2000) Existence and uniqueness of solutions to Cauchy problem of fuzzy differential equations. Fuzzy Sets Syst 110(1):55–67

Zabihi S, Ezzati R, Fattahzadeh F, Rashidinia J (2023) Numerical solutions of the fuzzy wave equation based on the fuzzy difference method. Fuzzy Sets Syst 465:108537. https://doi.org/10.1016/j.fss.2023.108537

Download references

Acknowledgements

The authors are thankful to the area editor and referees for giving valuable comments and suggestions.

Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK).

Author information

Authors and affiliations.

Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran

S. Soroush & T. Allahviranloo

Research Center of Performance and Productivity Analysis, Istinye University, Istanbul, Turkey

T. Allahviranloo

Department of Applied Mathematics, Faculty of Mathematics Sciences, Shahid Beheshti University, Tehran, Iran

H. Azari & M. Rostamy-Malkhalifeh

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to T. Allahviranloo .

Additional information

Communicated by Marcos Eduardo Valle.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Soroush, S., Allahviranloo, T., Azari, H. et al. Generalized fuzzy difference method for solving fuzzy initial value problem. Comp. Appl. Math. 43 , 129 (2024). https://doi.org/10.1007/s40314-024-02645-2

Download citation

Received : 30 March 2023

Revised : 12 January 2024

Accepted : 14 February 2024

Published : 27 March 2024

DOI : https://doi.org/10.1007/s40314-024-02645-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Fuzzy differential equation
• Generalized differentiability
• Adams–Bashforth method
• Fuzzy difference equations

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.2: Numerical Methods - Initial Value Problem

• Last updated
• Save as PDF
• Page ID 96065

• Jeffrey R. Chasnov
• Hong Kong University of Science and Technology

We begin with the simple Euler method, then discuss the more sophisticated RungeKutta methods, and conclude with the Runge-Kutta-Fehlberg method, as implemented in the MATLAB function ode45.m. Our differential equations are for \(x=\) \(x(t)\) , where the time \(t\) is the independent variable, and we will make use of the notation \(\dot{x}=d x / d t\) . This notation is still widely used by physicists and descends directly from the notation originally used by Newton.

7.2.1. Euler method

The Euler method is the most straightforward method to integrate a differential equation. Consider the first-order differential equation

\[\dot{x}=f(t, x), \nonumber \]

with the initial condition \(x(0)=x_{0}\) . Define \(t_{n}=n \Delta t\) and \(x_{n}=x\left(t_{n}\right)\) . A Taylor series expansion of \(x_{n+1}\) results in

\[\begin{aligned} x_{n+1} &=x\left(t_{n}+\Delta t\right) \\ &=x\left(t_{n}\right)+\Delta t \dot{x}\left(t_{n}\right)+\mathrm{O}\left(\Delta t^{2}\right) \\ &=x\left(t_{n}\right)+\Delta t f\left(t_{n}, x_{n}\right)+\mathrm{O}\left(\Delta t^{2}\right) \end{aligned} \nonumber \]

The Euler Method is therefore written as

\[x_{n+1}=x\left(t_{n}\right)+\Delta t f\left(t_{n}, x_{n}\right) \nonumber \]

We say that the Euler method steps forward in time using a time-step \(\Delta t\) , starting from the initial value \(x_{0}=x(0)\) . The local error of the Euler Method is \(\mathrm{O}\left(\Delta t^{2}\right)\) . The global error, however, incurred when integrating to a time \(T\) , is a factor of \(1 / \Delta t\) larger and is given by \(\mathrm{O}(\Delta t)\) . It is therefore customary to call the Euler Method a first-order method.

7.2.2. Modified Euler method

This method is of a type that is called a predictor-corrector method. It is also the first of what are Runge-Kutta methods. As before, we want to solve (7.3). The idea is to average the value of \(\dot{x}\) at the beginning and end of the time step. That is, we would like to modify the Euler method and write

\[x_{n+1}=x_{n}+\frac{1}{2} \Delta t\left(f\left(t_{n}, x_{n}\right)+f\left(t_{n}+\Delta t, x_{n+1}\right)\right) \nonumber \]

The obvious problem with this formula is that the unknown value \(x_{n+1}\) appears on the right-hand-side. We can, however, estimate this value, in what is called the predictor step. For the predictor step, we use the Euler method to find

\[x_{n+1}^{p}=x_{n}+\Delta t f\left(t_{n}, x_{n}\right) \nonumber \]

The corrector step then becomes

\[x_{n+1}=x_{n}+\frac{1}{2} \Delta t\left(f\left(t_{n}, x_{n}\right)+f\left(t_{n}+\Delta t, x_{n+1}^{p}\right)\right) \nonumber \]

The Modified Euler Method can be rewritten in the following form that we will later identify as a Runge-Kutta method:

\[\begin{aligned} k_{1} &=\Delta t f\left(t_{n}, x_{n}\right) \\ k_{2} &=\Delta t f\left(t_{n}+\Delta t, x_{n}+k_{1}\right) \\ x_{n+1} &=x_{n}+\frac{1}{2}\left(k_{1}+k_{2}\right) \end{aligned} \nonumber \]

7.2.3.  Second-order Runge-Kutta methods

We now derive all second-order Runge-Kutta methods. Higher-order methods can be similarly derived, but require substantially more algebra.

We consider the differential equation given by (7.3). A general second-order Runge-Kutta method may be written in the form

\[\begin{aligned} k_{1} &=\Delta t f\left(t_{n}, x_{n}\right) \\ k_{2} &=\Delta t f\left(t_{n}+\alpha \Delta t, x_{n}+\beta k_{1}\right) \\ x_{n+1} &=x_{n}+a k_{1}+b k_{2} \end{aligned} \nonumber \]

with \(\alpha, \beta, a\) and \(b\) constants that define the particular second-order Runge-Kutta method. These constants are to be constrained by setting the local error of the second-order Runge-Kutta method to be \(\mathrm{O}\left(\Delta t^{3}\right)\) . Intuitively, we might guess that two of the constraints will be \(a+b=1\) and \(\alpha=\beta\) .

We compute the Taylor series of \(x_{n+1}\) directly, and from the Runge-Kutta method, and require them to be the same to order \(\Delta t^{2}\) . First, we compute the Taylor series of \(x_{n+1}\) . We have

\[\begin{aligned} x_{n+1} &=x\left(t_{n}+\Delta t\right) \\ &=x\left(t_{n}\right)+\Delta t \dot{x}\left(t_{n}\right)+\frac{1}{2}(\Delta t)^{2} \ddot{x}\left(t_{n}\right)+\mathrm{O}\left(\Delta t^{3}\right) \end{aligned} \nonumber \]

\[\dot{x}\left(t_{n}\right)=f\left(t_{n}, x_{n}\right) . \nonumber \]

The second derivative is more complicated and requires partial derivatives. We have

\[\begin{aligned} \ddot{x}\left(t_{n}\right) &\left.=\frac{d}{d t} f(t, x(t))\right]_{t=t_{n}} \\ &=f_{t}\left(t_{n}, x_{n}\right)+\dot{x}\left(t_{n}\right) f_{x}\left(t_{n}, x_{n}\right) \\ &=f_{t}\left(t_{n}, x_{n}\right)+f\left(t_{n}, x_{n}\right) f_{x}\left(t_{n}, x_{n}\right) \end{aligned} \nonumber \]

\[x_{n+1}=x_{n}+\Delta t f\left(t_{n}, x_{n}\right)+\frac{1}{2}(\Delta t)^{2}\left(f_{t}\left(t_{n}, x_{n}\right)+f\left(t_{n}, x_{n}\right) f_{x}\left(t_{n}, x_{n}\right)\right) \nonumber \]

Second, we compute \(x_{n+1}\) from the Runge-Kutta method given by (7.5). Substituting in \(k_{1}\) and \(k_{2}\) , we have

\[x_{n+1}=x_{n}+a \Delta t f\left(t_{n}, x_{n}\right)+b \Delta t f\left(t_{n}+\alpha \Delta t, x_{n}+\beta \Delta t f\left(t_{n}, x_{n}\right)\right) . \nonumber \]

We Taylor series expand using

\[\begin{aligned} f\left(t_{n}+\alpha \Delta t, x_{n}+\beta \Delta t f\left(t_{n}, x_{n}\right)\right) & \\ =f\left(t_{n}, x_{n}\right)+\alpha \Delta t f_{t}\left(t_{n}, x_{n}\right)+\beta \Delta t f\left(t_{n}, x_{n}\right) f_{x}\left(t_{n}, x_{n}\right)+\mathrm{O}\left(\Delta t^{2}\right) \end{aligned} \nonumber \]

The Runge-Kutta formula is therefore

\[\begin{aligned} x_{n+1}=x_{n}+(a+b) & \Delta t f\left(t_{n}, x_{n}\right) \\ &+(\Delta t)^{2}\left(\alpha b f_{t}\left(t_{n}, x_{n}\right)+\beta b f\left(t_{n}, x_{n}\right) f_{x}\left(t_{n}, x_{n}\right)\right)+\mathrm{O}\left(\Delta t^{3}\right) \end{aligned} \nonumber \]

Comparing (7.6) and (7.7), we find

\[\begin{aligned} a+b &=1 \\ \alpha b &=1 / 2 \\ \beta b &=1 / 2 \end{aligned} \nonumber \]

There are three equations for four parameters, and there exists a family of secondorder Runge-Kutta methods.

The Modified Euler Method given by (7.4) corresponds to \(\alpha=\beta=1\) and \(a=\) \(b=1 / 2\) . Another second-order Runge-Kutta method, called the Midpoint Method, corresponds to \(\alpha=\beta=1 / 2, a=0\) and \(b=1 .\) This method is written as

\[\begin{aligned} k_{1} &=\Delta t f\left(t_{n}, x_{n}\right) \\ k_{2} &=\Delta t f\left(t_{n}+\frac{1}{2} \Delta t, x_{n}+\frac{1}{2} k_{1}\right) \\ x_{n+1} &=x_{n}+k_{2} \end{aligned} \nonumber \]

7.2.4.  Higher-order Runge-Kutta methods

The general second-order Runge-Kutta method was given by (7.5). The general form of the third-order method is given by

\[\begin{aligned} k_{1} &=\Delta t f\left(t_{n}, x_{n}\right) \\ k_{2} &=\Delta t f\left(t_{n}+\alpha \Delta t, x_{n}+\beta k_{1}\right) \\ k_{3} &=\Delta t f\left(t_{n}+\gamma \Delta t, x_{n}+\delta k_{1}+\epsilon k_{2}\right) \\ x_{n+1} &=x_{n}+a k_{1}+b k_{2}+c k_{3} \end{aligned} \nonumber \]

The following constraints on the constants can be guessed: \(\alpha=\beta, \gamma=\delta+\epsilon\) , and \(a+b+c=1\) . Remaining constraints need to be derived.

The fourth-order method has a \(k_{1}, k_{2}, k_{3}\) and \(k_{4}\) . The fifth-order method requires up to \(k_{6}\) . The table below gives the order of the method and the number of stages required.

Because of the jump in the number of stages required between the fourth-order and fifth-order method, the fourth-order Runge-Kutta method has some appeal. The general fourth-order method starts with 13 constants, and one then finds 11 constraints. A particularly simple fourth-order method that has been widely used is given by

\[\begin{aligned} k_{1} &=\Delta t f\left(t_{n}, x_{n}\right) \\ k_{2} &=\Delta t f\left(t_{n}+\frac{1}{2} \Delta t, x_{n}+\frac{1}{2} k_{1}\right) \\ k_{3} &=\Delta t f\left(t_{n}+\frac{1}{2} \Delta t, x_{n}+\frac{1}{2} k_{2}\right) \\ k_{4} &=\Delta t f\left(t_{n}+\Delta t, x_{n}+k_{3}\right) \\ x_{n+1} &=x_{n}+\frac{1}{6}\left(k_{1}+2 k_{2}+2 k_{3}+k_{4}\right) \end{aligned} \nonumber \]

7.2.5.  Adaptive Runge-Kutta Methods

As in adaptive integration, it is useful to devise an ode integrator that automatically finds the appropriate \(\Delta t\) . The Dormand-Prince Method, which is implemented in MATLAB’s ode45.m, finds the appropriate step size by comparing the results of a fifth-order and fourth-order method. It requires six function evaluations per time step, and constructs both a fifth-order and a fourth-order method from these function evaluations.

Suppose the fifth-order method finds \(x_{n+1}\) with local error \(\mathrm{O}\left(\Delta t^{6}\right)\) , and the fourth-order method finds \(x_{n+1}^{\prime}\) with local error \(\mathrm{O}\left(\Delta t^{5}\right)\) . Let \(\varepsilon\) be the desired error tolerance of the method, and let \(e\) be the actual error. We can estimate \(e\) from the difference between the fifth-and fourth-order methods; that is,

\[e=\left|x_{n+1}-x_{n+1}^{\prime}\right| \nonumber \]

Now \(e\) is of \(\mathrm{O}\left(\Delta t^{5}\right)\) , where \(\Delta t\) is the step size taken. Let \(\Delta \tau\) be the estimated step size required to get the desired error \(\varepsilon\) . Then we have

\[e / \varepsilon=(\Delta t)^{5} /(\Delta \tau)^{5} \nonumber \]

or solving for \(\Delta \tau\) ,

\[\Delta \tau=\Delta t\left(\frac{\varepsilon}{e}\right)^{1 / 5} \nonumber \]

On the one hand, if \(e<\varepsilon\) , then we accept \(x_{n+1}\) and do the next time step using the larger value of \(\Delta \tau\) . On the other hand, if \(e>\varepsilon\) , then we reject the integration step and redo the time step using the smaller value of \(\Delta \tau\) . In practice, one usually increases the time step slightly less and decreases the time step slightly more to prevent the waste of too many failed time steps.

7.2.6. System of differential equations

Our numerical methods can be easily adapted to solve higher-order differential equations, or equivalently, a system of differential equations. First, we show how a second-order differential equation can be reduced to two first-order equations. Consider

\[\ddot{x}=f(t, x, \dot{x}) . \nonumber \]

This second-order equation can be rewritten as two first-order equations by defining \(u=\dot{x} .\) We then have the system

\[\begin{aligned} &\dot{x}=u, \\ &\dot{u}=f(t, x, u) . \end{aligned} \nonumber \]

This trick also works for higher-order equation. For another example, the thirdorder equation

\[\dddot x=f(t, x, \dot{x}, \ddot{x}), \nonumber \]

can be written as

\[\begin{aligned} &\dot{x}=u \\ &\dot{u}=v \\ &\dot{v}=f(t, x, u, v) . \end{aligned} \nonumber \]

Now, we show how to generalize Runge-Kutta methods to a system of differential equations. As an example, consider the following system of two odes,

\[\begin{aligned} &\dot{x}=f(t, x, y), \\ &\dot{y}=g(t, x, y), \end{aligned} \nonumber \]

with the initial conditions \(x(0)=x_{0}\) and \(y(0)=y_{0}\) . The generalization of the commonly used fourth-order Runge-Kutta method would be

\[\begin{aligned} k_{1} &=\Delta t f\left(t_{n}, x_{n}, y_{n}\right) \\ l_{1} &=\Delta t g\left(t_{n}, x_{n}, y_{n}\right) \\ k_{2} &=\Delta t f\left(t_{n}+\frac{1}{2} \Delta t, x_{n}+\frac{1}{2} k_{1}, y_{n}+\frac{1}{2} l_{1}\right) \\ l_{2} &=\Delta t g\left(t_{n}+\frac{1}{2} \Delta t, x_{n}+\frac{1}{2} k_{1}, y_{n}+\frac{1}{2} l_{1}\right) \\ y_{3} &=\Delta t f\left(t_{n}+\frac{1}{2} \Delta t, x_{n}+\frac{1}{2} k_{2}, y_{n}+\frac{1}{2} l_{2}\right) \\ l_{3} &=\Delta t g\left(t_{n}+\frac{1}{2} \Delta t, x_{n}+\frac{1}{2} k_{2}, y_{n}+\frac{1}{2} l_{2}\right) \\ y_{n+1} &=y_{n}+\frac{1}{6}\left(l_{1}+2 l_{2}+2 l_{3}+l_{4}\right) \\ k_{4} &=\Delta t f\left(t_{n}+\Delta t, x_{n}+k_{3}, y_{n}+l_{3}\right) \\ l_{4} &=\Delta t g\left(t_{n}+\Delta t, x_{n}+k_{3}, y_{n}+l_{3}\right) \\ &=x_{n}+\frac{1}{6}\left(k_{1}+2 k_{2}+2 k_{3}+k_{4}\right) \\ &=\Delta \end{aligned} \nonumber \]