solving systems of equations using matrices practice problems

Solving Systems of Linear Equations Using Matrices

Hi there! This page is only going to make sense when you know a little about Systems of Linear Equations and Matrices , so please go and learn about those if you don't know them already.

The Example

One of the last examples on Systems of Linear Equations was this one:

Example: Solve

• x + y + z = 6
• 2y + 5z = −4
• 2x + 5y − z = 27

We went on to solve it using "elimination", but we can also solve it using Matrices!

Using Matrices makes life easier because we can use a computer program (such as the Matrix Calculator ) to do all the "number crunching".

But first we need to write the question in Matrix form.

In Matrix Form?

OK. A Matrix is an array of numbers:

Well, think about the equations:

They could be turned into a table of numbers like this:

We could even separate the numbers before and after the "=" into:

Now it looks like we have 2 Matrices.

In fact we have a third one, which is [x y z] :

Why does [x y z] go there? Because when we Multiply Matrices we use the "Dot Product" like this:

Which is the first of our original equations above (you might like to check that). Here it is for the second line.

 Try the third line for yourself.

The Matrix Solution

We can shorten this:

• A is the 3x3 matrix of x, y and z coefficients
• X is x, y and z , and
• B is 6, −4 and 27

Then (as shown on the Inverse of a Matrix page) the solution is this:

What does that mean?

It means that we can find the X matrix (the values of x, y and z) by multiplying the inverse of the A matrix by the B matrix .

So let's go ahead and do that.

First, we need to find the inverse of the A matrix (assuming it exists!)

Using the Matrix Calculator we get this:

(I left the 1/determinant outside the matrix to make the numbers simpler)

Then multiply A -1 by B (we can use the Matrix Calculator again):

And we are done! The solution is:

x = 5 y = 3 z = −2

Just like on the Systems of Linear Equations page.

Quite neat and elegant, and the human does the thinking while the computer does the calculating.

Just For Fun ... Do It Again!

For fun (and to help you learn), let us do this all again, but put matrix "X" first.

I want to show you this way, because many people think the solution above is so neat it must be the only way.

So we will solve it like this:

And because of the way that matrices are multiplied we need to set up the matrices differently now. The rows and columns have to be switched over ("transposed"):

And XA = B looks like this:

Then (also shown on the Inverse of a Matrix page) the solution is this:

This is what we get for A -1 :

In fact it is just like the Inverse we got before, but Transposed (rows and columns swapped over).

Next we multiply B by A -1 :

And the solution is the same:

x = 5 , y = 3 and z = −2

It didn't look as neat as the previous solution, but it does show us that there is more than one way to set up and solve matrix equations. Just be careful about the rows and columns!

4.4 Solve Systems of Equations with Three Variables

Learning objectives.

By the end of this section, you will be able to:

• Determine whether an ordered triple is a solution of a system of three linear equations with three variables
• Solve a system of linear equations with three variables
• Solve applications using systems of linear equations with three variables

Be Prepared 4.10

Before you get started, take this readiness quiz.

Evaluate 5 x − 2 y + 3 z 5 x − 2 y + 3 z when x = −2 , x = −2 , y = −4 , y = −4 , and z = 3 . z = 3 . If you missed this problem, review Example 1.21 .

Be Prepared 4.11

Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 . If you missed this problem, review Example 2.6 .

Be Prepared 4.12

Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 . If you missed this problem, review Example 2.8 .

Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables

In this section, we will extend our work of solving a system of linear equations. So far we have worked with systems of equations with two equations and two variables. Now we will work with systems of three equations with three variables. But first let's review what we already know about solving equations and systems involving up to two variables.

We learned earlier that the graph of a linear equation , a x + b y = c , a x + b y = c , is a line. Each point on the line, an ordered pair ( x , y ) , ( x , y ) , is a solution to the equation. For a system of two equations with two variables, we graph two lines. Then we can see that all the points that are solutions to each equation form a line. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions

We know when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

Similarly, for a linear equation with three variables a x + b y + c z = d , a x + b y + c z = d , every solution to the equation is an ordered triple, ( x , y , z ) ( x , y , z ) , that makes the equation true.

Linear Equation in Three Variables

A linear equation with three variables, where a, b, c, and d are real numbers and a, b , and c are not all 0, is of the form

Every solution to the equation is an ordered triple, ( x , y , z ) ( x , y , z ) that makes the equation true.

All the points that are solutions to one equation form a plane in three-dimensional space. And, by finding what the planes have in common, we’ll find the solution to the system.

When we solve a system of three linear equations represented by a graph of three planes in space, there are three possible cases.

To solve a system of three linear equations, we want to find the values of the variables that are solutions to all three equations. In other words, we are looking for the ordered triple ( x , y , z ) ( x , y , z ) that makes all three equations true. These are called the solutions of the system of three linear equations with three variables .

Solutions of a System of Linear Equations with Three Variables

Solutions of a system of equations are the values of the variables that make all the equations true. A solution is represented by an ordered triple ( x , y , z ) . ( x , y , z ) .

To determine if an ordered triple is a solution to a system of three equations, we substitute the values of the variables into each equation. If the ordered triple makes all three equations true, it is a solution to the system.

Example 4.31

Determine whether the ordered triple is a solution to the system: { x − y + z = 2 2 x − y − z = −6 2 x + 2 y + z = −3 . { x − y + z = 2 2 x − y − z = −6 2 x + 2 y + z = −3 .

ⓐ ( −2 , −1 , 3 ) ( −2 , −1 , 3 ) ⓑ ( −4 , −3 , 4 ) ( −4 , −3 , 4 )

Try It 4.61

Determine whether the ordered triple is a solution to the system: { 3 x + y + z = 2 x + 2 y + z = −3 3 x + y + 2 z = 4 . { 3 x + y + z = 2 x + 2 y + z = −3 3 x + y + 2 z = 4 .

ⓐ ( 1 , −3 , 2 ) ( 1 , −3 , 2 ) ⓑ ( 4 , −1 , −5 ) ( 4 , −1 , −5 )

Try It 4.62

Determine whether the ordered triple is a solution to the system: { x − 3 y + z = −5 − 3 x − y − z = 1 2 x − 2 y + 3 z = 1 . { x − 3 y + z = −5 − 3 x − y − z = 1 2 x − 2 y + 3 z = 1 .

ⓐ ( 2 , −2 , 3 ) ( 2 , −2 , 3 ) ⓑ ( −2 , 2 , 3 ) ( −2 , 2 , 3 )

Solve a System of Linear Equations with Three Variables

To solve a system of linear equations with three variables, we basically use the same techniques we used with systems that had two variables. We start with two pairs of equations and in each pair we eliminate the same variable. This will then give us a system of equations with only two variables and then we know how to solve that system!

Next, we use the values of the two variables we just found to go back to the original equation and find the third variable. We write our answer as an ordered triple and then check our results.

Example 4.32

How to solve a system of equations with three variables by elimination.

Solve the system by elimination: { x − 2 y + z = 3 2 x + y + z = 4 3 x + 4 y + 3 z = −1 . { x − 2 y + z = 3 2 x + y + z = 4 3 x + 4 y + 3 z = −1 .

Try It 4.63

Solve the system by elimination: { 3 x + y − z = 2 2 x − 3 y − 2 z = 1 4 x − y − 3 z = 0 . { 3 x + y − z = 2 2 x − 3 y − 2 z = 1 4 x − y − 3 z = 0 .

Try It 4.64

Solve the system by elimination: { 4 x + y + z = −1 − 2 x − 2 y + z = 2 2 x + 3 y − z = 1 . { 4 x + y + z = −1 − 2 x − 2 y + z = 2 2 x + 3 y − z = 1 .

The steps are summarized here.

Solve a system of linear equations with three variables.

• If any coefficients are fractions, clear them.
• Decide which variable you will eliminate.
• Work with a pair of equations to eliminate the chosen variable.
• Multiply one or both equations so that the coefficients of that variable are opposites.
• Add the equations resulting from Step 2 to eliminate one variable
• Step 3. Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
• Step 4. The two new equations form a system of two equations with two variables. Solve this system.
• Step 5. Use the values of the two variables found in Step 4 to find the third variable.
• Step 6. Write the solution as an ordered triple.
• Step 7. Check that the ordered triple is a solution to all three original equations.

Example 4.33

Solve: { 3 x − 4 z = 0 3 y + 2 z = −3 2 x + 3 y = −5 . { 3 x − 4 z = 0 3 y + 2 z = −3 2 x + 3 y = −5 .

We can eliminate z z from equations (1) and (2) by multiplying equation (2) by 2 and then adding the resulting equations.

Notice that equations (3) and (4) both have the variables x x and y y . We will solve this new system for x x and y y .

To solve for y , we substitute x = −4 x = −4 into equation (3).

We now have x = −4 x = −4 and y = 1 . y = 1 . We need to solve for z . We can substitute x = −4 x = −4 into equation (1) to find z .

We write the solution as an ordered triple. ( −4 , 1 , −3 ) ( −4 , 1 , −3 )

We check that the solution makes all three equations true.

3 x − 4 z = 0 ( 1 ) 3 ( −4 ) − 4 ( −3 ) = ? 0 0 = 0 ✓ 3 y + 2 z = −3 ( 2 ) 3 ( 1 ) + 2 ( −3 ) = ? − 3 −3 = −3 ✓ 2 x + 3 y = −5 ( 3 ) 2 ( −4 ) + 3 ( 1 ) = ? − 5 −5 = −5 ✓ The solution is ( −4 , 1 , −3 ) . 3 x − 4 z = 0 ( 1 ) 3 ( −4 ) − 4 ( −3 ) = ? 0 0 = 0 ✓ 3 y + 2 z = −3 ( 2 ) 3 ( 1 ) + 2 ( −3 ) = ? − 3 −3 = −3 ✓ 2 x + 3 y = −5 ( 3 ) 2 ( −4 ) + 3 ( 1 ) = ? − 5 −5 = −5 ✓ The solution is ( −4 , 1 , −3 ) .

Try It 4.65

Solve: { 3 x − 4 z = −1 2 y + 3 z = 2 2 x + 3 y = 6 . { 3 x − 4 z = −1 2 y + 3 z = 2 2 x + 3 y = 6 .

Try It 4.66

Solve: { 4 x − 3 z = −5 3 y + 2 z = 7 3 x + 4 y = 6 . { 4 x − 3 z = −5 3 y + 2 z = 7 3 x + 4 y = 6 .

When we solve a system and end up with no variables and a false statement, we know there are no solutions and that the system is inconsistent. The next example shows a system of equations that is inconsistent.

Example 4.34

Solve the system of equations: { x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2 . { x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2 .

Use equation (1) and (2) to eliminate z .

Use (2) and (3) to eliminate z z again.

Use (4) and (5) to eliminate a variable.

There is no solution.

We are left with a false statement and this tells us the system is inconsistent and has no solution.

Try It 4.67

Solve the system of equations: { x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1 . { x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1 .

Try It 4.68

Solve the system of equations: { 2 x − 2 y + 3 z = 6 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 . { 2 x − 2 y + 3 z = 6 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 .

When we solve a system and end up with no variables but a true statement, we know there are infinitely many solutions. The system is consistent with dependent equations. Our solution will show how two of the variables depend on the third.

Example 4.35

Solve the system of equations: { x + 2 y − z = 1 2 x + 7 y + 4 z = 11 x + 3 y + z = 4 . { x + 2 y − z = 1 2 x + 7 y + 4 z = 11 x + 3 y + z = 4 .

Use equation (1) and (3) to eliminate x .

Use equation (1) and (2) to eliminate x again.

Use equation (4) and (5) to eliminate y y .

The true statement 0 = 0 0 = 0 tells us that this is a dependent system that has infinitely many solutions. The solutions are of the form ( x , y , z ) ( x , y , z ) where x = 5 z − 5 ; y = −2 z + 3 x = 5 z − 5 ; y = −2 z + 3 and z is any real number.

Try It 4.69

Solve the system by equations: { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 . { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 .

Try It 4.70

Solve the system by equations: { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 . { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 .

Solve Applications using Systems of Linear Equations with Three Variables

Applications that are modeled by a systems of equations can be solved using the same techniques we used to solve the systems. Many of the application are just extensions to three variables of the types we have solved earlier.

Example 4.36

The community college theater department sold three kinds of tickets to its latest play production. The adult tickets sold for $15, the student tickets for $10 and the child tickets for $8. The theater department was thrilled to have sold 250 tickets and brought in $2,825 in one night. The number of student tickets sold is twice the number of adult tickets sold. How many of each type did the department sell?

Try It 4.71

The community college fine arts department sold three kinds of tickets to its latest dance presentation. The adult tickets sold for $20, the student tickets for $12 and the child tickets for $10.The fine arts department was thrilled to have sold 350 tickets and brought in $4,650 in one night. The number of child tickets sold is the same as the number of adult tickets sold. How many of each type did the department sell?

Try It 4.72

The community college soccer team sold three kinds of tickets to its latest game. The adult tickets sold for $10, the student tickets for $8 and the child tickets for $5. The soccer team was thrilled to have sold 600 tickets and brought in $4,900 for one game. The number of adult tickets is twice the number of child tickets. How many of each type did the soccer team sell?

Access this online resource for additional instruction and practice with solving a linear system in three variables with no or infinite solutions.

• Solving a Linear System in Three Variables with No or Infinite Solutions
• 3 Variable Application

Section 4.4 Exercises

Practice makes perfect.

In the following exercises, determine whether the ordered triple is a solution to the system.

{ 2 x − 6 y + z = 3 3 x − 4 y − 3 z = 2 2 x + 3 y − 2 z = 3 { 2 x − 6 y + z = 3 3 x − 4 y − 3 z = 2 2 x + 3 y − 2 z = 3

ⓐ ( 3 , 1 , 3 ) ( 3 , 1 , 3 ) ⓑ ( 4 , 3 , 7 ) ( 4 , 3 , 7 )

{ − 3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1 { − 3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1

ⓐ ( −5 , −7 , 4 ) ( −5 , −7 , 4 ) ⓑ ( 5 , 7 , 4 ) ( 5 , 7 , 4 )

{ y − 10 z = −8 2 x − y = 2 x − 5 z = 3 { y − 10 z = −8 2 x − y = 2 x − 5 z = 3

ⓐ ( 7 , 12 , 2 ) ( 7 , 12 , 2 ) ⓑ ( 2 , 2 , 1 ) ( 2 , 2 , 1 )

{ x + 3 y − z = 15 y = 2 3 x − 2 x − 3 y + z = −2 { x + 3 y − z = 15 y = 2 3 x − 2 x − 3 y + z = −2

ⓐ ( −6 , 5 , 1 2 ) ( −6 , 5 , 1 2 ) ⓑ ( 5 , 4 3 , −3 ) ( 5 , 4 3 , −3 )

In the following exercises, solve the system of equations.

{ 5 x + 2 y + z = 5 − 3 x − y + 2 z = 6 2 x + 3 y − 3 z = 5 { 5 x + 2 y + z = 5 − 3 x − y + 2 z = 6 2 x + 3 y − 3 z = 5

{ 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1 { 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1

{ 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3 { 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3

{ 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7 { 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7

{ 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3 { 3 x − 5 y + 4 z = 5 5 x + 2 y + z = 0 2 x + 3 y − 2 z = 3

{ 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7 { 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7

{ 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1 { 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1

{ 11 x + 9 y + 2 z = −9 7 x + 5 y + 3 z = −7 4 x + 3 y + z = −3 { 11 x + 9 y + 2 z = −9 7 x + 5 y + 3 z = −7 4 x + 3 y + z = −3

{ 1 3 x − y − z = 1 x + 5 2 y + z = −2 2 x + 2 y + 1 2 z = −4 { 1 3 x − y − z = 1 x + 5 2 y + z = −2 2 x + 2 y + 1 2 z = −4

{ x + 1 2 y + 1 2 z = 0 1 5 x − 1 5 y + z = 0 1 3 x − 1 3 y + 2 z = −1 { x + 1 2 y + 1 2 z = 0 1 5 x − 1 5 y + z = 0 1 3 x − 1 3 y + 2 z = −1

{ x + 1 3 y − 2 z = −1 1 3 x + y + 1 2 z = 0 1 2 x + 1 3 y − 1 2 z = −1 { x + 1 3 y − 2 z = −1 1 3 x + y + 1 2 z = 0 1 2 x + 1 3 y − 1 2 z = −1

{ 1 3 x − y + 1 2 z = 4 2 3 x + 5 2 y − 4 z = 0 x − 1 2 y + 3 2 z = 2 { 1 3 x − y + 1 2 z = 4 2 3 x + 5 2 y − 4 z = 0 x − 1 2 y + 3 2 z = 2

{ x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3 { x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3

{ 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3 { 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3

{ 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1 { 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1

{ 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8 { 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8

{ 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6 { 4 x − 3 y + 2 z = 0 − 2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6

{ x − 2 y + 2 z = 1 − 2 x + y − z = 2 x − y + z = 5 { x − 2 y + 2 z = 1 − 2 x + y − z = 2 x − y + z = 5

{ 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20 { 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20

{ x + 4 y + z = −8 4 x − y + 3 z = 9 2 x + 7 y + z = 0 { x + 4 y + z = −8 4 x − y + 3 z = 9 2 x + 7 y + z = 0

{ x + 2 y + z = 4 x + y − 2 z = 3 − 2 x − 3 y + z = −7 { x + 2 y + z = 4 x + y − 2 z = 3 − 2 x − 3 y + z = −7

{ x + y − 2 z = 3 − 2 x − 3 y + z = −7 x + 2 y + z = 4 { x + y − 2 z = 3 − 2 x − 3 y + z = −7 x + 2 y + z = 4

{ x + y − 3 z = −1 y − z = 0 − x + 2 y = 1 { x + y − 3 z = −1 y − z = 0 − x + 2 y = 1

{ x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7 { x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7

In the following exercises, solve the given problem.

The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is twice the measure of the first angle. The third angle is twelve more than the second. Find the measures of the three angles.

The sum of the measures of the angles of a triangle is 180. The sum of the measures of the second and third angles is three times the measure of the first angle. The third angle is fifteen more than the second. Find the measures of the three angles.

After watching a major musical production at the theater, the patrons can purchase souvenirs. If a family purchases 4 t-shirts, the video, and 1 stuffed animal, their total is $135.

A couple buys 2 t-shirts, the video, and 3 stuffed animals for their nieces and spends $115. Another couple buys 2 t-shirts, the video, and 1 stuffed animal and their total is $85. What is the cost of each item?

The church youth group is selling snacks to raise money to attend their convention. Amy sold 2 pounds of candy, 3 boxes of cookies and 1 can of popcorn for a total sales of $65. Brian sold 4 pounds of candy, 6 boxes of cookies and 3 cans of popcorn for a total sales of $140. Paulina sold 8 pounds of candy, 8 boxes of cookies and 5 cans of popcorn for a total sales of $250. What is the cost of each item?

Study Guides > Precalculus I

Solving a system of linear equations using matrices.

We have seen how to write a system of equations with an augmented matrix , and then how to use row operations and back-substitution to obtain row-echelon form . Now, we will take row-echelon form a step farther to solve a 3 by 3 system of linear equations. The general idea is to eliminate all but one variable using row operations and then back-substitute to solve for the other variables.

Example 6: Solving a System of Linear Equations Using Matrices

Example 7: solving a dependent system of linear equations using matrices, can any system of linear equations be solved by gaussian elimination, how to: given a system of equations, solve with matrices using a calculator..

• Save the augmented matrix as a matrix variable [latex]\left[A\right],\left[B\right],\left[C\right]\text{,} \dots [/latex].
• Use the ref( function in the calculator, calling up each matrix variable as needed.

Example 8: Solving Systems of Equations with Matrices Using a Calculator

Example 9: applying 2 × 2 matrices to finance, example 10: applying 3 × 3 matrices to finance, licenses & attributions, cc licensed content, specific attribution.

• Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

Forgot password? New user? Sign up

Existing user? Log in

Solving Linear Systems Using Matrices

Already have an account? Log in here.

• Worranat Pakornrat

Solving systems of linear equations is a common problem encountered in many disciplines. Solving such problems is so important that the techniques for solving them ( substitution , elimination ) are learned early on in algebra studies. This wiki will elaborate on the elementary technique of elimination and explore a few more techniques that can be obtained from linear algebra .

Row Reduction Techniques

Interpreting solutions from reduced row echelon form, multiplication by inverse of coefficient matrix, cramer's rule.

A system of equations can be represented in a couple of different matrix forms. One way is to realize the system as the matrix multiplication of the coefficients in the system and the column vector of its variables. The square matrix is called the coefficient matrix because it consists of the coefficients of the variables in the system of equations:

\[ \text{Product of matrices: } \quad \begin{array}{c c c c c c c} 2x & + & 4y & + & 7z & = & 4\\ 3x & + & 3y & + & 2z & = & 8\\ 5x & + & 6y & + & 3z & = & 0 \\ \end{array} \longrightarrow \left[ \begin{array}{c c c} 2 & 4 & 7\\ 3 & 3 & 2 \\ 5 & 6 & 3 \\ \end{array}\right] \left[ \begin{array}{c} x \\ y \\ z\\ \end{array} \right] = \left[ \begin{array}{c} 4 \\ 8 \\ 0 \end{array} \right]. \]

An alternate representation called an augmented matrix is created by stitching the columns of matrices together and divided by a vertical bar. The coefficient matrix is placed on the left of this vertical bar, while the constants on the right-hand side of each equation are placed on the right of the vertical bar:

\[ \text{Augmented matrix: } \quad \quad \begin{array}{c c c c c c c} 2x & + & 4y & + & 7z & = & 4\\ 3x & + & 3y & + & 2z & = & 8\\ 5x & + & 6y & + & 3z & = & 0 \\ \end{array} \longrightarrow \left[ \begin{array}{c c c | c} 2 & 4 & 7 & 4\\ 3 & 3 & 2 & 8\\ 5 & 6 & 3 & 0 \end{array}\right]. \]

The matrices that represent these systems can be manipulated in such a way as to provide easy to read solutions. This manipulation is called row reduction. Row reduction techniques transform the matrix into reduced row echelon form without changing the solutions to the system.

The reduced row echelon form of a matrix \(A\) \(\big(\)denoted \( \text{rref}(A)\big)\) is a matrix equal dimensions that satisfies: The leftmost non-zero element in each row is \( 1 \). This element is known as a pivot. Any column can have at most \( 1 \) pivot. If a column has a pivot, then the rest of the elements in the column will be \( 0 \). For any two columns \(C_{1} \) and \(C_{2}\) that have pivots in rows \( R_{1} \) and \( R_{2}, \) respectively, if pivot in \( C_{1} \) is to the left of pivot in \( C_{2}\), then \( R_{1} \) is above \( R_{2} \). In other words, for any two pivots \( P_{1}\) and \(P_{2}\), if \( P_{2} \) is to the right of \( P_{1} \), then \( P_{2} \) is below \( P_{1}\). Rows that consist of only zeroes are in the bottom of the matrix.

To convert any matrix to its reduced row echelon form, Gauss-Jordan elimination is performed. There are three elementary row operations used to achieve reduced row echelon form:

• Switch two rows.
• Multiply a row by any non-zero constant.
• Add a scalar multiple of one row to any other row.

Find \( \text{rref}(A)\) using Gauss-Jordan elimination, where \[ A = \left[ \begin{array}{c c c} 2 & 6 & -2\\ 1 & 6 & -4 \\ -1 & 4 & 9 \\ \end{array}\right].\] The leftmost element in the first row must be 1, so the first row is divided by 2: \[ \left[ \begin{array}{c c c} 2 & 6 & -2\\ 1 & 6 & -4 \\ -1 & 4 & 9 \\ \end{array}\right] \ce{->[\large \text{Divide the first row by 2.}]} \left[ \begin{array}{c c c} 1 & 3 & -1\\ 1 & 6 & -4 \\ -1 & 4 & 9 \\ \end{array}\right]. \] The top left element is a pivot, so the rest of the elements in the first column must be 0. This can be done by subtracting the first row from the second row. Furthermore, the first row can be added to the third row to obtain the necessary 0s in the first column: \[ \left[ \begin{array}{c c c} 1 & 3 & -1\\ 1 & 6 & -4 \\ -1 & 4 & 9 \\ \end{array}\right] \ce{->[\large R_2 - R_1 \text{ and } R_3 + R_1]} \left[ \begin{array}{c c c} 1 & 3 & -1\\ 0 & 3 & -3 \\ 0 & 7 & 8 \\ \end{array}\right]. \] Now that the leftmost column is \( \left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ \end{array}\right] \), the middle element can be made 1 by dividing the second row by 3: \[ \left[ \begin{array}{c c c} 1 & 3 & -1\\ 0 & 3 & -3 \\ 0 & 7 & 8 \\ \end{array}\right] \ce{->[\large \text{Divide the second row by 3.}]} \left[ \begin{array}{c c c} 1 & 3 & -1\\ 0 & 1 & -1 \\ 0 & 7 & 8 \\ \end{array}\right]. \] The top and bottom elements in the second column can be made 0 with the appropriate row operations: \[ \left[ \begin{array}{c c c} 1 & 3 & -1\\ 0 & 1 & -1 \\ 0 & 7 & 8 \\ \end{array}\right] \ce{->[\large R_1 - 3R_2 \text{ and } R_3 - 7R_2]} \left[ \begin{array}{c c c} 1 & 0 & 2\\ 0 & 1 & -1 \\ 0 & 0 & 15 \\ \end{array}\right]. \] With the middle column now \( \left[ \begin{array}{c} 0 \\ 1 \\ 0 \\ \end{array}\right] \), the method proceeds to the third column by dividing the third row by 15: \[ \left[ \begin{array}{c c c} 1 & 0 & 2\\ 0 & 1 & -1 \\ 0 & 0 & 15 \\ \end{array}\right] \ce{->[\large \text{Divide the third row by 15} ]} \left[ \begin{array}{c c c} 1 & 0 & 2\\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{array}\right]. \] In the final step of the process, multiples of the third row are added to the first and second rows so that the last column becomes \( \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array}\right]: \) \[ \left[ \begin{array}{c c c} 1 & 0 & 2\\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{array}\right] \ce{->[\large R_1 - 2R_3 \text{ and } R_2 + R_3 ]} \left[ \begin{array}{c c c} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right]. \ _\square \]

\[ A = \left[ \begin{array}{ccc} 1 & 4 & -5 \\ 6 & 4 & 0 \\ 2 & 2 & -1 \\ \end{array} \right] \]

What is the sum of all the entries in \( \text{rref}(A)?\)

Note : \(\text{rref}(A) \) stands for the "reduced row echelon form" of matrix \(A.\)

The following steps can be used to obtain the solutions to a system of linear equations:

• Convert the given equations to an augmented matrix.
• Perform row operations to get the reduced row echelon form of the matrix.
• Convert to augmented matrix back to a set of equations.

Once in this form, the possible solutions to a system of linear equations that the augmented matrix represents can be determined by three cases.

Case 1. If \(\text{rref}(A)\) is the identity matrix, then the system has a unique solution. When read row by row, this augmented matrix says \(x = -1, y = 2,\) and \(z = 3:\) \[ \left[ \begin{array}{c c c | c} 1 & 0 & 0 & -1\\ 0 & 1 & 0 & 2\\ 0 & 0 & 1 & 3\\ \end{array}\right]. \] Case 2. If \(\text{rref}(A)\) contains a row of zeroes followed by a zero augmented value, then the system has infinitely many solutions. Consider the following augmented matrix in reduced row echelon form. The last row reads \(\left[0 \hspace{.15cm} 0 \hspace{.15cm} 0 \hspace{.15cm} | \hspace{.15cm} 0\right] \) or \(0 = 0,\) which is not a contradiction. The other rows read \(x + 4y = -1\) and \(z = 2.\) This determines a value for \(z,\) but there are infinitely many pairs of real numbers \(x\) and \(y\) such that \(x + 4y = -1,\) so this system has an infinite number of solutions: \[ \left[ \begin{array}{c c c | c} 1 & 4 & 0 & -1\\ 0 & 0 & 1 & 2\\ 0 & 0 & 0 & 0\\ \end{array}\right]. \] Case 3. If \(\text{rref}(A)\) contains a row of zeroes followed by a nonzero augmented value, then the system has no solution. This case is similar to the first in that the bottom row contains mostly 0s. However, observe that the last row of the matrix reads \(\left[0 \hspace{.15cm} 0 \hspace{.15cm} 0 \hspace{.15cm} | \hspace{.15cm} 1\right] \), which reads as \(0 = 1.\) This is a contradiction; thus the system has no solutions: \[ \left[ \begin{array}{c c c | c} 1 & 4 & 0 & -1\\ 0 & 0 & 1 & 2\\ 0 & 0 & 0 & 1\\ \end{array}\right]. \]

Find the values of \( x \) and \( y \) satisfying the following system of equations: \[ \begin{cases} 5x - y =1\\ x + 2y = 9. \end{cases} \] For this example, row reduction techniques will be favored over standard elimination. The given system of equations can be written as the following augmented matrix: \[ \left[ \begin{array} {cc|c} 5 & -1 & 1\\ 1 & 2 & 9\\ \end{array} \right]. \] Gauss-Jordan elimination is performed to produce the reduced row echelon form of the matrix: \[ \left[ \begin{array} {cc|c} 5 & -1 & 1\\ 1 & 2 & 9\\ \end{array} \right] \ce{->[\text{Swap } R_1 \text{ and } R_2. ]} \left[ \begin{array} {cc|c} 1 & 2 & 9\\ 5 & -1 & 1\\ \end{array} \right] \] \[ \left[ \begin{array} {cc|c} 1 & 2 & 9\\ 5 & -1 & 1\\ \end{array} \right] \ce{->[R_2 - 5R_1 ]} \left[ \begin{array} {cc|c} 1 & 2 & 9\\ 0 & -11 & -44\\ \end{array} \right] \] \[ \left[ \begin{array} {cc|c} 1 & 2 & 9\\ 0 & -11 & -44\\ \end{array} \right] \ce{->[\text{Divide the second row by } -11.]} \left[ \begin{array} {cc|c} 1 & 2 & 9\\ 0 & 1 & 4\\ \end{array} \right] \] \[ \left[ \begin{array} {cc|c} 1 & 2 & 9\\ 0 & 1 & 4\\ \end{array} \right] \ce{->[R_1 - 2R_2]} \left[ \begin{array} {cc|c} 1 & 0 & 1\\ 0 & 1 & 4\\ \end{array} \right]. \] The first row of this reduced form reads \( x = 1 \) and the second row reads \( y = 4 \). \(_\square\) Note that this process is essentially the same as standard elimination. The main advantage of this procedure is the brevity of notation \((\)not having to write variable names such as \(x, y,\) and \(z,\) repetitively\()\) and ease of keeping track of steps taken.

As seen before, a system of equations can be represented by the matrix multiplication \(Ax = b.\) From here, the solution represented by the column matrix \(x\) can be obtained by left multiplying both sides of the equation by the inverse of the coefficient matrix \(A^{-1}\):

\[Ax = b \implies A^{-1}Ax = A^{-1}b \implies x = A^{-1}b. \]

One pitfall of this method arises when \(\det(A) = 0.\) Because the determinant of \(A\) is 0, it cannot have an inverse, meaning this method will fail. In fact, \(\det(A) = 0\) is equivalent to \(\text{rref}(A)\) containing a row of zeroes. As such, the system of equations that \(Ax = b\) represents will not have a unique solution. However, the system could have infinitely many solutions or no solution and a different method will be needed to discover it.

A system of equations is given by

\[\begin{align} ax + by &= 5 \\ cx + dy &= -1. \end{align} \]

If the inverse of \(\left[ \begin{array}{cc} a & b \\ c & d \end{array} \right]\) is \(\left[ \begin{array}{cc} 3 & 2 \\ -3 & 1 \end{array} \right]\), then what is \(x + y?\)

\[\begin{align} (2-3i)z + (5+i)w &= 19-4i\\ (1-i)z + (2+i)w &= 9-i \end{align}\]

Let \(z\) and \(w\) be the complex numbers satisfying the equations above.

Compute \(|z+w|^2\).

Note : \(i^2 = -1\), and \(|z|\) is the absolute value of \(z\).

Cramer's rule is a formula that uses determinants to provide a solution to a system of linear equations. The statement of the rule below uses only three variables, but the rule can be applied to a system of any size.

Consider a system of equations of three variables:

\[\begin{align*} a_{1} x + b_{1} y + c_{1} z &= d_{1} \\ a_{2} x + b_{2} y + c_{2} z &= d_{2} \\ a_{3} x + b_{3} y + c_{3} z &= d_{3}. \end{align*}\]

The solution to this system is given by

\[x=\dfrac{\det(A_{1})}{\det(A)} \quad y = \dfrac{\det(A_{2})}{\det(A)} \quad z= \dfrac{\det(A_{3})}{\det(A)},\]

where \(A= \begin{bmatrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{bmatrix} \) is the coefficient matrix and each \(A_{i}\) is \(A\) with the \(i^\text{th}\) column replaced with \( \begin{bmatrix} d_{1} \\ d_{2} \\ d_{3} \end{bmatrix}.\)

• If \(\det(A)=0\) and if any one of \(\det(A_1)\), \(\det(A_2),\) or \( \det(A_3)\) is not equal to \(0\), then the system has no solution.
• If \(\det(A) = 0\) and \(\det(A_1)\), \(\det(A_2),\) and \( \det(A_3)\) all equal 0, then a solution may or may not exist. If a solution does exist, then the system of equations will have infinitely many solutions.
• The computational complexity of this method increases on the order of \(O(n!),\) so it is unwieldy after \(3\times 3 \) systems.

As previously stated, a system of equations can be represented as a product of matrices like \[\begin{bmatrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} d_{1} \\ d_{2} \\ d_{3} \end{bmatrix}.\] The determinant of the coefficient matrix \(A\) is given by \[\det(A) = \left| \begin{array}{ccc} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array} \right|.\] If a column or row of a matrix is multiplied by a constant, then the value of its determinant is multiplied by that constant. So, in multiplying the first column by \(x,\) this equation becomes \[x\det(A) = \left| \begin{array}{ccc} a_{1}x & b_{1} & c_{1} \\ a_{2}x & b_{2} & c_{2} \\ a_{3}x & b_{3} & c_{3} \end{array} \right|.\] At this point, it is worth pointing out that column reduction techniques can be used as though they were row reduction techniques while preserving the solution. So adding \(y\) times the second column and \(z\) times the third column to the first column yields \[x\det(A) = \left| \begin{array}{ccc} a_{1}x & b_{1} & c_{1} \\ a_{2}x & b_{2} & c_{2} \\ a_{3}x & b_{3} & c_{3} \end{array} \right| \xrightarrow[]{C_{1} + yC_{2} + zC_{3}} \left| \begin{array}{ccc} a_{1}x+b_{1}y+c_{1}z & b_{1} & c_{1} \\ a_{2}x+b_{2}y+c_{2}z & b_{2} & c_{2} \\ a_{3}x+b_{3}y+c_{3}z & b_{3} & c_{3} \end{array} \right|. \] However, because \(a_{1}x + b_{1}y + c_{1}z = d_1\) \((\)and similarly for \(d_2\) and \(d_3),\) the new first column is precisely \( \left| \begin{array}{c} d_{1} \\ d_{2} \\ d_{3} \end{array} \right|.\) That is, \[\begin{align} x\det(A) = \left| \begin{array}{ccc} a_{1}x+b_{1}y+c_{1}z & b_{1} & c_{1} \\ a_{2}x+b_{2}y+c_{2}z & b_{2} & c_{2} \\ a_{3}x+b_{3}y+c_{3}z & b_{3} & c_{3} \end{array} \right| = \left| \begin{array}{ccc} d_{1} & b_{1} & c_{1} \\ d_{2} & b_{2} & c_{2} \\ d_{3} & b_{3} & c_{3} \end{array} \right| &= \det(A_1)\quad \text{ or } \\\\ x\det(A) &= \det(A_1) \longrightarrow x = \frac{\det(A_1)}{\det(A)}. \end{align} \] By a similar construction, \[y = \frac{\det(A_2)}{\det(A)}\quad \text{ and }\quad z = \frac{\det(A_3)}{\det(A)}. \ _\square\]

\[ \begin{cases} 5x - y =1\\ x + 2y = 9\\ \end{cases} \] According to Cramer's rule, the solution to the above system is \[x = \frac{\left| \begin{array}{cc} 1 & -1 \\ 9 & 2 \end{array} \right|}{\left| \begin{array}{cc} 5 & -1 \\ 1 & 2 \end{array} \right|} = 1 \quad \quad \text{ and } \quad \quad y = \frac{\left| \begin{array}{cc} 5 & 1 \\ 1 & 9 \end{array} \right|}{\left| \begin{array}{cc} 5 & -1 \\ 1 & 2 \end{array} \right|} = 4. \]

\[x = \frac{\left| \begin{array}{ccc} 1 & -4 & 1\\ 5 & 1 & 2 \\ 11 & -1 & -3 \end{array} \right|}{\left| \begin{array}{ccc} 3 & -4 & 1\\ 5 & 1 & 2 \\ 1 & -1 & -3 \end{array} \right|}, \quad \quad y = \frac{\left| \begin{array}{ccc} 3 & 1 & 1\\ 5 & 5 & 2 \\ 1 & 11 & -3 \end{array} \right|}{\left| \begin{array}{ccc} 3 & -4 & 1\\ 5 & 1 & 2 \\ 1 & -1 & -3 \end{array} \right|}, \quad \quad z = \frac{\left| \begin{array}{ccc} 3 & -4 & 1\\ 5 & 1 & 5 \\ 1 & -1 & 11 \end{array} \right|}{\left| \begin{array}{ccc} 3 & -4 & 1\\ 5 & 1 & 2 \\ 1 & -1 & -3 \end{array} \right|} \]

Using Cramer's rule, which equation is not solved by the solutions above?

Problem Loading...

Note Loading...

Set Loading...

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.6: Solving Systems with Gaussian Elimination

• Last updated
• Save as PDF
• Page ID 1388

Learning Objectives

• Write the augmented matrix of a system of equations.
• Write the system of equations from an augmented matrix.
• Perform row operations on a matrix.
• Solve a system of linear equations using matrices.

Carl Friedrich Gauss lived during the late \(18^{th}\) century and early \(19^{th}\) century, but he is still considered one of the most prolific mathematicians in history. His contributions to the science of mathematics and physics span fields such as algebra, number theory, analysis, differential geometry, astronomy, and optics, among others. His discoveries regarding matrix theory changed the way mathematicians have worked for the last two centuries.

We first encountered Gaussian elimination in Systems of Linear Equations: Two Variables . In this section, we will revisit this technique for solving systems, this time using matrices.

Writing the Augmented Matrix of a System of Equations

A matrix can serve as a device for representing and solving a system of equations. To express a system in matrix form, we extract the coefficients of the variables and the constants, and these become the entries of the matrix. We use a vertical line to separate the coefficient entries from the constants, essentially replacing the equal signs. When a system is written in this form, we call it an augmented matrix .

For example, consider the following \(2 × 2\) system of equations.

\[\begin{align*} 3x+4y&= 7\\ 4x-2y&= 5 \end{align*}\]

We can write this system as an augmented matrix:

\(\left[ \begin{array}{cc|c} 3&4&7\\4&-2&5\end{array} \right]\)

We can also write a matrix containing just the coefficients. This is called the coefficient matrix.

\(\begin{bmatrix}3&4\\4&−2\end{bmatrix}\)

A three-by-three system of equations such as

\[\begin{align*} 3x-y-z&= 0\\ x+y&= 5\\ 2x-3z&= 2 \end{align*}\]

has a coefficient matrix

\(\begin{bmatrix}3&−1&−1\\1&1&0\\2&0&−3\end{bmatrix}\)

and is represented by the augmented matrix

\(\left[ \begin{array}{ccc|c}3&−1&−1&0\\1&1&0&5\\2&0&−3&2\end{array} \right]\)

Notice that the matrix is written so that the variables line up in their own columns: \(x\)-terms go in the first column, \(y\)-terms in the second column, and \(z\)-terms in the third column. It is very important that each equation is written in standard form \(ax+by+cz=d\) so that the variables line up. When there is a missing variable term in an equation, the coefficient is \(0\).

How to: Given a system of equations, write an augmented matrix

• Write the coefficients of the \(x\)-terms as the numbers down the first column.
• Write the coefficients of the \(y\)-terms as the numbers down the second column.
• If there are \(z\)-terms, write the coefficients as the numbers down the third column.
• Draw a vertical line and write the constants to the right of the line.

Example \(\PageIndex{1}\): Writing the Augmented Matrix for a System of Equations

Write the augmented matrix for the given system of equations.

\[\begin{align*} x+2y-z&= 3\\ 2x-y+2z&= 6\\ x-3y+3z&= 4 \end{align*}\]

The augmented matrix displays the coefficients of the variables, and an additional column for the constants.

\(\left[ \begin{array}{ccc|c}1&2&−1&3\\2&−1&2&6\\1&−3&3&4\end{array} \right]\)

Exercise \(\PageIndex{1}\)

Write the augmented matrix of the given system of equations.

\[\begin{align*} 4x-3y&= 11\\ 3x+2y&= 4 \end{align*}\]

\(\left[ \begin{array}{cc|c} 4&−3&11\\3&2&4\end{array} \right]\)

Writing a System of Equations from an Augmented Matrix

We can use augmented matrices to help us solve systems of equations because they simplify operations when the systems are not encumbered by the variables. However, it is important to understand how to move back and forth between formats in order to make finding solutions smoother and more intuitive. Here, we will use the information in an augmented matrix to write the system of equations in standard form.

Example \(\PageIndex{2}\): Writing a System of Equations from an Augmented Matrix Form

Find the system of equations from the augmented matrix.

\(\left[ \begin{array}{ccc|c}1&−3&−5&-2\\2&−5&−4&5\\−3&5&4&6 \end{array} \right]\)

When the columns represent the variables \(x\), \(y\), and \(z\),

\[\left[ \begin{array}{ccc|c}1&-3&-5&-2\\2&-5&-4&5\\-3&5&4&6 \end{array} \right] \rightarrow \begin{align*} x-3y-5z&= -2\\ 2x-5y-4z&= 5\\ -3x+5y+4z&= 6 \end{align*}\]

Exercise \(\PageIndex{2}\)

Write the system of equations from the augmented matrix.

\(\left[ \begin{array}{ccc|c}1&−1& 1&5\\2&−1&3&1\\0&1&1&-9\end{array}\right]\)

\(\begin{align*} x-y+z&= 5\\ 2x-y+3z&= 1\\ y+z&= -9 \end{align*}\)

Performing Row Operations on a Matrix

Now that we can write systems of equations in augmented matrix form, we will examine the various row operations that can be performed on a matrix, such as addition, multiplication by a constant, and interchanging rows.

Performing row operations on a matrix is the method we use for solving a system of equations. In order to solve the system of equations, we want to convert the matrix to row-echelon form, in which there are ones down the main diagonal from the upper left corner to the lower right corner, and zeros in every position below the main diagonal as shown.

Row-echelon form \(\begin{bmatrix}1&a&b\\0&1&d\\0&0&1\end{bmatrix}\)

We use row operations corresponding to equation operations to obtain a new matrix that is row-equivalent in a simpler form. Here are the guidelines to obtaining row-echelon form.

• In any nonzero row, the first nonzero number is a \(1\). It is called a leading \(1\).
• Any all-zero rows are placed at the bottom on the matrix.
• Any leading \(1\) is below and to the right of a previous leading \(1\).
• Any column containing a leading \(1\) has zeros in all other positions in the column.

To solve a system of equations we can perform the following row operations to convert the coefficient matrix to row-echelon form and do back-substitution to find the solution.

• Interchange rows. (Notation: \(R_i ↔ R_j\))
• Multiply a row by a constant. (Notation: \(cR_i\))
• Add the product of a row multiplied by a constant to another row. (Notation: \(R_i+cR_j\))

Each of the row operations corresponds to the operations we have already learned to solve systems of equations in three variables. With these operations, there are some key moves that will quickly achieve the goal of writing a matrix in row-echelon form. To obtain a matrix in row-echelon form for finding solutions, we use Gaussian elimination, a method that uses row operations to obtain a \(1\) as the first entry so that row \(1\) can be used to convert the remaining rows.

GAUSSIAN ELIMINATION

The Gaussian elimination method refers to a strategy used to obtain the row-echelon form of a matrix. The goal is to write matrix \(A\) with the number \(1\) as the entry down the main diagonal and have all zeros below.

\(A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}\xrightarrow{After\space Gaussian\space elimination} A=\begin{bmatrix}1&b_{12}& b_{13}\\0&1&b_{23}\\0&0&1\end{bmatrix}\)

The first step of the Gaussian strategy includes obtaining a \(1\) as the first entry, so that row \(1\) may be used to alter the rows below.

How to: Given an augmented matrix, perform row operations to achieve row-echelon form

• The first equation should have a leading coefficient of \(1\). Interchange rows or multiply by a constant, if necessary.
• Use row operations to obtain zeros down the first column below the first entry of \(1\).
• Use row operations to obtain a \(1\) in row 2, column 2.
• Use row operations to obtain zeros down column 2, below the entry of 1.
• Use row operations to obtain a \(1\) in row 3, column 3.
• Continue this process for all rows until there is a \(1 in every entry down the main diagonal and there are only zeros below.
• If any rows contain all zeros, place them at the bottom.

Example \(\PageIndex{3}\): Solving a \(2×2\) System by Gaussian Elimination

Solve the given system by Gaussian elimination.

\[\begin{align*} 2x+3y&= 6\\ x-y&= \dfrac{1}{2} \end{align*}\]

First, we write this as an augmented matrix.

\(\left[ \begin{array}{cc|c} 2&3&6\\1&−1&12\end{array} \right]\)

We want a \(1\) in row 1, column 1. This can be accomplished by interchanging row 1 and row 2.

\(R_1\leftrightarrow R_2\rightarrow \left[ \begin{array}{cc|c} 1&−1&12\\2&3&6\end{array} \right]\)

We now have a \(1\) as the first entry in row 1, column 1. Now let’s obtain a \(0\) in row 2, column 1. This can be accomplished by multiplying row 1 by \(−2\), and then adding the result to row 2.

\(-2R_1+R_2=R_2\rightarrow \left[ \begin{array}{cc|c} 1&−1&12\\0&5&5\end{array} \right]\)

We only have one more step, to multiply row 2 by \(\dfrac{1}{5}\).

\(\dfrac{1}{5}R_2=R_2\rightarrow \left[ \begin{array}{cc|c} 1&−1&12\\0&1&1\end{array} \right]\)

Use back-substitution. The second row of the matrix represents \(y=1\). Back-substitute \(y=1\) into the first equation.

\[\begin{align*} x-(1)&= \dfrac{1}{2}\\ x&= \dfrac{3}{2} \end{align*}\]

The solution is the point \(\left(\dfrac{3}{2},1\right)\).

Exercise \(\PageIndex{3}\)

\[\begin{align*} 4x+3y&= 11\\ x-3y&= -1 \end{align*}\]

Example \(\PageIndex{4}\): Using Gaussian Elimination to Solve a System of Equations

Use Gaussian elimination to solve the given \(2 × 2\) system of equations .

\[\begin{align*} 2x+y&= 1\\ 4x+2y&= 6 \end{align*}\]

Write the system as an augmented matrix .

\(\left[ \begin{array}{cc|c} 2&1&1\\4&2&6\end{array} \right]\)

Obtain a \(1\) in row 1, column 1. This can be accomplished by multiplying the first row by \(\dfrac{1}{2}\).

\(\dfrac{1}{2} R_1=R_1\rightarrow \left[ \begin{array}{cc|c} 1&\dfrac{1}{2}&\dfrac{1}{2}\\4&2&6\end{array} \right]\)

Next, we want a \(0\) in row 2, column 1. Multiply row 1 by \(−4\) and add row 1 to row 2.

\(-4R_1+R_2=R_2\rightarrow \left[ \begin{array}{cc|c} 1&\dfrac{1}{2}&\dfrac{1}{2}\\0&0&4\end{array} \right]\)

The second row represents the equation \(0=4\). Therefore, the system is inconsistent and has no solution.

Example \(\PageIndex{5}\): Solving a Dependent System

Solve the system of equations.

\[\begin{align*} 3x+4y&= 12\\ 6x+8y&= 24 \end{align*}\]

Perform row operations on the augmented matrix to try and achieve row-echelon form .

\(A=\left[ \begin{array}{cc|c} 3&4&12\\6&8&24\end{array} \right]\)

\(-\dfrac{1}{2}R_2+R_1=R_1\rightarrow \left[ \begin{array}{cc|c} 0&0&0\\6&8&24\end{array} \right]\)

\(R_1\leftrightarrow R_2=\left[ \begin{array}{cc|c} 6&8&24\\0&0&0\end{array} \right]\)

The matrix ends up with all zeros in the last row: \(0y=0\). Thus, there are an infinite number of solutions and the system is classified as dependent. To find the generic solution, return to one of the original equations and solve for \(y\).

\[\begin{align*} 3x+4y&= 12\\ 4y&= 12-3x\\ y&= 3-\dfrac{3}{4}x \end{align*}\]

So the solution to this system is \(\left(x,3−\dfrac{3}{4}x\right)\).

Example \(\PageIndex{6}\): Performing Row Operations on a \(3×3\) Augmented Matrix to Obtain Row-Echelon Form

Perform row operations on the given matrix to obtain row-echelon form.

\(\left[ \begin{array}{ccc|c} 1&-3&4&3\\2&-5&6&6\\-3&3&4&6\end{array} \right]\)

The first row already has a \(1\) in row 1, column 1. The next step is to multiply row 1 by \(−2\) and add it to row 2. Then replace row 2 with the result.

\(-2R_1+R_2=R_2 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\-3&3&4&6\end{array} \right]\)

Next, obtain a zero in row 3, column 1.

\(3R_1+R_3=R_3 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\0&-6&16&15\end{array} \right]\)

Next, obtain a zero in row 3, column 2.

\(6R_2+R_3=R_3 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\0&0&4&15\end{array} \right]\)

The last step is to obtain a 1 in row 3, column 3.

\(\dfrac{1}{3}R_3=R_3 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\0&0&1&\dfrac{21}{2}\end{array} \right]\)

Exercise \(\PageIndex{4}\)

Write the system of equations in row-echelon form.

\[\begin{align*} x−2y+3z &= 9 \\ −x+3y &= −4 \\ 2x−5y+5z &= 17 \end{align*}\]

\(\left[ \begin{array}{ccc|c} 1&-\dfrac{5}{2}&\dfrac{5}{2}&\dfrac{17}{2}\\0&1&5&9\\0&0&1&2\end{array} \right]\)

Solving a System of Linear Equations Using Matrices

We have seen how to write a system of equations with an augmented matrix , and then how to use row operations and back-substitution to obtain row-echelon form. Now, we will take row-echelon form a step farther to solve a \(3\) by \(3\) system of linear equations. The general idea is to eliminate all but one variable using row operations and then back-substitute to solve for the other variables.

Example \(\PageIndex{7}\): Solving a System of Linear Equations Using Matrices

Solve the system of linear equations using matrices.

\[\begin{align*} x-y+z&= 8\\ 2x+3y-z&= -2\\ 3x-2y-9z&= 9 \end{align*}\]

First, we write the augmented matrix.

\(\left[ \begin{array}{ccc|c} 1&-1&1&8\\2&3&-1&-2\\3&-2&-9&9\end{array} \right]\)

Next, we perform row operations to obtain row-echelon form.

\(−2R_1+R_2=R_2\rightarrow \left[ \begin{array}{ccc|c} 1&-1&1&8\\0&5&-3&-18\\3&-2&-9&9\end{array} \right]\)

\(−3R_1+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&-1&1&8\\0&5&-3&-18\\0&1&-12&-15\end{array} \right]\)

The easiest way to obtain a \(1\) in row 2 of column 1 is to interchange \(R_2\) and \(R_3\).

\(Interchange\space R_2\space and\space R_3\rightarrow\left[ \begin{array}{ccc|c} 1&-1&1&8\\0&1&-12&-15\\0&5&-3&-18\end{array} \right]\)

\(−5R_2+R_3=R_3\rightarrow\left[ \begin{array}{ccc|c} 1&-1&1&8\\0&1&-12&-15\\0&0&57&57\end{array} \right]\)

\(−\dfrac{1}{57}R_3=R_3\rightarrow\left[ \begin{array}{ccc|c} 1&-1&1&8\\0&1&-12&-15\\0&0&1&1\end{array} \right]\)

The last matrix represents the equivalent system.

\[\begin{align*} x−y+z &= 8 \\ y−12z &= −15 \\ z &= 1 \end{align*}\]

Using back-substitution, we obtain the solution as \((4,−3,1)\).

Example \(\PageIndex{8}\): Solving a Dependent System of Linear Equations Using Matrices

Solve the following system of linear equations using matrices.

\[\begin{align*} −x−2y+z &= −1 \\ 2x+3y &= 2 \\ y−2z &= 0 \end{align*}\]

Write the augmented matrix.

\(\left[ \begin{array}{ccc|c} -1&-2&1&-1\\2&3&0&2\\0&1&-2&0\end{array} \right]\)

First, multiply row 1 by \(−1\) to get a \(1\) in row 1, column 1. Then, perform row operations to obtain row-echelon form.

\(-R_1\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\2&3&0&2\\0&1&-2&0\end{array} \right]\)

\(R_2\leftrightarrow R_3\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\0&1&-2&0\\2&3&0&2\end{array} \right]\)

\(−2R_1+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\0&1&-2&0\\0&-1&2&0\end{array} \right]\)

\(R_2+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\0&1&-2&0\\0&0&0&0\end{array} \right]\)

The last matrix represents the following system.

\[\begin{align*} x+2y−z &= 1 \\ y−2z &= 0 \\ 0 &= 0 \end{align*}\]

We see by the identity \(0=0\) that this is a dependent system with an infinite number of solutions. We then find the generic solution. By solving the second equation for \(y\) and substituting it into the first equation we can solve for \(z\) in terms of \(x\).

\[\begin{align*} x+2y−z &= 1 \\ y &= 2z \\ x+2(2z)−z &= 1 \\ x+3z &= 1 \\ z &=\dfrac{1−x}{3} \end{align*}\]

Now we substitute the expression for \(z\) into the second equation to solve for \(y\) in terms of \(x\).

\[\begin{align*} y−2z &= 0 \\ z &= \dfrac{1−x}{3} \\ y−2\left(\dfrac{1−x}{3}\right) &= 0 \\ y &= \dfrac{2−2x}{3} \end{align*}\]

The generic solution is \(\left(x,\dfrac{2−2x}{3},\dfrac{1−x}{3}\right)\).

Exercise \(\PageIndex{5}\)

Solve the system using matrices.

\[\begin{align*} x+4y-z&= 4\\ 2x+5y+8z&= 1\\ 5x+3y-3z&= 1 \end{align*}\]

\((1,1,1)\)

Q&A: Can any system of linear equations be solved by Gaussian elimination?

Yes, a system of linear equations of any size can be solved by Gaussian elimination.

How to: Given a system of equations, solve with matrices using a calculator

• Save the augmented matrix as a matrix variable \([A], [B], [C], ….\)
• Use the ref( function in the calculator, calling up each matrix variable as needed.

Example \(\PageIndex{9A}\): Solving Systems of Equations with Matrices Using a Calculator

\[\begin{align*} 5x+3y+9z&= -1\\ -2x+3y-z&= -2\\ -x-4y+5z&= 1 \end{align*}\]

Write the augmented matrix for the system of equations.

\(\left[ \begin{array}{ccc|c} 5&3&9&-1\\-2&3&-1&-2\\-1&-4&5&1\end{array} \right]\)

On the matrix page of the calculator, enter the augmented matrix above as the matrix variable \([A]\).

\([A]=\left[ \begin{array}{ccc|c} 5&3&9&-1\\-2&3&-1&-2\\-1&-4&5&1\end{array} \right]\)

Use the ref( function in the calculator, calling up the matrix variable \([A]\).

\[\begin{array}{cc} {\left[ \begin{array}{ccc|c} 1&\dfrac{3}{5}&\dfrac{9}{5}&\dfrac{1}{5}\\0&1&\dfrac{13}{21}&-\dfrac{4}{7}\\0&0&1&-\dfrac{24}{187}\end{array} \right] \rightarrow} & {\begin{align*} x+\dfrac{3}{5}y+\dfrac{9}{5}z &= -\dfrac{1}{5} \\ y+\dfrac{13}{21}z &= -\dfrac{4}{7} \\ z &= -\dfrac{24}{187} \end{align*}} \end{array}\]

Using back-substitution, the solution is \(\left(\dfrac{61}{187},−\dfrac{92}{187},−\dfrac{24}{187}\right)\).

Example \(\PageIndex{9B}\): Applying \(2×2\) Matrices to Finance

Carolyn invests a total of \($12,000\) in two municipal bonds, one paying \(10.5%\) interest and the other paying \(12%\) interest. The annual interest earned on the two investments last year was \($1,335\). How much was invested at each rate?

We have a system of two equations in two variables. Let \(x=\) the amount invested at \(10.5%\) interest, and \(y=\) the amount invested at \(12%\) interest.

\[\begin{align*} x+y&= 12,000\\ 0.105x+0.12y&= 1,335 \end{align*}\]

As a matrix, we have

\(\left[ \begin{array}{cc|c} 1&1&12,000\\0.105&0.12&1,335\end{array} \right]\)

Multiply row 1 by \(−0.105\) and add the result to row 2.

\(\left[ \begin{array}{cc|c} 1&1&12,000\\0&0.015&75\end{array} \right]\)

\[\begin{align*} 0.015y &= 75 \\ y &= 5,000 \end{align*}\]

So \(12,000−5,000=7,000\).

Thus, \($5,000\) was invested at \(12%\) interest and \($7,000\) at \(10.5%\) interest.

Example \(\PageIndex{10}\): Applying \(3×3\) Matrices to Finance

Ava invests a total of \($10,000\) in three accounts, one paying \(5%\) interest, another paying \(8%\) interest, and the third paying \(9%\) interest. The annual interest earned on the three investments last year was \($770\). The amount invested at \(9%\) was twice the amount invested at \(5%\). How much was invested at each rate?

We have a system of three equations in three variables. Let \(x\) be the amount invested at \(5%\) interest, let \(y\) be the amount invested at \(8%\) interest, and let \(z\) be the amount invested at \(9%\) interest. Thus,

\[\begin{align*} x+y+z &= 10,000 \\ 0.05x+0.08y+0.09z &= 770 \\ 2x−z &= 0 \end{align*}\]

\(\left[ \begin{array}{ccc|c} 1&1&1&10,000\\0.05&0.08&0.09&770\\2&0&-1&0\end{array} \right]\)

Now, we perform Gaussian elimination to achieve row-echelon form.

\(−0.05R_1+R_2=R_2\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&0.03&0.04&270\\2&0&-1&0\end{array} \right]\)

\(−2R_1+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&0.03&0.04&270\\0&-2&-3&-20,000\end{array} \right]\)

\(\dfrac{1}{0.03}R_2=R_2\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&1&\dfrac{4}{3}&9,000\\0&-2&-3&-20,000\end{array} \right]\)

\(2R_2+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&1&\dfrac{4}{3}&9,000\\0&0&-\dfrac{1}{3}&-2,000\end{array} \right]\)

The third row tells us \(−\dfrac{1}{3}z=−2,000\); thus \(z=6,000\).

The second row tells us \(y+\dfrac{4}{3}z=9,000\). Substituting \(z=6,000\),we get

\[\begin{align*} y+\dfrac{4}{3}(6,000) &= 9,000 \\ y+8,000 &= 9,000 \\ y &= 1,000 \end{align*}\]

The first row tells us \(x+y+z=10,000\). Substituting \(y=1,000\) and \(z=6,000\),we get

\[\begin{align*} x+1,000+6,000 &= 10,000 \\ x &= 3,000 \end{align*}\]

The answer is \($3,000\) invested at \(5%\) interest, \($1,000\) invested at \(8%\), and \($6,000\) invested at \(9%\) interest.

Exercise \(\PageIndex{6}\)

A small shoe company took out a loan of \($1,500,000\) to expand their inventory. Part of the money was borrowed at \(7%\), part was borrowed at \(8%\), and part was borrowed at \(10%\). The amount borrowed at \(10%\) was four times the amount borrowed at \(7%\), and the annual interest on all three loans was \($130,500\). Use matrices to find the amount borrowed at each rate.

\($150,000\) at \(7%\), \($750,000\) at \(8%\), \($600,000\) at \(10%\)

Access these online resources for additional instruction and practice with solving systems of linear equations using Gaussian elimination.

• Solve a System of Two Equations Using an Augmented Matrix
• Solve a System of Three Equations Using an Augmented Matrix
• Augmented Matrices on the Calculator

Key Concepts

• An augmented matrix is one that contains the coefficients and constants of a system of equations. See Example \(\PageIndex{1}\).
• A matrix augmented with the constant column can be represented as the original system of equations. See Example \(\PageIndex{2}\).
• Row operations include multiplying a row by a constant, adding one row to another row, and interchanging rows.
• We can use Gaussian elimination to solve a system of equations. See Example \(\PageIndex{3}\), Example \(\PageIndex{4}\), and Example \(\PageIndex{5}\).
• Row operations are performed on matrices to obtain row-echelon form. See Example \(\PageIndex{6}\).
• To solve a system of equations, write it in augmented matrix form. Perform row operations to obtain row-echelon form. Back-substitute to find the solutions. See Example \(\PageIndex{7}\) and Example \(\PageIndex{8}\).
• A calculator can be used to solve systems of equations using matrices. See Example \(\PageIndex{9}\).
• Many real-world problems can be solved using augmented matrices. See Example \(\PageIndex{10}\) and Example \(\PageIndex{11}\).

Math Made Easy

The Matrix and Solving Systems with Matrices

Introduction to the matrix.

A matrix (plural matrices ) is sort of like a “table” of information where you are keeping track of things both right and left ( columns ), and up and down ( rows ). Usually, a matrix contains numbers or algebraic expressions . You may have heard matrices called arrays , especially in computer science.

As an example, if you had three sisters, and you wanted an easy way to store their age and number of pairs of shoes, you could store this information in a matrix. The actual matrix is inside and includes the brackets:

$ \displaystyle \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}{c}} {\text{Ashley}} & {\text{Emma}} & {\text{Chloe}} \end{array}\\\begin{array}{*{20}{c}} {\text{Age}} \\ {\text{Number of Pairs of Shoes}} \end{array}\text{ }\left[ {\begin{array}{*{20}{c}} {\text{23}} & {\,\,\,\,\,\,\,\,\,\text{18}} & {\,\,\,\,\,\,\,\,\,\text{15}} \\ \text{5} & {\,\,\,\,\,\,\,\,\text{23}} & {\,\,\,\,\,\,\,\,\,\text{12}} \end{array}} \right]\end{array}$

Matrices are called multi-dimensional since we have data being stored in different directions in a grid. The dimensions of this matrix are “ 2 x 3 ” or “ 2 by 3 ”, since we have 2 rows and 3 columns. (You always go down first , and then over to get the dimensions of the matrix). Each number or variable inside the matrix is called an entry or element , and can be identified by subscripts . For example, for the matrix above, “Ashley’s number of pairs of shoes ( 5 )” would be identified as $ {{a}_{{2,1}}}$, since it’s on the 2 nd row and it’s the 1 st  entry. Again, matrices are great for storing numbers and variables – and also great for solving systems of equations, which we’ll see later. Note that we’ll address Solving Systems using   Reduced Row Echelon Form here .

Adding and Subtracting Matrices

Let’s look at a matrix that contains numbers and see how we can add and subtract matrices.

Let’s say you’re in avid reader, and in June, July, and August you read fiction and non-fiction books, and magazines, both in paper copies and online. You want to keep track of how many different types of books and magazines you read, and store that information in matrices.  Here is that information, and how it would look in matrix form:

Matrix Form:  $ \left[ {\begin{array}{*{20}{c}} 2 & 4 \\ \begin{array}{l}3\\4\end{array} & \begin{array}{l}1\\5\end{array} \end{array}} \right]$

Matrix Form:  $ \left[ {\begin{array}{*{20}{c}} 3 & 2 \\ \begin{array}{l}1\\5\end{array} & \begin{array}{l}1\\3\end{array} \end{array}} \right]$

Matrix Form:  $ \left[ {\begin{array}{*{20}{c}} 1 & 3 \\ \begin{array}{l}2\\4\end{array} & \begin{array}{l}3\\6\end{array} \end{array}} \right]$

We can add matrices if the dimensions are the same; since the three matrices are all “ 3  by   2 ”, we can add them. For example, if we wanted to know the total number of each type of book/magazine we read, we could add each of the elements to get the sum:

$ \displaystyle \require{cancel} \color{#800000}{{\left[ {\begin{array}{*{20}{c}} 2 & 4 \\ \begin{array}{l}3\\4\end{array} & \begin{array}{l}1\\5\end{array} \end{array}} \right]\,\,+\,\,\left[ {\begin{array}{*{20}{c}} 3 & 2 \\ \begin{array}{l}1\\5\end{array} & \begin{array}{l}1\\3\end{array} \end{array}} \right]\,\,\,+\,\,\left[ {\begin{array}{*{20}{c}} 1 & 3 \\ \begin{array}{l}2\\4\end{array} & \begin{array}{l}3\\6\end{array} \end{array}} \right]}}\,\,=\,\,\left[ {\begin{array}{*{20}{c}} {2+3+1} & {4+2+3} \\ \begin{array}{l}3+1+2\\4+5+4\end{array} & \begin{array}{l}1+1+3\\5+3+6\end{array} \end{array}} \right]\,\,=\,\,\left[ {\begin{array}{*{20}{c}} 6 & 9 \\ 6 & 5 \\ {13} & {14} \end{array}} \right]$

Thus we could see that we read 6 paper fiction, 9 online fiction, 6 paper non-fiction, 5 online non-fiction books, and 13 paper and 14 online magazines. We could also subtract matrices this same way. If we wanted to see how many books and magazines we would have read in August if we had doubled what we actually read, we could multiply the August matrix by the number 2 . This is called matrix scalar multiplication ; a scalar is just a single number that we multiply with every entry. Note that this is not the same as multiplying two matrices together (which we’ll get to next):

$ \displaystyle \color{#800000}{{2\left[ {\begin{array}{*{20}{c}} 1 & 3 \\ \begin{array}{l}2\\4\end{array} & \begin{array}{l}3\\6\end{array} \end{array}} \right]}}\,=\,\left[ {\begin{array}{*{20}{c}} {1\times 2} & {3\times 2} \\ {2\times 2} & {3\times 2} \\ {4\times 2} & {6\times 2} \end{array}} \right]\,=\,\left[ {\begin{array}{*{20}{c}} 2 & 6 \\ 4 & 6 \\ 8 & {12} \end{array}} \right]$

Multiplying Matrices

Multiplying matrices is a little trickier. First of all, you can only multiply matrices if the dimensions “match”; the second dimension (columns) of the first matrix has to match the first dimension (rows) of the second matrix , or you can’t multiply them. Think of it like the inner dimensions have to match , and the resulting dimensions of the new matrix are the outer dimensions .

Here’s an example of matrices with dimensions that would work. Again, always remember with matrices that you go down first and then over, to get their dimensions.

Notice how the “middle” or “inner” dimensions of the first matrices have to be the same (in this case, “ 2 ”), and the new matrix has the “outside” or “outer” dimensions of the first two matrices (“ 3 by 5 ”).

Now, let’s do a real-life example to see how the multiplication works .   Let’s say we want to find the final grades for 3 girls, and we know what their averages are for tests, projects, homework, and quizzes. We also know that tests are 40% of the grade, projects 15% , homework 25% , and quizzes 20% . Here’s the data we have:

Let’s organize the following data into two matrices, and perform matrix multiplication to find the final grades for Alexandra, Megan, and Brittney; this is a weighted average ! To do this, you have to multiply in the following way:

Just remember when you put matrices together with matrix multiplication , the columns (what you see across) on the first matrix have to correspond to the rows down on the second matrix . You should end up with entries that correspond with the entries of each row in the first matrix. For example, with the problem above, the columns of the first matrix each had something to do with Tests, Projects, Homework, and Quizzes (grades). The row down on the second matrix each had something to do with the same four items (weights of grades). But then we ended up with information on the three girls (rows down on the first matrix), and the middle “descriptions” (test, projects, etc.) went away.

Alexandra has a 90 , Megan has a 77 , and Brittney has an 87 . See how cool this is? Matrices are really useful for a lot of applications in “real life”!

Now let’s do another example; let’s multiply the following matrices : (And don’t worry too much; most of the time you’ll be doing matrix multiplication in the calculator!)

Matrices in the Graphing Calculator

The TI graphing calculator is great for matrix operations! Here are some basic steps for storing, multiplying, adding, and subtracting matrices. (Note that you can also enter matrices using  ALPHA ZOOM  and the arrow keys in the newer graphing calculators, but I still like “naming” the matrices.)

We’ll learn other ways to use the calculator with matrices a little later.

Determinants,  the Matrix Inverse, and the Identity Matrix

Soon we will be solving Systems of Equations using matrices, but we need to learn a few mechanics first!

Most square matrices (same dimension down and across) have what we call a determinant , designated by $ \det \left[ \text{A} \right]$ or $ \left| \text{A} \right|$, for example, which we’ll need to get the multiplicative inverse of that matrix. (The inverse of a matrix, designated by $ {{\text{A}}^{{-1}}}$, for example, is what we multiply that square matrix by to get the identity matrix, a matrix with 1 ‘s along the diagonal starting with the upper left element, and 0 ‘s everywhere else.)

We’ll use the inverses of matrices to solve Systems of Equations ; the inverses will allow us to get variables by themselves on one side (like “regular” algebra). You’ll solve these mainly by using your calculator , but you’ll also have to learn how to get them “by hand”.

I know all this sounds confusing, but let’s do some examples step-by-step. Let’s first get the determinant of matrices (which we can get easily on a calculator!). The determinant is always just a scalar (number), and you’ll see it with two lines around the matrix:

Now let’s use the determinant to get the inverse of a matrix . We’ll only work with 2 by 2 matrices, since you’ll probably be able to use the calculator for larger matrices. Note again that only square matrices have inverses , but there are square matrices that don’t have one (when the determinant is 0 ):

Note that a matrix, multiplied by its inverse, if it’s defined, will always result in what we call an  Identity Matrix : $ \displaystyle \left[ {\begin{array}{*{20}{c}} 3 & 1 \\ 4 & 8 \end{array}} \right]\,\times \,\left[ {\begin{array}{*{20}{c}} {\frac{2}{5}} & {-\frac{1}{{20}}} \\ {-\frac{1}{5}} & {\frac{3}{{20}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & 1 \end{array}} \right]$ . An identity matrix has 1 ’s along the diagonal starting with the upper left element, and 0 ’s everywhere else.

When you multiply a square matrix with an identity matrix, you just get that matrix back: $ \displaystyle \left[ {\begin{array}{*{20}{c}} 3 & 1 \\ 4 & 8 \end{array}} \right]\,\times \,\left[ {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & 1 \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 3 & 1 \\ 4 & 8 \end{array}} \right]$. Think of an  identity matrix  like “ 1 ” in regular multiplication (the multiplicative identity), and the  inverse matrix  like a  reciprocal  (the multiplicative inverse).

Solving Systems with Matrices

Why are we doing all this crazy math? Because we can  solve systems  with the  inverse of a matrix , since the inverse is sort of like dividing to get the variables all by themselves on one side.

To solve systems with matrices, we use $ \displaystyle X={{A}^{{-1}}}B$. Here is why, if you’re interested in the “theory” (the column on the right provides an example with “regular” multiplication). ( I  is the identity matrix.):

$ \displaystyle \begin{array}{l}\,\,\,\,\,\,\,\,AX=B\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5x=10\\{{A}^{{-1}}}AX={{A}^{{-1}}}B\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{5}\cdot 5x=\frac{1}{5}\cdot 10\\\,\,\,\,\,\,\,\,\,\,IX={{A}^{{-1}}}B\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1x=2\\\,\,\,\,\,\,\,\,\,\,\,X={{A}^{{-1}}}B\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=2\end{array}$

Here’s an example:

(It is important to note that if we are trying to solve a system of equations and the determinant turns out to be  0 , that system either has an  infinite number of solutions , or  no solution . See below. )

Solving Systems with Reduced Row Echelon Form

There’s another way to solve systems by converting a systems’ matrix into reduced row echelon form , where we can put everything in one matrix (called an augmented matrix ). I show how to use this method by hand here in the Solving Systems using   Reduced Row Echelon Form section , but here I’ll just show you how to easy it is to solve using RREF in a graphing calculator :

A little easier, right?

Solving Matrix Equations

Here are a couple more types of matrix problems you might see:

Cramer’s Rule

Sometimes you’ll have to learn Cramer’s Rule , which is another way to solve systems with matrices. Cramer’s Rule was named after the Swiss mathematician Gabriel Cramer, who also did a lot of other neat stuff with math. Cramer’s rule is all about getting determinants of the square matrices that are used to solve systems. It’s really not too difficult; it can just be a lot of work, so again, I’ll take the liberty of using the calculator to do most of the work :). Let’s just show an example: Solve the following system using Cramer’s rule:     $ \displaystyle \begin{array}{l}\,2x+3y-\,\,z\,=\,15\\4x-3y-\,\,z\,=\,19\\\,\,x\,-\,3y+\,3z\,=\,-4\end{array}$.

To solve for $ x, y$, and $ z$, we need to get the determinants of four matrices, the first one being the 3 by 3 matrix that holds the coefficients of $ x,y$, and $ z$. Let’s call this first determinant $ D$;  $ \displaystyle D=\det \left[ {\begin{array}{*{20}{c}} 2 & 3 & {-1} \\ 4 & {-3} & {-1} \\ 1 & {-3} & 3 \end{array}} \right]=-54$. Now get a matrix called $ {{D}_{x}}$, which is obtained by “throwing away” the first ($ x$) column, and replacing the numbers with the “answer” or constant column. Thus, $ \displaystyle {{D}_{x}}=\det \left[ {\begin{array}{*{20}{c}} {\boldsymbol{{15}}} & 3 & {-1} \\ {\boldsymbol{{19}}} & {-3} & {-1} \\ {\boldsymbol{{-4}}} & {-3} & 3 \end{array}} \right]=-270$. You can probably guess what the next determinant we need is: $ {{D}_{y}}$, which we get by “throwing away” the second column ($ y$) of the original matrix and replacing the numbers with the constant column like we did earlier for the $ x$. Thus, $ \displaystyle {{D}_{y}}=\det \left[ {\begin{array}{*{20}{c}} 2 & {\boldsymbol{{15}}} & {-1} \\ 4 & {\boldsymbol{{19}}} & {-1} \\ 1 & {\boldsymbol{{-4}}} & 3 \end{array}} \right]=-54$. Similarly, $ \displaystyle {{D}_{z}}=\det \left[ {\begin{array}{*{20}{c}} 2 & 3 & {\boldsymbol{{15}}} \\ 4 & {-3} & {\boldsymbol{{19}}} \\ 1 & {-3} & {\boldsymbol{{-4}}} \end{array}} \right]=108$. OK, now for the fun and easy part! To get the $ x, y$, and $ z$ answers to the system, you simply divide the determinants $ {{D}_{x}}$, $ {{D}_{y}}$, and $ {{D}_{z}}$, by the determinant $ D$, respectively. Thus, $ \displaystyle \left[ {\begin{array}{*{20}{c}} x \\ \begin{array}{l}y\\z\end{array} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\tfrac{{{{D}_{x}}}}{D}} \\ {\tfrac{{{{D}_{y}}}}{D}} \\ {\tfrac{{{{D}_{z}}}}{D}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\tfrac{{-270}}{{-54}}} \\ {\tfrac{{-54}}{{-54}}} \\ {\tfrac{{108}}{{-54}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 5 \\ 1 \\ {-2} \end{array}} \right]$. Now we know that $ x=5$, $ y=1$, and $ z=-2$. Note that, like the other systems, we can do this for any system where we have the same numbers of equations as unknowns .

Number of Solutions when Solving Systems with Matrices

Most systems problems that you’ll deal with will just have one solution. (These equations are called independent or consistent). But, like we learned here in the Systems of Linear Equations and Word Problems  section , sometimes we have systems where we either have no solutions or an infinite number of solutions.

Without going too much into Geometry, let’s look at what it looks like when three systems (each system looks like a “plane” or a piece of paper) have an infinite number of solutions , no solutions , and one solution , respectively:

Systems that have an infinite number of solution s (called dependent  or coincident ) will have two equations that are basically the same. One row of the coefficient matrix (and the corresponding constant matrix) is a multiple of another row. Thus, it’s like you’re trying to solve a system with only two equations, but three unknowns. A system that has an infinite number of solutions may look like this: $ \displaystyle \begin{align}2x+2y-z&=16\\4x+4y-2z&=32\\\,\,x-3y+3z&=-4\end{align}$ .

Systems with no solutions (called inconsistent ) will have one row of the coefficient matrix a multiple of another, but the rows in the constant matrix will not be in this same proportion. Thus, a system that has no solutions may look like this: $ \displaystyle \begin{align}2x+2y-z\,&=16\\4x+4y-2z&=10\\\,\,x\,-3y+3z&=-4\end{align}$ .

Applications of Matrices

Matrices can be used for many applications, including combining data, finding areas, and solving systems. Here are some examples of those applications; the most common is solving system of equations , as in the following problem:

Using the Determinant to get the Area of a Triangle

In your Geometry class, you may learn a neat trick where we can get the area of a triangle using the determinant of a matrix; let’s try an example. Let’s say we have the three coordinate points of that triangle, $ \left( {{{a}_{1}},{{b}_{1}}} \right),\left( {{{a}_{2}},{{b}_{2}}} \right)$, and $ \left( {{{a}_{3}},{{b}_{3}}} \right)$. The formula for the area of the triangle bounded by those points is:

$ \displaystyle \text{Area of Triangle with points }\left( {{{a}_{1}},{{b}_{1}}} \right),\,\left( {{{a}_{2}},{{b}_{2}}} \right)\,\,\text{and}\,\left( {{{a}_{3}},{{b}_{3}}} \right)=\pm \frac{1}{2}\left| {\begin{array}{*{20}{c}} {{{a}_{1}}} & {{{b}_{1}}} & 1 \\ {{{a}_{2}}} & {{{b}_{2}}} & 1 \\ {{{a}_{3}}} & {{{b}_{3}}} & 1 \end{array}} \right|$ (Try both the plus and minus, but only take positive answer.)

Matrix Multiplication Word Problem when Tables are Given

Here are some matrix multiplication applications:

The store wants to know how much their inventory is worth for all the shoes. How should we set up the matrix multiplication to determine this the best way?

Our matrix multiplication will look like this, even though our tables look a little different. We end up with numbers that relate to small, medium, and large shoes, so we can add up the amount in inventory (done on a calculator):

We’ll have $1050 worth of small shoes, $2315 worth of medium shoes, and $1255 worth of large shoes for a total of $4620 .

Her first mixture, Mixture 1, consists of 6 cups of almonds, 3 cups of cashews, and 1 cup of pecans. Her second mixture, Mixture 2, consists of 3 cups of almonds, 6 cups of cashews, and 1 cup of pecans. Her third mixture, Mixture 3, consists of 3 cups of almonds, 1 cup of cashews, and 6 cups of pecans.

Determine the amount of protein, carbs, and fats in a 1 cup serving of each of the mixtures.

Now we can multiply the matrices (using a graphing calculator) to end up with the amount of Protein, Carbs, and Fat (rows) in each of the mixtures (columns):

$ \displaystyle \require{cancel} \begin{array}{l}\cancel{{\text{Almonds, Cashews and Pecans}}}\,\,\,\,\,\,\,\,\,\text{Mixture 1, Mixture 2, Mixture 3 }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Mixture 1, Mixture 2, Mixture 3}\\\,\,\begin{array}{*{20}{c}} {\text{Protein}} \\ {\text{Carbs}} \\ {\text{Fat}} \end{array}\,\,\,\left[ {\begin{array}{*{20}{c}} {26.2} & {21} & {10.1} \\ {40.2} & {44.8} & {14.3} \\ {71.9} & {63.5} & {82.8} \end{array}} \right]\,\,\,\,\,\,\times \,\,\,\cancel{{\begin{array}{*{20}{c}} {\text{Almonds}} \\ {\text{Cashews}} \\ {\text{Pecans}} \end{array}}}\,\,\,\,\,\left[ {\begin{array}{*{20}{c}} 6 & 3 & 3 \\ 3 & 6 & 1 \\ 1 & 1 & 6 \end{array}} \right]\,\,\,\,\,\,=\,\,\,\,\,\,\begin{array}{*{20}{c}} {\text{Protein}} \\ {\text{Carbs}} \\ {\text{Fat}} \end{array}\,\,\,\,\left[ {\begin{array}{*{20}{c}} {230.3} & {214.7} & {160.2} \\ {389.9} & {403.7} & {251.2} \\ {704.7} & {679.5} & {776} \end{array}} \right]\end{array}$

But we have to be careful, since these amounts are for 10 cups (add down to see we’ll get 10 cups for each mixture in the matrix above). Also, notice how the cups unit “canceled out” when we did the matrix multiplication (grams/cup times cups = grams). To get the answers, we have to divide each answer by 10 to get grams per cup . The numbers in bold are our answers:

Here are a few more matrix application problems that can get a little tricky:

A Florist Must Make 5 Identical Bridesmaid Bouquets Systems Problem

Here’s a problem from the Systems of Linear Equations and Word Problems section ; we can see how much easier it is to solve with a matrix.

An Input Output Problem

Input-output problems  are seen in Economics , where we might have industries that produce for consumers, but also consume for themselves. An application of matrices is used in this input-output analysis, which was first proposed by Wassily Leontief; in fact, he won the Nobel Prize in economics in 1973 for this work.

We can express the amounts (proportions) the industries consume in matrices, such as in the following problem. Don’t worry if you don’t get this now; I’m sure there are whole courses dedicated to this topic!

Matrix Encoding/Decoding (Matrix Encryption) Problem

Matrix Encryption is a fun and interesting application; it involves using matrices in cryptology, where a (“secret”) encoded message can be sent to someone else (along with a random matrix) and decoded on the other end. Here’s an example:

a) For “ Math is Fun ”, (using 0 ’s for spaces), we have $ 13,1,20,8,0,9,19,0,6,21,14,0$; create matrix $ \displaystyle M=\left[ {\begin{array}{*{20}{c}} {13} & 8 & {19} & {21} \\ 1 & 0 & 0 & {14} \\ {20} & 9 & 6 & 0 \end{array}} \right]$ (go down columns first). To encode, multiply the given matrix E by matrix M :

$ \displaystyle EM=\left[ {\begin{array}{*{20}{c}} 2 & 4 & 1 \\ 3 & 9 & 5 \\ 6 & 8 & 0 \end{array}} \right]\times \left[ {\begin{array}{*{20}{c}} {13} & 8 & {19} & {21} \\ 1 & 0 & 0 & {14} \\ {20} & 9 & 6 & 0 \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {50} & {25} & {44} & {98} \\ {148} & {69} & {87} & {189} \\ {86} & {48} & {114} & {238} \end{array}} \right]$

Send the message as $ 50,148,86,25,69,48,44,87,114,98,189,238$ (go down columns first).

b) To decode the message, put the numbers received in matrix N and then compute $ {{E}^{{-1}}}N$:

$ \displaystyle {{E}^{{-1}}}N=\left[ {\begin{array}{*{20}{c}} {-4} & {.8} & {1.1} \\ 3 & {-.6} & {-.7} \\ {-3} & {.8} & {.6} \end{array}} \right]\times \left[ {\begin{array}{*{20}{c}} {50} & {25} & {44} & {98} \\ {148} & {69} & {87} & {189} \\ {86} & {48} & {114} & {238} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {13} & 8 & {19} & {21} \\ 1 & 0 & 0 & {14} \\ {20} & 9 & 6 & 0 \end{array}} \right]$

Convert the numbers back into the letters (going down columns first) to get “ Math is Fun ”. Wow!

Learn these rules, and practice, practice, practice!

On to Solving Systems using Reduced Row Echelon Form  – you are ready!

How to Solve Systems of Equations using Matrices

These lessons, with videos, examples, solutions, worksheets and activities, help Algebra students learn how to solve systems of equations using the inverse of matrices.

Related Pages Solving a System of Equations Inverse Matrix Types Of Matrices More Lessons On Matrices More Lessons for Grade 9 Math Worksheets

How to write a matrix equation from a systems of equations? How to solve a systems of equations using a matrix equation?

Solving Linear Systems Using Matrix Algebra One of the most commonly used applications of square matrices is solving systems of linear equations. The methods of solving systems of linear equations using matrix algebra are much more efficient than hand calculating the systems using substitution. This is especially true when dealing with systems of 3 or more variables. Two methods of matrix algebra include row reducing and finding the inverse.

How to solve a system of equations by using a matrix equation? The graphing calculator is integrated into the lesson.

Matrices to solve a system of equations Using the inverse of a matrix to solve a system of equations.

Use of matrices to solve a two unknown system of equations. The algebra is shown in a step by step method to get the equations into reduced row echelon form. The checking of the solutions is also shown.

Solving a System of Linear Equations Using Inverses

System of Equations - Matrix Method A tutorial on how to solve a simple system of equations using the Matrix Method or Inverse Method.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Unit Conversions
• Sets and Types of Numbers
• Common Multiple and Divisor
• Fractions and Decimals
• Algebraic Expressions and Polynomials
• Equations and Inequalities
• Sequences and Series
• Combinatorics
• Probability and Statistics
• Stereometry
• Analytical Geometry
• Sum, Difference and Product of Matrices
• Inverse Matrix
• Rank of a Matrix
• Determinant of a Matrix
• Matrix Equations
• System of Equations Solved by Matrices
• Matrix Word Problems
• Limits, Derivatives, Integrals
• Analysis of Functions
• Trig table and chart

• Link Partners
• Privacy Policy

Copyright © 2015-2023 math-exercises.com - All rights reserved. Any use of website content without written permission is prohibited.

Definition, Formulas, Solved Example Problems - Solved Example Problems on Applications of Matrices: Solving System of Linear Equations | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants

Chapter: 12th mathematics : unit 1 : applications of matrices and determinants, solved example problems on applications of matrices: solving system of linear equations.

Solution to a System of Linear equations

(i) Matrix Inversion Method

Example 1.22.

Solve the following system of linear equations, using matrix inversion method:

5 x  +  2  y  =  3, 3 x  +  2  y  =  5 .

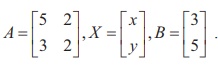
Then, applying the formula X = A −1 B , we get

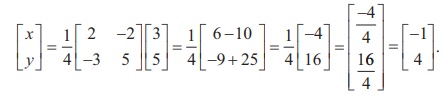
So the solution is ( x  = −1,  y  = 4).

Example 1.23

Solve the following system of equations, using matrix inversion method:

2 x 1  + 3 x 2  + 3 x 3  = 5,

x 1  – 2 x 2  +  x 3  = -4,

3 x 1  – x 2  – 2 x 3  = 3

The matrix form of the system is AX = B,where

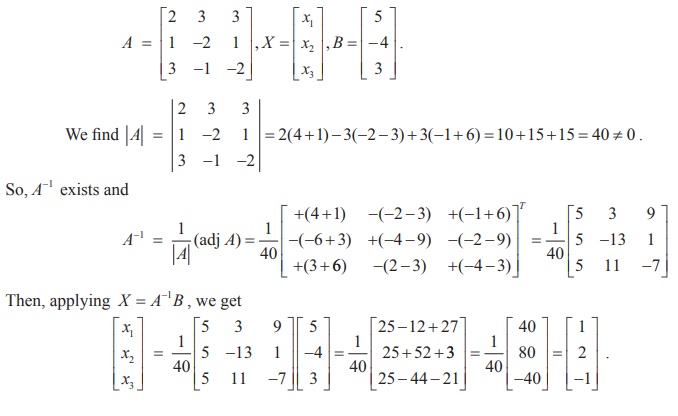
So, the solution is (  x 1  = 1,  x 2  = 2,  x 3  = −1) .

Example 1.24

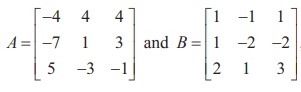
Writing the given system of equations in matrix form, we get

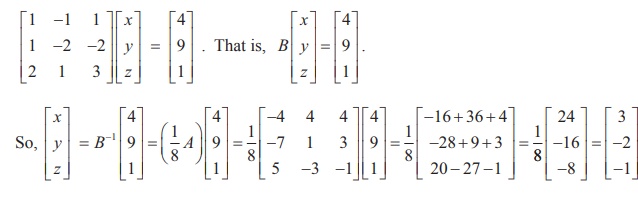
Hence, the solution is ( x  = 3,  y  = - 2,   z  = −1).

(ii) Cramer’s Rule

Example 1.25.

Solve, by Cramer’s rule, the system of equations

x 1   −   x 2   =  3, 2 x 1   +  3 x 2   +  4 x 3   =  17,  x 2   +  2 x 3   =  7.

First we evaluate the determinants

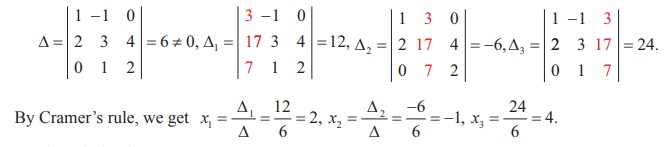
So, the solution is  ( x 1  = 2,  x 2  = - 1,   x 3  = 4).

Example 1.26

In a T20 match, Chennai Super Kings needed just 6 runs to win with 1 ball left to go in the last over. The last ball was bowled and the batsman at the crease hit it high up. The ball traversed along a path in a vertical plane and the equation of the path is  y  =   ax 2   +   bx  +   c  with respect to a  xy  -coordinate system in the  vertical  plane  and  the  ball  traversed   through   the   points  (10,8), (20,16), (30,18) , can you conclude that Chennai Super Kings won the  match?

Justify your answer. (All distances are measured in metres and the meeting point of the plane of  the path with the farthest boundary line is (70, 0).)

The path   y  =  ax 2  +  bx  +  c   passes through the points (10,8), (20,16), (40, 22) . So, we get   the   system   of   equations   100 a   + 10 b   +   c   =   8,   400 a   +   20 b   +   c =   16,1600 a   +   40 b   +   c   =   22.   To   apply   Cramer’s rule, we find

When  x  = 70, we get  y  = 6. 

So, the ball went by 6 metres high over the boundary line and it is impossible for a fielder  standing even just before theboundary line to jump and catch the ball.

    Hence the ball went for a super six and the Chennai Super Kings won the   match.

(iii) Gaussian Elimination Method

Example 1.27.

Solve the following system of linear equations, by Gaussian elimination method :

4 x  +  3 y  +  6 z  =  25,  x  +  5  y  +  7 z  =  13, 2 x  +  9  y  +   z  =  1.

Transforming the augmented matrix to echelon form, we get

The equivalent system is written by using the echelon form:

 x + 5y  + 7z = 13 , … (1)

 17y + 22z = 27 , … (2)

 199z = 398 . … (3)

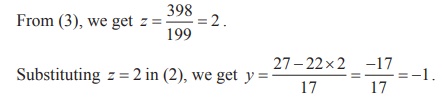
Substituting z = 2, y = -1  in (1), we get x = 13 - 5  × (−1 ) − 7 × 2 = 4 .

So, the solution is ( x =4, y = - 1, z = 2 ).

Note.  The above method of going from the last equation to the first equation is called the  method of back substitution .

Example 1.28

The  upward  speed   v ( t ) of a rocket  at time t is approximated by v(t) = at 2  + bt + c, 0 ≤  t ≤ 100 where a, b, and c are constants. It has been found that the speed at times t = 3, t = 6 , and t = 9 seconds are respectively, 64, 133, and 208 miles per second respectively. Find the speed at time  t = 15 seconds. (Use Gaussian elimination method.)

Since  v (3) =64,  v (6) = 133 and  v (9) = 208 , we get the following system of linear equations

 9a +3b + c = 64 ,

 36a + 6b + c = 133,

 81a + 9b + c = 208 .

We solve the above system of linear equations by Gaussian elimination method.

Reducing the augmented matrix to an equivalent row-echelon form by using elementary row  operations, we get

Writing the equivalent equations from the row-echelon matrix, we get

9a + 3b + c =  64, 2b + c = 41, c= 1.

By back substitution, we get 

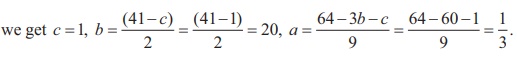
So, we get v (t) = 1/3 t 2    + 20t + 1.

Hence,  v (15) = 1/3 (225) + 20(15) + 1 = 75 + 300 + 1 = 376

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Solving Systems with Gaussian Elimination

Solving a system of linear equations using matrices.

We have seen how to write a system of equations with an augmented matrix , and then how to use row operations and back-substitution to obtain row-echelon form . Now, we will take row-echelon form a step farther to solve a 3 by 3 system of linear equations. The general idea is to eliminate all but one variable using row operations and then back-substitute to solve for the other variables.

Example 6: Solving a System of Linear Equations Using Matrices

Solve the system of linear equations using matrices.

First, we write the augmented matrix.

Next, we perform row operations to obtain row-echelon form.

The easiest way to obtain a 1 in row 2 of column 1 is to interchange [latex]{R}_{2}[/latex] and [latex]{R}_{3}[/latex].

The last matrix represents the equivalent system.

Using back-substitution, we obtain the solution as [latex]\left(4,-3,1\right)[/latex].

Example 7: Solving a Dependent System of Linear Equations Using Matrices

Solve the following system of linear equations using matrices.

Write the augmented matrix.

First, multiply row 1 by [latex]-1[/latex] to get a 1 in row 1, column 1. Then, perform row operations to obtain row-echelon form.

The last matrix represents the following system.

We see by the identity [latex]0=0[/latex] that this is a dependent system with an infinite number of solutions. We then find the generic solution. By solving the second equation for [latex]y[/latex] and substituting it into the first equation we can solve for [latex]z[/latex] in terms of [latex]x[/latex].

Now we substitute the expression for [latex]z[/latex] into the second equation to solve for [latex]y[/latex] in terms of [latex]x[/latex].

The generic solution is [latex]\left(x,\frac{2 - 2x}{3},\frac{1-x}{3}\right)[/latex].

Solve the system using matrices.

Can any system of linear equations be solved by Gaussian elimination?

Yes, a system of linear equations of any size can be solved by Gaussian elimination.

How To: Given a system of equations, solve with matrices using a calculator.

• Save the augmented matrix as a matrix variable [latex]\left[A\right],\left[B\right],\left[C\right]\text{,} \dots [/latex].
• Use the ref( function in the calculator, calling up each matrix variable as needed.

Example 8: Solving Systems of Equations with Matrices Using a Calculator

Solve the system of equations.

Write the augmented matrix for the system of equations.

On the matrix page of the calculator, enter the augmented matrix above as the matrix variable [latex]\left[A\right][/latex].

Use the ref( function in the calculator, calling up the matrix variable [latex]\left[A\right][/latex].

Using back-substitution, the solution is [latex]\left(\frac{61}{187},-\frac{92}{187},-\frac{24}{187}\right)[/latex].

Example 9: Applying 2 × 2 Matrices to Finance

Carolyn invests a total of $12,000 in two municipal bonds, one paying 10.5% interest and the other paying 12% interest. The annual interest earned on the two investments last year was $1,335. How much was invested at each rate?

We have a system of two equations in two variables. Let [latex]x=[/latex] the amount invested at 10.5% interest, and [latex]y=[/latex] the amount invested at 12% interest.

As a matrix, we have

Multiply row 1 by [latex]-0.105[/latex] and add the result to row 2.

So [latex]12,000 - 5,000=7,000[/latex].

Thus, $5,000 was invested at 12% interest and $7,000 at 10.5% interest.

Example 10: Applying 3 × 3 Matrices to Finance

Ava invests a total of $10,000 in three accounts, one paying 5% interest, another paying 8% interest, and the third paying 9% interest. The annual interest earned on the three investments last year was $770. The amount invested at 9% was twice the amount invested at 5%. How much was invested at each rate?

We have a system of three equations in three variables. Let [latex]x[/latex] be the amount invested at 5% interest, let [latex]y[/latex] be the amount invested at 8% interest, and let [latex]z[/latex] be the amount invested at 9% interest. Thus,

Now, we perform Gaussian elimination to achieve row-echelon form.

The third row tells us [latex]-\frac{1}{3}z=-2,000[/latex]; thus [latex]z=6,000[/latex].

The second row tells us [latex]y+\frac{4}{3}z=9,000[/latex]. Substituting [latex]z=6,000[/latex], we get

The first row tells us [latex]x+y+z=10,000[/latex]. Substituting [latex]y=1,000[/latex] and [latex]z=6,000[/latex], we get

The answer is $3,000 invested at 5% interest, $1,000 invested at 8%, and $6,000 invested at 9% interest.

A small shoe company took out a loan of $1,500,000 to expand their inventory. Part of the money was borrowed at 7%, part was borrowed at 8%, and part was borrowed at 10%. The amount borrowed at 10% was four times the amount borrowed at 7%, and the annual interest on all three loans was $130,500. Use matrices to find the amount borrowed at each rate.

• Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution

• IIT JEE Study Material

Solving Linear Equations Using Matrix

Solving linear equations using matrix is done by two prominent methods, namely the matrix method and row reduction or the Gaussian elimination method. In this article, we will look at solving linear equations with matrix and related examples. With the study notes provided below, students will develop a clear idea about the topic.

Download Complete Chapter Notes of Matrices & Determinants Download Now

How to Solve Linear Equations Using Matrix Method?

Let the equations be:

The first method to find the solution to the system of equations is the matrix method. The steps to be followed are given below:

• All the variables in the equations should be written in the appropriate order.
• The variables, their coefficients and constants are to be written on the respective sides.

Solving a system of linear equations by the method of finding the inverse consists of two new matrices, namely

• Matrix A: which represents the variables
• Matrix B: which represents the constants

A system of equations can be solved using matrix multiplication.

We can write the above equations in the matrix form as follows:

Where, \(\begin{array}{l}A=\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ {{c}_{1}} & {{c}_{2}} & {{c}_{3}} \\ \end{matrix} \right],\ X=\left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right],\ B=\left[ \begin{matrix} {{d}_{1}} \\ {{d}_{2}} \\ {{d}_{3}} \\ \end{matrix} \right]\end{array} \) .

A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.

The second method to find the solution for the system of equations is row reduction or Gaussian elimination.

• The augmented matrix for the linear equations is written.
• Use elementary such that all the elements below the main diagonal are zero. If a zero is obtained on the diagonal, perform the row operation such that a nonzero element is obtained.
• Back substitution is used to find the solution.

Related Topics:

• Introduction to Matrices
• Types of Matrices
• Matrix Operations
• Adjoint and Inverse of a Matrix
• Rank of a Matrix and Special Matrices

Solution to a System of Equations

A set of values of x, y, and z which simultaneously satisfy all the equations, is called a solution to the system of equations.

Consider, x + y + z = 9

2x – y + z = 5

4x + y – z = 7

Here, the set of values – x = 2, y = 3, z = 4, is a solution to the system of linear equations.

Because, 2 + 3 + 4 = 9, 4 – 3 + 4 = 5, 8 + 3 – 4 = 7

Consistent Equations

If the system of equations has one or more solutions, then it is said to be a consistent system of equations; otherwise, it is an inconsistent system of equations. For example, the system of linear equations x + 3y = 5;  x – y = 1 is consistent because x = 2, y = 1 is a solution to it. However, the system of linear equations x + 3y = 5; 2x + 6y = 8 is inconsistent because there is no set of values of x and y, which may satisfy the two equations simultaneously.

Condition for consistency of a system of linear equation AX = B

(b) If |A| = 0, and (Adj A) B ≠ 0, then the system is inconsistent.

(c) If |A| = 0, and (Adj A) B = 0, then the system is consistent and has infinitely many solutions.

Note AX = 0 is known as the homogeneous system of linear equations, and here, B = 0. A system of homogeneous equations is always consistent.

The system has a non-trivial solution (non-zero solution), if | A | = 0

Theorem 1: Let AX = B be a system of linear equations, where A is the coefficient matrix. If A is invertible, then the system has a unique solution, given by X = A -1 B

Uniqueness: If AX = B has two sets of solutions X 1 and X 2 , then AX 1 = B and AX 2 = B (Each equal to B).

⇒  AX 1 = AX 2

By cancellation law, A is invertible.

⇒  X 1 = X 2

Hence, the given system AX = B has a unique solution.

Note: A homogeneous system of equations is always consistent.

Problems on Solving Linear Equations Using Matrix Method

Illustration: Let A = \(\begin{array}{l}\left[ \begin{matrix} x+y & y \\ 2x & x-y \\ \end{matrix} \right],\ B=\left[ \begin{matrix} 2 \\ -1 \\ \end{matrix} \right],\ C = \left[ \begin{matrix} 3 \\ 2 \\ \end{matrix} \right]\end{array} \) . If AB = C, then find the matrix A 2 .

By solving AB = C, we get the values of x and y. Then by substituting these values in A, we obtain A 2

Here \(\begin{array}{l}\left[ \begin{matrix} x+y & y \\ 2x & x-y \\ \end{matrix} \right]\left[ \begin{matrix} 2 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} 3 \\ 2 \\ \end{matrix} \right]\\ \Rightarrow \left[ \begin{matrix} 2\left( x+y \right)-y \\ 2x.2-\left( x-y \right) \\ \end{matrix} \right]=\left[ \begin{matrix} 3 \\ 2 \\ \end{matrix} \right]\\ \Rightarrow 2\left( x+y \right)-y=3 \:\:and \:\:4x-\left( x-y \right)=2\end{array} \) \(\begin{array}{l}\Rightarrow \,\,2x+y=3\;\;\;\;and\;\;\;\;3x+y=2\end{array} \) Subtracting the two equations, we get, x = -1 So, y = 5 .

Illustration: Solve the following equations by matrix inversion

The given equation can be written in a matrix form as AX = D, and then by obtaining A -1 and multiplying it on both sides, we can solve the given problem.

then matrix A equals:

has no solution if a and b are

By applying row operation in the given matrices and comparing them, we can obtain the required result.

\(\begin{array}{l}\Rightarrow \,a=-3 \;\;and \;\;b\ne -1/3 \end{array} \) .

Applying \(\begin{array}{l}{{R}_{3}}\to {{R}_{3}}-2{{R}_{2}}+{{R}_{1}} \;\;and \;\;\;{{R}_{2}} to {{R}_{2}}-2{{R}_{1}}\end{array} \) we get;

Frequently Asked Questions

What do you mean by a linear equation.

A linear equation is an equation that has one or more variables having degree one.

Name two methods to solve linear equations using matrices.

The matrix multiplication method and the Gaussian elimination method are two methods to solve linear equations using matrices.

What do you mean by consistent equations?

A consistent system of equations is an equation having one or more solutions.

Give the formula used in the matrix multiplication method for solving linear equations.

We use the formula AX = B in the matrix multiplication method for solving linear equations. Here, A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.