system of linear inequalities problem solving

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.5: Solving Systems of Linear Inequalities (Two Variables)

• Last updated
• Save as PDF
• Page ID 18351

Learning Objectives

• Check solutions to systems of linear inequalities with two variables.
• Solve systems of linear inequalities.

Solutions to Systems of Linear Inequalities

A system of linear inequalities consists of a set of two or more linear inequalities with the same variables. The inequalities define the conditions that are to be considered simultaneously. For example,

We know that each inequality in the set contains infinitely many ordered pair solutions defined by a region in a rectangular coordinate plane. When considering two of these inequalities together, the intersection of these sets defines the set of simultaneous ordered pair solutions. When we graph each of the above inequalities separately, we have

4.7 Graphing Systems of Linear Inequalities

Learning objectives.

By the end of this section, you will be able to:

Determine whether an ordered pair is a solution of a system of linear inequalities

• Solve a system of linear inequalities by graphing
• Solve applications of systems of inequalities

Be Prepared 4.19

Before you get started, take this readiness quiz.

Solve the inequality 2 a < 5 a + 12 . 2 a < 5 a + 12 . If you missed this problem, review Example 2.52 .

Be Prepared 4.20

Determine whether the ordered pair ( 3 , 1 2 ) ( 3 , 1 2 ) is a solution to the system y > 2 x + 3 . y > 2 x + 3 . If you missed this problem, review Example 3.34 .

The definition of a system of linear inequalities is very similar to the definition of a system of linear equations.

System of Linear Inequalities

Two or more linear inequalities grouped together form a system of linear inequalities.

A system of linear inequalities looks like a system of linear equations, but it has inequalities instead of equations. A system of two linear inequalities is shown here.

To solve a system of linear inequalities, we will find values of the variables that are solutions to both inequalities. We solve the system by using the graphs of each inequality and show the solution as a graph. We will find the region on the plane that contains all ordered pairs ( x , y ) ( x , y ) that make both inequalities true.

Solutions of a System of Linear Inequalities

Solutions of a system of linear inequalities are the values of the variables that make all the inequalities true.

The solution of a system of linear inequalities is shown as a shaded region in the x, y coordinate system that includes all the points whose ordered pairs make the inequalities true.

To determine if an ordered pair is a solution to a system of two inequalities, we substitute the values of the variables into each inequality. If the ordered pair makes both inequalities true, it is a solution to the system.

Example 4.53

Determine whether the ordered pair is a solution to the system { x + 4 y ≥ 10 3 x − 2 y < 12 . { x + 4 y ≥ 10 3 x − 2 y < 12 .

ⓐ ( −2 , 4 ) ( −2 , 4 ) ⓑ ( 3 , 1 ) ( 3 , 1 )

ⓐ Is the ordered pair ( −2 , 4 ) ( −2 , 4 ) a solution?

The ordered pair ( −2 , 4 ) ( −2 , 4 ) made both inequalities true. Therefore ( −2 , 4 ) ( −2 , 4 ) is a solution to this system.

ⓑ Is the ordered pair ( 3 , 1 ) ( 3 , 1 ) a solution?

The ordered pair ( 3 , 1 ) ( 3 , 1 ) made one inequality true, but the other one false. Therefore ( 3 , 1 ) ( 3 , 1 ) is not a solution to this system.

Try It 4.105

Determine whether the ordered pair is a solution to the system: { x − 5 y > 10 2 x + 3 y > −2 . { x − 5 y > 10 2 x + 3 y > −2 .

ⓐ ( 3 , −1 ) ( 3 , −1 ) ⓑ ( 6 , −3 ) ( 6 , −3 )

Try It 4.106

Determine whether the ordered pair is a solution to the system: { y > 4 x − 2 4 x − y < 20 . { y > 4 x − 2 4 x − y < 20 .

ⓐ ( −2 , 1 ) ( −2 , 1 ) ⓑ ( 4 , −1 ) ( 4 , −1 )

Solve a System of Linear Inequalities by Graphing

The solution to a single linear inequality is the region on one side of the boundary line that contains all the points that make the inequality true. The solution to a system of two linear inequalities is a region that contains the solutions to both inequalities. To find this region, we will graph each inequality separately and then locate the region where they are both true. The solution is always shown as a graph.

Example 4.54

How to solve a system of linear inequalities by graphing.

Solve the system by graphing: { y ≥ 2 x − 1 y < x + 1 . { y ≥ 2 x − 1 y < x + 1 .

Try It 4.107

Solve the system by graphing: { y < 3 x + 2 y > − x − 1 . { y < 3 x + 2 y > − x − 1 .

Try It 4.108

Solve the system by graphing: { y < − 1 2 x + 3 y < 3 x − 4 . { y < − 1 2 x + 3 y < 3 x − 4 .

Solve a system of linear inequalities by graphing.

• Graph the boundary line.
• Shade in the side of the boundary line where the inequality is true.
• Shade in the side of that boundary line where the inequality is true.
• Step 3. The solution is the region where the shading overlaps.
• Step 4. Check by choosing a test point.

Example 4.55

Solve the system by graphing: { x − y > 3 y < − 1 5 x + 4 . { x − y > 3 y < − 1 5 x + 4 .

The point of intersection of the two lines is not included as both boundary lines were dashed. The solution is the area shaded twice—which appears as the darkest shaded region.

Try It 4.109

Solve the system by graphing: { x + y ≤ 2 y ≥ 2 3 x − 1 . { x + y ≤ 2 y ≥ 2 3 x − 1 .

Try It 4.110

Solve the system by graphing: { 3 x − 2 y ≤ 6 y > − 1 4 x + 5 . { 3 x − 2 y ≤ 6 y > − 1 4 x + 5 .

Example 4.56

Solve the system by graphing: { x − 2 y < 5 y > −4 . { x − 2 y < 5 y > −4 .

The point ( 0 , 0 ) ( 0 , 0 ) is in the solution and we have already found it to be a solution of each inequality. The point of intersection of the two lines is not included as both boundary lines were dashed.

The solution is the area shaded twice—which appears as the darkest shaded region.

Try It 4.111

Solve the system by graphing: { y ≥ 3 x − 2 y < − 1 . { y ≥ 3 x − 2 y < − 1 .

Try It 4.112

Solve the system by graphing: { x > −4 x − 2 y ≥ −4 . { x > −4 x − 2 y ≥ −4 .

Systems of linear inequalities where the boundary lines are parallel might have no solution. We’ll see this in the next example.

Example 4.57

Solve the system by graphing: { 4 x + 3 y ≥ 12 y < − 4 3 x + 1 . { 4 x + 3 y ≥ 12 y < − 4 3 x + 1 .

There is no point in both shaded regions, so the system has no solution.

Try It 4.113

Solve the system by graphing: { 3 x − 2 y ≥ 12 y ≥ 3 2 x + 1 . { 3 x − 2 y ≥ 12 y ≥ 3 2 x + 1 .

Try It 4.114

Solve the system by graphing: { x + 3 y > 8 y < − 1 3 x − 2 . { x + 3 y > 8 y < − 1 3 x − 2 .

Some systems of linear inequalities where the boundary lines are parallel will have a solution. We’ll see this in the next example.

Example 4.58

Solve the system by graphing: { y > 1 2 x − 4 x − 2 y < −4 . { y > 1 2 x − 4 x − 2 y < −4 .

No point on the boundary lines is included in the solution as both lines are dashed.

The solution is the region that is shaded twice which is also the solution to x − 2 y < −4 . x − 2 y < −4 .

Try It 4.115

Solve the system by graphing: { y ≥ 3 x + 1 −3 x + y ≥ −4 . { y ≥ 3 x + 1 −3 x + y ≥ −4 .

Try It 4.116

Solve the system by graphing: { y ≤ − 1 4 x + 2 x + 4 y ≤ 4 . { y ≤ − 1 4 x + 2 x + 4 y ≤ 4 .

Solve Applications of Systems of Inequalities

The first thing we’ll need to do to solve applications of systems of inequalities is to translate each condition into an inequality. Then we graph the system, as we did above, to see the region that contains the solutions. Many situations will be realistic only if both variables are positive, so we add inequalities to the system as additional requirements.

Example 4.59

Christy sells her photographs at a booth at a street fair. At the start of the day, she wants to have at least 25 photos to display at her booth. Each small photo she displays costs her $4 and each large photo costs her $10. She doesn’t want to spend more than $200 on photos to display.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could she display 10 small and 20 large photos? ⓓ Could she display 20 small and 10 large photos?

ⓑ Since x ≥ 0 x ≥ 0 and y ≥ 0 y ≥ 0 (both are greater than or equal to) all solutions will be in the first quadrant. As a result, our graph shows only quadrant one.

The solution of the system is the region of the graph that is shaded the darkest. The boundary line sections that border the darkly-shaded section are included in the solution as are the points on the x -axis from (25, 0) to (55, 0).

ⓒ To determine if 10 small and 20 large photos would work, we look at the graph to see if the point (10, 20) is in the solution region. We could also test the point to see if it is a solution of both equations.

It is not, Christy would not display 10 small and 20 large photos.

ⓓ To determine if 20 small and 10 large photos would work, we look at the graph to see if the point (20, 10) is in the solution region. We could also test the point to see if it is a solution of both equations.

It is, so Christy could choose to display 20 small and 10 large photos.

Notice that we could also test the possible solutions by substituting the values into each inequality.

Try It 4.117

A trailer can carry a maximum weight of 160 pounds and a maximum volume of 15 cubic feet. A microwave oven weighs 30 pounds and has 2 cubic feet of volume, while a printer weighs 20 pounds and has 3 cubic feet of space.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could 4 microwaves and 2 printers be carried on this trailer? ⓓ Could 7 microwaves and 3 printers be carried on this trailer?

Try It 4.118

Mary needs to purchase supplies of answer sheets and pencils for a standardized test to be given to the juniors at her high school. The number of the answer sheets needed is at least 5 more than the number of pencils. The pencils cost $2 and the answer sheets cost $1. Mary’s budget for these supplies allows for a maximum cost of $400.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could Mary purchase 100 pencils and 100 answer sheets? ⓓ Could Mary purchase 150 pencils and 150 answer sheets?

When we use variables other than x and y to define an unknown quantity, we must change the names of the axes of the graph as well.

Example 4.60

Omar needs to eat at least 800 calories before going to his team practice. All he wants is hamburgers and cookies, and he doesn’t want to spend more than $5. At the hamburger restaurant near his college, each hamburger has 240 calories and costs $1.40. Each cookie has 160 calories and costs $0.50.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could he eat 3 hamburgers and 1 cookie? ⓓ Could he eat 2 hamburgers and 4 cookies?

ⓑ Since h > = 0 h > = 0 and c > = 0 c > = 0 (both are greater than or equal to) all solutions will be in the first quadrant. As a result, our graph shows only quadrant one.

Graph 1.40 h + 0.50 c ≤ 5 . 1.40 h + 0.50 c ≤ 5 . The boundary line is 1.40 h + 0.50 c = 5 . 1.40 h + 0.50 c = 5 . We test (0, 0) and it makes the inequality true. We shade the side of the line that includes (0, 0).

The solution of the system is the region of the graph that is shaded the darkest. The boundary line sections that border the darkly shaded section are included in the solution as are the points on the x -axis from (5, 0) to (10, 0).

ⓒ To determine if 3 hamburgers and 1 cookie would meet Omar’s criteria, we see if the point (3, 2) is in the solution region. It is, so Omar might choose to eat 3 hamburgers and 1 cookie.

ⓓ To determine if 2 hamburgers and 4 cookies would meet Omar’s criteria, we see if the point (2, 4) is in the solution region. It is, Omar might choose to eat 2 hamburgers and 4 cookies.

We could also test the possible solutions by substituting the values into each inequality.

Try It 4.119

Tenison needs to eat at least an extra 1,000 calories a day to prepare for running a marathon. He has only $25 to spend on the extra food he needs and will spend it on $0.75 donuts which have 360 calories each and $2 energy drinks which have 110 calories.

ⓐ Write a system of inequalities that models this situation. ⓑ Graph the system. ⓒ Can he buy 8 donuts and 4 energy drinks and satisfy his caloric needs? ⓓ Can he buy 1 donut and 3 energy drinks and satisfy his caloric needs?

Try It 4.120

Philip’s doctor tells him he should add at least 1,000 more calories per day to his usual diet. Philip wants to buy protein bars that cost $1.80 each and have 140 calories and juice that costs $1.25 per bottle and have 125 calories. He doesn’t want to spend more than $12.

ⓐ Write a system of inequalities that models this situation. ⓑ Graph the system. ⓒ Can he buy 3 protein bars and 5 bottles of juice? ⓓ Can he buy 5 protein bars and 3 bottles of juice?

Access these online resources for additional instruction and practice with solving systems of linear inequalities by graphing.

• Solving Systems of Linear Inequalities by Graphing
• Systems of Linear Inequalities

Section 4.7 Exercises

Practice makes perfect.

Determine Whether an Ordered Pair is a Solution of a System of Linear Inequalities

In the following exercises, determine whether each ordered pair is a solution to the system.

{ 3 x + y > 5 2 x − y ≤ 10 { 3 x + y > 5 2 x − y ≤ 10

ⓐ ( 3 , −3 ) ( 3 , −3 ) ⓑ ( 7 , 1 ) ( 7 , 1 )

{ 4 x − y < 10 −2 x + 2 y > −8 { 4 x − y < 10 −2 x + 2 y > −8

ⓐ ( 5 , −2 ) ( 5 , −2 ) ⓑ ( −1 , 3 ) ( −1 , 3 )

{ y > 2 3 x − 5 x + 1 2 y ≤ 4 { y > 2 3 x − 5 x + 1 2 y ≤ 4

ⓐ (6, −4) (6, −4) ⓑ (3, 0) (3, 0)

{ y < 3 2 x + 3 3 4 x − 2 y < 5 { y < 3 2 x + 3 3 4 x − 2 y < 5

ⓐ ( −4 , −1 ) ( −4 , −1 ) ⓑ (8, 3) (8, 3)

{ 7 x + 2 y > 14 5 x − y ≤ 8 { 7 x + 2 y > 14 5 x − y ≤ 8

ⓐ (2, 3) (2, 3) ⓑ (7, −1) (7, −1)

{ 6 x − 5 y < 20 −2 x + 7 y > −8 { 6 x − 5 y < 20 −2 x + 7 y > −8

ⓐ (1, −3) (1, −3) ⓑ (−4, 4) (−4, 4)

In the following exercises, solve each system by graphing.

{ y ≤ 3 x + 2 y > x − 1 { y ≤ 3 x + 2 y > x − 1

{ y < − 2 x + 2 y ≥ − x − 1 { y < − 2 x + 2 y ≥ − x − 1

{ y < 2 x − 1 y ≤ − 1 2 x + 4 { y < 2 x − 1 y ≤ − 1 2 x + 4

{ y ≥ − 2 3 x + 2 y > 2 x − 3 { y ≥ − 2 3 x + 2 y > 2 x − 3

x − y > 1 y < − 1 4 x + 3 x − y > 1 y < − 1 4 x + 3

{ x + 2 y < 4 y < x − 2 { x + 2 y < 4 y < x − 2

{ 3 x − y ≥ 6 y ≥ − 1 2 x { 3 x − y ≥ 6 y ≥ − 1 2 x

{ 2 x + 4 y ≥ 8 y ≤ 3 4 x { 2 x + 4 y ≥ 8 y ≤ 3 4 x

{ 2 x − 5 y < 10 3 x + 4 y ≥ 12 { 2 x − 5 y < 10 3 x + 4 y ≥ 12

{ 3 x − 2 y ≤ 6 −4 x − 2 y > 8 { 3 x − 2 y ≤ 6 −4 x − 2 y > 8

{ 2 x + 2 y > −4 − x + 3 y ≥ 9 { 2 x + 2 y > −4 − x + 3 y ≥ 9

{ 2 x + y > −6 − x + 2 y ≥ −4 { 2 x + y > −6 − x + 2 y ≥ −4

{ x − 2 y < 3 y ≤ 1 { x − 2 y < 3 y ≤ 1

{ x − 3 y > 4 y ≤ − 1 { x − 3 y > 4 y ≤ − 1

{ y ≥ − 1 2 x − 3 x ≤ 2 { y ≥ − 1 2 x − 3 x ≤ 2

{ y ≤ − 2 3 x + 5 x ≥ 3 { y ≤ − 2 3 x + 5 x ≥ 3

{ y ≥ 3 4 x − 2 y < 2 { y ≥ 3 4 x − 2 y < 2

{ y ≤ − 1 2 x + 3 y < 1 { y ≤ − 1 2 x + 3 y < 1

{ 3 x − 4 y < 8 x < 1 { 3 x − 4 y < 8 x < 1

{ −3 x + 5 y > 10 x > −1 { −3 x + 5 y > 10 x > −1

{ x ≥ 3 y ≤ 2 { x ≥ 3 y ≤ 2

{ x ≤ −1 y ≥ 3 { x ≤ −1 y ≥ 3

{ 2 x + 4 y > 4 y ≤ − 1 2 x − 2 { 2 x + 4 y > 4 y ≤ − 1 2 x − 2

{ x − 3 y ≥ 6 y > 1 3 x + 1 { x − 3 y ≥ 6 y > 1 3 x + 1

{ −2 x + 6 y < 0 6 y > 2 x + 4 { −2 x + 6 y < 0 6 y > 2 x + 4

{ −3 x + 6 y > 12 4 y ≤ 2 x − 4 { −3 x + 6 y > 12 4 y ≤ 2 x − 4

{ y ≥ −3 x + 2 3 x + y > 5 { y ≥ −3 x + 2 3 x + y > 5

{ y ≥ 1 2 x − 1 −2 x + 4 y ≥ 4 { y ≥ 1 2 x − 1 −2 x + 4 y ≥ 4

{ y ≤ − 1 4 x − 2 x + 4 y < 6 { y ≤ − 1 4 x − 2 x + 4 y < 6

{ y ≥ 3 x − 1 −3 x + y > −4 { y ≥ 3 x − 1 −3 x + y > −4

{ 3 y > x + 2 −2 x + 6 y > 8 { 3 y > x + 2 −2 x + 6 y > 8

{ y < 3 4 x − 2 −3 x + 4 y < 7 { y < 3 4 x − 2 −3 x + 4 y < 7

In the following exercises, translate to a system of inequalities and solve.

Caitlyn sells her drawings at the county fair. She wants to sell at least 60 drawings and has portraits and landscapes. She sells the portraits for $15 and the landscapes for $10. She needs to sell at least $800 worth of drawings in order to earn a profit.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Will she make a profit if she sells 20 portraits and 35 landscapes? ⓓ Will she make a profit if she sells 50 portraits and 20 landscapes?

Jake does not want to spend more than $50 on bags of fertilizer and peat moss for his garden. Fertilizer costs $2 a bag and peat moss costs $5 a bag. Jake’s van can hold at most 20 bags.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Can he buy 15 bags of fertilizer and 4 bags of peat moss? ⓓ Can he buy 10 bags of fertilizer and 10 bags of peat moss?

Reiko needs to mail her Christmas cards and packages and wants to keep her mailing costs to no more than $500. The number of cards is at least 4 more than twice the number of packages. The cost of mailing a card (with pictures enclosed) is $3 and for a package the cost is $7.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Can she mail 60 cards and 26 packages? ⓓ Can she mail 90 cards and 40 packages?

Juan is studying for his final exams in chemistry and algebra. he knows he only has 24 hours to study, and it will take him at least three times as long to study for algebra than chemistry.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Can he spend 4 hours on chemistry and 20 hours on algebra? ⓓ Can he spend 6 hours on chemistry and 18 hours on algebra?

Jocelyn is pregnant and so she needs to eat at least 500 more calories a day than usual. When buying groceries one day with a budget of $15 for the extra food, she buys bananas that have 90 calories each and chocolate granola bars that have 150 calories each. The bananas cost $0.35 each and the granola bars cost $2.50 each.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could she buy 5 bananas and 6 granola bars? ⓓ Could she buy 3 bananas and 4 granola bars?

Mark is attempting to build muscle mass and so he needs to eat at least an additional 80 grams of protein a day. A bottle of protein water costs $3.20 and a protein bar costs $1.75. The protein water supplies 27 grams of protein and the bar supplies 16 gram. If he has $10 dollars to spend

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could he buy 3 bottles of protein water and 1 protein bar? ⓓ Could he buy no bottles of protein water and 5 protein bars?

Jocelyn desires to increase both her protein consumption and caloric intake. She desires to have at least 35 more grams of protein each day and no more than an additional 200 calories daily. An ounce of cheddar cheese has 7 grams of protein and 110 calories. An ounce of parmesan cheese has 11 grams of protein and 22 calories.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could she eat 1 ounce of cheddar cheese and 3 ounces of parmesan cheese? ⓓ Could she eat 2 ounces of cheddar cheese and 1 ounce of parmesan cheese?

Mark is increasing his exercise routine by running and walking at least 4 miles each day. His goal is to burn a minimum of 1500 calories from this exercise. Walking burns 270 calories/mile and running burns 650 calories.

ⓐ Write a system of inequalities to model this situation. ⓑ Graph the system. ⓒ Could he meet his goal by walking 3 miles and running 1 mile? ⓓ Could he meet his goal by walking 2 miles and running 2 miles?

Writing Exercises

Graph the inequality x − y ≥ 3 . x − y ≥ 3 . How do you know which side of the line x − y = 3 x − y = 3 should be shaded?

Graph the system { x + 2 y ≤ 6 y ≥ − 1 2 x − 4 . { x + 2 y ≤ 6 y ≥ − 1 2 x − 4 . What does the solution mean?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-7-graphing-systems-of-linear-inequalities

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Systems of Linear Inequalities: Solving by Graphing

Graphing Special Cases

Once you've learned how to graph two-variable linear inequalities , you can move on to solving systems of two-variable linear inequalities.

What is a system of linear inequalities?

A "system" of two-variable linear inequalities is a set of linear inequalities for which each of the inequalities is drawn on the same graph. On this graph, you shade the side of each line that is included in that line's inequality.

Content Continues Below

MathHelp.com

What is the solution to a system of linear inequalities?

The solution to the system of linear inequalities is the region of the plane where all of the individual lines' shading overlaps. This solution region is the intersection of the various lines' shadings; it is the area of the graph where all the inequalities are "happy".

What is an example of solving a system of linear inequalities?

• Solve the following system:

2 x − 3 y ≤ 12 x + 5 y ≤ 20 x > 0

Just as with solving single linear inequalities, it is usually best to solve as many of the inequalities as possible for " y " on one side. Solving the first two inequalities, I get the rearranged system:

Advertisement

y ≥ (2/3)  x − 4 y ≤ (−1/5)  x + 4 x > 0

"Solving" systems of two-variable linear inequalities means "graphing each individual inequality, and then finding the overlaps of the various solutions". So I graph each inequality individually, marking the "solution" side of each line as I go, and then I'll find the overlapping portion of the various solution regions.

The line for the first inequality in the above system, y ≥ (2/3)  x − 4 , looks like this:

The above line, shown in blue, represents the line y = (2/3)  x − 4 . The inequality part will be indicated by shading one side or the other of this line.

This inequality is an "or equal to" inequality, so the line is drawn as a solid line, rather than as a dashed line.

This inequality is a "greater than" inequality, so I want to shade above the line. However, since there will be more than one inequality on this graph, I don't know (yet) how much of that upper side of this line I will actually need.

How do I keep track of where the end solution region will be?

Until I know how much of a given single inequality's solution region I'll need, I can keep track of the fact that I want a certain side of an inequality's line (in this case, the top region) by drawing a little "fringe" along the top side of my solid line, like this:

Now I'll graph the line for the second inequality they gave me; namely, y ≤ (−1/5)  x + 4 :

This is another "or equal to" inequality, so the line is solid; and, since this is a "less than" inequality, I'll draw the fringe along the bottom of my solid line:

The last inequality is a common "real life" constraint, restricting the variable x to being positive only . The line " x = 0 " is just the y -axis, and I'll be wanting to shade the right-hand side. Because this is a strict inequality (that is, this inequality is not an "or equal to" inequality); the boundary (namely, the line dashed along the y -axis) is not to be included in the solution to the system:

The "solution" of the system is the region where all the inequalities are happy; that is, the solution is where all the inequalities work, the region where all three individual solution regions overlap. In this case, the solution is the shaded part in the middle:

The answer to this sort of exercise is typically a graph, as shown above. Nothing further should be required.

Notice how, in my graph, I made sure that the dashed line for the " x > 0 inequality is still clearly visible as being a dashed line. When your answer is a picture like this, make sure to draw it clearly. You're welcome to shade in your solution region right up to (and maybe onto) the solid lines, but make sure that your dashed lines are clearly dashed — by heavily over-drawing them, or maybe using a different color for contrast, if necessary. But make your meaning clear!

The solution region for the system graphed above is called a "bounded" solution, because there are lines closing it in on all sides. That is, the solution region is a bounded (finite) geometric figure; in the case above, the solution region was a triangle.

URL: https://www.purplemath.com/modules/syslneq.htm

Page 1 Page 2

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Systems of Linear Inequalities

How to find the solution of Linear Inequality Functions

• Interactive system of linear inequalities

A System of linear inequalities is simply two or more linear inequalities on the same plane. In other words, a system of linear inequalities is just two or more inequalities together.

The easiest way to remember what 'system' means in this context is by answering the following question: 'Does the word system ever refer to just one thing or does system always refer to more than one thing?'

Interactive System of Linear Inequalities

Click and drag on the points below and the system of linear inequalities will adjust accordingly. ( Full sized interactive system of linear inequalities )

Use it to enable or disable snapping

Click on the equation to change inequality type between ≤, <, > and ≥, you can drag the points to change the line equation.

Below are the graphs of the linear inequalities : y < x + 1 and y > x .

Pictured above is the system of inequalities made up the same two linear inequalities :

y < x + 1 y > x

When we take both of the linear inequalities pictured above and graph them on same Cartesian plane, we get a system of linear inequalities. The solution of this system is the yellow region which is the area of overlap. In other words, the solution of the system is the region where both inequalities are true. The y coordinates of all points in the yellow region are both greater than x + 1 as well as less than x.

Example of a system of Linear Inequalities

The picture below shows a system of linear inequalities.

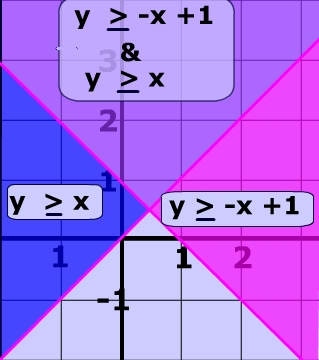
On the left is the graph of two linear inequalities. What is the solution to this system of linear inequalities?

(Reminder: the solution is the region that both inequalities cover)

Practice Problems

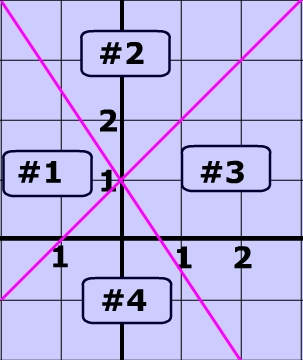
Below is the graph of the following system of inequalities:

• y > – x
• y > x + 1

From the picture can you determine which area is the solution of this system?

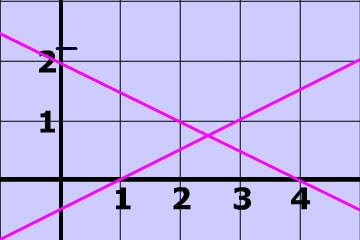
On the left is the graph of

• y = -3/2x + 1

Which region on the left is the solution to this system of linear inequalities ?

• y ≥ x + 1
• y ≥ –3/2x + 1

Remember: that simply means which region includes both of the following linear inequalities :

y ≥ x + 1 & y ≥ –x + 1

What is the solution to the following system of linear inequalities (whose lines are graphed on the right)

  y ≤ -½x + 2   y ≥ ½x - 1

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Systems of Linear Inequalities?

Linear inequalities are expressions in which two linear expressions are compared using the inequality symbols. In this step-by-step guide, you will learn about solving systems of linear inequalities.

The solution to a system of a linear inequality is the region where the graphs of all linear inequalities in the system overlap.

Related Topics

• How to Solve Linear Inequalities
• How to Solve Quadratic Inequalities

A step-by-step guide to solving systems of linear inequalities

The system of linear inequalities is a set of equations of linear inequality containing the same variables. Several methods of solving systems of linear equations translate to the system of linear inequalities. However, solving a system of linear inequalities is somewhat different from linear equations because the signs of inequality prevent us from solving by the substitution or elimination method. Perhaps the best way to solve systems of linear inequalities is by graphing the inequalities.

To solve a system of inequalities, graph each linear inequality in the system on the same \(x-y\) axis by following the steps below:

• Solve the inequality for \(y\).
• Treat the inequality as a linear equation and graph the line as either a solid line or a dashed line depending on the inequality sign. If the inequality sign does not contain an equals sign \((< or >)\) then draw the line as a dashed line. If the inequality sign does have an equals sign \((≤ or ≥)\) then draw the line as a solid line.
• Shade the region that satisfies the inequality.
• Repeat steps \(1 – 3\) for each inequality.
• The solution set will be the overlapped region of all the inequalities.

Solving Systems of Linear Inequalities – Example 1:

Solve the following system of inequalities.

\(\begin{cases}x\:-\:5y\ge \:6\\ \:3x\:+\:2y>1\end{cases}\)

First, isolate the variable \(y\) to the left in each inequality:

\(x -5y≥ 6\)

\(x≥6 + 5y\)

\(5y≤ x- 6\)

\(y≤0.2 x -1.2\)

\(3x+ 2y> 1\)

\(2y>1-3x\)

\(y> 0.5-1.5x\)

Now, graph \(y≤ 0.2x-1.2\) and \(y > 0.5 -1.5x\) using a solid line and a broken one, respectively.

The solution of the system of inequality is the darker shaded area which is the overlap of the two individual solution regions.

Exercises for Solving Systems of Linear Inequalities

Determine the solution to the following system of inequalities..

• \(\color{blue}{\begin{cases}5x-2y\le 10 \\ \:3x+2y>\:6\end{cases}}\)
• \(\color{blue}{\begin{cases}-2x-y<\:-1 \\ \:4x+\:2y\:\le -6\end{cases}}\)

by: Effortless Math Team about 2 years ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• How to Identify Statistical Questions
• Is ALEKS just for Mathematics?
• How to Overcome Praxis Core Math Anxiety?
• HSPT Math Practice Test Questions
• 7th Grade SBAC Math Practice Test Questions
• Top 10 7th Grade PSSA Math Practice Questions
• Full-Length 7th Grade STAAR Math Practice Test
• Best Laptop for High School Students in 2024
• How to Prepare for the SSAT Middle-Level Math Test?
• How to Compare Amounts of Money?

What people say about "How to Solve Systems of Linear Inequalities? - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

College Algebra and Trigonometry for Beginners The Ultimate Step by Step Guide to Acing the College Algebra and Trigonometry

10 full length pssa grade 7 math practice tests the practice you need to ace the pssa grade 7 math test, ged math workbook comprehensive math practices and solutions the ultimate test prep book with two full-length practice tests, calculus for beginners the ultimate step by step guide to acing calculus, statistics for beginners the ultimate step by step guide to acing statistics, ged math test prep in 30 days complete study guide and test tutor for ged mathematics. the ultimate book for beginners and pros + two practice tests, 10 full length gre math practice tests the practice you need to ace the gre math test, basic mathematics for beginners the ultimate step by step guide and a comprehensive basic math refresher, gre math for beginners the ultimate step by step guide to preparing for the gre math test, a comprehensive math workbook for grade 2, ged math made easy study guide to ace your test with key points, examples, and practices, the ultimate high school math bundle from algebra i to pre-calculus, the ultimate middle school math bundle grades 6-8, the ultimate elementary school math bundle grade 3-5, ap pre-calculus for beginners the ultimate step by step guide to acing ap precalculus.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos
• Google Play
• Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

A free service from Mattecentrum

Systems of linear inequalities

A system of linear inequalities in two variables consists of at least two linear inequalities in the same variables. The solution of a linear inequality is the ordered pair that is a solution to all inequalities in the system and the graph of the linear inequality is the graph of all solutions of the system.

Graph the system of inequalities

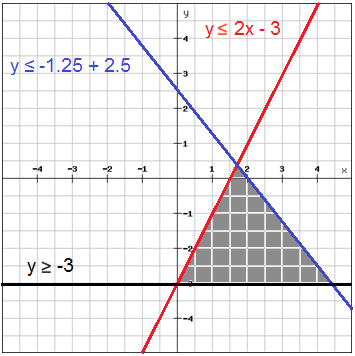
$$\\\left\{\begin{matrix} y\leq 2x-3\: \: \: \: \: \: \: \: \\ y\geq -3\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ y\leq -1.25x+2.5 \end{matrix}\right.\\$$

Graph one line at the time in the same coordinate plane and shade the half-plane that satisfies the inequality.

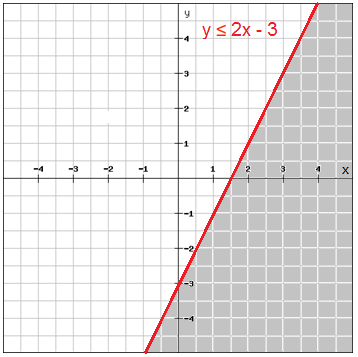
The solution region which is the intersection of the half-planes is shown in a darker shade

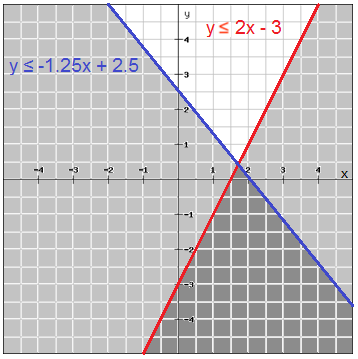
Usually only the solution region is shaded which makes it easier to see which region is the solution region

Video lesson

$$\\\left\{\begin{matrix} x > 3 \\ y \leq -x + 2 \end{matrix}\right.\\​$$

• Properties of exponents
• Scientific notation
• Exponential growth functions
• Monomials and polynomials
• Special products of polynomials
• Polynomial equations in factored form
• Use graphing to solve quadratic equations
• Completing the square
• The quadratic formula
• The graph of a radical function
• Simplify radical expressions
• Radical equations
• The Pythagorean Theorem
• The distance and midpoint formulas
• Simplify rational expression
• Multiply rational expressions
• Division of polynomials
• Add and subtract rational expressions
• Solving rational equations
• Algebra 2 Overview
• Geometry Overview
• SAT Overview
• ACT Overview

• Math Lessons
• For Teachers

Other Resources SAT Prep Blog

Support us merch donate.

• Other Resources

QUICK LINKS

Systems of linear inequalities calculator.

Introduction

Key Steps: How to Solve a System of Linear Inequalities

Solving Systems of Linear Inequalities

Practice: Solving Systems of Linear Inequalities

Back to all math lessons

We can solve a system of linear inequalities by graphing each inequality and identifying where the shaded areas overlap.

If we imagine that the shaded area for each inequality represents safety from a specific monster, then the space where all the shaded areas overlap represents the area we’re completely safe and contains the solutions to the system of inequalities .

Remember, a solid line means the boundary is also safe , and a dotted line means the boundary is not safe .

How do we check if a point is a solution to a system of linear inequalities?

We can plug in the x ​ and y ​ values of the point into each linear inequality and simplify.

If all of the inequalities simplify to a true statement, then the point is a solution.

If one or more of the inequalities simplify to a false statement, then the point is not a solution.

You can also use the Quick Links menu on the left to jump to a section of your choice.

You can also use the Quick Links dropdown above to jump to a section of your choice.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• y>2x,\:y<-x-3
• y\ge x,\:y>-x+1,\:y<11
• x+3>5,\:2x-1>11,\:y\le-\frac{4}{3}x-2,\:y>-\frac{1}{3}x+1
• y\ge 2x,\:y\le 2x
• y\ge 2x,\:y\le 2x,\:x<4
• y\ge 2x,\:y\le 2x,\:x\le 4,\:x\ge4

system-of-inequalities-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.

Systems of Linear Inequalities, Word Problems - Examples - Expii

Systems of linear inequalities, word problems - examples, explanations (3), word problems with systems of linear inequalities.

Solving word problems with systems of linear inequalities involves 2 steps:

Translate the word problem into mathematical expressions. We're finding a system of linear inequalities .

Solve! One strategy you can use to find solutions is to graph each inequality . Then, use the overlapping areas of the graphs to identify the solutions to the word problem.

Let's look at an example:

Image source: by Hannah Bonville

STEP 1: Translate the word problem into inequalities.

We're going to use x for the number of pizzas and y for the number of pounds of cookies.

Which inequality represents the number of pizzas Pilar needs?

Related Lessons

Systems of Linear Inequalities: Word Problems

When you are presented with a word problem that deals with inequalities, it may seem daunting at first to solve the problem. The good news is that there are two simple steps to follow in order to solve systems of linear inequalities!

Image source: by Anusha Rahman

Let's walk through an example problem together.

Jenn and John want to go on a road trip together. Jenn drives an average of 50mph, and John drives an average of 45mph. They want to drive less than 20 hours, but at least 500 miles. Write a system of linear inequalities to figure out how many miles John and Jenn must drive to make that happen.

Step 1: Translate the word problem into inequalities.

Let's start with establishing our variables. x=Jenn y=John

We know that Jenn and John want to drive at least 500 miles. At least generally means greater than or equal to . So if we incorporate the speed at which the two of them drive, we can say that:

50x+45y≥500

We also know that, combined, John and Jenn want to drive less than 20 hours. So, we can say that: x+y=20

Therefore, our system of linear equations is:

50x+45y≥500 x+y=20

Step 2: Solve the inequalities.

Let's solve these inequalities by graphing. Here is a graph of the two inequalities.

Made using Desmos

50x+45y≥500 is represented by the red shading. x+y=20 is represented by the blue shading. The overlap, or the solution, is represented by the purple shading.

(Video) Solving Inequalities: Word Problems

by Anusha Rahman

This video by Anusha Rahman walks you through an example word problem of how to solve a system of inequalities.

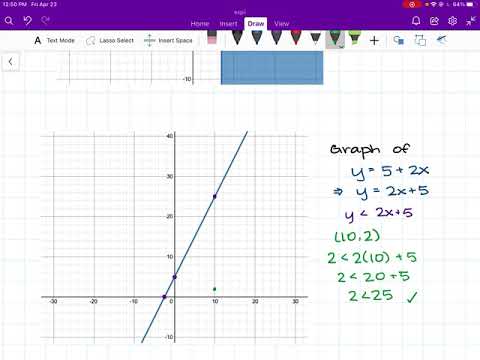
Example: Jackson is having a party for his friends on Saturday. Jackson expects at least 7 people to show up on Saturday. He is trying to figure out the total costs of all of the pizzas. He calls his local pizza place, Meredith’s pizza, who says that the cost of his pizzas will be less than 5 more than 2 times the number of people he needs pizza for.

Step 1: Establish variables x=the number of people y=the cost of all pizzas

Step 2: Set up the inequalities x≥7 y<5+2x

Step 3: Graph the inequalities to find the solution

Graph of: x≥7

Graph of y=5+2x

This is the graph of the line, y=5+2x. In order to graph the inequality, y<5+2x, we have to figure out what area on the graph to shade. To do that, we test out some points and see whether the inequality remains true!

Let's test the point (10,2). 2<2(10)+5 2<20+5 2<25 This statement is true ! So we will probably shade in this area, the bottom area of the graph. But, let's just check one more point to make sure.

Let's test the point (−10,2). 2<2(−10)+5 2<−20+5 2<−15 This statement is false .

So, we can see in the above graph that the area under the dotted line is shaded. This is the graph of y<5+2x.

Now, let's put both inequalities on the same graph to see the area of intersection!

The area shaded in purple is the solution to the system of inequalities! Because Jackson probably won't have negative friends or pay negative dollars, we can assume 0">x>0 and 0">y>0.

Jackson won’t know for certain what the price of his pizzas will be. Why? Because Jackson doesn’t know how many of his friends will be coming to his party. Especially when solving real-world problems, a system of inequalities is really helpful when we’re looking at something in the future, and we don’t have exact numbers, but we have a general idea, like Jackson does.

Online Systems of Equations Solver

Solve equations and systems of equations with wolfram|alpha, a powerful tool for finding solutions to systems of equations and constraints.

Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.

Learn more about:

• Systems of equations

Tips for entering queries

Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.

• solve y = 2x, y = x + 10
• solve system of equations {y = 2x, y = x + 10, 2x = 5y}
• y = x^2 - 2, y = 2 - x^2
• solve 4x - 3y + z = -10, 2x + y + 3z = 0, -x + 2y - 5z = 17
• solve system {x + 2y - z = 4, 2x + y + z = -2, z + 2y + z = 2}
• solve 4 = x^2 + y^2, 4 = (x - 2)^2 + (y - 2)^2
• x^2 + y^2 = 4, y = x
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

• Step-by-step solutions
• Wolfram Problem Generator

What are systems of equations?

A system of equations is a set of one or more equations involving a number of variables..

The solutions to systems of equations are the variable mappings such that all component equations are satisfied—in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.

Systems of linear equations are a common and applicable subset of systems of equations. In the case of two variables, these systems can be thought of as lines drawn in two-dimensional space. If all lines converge to a common point, the system is said to be consistent and has a solution at this point of intersection. The system is said to be inconsistent otherwise, having no solutions. Systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).

More general systems involving nonlinear functions are possible as well. These possess more complicated solution sets involving one, zero, infinite or any number of solutions, but work similarly to linear systems in that their solutions are the points satisfying all equations involved. Going further, more general systems of constraints are possible, such as ones that involve inequalities or have requirements that certain variables be integers.

Solving systems of equations is a very general and important idea, and one that is fundamental in many areas of mathematics, engineering and science.

Grade 8 Mathematics Module: “Solving Systems of Linear Inequalities in Two Variables”

This Self-Learning Module (SLM) is prepared so that you, our dear learners, can continue your studies and learn while at home. Activities, questions, directions, exercises, and discussions are carefully stated for you to understand each lesson.

Each SLM is composed of different parts. Each part shall guide you step-by-step as you discover and understand the lesson prepared for you.

Pre-tests are provided to measure your prior knowledge on lessons in each SLM. This will tell you if you need to proceed on completing this module or if you need to ask your facilitator or your teacher’s assistance for better understanding of the lesson. At the end of each module, you need to answer the post-test to self-check your learning. Answer keys are provided for each activity and test. We trust that you will be honest in using these.

Please use this module with care. Do not put unnecessary marks on any part of this SLM. Use a separate sheet of paper in answering the exercises and tests. And read the instructions carefully before performing each task.

If you have any questions in using this SLM or any difficulty in answering the tasks in this module, do not hesitate to consult your teacher or facilitator.

In this module, you will be acquainted with the application of systems of linear inequalities in two variables in solving problems related to real-life. The scope of this module enables you to use it in many different learning situations. The lesson is arranged following the standard sequence of the course. But the order in which you read them can be changed corresponding with the textbook you are now using.

This module is divided into two lessons:

• Lesson 1- Graphing Systems of Linear Inequalities in Two Variables
• Lesson 2– Solving Problems Involving Systems of Linear Inequalities in Two Variables

After going through this module, you are expected to:

1. define systems of linear inequalities in two variables;

2. graph systems of linear inequalities in two variables; and

3. solve problems involving systems of linear inequalities in two variables.

Grade 8 Mathematics Quarter 2 Self-Learning Module: “Solving Systems of Linear Inequalities in Two Variables”

Can't find what you're looking for.

We are here to help - please use the search box below.

Leave a Comment Cancel reply

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 7

• Intro to graphing two-variable inequalities
• Graphing two-variable inequalities
• Graphs of inequalities
• Two-variable inequalities from their graphs
• Intro to graphing systems of inequalities

Graphing systems of inequalities

• Systems of inequalities graphs
• Graphing inequalities (x-y plane) review

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• School Guide
• Class 11 Syllabus
• Class 11 Revision Notes
• Maths Notes Class 11
• Physics Notes Class 11
• Chemistry Notes Class 11
• Biology Notes Class 11
• NCERT Solutions Class 11 Maths
• RD Sharma Solutions Class 11
• Math Formulas Class 11
• CBSE Class 11 Maths Notes

Chapter 1: Sets

• Representation of a Set
• Types Of Sets
• Universal Sets
• Venn Diagram
• Operations on Sets
• Union of Sets

Chapter 2: Relations & Functions

• Cartesian Product of Sets
• Relation and Function
• Introduction to Domain and Range
• Piecewise Function
• Range of a Function

Chapter 3: Trigonometric Functions

• Measuring Angles
• Trigonometric Functions
• Trigonometric Functions of Sum and Difference of Two Angles

Chapter 4: Principle of Mathematical Induction

• Principle of Mathematical Induction

Chapter 5: Complex Numbers and Quadratic Equations

• Complex Numbers
• Algebra of Real Functions
• Algebraic Operations on Complex Numbers | Class 11 Maths
• Polar Representation of Complex Numbers
• Absolute Value of a Complex Number
• Conjugate of Complex Numbers
• Imaginary Numbers

Chapter 6: Linear Inequalities

• Compound Inequalities
• Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation - Linear Inequalities | Class 11 Maths
• Graphical Solution of Linear Inequalities in Two Variables

Solving Linear Inequalities Word Problems

Chapter 7: permutations and combinations.

• Fundamental Principle of Counting
• Permutation
• Combinations

Chapter 8: Binomial Theorem

• Binomial Theorem
• Pascal's Triangle

Chapter 9: Sequences and Series

• Sequences and Series
• General and Middle Terms - Binomial Theorem - Class 11 Maths
• Arithmetic Series
• Arithmetic Sequence
• Geometric Progression (GP) | Formula and Properties
• Geometric Series
• Arithmetic Progression and Geometric Progression
• Special Series - Sequences and Series | Class 11 Maths

Chapter 10: Straight Lines

• Slope of a Line
• Introduction to Two-Variable Linear Equations in Straight Lines
• Forms of Two-Variable Linear Equations - Straight Lines | Class 11 Maths
• Point-slope Form - Straight Lines | Class 11 Maths
• Slope Intercept Form
• Writing Slope-Intercept Equations
• Standard Form of a Straight Line
• X and Y Intercept
• Graphing slope-intercept equations - Straight Lines | Class 11 Maths

Chapter 11: Conic Sections

• Conic Sections
• Equation of a Circle
• Focus and Directrix of a Parabola
• Identifying Conic Sections from their Equation

Chapter 12: Introduction to Three-dimensional Geometry

• Coordinate Axes and Coordinate planes in 3D space
• 3D Distance Formula

Chapter 13: Limits and Derivatives

• Formal Definition of Limits
• Strategy in Finding Limits
• Determining Limits using Algebraic Manipulation
• Limits of Trigonometric Functions
• Properties of Limits
• Limits by Direct Substitution
• Estimating Limits from Graphs
• Estimating Limits from Tables
• Sandwich Theorem
• Average and Instantaneous Rate of Change
• Algebra of Derivative of Functions
• Product Rule in Derivatives
• Quotient Rule | Formula, Proof and Examples
• Derivatives of Polynomial Functions
• Application of Derivatives
• Applications of Power Rule

Chapter 14: Mathematical Reasoning

• Statements - Mathematical Reasoning
• Conditional Statements & Implications - Mathematical Reasoning | Class 11 Maths

Chapter 15: Statistics

• Measures of spread - Range, Variance, and Standard Deviation
• Mean Absolute Deviation
• Measures of Central Tendency in Statistics
• Difference Between Mean, Median, and Mode with Examples
• Frequency Distribution
• Variance and Standard Deviation

Chapter 16: Probability

• Random Experiment - Probability
• Types of Events in Probability
• Events in Probability
• Axiomatic Approach to Probability
• Measures of Dispersion | Types, Formula and Examples
• CBSE Class 11 Maths Formulas
• NCERT Solutions for Class 11 Maths - Chapter Wise PDF
• RD Sharma Class 11 Solutions for Maths

We are well versed with equations in multiple variables. Linear Equations represent a point in a single dimension, a line in a two-dimensional, and a plane in a three-dimensional world. Solutions to linear inequalities represent a region of the Cartesian plane. It becomes essential for us to know how to translate real-life problems into linear inequalities. 

Linear Inequalities 

Before defining the linear inequalities formally, let’s see them through a real-life situation and observe why their need arises in the first place. Let’s say Albert went to buy some novels for himself at the book fair. He has a total of Rs 200 with him. The book fair has a special sale policy which offers any book at Rs 70. Now he knows that he may not be able to spend the full amount on the books. Let’s say x is the number of books he bought. This situation can be represented mathematically by the following equation, 

70x < 200

Since he can’t spend all the amount on books, and also the amount spent by him will always be less than Rs 200. The present situation can only be represented by the equation given above. Now let’s study the linear inequalities with a formal description, 

Two real numbers or two algebraic expressions which are related by symbols such as ‘>’, ‘<‘, ‘≥’ and’≤’ form the inequalities. Linear inequalities are formed by linear equations which are connected with these symbols. These inequalities can be further classified into two parts:  Strict Inequalities: The inequalities with the symbols such as ‘>’ or ‘<‘. Slack Inequalities: The inequalities with the symbols such as ‘≥’ or ‘≤’.

Rules of Solving Linear Inequalities:

There are certain rules which we should keep in mind while solving linear inequalities. 

• Equal numbers can be added or subtracted from both sides of the inequality without affecting its sign.
• Both sides of Inequality can be divided or multiplied by any positive number but when they are multiplied or divided by a negative number, the sign of the linear inequality is reversed.

Now with this brief introduction to linear inequalities, let’s see some word problems on this concept. 

Sample Problems

Question 1: Considering the problem given in the beginning. Albert went to buy some novels for himself at the book fair. He has a total of Rs 200 with him. The book fair has a special sale policy which offers any book at Rs 70. Now he knows that he may not be able to spend the full amount on the books. Let’s say x is the number of books he bought. Represent this situation mathematically and graphically. 

Solution: 

We know that Albert cannot buy books for all the money he has. So, let’s say the number of books he buys is “x”. Then,  70x < 200 ⇒ x <  To plot the graph of this inequality, put x = 0.  0 <   Thus, x = 0 satisfies the inequality. So, the graph for the following inequality will look like, 

Question 2: Consider the performance of the strikers of the football club Real Madrid in the last 3 matches. Ronaldo and Benzema together scored less than 9 goals in the last three matches. It is also known that Ronaldo scored three more goals than Benzema. What can be the possible number of goals Ronaldo scored? 

Let’s say the number of goals scored by Benzema and Ronaldo are y and x respectively.  x = y + 3 …..(1) x + y < 9  …..(2)  Substituting the value of x from equation (1) in equation (2).  y + 3 + y < 9  ⇒2y  < 6  ⇒y < 3 Possible values of y: 0,1,2  Possible values of x: 3,4,5

Question 3: A classroom can fit at least 9 tables with an area of a one-meter square. We know that the perimeter of the classroom is 12m. Find the bounds on the length and breadth of the classroom. 

It can fit 9 tables, that means the area of the classroom is atleast 9m 2 . Let’s say the length of the classroom is x and breadth is y meters.  2(x + y) = 12 {Perimeter of the classroom} ⇒ x + y = 6  Area of the rectangle is given by,  xy > 9  ⇒x(6 – x) > 9  ⇒6x – x 2 > 9  ⇒ 0 > x 2 – 6x + 9  ⇒ 0 > (x – 3) 2 ⇒ 0 > x – 3  ⇒ x < 3  Thus, length of the classroom must be less than 3 m.  So, then the breadth of the classroom will be greater than 3 m. 

Question 4: Formulate the linear inequality for the following situation and plot its graph. 

Let’s say Aman and Akhil went to a stationery shop. Aman bought 3 notebooks and Akhil bought 4 books. Let’s say cost of each notebook was “x” and each book was “y”. The total expenditure was less than Rs 500. 

Cost of each notebook was “x” and for each book, it was “y”. Then the inequality can be described as, 3x + 4y < 500 Putting (x,y) → (0,0)  3(0) + 4(0) < 500 Origin satisfies the inequality. Thus, the graph of its solutions will look like, x.

Question 5: Formulate the linear inequality for the following situation and plot its graph. 

A music store sells its guitars at five times their cost price. Find the shopkeeper’s minimum cost price if his profit is more than Rs 3000. 

Let’s say the selling price of the guitar is y, and the cost price is x. y – x > 3000 ….(1) It is also given that,  y = 5x ….(2)  Substituting the value of y from equation (2) to equation (1).  5x – x > 3000  ⇒ 4x > 3000  ⇒  x >  ⇒ x> 750  Thus, the cost price must be greater than Rs 750. 

Question 6: The length of the rectangle is 4 times its breadth. The perimeter of the rectangle is less than 20. Formulate a linear inequality in two variables for the given situation, plot its graph and calculate the bounds for both length and breadth. 

Let’s say the length is “x” and breadth is “y”.  Perimeter = 2(x + y) < 20 ….(1) ⇒ x + y < 10  Given : x = 4y  Substituting the value of x in equation (1).  x + y < 10 ⇒ 5y < 10  ⇒ y < 2 So, x < 8 and y < 2. 

Question 7: Rahul and Rinkesh play in the same football team. In the previous game, Rahul scored 2 more goals than Rinkesh, but together they scored less than 8 goals. Solve the linear inequality and plot this on a graph.

The equations obtained from the given information in the question, Suppose Rahul scored x Number of goals and Rinkesh scored y number of goals, Equations obtained will be, x = y+2 ⇢ (1) x+y< 8 ⇢ (2) Solving both the equations, y+2 + y < 8 2y < 6 y< 3 Putting this value in equation (2), x< 5

Question 8: In a class of 100 students, there are more girls than boys, Can it be concluded that how many girls would be there?

Let’s suppose that B is denoted for boys and G is denoted for girls. Now, since Girls present in the class are more than boys, it can be written in equation form as, G > B  The total number of students present in class is 100 (given), It can be written as, G+ B= 100 B = 100- G Substitute G> B in the equation formed, G> 100 – G 2G > 100 G> 50 Hence, it is fixed that the number of girls has to be more than 50 in class, it can be 60, 65, etc. Basically any number greater than 50 and less than 100.

Question 9: In the previous question, is it possible for the number of girls to be exactly 50 or exactly 100? If No, then why?

No, It is not possible for the Number of girls to be exactly 50 since while solving, it was obtained that, G> 50  In any case if G= 50 is a possibility, from equation G+ B= 100, B = 50 will be obtained. This simply means that the number of boys is equal to the number of girls which contradicts to what is given in the question. No, it is not possible for G to be exactly 100 as well, as this proves that there are 0 boys in the class.

Question 10: Solve the linear inequality and plot the graph for the same,

7x+ 8y < 30

The linear inequality is given as, 7x+ 8y< 30  At x= 0, y= 30/8= 3.75 At y= 0, x= 30/7= 4.28 These values are the intercepts. The graph for the above shall look like,  Putting x= y/2, that is, y= 2x in the linear inequality, 7x + 16x < 30 x = 1.304 y = 2.609

Please Login to comment...

Similar reads.

• Linear Equations
• Mathematics
• School Learning
• 10 Ways to Use Slack for Effective Communication
• 10 Ways to Use Google Docs for Collaborative Writing
• NEET MDS 2024 Result: Toppers List, Category-wise Cutoff, and Important Dates
• NDA Admit Card 2024 Live Updates: Download Your Hall Ticket Soon on upsc.gov.in!
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Skip to primary navigation
• Skip to main content
• Skip to primary sidebar

Teaching Expertise

• Classroom Ideas
• Teacher’s Life
• Deals & Shopping
• Privacy Policy

14 Solving Inequalities Low-Tech Activities

December 9, 2022 //  by  Lauren Jannette

With numbers, symbols, and letters combined, inequalities can be a difficult math concept for students to understand. Help them visualize these equations with fun and engaging activities like graphs, charts, puzzles, and bingo! We’ve got activities catering to every student’s learning level and needs. Create a strong foundation in math by providing your students with flexible options for practicing their math skills. Ready, set, solve those equations!

1. Linear Inequalities Hangman

Turn hangman into math man ! This wonderful activity is great for independent practice. Students need to solve the inequalities to uncover the letters that create a word. Have them show their work on a separate sheet of paper so you can check for errors as they go.

Learn more: The Best of Teacher Entrepreneurs

2. Sorting Types of Inequalities

This organizational game is a great addition to your math classroom! Have students sort the cards into different groups. Then discuss what inequality means. After, introduce the symbol cards and have students re-sort their original cards into the new categories. Great for discussions on equality and inequality in other subjects too! 

Learn more: Teaching in an Organized Mess

3. Inequalities Anchor Chart

From time to time students need help remembering what math symbols mean. Work together to create this anchor chart for your math class. As you create it, discuss the difference between equations and when you would use them. The end result is a great, year-round resource for students to refer to!

Learn more: Joanna Gillen

4. Inequality Bingo

Who doesn’t love bingo? It’s the perfect way to get students excited about single-variable inequalities or multi-step inequalities. Simply create equations for the answer key. Then, give students the equation to solve and see if they can mark off a square!

Learn more: Everybody is a Genius

5. One-Step Inequalities

Graphing inequalities is an awesome way to help kids visualize math problems. This simple worksheet is perfect for one-step inequalities. Students solve the equation, then plot it on the graph. It’s perfect for a beginner inequalities lesson.

Learn more: Math Worksheets 4 Kids

6. Decoding Inequalities

Have students practice their decoding skills with inequalities! For each correct inequality answer, students earn a letter to help solve the mystery! You can use this activity in class or create a digital version to add to a digital math escape room! 

Learn more: Staley Algebra

7. Graphing Linear Inequalities

Creating a graph with inequalities is the perfect way to help students visualize math problems. Help them create this study guide by going through one-step, and then two-step, inequalities. This makes a fantastic resource that students can refer to all year long!

Learn more: Mathdyal

8. Truth and Lies

Discover the “truth” with these multi-step equations. Pair off your students and have them solve the solution sets to find the “lie”. Add a lesson on writing skills by having students explain why they chose the solution set they did. What’s great is that this activity is easily adaptable to a digital format!

Learn more: Mrs. Newell’s Math

9. Inequality Memory Game

Cut out and give your students a set of paper task cards containing inequalities and another with the solutions. Have them solve the equations and then glue the answer to the back of the problem set. Once they finish, get learners to match them to the correct points on a linear graph.

Learn more: Mrs. White’s 6th Grade Math

10. Compound Inequalities

This worksheet is designed to help students understand inequalities and number lines. Students solve the equations in white and then pair them with the answers and corresponding number lines. Pair students off for a partner practice activity.

Learn more: Chess Museum Template Library

11. Number Lines

Get back to basics! Number lines are a fantastic resource for understanding inequalities, whole numbers, and prime numbers. This answer key displays a variety of equations and math problems for students to solve. Simply erase the answers and let your students try them out!

Learn more: Cazoom Maths

12. Math Teacher Resource

Having a go-to presentation is a great resource for your math classroom! These easy-to-follow slides are perfect for students and are great for leading them through multi-step inequalities! Be sure to make time for students to ask questions.

Learn more: Made by Teachers

13. One-Step Inequalities Wheel

Give your students this handy visual study guide. The foldable sections reveal examples of each type of inequality. Leave the bottom circle blank so your students can add their own examples!

Learn more: Math in Demand

14. Inequality Puzzle Activity

Put your students into small groups and let them get their puzzles on! Each puzzle has an inequality, solution, number line, and word problem. Together,  students work to complete the puzzles. The first team to finish the set wins!

Help | Advanced Search

Mathematics > Optimization and Control

Title: convex reformulation of lmi-based distributed controller design with a class of non-block-diagonal lyapunov functions.

Abstract: This study addresses a distributed state feedback controller design problem for continuous-time linear time-invariant systems by means of linear matrix inequalities (LMI). As the exact convexification is still open, the block-diagonal relaxation of Lyapunov functions has been prevalent despite its conservatism. In this work, we target a class of non-block-diagonal Lyapunov functions that has the same sparsity as distributed controllers. By leveraging a block-diagonal factorization of sparse matrices and Finsler's lemma, we first present a (nonlinear) matrix inequality for stabilizing distributed controllers with such Lyapunov functions, which boils down to a necessary and sufficient condition for such controllers if the sparsity pattern is chordal. As a relaxation of the inequality, we derive an LMI that completely covers the conventional relaxation and then provide analogous results for $H_\infty$ control. Lastly, numerical examples underscore the efficacy of our results.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .