word problems math linear equations

Word Problems Linear Equations

Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?

\(\textbf{1)}\) Joe and Steve are saving money. Joe starts with $105 and saves $5 per week. Steve starts with $5 and saves $15 per week. After how many weeks do they have the same amount of money? Show Equations \(y= 5x+105,\,\,\,y=15x+5\) Show Answer 10 weeks ($155)

\(\textbf{2)}\) mike and sarah collect rocks. together they collected 50 rocks. mike collected 10 more rocks than sarah. how many rocks did each of them collect show equations \(m+s=50,\,\,\,m=s+10\) show answer mike collected 30 rocks, sarah collected 20 rocks., \(\textbf{3)}\) in a classroom the ratio of boys to girls is 2:3. there are 25 students in the class. how many are girls show equations \(b+g=50,\,\,\,3b=2g\) show answer 15 girls (10 boys), \(\textbf{4)}\) kyle makes sandals at home. the sandal making tools cost $100 and he spends $10 on materials for each sandal. he sells each sandal for $30. how many sandals does he have to sell to break even show equations \(c=10x+100,\,\,\,r=30x\) show answer 5 sandals ($150), \(\textbf{5)}\) molly is throwing a beach party. she still needs to buy beach towels and beach balls. towels are $3 each and beachballs are $4 each. she bought 10 items in total and it cost $34. how many beach balls did she get show equations show answer 4 beachballs (6 towels), \(\textbf{6)}\) anna volunteers at a pet shelter. they have cats and dogs. there are 36 pets in total at the shelter, and the ratio of dogs to cats is 4:5. how many cats are at the shelter show equations \(c+d=40,\,\,\,5d=4c\) show answer 20 cats (16 dogs), \(\textbf{7)}\) a store sells oranges and apples. oranges cost $1.00 each and apples cost $2.00 each. in the first sale of the day, 15 fruits were sold in total, and the price was $25. how many of each type of frust was sold show equations \(o+a=15,\,\,\,1o+2a=25\) show answer 10 apples and 5 oranges, \(\textbf{8)}\) the ratio of red marbles to green marbles is 2:7. there are 36 marbles in total. how many are red show equations \(r+g=36,\,\,\,7r=2g\) show answer 8 red marbles (28 green marbles), \(\textbf{9)}\) a tennis club charges $100 to join the club and $10 for every hour using the courts. write an equation to express the cost \(c\) in terms of \(h\) hours playing tennis. show equation the equation is \(c=10h+100\), \(\textbf{10)}\) emma and liam are saving money. emma starts with $80 and saves $10 per week. liam starts with $120 and saves $6 per week. after how many weeks will they have the same amount of money show equations \(e = 10x + 80,\,\,\,l = 6x + 120\) show answer 10 weeks ($180 each), \(\textbf{11)}\) mark and lisa collect stamps. together they collected 200 stamps. mark collected 40 more stamps than lisa. how many stamps did each of them collect show equations \(m + l = 200,\,\,\,m = l + 40\) show answer mark collected 120 stamps, lisa collected 80 stamps., \(\textbf{12)}\) in a classroom, the ratio of boys to girls is 3:5. there are 40 students in the class. how many are boys show equations \(b + g = 40,\,\,\,5b = 3g\) show answer 15 boys (25 girls), \(\textbf{13)}\) lisa is selling handmade jewelry. the materials cost $60, and she sells each piece for $20. how many pieces does she have to sell to break even show equations \(c=60,\,\,\,r=20x\) show answer 3 pieces, \(\textbf{14)}\) tom is buying books and notebooks for school. books cost $15 each, and notebooks cost $3 each. he bought 12 items in total, and it cost $120. how many notebooks did he buy show equations \(b + n = 12,\,\,\,15b+3n=120\) show answer 5 notebooks (7 books), \(\textbf{15)}\) emily volunteers at an animal shelter. they have rabbits and guinea pigs. there are 36 animals in total at the shelter, and the ratio of guinea pigs to rabbits is 4:5. how many guinea pigs are at the shelter show equations \(r + g = 36,\,\,\,5g=4r\) show answer 16 guinea pigs (20 rabbits), \(\textbf{16)}\) mike and sarah are going to a theme park. mike’s ticket costs $40, and sarah’s ticket costs $30. they also bought $20 worth of food. how much did they spend in total show equations \(m + s + f = t,\,\,\,m=40,\,\,\,s=30,\,\,\,f=20\) show answer they spent $90 in total., \(\textbf{17)}\) the ratio of red marbles to blue marbles is 2:3. there are 50 marbles in total. how many are blue show equations \(r + b = 50,\,\,\,3r=2b\) show answer 30 blue marbles (20 red marbles), \(\textbf{18)}\) a pizza restaurant charges $12 for a large pizza and $8 for a small pizza. if a customer buys 5 pizzas in total, and it costs $52, how many large pizzas did they buy show equations \(l + s = 5,\,\,\,12l+8s=52\) show answer they bought 3 large pizzas (2 small pizzas)., \(\textbf{19)}\) the area of a rectangle is 48 square meters. if the length is 8 meters, what is the width of the rectangle show equations \(a=l\times w,\,\,\,l=8,\,\,\,a=48\) show answer the width is 6 meters., \(\textbf{20)}\) two numbers have a sum of 50. one number is 10 more than the other. what are the two numbers show equations \(x+y=50,\,\,\,x=y+10\) show answer the numbers are 30 and 20., \(\textbf{21)}\) a store sells jeans for $40 each and t-shirts for $20 each. in the first sale of the day, they sold 8 items in total, and the price was $260. how many of each type of item was sold show equations \(j+t=8,\,\,\,40j+20t=260\) show answer 5 jeans and 3 t-shirts were sold., \(\textbf{22)}\) the ratio of apples to carrots is 3:4. there are 28 fruits in total. how many are apples show equations \(\)a+c=28,\,\,\,4a=3c show answer there are 12 apples and 16 carrots., \(\textbf{23)}\) a phone plan costs $30 per month, and there is an additional charge of $0.10 per minute for calls. write an equation to express the cost \(c\) in terms of \(m\) minutes. show equation the equation is \(\)c=30+0.10m, \(\textbf{24)}\) a triangle has a base of 8 inches and a height of 6 inches. calculate its area. show equations \(a=0.5\times b\times h,\,\,\,b=8,\,\,\,h=6\) show answer the area is 24 square inches., \(\textbf{25)}\) a store sells shirts for $25 each and pants for $45 each. in the first sale of the day, 4 items were sold, and the price was $180. how many of each type of item was sold show equations \(t+p=4,\,\,\,25t+45p=180\) show answer 0 shirts and 4 pants were sold., \(\textbf{26)}\) a garden has a length of 12 feet and a width of 10 feet. calculate its area. show equations \(a=l\times w,\,\,\,l=12,\,\,\,w=10\) show answer the area is 120 square feet., \(\textbf{27)}\) the sum of two consecutive odd numbers is 56. what are the two numbers show equations \(x+y=56,\,\,\,x=y+2\) show answer the numbers are 27 and 29., \(\textbf{28)}\) a toy store sells action figures for $15 each and toy cars for $5 each. in the first sale of the day, 10 items were sold, and the price was $110. how many of each type of item was sold show equations \(a+c=10,\,\,\,15a+5c=110\) show answer 6 action figures and 4 toy cars were sold., \(\textbf{29)}\) a bakery sells pie for $2 each and cookies for $1 each. in the first sale of the day, 14 items were sold, and the price was $25. how many of each type of item was sold show equations \(p+c=14,\,\,\,2p+c=25\) show answer 11 pies and 3 cookies were sold., \(\textbf{for 30-33}\) two car rental companies charge the following values for x miles. car rental a: \(y=3x+150 \,\,\) car rental b: \(y=4x+100\), \(\textbf{30)}\) which rental company has a higher initial fee show answer company a has a higher initial fee, \(\textbf{31)}\) which rental company has a higher mileage fee show answer company b has a higher mileage fee, \(\textbf{32)}\) for how many driven miles is the cost of the two companies the same show answer the companies cost the same if you drive 50 miles., \(\textbf{33)}\) what does the \(3\) mean in the equation for company a show answer for company a, the cost increases by $3 per mile driven., \(\textbf{34)}\) what does the \(100\) mean in the equation for company b show answer for company b, the initial cost (0 miles driven) is $100., \(\textbf{for 35-39}\) andy is going to go for a drive. the formula below tells how many gallons of gas he has in his car after m miles. \(g=12-\frac{m}{18}\), \(\textbf{35)}\) what does the \(12\) in the equation represent show answer andy has \(12\) gallons in his car when he starts his drive., \(\textbf{36)}\) what does the \(18\) in the equation represent show answer it takes \(18\) miles to use up \(1\) gallon of gas., \(\textbf{37)}\) how many miles until he runs out of gas show answer the answer is \(216\) miles, \(\textbf{38)}\) how many gallons of gas does he have after 90 miles show answer the answer is \(7\) gallons, \(\textbf{39)}\) when he has \(3\) gallons remaining, how far has he driven show answer the answer is \(162\) miles, \(\textbf{for 40-42}\) joe sells paintings. each month he makes no commission on the first $5,000 he sells but then makes a 10% commission on the rest., \(\textbf{40)}\) find the equation of how much money x joe needs to sell to earn y dollars per month. show answer the answer is \(y=.1(x-5,000)\), \(\textbf{41)}\) how much does joe need to sell to earn $10,000 in a month. show answer the answer is \($105,000\), \(\textbf{42)}\) how much does joe earn if he sells $45,000 in a month show answer the answer is \($4,000\), see related pages\(\), \(\bullet\text{ word problems- linear equations}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- averages}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- consecutive integers}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- distance, rate and time}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- break even}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- ratios}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- age}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- mixtures and concentration}\) \(\,\,\,\,\,\,\,\,\), linear equations are a type of equation that has a linear relationship between two variables, and they can often be used to solve word problems. in order to solve a word problem involving a linear equation, you will need to identify the variables in the problem and determine the relationship between them. this usually involves setting up an equation (or equations) using the given information and then solving for the unknown variables . linear equations are commonly used in real-life situations to model and analyze relationships between different quantities. for example, you might use a linear equation to model the relationship between the cost of a product and the number of units sold, or the relationship between the distance traveled and the time it takes to travel that distance. linear equations are typically covered in a high school algebra class. these types of problems can be challenging for students who are new to algebra, but they are an important foundation for more advanced math concepts. one common mistake that students make when solving word problems involving linear equations is failing to set up the problem correctly. it’s important to carefully read the problem and identify all of the relevant information, as well as any given equations or formulas that you might need to use. other related topics involving linear equations include graphing and solving systems. understanding linear equations is also useful for applications in fields such as economics, engineering, and physics., about andymath.com, andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. if you have any requests for additional content, please contact andy at [email protected] . he will promptly add the content. topics cover elementary math , middle school , algebra , geometry , algebra 2/pre-calculus/trig , calculus and probability/statistics . in the future, i hope to add physics and linear algebra content. visit me on youtube , tiktok , instagram and facebook . andymath content has a unique approach to presenting mathematics. the clear explanations, strong visuals mixed with dry humor regularly get millions of views. we are open to collaborations of all types, please contact andy at [email protected] for all enquiries. to offer financial support, visit my patreon page. let’s help students understand the math way of thinking thank you for visiting. how exciting.

Word Problems on Linear Equations

Worked-out word problems on linear equations with solutions explained step-by-step in different types of examples.

There are several problems which involve relations among known and unknown numbers and can be put in the form of equations. The equations are generally stated in words and it is for this reason we refer to these problems as word problems. With the help of equations in one variable, we have already practiced equations to solve some real life problems.

Steps involved in solving a linear equation word problem: ● Read the problem carefully and note what is given and what is required and what is given. ● Denote the unknown by the variables as x, y, ……. ● Translate the problem to the language of mathematics or mathematical statements. ● Form the linear equation in one variable using the conditions given in the problems. ● Solve the equation for the unknown. ● Verify to be sure whether the answer satisfies the conditions of the problem.

Step-by-step application of linear equations to solve practical word problems:

1. The sum of two numbers is 25. One of the numbers exceeds the other by 9. Find the numbers. 

Solution: Then the other number = x + 9 Let the number be x.  Sum of two numbers = 25 According to question, x + x + 9 = 25 ⇒ 2x + 9 = 25 ⇒ 2x = 25 - 9 (transposing 9 to the R.H.S changes to -9)  ⇒ 2x = 16 ⇒ 2x/2 = 16/2 (divide by 2 on both the sides)  ⇒ x = 8 Therefore, x + 9 = 8 + 9 = 17 Therefore, the two numbers are 8 and 17.

2.The difference between the two numbers is 48. The ratio of the two numbers is 7:3. What are the two numbers?  Solution:   Let the common ratio be x.  Let the common ratio be x.  Their difference = 48 According to the question,  7x - 3x = 48  ⇒ 4x = 48  ⇒ x = 48/4  ⇒ x = 12 Therefore, 7x = 7 × 12 = 84           3x = 3 × 12 = 36  Therefore, the two numbers are 84 and 36.

3. The length of a rectangle is twice its breadth. If the perimeter is 72 metre, find the length and breadth of the rectangle.  Solution: Let the breadth of the rectangle be x,  Then the length of the rectangle = 2x Perimeter of the rectangle = 72 Therefore, according to the question 2(x + 2x) = 72 ⇒ 2 × 3x = 72 ⇒ 6x = 72  ⇒ x = 72/6 ⇒ x = 12 We know, length of the rectangle = 2x                       = 2 × 12 = 24 Therefore, length of the rectangle is 24 m and breadth of the rectangle is 12 m.

4. Aaron is 5 years younger than Ron. Four years later, Ron will be twice as old as Aaron. Find their present ages. 

Solution: Let Ron’s present age be x.  Then Aaron’s present age = x - 5 After 4 years Ron’s age = x + 4, Aaron’s age x - 5 + 4.  According to the question;  Ron will be twice as old as Aaron.  Therefore, x + 4 = 2(x - 5 + 4)  ⇒ x + 4 = 2(x - 1)  ⇒ x + 4 = 2x - 2 ⇒ x + 4 = 2x - 2 ⇒ x - 2x = -2 - 4 ⇒ -x = -6 ⇒ x = 6 Therefore, Aaron’s present age = x - 5 = 6 - 5 = 1 Therefore, present age of Ron = 6 years and present age of Aaron = 1 year.

5. A number is divided into two parts, such that one part is 10 more than the other. If the two parts are in the ratio 5 : 3, find the number and the two parts.  Solution: Let one part of the number be x Then the other part of the number = x + 10 The ratio of the two numbers is 5 : 3 Therefore, (x + 10)/x = 5/3 ⇒ 3(x + 10) = 5x  ⇒ 3x + 30 = 5x ⇒ 30 = 5x - 3x ⇒ 30 = 2x  ⇒ x = 30/2  ⇒ x = 15 Therefore, x + 10 = 15 + 10 = 25 Therefore, the number = 25 + 15 = 40  The two parts are 15 and 25. 

More solved examples with detailed explanation on the word problems on linear equations.

6. Robert’s father is 4 times as old as Robert. After 5 years, father will be three times as old as Robert. Find their present ages.  Solution: Let Robert’s age be x years.  Then Robert’s father’s age = 4x After 5 years, Robert’s age = x + 5 Father’s age = 4x + 5 According to the question,  4x + 5 = 3(x + 5)  ⇒ 4x + 5 = 3x + 15  ⇒ 4x - 3x = 15 - 5  ⇒ x = 10 ⇒ 4x = 4 × 10 = 40  Robert’s present age is 10 years and that of his father’s age = 40 years.  

7. The sum of two consecutive multiples of 5 is 55. Find these multiples.  Solution: Let the first multiple of 5 be x.  Then the other multiple of 5 will be x + 5 and their sum = 55 Therefore, x + x + 5 = 55 ⇒ 2x + 5 = 55 ⇒ 2x = 55 - 5 ⇒ 2x = 50 ⇒ x = 50/2  ⇒ x = 25  Therefore, the multiples of 5, i.e., x + 5 = 25 + 5 = 30 Therefore, the two consecutive multiples of 5 whose sum is 55 are 25 and 30.  

8. The difference in the measures of two complementary angles is 12°. Find the measure of the angles.  Solution: Let the angle be x.  Complement of x = 90 - x Given their difference = 12° Therefore, (90 - x) - x = 12° ⇒ 90 - 2x = 12 ⇒ -2x = 12 - 90 ⇒ -2x = -78 ⇒ 2x/2 = 78/2 ⇒ x = 39 Therefore, 90 - x = 90 - 39 = 51  Therefore, the two complementary angles are 39° and 51°

9. The cost of two tables and three chairs is $705. If the table costs $40 more than the chair, find the cost of the table and the chair.  Solution: The table cost $ 40 more than the chair.  Let us assume the cost of the chair to be x.  Then the cost of the table = $ 40 + x The cost of 3 chairs = 3 × x = 3x and the cost of 2 tables 2(40 + x)  Total cost of 2 tables and 3 chairs = $705 Therefore, 2(40 + x) + 3x = 705 80 + 2x + 3x = 705 80 + 5x = 705 5x = 705 - 80 5x = 625/5 x = 125 and 40 + x = 40 + 125 = 165 Therefore, the cost of each chair is $125 and that of each table is $165. 

10. If 3/5 ᵗʰ of a number is 4 more than 1/2 the number, then what is the number?  Solution: Let the number be x, then 3/5 ᵗʰ of the number = 3x/5 Also, 1/2 of the number = x/2  According to the question,  3/5 ᵗʰ of the number is 4 more than 1/2 of the number.  ⇒ 3x/5 - x/2 = 4 ⇒ (6x - 5x)/10 = 4 ⇒ x/10 = 4 ⇒ x = 40 The required number is 40.  

Try to follow the methods of solving word problems on linear equations and then observe the detailed instruction on the application of equations to solve the problems.

●   Equations

What is an Equation?

What is a Linear Equation?

How to Solve Linear Equations?

Solving Linear Equations

Problems on Linear Equations in One Variable

Word Problems on Linear Equations in One Variable

Practice Test on Linear Equations

Practice Test on Word Problems on Linear Equations

●   Equations - Worksheets

Worksheet on Linear Equations

Worksheet on Word Problems on Linear Equation

7th Grade Math Problems   8th Grade Math Practice   From Word Problems on Linear Equations to HOME PAGE

New! Comments

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Properties of Division | Division of Property Overview|Math Properties

Apr 04, 24 03:22 PM

Long Division | Method | Steps | Examples | Long Division Worksheets

Apr 04, 24 01:09 PM

Division of Two-Digit by a One-Digit Numbers | Dividing Larger Numbers

Apr 04, 24 09:31 AM

Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer

Apr 04, 24 09:30 AM

Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr

Apr 02, 24 02:08 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.20: Word Problems for Linear Equations

• Last updated
• Save as PDF
• Page ID 45640

Word problems are important applications of linear equations. We start with examples of translating an English sentence or phrase into an algebraic expression.

Example 18.1

Translate the phrase into an algebraic expression:

a) Twice a variable is added to 4

Solution: We call the variable \(x .\) Twice the variable is \(2 x .\) Adding \(2 x\) to 4 gives:

\[4 + 2x\nonumber\]

b) Three times a number is subtracted from 7.

Solution: Three times a number is \(3 x .\) We need to subtract \(3 x\) from 7. This means:\

\[7-3 x\nonumber\]

c) 8 less than a number.

Solution: The number is denoted by \(x .8\) less than \(x\) mean, that we need to subtract 8 from it. We get:

\[x-8\nonumber\]

For example, 8 less than 10 is \(10-8=2\).

d) Subtract \(5 p^{2}-7 p+2\) from \(3 p^{2}+4 p\) and simplify.

Solution: We need to calculate \(3 p^{2}+4 p\) minus \(5 p^{2}-7 p+2:\)

\[\left(3 p^{2}+4 p\right)-\left(5 p^{2}-7 p+2\right)\nonumber\]

Simplifying this expression gives:

\[\left(3 p^{2}+4 p\right)-\left(5 p^{2}-7 p+2\right)=3 p^{2}+4 p-5 p^{2}+7 p-2 =-2 p^{2}+11 p-2\nonumber\]

e) The amount of money given by \(x\) dimes and \(y\) quarters.

Solution: Each dime is worth 10 cents, so that this gives a total of \(10 x\) cents. Each quarter is worth 25 cents, so that this gives a total of \(25 y\) cents. Adding the two amounts gives a total of

\[10 x+25 y \text{ cents or } .10x + .25y \text{ dollars}\nonumber\]

Now we deal with word problems that directly describe an equation involving one variable, which we can then solve.

Example 18.2

Solve the following word problems:

a) Five times an unknown number is equal to 60. Find the number.

Solution: We translate the problem to algebra:

\[5x = 60\nonumber\]

We solve this for \(x\) :

\[x=\frac{60}{5}=12\nonumber\]

b) If 5 is subtracted from twice an unknown number, the difference is \(13 .\) Find the number.

Solution: Translating the problem into an algebraic equation gives:

\[2x − 5 = 13\nonumber\]

We solve this for \(x\). First, add 5 to both sides.

\[2x = 13 + 5, \text{ so that } 2x = 18\nonumber\]

Dividing by 2 gives \(x=\frac{18}{2}=9\).

c) A number subtracted from 9 is equal to 2 times the number. Find the number.

Solution: We translate the problem to algebra.

\[9 − x = 2x\nonumber\]

We solve this as follows. First, add \(x\) :

\[9 = 2x + x \text{ so that } 9 = 3x\nonumber\]

Then the answer is \(x=\frac{9}{3}=3\)

d) Multiply an unknown number by five is equal to adding twelve to the unknown number. Find the number.

Solution: We have the equation:

\[5x = x + 12.\nonumber\]

Subtracting \(x\) gives

\[4x = 12.\nonumber\]

Dividing both sides by 4 gives the answer: \(x=3\).

e) Adding nine to a number gives the same result as subtracting seven from three times the number. Find the number.

Solution: Adding 9 to a number is written as \(x+9,\) while subtracting 7 from three times the number is written as \(3 x-7\). We therefore get the equation:

\[x + 9 = 3x − 7.\nonumber\]

We solve for \(x\) by adding 7 on both sides of the equation:

\[x + 16 = 3x.\nonumber\]

Then we subtract \(x:\)

\[16 = 2x.\nonumber\]

After dividing by \(2,\) we obtain the answer \(x=8\)

The following word problems consider real world applications. They require to model a given situation in the form of an equation.

Example 18.3

a) Due to inflation, the price of a loaf of bread has increased by \(5 \%\). How much does the loaf of bread cost now, when its price was \(\$ 2.40\) last year?

Solution: We calculate the price increase as \(5 \% \cdot \$ 2.40 .\) We have

\[5 \% \cdot 2.40=0.05 \cdot 2.40=0.1200=0.12\nonumber\]

We must add the price increase to the old price.

\[2.40+0.12=2.52\nonumber\]

The new price is therefore \(\$ 2.52\).

b) To complete a job, three workers get paid at a rate of \(\$ 12\) per hour. If the total pay for the job was \(\$ 180,\) then how many hours did the three workers spend on the job?

Solution: We denote the number of hours by \(x\). Then the total price is calculated as the price per hour \((\$ 12)\) times the number of workers times the number of hours \((3) .\) We obtain the equation

\[12 \cdot 3 \cdot x=180\nonumber\]

Simplifying this yields

\[36 x=180\nonumber\]

Dividing by 36 gives

\[x=\frac{180}{36}=5\nonumber\]

Therefore, the three workers needed 5 hours for the job.

c) A farmer cuts a 300 foot fence into two pieces of different sizes. The longer piece should be four times as long as the shorter piece. How long are the two pieces?

\[x+4 x=300\nonumber\]

Combining the like terms on the left, we get

\[5 x=300\nonumber\]

Dividing by 5, we obtain that

\[x=\frac{300}{5}=60\nonumber\]

Therefore, the shorter piece has a length of 60 feet, while the longer piece has four times this length, that is \(4 \times 60\) feet \(=240\) feet.

d) If 4 blocks weigh 28 ounces, how many blocks weigh 70 ounces?

Solution: We denote the weight of a block by \(x .\) If 4 blocks weigh \(28,\) then a block weighs \(x=\frac{28}{4}=7\)

How many blocks weigh \(70 ?\) Well, we only need to find \(\frac{70}{7}=10 .\) So, the answer is \(10 .\)

Note You can solve this problem by setting up and solving the fractional equation \(\frac{28}{4}=\frac{70}{x}\). Solving such equations is addressed in chapter 24.

e) If a rectangle has a length that is three more than twice the width and the perimeter is 20 in, what are the dimensions of the rectangle?

Solution: We denote the width by \(x\). Then the length is \(2 x+3\). The perimeter is 20 in on one hand and \(2(\)length\()+2(\)width\()\) on the other. So we have

\[20=2 x+2(2 x+3)\nonumber\]

Distributing and collecting like terms give

\[20=6 x+6\nonumber\]

Subtracting 6 from both sides of the equation and then dividing both sides of the resulting equation by 6 gives:

\[20-6=6 x \Longrightarrow 14=6 x \Longrightarrow x=\frac{14}{6} \text { in }=\frac{7}{3} \text { in }=2 \frac{1}{3} \text { in. }\nonumber\]

f) If a circle has circumference 4in, what is its radius?

Solution: We know that \(C=2 \pi r\) where \(C\) is the circumference and \(r\) is the radius. So in this case

\[4=2 \pi r\nonumber\]

Dividing both sides by \(2 \pi\) gives

\[r=\frac{4}{2 \pi}=\frac{2}{\pi} \text { in } \approx 0.63 \mathrm{in}\nonumber\]

g) The perimeter of an equilateral triangle is 60 meters. How long is each side?

Solution: Let \(x\) equal the side of the triangle. Then the perimeter is, on the one hand, \(60,\) and on other hand \(3 x .\) So \(3 x=60\) and dividing both sides of the equation by 3 gives \(x=20\) meters.

h) If a gardener has \(\$ 600\) to spend on a fence which costs \(\$ 10\) per linear foot and the area to be fenced in is rectangular and should be twice as long as it is wide, what are the dimensions of the largest fenced in area?

Solution: The perimeter of a rectangle is \(P=2 L+2 W\). Let \(x\) be the width of the rectangle. Then the length is \(2 x .\) The perimeter is \(P=2(2 x)+2 x=6 x\). The largest perimeter is \(\$ 600 /(\$ 10 / f t)=60\) ft. So \(60=6 x\) and dividing both sides by 6 gives \(x=60 / 6=10\). So the dimensions are 10 feet by 20 feet.

i) A trapezoid has an area of 20.2 square inches with one base measuring 3.2 in and the height of 4 in. Find the length of the other base.

Solution: Let \(b\) be the length of the unknown base. The area of the trapezoid is on the one hand 20.2 square inches. On the other hand it is \(\frac{1}{2}(3.2+b) \cdot 4=\) \(6.4+2 b .\) So

\[20.2=6.4+2 b\nonumber\]

Multiplying both sides by 10 gives

\[202=64+20 b\nonumber\]

Subtracting 64 from both sides gives

\[b=\frac{138}{20}=\frac{69}{10}=6.9 \text { in }\nonumber\]

and dividing by 20 gives

Exit Problem

Write an equation and solve: A car uses 12 gallons of gas to travel 100 miles. How many gallons would be needed to travel 450 miles?

Linear Equations Word Problems Worksheet with Solutions

The first equation family that many students learn about is linear equations. Linear equations have many applications in the real-world, which can make for a really great set of word problems! 

As a student studying algebra, you will encounter many linear equations word problems. That’s why I have put together this linear equations word problems worksheet with solutions!

My hope is that this linear equation word problems worksheet and answer key help you deepen your understanding of linear equations and linear systems!

What Are Linear Equations?

A linear equation is an  algebraic equation  where the highest power on the variable is one. When graphed, a linear equation will produce a straight line.

There are a few ways that we can write linear equations, with two of the most common being slope-intercept form and standard form .

Slope-intercept form is best way to identify the slope of the line and the y-intercept of the line. In general, the equation of a line in slope-intercept form is written as:

In this form,  a  represents the slope of the line and  b  represents the y-intercept of the line.

Equations of lines in standard form are easy to recognize because it is a uniformly recognized form of a line. Standard form allows for easy comparison of coefficients. When two linear equations are in standard form, you can quickly compare the coefficients of x and y.

In general, the standard form of a line is written as:

$$Ax+By=C$$

Note that A and B do not represent the slope of the line or the y-intercept in this form. Instead, A and B are simply constants.

Solving Linear Equations

Any set of word problems relating to linear equations will ask you to solve an equation of some sort. However, there are many different types of solving equations problems that you will encounter as you explore linear equations word problems.

Let’s take a look at a few different types to make sure you know what to expect when you check out the linear equation word problems worksheet with solutions below.

Solving Two-Step Equations and Multi-Step Equations

One of the simplest equation problems that you can solve is a two-step equation. A two-step equation requires you to perform just two steps in order to determine the unique solution to the linear equation.

The first step is to identify the side of the equation with the unknown variable. Your goal will be to isolate this variable (or get it by itself). Consider the following example:

In this example, the variable is on the right-hand side of the equation. To isolate x, we “undo” the operations on the right-hand side of the equation using inverse operations. This just means doing whatever the opposite operation is.

We can apply  order of operations  in reverse to start with the subtraction and then deal with the multiplication. Adding 5 to both sides and then dividing by 2 will result in:

$$\begin{split} 9+5&=2x-5+5 \\ \\ 14 &= 2x \\ \\ \frac{14}{2} &= \frac{2x}{2} \\ \\ 7 &= x \end{split} $$

This shows that the value of the unknown variable here is x = 7. This is a unique solution that will satisfy the equation.

If you want to learn more about finding the solution of linear equations and explore multi-step equations that use the distributive property, check out  these equation solving worksheets !

Systems of Linear Equations

Systems of linear equations are another type of problem that you will see on the linear equations word problems worksheet linked below. A system of linear equations involves two (or more!) linear equations that intersect in some way. 

There are a few different ways that linear equations can intersect :

• Once  at a single point of intersection
• Never  as a result of the lines being parallel 
• Always  as a result of the lines being on top of one another

When solving a system of linear equations, your goal is to determine both unknown variables. If the lines intersect, the solution to the system will be the point of intersection for the lines.

When given a linear equation, we can find the point of intersection between it and a second equation using a few different methods. I made a  video on the substitution method  and a  video on the elimination method  to help you understand these strategies for solving systems before you apply them to word problems involving systems of equations.

What Are Linear Equation Word Problems?

A linear equation word problem involves a real-world situation or scenario that can be solved by setting up and solving linear equations. The equations that are used model the relationships between different quantities in the real-world scenario. 

The topics of these problems vary, ranging from applications in science and physics (ie. calculate the speed of the boat) to business applications (ie. how many sales are required to break even?). The problems that you encounter will also vary in depth and difficulty. 

In my teaching experience, students tend to struggle with word problems because it isn’t always immediately clear what is being asked.  I have seen many students feel very confident in their equation solving skills, yet they still struggle when it comes to solving linear equation word problems.

One reason for this is that you aren’t always given equations from the start while solving word problems.

Tips for Solving Linear Equation Word Problems

During my time as a high school math teacher, I have come across a few tips that I think will help you solve linear equation word problems successfully.

To begin, the first step should always be to define two variables. Read the question carefully and think about the quantities involved. Use variables to represent these quantities.

The second step should be writing an equation that models the scenario. Depending on the problem, you may need to write a second equation as well.

Lastly, think about what the problem is asking you to find. 

For example, are you looking for the values of two unknown variables? If so, you are likely going to be setting up and solving a system of linear equations.

​If you are being asked for the value of a single variable, the chances are you will be solving a single linear equation.

Now that you have a basic understanding of the concepts involved in solving linear equations word problems, it’s time to try a few!

My goal here is to provide you with a worksheet that you can use to practice and feel confident that you understand linear equations word problems!

While I was writing this worksheet, I made sure to include a wide variety of problems that range in difficulty. You will see a few simpler problems involving a two-step equation or multi-step equations, but you will also see a few problems that involve systems of linear equations.

After solving each word problem, be sure to check the answer key to verify that you fully understand the process used to set up the problem and solve it. Reflecting on your understanding is an important part of developing comfort with any given math concept!

Click below to download the linear equations word problems worksheet with solutions!

Using This Linear Equation Word Problems Worksheet

Being able to read a  real-world algebra problem  and set up a linear equation (or a system of linear equations) to solve it is a very challenging skill. In my experience as a math teacher, many students struggle with this concept, even if they fully understand the mathematics that the problem requires.

This is the main reason that I put together this linear equation word problems worksheet with solutions. My goal is to provide you with a set of word problems that you can use to check your understanding of solving linear equations in the real-world.

I hope you found this practice worksheet helpful as you continue your studies of algebra and linear equations!

If you are looking for more linear equations math worksheets in PDF formats, check out my collection of  solving linear inequalities worksheets  and this  linear inequality word problems worksheet .

Did you find this linear equation word problems worksheet with solutions helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

Examples of One Solution Equations, Zero, and Infinite

Free Linear Inequalities Word Problems Worksheet

Linear Equations Word Problems Worksheets

Linear equations are equations that have two variables and are a straight line when graphed, based on their slope and y-intercept . Hence,linear equations word problems worksheets have a variety of word problems that help students practice key concepts and build a rock-solid foundation of the concepts.

Benefits of Linear Equations Word Problems Worksheets

Linear equations word problems worksheets are a great resource for students to practice a large variety of word type questions. These worksheets are supported by visuals which help students get a crystal clear understanding of the linear equations word type topic. The variety of problems that these worksheets offer helps students approach these concepts in an engaging and fun manner.

Linear equations word problems worksheets come with visual simulation for students to see the problems in action, an answer key that provides a detailed step-by-step solution for students to understand the process better, and a worksheet with detailed solutions.

Download Linear Equations Word Problems Worksheet PDFs

These math worksheets should be practiced regularly and are free to download in PDF formats.

☛ Check Grade wise Linear Equations Word Problems Worksheets

• 8th Grade Linear Equations Worksheets

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

By Subjects

• Trigonometry

Linear Equations Word Problems Worksheets

The free printables in this post present pupils with a set of word problems you need to answer by determining the linear equation represented by each.

About us Contact us

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

Linear Equations Word Problems Part 1 Lesson

• Demonstrate an understanding of how to solve a Linear Equation in One Variable
• Learn the six-step process for solving any word problem that involves a Linear Equation in One Variable
• Learn how to check the solution for a word problem
• Learn how to use phrases to set up equations
• Learn how to set up and solve word problems that involve sums of quantities
• Learn how to set up and solve consecutive integer word problems
• Learn how to set up and solve age word problems

How to Solve Word Problems with Linear Equations

Six-step method for applications of linear equations in one variable.

• Write down the main objective of the problem
• If more than one unknown exists, we express the other unknowns in terms of this variable
• Write out an equation that describes the given situation
• Solve the equation
• State the answer using a nice clear sentence
• We need to make sure the answer is reasonable. In other words, if asked how many miles were driven to the store, the answer shouldn't be (-3) as we can't drive a negative amount of miles.

Solve a Word Problem Involving Unknown Numbers

• We are asked to find an unknown number.
• Let x = the unknown number
• product of - means to multiply
• decreased by - means subtraction
• The keyword "is" means equals
• If we put this together:
• 6(x - 3) = 24
• 6 is multiplied by a number decreased by 3. This is the left part of the equation. Notice the parentheses. These are very important, as we want 6 to be multiplied by the result of x - 3. Then we have the keyword "is", which means equals. Lastly, we have 24, which is the right side of the equation.
• 6x - 18 = 24
• 6x - 18 + 18 = 24 + 18
• 6x = 42
• 6/6 x = 42/6
• x = 7
• Our unknown number is 7.
• Think about this in terms of the problem. The product of 6 and 7 decreased by 3, is 24
• 7 decreased by 3 is 4
• 6 • 4 = 24
• 24 = 24
• This tells us our solution is correct and 7 is our unknown number.

Solving a Word Problem Involving Sums of Quantities

• We are asked to find how many games each team (Cougars, Aztecs) won.
• Let x = the number of games won by the Cougars
• Then x - 5 = the number of games won by the Aztecs
• If we combine the number of games won by the Cougars (x) with the number of games won by the Aztecs (x - 5), the result is (=) 13.
• x + (x - 5) = 13
• 2x - 5 = 13
• 2x - 5 + 5 = 13 + 5
• 2x = 18
• 2/2 x = 18/2
• x = 9
• Since x represents the number of games won by the Cougars, we know that the Cougars won 9 games.
• Since the Aztecs won 5 less games, we subtract 9 - 5, to get 4. This is the number of games won by the Aztecs.
• During the regular season, the Cougars won 9 games and the Aztecs won 4 games.
• We know that the combined wins for the two teams were 13.
• Check: 9 (games won by Cougars) + 4 (games won by Aztecs) = 13
• We also know that the Cougars won 5 more games than the Aztecs.
• Check: 9 (games won by Cougars) - 5 = 4 (games won by the Aztecs)
• Since both checks are true, we have the correct answer.

Consecutive Integer Word Problems

• We are asked to find three consecutive integers.
• Let x = smallest consecutive integer
• Then x + 1 = the middle consecutive integer
• Then (x + 1) + 1 = the largest consecutive integer
• If we combine the three consecutive integers: x, (x + 1), (x + 1) + 1, our result is (equals) 21.
• x + (x + 1) + (x + 1) + 1 = 21
• x + x + 1 + x + 1 + 1 = 21
• 3x + 3 = 21
• 3x + 3 - 3 = 21 - 3
• 3x = 18
• 3/3 x = 18/3
• x = 6
• Since x represents the smallest consecutive integer, we know the smallest consecutive integer is 6.
• The middle consecutive integer is 7, from (6 + 1).
• The largest consecutive integer is 8, from (7 + 1).
• Our three consecutive integers are 6, 7, and 8.
• We know that the sum of the consecutive integers is 21.
• Check: 6 + 7 + 8 = 21
• 13 + 8 = 21
• 21 = 21
• Since our three consecutive integers sum to 21, our answer is correct.

Age Word Problems

• We are asked to find the age of each sibling.
• Let x = Jamie's age
• Then 2x = Steven's age (since it's twice the age of Jamie)
• If we add Jamie's age (x) with Steven's age (2x), the result is 15.
• x + 2x = 15
• 3x = 15
• 3/3 x = 15/3
• x = 5
• Since x represents Jamie's age, we know that Jamie is 5 years old.
• Since 2x represents Steven's age, we know that Steven is 2 • 5 or 10 years old
• Jamie is 5 years old and Steven is 10 years old.
• We know that the sum of their ages is 15.
• Check: 5 + 10 = 15
• 15 = 15
• We know that Steven is twice the age of Jamie
• Check: 2 • 5 = 10
• 10 = 10
• Since both of our checks were true, we can say our answer is correct.

Skills Check:

Solve each word problem.

The result of a number being increased by 6 and then multiplied by 8 is 104. Find the number.

Please choose the best answer.

Last week, a grocery store sold 8/5 as many cans of tomatoes as bags of chips. The total number of cans of tomatoes and bags of chips sold last week was 273. How many bags of chips were sold last week?

When five times the smaller of two consecutive integers is added to three times the larger, the result is 59. Find the smaller integer.

Congrats, Your Score is 100 %

Better Luck Next Time, Your Score is %

Ready for more? Watch the Step by Step Video Lesson   |   Take the Practice Test

Linear Equation Word Problems - Examples & Practice - Expii

Linear equation word problems - examples & practice, explanations (3), (video) slope-intercept word problems.

by cpfaffinator

This video by cpfaffinator explains how to translate word problems into variables while working through a couple of examples.

(Note: the answer at 3:34 should be y=0.50x+3 instead of y=0.5x+b .)

When writing linear equations (also called linear models) from word problems, you need to know what the x and y variables refer to, as well as what the slope and y-intercept are. Here are some tricks to help translate :

• The x variable. Usually, you'll be asked to find an equation in terms of some factor. This will usually be whatever affects the output of the equation.
• The y variable. The y variable is usually whatever you're trying to find in the problem. It'll depend on the x variable.
• The slope (m). The slope will be some sort of rate or other change over time.
• The y-intercept (b). Look for a starting point or extra fees—something that will be added (or subtracted) on , no matter what the x variable is.

Using these parts, we can write the word problem in slope intercept form , y=mx+b, and solve.

A city parking garage charges a flat rate of $3.00 for parking 2 hours or less, and $0.50 per hour for each additional hour. Write a linear model that gives the total charge in terms of additional hours parked.

First up, we want the equation, or model, to give us the total charge. This will be what the y variable represents. y=total charge for parking The total charge depends on how many additional hours you've parked. This is the x variables. x=additional hours parked

Next, we need to find the slope, m. If we look at the slope-intercept equation , y=mx+b, the slope is multiplied with the input x. So, we want to find some rate in our problem that goes with the number of additional hours parked . In the problem, we have $0.50 per hour for each additional hour. The number of hours is being multiplied by the price of 50 cents every hour. m=0.50

The y-intercept is the starting point. In other words, if we parked our car in the garage for 0 hours, what would the price be? The problem says the garage *charges a flat rate of $3.00. A flat rate means that no matter what we're being charged 3 dollars. b=3

Plugging these into the slope-intercept equation will give us our model. y=mx+by=0.50x+3

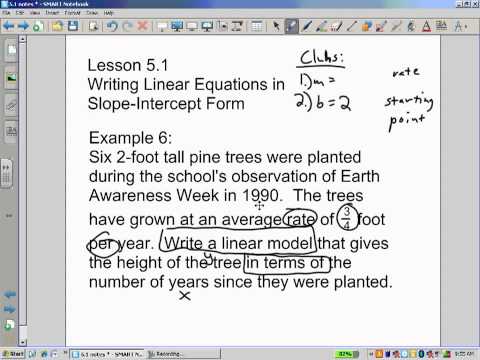
Six 2 foot tall pine trees were planted during the school's observation of Earth Awareness Week in 1990. The trees have grown at an average rate of 34 foot per year. Write a linear model that gives the height of the trees in terms of the number of years since they were planted.

What does the y variable represent in our equation?

Years since the trees were planted

Number of trees planted

Radius of trees' roots

Height of the trees

Related Lessons

Translate to a linear equation.

Sometimes, the trick to solving a word problem will be to translate it into a linear equation. To clue you in, linear equation word problems usually involve some sort of rate of change , or steady increase (or decrease) based on a single variable. If you see the word rate , or even "per" or "each" , it's a safe bet that a word problem is calling for a linear equation.

There are a couple steps when translating from a word problem to a linear equation. Review them, then we'll work through an example.

• Find the y variable, or output. What is the thing you're trying to find? This will often be a price, or an amount of time, or something else countable that depends on other things.
• Find the x variable, or input. What is affecting the price, or amount of time, etc.?
• Find the slope. What's the rate in the problem?
• Find the y-intercept. Is there anything that's added or subtracted on top of the rate, no matter what what x is?
• Plug all the numbers you know into y=mx+b !

Wally and Cobb are starting a catering business. They rent a kitchen for $350 a month, and charge $75 for each event they cater. If they cater 12 events in a month, how much do they profit?

First, let's find the y variable. What are we trying to find in this problem?

The name of the business

Word Problems with Linear Relationships

When you're faced with a linear word problem, it can feel daunting to work out a solution. The good news is that there are few simple steps that you can take to tackle linear word problems.

Image source: by Anusha Rahman

For future linear word problems, you can use these same steps to tackle the problem!

Math Made Easy

Systems of Linear Equations and Word Problems

Note that we saw how to solve linear inequalities here in the Coordinate System and Graphing Lines section . Note also that we solve Algebra Word Problems without Systems here , and we solve systems using matrices in the Matrices and Solving Systems with Matrices  section here.

Introduction to Systems

“Systems of equations” just means that we are dealing with more than one equation and variable. So far, we’ve basically just played around with the equation for a line, which is $ y=mx+b$. Let’s say we have the following situation:

Now, you can always do “guess and check” to see what would work, but you might as well use algebra! It’s much better to learn the algebra way, because even though this problem is fairly simple to solve, the algebra way will let you solve any algebra problem – even the really complicated ones.

The first trick in problems like this is to figure out what we want to know. This will help us decide what variables (unknowns) to use. What we want to know is how many pairs of jeans we want to buy (let’s say “$ j$”) and how many dresses we want to buy (let’s say “$ d$”). Always write down what your variables will be:

Let $ j=$ the number of jeans you will buy Let $ d=$ the number of dresses you’ll buy

Like we did before, let’s translate word-for-word from math to English:

Now we have the 2 equations as shown below. Notice that the $ j$ variable is just like the $ x$ variable and the $ d$ variable is just like the $ y$. It’s easier to put in $ j$   and $ d$ so we can remember what they stand for when we get the answers.

This is what we call a system, since we have to solve for more than one variable – we have to solve for 2 here. The cool thing is to solve for 2   variables , you typically need 2   equations , to solve for 3   variables , you need 3   equations , and so on. That’s easy to remember, right?

We need to get an answer that works in both equations ; this is what we’re doing when we’re solving; this is called solving simultaneous systems , or solving system simultaneously . There are several ways to solve systems; we’ll talk about graphing first.

Solving Systems by Graphing

Remember that when you graph a line, you see all the different coordinates (or $ x/y$ combinations) that make the equation work. In systems, you have to make both equations work, so the intersection of the two lines shows the point that fits both equations (assuming the lines do in fact intersect; we’ll talk about that later).  The points of intersections satisfy both equations simultaneously. 

Put these equations into the $ y=mx+b$ ($ d=mj+b$) format, by solving for the $ d$ (which is like the $ y$):

$ \displaystyle j+d=6;\text{ }\,\text{ }\text{solve for }d:\text{ }d=-j+6\text{ }$

$ \displaystyle 25j+50d=200;\text{ }\,\,\text{solve for }d:\text{ }d=\frac{{200-25j}}{{50}}=-\frac{1}{2}j+4$

Now graph both lines:

Note that with non-linear equations, there will most likely be more than one intersection; an example of how to get more than one solution via the Graphing Calculator can be found in the  Exponents and Radicals in Algebra section. Also, t here are some examples of systems of inequality  here in the Coordinate System and Graphing Lines section .

Solving Systems with Substitution

Substitution is the favorite way to solve for many students! It involves exactly what it says: substituting one variable in another equation so that you only have one variable in that equation. Here is the same problem:

You’re going to the mall with your friends and you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50 .  You really, really want to take home 6 items of clothing because you “need” that many new things. How many pairs of jeans and how many dresses you can buy so you use the whole $200 (tax not included)?

Below are our two equations, and let’s solve for “$ d$” in terms of “$ j$” in the first equation. Then, let’s substitute what we got for “$ d$” into the next equation. Even though it doesn’t matter which equation you start with, remember to always pick the “easiest” equation first (one that we can easily solve for a variable) to get a variable by itself.

We could buy 4 pairs of jeans and 2 dresses . Note that we could have also solved for “$ j$” first; it really doesn’t matter. You’ll want to pick the variable that’s most easily solved for. Let’s try another substitution problem that’s a little bit different:

Solving Systems with Linear Combination or Elimination

Probably the most useful way to solve systems is using linear combination, or linear elimination. The reason it’s most useful is that usually in real life we don’t have one variable in terms of another (in other words, a “$ y=$” situation).

The main purpose of the linear combination method is to add or subtract the equations so that one variable is eliminated. We can add, subtract, or multiply both sides of equations by the same numbers – let’s use real numbers as shown below. We are using the Additive Property of Equality , Subtraction Property of Equality , Multiplicative Property of Equality , and/or Division Property of Equality that we saw here in the Types of Numbers and Algebraic Properties section :

If we have a set of 2 equations with 2 unknowns, for example, we can manipulate them by adding, multiplying or subtracting (we usually prefer adding) so that we get one equation with one variable. Let’s use our previous problem:

We could buy 4 pairs of jeans and 2 dresses .

Here’s another example:

Types of equations

In the example above, we found one unique solution to the set of equations. Sometimes, however, for a set of equations, there are no solutions (when lines are parallel) or an infinite number of solutions or infinitely many solutions (when the two lines are actually the same line, and one is just a “multiple” of the other).

When there is at least one solution , the equations are consistent equations , since they have a solution. When there is only one solution, the system is called independent , since they cross at only one point. When equations have infinite solutions, they are the same equation, are consistent , and are called dependent or coincident (think of one just sitting on top of the other).

When equations have no solutions , they are called inconsistent equations , since we can never get a solution . 

Here are graphs of inconsistent and dependent equations that were created on a graphing calculator:

Systems with Three Equations

Let’s get a little more complicated with systems; in real life, we rarely just have two unknowns to solve for.

Let’s say at the same store, they also had pairs of shoes for $20 and we managed to get $60 more to spend! Now we have a new problem. To spend the even $260 , how many pairs of jeans, dresses, and pairs of shoes should we get if want, for example, exactly 10 total items (Remember that jeans cost $25 each and dresses cost $50 each).

Let’s let $ j=$ the number of pair of jeans, $ d=$ the number of dresses, and $ s=$ the number of pairs of shoes we should buy. So far, we’ll have the following equations:

$ \displaystyle \begin{array}{c}j+d+s=10\text{ }\\25j+\text{ }50d+\,20s=260\end{array}$

We’ll need another equation, since for three variables, we need three equations (otherwise, we theoretically might have infinite ways to solve the problem). In this type of problem, you would also need something like this: We want twice as many pairs of jeans as pairs of shoes . Now, since we have the same number of equations as variables , we can potentially get one solution for the system of equations. Here are the three equations:

We’ll learn later how to put these in our calculator to easily solve using matrices (see the  Matrices and Solving Systems with Matrices section). For now, we can use two equations at a time to eliminate a variable (using substitution and/or elimination), and keep doing this until we’ve solved for all variables. These can get really difficult to solve, but remember that in “real life”, there are computers to do all this work!

Remember again, that if we ever get to a point where we end up with something like this, it means there are an infinite number of solutions : $ 4=4$  (variables are gone and a number equals another number and they are the same). And if we up with something like this, it means there are no solutions : $ 5=2$ (variables are gone and two numbers are left and they don’t equal each other).

Let’s solve our system:      $ \displaystyle \begin{array}{c}j+d+s=10\text{ }\\25j+\text{ }50d+20s=260\\j=2s\end{array}$ :

We could buy 6 pairs of jeans, 1 dress, and 3 pairs of shoes .

Here’s one more example of a three-variable system of equations, where we’ll only use linear elimination:

$ \displaystyle \begin{align}5x-6y-\,7z\,&=\,7\\6x-4y+10z&=\,-34\\2x+4y-\,3z\,&=\,29\end{align}$

I know – this is really difficult stuff! But if you do it step-by-step and keep using the equations you need with the right variables, you can do it. Think of it like a puzzle – you may not know exactly where you’re going, but do what you can in baby steps, and you’ll get there (sort of like life sometimes, right?!). And we’ll learn much easier ways to do these types of problems.

Algebra Word Problems with Systems

Let’s do more word problems; you’ll notice that many of these are the same type that we did earlier in the Algebra Word Problems  section , but now we can use more than one variable. This will actually make the problems easier! Again, when doing these word problems:

• If you’re wondering what the variables (or unknowns) should be when working on a word problem, look at what the problem is asking. These are usually (but not always) what your variables are!
• If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!

Here are some problems:

Investment Word Problem

We also could have set up this problem with a table:

Mixture Word Problems

Here’s a mixture word problem . With mixture problems, remember if the problem calls for a pure solution or concentrate , use 100% (if the percentage is that solution) or 0% (if the percentage is another solution).

Let’s do the math (use substitution )!

$ \displaystyle \begin{array}{c}x\,\,+\,\,y=10\\.01x+.035y=10(.02)\end{array}$          $ \displaystyle \begin{array}{c}\,y=10-x\\.01x+.035(10-x)=.2\\.01x\,+\,.35\,\,-\,.035x=.2\\\,-.025x=-.15;\,\,\,\,\,x=6\\\,y=10-6=4\end{array}$

We would need 6 liters of the 1% milk, and 4 liters of the 3.5% milk.

Here’s another mixture problem:

$ \displaystyle \begin{array}{c}x+y=50\\8x+4y=50\left( {6.4} \right)\end{array}$                   $ \displaystyle \begin{array}{c}y=50-x\\8x+4\left( {50-x} \right)=320\\8x+200-4x=320\\4x=120\,;\,\,\,\,x=30\\y=50-30=20\\8x+4y=50(6.4)\end{array}$

We would need 30 pounds of the $8 coffee bean, and 20 pounds of the $4 coffee bean. See how similar this problem is to the one where we use percentages?

Distance Word Problem:

Here’s a distance word problem using systems ; distance problems have to do with an object’s speed, time, and distance. Note that, as well as the distance word problem here in the Algebra Word Problems section , there’s an example of a Parametric Distance Problem here in the Parametric Equations section .

Which Plumber Problem

Many word problems you’ll have to solve have to do with an initial charge or setup charge, and a charge or rate per time period. In these cases, the initial charge will be the $ \boldsymbol {y}$ -intercept , and the  rate will be the slope . Here is an example:

Geometry Word Problem:

Many times, we’ll have a geometry problem as an algebra word problem; these might involve perimeter, area, or sometimes angle measurements (so don’t forget these things!). Let’s do one involving angle measurements.

See – these are getting easier! Here’s one that’s a little tricky though:

Work Problem : 

Let’s do a “ work problem ” that is typically seen when studying Rational Equations (fraction with variables in them) and can be found here in the Rational Functions, E quations and Inequalities  section .

Note that there’s also a simpler version of this problem here in the Direct, Inverse, Joint and Combined Variation section .

Three Variable Word Problem:

Let’s do one more with three equations and three unknowns:

The “Candy” Problem

Sometimes we get lucky and can solve a system of equations where we have more unknowns (variables) then equations. (Actually, I think it’s not so much luck, but having good problem writers!) Here’s one like that:

There are more Systems Word Problems in the  Matrices and Solving Systems with Matrices section , Linear Programming section , and Right Triangle Trigonometry section .

Understand these problems, and practice, practice, practice!

For Practice : Use the Mathway  widget below to try a  Systems of Equations  problem. Click on Submit (the blue arrow to the right of the problem) and click on Solve by Substitution or Solve by Addition/Elimination  to see the answer .

You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.

If you click on Tap to view steps , or Click Here , you can register at Mathway for a free trial , and then upgrade to a paid subscription at any time (to get any type of math problem solved!).

On to Algebraic Functions, including Domain and Range   – you’re ready! 

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Word Problems on Linear Equations | How to Solve Linear Equations Word Problems?

We have provided several problems that involve relations among known and unknown numbers and can be put in the form of linear equations. Those equations can be stated in words and it is the main reason we prefer these Word Problems on Linear Equations. You can practice as many types of questions as you want to get an expert in this concept. For better understanding, we even listed linear equations examples with solutions.

Steps to Solve Word Problems on Linear Equations

Below are the simple steps to solve the linear equations word problems. Follow these instructions and solve the questions carefully.

• Read the problem carefully and make a note of what is given in the question and what is required.
• Denote the unknown things as the variables like x, y, z, a, b, . . .
• Translate the given word problem into mathematical statements.
• Form the linear equations in one variable by using the conditions provided in the question.
• Solve the unknown parameters from the equation.
• Verify the condition with the obtained answer ad cross check whether it is correct or not.

Linear Equations Examples with Answers

A motorboat goes downstream in the river and covers a distance between two coastal towns in 5 hours. It covers this distance upstream in 6 hours. If the speed of the stream is 3 km/hr, find the speed of the boat in still water?

Let the speed of the boat in still water = x km/hr

Speed of the boat down stream = (x + 3) km/hr

Time taken to cover the distance = 5 hrs

Therefore, distance covered in 5 hrs = (x + 3) x 5

Speed of the boat upstream = (x – 3) km/hr

Time taken to cover the distance = 6 hrs

Therefore, distance covered in 6 hrs – (x – 3) x 6

Therefore, the distance between the two coastal towns is fixed, i.e., the same.

As per the question

5(x + 3) = 6(x – 3)

5x + 15 = 6x – 18

15 + 18 = 6x – 5x

Required speed of the boat is 33 km/hr

The perimeter of a rectangular swimming pool is 144 m. Its length is 2 m more than twice its width. What are the length and width of the pool?

Let l be the length of the swimming pool, w be the width of the swimming pool.

According to the question,

length l = 2w + 2

The perimeter of swimming pool = 144 m

2l + 2w = 144

Substitute l = 2w + 2

2(2w + 2) + 2w = 144

4w + 4 + 2w = 144

6w = 144 – 4

w = 140 / 6

Then, the length is

l = 2(23.3) + 2

Hence, the length and width of the rectangular swimming pool is 48.6 m, 23.3 m.

The sum of three consecutive even numbers is 126. What are the numbers?

Let the first even number be x, the second number be (x + 2), the third number be (x + 4).

According to the question, the sum of consecutive even numbers is 126.

First Number + Second Number + Third Number = 126

x + (x + 2) + (x + 4) = 126

3x + 6 = 126

Subtract 6 from both sides.

3x + 6 – 6 = 126 – 6

Divide both sides by 3.

3x / 3 = 120 / 3

The first number is 40, the second number is (x + 2) = 40 + 2 = 42, third number is (x + 4) = 40 + 4 = 44.

Hence, the three consecutive even numbers are 40, 42, 44.

When five is added to three more than a certain number, the result is 19. What is the number?

Let us take the number as x.

Add 5 to the three more than a certain number.

5 + x + 3 = 19

Subtract 8 from both sides of the equation.

x + 8 – 8 = 19 – 8

So, the number is 11.

Eleven less than seven times a number is five more than six times the number. Find the number?

Let the number be x.

11 less than the seven times a number is five more than six times the number.

7x – 11 = 6x + 5

7x – 6x = 5 + 11

Hence the required number is 16.

Two angles of a triangle are the same size. The third angle is 12 degrees smaller than the first angle. Find the measure of the angles.

Let the triangle be ∆ABC.

So, ∠A = ∠B and ∠C = ∠A – 12 degrees

The sum of three angles of a triangle = 180 degrees

∠A + ∠B + ∠C = 180

∠A + ∠A + ∠A – 12 = 180

3∠A – 12 = 180

Add 12 to both sides of the equation.

3∠A – 12 + 12 = 180 + 12

3∠A / 3 = 192/3

Hence, the first and second angles of the triangle are 64 degrees, 64 degrees and the third angle is 64 – 12 = 52 degrees.

The perimeter of a rectangle is 150 cm. The length is 15 cm greater than the width. Find the dimensions.

Let the rectangle width is w.

Length of rectangle l = w + 15 cm

Given that, the perimeter of a rectangle is 150 cm

2l + 2w = 150

Substitute l = w + 15 cm in above equation.

2(w + 15) + 2w = 150

2w + 30 + 2w = 150

4w + 30 = 150

Subtract 30 from both sides.

4w + 30 – 30 = 150 – 30

Divide both sides by 4.

4w/4 = 120/4

Hence, the rectangle width is 30 cm, the length is (30 + 15) = 45 cm.

If Mr. David and his son together had 220 dollars, and Mr. David had 10 times as much as his son, how much money had each?

Let Mr. David’s son has x dollars.

The amount at Mr. David = 10x dollars

Given that, Mr. David and his son together had 220 dollars

x + 10x = 220

Divide both sides by 11.

x = 220 / 11

Hence, Mr. David has 20 x 10 = 200 dollars and his son has 20 dollars.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• Middle School Math Solutions – Inequalities Calculator Next up in our Getting Started maths solutions series is help with another middle school algebra topic - solving...

Please add a message.

Message received. Thanks for the feedback.

• For a new problem, you will need to begin a new live expert session.
• You can contact support with any questions regarding your current subscription.
• You will be able to enter math problems once our session is over.
• I am only able to help with one math problem per session. Which problem would you like to work on?
• Does that make sense?
• I am currently working on this problem.
• Are you still there?
• It appears we may have a connection issue. I will end the session - please reconnect if you still need assistance.
• Let me take a look...
• Can you please send an image of the problem you are seeing in your book or homework?
• If you click on "Tap to view steps..." you will see the steps are now numbered. Which step # do you have a question on?
• Please make sure you are in the correct subject. To change subjects, please exit out of this live expert session and select the appropriate subject from the menu located in the upper left corner of the Mathway screen.
• What are you trying to do with this input?
• While we cover a very wide range of problems, we are currently unable to assist with this specific problem. I spoke with my team and we will make note of this for future training. Is there a different problem you would like further assistance with?
• Mathway currently does not support this subject. We are more than happy to answer any math specific question you may have about this problem.
• Mathway currently does not support Ask an Expert Live in Chemistry. If this is what you were looking for, please contact support.
• Mathway currently only computes linear regressions.
• We are here to assist you with your math questions. You will need to get assistance from your school if you are having problems entering the answers into your online assignment.
• Have a great day!
• Hope that helps!
• You're welcome!
• Per our terms of use, Mathway's live experts will not knowingly provide solutions to students while they are taking a test or quiz.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Digital SAT Math

Course: digital sat math   >   unit 2.

• Understanding linear relationships | Lesson
• Linear equation word problems — Basic example
• Linear equation word problems — Harder example

Linear equation word problems: foundations

• (Choice A)   x − 2 ‍   A x − 2 ‍  
• (Choice B)   x + 2 ‍   B x + 2 ‍  
• (Choice C)   2 x ‍   C 2 x ‍  
• (Choice D)   x 2 ‍   D x 2 ‍