general solution eigenvalue problem calculator

Online Eigenvalue Calculator

Compute eigenvalues with wolfram|alpha.

• Natural Language

More than just an online eigenvalue calculator

Wolfram|Alpha is a great resource for finding the eigenvalues of matrices. You can also explore eigenvectors, characteristic polynomials, invertible matrices, diagonalization and many other matrix-related topics.

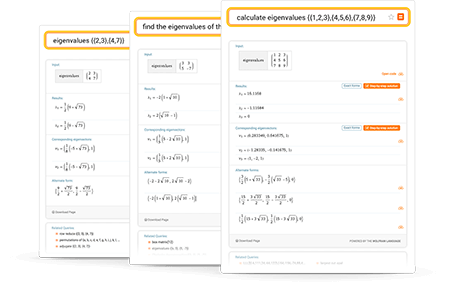
Learn more about:

• Eigenvalues

Tips for entering queries

Use plain English or common mathematical syntax to enter your queries. To enter a matrix, separate elements with commas and rows with curly braces, brackets or parentheses.

• eigenvalues {{2,3},{4,7}}
• calculate eigenvalues {{1,2,3},{4,5,6},{7,8,9}}
• find the eigenvalues of the matrix ((3,3),(5,-7))
• [[2,3],[5,6]] eigenvalues
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

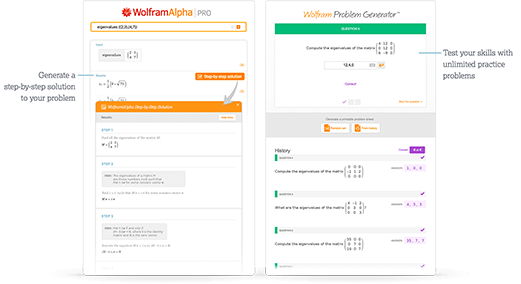
• Step-by-step solutions
• Wolfram Problem Generator

Eigenvalue and Eigenvector Calculator

Calculating the trace and determinant, how to find eigenvalues, eigenvalue and eigenvector calculator – 2x2 matrices, how to find eigenvalues and eigenvectors of 3x3 matrices, complex eigenvalues and eigenvectors.

If analyzing matrices gives you a headache, this eigenvalue and eigenvector calculator is the perfect tool for you. It will allow you to find the eigenvalues of a matrix of size 2x2 or 3x3 matrix and will even save you time by finding the eigenvectors as well. In this article, we will provide you with explanations and handy formulas to ensure you understand how this calculator works and how to find eigenvalues and eigenvectors in general.

Let's dive right in!

A 2x2 matrix A A A has the following form:

where a 1 a_1 a 1 ​ , a 2 a_2 a 2 ​ , b 1 b_1 b 1 ​ and b 2 b_2 b 2 ​ are the elements of the matrix. Our eigenvalue and eigenvector calculator uses the form above, so make sure to input the numbers properly – don't mix them up!

In the case of a 2x2 matrix, in order to find the eigenvectors and eigenvalues, it's helpful first to get two very special numbers: the trace and the determinant of the array. Lucky for us, the eigenvalue and eigenvector calculator will find them automatically, and if you'd like to see them, click on the advanced mode button . In case you want to check if it gave you the correct answer or simply perform the calculations by hand, follow the steps below:

• Trace : the trace of a matrix is defined as the sum of the elements on the main diagonal (from the upper left to the lower right). It is also equal to the sum of the eigenvalues (counted with their multiplicities). In the case of a 2x2 matrix, it is:
• Determinant : the determinant of a matrix is useful in multiple further operations – for example, finding the inverse of a matrix (you can learn how to do it at our inverse matric calculator ). For a 2x2 matrix, the determinant is:

Each 2x2 matrix A A A has two eigenvalues: λ 1 \lambda_1 λ 1 ​ and λ 2 \lambda_2 λ 2 ​ . These are defined as numbers that fulfill the following condition for a nonzero column vector v = ( v 1 , v 2 ) \bold{v} = (v_1, v_2) v = ( v 1 ​ , v 2 ​ ) , which we call an eigenvector:

You can also find another equivalent version of the equation above:

where I \mathbb{I} I is the 2x2 identity matrix.

Knowing the trace and determinant, it is a trivial task to find the eigenvalues of a matrix – all you have to do is input these values into the following equations:

Some matrices have only one eigenvalue. Examples of such arrays include matrices of the form:

Make sure to experiment with our calculator to see which matrices have only one eigenvalue!

You can also use our calculator for finding eigenvectors . In essence, learning how to find eigenvectors boils down to directly solving the equation:

Note that if a matrix has only one eigenvalue, it can still have multiple eigenvectors corresponding to it. For instance, the identity matrix:

...has only one (double) eigenvalue λ = 1 \lambda = 1 λ = 1 , but two eigenvectors: v 1 = ( 1 , 0 ) v_1 = (1,0) v 1 ​ = ( 1 , 0 ) and v 2 = ( 0 , 1 ) v_2 = (0,1) v 2 ​ = ( 0 , 1 ) .

Remember that if a vector v v v is an eigenvector, then the same vector multiplied by a scalar is also an eigenvector of the same matrix. If you would like to simplify the solution provided by our calculator, head over to the unit vector calculator .

Let's now try to translate all this into the language of 3x3 matrices . First of all, let's see an example of such an object:

where for us, the entries a 1 a_1 a 1 ​ , a 2 a_2 a 2 ​ , up to c 3 c_3 c 3 ​ are real numbers.

In general, most of the definitions above are the same for 3x3 matrices. For instance, the trace is the sum of the cells on the main diagonal:

However, the determinant is now a more complicated manner:

Now, when it comes to how to find eigenvectors and eigenvalues, the definition is again the same : they are the numbers λ \lambda λ and vectors v v v that satisfy the matrix equation:

where the multiplication on the left is matrix multiplication (a rather complex operations we detailed at our matrix multiplication calculator ). However, the trick is that this time the equation is far more complicated . In particular, the formulas from above don't work here.

In the case of 2x2 matrices, it all boils down to the quadratic formula: if you don't remember how to solve it, check out our quadratic formula calculator . However, when the arrays are of size 3x3, we obtain a cubic equation , i.e., an equation with the variable to the third power. And such things are not so easy to calculate.

Fortunately, we have the eigenvalue and eigenvector calculator that can hide all these ugly formulas and effortlessly give us a pretty answer .

But is the answer always a pretty one?

Quadratic and cubic equations sometimes have no real solutions . This means that there is no real number (the kind of number that we learned when we were little kids) that satisfies this formula. Therefore, in the field of real numbers, it's not always possible to find the eigenvalues of a matrix. However, in mathematics, there is an extension in which that can never happen: every equation has as many solutions (counted with their multiplicities) as its degree .

Complex numbers, formally speaking, are pairs of real numbers . The first of the pair is called the real part , and the second the imaginary part (yup, that's exactly what professional mathematicians called it). The second one has the mysterious number i \mathrm i i , which we define as the square root of ( − 1 -1 − 1 ). They told us at school that such things don't exist, didn't they? Well, they do, but they're imaginary .

For us, this means that the calculator will always know how to find the eigenvectors and eigenvalues of a matrix. Once it does that, it's crucial to know if the problem you're solving uses complex numbers or just the real ones . Just to be on the safe side, our eigenvalue and eigenvector calculator will show you all the values and their corresponding eigenvectors, be they real or complex.

However, if you only need the real ones, feel free to ignore all that have an i \mathrm i i in them . Just keep in mind that they do exist, even though they're imaginary.

How do I find eigenvalues and eigenvectors?

To find an eigenvalue , λ , and its eigenvector, v , of a square matrix, A , you need to:

Write the determinant of the matrix, which is A - λI with I as the identity matrix.

Solve the equation det(A - λI) = 0 for λ (these are the eigenvalues).

Write the system of equations Av = λv with coordinates of v as the variable.

For each λ , solve the system of equations , Av = λv .

Write the solution of Av = λv with parameters.

For each parameter, its coefficient is the coordinate of an eigenvector.

Group the coefficients corresponding to each parameter to form an eigenvector v .

How do I find eigenvalues of a 3x3 matrix?

To find the eigenvalues λ₁ , λ₂ , λ₃ of a 3x3 matrix, A , you need to:

• Subtract λ (as a variable) from the main diagonal of A to get A - λI .
• Write the determinant of the matrix, which is A - λI .
• Solve the cubic equation, which is det(A - λI) = 0 , for λ .
• The (at most three) solutions of the equation are the eigenvalues of A .
• If needed, proceed to find the eigenvectors of the eigenvalues .

How do I find eigenvectors from eigenvalues?

When you have an eigenvalue, λ , of a square matrix, A , and you want to find its corresponding eigenvector, v , you need to:

• Denote the coordinates of v as variables (e.g., v = (x,y,z) for 3x3 matrices).
• Write the system of equations, Av = λv (each coordinate gives one equation).
• Solve the system of equations for the coordinates of v .
• Write the solution using parameters.
• For each parameter, its coefficient is the coordinate of an eigenvector .
• Group the coefficients corresponding to each parameter to form an eigenvector, v .

How many eigenvalues does a matrix have?

A square matrix with n rows and columns can have at most n eigenvalues . If we don't allow complex numbers, it may happen that it will have none (i.e., when the characteristic polynomial has no real solutions).

Are eigenvectors orthogonal?

In general, no . If the initial matrix is symmetric, then the eigenvectors of distinct eigenvalues are always orthogonal.

Can 0 be an eigenvalue?

Yes , it can. For that to happen, there must exist a non-zero vector, v , such that Av = 0 (as a matrix multiplication).

Helium balloons

Integration by completing the square, plant spacing, set builder.

• Biology (99)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (508)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Finding of eigenvalues and eigenvectors

This calculator allows to find eigenvalues and eigenvectors using the Characteristic polynomial .

• Leave extra cells empty to enter non-square matrices.
• decimal (finite and periodic) fractions: 1/3 , 3.14 , -1.3(56) , or 1.2e-4
• mathematical expressions : 2/3+3*(10-4) , (1+x)/y^2 , 2^0.5 (= 2 ) , 2^(1/3) , 2^n , sin(phi) , cos(3.142rad) , a_1 , or (root of x^5-x-1 near 1.2)
• matrix literals: {{1,3},{4,5}}
• operators: + , - , * , / , \ , ! , ^ , ^{*} , , , ; , ≠ , = , ⩾ , ⩽ , > , and
• functions: sqrt , cbrt , exp , log , abs , conjugate , arg , min , max , gcd , rank , adjugate , inverse , determinant , transpose , pseudoinverse , cos , sin , tan , cot , cosh , sinh , tanh , coth , arccos , arcsin , arctan , arccot , arcosh , arsinh , artanh , arcoth , derivative , factor , and resultant
• units: rad , deg
• pi , e , i — mathematical constants
• k , n — integers
• I or E — identity matrix
• X , Y — matrix symbols
• Use ↵ Enter , Space , ← ↑ ↓ → , Backspace , and Delete to navigate between cells, Ctrl ⌘ Cmd + C / Ctrl ⌘ Cmd + V to copy/paste matrices.
• Drag-and-drop matrices from the results, or even from/to a text editor.
• To learn more about matrices use Wikipedia .
• Find eigenvectors of ({{-26,-33,-25},{31,42,23},{-11,-15,-4}})

•  All online calculators
•  Suggest a calculator
•  Translation

PLANETCALC Online calculators

•  English

Eigenvalue calculator

This online calculator computes the eigenvalues of a square matrix up to the fourth degree by solving the characteristic equation.

This online calculator computes the eigenvalues of a square matrix by solving the characteristic equation. The characteristic equation is the equation obtained by equating the characteristic polynomial to zero. Thus, this calculator first gets the characteristic equation using the Characteristic polynomial calculator, then solves it analytically to obtain eigenvalues (either real or complex). It does so only for matrices 2x2, 3x3, and 4x4, using the The solution of a quadratic equation , Cubic equation and Quartic equation solution calculators. Thus it can find eigenvalues of a square matrix up to the fourth degree.

It is very unlikely that you would have a square matrix of a higher degree in math problems, because, according to the Abel–Ruffini theorem, a general polynomial equation of degree five or higher has no solution in radicals, thus, it can be solved only by numerical methods. (Note that the degree of a characteristic polynomial is the degree of its square matrix). More theory can be found below the calculator.

Eigenvalues

Eigenvalues are easier to explain with eigenvectors. Suppose we have a square matrix A . This matrix defines a linear transformation, that is, if we multiply any vector by A, we get the new vector that changes direction:

However, there are some vectors for which this transformation produces the vector that is parallel to the original vector. In other words:

These vectors are eigenvectors of A, and these numbers are eigenvalues of A.

This equation can be rewritten as

where I is the identity matrix.

The roots of this equation are eigenvalues of A, also called characteristic values , or characteristic roots .

The characteristic equation of A is a polynomial equation, and to get polynomial coefficients you need to expand the determinant of matrix

For a 2x2 case we have a simple formula:

where trA is the trace of A (sum of its diagonal elements) and detA is the determinant of A. That is

For other cases you can use the Faddeev–LeVerrier algorithm as it is done in the Characteristic polynomial calculator.

Once you get the characteristic equation in polynomial form, you can solve it for eigenvalues. And here you can find an excellent introduction as to why we would ever care about finding eigenvalues and eigenvectors, and why they are very important concepts in linear algebra.

Similar calculators

• • Characteristic polynomial
• • Solution of nonhomogeneous system of linear equations using matrix inverse
• • Modular inverse of a matrix
• • Inverse matrix calculator
• • Matrix Transpose
• • Algebra section ( 112 calculators )

Share this page

Online Eigenvalue Calculator

Compute eigenvalues with wolfram|alpha.

• Natural Language

More than just an online eigenvalue calculator

Wolfram|Alpha is a great resource for finding the eigenvalues of matrices. You can also explore eigenvectors, characteristic polynomials, invertible matrices, diagonalization and many other matrix-related topics.

Learn more about:

• Eigenvalues

Tips for entering queries

Use plain English or common mathematical syntax to enter your queries. To enter a matrix, separate elements with commas and rows with curly braces, brackets or parentheses.

• eigenvalues {{2,3},{4,7}}
• calculate eigenvalues {{1,2,3},{4,5,6},{7,8,9}}
• find the eigenvalues of the matrix ((3,3),(5,-7))
• [[2,3],[5,6]] eigenvalues
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

• Step-by-step solutions
• Wolfram Problem Generator

Related Content

• Riemann Sum Calculator
• Synthetic Division
• Euler’s Method Calculator
• Relative Extrema Calculator
• Inflection Point Calculator
• L’Hopital’s Rule Calculator
• Tangent Plane Calculator

On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!

Nikkolas and Alex Founders and Owners of Voovers

Eigenvector Calculator

Eigenvector Lesson

Lesson contents, what is an eigenvector.

Eigenvectors are a set of vectors associated with a system of linear equations/matrix. The combination of the eigenvalues and eigenvalues of a system of equations/matrix is very useful in various mathematics, physics, and engineering problems.

“Eigen” is German for “own”. These semantics describe the relationship between the eigenvalues and eigenvectors; each eigenvalue has a corresponding eigenvector, and vice versa. The eigenvalues and eigenvectors of any linear system of equations/matrix can be found if the matrix is square. A square matrix is one that has an equal number of columns and rows. Non-square matrices will have complex/imaginary eigenvalues and eigenvectors.

How to Hand Calculate Eigenvectors

The basic representation of the relationship between an eigenvector and its corresponding eigenvalue is given as Av = λv, where A is a matrix of m rows and m columns, λ is a scalar, and v is a vector of m columns. In this relation, true values of v are the eigenvectors, and true values of λ are the eigenvalues.

For the value of a variable to be true, it must satisfy the equation such that the left and right sides of the equation are equal. Since we will solve for the eigenvalues first, the eigenvectors will satisfy the equation for each given eigenvalue. There may be more eigenvectors than eigenvalues, so each value of λ may have multiple values of v that satisfy the equation. It is possible for there to be an infinite number of eigenvectors for an eigenvalue, but usually there will only be a few distinct eigenvectors.

The equation Av = λv can be rearranged to A – I = 0 where I is the identity matrix. Then, we can proceed to carrying out the matrix multiplication and subtraction operations which will result in a polynomial. This polynomial is set equal to zero. Then, the roots of the terms can be solved for. The roots of these terms are the eigenvalues. When the eigenvalues are known, we can plug them into the equation Av = λv and find out eigenvectors.

In a matrix of m columns and rows, there can be as few as zero eigenvalues, and as many as m eigenvalues. As stated earlier, each of these eigenvalues could have any number of eigenvectors associated with it. This means that we can expect the number of eigenvectors of a system to be anywhere from zero to infinity. Now, that’s not a particularly small range of values, but we can expect the number of eigenvectors to be less than twenty when working with standard 3×3 and 4×4 matrices.

How the Calculator Works

This calculator is written in JavaScript (JS) and uses a JS native computer algebra system (CAS) for computations. Your inputted matrix is converted to a 2-dimensional JS array and then fed to the CAS.

The CAS then uses a numerical routine called the “Jacobi method” to find the eigenvectors and eigenvalues. This numerical routine involves stepping through approximated calculations that are repeated very many times until convergence to an accurate solution is reached. It then returns the eigenvalues and eigenvectors. The eigenvectors are built into an output array that is formatted into LaTeX (a math rendering language) and displayed in the answer area.

Because computer processors are so much more capable of fast, simple calculations than a human, the calculator can go through these routines in the blink of an eye and return you a result that is accurate to a minimum of the fifth decimal place.

This calculator finds the eigenvectors and eigenvalues simultaneously but displaying both can get messy for large systems/matrices. If you would like to see the eigenvalues of your matrix, visit our eigenvalue calculator . Between the two calculators, the order of eigenvalues will match the order of eigenvectors.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^4-5x^2+4=0
• \sqrt{x-1}-x=-7
• \left|3x+1\right|=4
• \log _2(x+1)=\log _3(27)
• 3^x=9^{x+5}

equation-calculator

general solution

• High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.1: Eigenvalue Problems for y'' + λy = 0

• Last updated
• Save as PDF
• Page ID 9460

• William F. Trench
• Trinity University

In Chapter 12 we’ll study partial differential equations that arise in problems of heat conduction, wave propagation, and potential theory. The purpose of this chapter is to develop tools required to solve these equations. In this section we consider the following problems, where \(\lambda\) is a real number and \(L>0\):

• Problem 1: \(y''+\lambda y=0,\quad y(0)=0,\quad y(L)=0\)
• Problem 2: \(y''+\lambda y=0,\quad y'(0)=0,\quad y'(L)=0\)
• Problem 3: \(y''+\lambda y=0,\quad y(0)=0,\quad y'(L)=0\)
• Problem 4: \(y''+\lambda y=0,\quad y'(0)=0,\quad y(L)=0\)
• Problem 5: \(y''+\lambda y=0,\quad y(-L)=y(L), \quad y'(-L)=y'(L)\)

In each problem the conditions following the differential equation are called boundary conditions . Note that the boundary conditions in Problem 5, unlike those in Problems 1-4, don’t require that \(y\) or \(y'\) be zero at the boundary points, but only that \(y\) have the same value at \(x=\pm L\), and that \(y'\) have the same value at \(x=\pm L\). We say that the boundary conditions in Problem 5 are periodic .

Obviously, \(y\equiv0\) (the trivial solution) is a solution of Problems 1-5 for any value of \(\lambda\). For most values of \(\lambda\), there are no other solutions. The interesting question is this:

For what values of \(\lambda\) does the problem have nontrivial solutions, and what are they?

A value of \(\lambda\) for which the problem has a nontrivial solution is an eigenvalue of the problem, and the nontrivial solutions are \(\lambda\)- eigenfunctions , or eigenfunctions associated with \(\lambda\) . Note that a nonzero constant multiple of a \(\lambda\)-eigenfunction is again a \(\lambda\)-eigenfunction.

Problems 1-5 are called eigenvalue problems . Solving an eigenvalue problem means finding all its eigenvalues and associated eigenfunctions. We’ll take it as given here that all the eigenvalues of Problems 1-5 are real numbers. This is proved in a more general setting in Section 13.2.

Theorem 11.1.1

Problems \(1\)–\(5\) have no negative eigenvalues. Moreover\(,\) \(\lambda=0\) is an eigenvalue of Problems \(2\) and \(5,\) with associated eigenfunction \(y_0=1,\) but \(\lambda=0\) isn’t an eigenvalue of Problems \(1,\) \(3,\) or \(4\).

We consider Problems 1-4, and leave Problem 5 to you ( Exercise 11.1.1 ). If \(y''+\lambda y=0\), then \(y(y''+\lambda y)=0\), so

\[\int_0^L y(x)(y''(x)+\lambda y(x))\,dx=0;\nonumber \]

\[\label{eq:11.1.1} \lambda\int_0^L y^2(x)\,dx=-\int_0^L y(x)y''(x)\, dx.\]

Integration by parts yields

\[\label{eq:11.1.2} \begin{array}{rcl} \int_0^L y(x)y''(x)\, dx &= \left.\ y(x)y'(x)\right| _{0}^{L} -\int_0^L (y'(x))^2\,dx \\ &=\ y(L)y'(L)-y(0)y'(0)-\int_0^L (y'(x))^2\,dx. \end{array}\]

However, if \(y\) satisfies any of the boundary conditions of Problems 1-4, then

\[y(L)y'(L)-y(0)y'(0)=0;\nonumber \]

hence, Equation \ref{eq:11.1.1} and Equation \ref{eq:11.1.2} imply that

\[\lambda\int_0^L y^2(x)\,dx=\int_0^L (y'(x))^2\, dx.\nonumber \]

If \(y\not\equiv0\), then \(\int_0^L y^2(x)\,dx>0\). Therefore \(\lambda\ge0\) and, if \(\lambda=0\), then \(y'(x)=0\) for all \(x\) in \((0,L)\) (why?), and \(y\) is constant on \((0,L)\). Any constant function satisfies the boundary conditions of Problem 2, so \(\lambda=0\) is an eigenvalue of Problem 2 and any nonzero constant function is an associated eigenfunction. However, the only constant function that satisfies the boundary conditions of Problems \(1\), \(3\), or \(4\) is \(y\equiv0\). Therefore \(\lambda=0\) isn’t an eigenvalue of any of these problems.

Example 11.1.1

Solve the eigenvalue problem

\[\label{eq:11.1.3} y''+\lambda y=0,\quad y(0)=0,\quad y(L)=0.\]

From Theorem 11.1.1 , any eigenvalues of Equation \ref{eq:11.1.3} must be positive. If \(y\) satisfies Equation \ref{eq:11.1.3} with \(\lambda>0\), then

\[y=c_1\cos\sqrt\lambda\, x+c_2\sin\sqrt\lambda\, x,\nonumber \]

where \(c_1\) and \(c_2\) are constants. The boundary condition \(y(0)=0\) implies that \(c_1=0\). Therefore \(y=c_2\sin\sqrt\lambda\, x\). Now the boundary condition \(y(L)=0\) implies that \(c_2\sin\sqrt\lambda\, L=0\). To make \(c_2\sin\sqrt\lambda\, L=0\) with \(c_2\ne0\), we must choose \(\sqrt\lambda=n\pi/L\), where \(n\) is a positive integer. Therefore \(\lambda_n=n^2\pi^2/L^2\) is an eigenvalue and

\[y_n=\sin{n\pi x\over L}\nonumber \]

is an associated eigenfunction.

For future reference, we state the result of Example 11.1.1 as a theorem.

Theorem 11.1.2

The eigenvalue problem

\[y''+\lambda y=0,\quad y(0)=0,\quad y(L)=0\nonumber \]

has infinitely many positive eigenvalues \(\lambda_n=n^2\pi^2/L^2\), with associated eigenfunctions

\[y_n=\sin {n\pi x\over L},\quad n=1,2,3,\dots.\nonumber\]

There are no other eigenvalues.

We leave it to you to prove the next theorem about Problem 2 by an argument like that of Example 11.1.1 ( Exercise 11.1.17 ).

Theorem 11.1.3

\[y''+\lambda y=0,\quad y'(0)=0,\quad y'(L)=0\nonumber \]

has the eigenvalue \(\lambda_0=0\), with associated eigenfunction \(y_0=1\), and infinitely many positive eigenvalues \(\lambda_n=n^2\pi^2/L^2\), with associated eigenfunctions

\[y_n=\cos {n\pi x\over L}, n=1,2,3\dots.\nonumber\]

Example 11.1.2

\[\label{eq:11.1.4} y''+\lambda y=0,\quad y(0)=0,\quad y'(L)=0.\]

From Theorem 11.1.1 , any eigenvalues of Equation \ref{eq:11.1.4} must be positive. If \(y\) satisfies Equation \ref{eq:11.1.4} with \(\lambda>0\), then

where \(c_1\) and \(c_2\) are constants. The boundary condition \(y(0)=0\) implies that \(c_1=0\). Therefore \(y=c_2\sin\sqrt\lambda\, x\). Hence, \(y'=c_2\sqrt\lambda\cos\sqrt\lambda\,x\) and the boundary condition \(y'(L)=0\) implies that \(c_2\cos\sqrt\lambda\,L=0\). To make \(c_2\cos\sqrt\lambda\,L=0\) with \(c_2\ne0\) we must choose

\[\sqrt\lambda={(2n-1)\pi\over2L},\nonumber \]

where \(n\) is a positive integer. Then \(\lambda_n=(2n-1)^2\pi^2/4L^2\) is an eigenvalue and

\[y_n=\sin{(2n-1)\pi x\over2L}\nonumber \]

For future reference, we state the result of Example 11.1.2 as a theorem.

Theorem 11.1.4

\[y''+\lambda y=0,\quad y(0)=0,\quad y'(L)=0\nonumber \]

has infinitely many positive eigenvalues \(\lambda_n=(2n-1)^2\pi^2/4L^2,\) with associated eigenfunctions

\[y_n=\sin{(2n-1)\pi x\over2L},\quad n=1,2,3,\dots.\nonumber \]

We leave it to you to prove the next theorem about Problem 4 by an argument like that of Example 11.1.2 ( Exercise 11.1.18 ).

Theorem 11.1.5

\[y''+\lambda y=0,\quad y'(0)=0,\quad y(L)=0\nonumber \]

\[y_n=\cos{(2n-1)\pi x\over2L},\quad n=1,2,3,\dots.\nonumber\]

Example 11.1.3

\[\label{eq:11.1.5} y''+\lambda y=0,\quad y(-L)=y(L),\quad y'(-L)=y'(L).\]

From Theorem 11.1.1 , \(\lambda=0\) is an eigenvalue of Equation \ref{eq:11.1.5} with associated eigenfunction \(y_0=1\), and any other eigenvalues must be positive. If \(y\) satisfies Equation \ref{eq:11.1.5} with \(\lambda>0\), then

\[\label{eq:11.1.6} y=c_1\cos\sqrt\lambda\, x+c_2\sin\sqrt\lambda\, x,\]

where \(c_1\) and \(c_2\) are constants. The boundary condition \(y(-L)=y(L)\) implies that

\[\label{eq:11.1.7} c_1\cos(-\sqrt\lambda\,L)+c_2\sin(-\sqrt\lambda\,L)=c_1\cos \sqrt\lambda\,L+c_2\sin \sqrt\lambda\,L.\]

\[\label{eq:11.1.8} \cos(-\sqrt\lambda\,L)=\cos \sqrt\lambda\,L\quad \text{and} \quad \sin(-\sqrt\lambda\,L)=-\sin \sqrt\lambda\,L,\]

Equation \ref{eq:11.1.7} implies that

\[\label{eq:11.1.9} c_2\sin \sqrt\lambda\,L=0.\]

Differentiating Equation \ref{eq:11.1.6} yields

\[y'=\sqrt\lambda\left(-c_1\sin\sqrt\lambda x+c_2\cos\sqrt\lambda x\right).\nonumber\]

The boundary condition \(y'(-L)=y'(L)\) implies that

\[-c_1\sin(-\sqrt\lambda\,L)+c_2\cos(-\sqrt\lambda\,L)=-c_1\sin \sqrt\lambda\,L+c_2\cos \sqrt\lambda\,L,\nonumber\]

and Equation \ref{eq:11.1.8} implies that

\[\label{eq:11.1.10} c_1\sin \sqrt\lambda\,L=0.\]

Eqns. Equation \ref{eq:11.1.9} and Equation \ref{eq:11.1.10} imply that \(c_1=c_2=0\) unless \(\sqrt\lambda =n\pi /L\), where \(n\) is a positive integer. In this case Equation \ref{eq:11.1.9} and Equation \ref{eq:11.1.10} both hold for arbitrary \(c_1\) and \(c_2\). The eigenvalue determined in this way is \(\lambda_n=n^2\pi^2/L^2\), and each such eigenvalue has the linearly independent associated eigenfunctions

\[\cos {n\pi x\over L} \quad \text{and} \quad \sin{ n\pi x\over L}. \nonumber\]

For future reference we state the result of Example 11.1.3 as a theorem.

Theorem 11.1.6

\[y''+\lambda y=0,\quad y(-L)=y(L),\quad y'(-L)=y'(L),\nonumber\]

has the eigenvalue \(\lambda_0=0\), with associated eigenfunction \(y_0=1\) and infinitely many positive eigenvalues \(\lambda_n=n^2\pi^2/L^2,\) with associated eigenfunctions

\[y_{1n}=\cos {n\pi x\over L} \quad \text{and} \quad y_{2n}=\sin {n\pi x\over L},\quad n=1,2,3,\dots.\nonumber\]

Orthogonality

We say that two integrable functions \(f\) and \(g\) are orthogonal on an interval \([a,b]\) if

\[\int_a^bf(x)g(x)\,dx=0.\nonumber\]

More generally, we say that the functions \(\phi_1\), \(\phi_2\), …, \(\phi_n\), …(finitely or infinitely many) are orthogonal on \([a,b]\) if

\[\int_a^b\phi_i(x)\phi_j(x)\,dx=0\quad \text{whenever} \quad i\ne j.\nonumber\]

The importance of orthogonality will become clear when we study Fourier series in the next two sections.

Example 11.1.4

Show that the eigenfunctions

\[\label{eq:11.1.11} 1,\, \cos{\pi x\over L},\, \sin{\pi x\over L}, \, \cos{2\pi x\over L}, \, \sin{2\pi x\over L},\dots, \cos{n\pi x\over L}, \, \sin{n\pi x\over L},\dots\]

of Problem 5 are orthogonal on \([-L,L]\).

We must show that

\[\label{eq:11.1.12} \int_{-L}^L f(x)g(x)\,dx=0\]

whenever \(f\) and \(g\) are distinct functions from Equation \ref{eq:11.1.11}. If \(r\) is any nonzero integer, then

\[\label{eq:11.1.13} \int_{-L}^L\cos{r\pi x\over L}\,dx ={L\over r\pi}\sin{r\pi x\over L}\bigg|_{-L}^L=0.\]

\[\int_{-L}^L\sin{r\pi x\over L}\,dx =-{L\over r\pi}\cos{r\pi x\over L}\bigg|_{-L}^L=0.\nonumber\]

Therefore Equation \ref{eq:11.1.12} holds if \(f\equiv1\) and \(g\) is any other function in Equation \ref{eq:11.1.11}.

If \(f(x)=\cos m\pi x/L\) and \(g(x)=\cos n\pi x/L\) where \(m\) and \(n\) are distinct positive integers, then

\[\label{eq:11.1.14} \int_{-L}^L f(x)g(x)\,dx=\int_{-L}^L\cos{m\pi x\over L} \cos{n\pi x\over L}\,dx.\]

To evaluate this integral, we use the identity

\[\cos A\cos B={1\over2}[\cos(A-B)+\cos(A+B)]\nonumber\]

with \(A=m\pi x/L\) and \(B=n\pi x/L\). Then Equation \ref{eq:11.1.14} becomes

\[\int_{-L}^L f(x)g(x)\,dx={1\over2}\left[\int_{-L}^L\cos{(m-n)\pi x\over L}\,dx +\int_{-L}^L\cos{(m+n)\pi x\over L}\,dx\right].\nonumber\]

Since \(m-n\) and \(m+n\) are both nonzero integers, Equation \ref{eq:11.1.13} implies that the integrals on the right are both zero. Therefore Equation \ref{eq:11.1.12} is true in this case.

If \(f(x)=\sin m\pi x/L\) and \(g(x)=\sin n\pi x/L\) where \(m\) and \(n\) are distinct positive integers, then

\[\label{eq:11.1.15} \int_{-L}^L f(x)g(x)\,dx=\int_{-L}^L\sin{m\pi x\over L} \sin{n\pi x\over L}\,dx.\]

\[\sin A\sin B={1\over2}[\cos(A-B)-\cos(A+B)]\nonumber\]

with \(A=m\pi x/L\) and \(B=n\pi x/L\). Then Equation \ref{eq:11.1.15} becomes

\[\int_{-L}^L f(x)g(x)\,dx={1\over2}\left[\int_{-L}^L\cos{(m-n)\pi x\over L}\,dx -\int_{-L}^L\cos{(m+n)\pi x\over L}\,dx\right]=0.\nonumber\]

If \(f(x)=\sin m\pi x/L\) and \(g(x)=\cos n\pi x/L\) where \(m\) and \(n\) are positive integers (not necessarily distinct), then

\[\int_{-L}^L f(x)g(x)\,dx=\int_{-L}^L\sin{m\pi x\over L} \cos{n\pi x\over L}\,dx=0\nonumber\]

because the integrand is an odd function and the limits are symmetric about \(x=0\).

Exercises 11.1.19-11.1.22 ask you to verify that the eigenfunctions of Problems 1-4 are orthogonal on \([0,L]\). However, this also follows from a general theorem that we'll prove in Chapter 13.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)

Eigenvectors Calculator

This calculator computes eigenvectors of a square matrix using the characteristic polynomial. The calculator will show all steps and detailed explanation.

Most popular calculators

• Factoring Polynomials
• Solving equations
• Rationalize Denominator
• Arithmetic sequences

Polynomial Calculators

• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Expand & Simplify
• Generate From Roots

Rational Expressions

• Simplifying
• Multiplication / Division
• Addition / Subtraction

Radical Expressions

Solving equations.

• Quadratic Equations (with steps)
• Polynomial Equations
• Solving Equations - With Steps

Quadratic Equation

• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism

Complex Numbers

• Modulus, inverse, polar form
• Simplify Expression

Systems of equations

• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition

Calculus Calculators

• Limit Calculator
• Derivative Calculator
• Integral Calculator

Sequences & Series

• Arithmetic Sequences
• Geometric Sequences
• Find n th Term

Analytic Geometry

• Distance and Midpoint
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection

Trigonometry

• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex

Statistics and probability

• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression

Financial Calculators

• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator

Other Calculators

• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

How to input matrix ?

1: input matrix starting from the upper left-hand corner., 2: you don't need to enter zeros., 3: you can copy and paste matrix from excel in 3 steps., 4: you don't need to use scroll bars, since the calculator will automatically remove empty rows and columns., 5: to delete matrix.

Related Calculators

Was this calculator helpful?

Please tell me how can I make this better.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)