problem solving inverse proportion

Direct & Inverse Proportions/Variations

In these lessons, we will learn how to solve direct proportions (variations) and inverse proportions (inverse variations) problems. (Note: Some texts may refer to inverse proportions/variations as indirect proportions/variations.)

Related Pages: Direct Variations Proportion Word Problems More Algebra Lessons

The following diagram gives the steps to solve ratios and direct proportion word problems. Scroll down the page for examples and step-by-step solutions.

Direct Proportions/Variations

Knowing that the ratio does not change allows you to form an equation to find the value of an unknown variable.

Example : If two pencils cost $1.50, how many pencils can you buy with $9.00?

How To Solve Directly Proportional Questions?

Example 1: F is directly proportional to x. When F is 6, x is 4. Find the value of F when x is 5. Example 2: A is directly proportional to the square of B. When A is 10, B is 2. Find the value of A when B is 3.

How To Use Direct Proportion?

How To Solve Word Problems Using Proportions?

This video shows how to solve word problems by writing a proportion and solving 1. A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour, how much sugar do I use? 2. A syrup is made by dissolving 2 cups of sugar in 2/3 cups of boiling water. How many cups of sugar should be used for 2 cups of boiling water? 3. A school buys 8 gallons of juice for 100 kids. how many gallons do they need for 175 kids?

Solving More Word Problems Using Proportions

1. On a map, two cities are 2 5/8 inches apart. If 3/8 inches on the map represents 25 miles, how far apart are the cities (in miles)? 2. Solve for the sides of similar triangles using proportions

Inverse Proportions/Variations Or Indirect Proportions

Two values x and y are inversely proportional to each other when their product xy is a constant (always remains the same). This means that when x increases y will decrease, and vice versa, by an amount such that xy remains the same.

Knowing that the product does not change also allows you to form an equation to find the value of an unknown variable

Example : It takes 4 men 6 hours to repair a road. How long will it take 8 men to do the job if they work at the same rate?

Solution : The number of men is inversely proportional to the time taken to do the job. Let t be the time taken for the 8 men to finish the job. 4 × 6 = 8 × t 24 = 8t t = 3 hours

Usually, you will be able to decide from the question whether the values are directly proportional or inversely proportional.

How To Solve Inverse Proportion Questions?

This video shows how to solve inverse proportion questions. It goes through a couple of examples and ends with some practice questions Example 1: A is inversely proportional to B. When A is 10, B is 2. Find the value of A when B is 8 Example 2: F is inversely proportional to the square of x. When A is 20, B is 3. Find the value of F when x is 5.

How To Use Inverse Proportion To Work Out Problems?

How to use a more advanced form of inverse proportion where the use of square numbers is involved.

More examples to explain direct proportions / variations and inverse proportions / variations

How to solve Inverse Proportion Math Problems on pressure and volume?

In math, an inverse proportion is when an increase in one quantity results in a decrease in another quantity. This video will show how to solve an inverse proportion math problem. Example : The pressure in a piston is 2.0 atm at 25°C and the volume is 4.0L. If the pressure is increased to 6.0 atm at the same temperature, what will be the volume?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Inverse Variation

Inverse Variation or Inverse Proportion:

Two quantities are said to vary inversely the increase (or decrease) in one quantity causes the decrease (or increase) in the other quantity.

Examples on Inverse Variation or Inverse Proportion:

(i) The time taken to finish a piece of work varies inversely as the number of men at work. (More men at work, less is the time taken to finish it)

(ii) The speed varies inversely as the time taken to cover a distance. (More is the speed, less is the time taken to cover a distance)

Solved worked-out problems on Inverse Variation:

1. If 35 men can reap a field in 8 days; in how many days can 20 men reap the same field? Solution: 35 men can reap the field in 8 days 1 man can reap the field in (35 × 8) days   [less men, more days] 20 men can reap the field in (35 × 8)/20 days   [more men, more days]                                           = 14 days Hence, 20 men can reap the field in 14 days.

2. A fort had provisions for 300 men for 90 days. After 20 days, 50 men left the fort. How long would the food last at the same rate? Solution: Remaining number of men = (300 - 50) = 250. Remaining number of days = (90 - 20) days = 70 days. 300 men had provisions for 70 days 1 man had provisions for (300 × 70) days   [less men, more days] 250 men had provisions for (300 × 70)/250 days                                                                     [more men, more days]                                           = 84 days. Hence, the remaining food will last for 84 days.

More examples on Inverse Variation word problems:

3. 6 oxen or 8 cows can graze a field in 28 days. How long would 9 oxen and 2 cows take to graze the same field? Solution: 6 oxen = 8 cows ⇒ 1 ox = 8/6 cows ⇒ 9 oxen ≡ (8/6 × 9) cows = 12 cows ⇒ (9 oxen + 2 cows) ≡ (12 cows + 2 cows) = 14 cows Now, 8 cows can graze the field in 28 days 1 cow can graze the field in (28 × 8) days   [less cows, more days] 14 cows can graze the field in (28 × 8)/14 days                                                                    [more cows, less days]                                               = 16 days Hence, 9 oxen and 2 cows can graze the field in 16 days.

4. 6 typists working 5 hours a day can type the manuscript of a book in 16 days. How many days will 4 typists take to do the same job, each working 6 hours a day? Solution: 6 typists working 5 hours a day can finish the job in 16 days 6 typists working 1 hour a day can finish it in (16 × 5) days                                                            [less hours per day, more days] 1 typist working 1 hour a day can finish it in (16 × 5 x 6)/6 days                                                             [less typists, more days] 1 typist working 6 hours a day can finish it in 6 days                                                            [more hours per day, less days] 4 typists working 6 hours a day can finish it (16 × 5 × 6)/(6 × 4) days

                                                                   = 20 days. Hence, 4 typists working 6 hours a day can finish the job in 20 days.

●   Ratio and Proportion (Direct & Inverse Variation)

Direct Variation

Practice Test on Direct Variation and Inverse Variation

●   Ratio and Proportion - Worksheets

Worksheet on Direct Variation

Worksheet on Inverse Variation

8th Grade Math Practice

From Inverse Variation to HOME PAGE

New! Comments

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

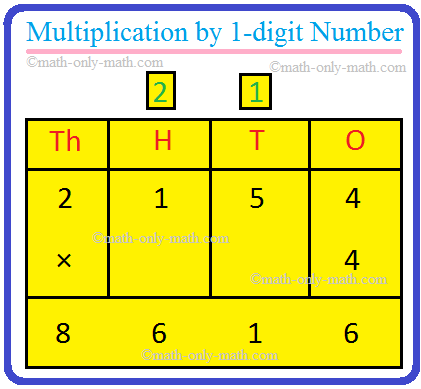
Multiplication by Ten, Hundred and Thousand |Multiply by 10, 100 &1000

Mar 29, 24 06:35 PM

Properties of Multiplication | Multiplicative Identity | Whole Numbers

Mar 29, 24 05:08 PM

Multiplication of a Number by a 3-Digit Number |3-Digit Multiplication

Mar 28, 24 06:33 PM

Multiply a Number by a 2-Digit Number | Multiplying 2-Digit by 2-Digit

Mar 27, 24 05:21 PM

Multiplication by 1-digit Number | Multiplying 1-Digit by 4-Digit

Mar 26, 24 04:14 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.3: Use Direct and Inverse Variation

• Last updated
• Save as PDF
• Page ID 142722

Learning Objectives

By the end of this section, you will be able to:

• Solve direct variation problems
• Solve inverse variation problems

Before you get started, take this readiness quiz.

If you miss a problem, go back to the section listed and review the material.

• Find the multiplicative inverse of −8 If you missed this problem, review Exercise 1.10.13 .
• Solve for n: 45=20n If you missed this problem, review Exercise 2.2.1 .
• Evaluate \(5x^2\) when x=10 If you missed this problem, review Exercise 1.3.25 .

When two quantities are related by a proportion, we say they are proportional to each other. Another way to express this relation is to talk about the variation of the two quantities. We will discuss direct variation and inverse variation in this section.

Solve Direct Variation Problems

Lindsay gets paid $15 per hour at her job. If we let s be her salary and h be the number of hours she has worked, we could model this situation with the equation

Lindsay’s salary is the product of a constant, 15, and the number of hours she works. We say that Lindsay’s salary varies directly with the number of hours she works. Two variables vary directly if one is the product of a constant and the other.

Definition: DIRECT VARIATION

For any two variables x and y , y varies directly with x if

y=kx, where \(n \ne 0\)

In applications using direct variation, generally we will know values of one pair of the variables and will be asked to find the equation that relates x and y . Then we can use that equation to find values of y for other values of x .

How to Solve Direct Variation Problems

Example \(\PageIndex{1}\)

If y varies directly with x and y=20 when x=8, find the equation that relates x and y .

Example \(\PageIndex{2}\)

If y varies directly as x and y=3, when x=10, find the equation that relates x and y .

\(y=\frac{3}{10}x\)

Example \(\PageIndex{3}\)

If y varies directly as x and y=12 when x=4, find the equation that relates x and y .

We’ll list the steps below.

Definition: SOLVE DIRECT VARIATION PROBLEMS

• Write the formula for direct variation.
• Substitute the given values for the variables.
• Solve for the constant of variation.
• Write the equation that relates x and y.

Now we’ll solve a few applications of direct variation.

Example \(\PageIndex{4}\)

When Raoul runs on the treadmill at the gym, the number of calories, c , he burns varies directly with the number of minutes, m , he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.

• Write the equation that relates c and m .
• How many calories would he burn if he ran on the treadmill for 25 minutes?

Example \(\PageIndex{5}\)

The number of calories, c , burned varies directly with the amount of time, t, spent exercising. Arnold burned 312 calories in 65 minutes exercising.

• Write the equation that relates c and t .
• How many calories would he burn if he exercises for 90 minutes?
• 432 calories

Example \(\PageIndex{6}\)

The distance a moving body travels, d , varies directly with time, t , it moves. A train travels 100 miles in 2 hours

• Write the equation that relates d and t .
• How many miles would it travel in 5 hours?

In the previous example, the variables c and m were named in the problem. Usually that is not the case. We will have to name the variables in the next example as part of the solution, just like we do in most applied problems.

Example \(\PageIndex{7}\)

The number of gallons of gas Eunice’s car uses varies directly with the number of miles she drives. Last week she drove 469.8 miles and used 14.5 gallons of gas.

• Write the equation that relates the number of gallons of gas used to the number of miles driven.
• How many gallons of gas would Eunice’s car use if she drove 1000 miles?

Notice that in this example, the units on the constant of variation are gallons/mile. In everyday life, we usually talk about miles/gallon.

Example \(\PageIndex{8}\)

The distance that Brad travels varies directly with the time spent traveling. Brad travelled 660 miles in 12 hours,

• Write the equation that relates the number of miles travelled to the time.
• How many miles could Brad travel in 4 hours?

Example \(\PageIndex{9}\)

The weight of a liquid varies directly as its volume. A liquid that weighs 24 pounds has a volume of 4 gallons.

• Write the equation that relates the weight to the volume.
• If a liquid has volume 13 gallons, what is its weight?

In some situations, one variable varies directly with the square of the other variable. When that happens, the equation of direct variation is \(y=kx^2\).

Example \(\PageIndex{10}\)

The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 4” will support a maximum load of 75 pounds.

• Write the equation that relates the maximum load to the cross-section.
• What is the maximum load that can be supported by a beam with diagonal 8”?

Example \(\PageIndex{11}\)

The distance an object falls is directly proportional to the square of the time it falls. A ball falls 144 feet in 3 seconds.

• Write the equation that relates the distance to the time.
• How far will an object fall in 4 seconds?
• \(d=16t^2\)

Example \(\PageIndex{12}\)

The area of a circle varies directly as the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.04 square inches.

• Write the equation that relates the area to the radius.
• What is the area of a pizza with a radius of 9 inches?
• \(A=3.14r^2\)
• 254.34 square inches

Solve Inverse Variation Problems

Many applications involve two variable that vary inversely . As one variable increases, the other decreases. The equation that relates them is \(y=\frac{k}{x}\).

Definition: INVERSE VARIATION

For any two variables x and y , y varies inversely with x if

y=\(\frac{k}{x}\),where \(k \ne 0\)

The word ‘inverse’ in inverse variation refers to the multiplicative inverse. The multiplicative inverse of x is \(\frac{1}{x}\).

We solve inverse variation problems in the same way we solved direct variation problems. Only the general form of the equation has changed. We will copy the procedure box here and just change ‘direct’ to ‘inverse’.

Definition: SOLVE INVERSE VARIATION PROBLEMS

• Write the formula for inverse variation.

Example \(\PageIndex{13}\)

If y varies inversely with x and y=20 when x=8 x and y .

Example \(\PageIndex{14}\)

If p varies inversely with q and p=30 when q=12 find the equation that relates p and q.

\(p=\frac{360}{q}\)

Example \(\PageIndex{15}\)

If y varies inversely with x and y=8 when x=2 find the equation that relates x and y.

\(y=\frac{16}{x}\)

Example \(\PageIndex{16}\)

The fuel consumption (mpg) of a car varies inversely with its weight. A car that weighs 3100 pounds gets 26 mpg on the highway.

• Write the equation of variation.
• What would be the fuel consumption of a car that weighs 4030 pounds?

Example \(\PageIndex{17}\)

A car’s value varies inversely with its age. Elena bought a two-year-old car for $20,000.

• What will be the value of Elena’s car when it is 5 years old?
• \(v=\frac{40,000}{a}\)

Example \(\PageIndex{18}\)

The time required to empty a pool varies inversely as the rate of pumping. It took Lucy 2.5 hours to empty her pool using a pump that was rated at 400 gpm (gallons per minute).

• How long will it take her to empty the pool using a pump rated at 500 gpm?
• \(t=\frac{1000}{r}\)

Example \(\PageIndex{19}\)

The frequency of a guitar string varies inversely with its length. A 26” long string has a frequency of 440 vibrations per second.

• How many vibrations per second will there be if the string’s length is reduced to 20” by putting a finger on a fret?

Example \(\PageIndex{20}\)

The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a block of ice melts in 2 hours when the temperature is 65 degrees.

• How many hours would it take for the same block of ice to melt if the temperature was 78 degrees?
• \(h=\frac{130}{t}\)
• \(1\frac{2}{3}\) hours

Example \(\PageIndex{21}\)

The force needed to break a board varies inversely with its length. Richard uses 24 pounds of pressure to break a 2-foot long board.

• How many pounds of pressure is needed to break a 5-foot long board?
• \(F=\frac{48}{L}\)

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Inversely Proportional – Explanation & Examples

JUMP TO TOPIC

Direct proportion

Inverse proportion, real life examples of the concept of inverse proportion, practice questions, inversely proportional – explanation & examples, what does inversely proportional mean.

In our day-to-day life, we frequently encounter situations where the variation in values of a certain quantity is influenced by the variation in values of another quantity.

For example , the siren of an approaching fire engine or ambulance is becoming as louder as the vehicle nears you and as quieter as it gets farther away. You noticed that the less the distance between you and the vehicle, the louder the siren and the more the distance, the quieter the siren becomes. This type of situation is referred to as inverse proportion or sometimes indirect proportion.

Direct and indirect proportion are two concepts that we are all familiar with, just maybe not on a mathematical level. Direct and inverse proportion are both used to show how two quantities are related to each other.

In this article, we are going to learn about inverse and indirect proportion and how these concepts are important to real life situations. but before we begin, let’s remind ourselves about the concept of direct proportion.

Two variables a and b are said to be directly proportional if an increase in one variable cause the other variable to increases too and vice versa. This mean that in direct proportion, the ratio of the corresponding values of variables remains constant. In this case if the values of b; b 1 , b 2  corresponds to the values of a; a 1 , a 2  respectively then, their ratio is constant;

a 1/ /b 1  = a 2  /b 2

Direct proportion is represented the proportional sign ‘∝’ as a ∝ b.  The formula for direct variation is given by:

where k is called the constant of proportionality.

In contrast with direct proportion, where one quantity varies directly as per changes in other quantity, in inverse proportion, an increase in one variable causes a decrease in the other variable, and vice versa. Two variables a and b are said to be inversely proportional if; a∝1/b. In this case, an increase in variable b causes a reduction in the value of variable a. Similarly, a decrease in variable b causes an increment in the value of variable a.

Indirectly Proportional Formula

If variable a is inversely proportional to variable b then, this can be represented in the formula:

ab = k; where k is the proportional constant.

To set up an inverse proportional equation, the following steps are considered:

• Write down the proportional relationship
• Write the equation using the proportional constant
• Now find the value of the constant using the given values

• The time taken by a certain number of workers to accomplish a piece of work inversely varies as the number of workers at work. This means that, the lesser the number of workers, the more time taken to finish the work and vice versa.
• The speed of a moving vessel such as a train, vehicle or ship inversely varies as the time taken to cover a certain distance. The higher the speed, the lesser the time taken to cover the distance.

It takes 8 days for 35 laborers to harvest coffee on a plantation. How long will 20 laborers take to harvest coffee on the same plantation.

• 35 laborers harvest coffee in 8 days

Duration taken by one worker = (35 × 8) days

• Now calculate the duration taken by 20 workers

= (35 × 8)/20

= 14 days Therefore, 20 laborers will take 14 days.

It takes 28 days for 6 goats or 8 sheep to graze a field. How long will 9 goats and 2 sheep take to graze the same field. Solution 6 goats = 8 sheep ⇒ 1 goat = 8/6 sheep ⇒ 9 goats ≡ (8/6 × 9) sheep = 12 sheep ⇒ (9 goats + 2 sheep) ≡ (12 sheep + 2 sheep) = 14 sheep

Now, 8 sheep => 28 days

One sheep will graze in (28 × 8) days

⇒ 14 sheep will take (28 × 8)/14 days = 16 days Hence, 9 goats and 2 sheep will take 16 days to graze the field.

Nine taps can fill a tank in four hours. How long will it take twelve taps of similar flowrate to fill the same tank?

Let the ratios;

x 1 /x 2  = y 2/ y 1

⇒ 9/x = 12/4

Therefore, 12 taps will take 3 hours to fill the tank.

Previous Lesson  |  Main Page | Next Lesson

Inverse Proportion

When two quantities are related to each other inversely, i.e., when an increase in one quantity brings a decrease in the other and vice versa then they are said to be in inverse proportion. In inverse proportion, the product of the given two quantities is equal to a constant value. Let's learn more about it in detail in this article.

What is Inverse Proportion?

The definition of inverse proportion states that "Two quantities are said to be in inverse proportion if an increase in one leads to a decrease in the other quantity and a decrease in one leads to an increase in the other quantity". In other words, if the product of both the quantities, irrespective of a change in their values, is equal to a constant value, then they are said to be in inverse proportion . For example, let us take the number of workers and the number of days required by them to complete a given amount of work as x and y respectively.

Are the number of workers and the number of days in inverse proportional relation? Let's find out.

Observe the values written in the table carefully. You will find out that for each row, the product of x and y are the same. That means if there are 16 workers, they will complete the work in 3 days. So, here x × y = 16 × 3 = 48. Now, we decrease the number of workers, it is obvious that the less number of workers will do the same work in more time. But we see the product of x and y here, it is 12 × 4 = 48. Again, for 8 workers in 6 days, the product is 48. And same for 4 workers in 12 days. So, the product of two quantities in inverse proportion is always equal.

Inverse Proportion Formula

Inverse proportion formula help in establishing a relationship between two inversely proportional quantities. Let x and y be two quantities and assume that x is decreasing when y is increasing and vice versa. Example: The speed is inversely proportional to the time. As the speed increases, the time taken by us to cover the same distance decreases. Taking speed as y and time as x, we can say that y is said to be inversely proportional to x and is written mathematically as inverse proportion formula.

The inverse proportional formula is written as

• k is the constant of proportionality .
• y increases as x decreases.
• y decreases as x increases.

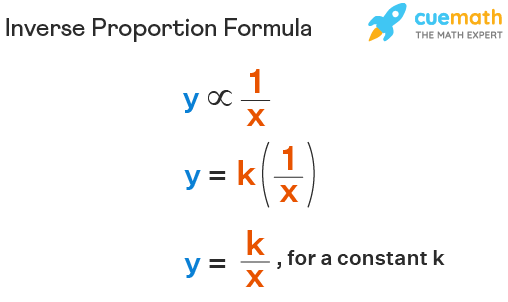
Here the symbol ∝ denotes the proportional relationship between two quantities.

Inverse Proportion Graph

The graph of inverse proportion is usually a curve that bends towards the origin forming the shape of a hyperbola . If there are any two random points each on the x-axis and y-axis on the inverse proportion graph (x) 1 , (x) 2 , (y) 1 , and (y) 2 , such that (x) 1 < (x) 2 and (y) 1 < (y) 2 , the graph will be shown like this:

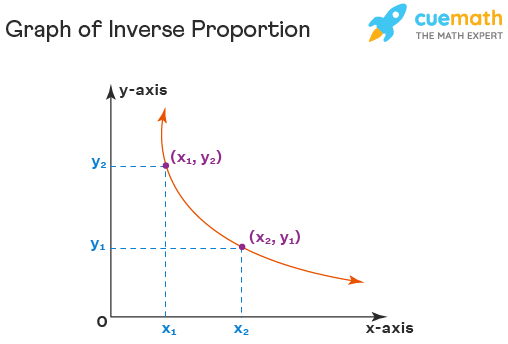
It means if we are increasing the value of x from \(x_{1}\) to \(x_{2}\), the value of y decreases from \(y_{2}\) to \(y_{1}\).

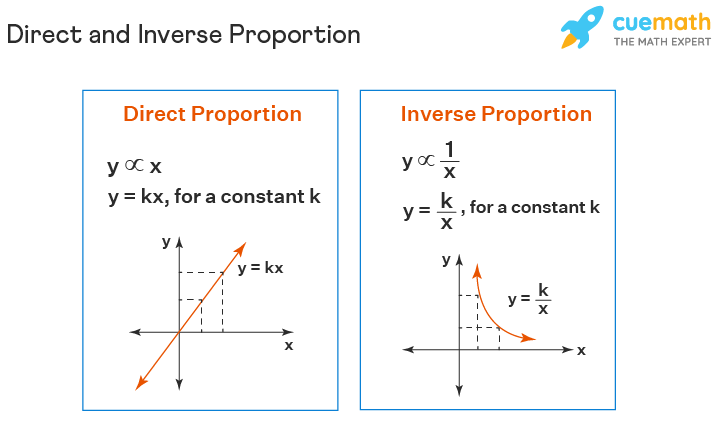
Direct and Inverse Proportion

There are two main types of proportionality - direct proportion and inverse proportion. Two variables x and y are said to be in direct proportion when y ∝ x (or x ∝ y). This implies, y = kx, for a constant k. While two variables x and y are said to be in inverse proportion if y ∝ 1/x (or x ∝ 1/y). This implies y = k/x, for a constant k. In a direct variation relationship, the ratio of two variables is equal for any values, while in inverse proportion the product of two variables is equal for any values. Look at the image given below to understand the distinction between direct and inverse proportion pictorially.

Related Topics

Check these interesting articles related to the concept of inverse proportion.

• Constant of Proportionality
• Direct Proportion
• Percent Proportion

Inverse Proportion Examples

Example 1: Suppose x and y are in an inverse proportion such that when x = 120, y = 5. Find the value of y when x = 150 using the inverse proportion formula.

To find: Value of y. Given: x = 120 when y = 5. x ∝ 1/y x = k / y, where k is a constant, or k = xy Putting, x = 120 and y = 5, we get; k = 120 × 5 = 600 Now, when x = 150, then; 150 y = 600 y = 600/150 = 4 That means when x is increased to 150 then y decreases to 4.

Answer: The value of y is 4 when x = 150.

Example 2: The time taken by a vehicle is 3 hours at a speed of 60 miles/hour. What would be the speed taken to cover the same distance at 4 hours?

Consider speed as m and time parameter as n.

If the time taken increases, then the speed decreases. This is an inverse proportional relation, hence m ∝ 1/n. Using the inverse proportion formula, m = k/ n m × n = k At speed of 60 miles/hour, time = 3 hours, from this we get, k = 60 × 3 = 180 Now, we need to find speed when time, n = 4. m × n = k m × 4 = 180 ∴ m = 180/4 = 45

Therefore, the speed at 4 hours is 45 miles/hour.

Example 3: In a construction company, a supervisor claims that 7 men can complete a task in 42 days. In how many days will 14 men finish the same task?

Consider the number of men be M and the number of days be D. Given: \(M_1\)= 7 , \(D_1\) = 42, and \(M_2\) = 14.

This is an inverse proportional relation, as if the number of workers increases, the number of days decreases.

Considering the first situation, \(M_1\) = k/ \(D_1\)

k = 7 × 42 = 294

Considering the second situation, \(M_2\) = k/ \(D_2\)

14 = 294/ \(D_2\)

\(D_2\) = 294/14 = 21

Answer: It will take 21 days for 14 men to do the same task.

go to slide go to slide go to slide

Book a Free Trial Class

Inverse Proportion Practice Questions

go to slide go to slide

FAQs on Inverse Proportion

What is an indirect proportion.

Indirect or inverse proportion is a relation between two quantities where an increase in one leads to a decrease in the other, and vice-versa. It is just the opposite of direct proportion.

What is the Symbol ∝ Denotes in Inverse Proportion Formula?

In the inverse proportion formula, the proportionate symbol ∝ denotes the relationship between two quantities. It is expressed as x ∝ 1/y. This implies x = k/y, where k is the constant of proportionality.

How do you Find K in Inverse Proportion?

K in inverse proportion represents the constant of proportionality which is the same irrespective of the values of the given variables. To find k in inverse proportion, find the product of x and y. The formula is y = k/x, which gives us k=xy.

How do you Represent the Inverse Proportional Formula?

The inverse proportional formula depicts the relationship between two quantities which can be understood by the formula given below:

• Identify the two quantities which vary in the given problem.
• Identify that there is an inverse variation. x ∝ 1/y
• Apply the Inverse proportion formula x = k/y.

What is the Difference Between Direct and Inverse Proportion?

The difference between direct and inverse proportion is that the direct proportion shows a direct relationship between the two quantities where an increase in one also leads to an increase in the other quantity and vice-versa. On the other hand, inverse proportion represents an indirect relation between two quantities or variables where an increase in one leads to a decrease in the other variable, and vice-versa.

What is the Formula of Inverse Proportion?

The formula of inverse proportion is y = k/x, where x and y are two quantities in inverse proportion and k is the constant of proportionality.

How to Show Relationship Between Two Quantities Using Inverse Proportion Formula?

The inverse proportional relationship between two quantities can be shown if the product of two quantities (x × y) is constant, then they depict an inversely proportional relationship. It is expressed as x ∝ 1/y or x = k/y, where k is the constant of proportionality.

Directly Proportional and Inversely Proportional

Directly proportional: as one amount increases, another amount increases at the same rate.

Example: you are paid $20 an hour

How much you earn is directly proportional to how many hours you work

Work more hours, get more pay; in direct proportion.

This could be written:

Earnings ∝ Hours worked

• If you work 2 hours you get paid $40
• If you work 3 hours you get paid $60

Constant of Proportionality

The "constant of proportionality" is the value that relates the two amounts

Example: you are paid $20 an hour (continued)

The constant of proportionality is 20 because:

Earnings = 20 × Hours worked

This can be written:

Where k is the constant of proportionality

Example: y is directly proportional to x, and when x=3 then y=15. What is the constant of proportionality?

They are directly proportional, so:

Put in what we know (y=15 and x=3):

Solve (by dividing both sides by 3):

The constant of proportionality is 5:

When we know the constant of proportionality we can then answer other questions

Example: (continued)

What is the value of y when x = 9?

What is the value of x when y = 2?

Inversely Proportional

Example: speed and travel time.

Speed and travel time are Inversely Proportional because the faster we go the shorter the time.

• As speed goes up, travel time goes down
• And as speed goes down, travel time goes up

Example: 4 people can paint a fence in 3 hours. How long will it take 6 people to paint it? (Assume everyone works at the same rate)

It is an Inverse Proportion:

• As the number of people goes up, the painting time goes down.
• As the number of people goes down, the painting time goes up.

We can use:

• t = number of hours
• k = constant of proportionality
• n = number of people

"4 people can paint a fence in 3 hours" means that t = 3 when n = 4

So now we know:

And when n = 6:

So 6 people will take 2 hours to paint the fence.

How many people are needed to complete the job in half an hour?

So it needs 24 people to complete the job in half an hour. (Assuming they don't all get in each other's way!)

Proportional to ...

It is also possible to be proportional to a square, a cube, an exponential, or other function!

Example: Proportional to x 2

A stone is dropped from the top of a high tower.

The distance it falls is proportional to the square of the time of fall.

The stone falls 19.6 m after 2 seconds, how far does it fall after 3 seconds?

• d is the distance fallen and
• t is the time of fall

When d = 19.6 then t = 2

And when t = 3:

So it has fallen 44.1 m after 3 seconds.

Inverse Square

Inverse Square : when one value decreases as the square of the other value.

Example: light and distance

The further away we are from a light, the less bright it is.

In fact the brightness decreases as the square of the distance. Because the light is spreading out in all directions.

So a brightness of "1" at 1 meter is only "0.25" at 2 meters (double the distance leads to a quarter of the brightness), and so on.

Helping with Math

Inverse Proportion

Introduction

We frequently come into situations in our daily lives when the change in values of one quantity is affected by the change in values of another quantity. Two quantities can be related through proportionality. A change in one quantity’s proportion could sometimes result in a change in the proportion of another. Let us say, for instance, that if we drive faster, it takes less time to travel a certain distance. This scenario shows inverse proportionality between two quantities. 

The definition of inverse proportion, how it differs from direct proportion , real-life applications, and various examples of inverse proportion will all be covered in this article.

What is Inverse Proportion?

Inverse proportion refers to the relationship between two quantities if an increase in one causes a decrease in the other and a decrease in one causes an increase in the other. In other terms, two quantities are said to be in inverse proportion if their product is equal to a constant value regardless of changes in their values.

They are said to be in inverse proportion when one quantity increases while the other decreases and vice versa. Let’s examine the table below to provide an example of inverse proportion.

Let us find out how the numbers show an inverse proportion by getting the product of each row. The table third column, ab, shows that the product of a and b are the same.

We can say that the numbers in columns a and b as “ a is inversely proportional to b” or may be represented as a∝b. Let us use the equation below to calculate the other values.

a=$\frac{64}{b}$

When b=32, a=$\frac{64}{32}$=2.

When b=16, a=$\frac{64}{16}$=4.

When b=8, a=$\frac{64}{32}$=8.

When b=4, a=$\frac{64}{4}$=16.

When b=2, a=$\frac{64}{2}$=32.

When b=1, a=$\frac{64}{1}$=64.

Formula: Inverse Proportion

The inverse proportion formula can determine a relationship between two inversely proportional quantities. Assume that x decreases when y increases and vice versa for the two values, x and y. 

As an illustration, consider the relationship between speed and time. With increasing speed, it takes less time for us to cover a certain distance.

Time travel decreases as speed increases. Time travel increases as speed decreases.

The relationship between speed and time, denoted as y and x, can be expressed mathematically as the inverse proportion formula.

Written as follows is the inverse proportional formula:

y=$\frac{k}{x}$

Take note of the following:

k is the constant of proportionality As x decreases, y increases. As x increases, y decreases.

The formulas below also show inverse proportionality. 

y∝$\frac{1}{x}$; y=k⋅$\frac{1}{x}$; y=k ($\frac{1}{x}$)

The proportional relationship between two quantities is indicated here by the symbol .

Real World Examples of Inverse Proportion

Among the many inverse proportions scenarios are the following examples:

( 1 ) A moving object’s speed, such as a moving train, car, or ship, inversely varies with the time necessary to travel a specific distance. Less time is needed to complete a distance as speed increases.

As speed increases , time travel decreases . As speed decreases , time travel increases .

( 2 )The number of people or workers present at work is inversely proportional to the amount of time it takes for a given number of people or workers to perform a task. This implies that the length of time it takes to complete the work increases with the number of workers and vice versa.

As the number of people or workers increases , the time it takes to finish a task decreases.   As the number of people or workers decreases , the time it takes to finish a task increases.  

( 3 ) The distance between you and an ambulance as it is approaching impacts how loud its siren will be. As the ambulance approaches you, the siren becomes louder, and as it moves away, it gets quieter. The siren gets louder and quieter depending on how far away you are from the ambulance. The louder the siren, the closer you are.

As the distance between you and an ambulance increases , the sound of the siren decreases . As the distance between you and an ambulance decreases , the sound of the siren increases .

( 4 ) The brightness of a streetlight has an inverse relationship with the distance between you and it. This indicates that the streetlight’s brightness decreases as you get farther away. The streetlight will typically be brighter if you are 50 meters from it than if you are 200 meters away.

As the distance between you and the streetlight increases, its brightness decreases. As the distance between you and the streetlight decreases, its brightness increases.

( 5 ) The number of goods you can buy is inversely related to the price of each item. Suppose you were to consider your spending limit when purchasing some apples from the market. If the price of each apple is \$0.50 instead of \$0.75, you can buy more apples.

( 6 ) A device’s battery life is inversely proportional to the amount of time it is utilized. Consider charging a device, let us say for example a laptop, to 95% before using it. Let us suppose that after an hour of use, the battery lowers to 85%, after two hours, it reduces to 77%. A considerable and proportional decline in the battery percentage may be immediately detected with an increase in the amount of time that the device is being utilized.

Aside from the listed above, there are more examples of scenarios that involve inverse proportion. Remember that when two things are said to be in inverse proportion, a change in one quantity corresponds to a corresponding decrease or increase in the other. If we know essential information pertaining to the problem statement, the concept of inverse proportion makes it easy for us to calculate the amount or value of a missing entity. 

Direct vs Inverse Proportion

Direct proportion and inverse proportion are the two main types of proportionality. To illustrate how the amounts and quantities relate to one another, a direct and inverse proportion is used. The symbol is used to denote proportionality. Let us say, for example, the variable x and y; if y is proportional to x, then it is represented as y∝x. If we have y is inversely proportional to x, then it is represented as y∝$\frac{1}{x}$. Now in both instances, the value of “y” changes in relation to “x,” or the value of “x” changes in relation to “y”. A proportionality constant is equivalent to the change in both values. 

Direct Proportion

When y∝x, two variables x and y are said to be in direct proportion. This suggests that, for a constant k, y = kx. The ratio of two variables in a direct variation relationship is equal for all values.

When y∝1/x, two variables, x and y, are said to be in inverse proportion. This means that, for a constant k, y = k/x. The product of two variables in an inverse proportion relationship is equal for all values. 

To visualize the difference between direct and inverse proportion, look at the illustration below.

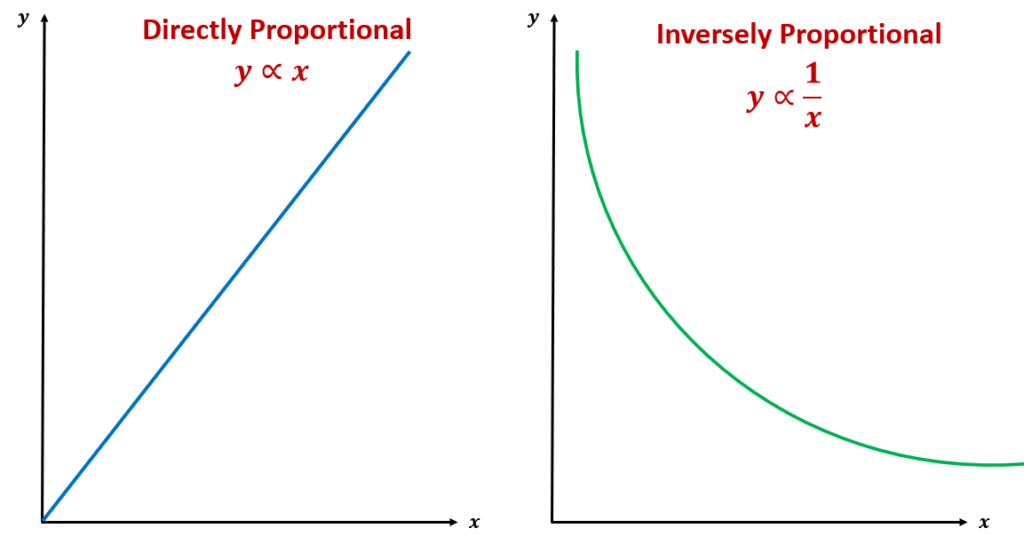
For the graph of directly proportional, it shows that as the value of x increases, the value of y increases also. We may also say that as y decreases, x also decreases. On the other hand, for the graph inversely proportional, as the value of x increases, the value of y decreases or when x decreases, the value of y increases.

Graph of Inverse Proportion

The graph below shows that the quantities are in inverse proportion. It shows the relationship between the x and y values. It reads as y is inversely proportional to x.

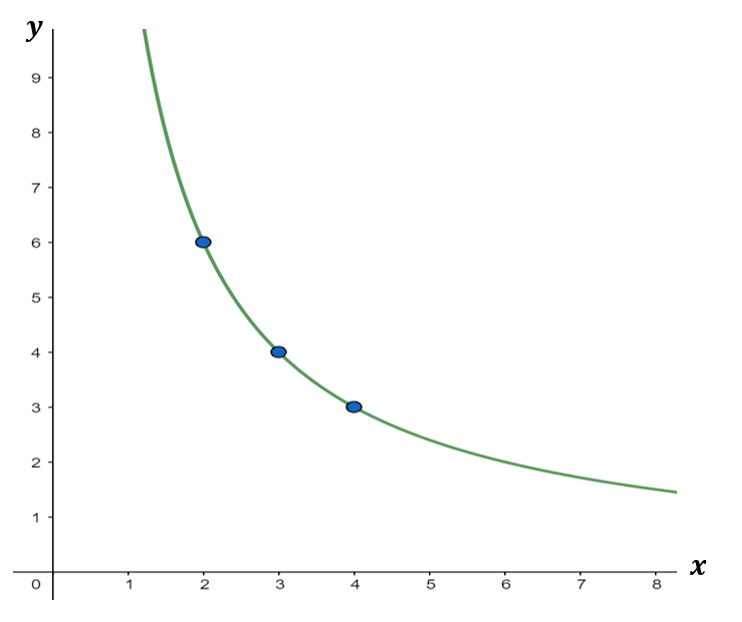
Using the graph above, let us identify some points and arrange them in a table. 

Let us say that Point A has the coordinates ( 2, 6 ), Point B has the coordinates ( 3, 4 ), and Point C has the coordinates ( 4, 3 ). 

By the inverse proportion formula, let us check if the graph indeed shows an inverse proportion.

Since the product of x and y is constant, the given data shows inverse proportionality with an equation y=$\frac{12}{x}$. Thus, if we want to find the values of x given y or vice versa, we can easily identify them. For example, 

Therefore, the other coordinates on the graph are ( 6, 2 ) and ( $\frac{2}{3}$, 18 ).

How Should I Write Indirect Proportion Equations?

The steps listed here should be followed when writing an inverse proportion equation.

1. Find the constant of proportionality.

2. Enter the proportionality constant into an equation after finding it.

Let us use the table below as an example and figure out its inverse proportion equation.

Using the steps mentioned above, let us write the indirect proportion equation of the given data. 

Since the formula for indirect proportion is y=$\frac{k}{x}$, where k is the constant of proportionality, we will have,

The given data indeed shows an inverse proportion since the product of the shared x and y values is constant.

The proportion equation of the data given is:

y=$\frac{100}{x}$

Knowing the indirect proportion equation will help us to identify unknown values. For example, if y=10, then x must be equal to 10.

More Examples

Assume that 4 people work at the same rate in painting a fence for 6 hours. 

( a ) How long will it take 8 people to paint the fence?

( b ) How long will it take 12 people to paint the fence?

( c ) How many people are needed to complete the task in 30 minutes?

This scenario shows an inverse proportion since. The painting time will go down if the number of people goes up. Let us use the inverse proportion equation,

where y is the number of hours spent painting the fence, x is the number of people working, and k is the constant of proportionality.

Since 4 people can paint the fence in 6 hours, we have x=4 and y=6. Plugging in these values in the equation, we have,

6=$\frac{k}{4}$ 6⋅4=k 24=k k=24

Now that we already know the constant of proportionality, which is 24, we now have the equation,

 y=$\frac{24}{x}$

Let us plug in 8 to the value of x in the equation.

y=$\frac{24}{8}$ y=3

Therefore, it will take 3 hours for 8 people to paint the fence.

Plugging in x=12 to the inverse proportion equation we have,

y=$\frac{24}{12}$ y=2

Hence, 12 people can finish painting the fence in 2 hours.

In this question, we will use ½ or 0.5 hours since it is equivalent to 30 minutes. This time y=½, and we are solving for x.

Substituting ½ in the equation,

12=$\frac{24}{x}$ x=24⋅2 x=48

Thus, 48 people are needed to finish the task in 30 minutes.

The value p is inversely proportional to r. If p=40 and r=2,

( a ) Find the equation relating the given data. ( b ) If p=20, what is r? ( c ) If r=5, find p.

( a ) Find the equation relating the given data.

The statement p is inversely proportional to r is written as,

p∝$\frac{1}{r}$

To find the equation relating p and r, let us use the formula p=kr to identify the constant of proportionality.

p=$\frac{k}{r}$ 40=$\frac{k}{2}$ 40⋅2=k 80=k k=80

Since we already know that 80 is the constant of proportionality, we have the equation,

p=$\frac{80}{r}$

( b ) If p=20 , what is r?

Let us substitute the given value of p to the inverse proportion equation.

p=$\frac{80}{r}$ 20=$\frac{80}{r}$ r=$\frac{80}{20}$ r=4

Therefore, the value of r is equal to 4 when p is 20. 

( c ) If r=5, find p.

This time, r is given, and we must find the value of p.

p=$\frac{80}{5}$ p=16

Hence, when r=5, the value of p is 16.

Suppose it takes 3 students to finish a project in 6 hours. When 9 students are working on the same project, how long does it take to complete the task?

Let x=number of students and y=hours spent doing the project.

Let us first find the constant of proportionality. Thus, we have

y=$\frac{k}{x}$ 6=$\frac{k}{3}$ 6⋅3=k 18=k k=18

Hence, the inverse proportion equation to represent the scenario is,

y=$\frac{18}{x}$

Since k=18, let us now solve for hours spent in doing the project if 9 students will be working on it.

y=$\frac{k}{9}$ y=2

Therefore, it will take 2 hours to finish the project by 9 students.

Suppose the table below shows an inverse proportion. 

( a ) Find the constant of proportionality ( b ) Write the equation of inverse proportion ( c ) Complete the table.

The table has given the values for x and y. Since they are inversely proportional, we may have the equation,

 ( a ) Find the constant of proportionality

Let us find the constant of proportionality from the table where both x and y are given.

Hence, the constant of proportionality is 60.

( b ) Write the equation of inverse proportion.

By substituting the computed constant of proportionality, the equation is,

( c ) Complete the table.

Here is the complete table.

y=$\frac{60}{x}$ 10=$\frac{60}{x}$ x=$\frac{60}{10}$ x=6

y=$\frac{60}{x}$ y=$\frac{60}{4}$ x=15

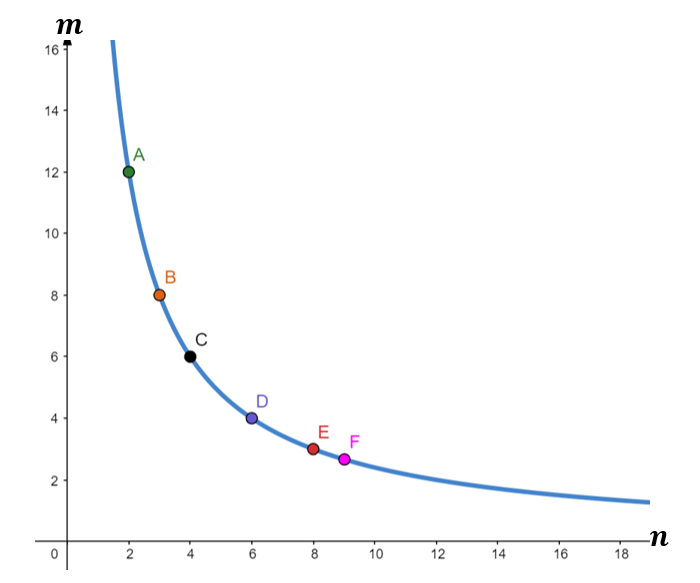
m is inversely proportional to n. When m=4, n=6.

Draw the graph after filling out the values in the table below.

Since m is inversely proportional to n, in symbols, it is written as m∝$\frac{1}{n}$. 

Let us use the given values of n and m to find the constant of proportionality. Hence, we will use the formula,

m=$\frac{k}{n}$

Substituting the given values, we have, 

Knowing the value of the constant of proportionality makes it easy to complete the data.

We will now utilize the equation m=$\frac{24}{n}$.

The table below shows the completed data.

Let us write each pair as coordinates of points A, B, C, D, E, and F. Hence, we may have, 

Point A ( 2, 12 )

Point B ( 3, 8 )

Point C ( 4, 6 )

Point D ( 6, 4 )

Point E ( 8, 3 )

Point F ( 9, $\frac{8}{3}$ )

The figure below shows the graph of m=$\frac{24}{n}$.

Definition: Two quantities are said to be in inverse proportion when one quantity increases while the other decreases and vice versa.

Formula:  

How do I Write inverse proportion Equations?

1. Find the constant of proportionality. 2. Enter the proportionality constant into an equation after finding it.

Frequently Asked Questions on Inverse Proportion (FAQs)

What is meant by inverse proportion.

One kind of proportionality relationship is inverse proportion. There is an inverse proportionality in two quantities when one quantity’s value increases relative to a decrease in another or vice versa.

Other names for inverse proportion include indirect proportion and inverse variation. Examples of inverse proportion include the amount of time it takes to travel a certain distance lowers as our speed rises, and the time it takes to finish a task decreases as more people work on it. 

How do the inverse and direct proportions differ from one another?

Direct proportion and inverse proportion are the two main types of proportionality. To illustrate how the amounts and quantities relate to one another, a direct and inverse proportion is used. The symbol is used to denote proportionality. 

y∝x is read as “y is directly proportional to x”. y∝$\frac{1}{x}$ is read as “y is inversely proportional to x”.

What is the equation for inverse proportion?

The equation for inverse proportion is y=$\frac{k}{x}$ or xy=k, where k is the constant of proportionality. You can use the known values to get the value of the constant k and then apply this formula to determine all the other unknown values.

How do you find the value of “k” in an inverse proportion?

The variable “k” is the constant of proportionality. In inverse proportion, we follow the formula y=$\frac{k}{x}$ when y is inversely proportional to x. Hence, to find the value of “k”, you must get the product of the given values of x and y.

Let us say, for instance, that y is inversely proportional to x, and we know that x=5 and y=6. Here is how to find the constant of proportionality, “k”.

k=xy k=5⋅6 k=30

Hence, the constant of proportionality for the inverse proportion is 30. The equation that represents the given value is,

y=$\frac{30}{x}$

Finding the value of the constant of proportionality is very helpful for solving the equation for the inverse proportion and for determining other values. Therefore, we can readily determine y as 3 or 2, respectively, if x is 10 or 15.

Recommended Worksheets

Inverse Proportion (Summer Themed) Math Worksheets Direct Proportion (Labor Day Themed) Math Worksheets Proportion (Thanksgiving Day Themed) Math Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

<a href="https://helpingwithmath.com/inverse-proportion/">Inverse Proportion</a>

"Inverse Proportion". Helping with Math . Accessed on March 31, 2024. https://helpingwithmath.com/inverse-proportion/.

"Inverse Proportion". Helping with Math , https://helpingwithmath.com/inverse-proportion/. Accessed 31 March, 2024.

Additional Numbers Theory:

Latest worksheets.

The worksheets below are the mostly recently added to the site.

Expressing the Sum of Numbers Using Rectangular Array 2nd Grade Math Worksheets

Addition of Three-Digit Numbers (Halloween themed) Worksheets

Comparing Measurement using the SI Unit 2nd Grade Math Worksheets

Different Measuring Tools for Length 2nd Grade Math Worksheets

Understanding Basic Money Denominations 2nd Grade Math Worksheets

Understanding Number Lines 2nd Grade Math Worksheets

Shape Partitions (Rectangles and Circles) 2nd Grade Math Worksheets

Understanding the Metric System Unit of Measurement for Length 2nd Grade Math Worksheets

Naming Numbers Up To 1000 2nd Grade Math Worksheets

Understanding Picture Graph and Bar Graph 2nd Grade Math Worksheets

WORD PROBLEMS ON INVERSE PROPORTION

Inverse proportion :

Inverse proportion is a situation where an increases in one quantity causes a corresponding decreases in the other quantity.

Inverse proportion is a situation where an decreases in one quantity causes a corresponding increases in the other quantity.  

Problem 1 :

6 pumps are required to fill a water sump in 1 hr 30 minutes. What will be the time taken to fill the sump if one pump is switched off ?

Let x be the required time taken.

As the number of pumps increases the time taken to fill the sump will be less.

It comes under inverse proportion.

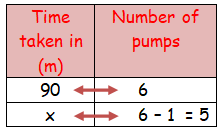
90  ⋅  6 = x  ⋅ 5

540 = x  ⋅   5

540/5 = x 

108/60 = 1 hour 48 min

Therefore, the time taken to fill the sump is 1 hour 48 min.

Problem 2 :

A farmer has enough food for 144 ducks for 28 days. If he sells 32 ducks, how long will the food last? 

Let the required number of days be x.

As the number of ducks decreases the food will last for more days.

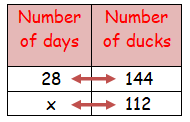
28  ⋅  144 =  x   ⋅   112

4032 = x   ⋅   112

4032/112 = x

  36 = x

Therefore, the food last for 36 days.

Problem 3 :

If takes 60 days for 10 machines to dig a hole. Assuming that all machines work at the same speed, how long will it take 30 machines to dig the same hole?

Let the number of days required be x.

As the number of machines increases it takes less days to complete the work.

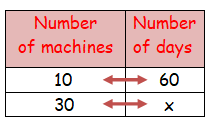
  10  ⋅   60 = 30  ⋅  x

600 = 30  ⋅  x

Therefore, it takes 20 days to dig the hole.

Problem 4 :

Forty students stay in a hostel. They had food stock for 30 days. If the students are doubled then for how many days the stock will last?

Let x be the required number of days.

As the number of students increases the food last for less number of days.

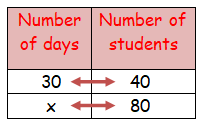
30  ⋅   40 = x  ⋅  80

1200 = x  ⋅  80

1200/80 = x

Therefore, the food stock lasts for 15 days.

Problem 5 :

Meena had enough money to send 8 parcels each weighing 500 grams through a courier service. What would be the weight of each parcel, if she has to send 40 parcels for the same money?

Let the weight of parcel be x grams.

As the number of parcels increases weight of a parcel decreases.

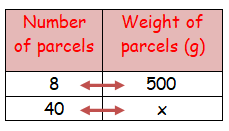
8  ⋅  500 = 40  ⋅  x

4000 = 40  ⋅  x

4000/40 = x

Therefore, the weight of each parcel is 100 grams.

Problem 6 :

If takes 120 minutes to weed a garden with 6 gardeners if the same work is to be done in 30 minutes, how many more gardeners are needed?

Let the number of gardeners needed be x.

As the number of gardeners increases the time decreases.

6  ⋅   120 = x  ⋅   30

720 = x  ⋅   30

To complete the work in 30 min gardeners needed = 24.

Already existing gardeners = 6

Therefore, 18 more gardeners are needed.

Problem 7 :

Heena goes by bi-cycle to her school every day. Her average speed is 12 km/hr. and she reaches school in 20 minutes. What is the increase in speed, if she reaches the school in 15 minutes?

Let the speed to reach school in 15 minutes be x.

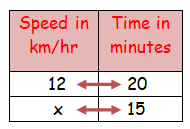
If she reaches the school in 15 minutes the speed = 16   km/hr.

Already running with 12 km/hr.

Increased speed = 16 – 12 = 4  km/hr.

Therefore, the increase in speed is 4 km/hr.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Honors Algebra 2 Problems on Solving Exponential Equations

Mar 30, 24 11:45 PM

Properties of Parallelograms Worksheet

Mar 30, 24 09:11 PM

Division by Zero

Mar 30, 24 08:11 AM

• Maths Questions
• Direct And Inverse Proportion Questions

Direct and Inverse Proportion Questions

Direct and inverse proportions are two important basic concepts of algebra in mathematics. These concepts are useful in identifying the relationship between two quantities and establishing the equation for the same. Solving direct and inverse proportion questions will help you to solve many real-world problems. Also, practise additional questions on direct proportion and inverse proportion here in this article.

Direct and Inverse Proportion – Meaning

Suppose two variables or quantities change in the same direction, they are said to be in direct proportion. That means if one quantity or variable increases, the other quantity or variable also increases and vice versa.

Suppose two variables or quantities change in the opposite direction, they are said to be in inverse proportion. That means if one quantity or variable increases, the other quantity or variable will decrease and vice versa.

Click here to get more information about direct and inverse proportions .

Direct and Inverse Proportion Questions and Answers

1. Suppose x and y are in inverse proportion. If y = 12 then x = 4, find the value of y when x = 8.

Given, x and y are in inverse proportion.

4 = k/12 (where k is a constant)

k = 4 × 12 = 48

Also, given that, x = 8

Thus, the value of y is 6 when x = 8.

2. The variable x is inversely proportional to y. If x increases by m%, then by what percent will y decrease?

By the definition of inverse proportion, two quantities, x and y, are said to be inversely proportional if a decrease in x causes a proportional increase in y and vice-versa.

If the variable x is inversely proportional to y, then xy = k(constant).

Thus, if x increases by m%, then y decreases by m%.

3. If two cardboard boxes occupy 500 cubic centimetres of space, then how much space is required to keep 200 such boxes?

2 cardboard boxes occupy 500 cubic centimetres.

Space required for 200 boxes = ?

As the number of boxes increases, the space required to keep them increases, so this is a case of direct proportion.

Let x cubic centimetres be the required space.

So, 2/500 = 200/x

2x = 200 × 500

x = (200 × 500)/2

Therefore, the required space is 50,000 cubic centimetres.

4. If 35 men can finish a piece of work in 8 days, in how many days can 20 men complete the same work?

35 men can finish a piece of work in 8 days.

1 man can finish the work in (35 × 8) days.

That means less men and more days.

Here, we can see the inverse proportion between men and the amount of work done.

20 men can complete the work in (35 × 8)/20 days = 14 days

Therefore, 20 men can finish the same work in 14 days.

5. If 270 kg of corn would feed 42 horses for 21 days, for how many days would 360 kg of corn feed 21 horses?

270 kg of corn would feed 42 horses for 21 days.

We have to find the number of days it would take to feed 360 kg of corn to 21 horses.

As we know, N₁D₁/W₁ = N₂D₂/W₂

where N = Number of horses

D = Number of days

W = Amount of corn

From the given,

N₁ = 42 , D₁ = 21, W₁ = 270 kg

N₂ = 21 , W₂ = 360 kg and D₂ = ?

∴ (42 × 21)/270 = (21 × D₂)/360

⇒ D₂ = (42 × 21 × 360)/(270 × 21)

Therefore, the number of days taken to feed 360 kg of corn to 21 horses is 56 days.

6. l varies directly as m, and l is equal to 5 when m = 2/3. Find l when m = 16/3.

If l varies directly as m.

l/m = k….(i)

l/m = 5/(2/3)

That means k = 15/2

Now, m = 16/3

Substituting m = 16/3 and k = 15/2 in equation (i), we get;

l/(16/3) = 15/2

3l/16 = 15/2

l = (15/2) × (16/3)

Therefore, l = 40 when m = 16/3.

7. Find the values of x and y if a and b are in inverse proportion:

When a and b are inversely proportional, then ab = k, where k is any constant.

i.e., 12 × 30 = k

Now consider the values in the next column.

Similarly, 8y = k

Hence, x = 72 and y = 45.

8. If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get if the number of children is reduced by 4?

Given that a box of sweets was distributed among 24 children.

The number of sweets that can be given to each child = 5

Total number of sweets = 24 × 5 = 120 sweets.

If the number of children is reduced by 4, then the remaining number of children = 24 – 4 = 20

Here, the number of children is reduced and the number of sweets for each child will be reduced.

Thus, both are in inverse proportion.

Hence, the number of sweets that can be given to each child = 120/20 = 6

9. A worker is paid Rs. 225 for 9 days of work. If he works for 22 days, how much will he get?

Amount paid for 9 days of work = Rs. 225

Let x be the amount to be paid to the worker for 22 days.

Here, the amount to be paid for 22 days will be more than the amount paid for 9 days.

That means both are in direct proportion.

So, 9/225 = 22/x

x = (22 × 225)/9

x = 22 × 25 = 550

Therefore, the worker gets Rs. 550 for 22 working days.

10. P is directly proportional to Q².

When P = 50, Q = 5

(i) Find a formula for P in terms of Q.

(ii) Find the value of P when Q = 3

(iii) Find the value of Q when P = 200

Given that P is directly proportional to Q².

So, P/Q² = k

When P = 50 and Q = 5,

(i) Formula for P in terms of Q is: P = kQ²

Using the relation, P = kQ², we have;

P = 2 × (3)² {since k = 2}

Thus, P = 18 when Q = 3.

(iii) P = 200

200 = 2Q² {since k = 2}

⇒ Q² = 200/2 = 100

Therefore, Q = 10 when P = 200.

Practice Questions on Direct and Inverse Proportion

• If a car covers 102 km in 6.8 litres of petrol, how much distance will it cover in 24.2 litres?
• Reena takes 125 minutes to walk a distance of a hundred metres. What distance would she cover in 315 minutes?
• Both x and y vary directly, and when x is 10, y is 14. Find the value of x when y is 49.
• If x and y are inversely proportional, then find the values of p, q, and r.
• A school has 8 periods a day, each of 45 minutes duration. How long would each period be if the school has 9 periods a day, assuming the number of school hours to be the same?

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Direct and Inverse Proportion Practice Questions

Click here for questions, click here for answers .

variation, proportionality

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024