problem solving involving exponential functions

Forgot password? New user? Sign up

Existing user? Log in

Exponential Functions - Problem Solving

Already have an account? Log in here.

Recommended Course

Complex numbers.

The beauty of Algebra through complex numbers, fractals, and Euler’s formula.

• Andrew Hayes

An exponential function is a function of the form \(f(x)=a \cdot b^x,\) where \(a\) and \(b\) are real numbers and \(b\) is positive. Exponential functions are used to model relationships with exponential growth or decay. Exponential growth occurs when a function's rate of change is proportional to the function's current value. Whenever an exponential function is decreasing, this is often referred to as exponential decay .

To solve problems on this page, you should be familiar with

• rules of exponents - algebraic
• solving exponential equations
• graphs of exponential functions .

Growth and Decay

Problem solving - basic, problem solving - intermediate, problem solving - advanced.

Suppose that the population of rabbits increases by 1.5 times a month. When the initial population is 100, what is the approximate integer population after a year? The population after \(n\) months is given by \(100 \times 1.5^n.\) Therefore, the approximate population after a year is \[100 \times 1.5^{12} \approx 100 \times 129.75 = 12975. \ _\square \]

Suppose that the population of rabbits increases by 1.5 times a month. At the end of a month, 10 rabbits immigrate in. When the initial population is 100, what is the approximate integer population after a year? Let \(p(n)\) be the population after \(n\) months. Then \[p(n+2) = 1.5 p(n+1) + 10\] and \[p(n+1) = 1.5 p(n) + 10,\] from which we have \[p(n+2) - p(n+1) = 1.5 \big(p(n+1) - p(n)\big).\] Then the population after \(n\) months is given by \[p(0) + \big(p(1) - p(0)\big) \frac{1.5^{n} - 1}{1.5 - 1} .\] Therefore, the population after a year is given by \[\begin{align} 100 + (160 - 100) \frac{1.5^{12} - 1}{1.5 - 1} \approx& 100 + 60 \times 257.493 \\ \approx& 15550. \ _\square \end{align}\]

Suppose that the annual interest is 3 %. When the initial balance is 1,000 dollars, how many years would it take to have 10,000 dollars? The balance after \(n\) years is given by \(1000 \times 1.03^n.\) To have the balance 10,000 dollars, we need \[\begin{align} 1000 \times 1.03^n \ge& 10000 \\ 1.03^n \ge& 10\\ n \log_{10}{1.03} \ge& 1 \\ n \ge& 77.898\dots. \end{align}\] Therefore, it would take 78 years. \( _\square \)

The half-life of carbon-14 is approximately 5730 years. Humans began agriculture approximately ten thousand years ago. If we had 1 kg of carbon-14 at that moment, how much carbon-14 in grams would we have now? The weight of carbon-14 after \(n\) years is given by \(1000 \times \left( \frac{1}{2} \right)^{\frac{n}{5730}}\) in grams. Therefore, the weight after 10000 years is given by \[1000 \times \left( \frac{1}{2} \right)^{\frac{10000}{5730}} \approx 1000 \times 0.298 = 298.\] Therefore, we would have approximately 298 g. \( _\square \)

Given three numbers such that \( 0 < a < b < c < 1\), define

\[ A = a^{a}b^{b}c^{c}, \quad B = a^{a}b^{c}c^{b} , \quad C = a^{b}b^{c}c^{a}. \]

How do the values of \(A, B, C \) compare to each other?

\[\large 2^{x} = 3^{y} = 12^{z} \]

If the equation above is fulfilled for non-zero values of \(x,y,z,\) find the value of \(\frac { z(x+2y) }{ xy }\).

If \(5^x = 6^y = 30^7\), then what is the value of \( \frac{ xy}{x+y} \)?

If \(27^{x} = 64^{y} = 125^{z} = 60\), find the value of \(\large\frac{2013xyz}{xy+yz+xz}\).

\[\large f(x)=\frac{e^x+e^{-x}}{e^x-e^{-x}} \]

Suppose we define the function \(f(x) \) as above. If \(f(a)=\frac{5}{3}\) and \(f(b)=\frac{7}{5},\) what is the value of \(f(a+b)?\)

\[\large \left(1+\frac{1}{x}\right)^{x+1}=\left(1+\frac{1}{2000}\right)^{2000}\]

Given that \(x\) is an integer that satisfies the equation above, find the value of \(x\).

\[\Large a^{(a-1)^{(a-2)}} = a^{a^2-3a+2}\]

Find the sum of all positive integers \(a\) that satisfy the equation above.

Find the sum of all solutions to the equation

\[ \large (x^2+5x+5)^{x^2-10x+21}=1 .\]

\[\large |x|^{(x^2-x-2)} < 1 \]

If the solution to the inequality above is \(x\in (A,B) \), then find the value of \(A+B\).

Master concepts like these

Learn more in our Complex Numbers course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 2   >   Unit 6

Solving exponential equations using exponent properties.

• Solve exponential equations using exponent properties
• Solving exponential equations using exponent properties (advanced)
• Solve exponential equations using exponent properties (advanced)
• Rational exponents and radicals: FAQ

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

6.6 Exponential and Logarithmic Equations

Learning objectives.

In this section, you will:

• Use like bases to solve exponential equations.
• Use logarithms to solve exponential equations.
• Use the definition of a logarithm to solve logarithmic equations.
• Use the one-to-one property of logarithms to solve logarithmic equations.
• Solve applied problems involving exponential and logarithmic equations.

In 1859, an Australian landowner named Thomas Austin released 24 rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.

Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.

Using Like Bases to Solve Exponential Equations

The first technique involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers b , b , S , S , and T , T , where b > 0 , b ≠ 1 , b > 0 , b ≠ 1 , b S = b T b S = b T if and only if S = T . S = T .

In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.

For example, consider the equation 3 4 x − 7 = 3 2 x 3 . 3 4 x − 7 = 3 2 x 3 . To solve for x , x , we use the division property of exponents to rewrite the right side so that both sides have the common base, 3. 3. Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for x x :

Using the One-to-One Property of Exponential Functions to Solve Exponential Equations

For any algebraic expressions S and  T , S and  T , and any positive real number b ≠ 1 , b ≠ 1 ,

Given an exponential equation with the form b S = b T , b S = b T , where S S and T T are algebraic expressions with an unknown, solve for the unknown.

• Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form b S = b T . b S = b T .
• Use the one-to-one property to set the exponents equal.
• Solve the resulting equation, S = T , S = T , for the unknown.

Solving an Exponential Equation with a Common Base

Solve 2 x − 1 = 2 2 x − 4 . 2 x − 1 = 2 2 x − 4 .

Solve 5 2 x = 5 3 x + 2 . 5 2 x = 5 3 x + 2 .

Rewriting Equations So All Powers Have the Same Base

Sometimes the common base for an exponential equation is not explicitly shown. In these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one-to-one property.

For example, consider the equation 256 = 4 x − 5 . 256 = 4 x − 5 . We can rewrite both sides of this equation as a power of 2. 2. Then we apply the rules of exponents, along with the one-to-one property, to solve for x : x :

Given an exponential equation with unlike bases, use the one-to-one property to solve it.

• Rewrite each side in the equation as a power with a common base.

Solving Equations by Rewriting Them to Have a Common Base

Solve 8 x + 2 = 16 x + 1 . 8 x + 2 = 16 x + 1 .

Solve 5 2 x = 25 3 x + 2 . 5 2 x = 25 3 x + 2 .

Solving Equations by Rewriting Roots with Fractional Exponents to Have a Common Base

Solve 2 5 x = 2 . 2 5 x = 2 .

Solve 5 x = 5 . 5 x = 5 .

Do all exponential equations have a solution? If not, how can we tell if there is a solution during the problem-solving process?

No. Recall that the range of an exponential function is always positive. While solving the equation, we may obtain an expression that is undefined.

Solving an Equation with Positive and Negative Powers

Solve 3 x + 1 = −2. 3 x + 1 = −2.

This equation has no solution. There is no real value of x x that will make the equation a true statement because any power of a positive number is positive.

Figure 2 shows that the two graphs do not cross so the left side is never equal to the right side. Thus the equation has no solution.

Solve 2 x = −100. 2 x = −100.

Solving Exponential Equations Using Logarithms

Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall, since log ( a ) = log ( b ) log ( a ) = log ( b ) is equivalent to a = b , a = b , we may apply logarithms with the same base on both sides of an exponential equation.

Given an exponential equation in which a common base cannot be found, solve for the unknown.

• If one of the terms in the equation has base 10, use the common logarithm.
• If none of the terms in the equation has base 10, use the natural logarithm.
• Use the rules of logarithms to solve for the unknown.

Solving an Equation Containing Powers of Different Bases

Solve 5 x + 2 = 4 x . 5 x + 2 = 4 x .

Solve 2 x = 3 x + 1 . 2 x = 3 x + 1 .

Is there any way to solve 2 x = 3 x ? 2 x = 3 x ?

Yes. The solution is 0. 0.

Equations Containing e

One common type of exponential equations are those with base e . e . This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base e e on either side, we can use the natural logarithm to solve it.

Given an equation of the form y = A e k t , y = A e k t , solve for t . t .

• Divide both sides of the equation by A . A .
• Apply the natural logarithm of both sides of the equation.
• Divide both sides of the equation by k . k .

Solve an Equation of the Form y = Ae kt

Solve 100 = 20 e 2 t . 100 = 20 e 2 t .

Using laws of logs, we can also write this answer in the form t = ln 5 . t = ln 5 . If we want a decimal approximation of the answer, we use a calculator.

Solve 3 e 0.5 t = 11. 3 e 0.5 t = 11.

Does every equation of the form y = A e k t y = A e k t have a solution?

No. There is a solution when k ≠ 0 , k ≠ 0 , and when y y and A A are either both 0 or neither 0, and they have the same sign. An example of an equation with this form that has no solution is 2 = −3 e t . 2 = −3 e t .

Solving an Equation That Can Be Simplified to the Form y = Ae kt

Solve 4 e 2 x + 5 = 12. 4 e 2 x + 5 = 12.

Solve 3 + e 2 t = 7 e 2 t . 3 + e 2 t = 7 e 2 t .

Extraneous Solutions

Sometimes the methods used to solve an equation introduce an extraneous solution , which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when the logarithm is taken on both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the number we are evaluating in a logarithm function is negative, there is no output.

Solving Exponential Functions in Quadratic Form

Solve e 2 x − e x = 56. e 2 x − e x = 56.

When we plan to use factoring to solve a problem, we always get zero on one side of the equation, because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation e x = −7 e x = −7 because a positive number never equals a negative number. The solution ln ( −7 ) ln ( −7 ) is not a real number, and in the real number system this solution is rejected as an extraneous solution.

Solve e 2 x = e x + 2. e 2 x = e x + 2.

Does every logarithmic equation have a solution?

No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.

Using the Definition of a Logarithm to Solve Logarithmic Equations

We have already seen that every logarithmic equation log b ( x ) = y log b ( x ) = y is equivalent to the exponential equation b y = x . b y = x . We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation log 2 ( 2 ) + log 2 ( 3 x − 5 ) = 3. log 2 ( 2 ) + log 2 ( 3 x − 5 ) = 3. To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x : x :

For any algebraic expression S S and real numbers b b and c , c , where b > 0 , b ≠ 1 , b > 0 , b ≠ 1 ,

Using Algebra to Solve a Logarithmic Equation

Solve 2 ln x + 3 = 7. 2 ln x + 3 = 7.

Solve 6 + ln x = 10. 6 + ln x = 10.

Using Algebra Before and After Using the Definition of the Natural Logarithm

Solve 2 ln ( 6 x ) = 7. 2 ln ( 6 x ) = 7.

Solve 2 ln ( x + 1 ) = 10. 2 ln ( x + 1 ) = 10.

Using a Graph to Understand the Solution to a Logarithmic Equation

Solve ln x = 3. ln x = 3.

Figure 3 represents the graph of the equation. On the graph, the x -coordinate of the point at which the two graphs intersect is close to 20. In other words e 3 ≈ 20. e 3 ≈ 20. A calculator gives a better approximation: e 3 ≈ 20.0855. e 3 ≈ 20.0855.

Use a graphing calculator to estimate the approximate solution to the logarithmic equation 2 x = 1000 2 x = 1000 to 2 decimal places.

Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers x > 0 , x > 0 , S > 0 , S > 0 , T > 0 T > 0 and any positive real number b , b , where b ≠ 1 , b ≠ 1 ,

For example,

So, if x − 1 = 8 , x − 1 = 8 , then we can solve for x , x , and we get x = 9. x = 9. To check, we can substitute x = 9 x = 9 into the original equation: log 2 ( 9 − 1 ) = log 2 ( 8 ) = 3. log 2 ( 9 − 1 ) = log 2 ( 8 ) = 3. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.

For example, consider the equation log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for x : x :

To check the result, substitute x = 10 x = 10 into log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) .

For any algebraic expressions S S and T T and any positive real number b , b , where b ≠ 1 , b ≠ 1 ,

Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.

Given an equation containing logarithms, solve it using the one-to-one property.

• Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form log b S = log b T . log b S = log b T .
• Use the one-to-one property to set the arguments equal.

Solving an Equation Using the One-to-One Property of Logarithms

Solve ln ( x 2 ) = ln ( 2 x + 3 ) . ln ( x 2 ) = ln ( 2 x + 3 ) .

There are two solutions: 3 3 or −1. −1. The solution −1 −1 is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.

Solve ln ( x 2 ) = ln 1. ln ( x 2 ) = ln 1.

Solving Applied Problems Using Exponential and Logarithmic Equations

In previous sections, we learned the properties and rules for both exponential and logarithmic functions. We have seen that any exponential function can be written as a logarithmic function and vice versa. We have used exponents to solve logarithmic equations and logarithms to solve exponential equations. We are now ready to combine our skills to solve equations that model real-world situations, whether the unknown is in an exponent or in the argument of a logarithm.

One such application is in science, in calculating the time it takes for half of the unstable material in a sample of a radioactive substance to decay, called its half-life . Table 1 lists the half-life for several of the more common radioactive substances.

We can see how widely the half-lives for these substances vary. Knowing the half-life of a substance allows us to calculate the amount remaining after a specified time. We can use the formula for radioactive decay:

• A 0 A 0 is the amount initially present
• T T is the half-life of the substance
• t t is the time period over which the substance is studied
• A ( t ) A ( t ) is the amount of the substance present after time t t

Using the Formula for Radioactive Decay to Find the Quantity of a Substance

How long will it take for ten percent of a 1000-gram sample of uranium-235 to decay?

Ten percent of 1000 grams is 100 grams. If 100 grams decay, the amount of uranium-235 remaining is 900 grams.

How long will it take before twenty percent of our 1000-gram sample of uranium-235 has decayed?

Access these online resources for additional instruction and practice with exponential and logarithmic equations.

• Solving Logarithmic Equations
• Solving Exponential Equations with Logarithms

6.6 Section Exercises

How can an exponential equation be solved?

When does an extraneous solution occur? How can an extraneous solution be recognized?

When can the one-to-one property of logarithms be used to solve an equation? When can it not be used?

For the following exercises, use like bases to solve the exponential equation.

4 − 3 v − 2 = 4 − v 4 − 3 v − 2 = 4 − v

64 ⋅ 4 3 x = 16 64 ⋅ 4 3 x = 16

3 2 x + 1 ⋅ 3 x = 243 3 2 x + 1 ⋅ 3 x = 243

2 − 3 n ⋅ 1 4 = 2 n + 2 2 − 3 n ⋅ 1 4 = 2 n + 2

625 ⋅ 5 3 x + 3 = 125 625 ⋅ 5 3 x + 3 = 125

36 3 b 36 2 b = 216 2 − b 36 3 b 36 2 b = 216 2 − b

( 1 64 ) 3 n ⋅ 8 = 2 6 ( 1 64 ) 3 n ⋅ 8 = 2 6

For the following exercises, use logarithms to solve.

9 x − 10 = 1 9 x − 10 = 1

2 e 6 x = 13 2 e 6 x = 13

e r + 10 − 10 = −42 e r + 10 − 10 = −42

2 ⋅ 10 9 a = 29 2 ⋅ 10 9 a = 29

− 8 ⋅ 10 p + 7 − 7 = −24 − 8 ⋅ 10 p + 7 − 7 = −24

7 e 3 n − 5 + 5 = −89 7 e 3 n − 5 + 5 = −89

e − 3 k + 6 = 44 e − 3 k + 6 = 44

− 5 e 9 x − 8 − 8 = −62 − 5 e 9 x − 8 − 8 = −62

− 6 e 9 x + 8 + 2 = −74 − 6 e 9 x + 8 + 2 = −74

2 x + 1 = 5 2 x − 1 2 x + 1 = 5 2 x − 1

e 2 x − e x − 132 = 0 e 2 x − e x − 132 = 0

7 e 8 x + 8 − 5 = −95 7 e 8 x + 8 − 5 = −95

10 e 8 x + 3 + 2 = 8 10 e 8 x + 3 + 2 = 8

4 e 3 x + 3 − 7 = 53 4 e 3 x + 3 − 7 = 53

8 e − 5 x − 2 − 4 = −90 8 e − 5 x − 2 − 4 = −90

3 2 x + 1 = 7 x − 2 3 2 x + 1 = 7 x − 2

e 2 x − e x − 6 = 0 e 2 x − e x − 6 = 0

3 e 3 − 3 x + 6 = −31 3 e 3 − 3 x + 6 = −31

For the following exercises, use the definition of a logarithm to rewrite the equation as an exponential equation.

log ( 1 100 ) = −2 log ( 1 100 ) = −2

log 324 ( 18 ) = 1 2 log 324 ( 18 ) = 1 2

For the following exercises, use the definition of a logarithm to solve the equation.

5 log 7 n = 10 5 log 7 n = 10

− 8 log 9 x = 16 − 8 log 9 x = 16

4 + log 2 ( 9 k ) = 2 4 + log 2 ( 9 k ) = 2

2 log ( 8 n + 4 ) + 6 = 10 2 log ( 8 n + 4 ) + 6 = 10

10 − 4 ln ( 9 − 8 x ) = 6 10 − 4 ln ( 9 − 8 x ) = 6

For the following exercises, use the one-to-one property of logarithms to solve.

ln ( 10 − 3 x ) = ln ( − 4 x ) ln ( 10 − 3 x ) = ln ( − 4 x )

log 13 ( 5 n − 2 ) = log 13 ( 8 − 5 n ) log 13 ( 5 n − 2 ) = log 13 ( 8 − 5 n )

log ( x + 3 ) − log ( x ) = log ( 74 ) log ( x + 3 ) − log ( x ) = log ( 74 )

ln ( − 3 x ) = ln ( x 2 − 6 x ) ln ( − 3 x ) = ln ( x 2 − 6 x )

log 4 ( 6 − m ) = log 4 3 m log 4 ( 6 − m ) = log 4 3 m

ln ( x − 2 ) − ln ( x ) = ln ( 54 ) ln ( x − 2 ) − ln ( x ) = ln ( 54 )

log 9 ( 2 n 2 − 14 n ) = log 9 ( − 45 + n 2 ) log 9 ( 2 n 2 − 14 n ) = log 9 ( − 45 + n 2 )

ln ( x 2 − 10 ) + ln ( 9 ) = ln ( 10 ) ln ( x 2 − 10 ) + ln ( 9 ) = ln ( 10 )

For the following exercises, solve each equation for x . x .

log ( x + 12 ) = log ( x ) + log ( 12 ) log ( x + 12 ) = log ( x ) + log ( 12 )

ln ( x ) + ln ( x − 3 ) = ln ( 7 x ) ln ( x ) + ln ( x − 3 ) = ln ( 7 x )

log 2 ( 7 x + 6 ) = 3 log 2 ( 7 x + 6 ) = 3

ln ( 7 ) + ln ( 2 − 4 x 2 ) = ln ( 14 ) ln ( 7 ) + ln ( 2 − 4 x 2 ) = ln ( 14 )

log 8 ( x + 6 ) − log 8 ( x ) = log 8 ( 58 ) log 8 ( x + 6 ) − log 8 ( x ) = log 8 ( 58 )

ln ( 3 ) − ln ( 3 − 3 x ) = ln ( 4 ) ln ( 3 ) − ln ( 3 − 3 x ) = ln ( 4 )

log 3 ( 3 x ) − log 3 ( 6 ) = log 3 ( 77 ) log 3 ( 3 x ) − log 3 ( 6 ) = log 3 ( 77 )

For the following exercises, solve the equation for x , x , if there is a solution . Then graph both sides of the equation, and observe the point of intersection (if it exists) to verify the solution.

log 9 ( x ) − 5 = −4 log 9 ( x ) − 5 = −4

log 3 ( x ) + 3 = 2 log 3 ( x ) + 3 = 2

ln ( 3 x ) = 2 ln ( 3 x ) = 2

ln ( x − 5 ) = 1 ln ( x − 5 ) = 1

log ( 4 ) + log ( − 5 x ) = 2 log ( 4 ) + log ( − 5 x ) = 2

− 7 + log 3 ( 4 − x ) = −6 − 7 + log 3 ( 4 − x ) = −6

ln ( 4 x − 10 ) − 6 = − 5 ln ( 4 x − 10 ) − 6 = − 5

log ( 4 − 2 x ) = log ( − 4 x ) log ( 4 − 2 x ) = log ( − 4 x )

log 11 ( − 2 x 2 − 7 x ) = log 11 ( x − 2 ) log 11 ( − 2 x 2 − 7 x ) = log 11 ( x − 2 )

ln ( 2 x + 9 ) = ln ( − 5 x ) ln ( 2 x + 9 ) = ln ( − 5 x )

log 9 ( 3 − x ) = log 9 ( 4 x − 8 ) log 9 ( 3 − x ) = log 9 ( 4 x − 8 )

log ( x 2 + 13 ) = log ( 7 x + 3 ) log ( x 2 + 13 ) = log ( 7 x + 3 )

3 log 2 ( 10 ) − log ( x − 9 ) = log ( 44 ) 3 log 2 ( 10 ) − log ( x − 9 ) = log ( 44 )

ln ( x ) − ln ( x + 3 ) = ln ( 6 ) ln ( x ) − ln ( x + 3 ) = ln ( 6 )

For the following exercises, solve for the indicated value, and graph the situation showing the solution point.

An account with an initial deposit of $6,500 $6,500 earns 7.25 % 7.25 % annual interest, compounded continuously. How much will the account be worth after 20 years?

The formula for measuring sound intensity in decibels D D is defined by the equation D = 10 log ( I I 0 ) , D = 10 log ( I I 0 ) , where I I is the intensity of the sound in watts per square meter and I 0 = 10 − 12 I 0 = 10 − 12 is the lowest level of sound that the average person can hear. How many decibels are emitted from a jet plane with a sound intensity of 8.3 ⋅ 10 2 8.3 ⋅ 10 2 watts per square meter?

The population of a small town is modeled by the equation P = 1650 e 0.5 t P = 1650 e 0.5 t where t t is measured in years. In approximately how many years will the town’s population reach 20,000? 20,000?

For the following exercises, solve each equation by rewriting the exponential expression using the indicated logarithm. Then use a calculator to approximate the variable to 3 decimal places.

1000 ( 1.03 ) t = 5000 1000 ( 1.03 ) t = 5000 using the common log.

e 5 x = 17 e 5 x = 17 using the natural log

3 ( 1.04 ) 3 t = 8 3 ( 1.04 ) 3 t = 8 using the common log

3 4 x − 5 = 38 3 4 x − 5 = 38 using the common log

50 e − 0.12 t = 10 50 e − 0.12 t = 10 using the natural log

For the following exercises, use a calculator to solve the equation. Unless indicated otherwise, round all answers to the nearest ten-thousandth.

7 e 3 x − 5 + 7.9 = 47 7 e 3 x − 5 + 7.9 = 47

ln ( 3 ) + ln ( 4.4 x + 6.8 ) = 2 ln ( 3 ) + ln ( 4.4 x + 6.8 ) = 2

log ( − 0.7 x − 9 ) = 1 + 5 log ( 5 ) log ( − 0.7 x − 9 ) = 1 + 5 log ( 5 )

Atmospheric pressure P P in pounds per square inch is represented by the formula P = 14.7 e − 0.21 x , P = 14.7 e − 0.21 x , where x x is the number of miles above sea level. To the nearest foot, how high is the peak of a mountain with an atmospheric pressure of 8.369 8.369 pounds per square inch? ( Hint : there are 5280 feet in a mile)

The magnitude M of an earthquake is represented by the equation M = 2 3 log ( E E 0 ) M = 2 3 log ( E E 0 ) where E E is the amount of energy released by the earthquake in joules and E 0 = 10 4.4 E 0 = 10 4.4 is the assigned minimal measure released by an earthquake. To the nearest hundredth, what would the magnitude be of an earthquake releasing 1.4 ⋅ 10 13 1.4 ⋅ 10 13 joules of energy?

Use the definition of a logarithm along with the one-to-one property of logarithms to prove that b log b x = x . b log b x = x .

Recall the formula for continually compounding interest, y = A e k t . y = A e k t . Use the definition of a logarithm along with properties of logarithms to solve the formula for time t t such that t t is equal to a single logarithm.

Recall the compound interest formula A = a ( 1 + r k ) k t . A = a ( 1 + r k ) k t . Use the definition of a logarithm along with properties of logarithms to solve the formula for time t . t .

Newton’s Law of Cooling states that the temperature T T of an object at any time t can be described by the equation T = T s + ( T 0 − T s ) e − k t , T = T s + ( T 0 − T s ) e − k t , where T s T s is the temperature of the surrounding environment, T 0 T 0 is the initial temperature of the object, and k k is the cooling rate. Use the definition of a logarithm along with properties of logarithms to solve the formula for time t t such that t t is equal to a single logarithm.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/6-6-exponential-and-logarithmic-equations

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Exponential and Logarithmic Equations

Solve applied problems involving exponential and logarithmic equations.

In previous sections, we learned the properties and rules for both exponential and logarithmic functions. We have seen that any exponential function can be written as a logarithmic function and vice versa. We have used exponents to solve logarithmic equations and logarithms to solve exponential equations. We are now ready to combine our skills to solve equations that model real-world situations, whether the unknown is in an exponent or in the argument of a logarithm.

One such application is in science, in calculating the time it takes for half of the unstable material in a sample of a radioactive substance to decay, called its half-life . The table below lists the half-life for several of the more common radioactive substances.

We can see how widely the half-lives for these substances vary. Knowing the half-life of a substance allows us to calculate the amount remaining after a specified time. We can use the formula for radioactive decay:

• [latex]{A}_{0}[/latex] is the amount initially present
• T  is the half-life of the substance
• t  is the time period over which the substance is studied
• y  is the amount of the substance present after time  t

Example 13: Using the Formula for Radioactive Decay to Find the Quantity of a Substance

How long will it take for ten percent of a 1000-gram sample of uranium-235 to decay?

[latex]\begin{cases}\text{ }y=\text{1000}e\frac{\mathrm{ln}\left(0.5\right)}{\text{703,800,000}}t\hfill & \hfill \\ \text{ }900=1000{e}^{\frac{\mathrm{ln}\left(0.5\right)}{\text{703,800,000}}t}\hfill & \text{After 10% decays, 900 grams are left}.\hfill \\ \text{ }0.9={e}^{\frac{\mathrm{ln}\left(0.5\right)}{\text{703,800,000}}t}\hfill & \text{Divide by 1000}.\hfill \\ \mathrm{ln}\left(0.9\right)=\mathrm{ln}\left({e}^{\frac{\mathrm{ln}\left(0.5\right)}{\text{703,800,000}}t}\right)\hfill & \text{Take ln of both sides}.\hfill \\ \mathrm{ln}\left(0.9\right)=\frac{\mathrm{ln}\left(0.5\right)}{\text{703,800,000}}t\hfill & \text{ln}\left({e}^{M}\right)=M\hfill \\ \text{ }\text{ }t=\text{703,800,000}\times \frac{\mathrm{ln}\left(0.9\right)}{\mathrm{ln}\left(0.5\right)}\text{years}\begin{cases}{cccc}& & & \end{cases}\hfill & \text{Solve for }t.\hfill \\ \text{ }\text{ }t\approx \text{106,979,777 years}\hfill & \hfill \end{cases}[/latex]

Analysis of the Solution

Ten percent of 1000 grams is 100 grams. If 100 grams decay, the amount of uranium-235 remaining is 900 grams.

How long will it take before twenty percent of our 1000-gram sample of uranium-235 has decayed?

• Precalculus. Authored by : Jay Abramson, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download For Free at : http://cnx.org/contents/[email protected].

WORD PROBLEMS ON EXPONENTIAL FUNCTIONS

Every exponential function will be in the form of y = ab x

Here a = initial value and b = base.

Based on the value of b, we can see two types of exponential function.

• Exponential growth, if b > 1
• Exponential decay, if 0 < b < 1

Some times exponential functions will be in the form

Here r is the growth or decay factor.

If the function is changes exponentially, then

Problem 1 :

A cup of green tea contains 35 milligrams of caffeine. The average teen can eliminate approximately 12.5% of the caffeine from their system per hour.

a) Write an exponential function to represent the amount of caffeine remaining after drinking a cup of green tea.

b) Estimate the amount of caffeine in a teenager’s body 3 hours after drinking a cup of green tea.

a)  a = 35

Per hour 12.5 % of caffeine is being eliminated each hour.

then, r = 12.5

y = 35(1 - 12.5%) x  

Here x is the number of hours.

y = 35(1 - 0.125) x  

y = 35(0.875) x  

b) Number of hours = 3

y = 35(0.875) 3  

= 35(0.6699) 

So, the amount caffeine after 3 hours is 23.45 milligrams

Problem 2 :

From 1990 to 2000, the population of California can be modeled by

P = 29,816,591(1.0128) t

where t is the number of years since 1990. Estimate the population in 2007.

To estimate the population in 2007, we have to apply t as 17.

P = 29,816,591(1.0128) 17

= 37013551.9

Approximately  37013552.

So, the required population at 2007 is 37013552..

Problem 3 :

You buy a new car for $22,500. The value of the car decreases by 25% each year.

Write an exponential decay model giving the car's value V (in dollars) after t years. What is the value of the car after three years?

Initial value = 22500

Decreasing rate = 25%

y = 22500(1 - 25%) x  

= 22500(1- 0.25) x  

= 22500(0.75) x  

Problem 4 :

A virus spreads through a network of computers such that each minute, 25% more computers are infected. If the virus began at only one computer, find the model for this situation and find the number of computers affected after 40 minutes.

Number of virus in the initial stage = 1

Increasing factor = 25%

y = 1(1 + 25%) x  

= 1(1 + 0.25) x  

= 1(1.25) x  

The total number of computer after 40 minutes.

= 1(1.25) 40

Problem 5 :

A radioactive substance decays exponentially. A scientist begins with 100 milligrams of a radioactive substance. After 35 hours, 50 mg of the substance remains. How many milligrams will remain after 54 hours?

Exponential function for growth or decay

A(t) = ae rt ---(1)

Here A(t) is the quantity of substance after t hours.

Initial value = 100

100 = a(e) r(0)  

100 = a(e) 0

Applying the value of a in (1), we get

A(t) = 100e rt

Here t = 35, A(t) = 50

50 = 100e r(35)

1/2 =  e r(35)

ln (1/2) = 35r

r = ln(0.5)/35

r = -0.693/35

Approximately r = -0.02

Rate of decreasing = 2%

Quantity of substance after 54 hours.

A(t) = 100e (-0.02) 54

= 100e (-1.08)

Approximately 34 milligrams.

Problem 6 :

A radioactive substance decays exponentially. A scientist begins with 110 milligrams of a radioactive substance. After 31 hours, 55 mg of the substance remains. How many milligrams will remain after 42 hours?

Initial value = 110

110 = a(e) r(0)  

110 = a(e) 0

A(t) = 110e rt

Here t = 31, A(t) = 55

55 = 110e r(31)

1/2 =  e r(31)

ln (1/2) = 31r

r = ln(0.5)/31

r = -0.693/31

Approximately r = -0.022

Rate of decreasing = 2.2%

Quantity of substance after 42 hours.

A(t) = 110e (-0.022) 42

= 110e (-0.924)

= 110/2.519

Approximately 44 milligrams.

Problem 7 :

A house was valued at $110,000 in the year 1985. The value appreciated to $145,000 by the year 2005. What was the annual growth rate between 1985 and 2005?

Assume that the house value continues to grow by the same percentage. What did the value equal in the year 2010?

By observing the given situation, the required function will be exponential growth function.

P(t) = a(1 + r%) x  

At 1985, the population is  $110,000

110000 = a(1 + r%) 0  

Applying the initial value in (1), we get

P(t) = 110000(1 + r%) x  

In the year 2005, the value of x = 20

145000 = 110000(1 + r%) 20  

(1 + r%) 20   = 145000/110000

(1 + r%) 20  = 1.318

1 + r% = (1.318) 1/20

1 + r% = (1.318) 0.05

r% = 1.014 - 1

In the year 2010, the value of x = 25

P(t) = 110000(1 + 1.4%) 25  

= 110000(1.416)

So, the population at 2010 is  155760.

• Variables and Expressions
• Variables and Expressions Worksheet
• Place Value of Number
• Formation of Large Numbers
• Laws of Exponents
• Angle Bisector Theorem
• Pre Algebra
• SAT Practice Topic Wise
• Geometry Topics
• SMO Past papers
• Parallel Lines and Angles
• Properties of Quadrilaterals
• Circles and Theorems
• Transformations of 2D Shapes
• Quadratic Equations and Functions
• Composition of Functions
• Polynomials
• Fractions Decimals and Percentage
• Customary Unit and Metric Unit
• Honors Geometry
• 8th grade worksheets
• Linear Equations
• Precalculus Worksheets
• 7th Grade Math Worksheets
• Vocabulary of Triangles and Special right triangles
• 6th Grade Math Topics
• STAAR Math Practice
• Math 1 EOC Review Worksheets
• 11 Plus Math Papers
• CA Foundation Papers

Recent Articles

Factoring Exponential Expression Using Algebraic Identities Worksheet

Mar 14, 24 10:44 PM

Positive and Negative Numbers Connecting in Real Life Worksheet

Mar 14, 24 10:12 AM

Positive and Negative Numbers Connecting in Real Life

Mar 14, 24 09:52 AM

© All rights reserved. intellectualmath.com

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.6: Integrals Involving Exponential and Logarithmic Functions

• Last updated
• Save as PDF
• Page ID 2516

• Gilbert Strang & Edwin “Jed” Herman

Learning Objectives

• Integrate functions involving exponential functions.
• Integrate functions involving logarithmic functions.

Exponential and logarithmic functions are used to model population growth, cell growth, and financial growth, as well as depreciation, radioactive decay, and resource consumption, to name only a few applications. In this section, we explore integration involving exponential and logarithmic functions.

• Integrals of Exponential Functions

The exponential function is perhaps the most efficient function in terms of the operations of calculus. The exponential function, \(y=e^x\), is its own derivative and its own integral.

Rule: Integrals of Exponential Functions

Exponential functions can be integrated using the following formulas.

\[ \begin{align} ∫e^x\,dx &= e^x+C \\[4pt] ∫a^x\,dx &=\dfrac{a^x}{\ln a}+C \end{align} \nonumber \]

Example \(\PageIndex{1}\): Finding an Antiderivative of an Exponential Function

Find the antiderivative of the exponential function \(e^{−x}\).

Use substitution, setting \(u=−x,\) and then \(du=−1\,dx\). Multiply the \(du\) equation by \(−1\), so you now have \(−du=\,dx\). Then,

\[∫e^{−x}\,dx=−∫e^u\,du=−e^u+C=−e^{−x}+C. \nonumber \]

Exercise \(\PageIndex{1}\)

Find the antiderivative of the function using substitution: \(x^2e^{−2x^3}\).

Let \(u\) equal the exponent on \(e\).

\(\displaystyle ∫x^2e^{−2x^3}\,dx=−\dfrac{1}{6}e^{−2x^3}+C\)

A common mistake when dealing with exponential expressions is treating the exponent on \(e\) the same way we treat exponents in polynomial expressions. We cannot use the power rule for the exponent on \(e\). This can be especially confusing when we have both exponentials and polynomials in the same expression, as in the previous checkpoint. In these cases, we should always double-check to make sure we’re using the right rules for the functions we’re integrating.

Example \(\PageIndex{2}\): Square Root of an Exponential Function

Find the antiderivative of the exponential function \(e^x\sqrt{1+e^x}\).

First rewrite the problem using a rational exponent:

\[∫e^x\sqrt{1+e^x}\,dx=∫e^x(1+e^x)^{1/2}\,dx.\nonumber \]

Using substitution, choose \(u=1+e^x\). Then, \(du=e^x\,dx\). We have

\[∫e^x(1+e^x)^{1/2}\,dx=∫u^{1/2}\,du.\nonumber \]

\[∫u^{1/2}\,du=\dfrac{u^{3/2}}{3/2}+C=\dfrac{2}{3}u^{3/2}+C=\dfrac{2}{3}(1+e^x)^{3/2}+C\nonumber \]

Exercise \(\PageIndex{2}\)

Find the antiderivative of \(e^x(3e^x−2)^2\).

Let \(u=3e^x−2\).

\(\displaystyle ∫e^x(3e^x−2)^2\,dx=\dfrac{1}{9}(3e^x−2)^3+C\)

Example \(\PageIndex{3}\): Using Substitution with an Exponential Function

Use substitution to evaluate the indefinite integral \(\displaystyle ∫3x^2e^{2x^3}\,dx.\)

Here we choose to let \(u\) equal the expression in the exponent on \(e\). Let \(u=2x^3\) and \(du=6x^2\,dx\). Again, \(du\) is off by a constant multiplier; the original function contains a factor of \(3x^2,\) not \(6x^2\). Multiply both sides of the equation by \(\dfrac{1}{2}\) so that the integrand in \(u\) equals the integrand in \(x\). Thus,

\[∫3x^2e^{2x^3}\,dx=\frac{1}{2}∫e^u\,du. \nonumber \]

Integrate the expression in \(u\) and then substitute the original expression in \(x\) back into the \(u\)-integral:

\[\frac{1}{2}∫e^u\,du=\frac{1}{2}e^u+C=\frac{1}{2}e^{2x^3}+C. \nonumber \]

Exercise \(\PageIndex{3}\)

Evaluate the indefinite integral \(\displaystyle ∫2x^3e^{x^4}\,dx\).

Let \(u=x^4.\)

\(\displaystyle ∫2x^3e^{x^4}\,dx=\frac{1}{2}e^{x^4}+C\)

As mentioned at the beginning of this section, exponential functions are used in many real-life applications. The number \(e\) is often associated with compounded or accelerating growth, as we have seen in earlier sections about the derivative. Although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total growth. Let’s look at an example in which integration of an exponential function solves a common business application.

A price–demand function tells us the relationship between the quantity of a product demanded and the price of the product. In general, price decreases as quantity demanded increases. The marginal price–demand function is the derivative of the price–demand function and it tells us how fast the price changes at a given level of production. These functions are used in business to determine the price–elasticity of demand, and to help companies determine whether changing production levels would be profitable.

Example \(\PageIndex{4}\): Finding a Price–Demand Equation

Find the price–demand equation for a particular brand of toothpaste at a supermarket chain when the demand is \(50\) tubes per week at $2.35 per tube, given that the marginal price—demand function, \(p′(x),\) for \(x\) number of tubes per week, is given as

\[p'(x)=−0.015e^{−0.01x}. \nonumber \]

If the supermarket chain sells \(100\) tubes per week, what price should it set?

To find the price–demand equation, integrate the marginal price–demand function. First find the antiderivative, then look at the particulars. Thus,

\[p(x)=∫−0.015e^{−0.01x}\,dx=−0.015∫e^{−0.01x}\,dx. \nonumber \]

Using substitution, let \(u=−0.01x\) and \(du=−0.01\,dx\). Then, divide both sides of the \(du\) equation by \(−0.01\). This gives

\[\dfrac{−0.015}{−0.01}∫e^u\,du=1.5∫e^u\,du=1.5e^u+C=1.5e^{−0.01}x+C. \nonumber \]

The next step is to solve for \(C\). We know that when the price is $2.35 per tube, the demand is \(50\) tubes per week. This means

\[p(50)=1.5e^{−0.01(50)}+C=2.35. \nonumber \]

Now, just solve for \(C\):

\[C=2.35−1.5e^{−0.5}=2.35−0.91=1.44. \nonumber \]

\[p(x)=1.5e^{−0.01x}+1.44. \nonumber \]

If the supermarket sells \(100\) tubes of toothpaste per week, the price would be

\[p(100)=1.5e−0.01(100)+1.44=1.5e−1+1.44≈1.99. \nonumber \]

The supermarket should charge $1.99 per tube if it is selling \(100\) tubes per week.

Example \(\PageIndex{5}\): Evaluating a Definite Integral Involving an Exponential Function

Evaluate the definite integral \(\displaystyle ∫^2_1e^{1−x}\,dx.\)

Again, substitution is the method to use. Let \(u=1−x,\) so \(\,du=−1\,dx\) or \(−\,du=\,dx\). Then \(\displaystyle ∫e^{1−x}\,dx=−∫e^u\,du.\)

Next, change the limits of integration. Using the equation \(u=1−x\), we have:

\[\text{When }x = 1, \quad u=1−(1)=0, \nonumber \]

\[\text{and when }x = 2, \quad u=1−(2)=−1. \nonumber \]

The integral then becomes

\[\begin{align*} ∫^2_1e^{1−x}\,\,dx &= −∫^{−1}_0e^u\,\,du \\[4pt] &=∫^0_{−1}e^u\,\,du \\[4pt] &=e^u\bigg|^0_{−1}=e^0−(e^{−1}) \\[4pt] &=−e^{−1}+1. \end{align*}\]

See Figure \(\PageIndex{2}\).

Exercise \(\PageIndex{4}\)

Evaluate \(\displaystyle ∫^2_0e^{2x}\,dx.\)

Let \(u=2x.\)

\(\displaystyle \frac{1}{2}∫^4_0e^u\,du=\dfrac{1}{2}(e^4−1)\)

Example \(\PageIndex{6}\): Growth of Bacteria in a Culture

Suppose the rate of growth of bacteria in a Petri dish is given by \(q(t)=3^t\), where \(t\) is given in hours and \(q(t)\) is given in thousands of bacteria per hour. If a culture starts with \(10,000\) bacteria, find a function \(Q(t)\) that gives the number of bacteria in the Petri dish at any time \(t\). How many bacteria are in the dish after \(2\) hours?

\[Q(t)=∫3^tdt=\dfrac{3^t}{\ln 3}+C. \nonumber \]

Then, at \(t=0\) we have \(Q(0)=10=\dfrac{1}{\ln 3}+C,\) so \(C≈9.090\) and we get

\[Q(t)=\dfrac{3^t}{\ln 3}+9.090. \nonumber \]

At time \(t=2\), we have

\[\begin{align*} Q(2) &=\dfrac{3^2}{\ln 3}+9.090 \\[4pt] &\approx 17.282. \end{align*}\]

After 2 hours, there are 17,282 bacteria in the dish.

Exercise \(\PageIndex{5}\)

From Example, suppose the bacteria grow at a rate of \(q(t)=2^t\). Assume the culture still starts with \(10,000\) bacteria. Find \(Q(t)\). How many bacteria are in the dish after \(3\) hours?

Use the procedure from Example \(\PageIndex{6}\) to solve the problem

\[\begin{align*} Q(t) &= \dfrac{2^t}{\ln 2} + 8.557. \\[4pt] Q(3) &\approx 20,099 \end{align*}\]

So there are \(20,099\) bacteria in the dish after \(3\) hours.

Example \(\PageIndex{7}\): Fruit Fly Population Growth

Suppose a population of fruit flies increases at a rate of \(g(t)=2e^{0.02t}\), in flies per day. If the initial population of fruit flies is \(100\) flies, how many flies are in the population after \(10\) days?

Let \(G(t)\) represent the number of flies in the population at time \(t\). Applying the net change theorem, we have

\[ \begin{align*} G(10)=G(0)+∫^{10}_02e^{0.02t}\,dt \\[4pt] &=100+\left[\dfrac{2}{0.02}e^{0.02t}\right]∣^{10}_0 \\[4pt] &=100+\left[100e^{0.02t}\right]∣^{10}_0 \\[4pt] &=100+100e^{0.2}−100 \\[4pt] &≈122. \end{align*}\]

There are \(122\) flies in the population after \(10\) days.

Exercise \(\PageIndex{6}\)

Suppose the rate of growth of the fly population is given by \(g(t)=e^{0.01t},\) and the initial fly population is \(100\) flies. How many flies are in the population after \(15\) days?

Use the process from Example \(\PageIndex{7}\) to solve the problem.

There are \(116\) flies.

Example \(\PageIndex{8}\): Evaluating a Definite Integral Using Substitution

Evaluate the definite integral using substitution: \[∫^2_1\dfrac{e^{1/x}}{x^2}\,dx.\nonumber \]

This problem requires some rewriting to simplify applying the properties. First, rewrite the exponent on e as a power of \(x\), then bring the \(x^2\) in the denominator up to the numerator using a negative exponent. We have

\[∫^2_1\dfrac{e^{1/x}}{x^2}\,\,dx=∫^2_1e^{x^{−1}}x^{−2}\,dx. \nonumber \]

Let \(u=x^{−1},\) the exponent on \(e\). Then

\[du=−x^{−2}\,dx \nonumber \]

\[−du=x^{−2}\,dx. \nonumber \]

Bringing the negative sign outside the integral sign, the problem now reads

\[−∫e^u\,du. \nonumber \]

Next, change the limits of integration:

\[u=(1)^{−1}=1 \nonumber \]

\[u=(2)^{−1}=\dfrac{1}{2}. \nonumber \]

Notice that now the limits begin with the larger number, meaning we can multiply by \(−1\) and interchange the limits. Thus,

\[−∫^{1/2}_1e^u\,du=∫^1_{1/2}e^u\,du=e^u\big|^1_{1/2}=e−e^{1/2}=e−\sqrt{e}.\nonumber \]

Exercise \(\PageIndex{7}\)

Evaluate the definite integral using substitution: \[∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}\,dx.\nonumber \]

Let \(u=4x^{−2}.\)

\(\displaystyle ∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}\,dx=\dfrac{1}{8}[e^4−e]\).

Integrals Involving Logarithmic Functions

Integrating functions of the form \(f(x)=x^{−1}\) result in the absolute value of the natural log function, as shown in the following rule. Integral formulas for other logarithmic functions, such as \(f(x)=\ln x\) and \(f(x)=\log_a x\), are also included in the rule.

Rule: Integration Formulas Involving Logarithmic Functions

The following formulas can be used to evaluate integrals involving logarithmic functions.

\[\begin{align*} ∫x^{−1}\,dx &=\ln |x|+C \\[4pt] ∫\ln x\,\,dx &= x\ln x−x+C =x (\ln x−1)+C \\[4pt] ∫\log_a x\,dx &=\dfrac{x}{\ln a}(\ln x−1)+C \end{align*}\]

Example \(\PageIndex{9}\): Finding an Antiderivative Involving \(\ln x\)

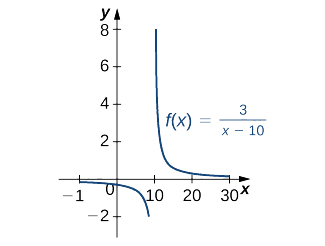
Find the antiderivative of the function \(\dfrac{3}{x−10}. \)

First factor the \(3\) outside the integral symbol. Then use the \(u^{−1}\) rule. Thus,

\[∫\dfrac{3}{x−10}\,dx=3∫\dfrac{1}{x−10}\,dx=3∫\dfrac{du}{u}=3\ln |u|+C=3\ln |x−10|+C,\quad x≠10. \nonumber \]

See Figure \(\PageIndex{3}\).

Exercise \(\PageIndex{8}\)

Find the antiderivative of \(\dfrac{1}{x+2}.\)

Follow the pattern from Example \(\PageIndex{9}\) to solve the problem.

\(\displaystyle \int \dfrac{1}{x+2}\,dx = \ln |x+2|+C\)

Example \(\PageIndex{10}\): Finding an Antiderivative of a Rational Function

Find the antiderivative of \(\dfrac{2x^3+3x}{x^4+3x^2}. \)

This can be rewritten as \(\displaystyle ∫(2x^3+3x)(x^4+3x^2)^{−1}\,dx.\) Use substitution.

Let \(u=x^4+3x^2\), then \(du=(4x^3+6x)\,dx.\) Alter \(du\) by factoring out the \(2\). Thus,

\[du=(4x^3+6x)\,dx=2(2x^3+3x)\,dx \nonumber \]

\[\dfrac{1}{2}\,du=(2x^3+3x)\,dx. \nonumber \]

Rewrite the integrand in \(u\):

\[∫(2x^3+3x)(x^4+3x^2)^{−1}\,dx=\dfrac{1}{2}∫u^{−1}\,du. \nonumber \]

Then we have

\[\dfrac{1}{2}∫u^{−1}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln ∣x^4+3x^2∣+C. \nonumber \]

Example \(\PageIndex{11}\): Finding an Antiderivative of a Logarithmic Function

Find the antiderivative of the log function \(\log_2 x.\)

Follow the format in the formula listed in the rule on integration formulas involving logarithmic functions. Based on this format, we have

\[∫\log_2 x\,dx=\dfrac{x}{\ln 2}(\ln x−1)+C.\nonumber \]

Exercise \(\PageIndex{9}\)

Find the antiderivative of \(\log_3 x\).

Follow Example \(\PageIndex{11}\) and refer to the rule on integration formulas involving logarithmic functions.

\(\displaystyle ∫\log_3 x\,dx=\dfrac{x}{\ln 3}(\ln x−1)+C\)

Example \(\PageIndex{12}\) is a definite integral of a trigonometric function. With trigonometric functions, we often have to apply a trigonometric property or an identity before we can move forward. Finding the right form of the integrand is usually the key to a smooth integration.

Example \(\PageIndex{12}\): Evaluating a Definite Integral

Evaluate the definite integral \[∫^{π/2}_0\dfrac{\sin x}{1+\cos x}\,dx.\nonumber \]

We need substitution to evaluate this problem. Let \(u=1+\cos x\) so \(du=−\sin x\,\,dx.\)

Rewrite the integral in terms of \(u\), changing the limits of integration as well. Thus,

\[ \begin{align*} u &= 1+\cos(0)=2 \\[4pt] u &=1+\cos \left(\dfrac{π}{2}\right)=1.\end{align*}\]

\[ \begin{align*}∫^{π/2}_0\dfrac{\sin x}{1+\cos x} &=−∫^1_2 u^{−1}\,du \\[4pt] &=∫^2_1u^{−1}\,du \\[4pt] &=\ln |u|\,\bigg|^2_1 \\[4pt] &=[\ln 2−\ln 1]=\ln 2 \end{align*}\]

Key Concepts

• Exponential and logarithmic functions arise in many real-world applications, especially those involving growth and decay.
• Substitution is often used to evaluate integrals involving exponential functions or logarithms.

Key Equations

\[∫e^x\,dx=e^x+C \nonumber \]

\[\int a^x\,dx=\dfrac{a^x}{\ln a}+C \nonumber \]

• Integration Formulas Involving Logarithmic Functions

\[∫x^{−1}\,dx=\ln |x|+C \nonumber \]

\[∫\ln x\,dx=x\ln x−x+C=x(\ln x−1)+C \nonumber \]

\[∫\log_a x\,dx=\dfrac{x}{\ln a}(\ln x−1)+C \nonumber \]

• Toggle navigation

Lee | D379 | Spring 2024

• Course Profile
• Course Outline
• Syllabus/Grading Policy
• Academic Calendar
• Class Meeting Grid

Class Agendas

• WeBWorK Site
• Module Assignments
• Online Lessons
• Final Exam Review Questions
• Final Exam Review videos
• MAT 1375 Video Resources
• WeBWorK site
• WeBWorK Guide for Students
• Homework help – Q&A site
• Desmos – online calculator
• College Resources

OpenLab Help

• 15. Exponential equations and applications

Course Hub – Handout Textbook – Session 15

Assignments

• Exponential Functions – Equations

Prep for Next Class (Please look at them and prepare questions for the next class).

Course Hub – Handout Textbook – Session 16

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Name: Mr. Victor Lee Class Days: Monday, Wednesday Class Times: 2:15 pm – 3:55 pm Room: N703 Office: N825 Office Hours: Monday, Wednesday 11:00 am – 12:00 pm Online Classroom/Office

Textbook: Precalculus ( 3rd Edition) by Tradler and Carley

Topics include an in-depth study of functions such as polynomial functions, radical functions, trigonometric functions, exponential and logarithmic functions; connections to vectors and complex numbers; solving trigonometric equations, and identities involving sum, double and half-angle formulas; Binomial Theorem and progressions.  

This class uses  WeBWorK , an online homework system.  Login information will be provided by your professor.  For information about how to use the WeBWorK system, please see the  WeBWorK  Guide for Students .

Need Help with MAT 1375?

The Mathematics Department’s MAT 1375 Course Hub has many resources for both students and faculty, including online lessons , review information , and more.

The WeBWorK Q&A site is a place to ask and answer questions about your homework problems.  HINT: To ask a question, start by logging in to your WeBWorK section, then click  “Ask for Help” after any problem.

Search This Course

• All Categories Announcements Assignment Instructions Assignment Posts Class Agendas Course Activities Discussions Resources

Logged-in faculty members can clone this course. Learn More!

Recent Posts

• 16. Applications of exp and log
• News: Test 2
• 14. Properties of Logarithms and Logarithmic Equations
• 13. Exponential and Logarithmic Functions

Recent Comments

Member portfolios, find library materials, library information.

Ursula C. Schwerin Library New York City College of Technology, C.U.N.Y 300 Jay Street, Library Building - 4th Floor

Acknowledgments

This course is based on the following course(s):

• MAT1375 by Jonas Reitz

Unless otherwise noted, this site has a Creative Commons Attribution-NonCommercial (CC BY-NC) license. Learn more.

© 2024 MAT1375 Precalculus, Spring 2024

Theme by Anders Noren — Up ↑

The OpenLab at City Tech: A place to learn, work, and share

The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.

New York City College of Technology | City University of New York

Accessibility

Our goal is to make the OpenLab accessible for all users.

Learn more about accessibility on the OpenLab

Creative Commons

• - Attribution
• - NonCommercial
• - ShareAlike

© New York City College of Technology | City University of New York