quadratic equation solve by completing the square

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• complete\:the\:square\:x^{2}+5x+4=0
• complete\:the\:square\:x^{2}+5x+6=0
• complete\:the\:square\:x^{2}=7x+18
• complete\:the\:square\:x^{2}=4x+21

quadratic-equation-solve-by-completing-square-calculator

• High School Math Solutions – Quadratic Equations Calculator, Part 3 On the last post we covered completing the square (see link). It is pretty strait forward if you follow all the...

Please add a message.

Message received. Thanks for the feedback.

Completing the Square

" Completing the Square " is where we ...

But if you have time, let me show you how to " Complete the Square " yourself.

Say we have a simple expression like x 2 + bx . Having x twice in the same expression can make life hard. What can we do?

Well, with a little inspiration from Geometry we can convert it, like this:

As you can see x 2 + bx can be rearranged nearly into a square ...

... and we can complete the square with (b/2) 2

In Algebra it looks like this:

So, by adding (b/2) 2 we can complete the square.

The result of (x+b/2) 2 has x only once , which is easier to use.

Keeping the Balance

Now ... we can't just add (b/2) 2 without also subtracting it too! Otherwise the whole value changes.

So let's see how to do it properly with an example:

The result:

x 2 + 6x + 7   =   (x+3) 2 − 2

And now x only appears once, and our job is done!

A Shortcut Approach

Here is a method you may like, it is quick when you get used to it.

First think about the result we want: (x+d) 2 + e

After expanding (x+d) 2 we get: x 2 + 2dx + d 2 + e

Now see if we can turn our example into that form to discover d and e.

Example: try to fit x 2 + 6x + 7 into x 2 + 2dx + d 2 + e

Now we can "force" an answer:

• We know that 6x must end up as 2dx , so d must be 3
• Next we see that 7 must become d 2 + e = 9 + e , so e must be −2

And we get the same result (x+3) 2 − 2 as above!

Now, let us look at a useful application: solving Quadratic Equations ...

Solving General Quadratic Equations by Completing the Square

We can complete the square to solve a Quadratic Equation (find where it is equal to zero).

But a general Quadratic Equation may have a coefficient of a in front of x 2 :

ax 2 + bx + c = 0

To deal with that we divide the whole equation by "a" first, then carry on:

x 2 + (b/a)x + c/a = 0

Now we can solve a Quadratic Equation in 5 steps:

• Step 1 Divide all terms by a (the coefficient of x 2 ).
• Step 2 Move the number term ( c/a ) to the right side of the equation.
• Step 3 Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation.

We now have something that looks like (x + p) 2 = q, which can be solved this way:

• Step 4 Take the square root on both sides of the equation.
• Step 5 Subtract the number that remains on the left side of the equation to find x .

OK, some examples will help!

Example 1: Solve x 2 + 4x + 1 = 0

Step 1 can be skipped in this example since the coefficient of x 2 is 1

Step 2 Move the number term to the right side of the equation:

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation.

(b/2) 2 = (4/2) 2 = 2 2 = 4

Step 4 Take the square root on both sides of the equation:

Step 5 Subtract 2 from both sides:

Example 2: Solve 5x 2 – 4x – 2 = 0

Step 1 Divide all terms by 5

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:

(b/2) 2 = (0.8/2) 2 = 0.4 2 = 0.16

Step 5 Subtract (-0.4) from both sides (in other words, add 0.4):

Why "Complete the Square"?

Why complete the square when we can just use the Quadratic Formula to solve a Quadratic Equation?

Well, one reason is given above, where the new form not only shows us the vertex, but makes it easier to solve.

There are also times when the form ax 2 + bx + c may be part of a larger question and rearranging it as a(x+ d ) 2 + e makes the solution easier, because x only appears once.

For example "x" may itself be a function (like cos(z) ) and rearranging it may open up a path to a better solution.

Also Completing the Square is the first step in the Derivation of the Quadratic Formula

Just think of it as another tool in your mathematics toolbox.

Footnote: Values of "d" and "e"

How did I get the values of d and e from the top of the page?

9.2 Solve Quadratic Equations by Completing the Square

Learning objectives.

By the end of this section, you will be able to:

• Complete the square of a binomial expression
• Solve quadratic equations of the form x 2 + b x + c = 0 x 2 + b x + c = 0 by completing the square
• Solve quadratic equations of the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 by completing the square

Be Prepared 9.4

Before you get started, take this readiness quiz.

Expand: ( x + 9 ) 2 . ( x + 9 ) 2 . If you missed this problem, review Example 5.32 .

Be Prepared 9.5

Factor y 2 − 14 y + 49 . y 2 − 14 y + 49 . If you missed this problem, review Example 6.9 .

Be Prepared 9.6

Factor 5 n 2 + 40 n + 80 . 5 n 2 + 40 n + 80 . If you missed this problem, review Example 6.14 .

So far we have solved quadratic equations by factoring and using the Square Root Property. In this section, we will solve quadratic equations by a process called completing the square , which is important for our work on conics later.

Complete the Square of a Binomial Expression

In the last section, we were able to use the Square Root Property to solve the equation ( y − 7) 2 = 12 because the left side was a perfect square.

We also solved an equation in which the left side was a perfect square trinomial, but we had to rewrite it the form ( x − k ) 2 ( x − k ) 2 in order to use the Square Root Property.

What happens if the variable is not part of a perfect square? Can we use algebra to make a perfect square?

Let’s look at two examples to help us recognize the patterns.

We restate the patterns here for reference.

Binomial Squares Pattern

If a and b are real numbers,

We can use this pattern to “make” a perfect square.

We will start with the expression x 2 + 6 x . Since there is a plus sign between the two terms, we will use the ( a + b ) 2 pattern, a 2 + 2 ab + b 2 = ( a + b ) 2 .

We ultimately need to find the last term of this trinomial that will make it a perfect square trinomial. To do that we will need to find b . But first we start with determining a . Notice that the first term of x 2 + 6 x is a square, x 2 . This tells us that a = x .

What number, b, when multiplied with 2 x gives 6 x ? It would have to be 3, which is 1 2 ( 6 ) . 1 2 ( 6 ) . So b = 3.

Now to complete the perfect square trinomial, we will find the last term by squaring b , which is 3 2 = 9.

We can now factor.

So we found that adding 9 to x 2 + 6 x ‘completes the square’, and we write it as ( x + 3) 2 .

Complete a square of x 2 + b x . x 2 + b x .

• Step 1. Identify b , the coefficient of x .
• Step 2. Find ( 1 2 b ) 2 , ( 1 2 b ) 2 , the number to complete the square.
• Step 3. Add the ( 1 2 b ) 2 ( 1 2 b ) 2 to x 2 + bx .
• Step 4. Factor the perfect square trinomial, writing it as a binomial squared.

Example 9.11

Complete the square to make a perfect square trinomial. Then write the result as a binomial squared.

ⓐ x 2 − 26 x x 2 − 26 x ⓑ y 2 − 9 y y 2 − 9 y ⓒ n 2 + 1 2 n n 2 + 1 2 n

Try It 9.21

ⓐ a 2 − 20 a a 2 − 20 a ⓑ m 2 − 5 m m 2 − 5 m ⓒ p 2 + 1 4 p p 2 + 1 4 p

Try It 9.22

ⓐ b 2 − 4 b b 2 − 4 b ⓑ n 2 + 13 n n 2 + 13 n ⓒ q 2 − 2 3 q q 2 − 2 3 q

Solve Quadratic Equations of the Form x 2 + bx + c = 0 by Completing the Square

In solving equations, we must always do the same thing to both sides of the equation. This is true, of course, when we solve a quadratic equation by completing the square too. When we add a term to one side of the equation to make a perfect square trinomial, we must also add the same term to the other side of the equation.

For example, if we start with the equation x 2 + 6 x = 40, and we want to complete the square on the left, we will add 9 to both sides of the equation.

Now the equation is in the form to solve using the Square Root Property ! Completing the square is a way to transform an equation into the form we need to be able to use the Square Root Property.

Example 9.12

How to solve a quadratic equation of the form x 2 + b x + c = 0 x 2 + b x + c = 0 by completing the square.

Solve by completing the square: x 2 + 8 x = 48 . x 2 + 8 x = 48 .

Try It 9.23

Solve by completing the square: x 2 + 4 x = 5 . x 2 + 4 x = 5 .

Try It 9.24

Solve by completing the square: y 2 − 10 y = −9 . y 2 − 10 y = −9 .

The steps to solve a quadratic equation by completing the square are listed here.

Solve a quadratic equation of the form x 2 + b x + c = 0 x 2 + b x + c = 0 by completing the square.

• Step 1. Isolate the variable terms on one side and the constant terms on the other.
• Step 2. Find ( 1 2 · b ) 2 , ( 1 2 · b ) 2 , the number needed to complete the square. Add it to both sides of the equation.
• Step 3. Factor the perfect square trinomial, writing it as a binomial squared on the left and simplify by adding the terms on the right
• Step 4. Use the Square Root Property.
• Step 5. Simplify the radical and then solve the two resulting equations.
• Step 6. Check the solutions.

When we solve an equation by completing the square, the answers will not always be integers.

Example 9.13

Solve by completing the square: x 2 + 4 x = −21 . x 2 + 4 x = −21 .

Try It 9.25

Solve by completing the square: y 2 − 10 y = −35 . y 2 − 10 y = −35 .

Try It 9.26

Solve by completing the square: z 2 + 8 z = −19 . z 2 + 8 z = −19 .

In the previous example, our solutions were complex numbers. In the next example, the solutions will be irrational numbers.

Example 9.14

Solve by completing the square: y 2 − 18 y = −6 . y 2 − 18 y = −6 .

Another way to check this would be to use a calculator. Evaluate y 2 − 18 y y 2 − 18 y for both of the solutions. The answer should be −6 . −6 .

Try It 9.27

Solve by completing the square: x 2 − 16 x = −16 . x 2 − 16 x = −16 .

Try It 9.28

Solve by completing the square: y 2 + 8 y = 11 . y 2 + 8 y = 11 .

We will start the next example by isolating the variable terms on the left side of the equation.

Example 9.15

Solve by completing the square: x 2 + 10 x + 4 = 15 . x 2 + 10 x + 4 = 15 .

Try It 9.29

Solve by completing the square: a 2 + 4 a + 9 = 30 . a 2 + 4 a + 9 = 30 .

Try It 9.30

Solve by completing the square: b 2 + 8 b − 4 = 16 . b 2 + 8 b − 4 = 16 .

To solve the next equation, we must first collect all the variable terms on the left side of the equation. Then we proceed as we did in the previous examples.

Example 9.16

Solve by completing the square: n 2 = 3 n + 11 . n 2 = 3 n + 11 .

Try It 9.31

Solve by completing the square: p 2 = 5 p + 9 . p 2 = 5 p + 9 .

Try It 9.32

Solve by completing the square: q 2 = 7 q − 3 . q 2 = 7 q − 3 .

Notice that the left side of the next equation is in factored form. But the right side is not zero. So, we cannot use the Zero Product Property since it says “If a · b = 0 , a · b = 0 , then a = 0 or b = 0.” Instead, we multiply the factors and then put the equation into standard form to solve by completing the square.

Example 9.17

Solve by completing the square: ( x − 3 ) ( x + 5 ) = 9 . ( x − 3 ) ( x + 5 ) = 9 .

Try It 9.33

Solve by completing the square: ( c − 2 ) ( c + 8 ) = 11 . ( c − 2 ) ( c + 8 ) = 11 .

Try It 9.34

Solve by completing the square: ( d − 7 ) ( d + 3 ) = 56 . ( d − 7 ) ( d + 3 ) = 56 .

Solve Quadratic Equations of the Form ax 2 + bx + c = 0 by Completing the Square

The process of completing the square works best when the coefficient of x 2 is 1, so the left side of the equation is of the form x 2 + bx + c . If the x 2 term has a coefficient other than 1, we take some preliminary steps to make the coefficient equal to 1.

Sometimes the coefficient can be factored from all three terms of the trinomial. This will be our strategy in the next example.

Example 9.18

Solve by completing the square: 3 x 2 − 12 x − 15 = 0 . 3 x 2 − 12 x − 15 = 0 .

To complete the square, we need the coefficient of x 2 x 2 to be one. If we factor out the coefficient of x 2 x 2 as a common factor, we can continue with solving the equation by completing the square.

Try It 9.35

Solve by completing the square: 2 m 2 + 16 m + 14 = 0 . 2 m 2 + 16 m + 14 = 0 .

Try It 9.36

Solve by completing the square: 4 n 2 − 24 n − 56 = 8 . 4 n 2 − 24 n − 56 = 8 .

To complete the square, the coefficient of the x 2 must be 1. When the leading coefficient is not a factor of all the terms, we will divide both sides of the equation by the leading coefficient! This will give us a fraction for the second coefficient. We have already seen how to complete the square with fractions in this section.

Example 9.19

Solve by completing the square: 2 x 2 − 3 x = 20 . 2 x 2 − 3 x = 20 .

To complete the square we need the coefficient of x 2 x 2 to be one. We will divide both sides of the equation by the coefficient of x 2 . Then we can continue with solving the equation by completing the square.

Try It 9.37

Solve by completing the square: 3 r 2 − 2 r = 21 . 3 r 2 − 2 r = 21 .

Try It 9.38

Solve by completing the square: 4 t 2 + 2 t = 20 . 4 t 2 + 2 t = 20 .

Now that we have seen that the coefficient of x 2 must be 1 for us to complete the square, we update our procedure for solving a quadratic equation by completing the square to include equations of the form ax 2 + bx + c = 0.

Solve a quadratic equation of the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 by completing the square.

• Step 1. Divide by a a to make the coefficient of x 2 term 1.
• Step 2. Isolate the variable terms on one side and the constant terms on the other.
• Step 3. Find ( 1 2 · b ) 2 , ( 1 2 · b ) 2 , the number needed to complete the square. Add it to both sides of the equation.
• Step 4. Factor the perfect square trinomial, writing it as a binomial squared on the left and simplify by adding the terms on the right
• Step 5. Use the Square Root Property.
• Step 6. Simplify the radical and then solve the two resulting equations.
• Step 7. Check the solutions.

Example 9.20

Solve by completing the square: 3 x 2 + 2 x = 4 . 3 x 2 + 2 x = 4 .

Again, our first step will be to make the coefficient of x 2 one. By dividing both sides of the equation by the coefficient of x 2 , we can then continue with solving the equation by completing the square.

Try It 9.39

Solve by completing the square: 4 x 2 + 3 x = 2 . 4 x 2 + 3 x = 2 .

Try It 9.40

Solve by completing the square: 3 y 2 − 10 y = −5 . 3 y 2 − 10 y = −5 .

Access these online resources for additional instruction and practice with completing the square.

• Completing Perfect Square Trinomials
• Completing the Square 1
• Completing the Square to Solve Quadratic Equations
• Completing the Square to Solve Quadratic Equations: More Examples
• Completing the Square 4

Section 9.2 Exercises

Practice makes perfect.

In the following exercises, complete the square to make a perfect square trinomial. Then write the result as a binomial squared.

ⓐ m 2 − 24 m m 2 − 24 m ⓑ x 2 − 11 x x 2 − 11 x ⓒ p 2 − 1 3 p p 2 − 1 3 p

ⓐ n 2 − 16 n n 2 − 16 n ⓑ y 2 + 15 y y 2 + 15 y ⓒ q 2 + 3 4 q q 2 + 3 4 q

ⓐ p 2 − 22 p p 2 − 22 p ⓑ y 2 + 5 y y 2 + 5 y ⓒ m 2 + 2 5 m m 2 + 2 5 m

ⓐ q 2 − 6 q q 2 − 6 q ⓑ x 2 − 7 x x 2 − 7 x ⓒ n 2 − 2 3 n n 2 − 2 3 n

Solve Quadratic Equations of the form x 2 + bx + c = 0 by Completing the Square

In the following exercises, solve by completing the square.

u 2 + 2 u = 3 u 2 + 2 u = 3

z 2 + 12 z = −11 z 2 + 12 z = −11

x 2 − 20 x = 21 x 2 − 20 x = 21

y 2 − 2 y = 8 y 2 − 2 y = 8

m 2 + 4 m = −44 m 2 + 4 m = −44

n 2 − 2 n = −3 n 2 − 2 n = −3

r 2 + 6 r = −11 r 2 + 6 r = −11

t 2 − 14 t = −50 t 2 − 14 t = −50

a 2 − 10 a = −5 a 2 − 10 a = −5

b 2 + 6 b = 41 b 2 + 6 b = 41

x 2 + 5 x = 2 x 2 + 5 x = 2

y 2 − 3 y = 2 y 2 − 3 y = 2

u 2 − 14 u + 12 = −1 u 2 − 14 u + 12 = −1

z 2 + 2 z − 5 = 2 z 2 + 2 z − 5 = 2

r 2 − 4 r − 3 = 9 r 2 − 4 r − 3 = 9

t 2 − 10 t − 6 = 5 t 2 − 10 t − 6 = 5

v 2 = 9 v + 2 v 2 = 9 v + 2

w 2 = 5 w − 1 w 2 = 5 w − 1

x 2 − 5 = 10 x x 2 − 5 = 10 x

y 2 − 14 = 6 y y 2 − 14 = 6 y

( x + 6 ) ( x − 2 ) = 9 ( x + 6 ) ( x − 2 ) = 9

( y + 9 ) ( y + 7 ) = 80 ( y + 9 ) ( y + 7 ) = 80

( x + 2 ) ( x + 4 ) = 3 ( x + 2 ) ( x + 4 ) = 3

( x − 2 ) ( x − 6 ) = 5 ( x − 2 ) ( x − 6 ) = 5

Solve Quadratic Equations of the form ax 2 + bx + c = 0 by Completing the Square

3 m 2 + 30 m − 27 = 6 3 m 2 + 30 m − 27 = 6

2 x 2 − 14 x + 12 = 0 2 x 2 − 14 x + 12 = 0

2 n 2 + 4 n = 26 2 n 2 + 4 n = 26

5 x 2 + 20 x = 15 5 x 2 + 20 x = 15

2 c 2 + c = 6 2 c 2 + c = 6

3 d 2 − 4 d = 15 3 d 2 − 4 d = 15

2 x 2 + 7 x − 15 = 0 2 x 2 + 7 x − 15 = 0

3 x 2 − 14 x + 8 = 0 3 x 2 − 14 x + 8 = 0

2 p 2 + 7 p = 14 2 p 2 + 7 p = 14

3 q 2 − 5 q = 9 3 q 2 − 5 q = 9

5 x 2 − 3 x = −10 5 x 2 − 3 x = −10

7 x 2 + 4 x = −3 7 x 2 + 4 x = −3

Writing Exercises

Solve the equation x 2 + 10 x = −25 x 2 + 10 x = −25

ⓐ by using the Square Root Property

ⓑ by Completing the Square

ⓒ Which method do you prefer? Why?

Solve the equation y 2 + 8 y = 48 y 2 + 8 y = 48 by completing the square and explain all your steps.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/9-2-solve-quadratic-equations-by-completing-the-square

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Math Article
• Completing The Square

Completing The Square Method

A polynomial equation with a degree equal to two is known as a quadratic equation . ‘Quad’ means four, but ‘Quadratic’ means ‘to make square’. A quadratic equation in its standard form is represented as:

ax 2 + bx + c = 0, where a, b and c are real numbers such that a ≠ 0 and x is a variable.

Since the degree of the above-written equation is two, it will have two roots or solutions. The roots of polynomials are the values of x, which satisfy the equation. There are several methods to find the roots of a quadratic equation. One of them is by completing the square . The ways of solving these quadratics have been introduced to the students in Class 10 and 11. In this article, you can learn how to solve a given quadratic equation using the method of completing the square.

Completing the square method is one of the methods to find the roots of the given quadratic equation. In this method, we have to convert the given equation into a perfect square. We can also evaluate the roots of the quadratic equation by using the quadratic formula .

Completing the Square for Quadratic Equation

For completing the square to solve quadratic equations , first, we need to write the standard form as:

ax 2   + bx + c = 0

For simplification, let us take a = 1 so that the equation becomes,

x 2  + bx + c = 0

If we wanted to represent a quadratic equation using geometry, one way would be to describe the terms of the expression in the L.H.S. of the equation using geometric figures such as squares, rectangles etc. If we take a square with the side equal to x units, its area would be equivalent to x 2  square units. This area will hence represent the first term of the expression. Similarly, a rectangle with two sides as x units and b units will have an area equal to bx square units. And let us take a square with an area equal to c square units to represent the last term of the expression. In the figure below, we have the geometrical equivalent of the expressions x 2 , bx and c.

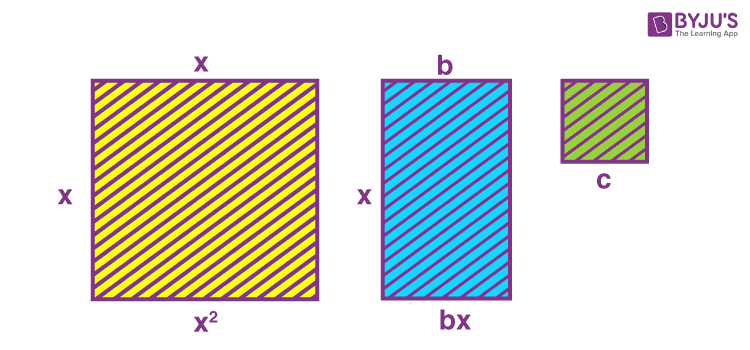
Geometrical equivalent of x 2 , bx and c

Let us complete some squares as mentioned in the previous figure. If we break the rectangle representing bx into two equal parts, cutting vertically, we will have two figures with an area of each equal to b/2 x square units. The figures are arranged accordingly in the second figure below.

Rearranging the figures

But our square is not complete yet. One square of side b/2 units is needed to complete the square shape. We can take this final part of the main square from the square with the area c square units. After cutting it out and putting it in place, it results in the below figure.

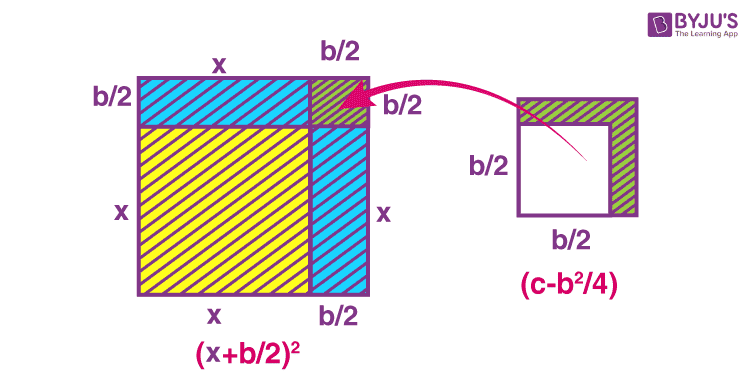
Let us derive the formula for completing the square with the help of the above procedure.

Completing The Square Formula

The square is finally completed in the above figure. The area of the square is equal to

(x + b/2) 2  square units

The remaining area is equal to

(c – b 2 /4) square units

All this time, we were rearranging the same figures that we had initially. Thus, the actual representation can be:

x 2  + bx + c = (x + b/2) 2  + (c – b 2 /4)

This method is known as completing the square method. We have achieved it geometrically. 

We know that, 

This can be written as:

(x + b/2) 2  + (c – b 2 /4) = 0

⇒ (x + b/2) 2  = -(c – b 2 /4)

This formula can be used to solve the quadratic equations by completing the square technique.

All the terms in the R.H.S. of the above equation are known. That’s why it is easy to determine the roots. 

Steps for Completing the square method

Suppose ax 2  + bx + c = 0 is the given quadratic equation. Then follow the given steps to solve it by completing the square method.

Step 1: Write the equation in the form, such that c is on the right side.

Step 2: If a is not equal to 1, divide the complete equation by a such that the coefficient of x 2  will be 1.

Step 3: Now add the square of half of the coefficient of term-x, (b/2a) 2 , on both sides.

Step 4: Factorize the left side of the equation as the square of the binomial term.

Step 5: Take the square root on both the sides

Step 6: Solve for variable x and find the roots.

The above steps can be implemented as shown below.

Consider the quadratic equation ax 2  + bx + c = 0 (a ≠ 0). 

Dividing throughout by a, we get

x 2  + (b/a)x + (c/a) = 0

This can also be written by adding and subtracting (b/2a) 2  as,

[x + (b/2a)] 2  – (b/2a) 2  + (c/a) = 0

[x + (b/2a)] 2  – [(b 2  – 4ac)/4a 2 ] = 0

[x + (b/2a)] 2  = [(b 2 – 4ac)/4a 2 ]

If b 2  – 4ac ≥ 0, then by taking the square root, we get

x + (b/2a) = ± √(b 2  – 4ac)/ 2a

Further simplification of this will give you the quadratic formula .

Otherwise, we can directly apply the completing the square method formula while solving the equations.

Let us look at some examples for a better understanding of this technique.

Completing the Square Examples

Example 1: Find the roots of the quadratic equation x 2  + 4x – 5 = 0 by the method of completing the square.

Given quadratic equation is:

x 2  + 4x – 5 = 0

Comparing the equation with the standard form,

b = 4, c = -5

(x + b/2) 2  = -(c – b 2 /4)

So, [x + (4/2)] 2  = -[-5 – (4 2 /4)]

(x + 2) 2  = 5 + 4

⇒ (x + 2) 2  = 9

⇒ (x + 2) = ±√9

⇒ (x + 2) = ± 3

⇒ x + 2 = 3, x + 2 = -3

⇒ x = 1 , -5

Therefore, the roots of the given equation are 1 and -5.

Example 2: Find the roots of the quadratic equation 3x 2  – 5x + 2 = 0 by completing the square.

3x 2  – 5x + 2 = 0

The given equation is not in the form to which we apply the method of completing squares, i.e. the coefficient of x 2  is not 1. To make it 1, we need to divide the whole equation with 3.

x 2  – 5/3 x + 2/3 = 0

Comparing with the standard form,

b = -5/3; c = ⅔

c – b 2 /4 = ⅔ – [(-5/3) 2 /4] = (2/3) – (25/36) = (24 – 25)/36 =  -1/36

Substituting these values in the equation (x + b/2) 2  = -(c – b 2 /4) we get,

⇒ (x – 5/6) 2  = 1/36

⇒ (x – 5/6)= ± √(1/36)

⇒ x – 5/6 = ±1/6

⇒ x = 1, -2/3

Therefore, the roots of the given equation are 1 and -⅔.

The below video will help you visualize the concepts of solving quadratic equations.

Completing the Square Problems

Let’s practice the questions on completing the square method of solving quadratic equations.

• Find the roots of 4x 2  + 3x + 5 = 0 by the method of completing the square.
• Find the roots of the equation 5x 2  – 6x – 2 = 0 by the method of completing the square.
• Find two consecutive odd positive integers, the sum of whose squares is 290.

To solve more problems on the topic, download BYJU’S – The Learning App from Google Play Store.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

I understand the method of completing square in very clear manners thank you for your suggestions

this is very help full. i understood each and every step clearly.

Easily understood Nice way of learning

I UNDERSTAND EACH AND EVERY STEPS CLEARLY THANKS BYJU’S ANSHIKA:)

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Quadratic Equation Solver

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Step-By-Step Example

Example (click to try), choose your method, solve by factoring.

Example: 3x^2-2x-1=0

Complete The Square

Example: 3x^2-2x-1=0 (After you click the example, change the Method to 'Solve By Completing the Square'.)

Take the Square Root

Example: 2x^2=18

Quadratic Formula

Example: 4x^2-2x-1=0

About quadratic equations

Need more problem types? Try MathPapa Algebra Calculator

Clear Quadratic Equation Solver »

Solving Quadratic Equations by Completing the Square

Are you preparing for O-level exams?

Here is a quick crash course on solving Quadratic Equations by completing the square.

Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later. This will be delivered to your email inbox.

To solve the quadratic equation ax 2 + bx + c = 0 by completing the square, you can follow the steps below:

Step 1: Change coefficient of x 2 equal to 1

a( x 2 + b x /a + c/a) = 0

Step 2: Leave x 2 and x terms on the Left Hand Side (LHS)

x 2 + b x /a = – c/a

Step 3: Coefficient of x ÷2, square it, add to both sides

x 2 + b x /a + (b/2a) 2 = – c/a + (b/2a) 2

Step 4: Factorise the LHS of the equation

(x + b/2a) 2 = – c/a + (b/2a) 2

Step 5: Simplify to solve for x

= –4ac/4a 2 + b 2 /4a 2

= (b 2 – 4ac)/4a 2

x + b/2a = ±√( (b 2 – 4ac)/4a 2 )

x = – b/2a  ±√( (b 2 – 4ac)/4a 2 )

x =( – b ±√( (b 2 – 4ac) ) /2a

Does the answer look familiar to you?

Yes, it is the Quadratic Formula!

In fact, the answer to the “Completed Square” equation is the same as the Quadratic Formula.

But you are required to show the steps to completing the square.

Let’s look at an example below.

Example (Solve Quadratic Equations by Completing the Square)

2 x 2 – 3 x – 9 = 0

x 2 – 3 x/2 – 9/2 = 0

x 2 – 3 x /2 =  9/2

x 2 – 3 x /2 + (– 3/4) 2 =  9/2 + (– 3/4) 2

( x – 3/4) 2 = 9/2 + 9/16

( x – 3/4) 2 = ± 9/4

x = 3/4 + 9/4  or x = 3/4 – 9/4

   = 3                      = –3/2 (ans)

Last Minute Revision for O Level Math?

Check out our exam guide on other topics here.

Secondary Math Revision Notes

Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later. 

This will be delivered to your email inbox.

Does your child need help in his or her studies?

1) live zoom lessons at grade solution learning centre.

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:

– Live Zoom lessons – EdaptIQ™, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital worksheets. – 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.

We specialise in English, Math, and Science subjects.

You can see our fees and schedules here >>

Primary Math Tuition

Secondary Math Tuition

2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >>

Math Online Courses

YOU HAVE THE FOLLOWING POINTS

• PRIMARY SCHOOL
• SECONDARY SCHOOL
• LOGIN / REGISTER

Completing the square

You already know there’s more than one way to solve quadratic equations . Have you tried completing the square yet?

Let’s try it now!

What does it mean to complete the square?

Completing the square is a method by which the same value is added to and subtracted from an expression in order to write it as a perfect square.

Remember: A quadratic equation is an equation in which the variable is raised to the second power.

We’ll also need a reminder of the standard form of a quadratic equation, which looks like this:

Why is completing the square so useful?

Completing the square is another tool in your tool chest for solving quadratic equations. You’ll find that, even beyond quadratic equations, you can work so much more efficiently once you start recognizing which method to use when. Think of it as a fun challenge — see how simple you can make things!

How to complete the square

Let’s get into some math and learn how to complete the square! The best way to learn something is to see it in action, so we’ll walk through a few examples together.

Solve this quadratic equation by completing the square:

Move the constant to the right side of the equation and change its sign:

$$x^2+4x={-}{1}$$

To complete the square while preserving the relation between each side of the equation, the same value needs to be added to both sides (remember the addition and subtraction property of equality!):

$$x^2+{4x}+\mathord{?} =-1+\mathord{?}$$

Write the expression as a product with the factors $$2$$ and $$x$$ so that our expression has the same structure as the formula we want to use:

$$x^2+{2\times x\times2}+\mathord{?} =-1+\mathord{?}$$

Since $$2$$ is part of the middle term, add $$2^2$$ to both sides of the equation:

$${x}^2+{2\times {x}\times{2}}+{2^2} =-1+{2^2}$$

Remember the square of the sum formula $${a}^2+2{a}{b}+{b}^2=({a}+{b})^2$$? We’ll use that to factor the expression on the left-hand side of the equation:

$$({x}+{2})^2 =-1+{2^2}$$

Evaluate the power:

$$({x}+{2})^2 =-1+4$$

Calculate the sum:

$$({x}+{2})^2 =3$$

Take the square root of both sides of the equation, and remember to use both positive and negative roots! We can do this because of the rule stating that, if two expressions are equal, their square roots are also equal:

$${x}+{2} =\pm\sqrt{3}$$

Separate the equation into $$2$$ possible cases (one with the minus root and one with the plus root):

$${x}{+}{2} =-\sqrt{3}$$

$${x}{+}{2} =\sqrt{3}$$

Move the constants to the right-hand side of the equation and change their signs:

$${x} =-\sqrt{3}{-}2$$

$${x} =\sqrt{3}{-}2$$

Our equation has $$2$$ solutions:

$$-2t^{2} + 3t = {-} {2}$$

We want to isolate the unknown variable on one side, so divide both sides of the equation by $$-2$$:

$$t^{2} -\frac32t = 1$$

To complete the square while preserving the relation between the sides of the equation, we need to add the same value to both sides (there’s the addition and subtraction property of equality again):

$$t^{2} -{\frac32t} + \mathord{?} = 1+ \mathord{?}$$

Write the expression as a product with the factors $$2$$ and $$t$$ so that our expression has the same structure as the formula we want to use:

$$t^2-{2\times t\times\frac34}+{\mathord{?}} =1+{\mathord{?}}$$

Since $$\frac34$$ is part of the middle term, add $$\left(\frac34\right)^2$$ to both sides of the equation:

$${t}^2-{2\times {t}\times{\frac34}}+{\left(\frac34\right)^2}=1+\left(\frac34\right)^2$$

The square of the sum formula is $${a}^2+2{a}{b}+{b}^2=({a}+{b})^2$$, so let’s use it to factor the expression on the left-hand side:

$$\left({t}-{\frac34}\right)^2 =1+{\left(\frac34\right)^2}$$

$$\left(t-\frac34\right)^2 =1+{\frac9{16}}$$

$$\left(t-\frac34\right)^2 =\frac{25}{16}$$

Take the square root of both sides of the equation, remembering to use both positive and negative roots. We can do this because of the rule stating if two expressions are equal, then their square roots are also equal:

$$t-\frac34 =\pm\frac{5}{4}$$

$$t{-}{\frac34} =-\frac{5}{4}$$

$$t{-}{\frac34} =\frac{5}{4}$$

$$t =-\frac{5}{4}{+}{\frac34}$$

$$t =\frac{5}{4}{+}{\frac34}$$

Add the fractions:

$$t =-\frac12$$

There we go! The equation has $$2$$ solutions:

That wasn’t so bad, right? Let’s review the process so you can try this again any time:

Study summary

• Move the constant to the right side of the equation.
• Divide both sides by the constant.
• To complete the square, add or subtract the same value to both sides.
• Factor the expression on the left side of the equation.
• Calculate the sum or difference on the right side of the equation.
• Solve the equation.

Do it yourself!

How did it go with the examples? Are you ready to try some on your own? Here are a few practice problems for you to work through:

Solve a quadratic equation by completing the square:

• $$x^2-4x+3=8$$
• $$9t^2+6t+5=13$$
• $$t^2+3t+\frac{1}{4}=7$$
• $$a^2+\frac{10}{3}a=\frac{11}{9}$$
• $$x_1=-1, x_2=5$$
• $$t_1=-\frac43, ~t_2=\frac23$$
• $$t_1=-\frac92, ~x_2=\frac32$$
• $$a_1=-\frac{11}3, ~a_2=\frac13$$

If you’re struggling through the solving process, that’s totally okay! Making mistakes can actually help you learn! If you’re getting too stuck or confused, scan the problem using your Photomath app , and we’ll walk you through to the other side!

Here’s a sneak peek of what you’ll see:

Related Topics

• Math Explained: Algebra
• Quadratic Equations

Related Articles

Algebra - Basics, Concepts, Examples, Practice

Taking the square root

Number of solutions

ABC formula

Algebra Examples

• Terms ( Premium )
• DO NOT SELL MY INFO
• Mathway © 2024

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.25: Solving Quadratic Equations by Completing the Square

• Last updated
• Save as PDF
• Page ID 95698

• Katherine Skelton
• Highline College

So far we have solved quadratic equations by factoring and using the Square Root Property. In this section, we will solve quadratic equations by a process called completing the square , which is important for our work on conics later.

Completing the Square of a Binomial Expression

In the last section, we were able to use the Square Root Property to solve the equation \((y-7)^{2}=12\) because the left side was a perfect square.

\(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)

We also solved an equation in which the left side was a perfect square trinomial, but we had to rewrite it the form \((x−k)^{2}\) in order to use the Square Root Property.

\(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)

What happens if the variable is not part of a perfect square? Can we use algebra to make a perfect square?

Let’s look at two examples to help us recognize the patterns.

\(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)

We restate the patterns here for reference.

Binomial Squares Pattern

If \(a\) and \(b\) are real numbers,

\(\begin{array}{l}(a+b)^2=a^2+2 a b+b^2 \quad \quad  \underbrace{(a+b)^2}_{(\text {binomial })^2}=\underbrace{a^2}_{\text {(first term) })^2}+\underbrace{2 a b}_{2 \cdot(\text { product of }}+\underbrace{b^2}_{\text {(second term) })^2} \end{array}\)

\((a-b)^2=a^2-2 a b+b^2 \quad \quad \underbrace{(a-b)^2}_{\text {(binomial) })^2}=\underbrace{a^2}_{\text {(first term) })^2}-\underbrace{2 a b}_{\substack{\text { terms) } \\ \text { tiroduct of }}}+\underbrace{b^2}_{\text {(second term) })^2}\)

We can use this pattern to “make” a perfect square.

We will start with the expression \(x^{2}+6 x\). Since there is a plus sign between the two terms, we will use the \((a+b)^{2}\) pattern, \(a^{2}+2 a b+b^{2}=(a+b)^{2}\).

We ultimately need to find the last term of this trinomial that will make it a perfect square trinomial. To do that we will need to find \(b\). But first we start with determining \(a\). Notice that the first term of \(x^{2}+6x\) is a square, \(x^{2}\). This tells us that \(a=x\).

What number, \(b\) , when multiplied with \(2x\) gives \(6x\)? It would have to be \(3\), which is \(\frac{1}{2}(6)\). So \(b=3\).

Now to complete the perfect square trinomial, we will find the last term by squaring \(b\), which is \(3^{2}=9\).

We can now factor.

So we found that adding \(9\) to \(x^{2}+6 x\) ‘completes the square’, and we write it as \((x+3)^{2}\).

How To Complete a Square of \(x^{2}+bx\)

• Identify \(b\), the coefficient of \(x\).
• Find \(\left(\frac{1}{2} b\right)^{2}\), the number to complete the square.
• Add the\(\left(\frac{1}{2} b\right)^{2}\) to \(x^{2}+bx\).
• Factor the perfect square trinomial, writing it as a binomial squared.

Example \(\PageIndex{1}\)

Complete the square to make a perfect square trinomial. Then write the result as a binomial squared.

• \(x^{2}-26 x\)
• \(y^{2}-9 y\)
• \(n^{2}+\frac{1}{2} n\)

You Try \(\PageIndex{1}\)

• \(b^{2}-4 b\)
• \(n^{2}+13 n\)
• \(q^{2}-\frac{2}{3} q\)
• \((b-2)^{2}\)
• \(\left(n+\frac{13}{2}\right)^{2}\)
• \(\left(q-\frac{1}{3}\right)^{2}\)

Solving Quadratic Equations of the Form \(x^{2}+bx+c=0\) by Completing the Square

In solving equations, we must always do the same thing to both sides of the equation. This is true, of course, when we solve a quadratic equation by completing the square too. When we add a term to one side of the equation to make a perfect square trinomial, we must also add the same term to the other side of the equation.

For example, if we start with the equation \(x^{2}+6x=40\), and we want to complete the square on the left, we will add 9 to both sides of the equation.

Now the equation is in the form to solve using the Square Root Property ! Completing the square is a way to transform an equation into the form we need to be able to use the Square Root Property.

Example \(\PageIndex{2}\)

Solve by completing the square: \(x^{2}+8x=48\)

You Try \(\PageIndex{2}\)

Solve by completing the square: \(y^{2}−10y=−9\)

\(y=1, y=9\)

The steps to solve a quadratic equation by completing the square are listed here.

Solving Quadratic Equation of the Form \(x^{2}+bx+c=0\) by Completing the Square

• Isolate the variable terms on one side and the constant terms on the other.
• Find \(\left(\frac{1}{2} \cdot b\right)^{2}\), the number needed to complete the square. Add it to both sides of the equation.
• Factor the perfect square trinomial, writing it as a binomial squared on the left and simplify by adding the terms on the right
• Use the Square Root Property.
• Simplify the radical and then solve the two resulting equations.
• Check the solutions.

When we solve an equation by completing the square, the answers will not always be integers.

Example \(\PageIndex{3}\)

Solve by completing the square: \(x^{2}+4 x=-21\)

You Try \(\PageIndex{3}\)

Solve by completing the square: \(y^{2}-10 y=-35\)

\(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)

In the previous example, our solutions were complex numbers. In the next example, the solutions will be irrational numbers.

Example \(\PageIndex{4}\)

Solve by completing the square: \(y^{2}-18 y=-6\)

Another way to check this would be to use a calculator. Evaluate \(y^{2}−18y\) for both of the solutions. The answer should be \(−6\).

You Try \(\PageIndex{4}\)

Solve by completing the square: \(y^{2}+8 y=11\)

\(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)

We will start the next example by isolating the variable terms on the left side of the equation.

Example \(\PageIndex{5}\)

Solve by completing the square: \(x^{2}+10 x+4=15\)

You Try \(\PageIndex{5}\)

Solve by completing the square: \(b^{2}+8 b-4=16\)

\(b=-10, b=2\)

To solve the next equation, we must first collect all the variable terms on the left side of the equation. Then we proceed as we did in the previous examples.

Example \(\PageIndex{6}\)

Solve by completing the square: \(n^{2}=3 n+11\)

You Try \(\PageIndex{6}\)

Solve by completing the square: \(q^{2}=7 q-3\)

\(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)

Notice that the left side of the next equation is in factored form. But the right side is not zero. So, we cannot use the Zero Product Property since it says “If \(a⋅b=0\), then \(a=0\) or \(b=0\).” Instead, we multiply the factors and then put the equation into standard form to solve by completing the square.

Example \(\PageIndex{7}\)

Solve by completing the square: \((x-3)(x+5)=9\)

You Try \(\PageIndex{7}\)

Solve by completing the square: \((c-2)(c+8)=11\)

\(c=-9, c=3\)

Solving Quadratic Equations of the Form \(ax^{2}+bx+c=0\) by Completing the Square

The process of completing the square works best when the coefficient of \(x^{2}\) is \(1\), so the left side of the equation is of the form \(x^{2}+bx+c\). If the \(x^{2}\) term has a coefficient other than \(1\), we take some preliminary steps to make the coefficient equal to \(1\).

Sometimes the coefficient can be factored from all three terms of the trinomial. This will be our strategy in the next example.

Example \(\PageIndex{8}\)

Solve by completing the square: \(3 x^{2}-12 x-15=0\)

To complete the square, we need the coefficient of \(x^{2}\) to be one. If we factor out the coefficient of \(x^{2}\) as a common factor, we can continue with solving the equation by completing the square.

You Try \(\PageIndex{8}\)

Solve by completing the square: \(2 m^{2}+16 m+14=0\)

\(m=-7, m=-1\)

To complete the square, the coefficient of the \(x^{2}\) must be \(1\). When the leading coefficient is not a factor of all the terms, we will divide both sides of the equation by the leading coefficient! This will give us a fraction for the second coefficient. We have already seen how to complete the square with fractions in this section.

Example \(\PageIndex{9}\)

Solve by completing the square: \(2 x^{2}-3 x=20\)

To complete the square we need the coefficient of \(x^{2}\) to be one. We will divide both sides of the equation by the coefficient of \(x^{2}\). Then we can continue with solving the equation by completing the square.

You Try \(\PageIndex{9}\)

Solve by completing the square: \(4 t^{2}+2 t=20\)

\(t=-\frac{5}{2}, t=2\)

Now that we have seen that the coefficient of \(x^{2}\) must be \(1\) for us to complete the square, we update our procedure for solving a quadratic equation by completing the square to include equations of the form \(a x^{2}+b x+c=0\).

How to Solve a Quadratic Equation of the Form \(a x^{2}+b x+c=0\) by Completing the Square

• Divide by the leading coefficient, "a", to make the coefficient of \(x^{2}\) term \(1\).

Example \(\PageIndex{10}\)

Solve by completing the square: \(3 x^{2}+2 x=4\)

Again, our first step will be to make the coefficient of \(x^{2}\) one. By dividing both sides of the equation by the coefficient of \(x^{2}\), we can then continue with solving the equation by completing the square.

You Try \(\PageIndex{10}\)

Solve by completing the square: \(3 y^{2}-10 y=-5\)

\(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)