solving problems exponential and logarithmic

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 2   >   Unit 8

• Solving exponential equations using logarithms: base-10

Solving exponential equations using logarithms

• Solve exponential equations using logarithms: base-10 and base-e
• Solving exponential equations using logarithms: base-2
• Solve exponential equations using logarithms: base-2 and other bases

Solving exponential equations of the form a ⋅ b x = d ‍  

Check your understanding.

• (Choice A)   x = log 2 ⁡ ( 39.3 ) ‍   A x = log 2 ⁡ ( 39.3 ) ‍  
• (Choice B)   x = log 6 ⁡ ( 118 ) ‍   B x = log 6 ⁡ ( 118 ) ‍  
• (Choice C)   x = log 12 ⁡ ( 236 ) ‍   C x = log 12 ⁡ ( 236 ) ‍  
• (Choice D)   x = log 118 ⁡ ( 6 ) ‍   D x = log 118 ⁡ ( 6 ) ‍  
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Solving exponential equations of the form a ⋅ b c x = d ‍  

• (Choice A)   t = log ⁡ ( 43.5 ) ‍   A t = log ⁡ ( 43.5 ) ‍  
• (Choice B)   t = log 30 ⁡ ( 130.5 ) ‍   B t = log 30 ⁡ ( 130.5 ) ‍  
• (Choice C)   t = log ⁡ ( 174 ) 4 ‍   C t = log ⁡ ( 174 ) 4 ‍  
• (Choice D)   t = log 30 ⁡ ( 522 ) 4 ‍   D t = log 30 ⁡ ( 522 ) 4 ‍  

Challenge problem

• (Choice A)   2 ‍   A 2 ‍  
• (Choice B)   3 ‍   B 3 ‍  
• (Choice C)   4 ‍   C 4 ‍  
• (Choice D)   log 2 ⁡ ( 3 ) ‍   D log 2 ⁡ ( 3 ) ‍  
• (Choice E)   log 3 ⁡ ( 2 ) ‍   E log 3 ⁡ ( 2 ) ‍  
• (Choice F)   log ⁡ ( 3 ) ‍   F log ⁡ ( 3 ) ‍  

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

10.5 Solve Exponential and Logarithmic Equations

Learning objectives.

By the end of this section, you will be able to:

• Solve logarithmic equations using the properties of logarithms
• Solve exponential equations using logarithms
• Use exponential models in applications

Be Prepared 10.13

Before you get started, take this readiness quiz.

Solve: x 2 = 16 . x 2 = 16 . If you missed this problem, review Example 6.46 .

Be Prepared 10.14

Solve: x 2 − 5 x + 6 = 0 . x 2 − 5 x + 6 = 0 . If you missed this problem, review Example 6.45 .

Be Prepared 10.15

Solve: x ( x + 6 ) = 2 x + 5 . x ( x + 6 ) = 2 x + 5 . If you missed this problem, review Example 6.47 .

Solve Logarithmic Equations Using the Properties of Logarithms

In the section on logarithmic functions, we solved some equations by rewriting the equation in exponential form. Now that we have the properties of logarithms, we have additional methods we can use to solve logarithmic equations.

If our equation has two logarithms we can use a property that says that if log a M = log a N log a M = log a N then it is true that M = N . M = N . This is the One-to-One Property of Logarithmic Equations .

One-to-One Property of Logarithmic Equations

For M > 0 , N > 0 , a > 0 , M > 0 , N > 0 , a > 0 , and a ≠ 1 a ≠ 1 is any real number:

To use this property, we must be certain that both sides of the equation are written with the same base.

Remember that logarithms are defined only for positive real numbers. Check your results in the original equation. You may have obtained a result that gives a logarithm of zero or a negative number.

Example 10.38

Solve: 2 log 5 x = log 5 81 . 2 log 5 x = log 5 81 .

Try It 10.75

Solve: 2 log 3 x = log 3 36 2 log 3 x = log 3 36

Try It 10.76

Solve: 3 log x = log 64 3 log x = log 64

Another strategy to use to solve logarithmic equations is to condense sums or differences into a single logarithm.

Example 10.39

Solve: log 3 x + log 3 ( x − 8 ) = 2 . log 3 x + log 3 ( x − 8 ) = 2 .

Try It 10.77

Solve: log 2 x + log 2 ( x − 2 ) = 3 log 2 x + log 2 ( x − 2 ) = 3

Try It 10.78

Solve: log 2 x + log 2 ( x − 6 ) = 4 log 2 x + log 2 ( x − 6 ) = 4

When there are logarithms on both sides, we condense each side into a single logarithm. Remember to use the Power Property as needed.

Example 10.40

Solve: log 4 ( x + 6 ) − log 4 ( 2 x + 5 ) = − log 4 x . log 4 ( x + 6 ) − log 4 ( 2 x + 5 ) = − log 4 x .

Try It 10.79

Solve: log ( x + 2 ) − log ( 4 x + 3 ) = − log x . log ( x + 2 ) − log ( 4 x + 3 ) = − log x .

Try It 10.80

Solve: log ( x − 2 ) − log ( 4 x + 16 ) = log 1 x . log ( x − 2 ) − log ( 4 x + 16 ) = log 1 x .

Solve Exponential Equations Using Logarithms

In the section on exponential functions, we solved some equations by writing both sides of the equation with the same base. Next we wrote a new equation by setting the exponents equal.

It is not always possible or convenient to write the expressions with the same base. In that case we often take the common logarithm or natural logarithm of both sides once the exponential is isolated.

Example 10.41

Solve 5 x = 11 . 5 x = 11 . Find the exact answer and then approximate it to three decimal places.

Try It 10.81

Solve 7 x = 43 . 7 x = 43 . Find the exact answer and then approximate it to three decimal places.

Try It 10.82

Solve 8 x = 98 . 8 x = 98 . Find the exact answer and then approximate it to three decimal places.

When we take the logarithm of both sides we will get the same result whether we use the common or the natural logarithm (try using the natural log in the last example. Did you get the same result?) When the exponential has base e , we use the natural logarithm.

Example 10.42

Solve 3 e x + 2 = 24 . 3 e x + 2 = 24 . Find the exact answer and then approximate it to three decimal places.

Try It 10.83

Solve 2 e x − 2 = 18 . 2 e x − 2 = 18 . Find the exact answer and then approximate it to three decimal places.

Try It 10.84

Solve 5 e 2 x = 25 . 5 e 2 x = 25 . Find the exact answer and then approximate it to three decimal places.

Use Exponential Models in Applications

In previous sections we were able to solve some applications that were modeled with exponential equations. Now that we have so many more options to solve these equations, we are able to solve more applications.

We will again use the Compound Interest Formulas and so we list them here for reference.

Compound Interest

For a principal, P , invested at an interest rate, r , for t years, the new balance, A is:

Example 10.43

Jermael’s parents put $10,000 in investments for his college expenses on his first birthday. They hope the investments will be worth $50,000 when he turns 18. If the interest compounds continuously, approximately what rate of growth will they need to achieve their goal?

Try It 10.85

Hector invests $ 10,000 $ 10,000 at age 21. He hopes the investments will be worth $ 150,000 $ 150,000 when he turns 50. If the interest compounds continuously, approximately what rate of growth will he need to achieve his goal?

Try It 10.86

Rachel invests $ 15,000 $ 15,000 at age 25. She hopes the investments will be worth $ 90,000 $ 90,000 when she turns 40. If the interest compounds continuously, approximately what rate of growth will she need to achieve her goal?

We have seen that growth and decay are modeled by exponential functions. For growth and decay we use the formula A = A 0 e k t . A = A 0 e k t . Exponential growth has a positive rate of growth or growth constant, k k , and exponential decay has a negative rate of growth or decay constant, k .

Exponential Growth and Decay

For an original amount, A 0 , A 0 , that grows or decays at a rate, k , for a certain time, t , the final amount, A , is:

We can now solve applications that give us enough information to determine the rate of growth. We can then use that rate of growth to predict other situations.

Example 10.44

Researchers recorded that a certain bacteria population grew from 100 to 300 in 3 hours. At this rate of growth, how many bacteria will there be 24 hours from the start of the experiment?

This problem requires two main steps. First we must find the unknown rate, k . Then we use that value of k to help us find the unknown number of bacteria.

Try It 10.87

Researchers recorded that a certain bacteria population grew from 100 to 500 in 6 hours. At this rate of growth, how many bacteria will there be 24 hours from the start of the experiment?

Try It 10.88

Researchers recorded that a certain bacteria population declined from 700,000 to 400,000 in 5 hours after the administration of medication. At this rate of decay, how many bacteria will there be 24 hours from the start of the experiment?

Radioactive substances decay or decompose according to the exponential decay formula. The amount of time it takes for the substance to decay to half of its original amount is called the half-life of the substance.

Similar to the previous example, we can use the given information to determine the constant of decay, and then use that constant to answer other questions.

Example 10.45

The half-life of radium-226 is 1,590 years. How much of a 100 mg sample will be left in 500 years?

This problem requires two main steps. First we must find the decay constant k . If we start with 100-mg, at the half-life there will be 50-mg remaining. We will use this information to find k . Then we use that value of k to help us find the amount of sample that will be left in 500 years.

Try It 10.89

The half-life of magnesium-27 is 9.45 minutes. How much of a 10-mg sample will be left in 6 minutes?

Try It 10.90

The half-life of radioactive iodine is 60 days. How much of a 50-mg sample will be left in 40 days?

Access these online resources for additional instruction and practice with solving exponential and logarithmic equations.

• Solving Logarithmic Equations
• Solving Logarithm Equations
• Finding the rate or time in a word problem on exponential growth or decay

Section 10.5 Exercises

Practice makes perfect.

In the following exercises, solve for x .

log 4 64 = 2 log 4 x log 4 64 = 2 log 4 x

log 49 = 2 log x log 49 = 2 log x

3 log 3 x = log 3 27 3 log 3 x = log 3 27

3 log 6 x = log 6 64 3 log 6 x = log 6 64

log 5 ( 4 x − 2 ) = log 5 10 log 5 ( 4 x − 2 ) = log 5 10

log 3 ( x 2 + 3 ) = log 3 4 x log 3 ( x 2 + 3 ) = log 3 4 x

log 3 x + log 3 x = 2 log 3 x + log 3 x = 2

log 4 x + log 4 x = 3 log 4 x + log 4 x = 3

log 2 x + log 2 ( x − 3 ) = 2 log 2 x + log 2 ( x − 3 ) = 2

log 3 x + log 3 ( x + 6 ) = 3 log 3 x + log 3 ( x + 6 ) = 3

log x + log ( x + 3 ) = 1 log x + log ( x + 3 ) = 1

log x + log ( x − 15 ) = 2 log x + log ( x − 15 ) = 2

log ( x + 4 ) − log ( 5 x + 12 ) = − log x log ( x + 4 ) − log ( 5 x + 12 ) = − log x

log ( x − 1 ) − log ( x + 3 ) = log 1 x log ( x − 1 ) − log ( x + 3 ) = log 1 x

log 5 ( x + 3 ) + log 5 ( x − 6 ) = log 5 10 log 5 ( x + 3 ) + log 5 ( x − 6 ) = log 5 10

log 5 ( x + 1 ) + log 5 ( x − 5 ) = log 5 7 log 5 ( x + 1 ) + log 5 ( x − 5 ) = log 5 7

log 3 ( 2 x − 1 ) = log 3 ( x + 3 ) + log 3 3 log 3 ( 2 x − 1 ) = log 3 ( x + 3 ) + log 3 3

log ( 5 x + 1 ) = log ( x + 3 ) + log 2 log ( 5 x + 1 ) = log ( x + 3 ) + log 2

In the following exercises, solve each exponential equation. Find the exact answer and then approximate it to three decimal places.

3 x = 89 3 x = 89

2 x = 74 2 x = 74

5 x = 110 5 x = 110

4 x = 112 4 x = 112

e x = 16 e x = 16

e x = 8 e x = 8

( 1 2 ) x = 6 ( 1 2 ) x = 6

( 1 3 ) x = 8 ( 1 3 ) x = 8

4 e x + 1 = 16 4 e x + 1 = 16

3 e x + 2 = 9 3 e x + 2 = 9

6 e 2 x = 24 6 e 2 x = 24

2 e 3 x = 32 2 e 3 x = 32

1 4 e x = 3 1 4 e x = 3

1 3 e x = 2 1 3 e x = 2

e x + 1 + 2 = 16 e x + 1 + 2 = 16

e x − 1 + 4 = 12 e x − 1 + 4 = 12

In the following exercises, solve each equation.

3 3 x + 1 = 81 3 3 x + 1 = 81

6 4 x − 17 = 216 6 4 x − 17 = 216

e x 2 e 14 = e 5 x e x 2 e 14 = e 5 x

e x 2 e x = e 20 e x 2 e x = e 20

log a 64 = 2 log a 64 = 2

log a 81 = 4 log a 81 = 4

ln x = −8 ln x = −8

ln x = 9 ln x = 9

log 5 ( 3 x − 8 ) = 2 log 5 ( 3 x − 8 ) = 2

log 4 ( 7 x + 15 ) = 3 log 4 ( 7 x + 15 ) = 3

ln e 5 x = 30 ln e 5 x = 30

ln e 6 x = 18 ln e 6 x = 18

3 log x = log 125 3 log x = log 125

7 log 3 x = log 3 128 7 log 3 x = log 3 128

log 6 x + log 6 ( x − 5 ) = log 6 24 log 6 x + log 6 ( x − 5 ) = log 6 24

log 9 x + log 9 ( x − 4 ) = log 9 12 log 9 x + log 9 ( x − 4 ) = log 9 12

log 2 ( x + 2 ) − log 2 ( 2 x + 9 ) = − log 2 x log 2 ( x + 2 ) − log 2 ( 2 x + 9 ) = − log 2 x

log 6 ( x + 1 ) − log 6 ( 4 x + 10 ) = log 6 1 x log 6 ( x + 1 ) − log 6 ( 4 x + 10 ) = log 6 1 x

In the following exercises, solve for x , giving an exact answer as well as an approximation to three decimal places.

6 x = 91 6 x = 91

( 1 2 ) x = 10 ( 1 2 ) x = 10

7 e x − 3 = 35 7 e x − 3 = 35

8 e x + 5 = 56 8 e x + 5 = 56

In the following exercises, solve.

Sung Lee invests $ 5,000 $ 5,000 at age 18. He hopes the investments will be worth $ 10,000 $ 10,000 when he turns 25. If the interest compounds continuously, approximately what rate of growth will he need to achieve his goal? Is that a reasonable expectation?

Alice invests $ 15,000 $ 15,000 at age 30 from the signing bonus of her new job. She hopes the investments will be worth $ 30,000 $ 30,000 when she turns 40. If the interest compounds continuously, approximately what rate of growth will she need to achieve her goal?

Coralee invests $ 5,000 $ 5,000 in an account that compounds interest monthly and earns 7 % . 7 % . How long will it take for her money to double?

Simone invests $ 8,000 $ 8,000 in an account that compounds interest quarterly and earns 5 % . 5 % . How long will it take for his money to double?

Researchers recorded that a certain bacteria population declined from 100,000 to 100 in 24 hours. At this rate of decay, how many bacteria will there be in 16 hours?

Researchers recorded that a certain bacteria population declined from 800,000 to 500,000 in 6 hours after the administration of medication. At this rate of decay, how many bacteria will there be in 24 hours?

A virus takes 6 days to double its original population ( A = 2 A 0 ) . ( A = 2 A 0 ) . How long will it take to triple its population?

A bacteria doubles its original population in 24 hours ( A = 2 A 0 ) . ( A = 2 A 0 ) . How big will its population be in 72 hours?

Carbon-14 is used for archeological carbon dating. Its half-life is 5,730 years. How much of a 100-gram sample of Carbon-14 will be left in 1000 years?

Radioactive technetium-99m is often used in diagnostic medicine as it has a relatively short half-life but lasts long enough to get the needed testing done on the patient. If its half-life is 6 hours, how much of the radioactive material form a 0.5 ml injection will be in the body in 24 hours?

Writing Exercises

Explain the method you would use to solve these equations: 3 x + 1 = 81 , 3 x + 1 = 81 , 3 x + 1 = 75 . 3 x + 1 = 75 . Does your method require logarithms for both equations? Why or why not?

What is the difference between the equation for exponential growth versus the equation for exponential decay?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/10-5-solve-exponential-and-logarithmic-equations

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Working with Exponents and Logarithms

What is an exponent, what is a logarithm.

A Logarithm goes the other way.

It asks the question "what exponent produced this?":

And answers it like this:

In that example:

• The Exponent takes 2 and 3 and gives 8 (2, used 3 times in a multiplication, makes 8)
• The Logarithm takes 2 and 8 and gives 3 (2 makes 8 when used 3 times in a multiplication)

A Logarithm says how many of one number to multiply to get another number

So a logarithm actually gives us the exponent as its answer :

Working Together

Exponents and Logarithms work well together because they "undo" each other (so long as the base "a" is the same):

They are " Inverse Functions "

Doing one, then the other, gets us back to where we started:

It is too bad they are written so differently ... it makes things look strange. So it may help to think of a x as "up" and log a (x) as "down":

Anyway, the important thing is that:

The Logarithmic Function is "undone" by the Exponential Function.

(and vice versa)

Like in this example:

Example, what is x in log 3 (x) = 5

We want to "undo" the log 3 so we can get "x ="

Example: Calculate y in y = log 4 ( 1 4 )

Now a simple trick: 1 4 = 4 -1

Properties of Logarithms

One of the powerful things about Logarithms is that they can turn multiply into add .

log a ( m × n ) = log a m + log a n

"the log of multiplication is the sum of the logs"

Why is that true? See Footnote .

Using that property and the Laws of Exponents we get these useful properties:

Remember: the base "a" is always the same!

And there were books full of Logarithm tables to help.

Let us have some fun using the properties:

Example: Simplify log a ( (x 2 +1) 4 √x )

That is as far as we can simplify it ... we can't do anything with log a (x 2 +1)

Answer: 4 log a (x 2 +1) + ½ log a (x)

Note: there is no rule for handling log a (m+n) or log a (m−n)

We can also apply the logarithm rules "backwards" to combine logarithms:

Example: Turn this into one logarithm: log a (5) + log a (x) − log a (2)

Answer: log a (5x/2)

The Natural Logarithm and Natural Exponential Functions

When the base is Euler's Number e = 2.718281828459... we get:

• The Natural Logarithm log e (x) which is more commonly written ln(x)
• The Natural Exponential Function e x

And the same idea that one can "undo" the other is still true:

ln(e x ) = x

e (ln x) = x

And here are their graphs:

They are the same curve with x-axis and y-axis flipped .

Which is another thing showing us they are inverse functions.

Always try to use Natural Logarithms and the Natural Exponential Function whenever possible.

The Common Logarithm

When the base is 10 we get:

• The Common Logarithm log 10 (x) , which is sometimes written as log(x)

Engineers love to use it, but it is not used much in mathematics.

Example: Calculate log 10 100

Well, 10 × 10 = 100, so when 10 is used 2 times in a multiplication we get 100:

log 10 100 = 2

Likewise log 10 1,000 = 3, log 10 10,000 = 4, and so on.

Example: Calculate log 10 369

OK, best to use my calculator's "log" button:

log 10 369 = 2.567...

Changing the Base

What if we want to change the base of a logarithm?

Easy! Just use this formula:

"x goes up, a goes down"

1 log b a works as a "conversion factor" from one base to any other base.

Another useful property is:

log a x = 1 / log x a

See how "x" and "a" swap positions?

Example: Calculate 1 / log 8 2

1 / log 8 2 = log 2 8

And 2 × 2 × 2 = 8, so when 2 is used 3 times in a multiplication we get 8:

1 / log 8 2 = log 2 8 = 3

And we use the Natural Logarithm so often it is worth remembering this:

log a x = ln x / ln a

Example: Calculate log 4 22

What does this answer mean? It means that 4 with an exponent of 2.23 equals 22. So we can check that answer:

Check: 4 2.23 = 22.01 (close enough!)

Here is another example:

Example: Calculate log 5 125

We can use the "ln" function on the calculator:

Is it exactly 3? We should not trust a calculator as there could be rounding errors, but in this case we can check that 5 3 = 5 × 5 × 5 = 125 exactly , so:

Real World Usage

Here are some uses for Logarithms in the real world:

Earthquakes

The magnitude of an earthquake is a Logarithmic scale.

The famous "Richter Scale" uses this formula:

M = log 10 A + B

Where A is the amplitude (in mm) measured by the Seismograph and B is a distance correction factor

Nowadays there are more complicated formulas, but they still use a logarithmic scale.

Loudness is measured in Decibels (dB for short):

Loudness in dB = 10 log 10 (p × 10 12 )

where p is the sound pressure.

Acidic or Alkaline

Acidity (or Alkalinity) is measured in pH:

pH = −log 10 [H + ]

where H + is the molar concentration of dissolved hydrogen ions. Note: in chemistry [ ] means molar concentration (moles per liter).

More Examples

Example: solve 2 log 8 x = log 8 16.

But ... but ... but ... we can't have a log of a negative number!

So the −4 case is not defined.

Check: use a calculator to see if this is the right answer ... also try the "−4" case.

Example: Solve e − w = e 2w+6

Answer: w = − 2

Check: e -(−2) = e 2 and e 2(−2)+6 = e 2

Footnote : Why does log(m × n) = log(m) + log(n) ?

It is one of those clever things we do in mathematics which can be described as "we can't do it here, so let's go over there , do it, then come back".

Module 12: Exponential and Logarithmic Equations and Models

Exponential and logarithmic equations, learning outcomes.

• Solve an exponential equation with a common base.
• Rewrite an exponential equation so all terms have a common base then solve.
• Recognize when an exponential equation does not have a solution.
• Use logarithms to solve exponential equations.
• Solve a logarithmic equation algebraically.
• Solve a logarithmic equation graphically.
• Use the one-to-one property of logarithms to solve a logarithmic equation.
• Solve a radioactive decay problem.

In 1859, an Australian landowner named Thomas Austin released 24 rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.

Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section we will learn techniques for solving exponential and logarithmic equations.

Exponential Equations

The first technique we will introduce for solving exponential equations involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers b , S , and T , where [latex]b>0,\text{ }b\ne 1[/latex], [latex]{b}^{S}={b}^{T}[/latex] if and only if S  = T .

In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then we use the fact that exponential functions are one-to-one to set the exponents equal to one another and solve for the unknown.

For example, consider the equation [latex]{3}^{4x - 7}=\frac{{3}^{2x}}{3}[/latex]. To solve for x , we use the division property of exponents to rewrite the right side so that both sides have the common base 3. Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for x :

[latex]\begin{array}{l}{3}^{4x - 7}\hfill & =\frac{{3}^{2x}}{3}\hfill & \hfill \\ {3}^{4x - 7}\hfill & =\frac{{3}^{2x}}{{3}^{1}}\hfill & {\text{Rewrite 3 as 3}}^{1}.\hfill \\ {3}^{4x - 7}\hfill & ={3}^{2x - 1}\hfill & \text{Use the division property of exponents}\text{.}\hfill \\ 4x - 7\hfill & =2x - 1\text{ }\hfill & \text{Apply the one-to-one property of exponents}\text{.}\hfill \\ 2x\hfill & =6\hfill & \text{Subtract 2}x\text{ and add 7 to both sides}\text{.}\hfill \\ x\hfill & =3\hfill & \text{Divide by 3}\text{.}\hfill \end{array}[/latex]

A General Note: Using the One-to-One Property of Exponential Functions to Solve Exponential Equations

For any algebraic expressions S  and T , and any positive real number [latex]b\ne 1[/latex],

[latex]{b}^{S}={b}^{T}\text{ if and only if }S=T[/latex]

How To: Given an exponential equation Of the form [latex]{b}^{S}={b}^{T}[/latex], where S  and  T  are algebraic expressions with an unknown, solve for the unknown

• Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form [latex]{b}^{S}={b}^{T}[/latex].
• Use the one-to-one property to set the exponents equal to each other.
• Solve the resulting equation, S  = T , for the unknown.

Example: Solving an Exponential Equation with a Common Base

Solve [latex]{2}^{x - 1}={2}^{2x - 4}[/latex].

[latex]\begin{array}{l} {2}^{x - 1}={2}^{2x - 4}\hfill & \text{The common base is }2.\hfill \\ \text{ }x - 1=2x - 4\hfill & \text{By the one-to-one property the exponents must be equal}.\hfill \\ \text{ }x=3\hfill & \text{Solve for }x.\hfill \end{array}[/latex]

Solve [latex]{5}^{2x}={5}^{3x+2}[/latex].

[latex]x=–2[/latex]

Rewriting Equations So All Powers Have the Same Base

Sometimes the common base for an exponential equation is not explicitly shown. In these cases we simply rewrite the terms in the equation as powers with a common base and solve using the one-to-one property.

For example, consider the equation [latex]256={4}^{x - 5}[/latex]. We can rewrite both sides of this equation as a power of 2. Then we apply the rules of exponents along with the one-to-one property to solve for x :

[latex]\begin{array}{l}256={4}^{x - 5}\hfill & \hfill \\ {2}^{8}={\left({2}^{2}\right)}^{x - 5}\hfill & \text{Rewrite each side as a power with base 2}.\hfill \\ {2}^{8}={2}^{2x - 10}\hfill & \text{To take a power of a power, multiply the exponents}.\hfill \\ 8=2x - 10\hfill & \text{Apply the one-to-one property of exponents}.\hfill \\ 18=2x\hfill & \text{Add 10 to both sides}.\hfill \\ x=9\hfill & \text{Divide by 2}.\hfill \end{array}[/latex]

How To: Given an exponential equation with unlike bases, use the one-to-one property to solve it

• Rewrite each side in the equation as a power with a common base.

Example: Solving Equations by Rewriting Them to Have a Common Base

Solve [latex]{8}^{x+2}={16}^{x+1}[/latex].

[latex]\begin{array}{llllll}\text{ }{8}^{x+2}={16}^{x+1}\hfill & \hfill \\ {\left({2}^{3}\right)}^{x+2}={\left({2}^{4}\right)}^{x+1}\hfill & \text{Write }8\text{ and }16\text{ as powers of }2.\hfill \\ \text{ }{2}^{3x+6}={2}^{4x+4}\hfill & \text{To take a power of a power, multiply the exponents}.\hfill \\ \text{ }3x+6=4x+4\hfill & \text{Use the one-to-one property to set the exponents equal to each other}.\hfill \\ \text{ }x=2\hfill & \text{Solve for }x.\hfill \end{array}[/latex]

Solve [latex]{5}^{2x}={25}^{3x+2}[/latex].

[latex]x=–1[/latex]

Example: Solving Equations by Rewriting Roots with Fractional Exponents to Have a Common Base

Solve [latex]{2}^{5x}=\sqrt{2}[/latex].

[latex]\begin{array}{l}{2}^{5x}={2}^{\frac{1}{2}}\hfill & \text{Write the square root of 2 as a power of }2.\hfill \\ 5x=\frac{1}{2}\hfill & \text{Use the one-to-one property}.\hfill \\ x=\frac{1}{10}\hfill & \text{Solve for }x.\hfill \end{array}[/latex]

Solve [latex]{5}^{x}=\sqrt{5}[/latex].

[latex]x=\frac{1}{2}[/latex]

Do all exponential equations have a solution? If not, how can we tell if there is a solution during the problem-solving process?

No. Recall that the range of an exponential function is always positive. While solving the equation we may obtain an expression that is undefined.

Example: Determining When an Equation has No Solution

Solve [latex]{3}^{x+1}=-2[/latex].

This equation has no solution. There is no real value of x  that will make the equation a true statement because any power of a positive number is positive.

Analysis of the Solution

The figure below shows that the two graphs do not cross so the left side of the equation is never equal to the right side of the equation. Thus the equation has no solution.

Solve [latex]{2}^{x}=-100[/latex].

The equation has no solution.

Using Logarithms to Solve Exponential Equations

Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall that since [latex]\mathrm{log}\left(a\right)=\mathrm{log}\left(b\right)[/latex] is equal to a  = b ,   we may apply logarithms with the same base to both sides of an exponential equation.

How To: Given an exponential equation Where a common base cannot be found, solve for the unknown

• If one of the terms in the equation has base 10, use the common logarithm.
• If none of the terms in the equation has base 10, use the natural logarithm.
• Use the rules of logarithms to solve for the unknown.

Example: Solving an Equation Containing Powers of Different Bases

Solve [latex]{5}^{x+2}={4}^{x}[/latex].

[latex]\begin{array}{l}\text{ }{5}^{x+2}={4}^{x}\hfill & \text{There is no easy way to get the powers to have the same base}.\hfill \\ \text{ }\mathrm{ln}{5}^{x+2}=\mathrm{ln}{4}^{x}\hfill & \text{Take ln of both sides}.\hfill \\ \text{ }\left(x+2\right)\mathrm{ln}5=x\mathrm{ln}4\hfill & \text{Use the power rule for logs}.\hfill \\ \text{ }x\mathrm{ln}5+2\mathrm{ln}5=x\mathrm{ln}4\hfill & \text{Use the distributive property}.\hfill \\ \text{ }x\mathrm{ln}5-x\mathrm{ln}4=-2\mathrm{ln}5\hfill & \text{Get terms containing }x\text{ on one side, terms without }x\text{ on the other}.\hfill \\ x\left(\mathrm{ln}5-\mathrm{ln}4\right)=-2\mathrm{ln}5\hfill & \text{On the left hand side, factor out }x.\hfill \\ \text{ }x\mathrm{ln}\left(\frac{5}{4}\right)=\mathrm{ln}\left(\frac{1}{25}\right)\hfill & \text{Use the properties of logs}.\hfill \\ \text{ }x=\frac{\mathrm{ln}\left(\frac{1}{25}\right)}{\mathrm{ln}\left(\frac{5}{4}\right)}\hfill & \text{Divide by the coefficient of }x.\hfill \end{array}[/latex]

Solve [latex]{2}^{x}={3}^{x+1}[/latex].

[latex]x=\frac{\mathrm{ln}3}{\mathrm{ln}\left(\frac{2}{3}\right)}[/latex]

Is there any way to solve [latex]{2}^{x}={3}^{x}[/latex]?

Yes. The solution is x = 0.

Equations Containing [latex]e[/latex]

One common type of exponential equations are those with base e . This constant occurs again and again in nature, mathematics, science, engineering, and finance. When we have an equation with a base e  on either side, we can use the natural logarithm to solve it.

How To: Given an equation of the form [latex]y=A{e}^{kt}[/latex], solve for [latex]t[/latex]

• Divide both sides of the equation by A .
• Apply the natural logarithm to both sides of the equation.
• Divide both sides of the equation by k .

Example: Solving an Equation of the Form [latex]y=A{e}^{kt}[/latex]

Solve [latex]100=20{e}^{2t}[/latex].

[latex]\begin{array}{l}100\hfill & =20{e}^{2t}\hfill & \hfill \\ 5\hfill & ={e}^{2t}\hfill & \text{Divide by the coefficient 20}\text{.}\hfill \\ \mathrm{ln}5\hfill & =\mathrm{ln}{{e}^{2t}}\hfill & \text{Take ln of both sides.}\hfill \\ \mathrm{ln}5\hfill & =2t\hfill & \text{Use the fact that }\mathrm{ln}\left(x\right)\text{ and }{e}^{x}\text{ are inverse functions}\text{.}\hfill \\ t\hfill & =\frac{\mathrm{ln}5}{2}\hfill & \text{Divide by the coefficient of }t\text{.}\hfill \end{array}[/latex]

Using laws of logs, we can also write this answer in the form [latex]t=\mathrm{ln}\sqrt{5}[/latex]. If we want a decimal approximation of the answer, then we use a calculator.

Solve [latex]3{e}^{0.5t}=11[/latex].

Does every equation of the form [latex]y=A{e}^{kt}[/latex] have a solution?

No. There is a solution when [latex]k\ne 0[/latex], and when  [latex]y[/latex]  and [latex] A [/latex] are either both 0 or neither 0 and they have the same sign. An example of an equation with this form that has no solution is [latex]2=-3{e}^{t}[/latex].

Example: Solving an Equation That Can Be Simplified to the Form [latex]y=A{e}^{kt}[/latex]

Solve [latex]4{e}^{2x}+5=12[/latex].

[latex]\begin{array}{l}4{e}^{2x}+5=12\hfill & \hfill \\ 4{e}^{2x}=7\hfill & \text{Subtract 5 from both sides}.\hfill \\ {e}^{2x}=\frac{7}{4}\hfill & \text{Divide both sides by 4}.\hfill \\ 2x=\mathrm{ln}\left(\frac{7}{4}\right)\hfill & \text{Take ln of both sides}.\hfill \\ x=\frac{1}{2}\mathrm{ln}\left(\frac{7}{4}\right)\hfill & \text{Solve for }x.\hfill \end{array}[/latex]

Solve [latex]3+{e}^{2t}=7{e}^{2t}[/latex].

Extraneous Solutions

Sometimes the methods used to solve an equation introduce an extraneous solution , which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when taking the logarithm of both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the number we are evaluating in a logarithm function is negative, there is no output.

Example: Solving Exponential Functions in Quadratic Form

Solve [latex]{e}^{2x}-{e}^{x}=56[/latex].

[latex]\begin{array}{l}{e}^{2x}-{e}^{x}=56\hfill \\ {e}^{2x}-{e}^{x}-56=0\hfill & \text{Get one side of the equation equal to zero}.\hfill \\ \left({e}^{x}+7\right)\left({e}^{x}-8\right)=0\hfill & \text{Factor by the FOIL method}.\hfill \\ {e}^{x}+7=0\text{ or }{e}^{x}-8=0 & \text{If a product is zero, then one factor must be zero}.\hfill \\ {e}^{x}=-7{\text{ or e}}^{x}=8\hfill & \text{Isolate the exponentials}.\hfill \\ {e}^{x}=8\hfill & \text{Reject the equation in which the power equals a negative number}.\hfill \\ x=\mathrm{ln}8\hfill & \text{Solve the equation in which the power equals a positive number}.\hfill \end{array}[/latex]

When we plan to use factoring to solve a problem, we always get zero on one side of the equation because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation [latex]{e}^{x}=-7[/latex] because a positive number never equals a negative number. The solution [latex]x=\mathrm{ln}\left(-7\right)[/latex] is not a real number and in the real number system, this solution is rejected as an extraneous solution.

Solve [latex]{e}^{2x}={e}^{x}+2[/latex].

[latex]x=\mathrm{ln}2[/latex]

Does every logarithmic equation have a solution?

No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.

Logarithmic Equations

We have already seen that every logarithmic equation [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex] is equal to the exponential equation [latex]{b}^{y}=x[/latex]. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation [latex]{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3[/latex]. To solve this equation, we can use rules of logarithms to rewrite the left side as a single log and then apply the definition of logs to solve for [latex]x[/latex]:

[latex]\begin{array}{l}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3\hfill & \hfill \\ \text{ }{\mathrm{log}}_{2}\left(2\left(3x - 5\right)\right)=3\hfill & \text{Apply the product rule of logarithms}.\hfill \\ \text{ }{\mathrm{log}}_{2}\left(6x - 10\right)=3\hfill & \text{Distribute}.\hfill \\ \text{ }{2}^{3}=6x - 10\hfill & \text{Convert to exponential form}.\hfill \\ \text{ }8=6x - 10\hfill & \text{Calculate }{2}^{3}.\hfill \\ \text{ }18=6x\hfill & \text{Add 10 to both sides}.\hfill \\ \text{ }x=3\hfill & \text{Divide both sides by 6}.\hfill \end{array}[/latex]

A General Note: Using the Definition of a Logarithm to Solve Logarithmic Equations

For any algebraic expression S and real numbers b and c , where [latex]b>0,\text{ }b\ne 1[/latex],

[latex]{\mathrm{log}}_{b}\left(S\right)=c\text{ if and only if }{b}^{c}=S[/latex]

Example: Using Algebra to Solve a Logarithmic Equation

Solve [latex]2\mathrm{ln}x+3=7[/latex].

[latex]\begin{array}{l}2\mathrm{ln}x+3=7\hfill & \hfill \\ \text{}2\mathrm{ln}x=4\hfill & \text{Subtract 3 from both sides}.\hfill \\ \text{}\mathrm{ln}x=2\hfill & \text{Divide both sides by 2}.\hfill \\ \text{}x={e}^{2}\hfill & \text{Rewrite in exponential form}.\hfill \end{array}[/latex]

Solve [latex]6+\mathrm{ln}x=10[/latex].

[latex]x={e}^{4}[/latex]

Example: Using Algebra Before and After Using the Definition of the Natural Logarithm

Solve [latex]2\mathrm{ln}\left(6x\right)=7[/latex].

[latex]\begin{array}{l}2\mathrm{ln}\left(6x\right)=7\hfill & \hfill \\ \text{}\mathrm{ln}\left(6x\right)=\frac{7}{2}\hfill & \text{Divide both sides by 2}.\hfill \\ \text{}6x={e}^{\left(\frac{7}{2}\right)}\hfill & \text{Use the definition of }\mathrm{ln}.\hfill \\ \text{}x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}\hfill & \text{Divide both sides by 6}.\hfill \end{array}[/latex]

Solve [latex]2\mathrm{ln}\left(x+1\right)=10[/latex].

[latex]x={e}^{5}-1[/latex]

Example: Using a Graph to Understand the Solution to a Logarithmic Equation

Solve [latex]\mathrm{ln}x=3[/latex].

[latex]\begin{array}{l}\mathrm{ln}x=3\hfill & \hfill \\ x={e}^{3}\hfill & \text{Use the definition of }\mathrm{ln}\text{.}\hfill \end{array}[/latex]

Below is a graph of the equation. On the graph the x -coordinate of the point where the two graphs intersect is close to 20. In other words [latex]{e}^{3}\approx 20[/latex]. A calculator gives a better approximation: [latex]{e}^{3}\approx 20.0855[/latex].

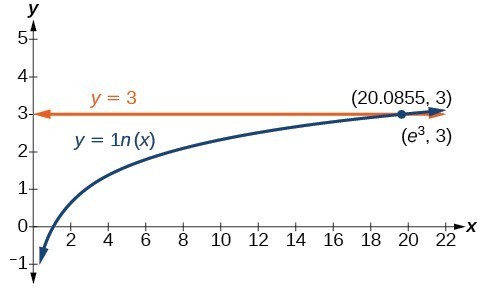
The graphs of [latex]y=\mathrm{ln}x[/latex] and y = 3 cross at the point [latex]\left(e^3,3\right)[/latex] which is approximately (20.0855, 3).

Use a graphing calculator to estimate the approximate solution to the logarithmic equation [latex]{2}^{x}=1000[/latex] to 2 decimal places.

[latex]x\approx 9.97[/latex]

Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers x  > 0, S  > 0, T  > 0 and any positive real number b , where [latex]b\ne 1[/latex],

[latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex]

For example,

[latex]\text{If }{\mathrm{log}}_{2}\left(x - 1\right)={\mathrm{log}}_{2}\left(8\right),\text{then }x - 1=8[/latex]

So if [latex]x - 1=8[/latex], then we can solve for x  and we get x  = 9. To check, we can substitute x  = 9 into the original equation: [latex]{\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3[/latex]. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.

For example, consider the equation [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex]. To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm and then apply the one-to-one property to solve for x :

[latex]\begin{array}{l}\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{3x - 2}{2}\right)=\mathrm{log}\left(x+4\right)\hfill & \text{Apply the quotient rule of logarithms}.\hfill \\ \text{}\frac{3x - 2}{2}=x+4\hfill & \text{Apply the one-to-one property}.\hfill \\ \text{}3x - 2=2x+8\hfill & \text{Multiply both sides of the equation by }2.\hfill \\ \text{}x=10\hfill & \text{Subtract 2}x\text{ and add 2}.\hfill \end{array}[/latex]

To check the result, substitute x  = 10 into [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex].

[latex]\begin{array}{l}\mathrm{log}\left(3\left(10\right)-2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(\left(10\right)+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(28\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(14\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{28}{2}\right)=\mathrm{log}\left(14\right)\hfill & \text{The solution checks}.\hfill \end{array}[/latex]

A General Note: Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

For any algebraic expressions S and T and any positive real number b , where [latex]b\ne 1[/latex],

Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.

How To: Given an equation containing logarithms, solve it using the one-to-one property

• Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation is of the form [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T[/latex].
• Use the one-to-one property to set the arguments equal to each other.
• Solve the resulting equation, S =  T , for the unknown.

Example: Solving an Equation Using the One-to-One Property of Logarithms

Solve [latex]\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)[/latex].

[latex]\begin{array}{l}\text{ }\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)\hfill & \hfill \\ \text{ }{x}^{2}=2x+3\hfill & \text{Use the one-to-one property of the logarithm}.\hfill \\ \text{ }{x}^{2}-2x - 3=0\hfill & \text{Get zero on one side before factoring}.\hfill \\ \left(x - 3\right)\left(x+1\right)=0\hfill & \text{Factor using FOIL}.\hfill \\ \text{ }x - 3=0\text{ or }x+1=0\hfill & \text{If a product is zero, one of the factors must be zero}.\hfill \\ \text{ }x=3\text{ or }x=-1\hfill & \text{Solve for }x.\hfill \end{array}[/latex]

There are two solutions: x  = 3 or x  = –1. The solution x  = –1 is negative, but it checks when substituted into the original equation because the argument of the logarithm function is still positive.

Solve [latex]\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}1[/latex].

[latex]x=1[/latex] or [latex]x=–1[/latex]

Key Equations

Key concepts.

• We can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then we use the fact that exponential functions are one-to-one to set the exponents equal to one another and solve for the unknown.
• When we are given an exponential equation where the bases are explicitly shown as being equal, set the exponents equal to one another and solve for the unknown.
• When we are given an exponential equation where the bases are not explicitly shown as being equal, rewrite each side of the equation as powers of the same base, then set the exponents equal to one another and solve for the unknown.
• When an exponential equation cannot be rewritten with a common base, solve by taking the logarithm of each side.
• We can solve exponential equations with base e  by applying the natural logarithm to both sides because exponential and logarithmic functions are inverses of each other.
• After solving an exponential equation, check each solution in the original equation to find and eliminate any extraneous solutions.
• When given an equation of the form [latex]{\mathrm{log}}_{b}\left(S\right)=c[/latex], where S  is an algebraic expression, we can use the definition of a logarithm to rewrite the equation as the equivalent exponential equation [latex]{b}^{c}=S[/latex] and solve for the unknown.
• We can also use graphing to solve equations of the form [latex]{\mathrm{log}}_{b}\left(S\right)=c[/latex]. We graph both equations [latex]y={\mathrm{log}}_{b}\left(S\right)[/latex] and [latex]y=c[/latex] on the same coordinate plane and identify the solution as the x- value of the point of intersecting.
• When given an equation of the form [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T[/latex], where S  and T  are algebraic expressions, we can use the one-to-one property of logarithms to solve the equation S  = T  for the unknown.
• Combining the skills learned in this and previous sections, we can solve equations that model real world situations whether the unknown is in an exponent or in the argument of a logarithm.
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Precalculus. Authored by : Jay Abramson, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download For Free at : http://cnx.org/contents/[email protected].
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Question ID 2637, 2620, 2638. Authored by : Greg Langkamp. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 98554, 98555, 98596. Authored by : Michael Jenck. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 14406. Authored by : James Sousa. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 122911. Authored by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL

• Toggle navigation

Lee | D379 | Spring 2024

• Course Profile
• Course Outline
• Syllabus/Grading Policy
• Academic Calendar
• Class Meeting Grid

Class Agendas

• WeBWorK Site
• Module Assignments
• Online Lessons
• Final Exam Review Questions
• Final Exam Review videos
• MAT 1375 Video Resources
• WeBWorK site
• WeBWorK Guide for Students
• Homework help – Q&A site
• Desmos – online calculator
• College Resources

OpenLab Help

• 15. Exponential equations and applications

Course Hub – Handout Textbook – Session 15

Assignments

• Exponential Functions – Equations

Prep for Next Class (Please look at them and prepare questions for the next class).

Course Hub – Handout Textbook – Session 16

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Name: Mr. Victor Lee Class Days: Monday, Wednesday Class Times: 2:15 pm – 3:55 pm Room: N703 Office: N825 Office Hours: Monday, Wednesday 11:00 am – 12:00 pm Online Classroom/Office

Textbook: Precalculus ( 3rd Edition) by Tradler and Carley

Topics include an in-depth study of functions such as polynomial functions, radical functions, trigonometric functions, exponential and logarithmic functions; connections to vectors and complex numbers; solving trigonometric equations, and identities involving sum, double and half-angle formulas; Binomial Theorem and progressions.  

This class uses  WeBWorK , an online homework system.  Login information will be provided by your professor.  For information about how to use the WeBWorK system, please see the  WeBWorK  Guide for Students .

Need Help with MAT 1375?

The Mathematics Department’s MAT 1375 Course Hub has many resources for both students and faculty, including online lessons , review information , and more.

The WeBWorK Q&A site is a place to ask and answer questions about your homework problems.  HINT: To ask a question, start by logging in to your WeBWorK section, then click  “Ask for Help” after any problem.

Search This Course

• All Categories Announcements Assignment Instructions Assignment Posts Class Agendas Course Activities Discussions Resources

Logged-in faculty members can clone this course. Learn More!

Recent Posts

• 16. Applications of exp and log
• News: Test 2
• 14. Properties of Logarithms and Logarithmic Equations
• 13. Exponential and Logarithmic Functions

Recent Comments

Member portfolios, find library materials, library information.

Ursula C. Schwerin Library New York City College of Technology, C.U.N.Y 300 Jay Street, Library Building - 4th Floor

Acknowledgments

This course is based on the following course(s):

• MAT1375 by Jonas Reitz

Unless otherwise noted, this site has a Creative Commons Attribution-NonCommercial (CC BY-NC) license. Learn more.

© 2024 MAT1375 Precalculus, Spring 2024

Theme by Anders Noren — Up ↑

The OpenLab at City Tech: A place to learn, work, and share

The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.

New York City College of Technology | City University of New York

Accessibility

Our goal is to make the OpenLab accessible for all users.

Learn more about accessibility on the OpenLab

Creative Commons

• - Attribution
• - NonCommercial
• - ShareAlike

© New York City College of Technology | City University of New York

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.6: Application Problems with Exponential and Logarithmic Functions

• Last updated
• Save as PDF
• Page ID 38600

• Rupinder Sekhon and Roberta Bloom
• De Anza College

Learning Objectives

In this section, you will:

• review strategies for solving equations arising from exponential formulas
• solve application problems involving exponential functions and logarithmic functions

STRATEGIES FOR SOLVING EQUATIONS THAT CONTAIN EXPONENTS

When solving application problems that involve exponential and logarithmic functions, we need to pay close attention to the position of the variable in the equation to determine the proper way solve the equation we investigate solving equations that contain exponents.

Suppose we have an equation in the form : value = coefficient(base) exponent

We consider four strategies for solving the equation:

STRATEGY A : If the coefficient, base, and exponent are all known, we only need to evaluate the expression for coefficient(base) exponent to evaluate its value.

STRATEGY B: If the variable is the coefficient, evaluate the expression for (base) exponent . Then it becomes a linear equation which we solve by dividing to isolate the variable.

STRATEGY C : If the variable is in the exponent, use logarithms to solve the equation.

STRATEGY D: If the variable is not in the exponent, but is in the base, use roots to solve the equation.

Below we examine each strategy with one or two examples of its use.

Example \(\PageIndex{1}\)

Suppose that a stock’s price is rising at the rate of 7% per year, and that it continues to increase at this rate. If the value of one share of this stock is $43 now, find the value of one share of this stock three years from now.

The problem tells us that \(a\) = 43 and \(r\) = 0.07, so \(b = 1+ r = 1+ 0.07 = 1.07\)

Therefore, function is \(y = 43(1.07)^t\).

In this case we know that \(t\) = 3 years, and we need to evaluate \(y\) when \(t\) = 3.

At the end of 3 years, the value of this one share of this stock will be

\[y=43(1.07)^{3}=\$ 52.68 \nonumber \]

Example \(\PageIndex{2}\)

The value of a new car depreciates (decreases) after it is purchased. Suppose that the value of the car depreciates according to an exponential decay model. Suppose that the value of the car is $12000 at the end of 5 years and that its value has been decreasing at the rate of 9% per year. Find the value of the car when it was new.

The function is \(y = a(0.91)^t\)

In this case we know that when \(t\) = 5, then \(y\) = 12000; substituting these values gives

\[12000 = a(0.91)^5 \nonumber \]

We need to solve for the initial value a, the purchase price of the car when new.

First evaluate (0.91) 5 ; then solve the resulting linear equation to find \(a\).

\[ 1200 = a(0.624) \nonumber \]

\(a=\frac{12000}{0.624} = \$ 19,230.77\); The car's value was $19,230.77 when it was new.

Example \(\PageIndex{3}\)

A national park has a population of 5000 deer in the year 2016. Conservationists are concerned because the deer population is decreasing at the rate of 7% per year. If the population continues to decrease at this rate, how long will it take until the population is only 3000 deer?

\(r\) = -0.07 and \(b = 1+r = 1+(-0.07) = 0.93\) and the initial population is \(a\) = 5000

The exponential decay function is \(y = 5000(0.93)^t\)

To find when the population will be 3000, substitute \(y\) = 3000

\[ 3000 = 5000(0.93)^t \nonumber \]

Next, divide both sides by 5000 to isolate the exponential expression

\[\begin{array}{l} \frac{3000}{5000}=\frac{5000}{5000}(0.93)^{2} \\ 0.6=0.93^{t} \end{array} \nonumber \]

Rewrite the equation in logarithmic form; then use the change of base formula to evaluate.

\[t=\log _{0.93}(0.6) \nonumber \]

\(t = \frac{\ln(0.6)}{\ln(0.93)}=7.039\) years; After 7.039 years, there are 3000 deer.

Note: In Example \(\PageIndex{3}\), we needed to state the answer to several decimal places of precision to remain accurate. Evaluating the original function using a rounded value of \(t\) = 7 years gives a value that is close to 3000, but not exactly 3000.

\[y=5000(0.93)^{7}=3008.5 \text { deer } \nonumber \]

However using \(t\) = 7.039 years produces a value of 3000 for the population of deer

\[ y=5000(0.93)^{7.039}=3000.0016 \approx 3000 \text { deer } \nonumber \]

Example \(\PageIndex{4}\)

A video posted on YouTube initially had 80 views as soon as it was posted. The total number of views to date has been increasing exponentially according to the exponential growth function \(y = 80e^{0.2t}\), where \(t\) represents time measured in days since the video was posted. How many days does it take until 2500 people have viewed this video?

Let \(y\) be the total number of views \(t\) days after the video is initially posted. We are given that the exponential growth function is \(y = 80e^{0.2t}\) and we want to find the value of \(t\) for which \(y\) = 2500. Substitute \(y\) = 2500 into the equation and use natural log to solve for \(t\).

\[2500 = 80e^{0.12t} \nonumber \]

Divide both sides by the coefficient, 80, to isolate the exponential expression.

\[\begin{array}{c} \frac{2500}{80}=\frac{80}{80} e^{0.12 t} \\ 31.25=e^{0.12 t} \end{array} \nonumber \]

Rewrite the equation in logarithmic form

\[ 0.12t = \ln(31.25) \nonumber \]

Divide both sides by 0.04 to isolate \(t\); then use your calculator and its natural log function to evaluate the expression and solve for \(t\).

\[\begin{array}{l} \mathrm{t}=\frac{\ln (31.25)}{0.12} \\ \mathrm{t}=\frac{3.442}{0.12} \\ \mathrm{t} \approx 28.7 \text { days } \end{array} \nonumber \]

This video will have 2500 total views approximately 28.7 days after it was posted.

STRATEGY D: If the variable is not in the exponent, but is in the base, we use roots to solve the equation. It is important to remember that we only use logarithms when the variable is in the exponent.

Example \(\PageIndex{5}\)

A statistician creates a website to analyze sports statistics. His business plan states that his goal is to accumulate 50,000 followers by the end of 2 years (24 months from now). He hopes that if he achieves this goal his site will be purchased by a sports news outlet. The initial user base of people signed up as a result of pre-launch advertising is 400 people. Find the monthly growth rate needed if the user base is to accumulate to 50,000 users at the end of 24 months.

Let \(y\) be the total user base \(t\) months after the site is launched.

The growth function for this site is \(y = 400(1+r)^t\);

We don’t know the growth rate \(r\). We do know that when \(t\) = 24 months, then \(y\) = 50000.

Substitute the values of \(y\) and \(t\); then we need to solve for \(r\).

\[5000 = 400(1+r)^{24} \nonumber \]

Divide both sides by 400 to isolate (1+r) 24 on one side of the equation

\[\begin{array}{l} \frac{50000}{400}=\frac{400}{400}(1+r)^{24} \\ 125=(1+r)^{24} \end{array} \nonumber \]

Because the variable in this equation is in the base, we use roots:

\[\begin{array}{l} \sqrt[24]{125}=1+r \\ 125^{1 / 24}=1+r \\ 1.2228 \approx 1+r \\ 0.2228 \approx r \end{array} \nonumber \]

The website’s user base needs to increase at the rate of 22.28% per month in order to accumulate 50,000 users by the end of 24 months.

Example \(\PageIndex{6}\)

A fact sheet on caffeine dependence from Johns Hopkins Medical Center states that the half life of caffeine in the body is between 4 and 6 hours. Assuming that the typical half life of caffeine in the body is 5 hours for the average person and that a typical cup of coffee has 120 mg of caffeine.

• Write the decay function.
• Find the hourly rate at which caffeine leaves the body.
• How long does it take until only 20 mg of caffiene is still in the body? www.hopkinsmedicine.org/psyc...fact_sheet.pdf

a. Let \(y\) be the total amount of caffeine in the body \(t\) hours after drinking the coffee.

Exponential decay function \(y = ab^t\) models this situation.

The initial amount of caffeine is \(a\) = 120.

We don’t know \(b\) or \(r\), but we know that the half- life of caffeine in the body is 5 hours. This tells us that when \(t\) = 5, then there is half the initial amount of caffeine remaining in the body.

\[\begin{array}{l} y=120 b^{t} \\ \frac{1}{2}(120)=120 b^{5} \\ 60=120 b^{5} \end{array} \nonumber \]

Divide both sides by 120 to isolate the expression \(b^5\) that contains the variable.

\[\begin{array}{l} \frac{60}{120}=\frac{120}{120} \mathrm{b}^{5} \\ 0.5=\mathrm{b}^{5} \end{array} \nonumber \]

The variable is in the base and the exponent is a number. Use roots to solve for \(b\):

\[\begin{array}{l} \sqrt[5]{0.5}=\mathrm{b} \\ 0.5^{1 / 5}=\mathrm{b} \\ 0.87=\mathrm{b} \end{array} \nonumber \]

We can now write the decay function for the amount of caffeine (in mg.) remaining in the body \(t\) hours after drinking a cup of coffee with 120 mg of caffeine

\[y=f(t)=120(0.87)^{t} \nonumber \]

b. Use \(b = 1 + r\) to find the decay rate \(r\). Because \(b = 0.87 < 1\) and the amount of caffeine in the body is decreasing over time, the value of \(r\) will be negative.

\[\begin{array}{l} 0.87=1+r \\ r=-0.13 \end{array} \nonumber \]

The decay rate is 13%; the amount of caffeine in the body decreases by 13% per hour.

c. To find the time at which only 20 mg of caffeine remains in the body, substitute \(y\) = 20 and solve for the corresponding value of \(t\).

\[\begin{array}{l} y=120(.87)^{t} \\ 20=120(.87)^{t} \end{array} \nonumber \]

Divide both sides by 120 to isolate the exponential expression.

\[\begin{array}{l} \frac{20}{120}=\frac{120}{120}\left(0.87^{t}\right) \\ 0.1667=0.87^{t} \end{array} \nonumber \]

Rewrite the expression in logarithmic form and use the change of base formula

\[\begin{array}{l} t=\log _{0.87}(0.1667) \\ t=\frac{\ln (0.1667)}{\ln (0.87)} \approx 12.9 \text { hours } \end{array} \nonumber \]

After 12.9 hours, 20 mg of caffeine remains in the body.

EXPRESSING EXPONENTIAL FUNCTIONS IN THE FORMS y = ab t and y = ae kt

Now that we’ve developed our equation solving skills, we revisit the question of expressing exponential functions equivalently in the forms \(y = ab^t\) and \(y = ae^{kt}\)

We’ve already determined that if given the form \(y = ae^{kt}\), it is straightforward to find \(b\).

Example \(\PageIndex{7}\)

For the following examples, assume \(t\) is measured in years.

• Express \(y = 3500e^{0.25t}\) in form \(y = ab^t\) and find the annual percentage growth rate.
• Express \(y = 28000e^{-0.32t}\) in form \(y = ab^t\) and find the annual percentage decay rate.

a. Express \(y = 3500e^{0.25t}\) in the form \(y = ab^t\)

\[\begin{array}{l} y=a e^{k t}=a b^{t} \\ a\left(e^{k}\right)^{t}=a b^{t} \end{array} \nonumber \]

Thus \(e^k=b\)

In this example \(b=e^{0.25} \approx 1.284\)

We rewrite the growth function as y = 3500(1.284 t )

To find \(r\), recall that \(b = 1+r\) \[\begin{aligned} &1.284=1+r\\ &0.284=\mathrm{r} \end{aligned} \nonumber \]

The continuous growth rate is \(k\) = 0.25 and the annual percentage growth rate is 28.4% per year.

b. Express \(y = 28000e^{-0.32t}\) in the form \(y = ab^t\)

In this example \(\mathrm{b}=e^{-0.32} \approx 0.7261\)

We rewrite the growth function as y = 28000(0.7261 t )

To find \(r\), recall that \(b = 1+r\) \[\begin{array}{l} 0.7261=1+r \\ 0.2739=r \end{array} \nonumber \]

The continuous decay rate is \(k\) = -0.32 and the annual percentage decay rate is 27.39% per year.

In the sentence, we omit the negative sign when stating the annual percentage decay rate because we have used the word “decay” to indicate that r is negative.

Example \(\PageIndex{8}\)

• Express \(y = 4200 (1.078)^t\) in the form \(y =ae^{kt}\)
• Express \(y = 150 (0.73)^t\) in the form \(y =ae^{kt}\)

a. Express \(y = 4200 (1.078)^t\) in the form \(y =ae^{kt}\)

\[\begin{array}{l} \mathrm{y}=\mathrm{a} e^{\mathrm{k} t}=\mathrm{ab}^{\mathrm{t}} \\ \mathrm{a}\left(e^{\mathrm{k}}\right)^{\mathrm{t}}=\mathrm{ab}^{\mathrm{t}} \\ e^{\mathrm{k}}=\mathrm{b} \\ e^{k}=1.078 \end{array} \nonumber \]

Therefore \(\mathrm{k}=\ln 1.078 \approx 0.0751\)

We rewrite the growth function as \(y = 3500e^{0.0751t}\)

b. Express \(y =150 (0.73)^t\) in the form \(y = ae^{kt}\)

\[\begin{array}{l} y=a e^{k t}=a b^{t} \\ a\left(e^{k}\right)^{t}=a b^{t} \\ e^{k}=b \\ e^{k}=0.73 \end{array} \nonumber \]

Therefore \(\mathrm{k}=\ln 0.73 \approx-0.3147\)

We rewrite the growth function as \(y = 150e^{-0.3147t}\)

AN APPLICATION OF A LOGARITHMIC FUNCTON

Suppose we invest $10,000 today and want to know how long it will take to accumulate to a specified amount, such as $15,000. The time \(t\) needed to reach a future value \(y\) is a logarithmic function of the future value: \(t = g(y)\)

Example \(\PageIndex{9}\)

Suppose that Vinh invests $10000 in an investment earning 5% per year. He wants to know how long it would take his investment to accumulate to $12000, and how long it would take to accumulate to $15000.

We start by writing the exponential growth function that models the value of this investment as a function of the time since the $10000 is initially invested

\[y=10000(1.05)^{t} \nonumber \]

We divide both sides by 10000 to isolate the exponential expression on one side.

\[\frac{y}{10000}=1.05^{t} \nonumber \]

Next we rewrite this in logarithmic form to express time as a function of the accumulated future value. We’ll use function notation and call this function \(g(y)\).

\[\mathrm{t}=\mathrm{g}(\mathrm{y})=\log _{1.05}\left(\frac{\mathrm{y}}{10000}\right) \nonumber \]

Use the change of base formula to express \(t\) as a function of \(y\) using natural logarithm:

\[\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)} \nonumber \]

We can now use this function to answer Vinh’s questions.

To find the number of years until the value of this investment is $12,000, we substitute \(y\) = $12,000 into function \(g\) and evaluate \(t\):

\[\mathrm{t}=\mathrm{g}(12000)=\frac{\ln \left(\frac{12000}{10000}\right)}{\ln (1.05)}=\frac{\ln (1.2)}{\ln (1.05)}=3.74 \text { years } \nonumber \]

To find the number of years until the value of this investment is $15,000, we substitute \(y\) = $15,000 into function \(g\) and evaluate \(t\):

\[\mathrm{t}=\mathrm{g}(15000)=\frac{\ln \left(\frac{15000}{10000}\right)}{\ln (1.05)}=\frac{\ln (1.5)}{\ln (1.05)}=8.31 \text { years } \nonumber \]

Before ending this section, we investigate the graph of the function \(\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)}\). We see that the function has the general shape of logarithmic functions that we examined in section 5.5. From the points plotted on the graph, we see that function \(g\) is an increasing function but it increases very slowly.

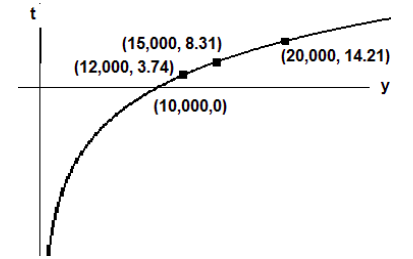
If we consider just the function \(\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)}\), then the domain of function would be \(y > 0\), all positive real numbers, and the range for \(t\) would be all real numbers.

In the context of this investment problem, the initial investment at time \(t\) = 0 is \(y\) =$10,000. Negative values for time do not make sense. Values of the investment that are lower than the initial amount of $10,000 also do not make sense for an investment that is increasing in value.

Therefore the function and graph as it pertains to this problem concerning investments has domain \(y ≥ 10,000\) and range \(t ≥ 0\).

The graph below is restricted to the domain and range that make practical sense for the investment in this problem.