problem solving about geometric figures

Geometry Math Problems - Perimeters

In these lessons, we will learn to solve geometry math problems that involve perimeter.

Related Pages Geometry math problems involving area Area Formula Geometry math problems involving angles More Algebra Word Problems

Geometry word problems involves geometric figures and angles described in words. You would need to be familiar with the formulas in geometry.

Making a sketch of the geometric figure is often helpful.

Geometry Word Problems Involving Perimeter

Example: A triangle has a perimeter of 50. If 2 of its sides are equal and the third side is 5 more than the equal sides, what is the length of the third side?

Solution: Step 1: Assign variables:

Let x = length of the equal sides Sketch the figure

Step 2: Write out the formula for perimeter of triangle .

P = sum of the three sides

Step 3: Plug in the values from the question and from the sketch.

50 = x + x + x+ 5

Combine like terms 50 = 3x + 5

Isolate variable x 3x = 50 – 5 3x = 45 x = 15

Be careful! The question requires the length of the third side.

The length of third side = 15 + 5 = 20

Answer: The length of third side is 20.

Geometry Math Problem involving the perimeter of a rectangle

The following two videos give the perimeter of a rectangle, a relationship between the length and width of the rectangle, and use that information to find the exact value of the length and width.

Example: A rectangular garden is 2.5 times as long as it is wide. It has a perimeter of 168 ft. How long and wide is the garden?

Example: A rectangular landing strip for an airplane has perimeter 8000 ft. If the length is 10 ft longer than 35 times the width, what is the length and width?

Examples of perimeter geometry word problems This video shows how to write an equation and find the dimensions of a rectangle knowing the perimeter and some information about the about the length and width.

Example: The width of a rectangle is 3 ft less than its length. The perimeter of the rectangle is 110 ft. Find the dimensions.

Perimeter Word Problems

Example: The length of a rectangle is 7 cm more than 4 times its width. Its perimeter is 124 cm. Find its dimensions.

Geometry Math Problem involving the perimeter of a triangle

The following two videos give the perimeter of a triangle, a relationship between the sides of the triangle, and use that information to find the exact value or values of the required side or sides.

Example: Patrick’s bike ride follows a triangular path; two legs are equal, the third is 8 miles longer than the other legs. If Patrick rides 30 miles total, what is the length of the longest leg?

Example: The perimeter of a triangle is 56 cm. The first side is 6 cm shorter than the second side. The third side is 2 cm shorter than twice the length of the first side. What is the length of each side?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Free Mathematics Tutorials

Free geometry problems and questions writh solutions.

Free geometry tutorials on topics such as perpendicular bisector, central and inscribed angles, circumcircles, sine law and triangle properties to solve triangle problems. Also geometry problems with detailed solutions on triangles, polygons, parallelograms, trapezoids, pyramids and cones are included. Polar coordinates equations, conversion and graphing are also included. More challenging geometry problems are also included.

Geometry Problems

• Triangle Problems . Triangle problems with detailed solutions.
• Congruent Triangles Examples and Problems with Solutions .
• Similar Triangles Examples and Problems with Solutions . Definition and theorems on similar triangles including examples and problems with detailed solutions.
• Equilateral Triangles Problems with Solutions .
• Isosceles Triangles Problems with Solutions .
• Area and Perimeter of Right Triangles Problems With Solution .
• Cosine Law Problems . The cosine law is used to solve word problems.
• Sine Law Problems . The sine law is used to solve word problems.
• Triangle Inscribed in a Circle - Problem With Solution . Inscribed right triangle problem with detailed solution.
• Circle Tangent to Right Triangle - Problem With Solution . Solve a right triangle whose sides are all tangent to a circle. Both the problem and its detailed solution are presented.
• Overlapping Circles Problem . Find the overlapping area of two circles: problem with detailed solutions.
• Sectors and Circles Problems . Problems, with detailed solutions, related to sectors and circles.
• Two Squares and a Circle - Problem With Solution . A problem, with a detailed solution, on a circle inscribed in one square and circumscribed to another, is presented.
• Two Circles and a Square - Problem With Solution . A problem, with a detailed solution, on a square inscribed in one circle and circumscribed to another is presented.

Quadrilaterals

• Rectangle Problems . Rectangle problems on area, dimensions, perimeter and diagonal with detailed solutions.
• Geometry Problems on Squares . Square problems on area, diagonal and perimeter, with detailed solutions.
• Parallelogram Problems . Word problems related to parallelograms are presented along with detailed solutions.
• Trapezoid Problems . Trapezoid problems are presented along with detailed solutions.
• Solve a Trapezoid Given its Bases and Legs .
• Rhombus Problems . Rhombus definition and properties are presented along with problems with detailed solutions.
• Polygons Problems . Problems related to regular polygons.
• Area Of Octagon - Problem With Solution . Find the length of one side, the perimeter and area of a regular octagon given the distance between two opposite sides (span).
• Angles in Parallel Lines and Transversals Problems . Problems related to parallel lines and alternate and corresponding angles.
• 3D Shapes Volume Problems . 3D shapes, such as prisms, volume problems with detailed solutions.
• Compare Volumes of 3D shapes . A problem to compare the volumes of a cone, a cylinder and a hemisphere.
• How to construct a frustum? . If you cut off the top part of a cone with a plane perpendicular to the height of the cone, you obtain a conical frustum. How to construct a frustum given the radius of the base, the radius of the top and the height?
• Cone Problems . Problems related to the surface area and volume of a cone with detailed solutions are presented.
• Pyramid Problems . Pyramid problems related to surface area and volume with detailed solutions.
• Intercept Theorem and Problems with Solutions .

Geometry Tutorials

• Parts of a Circle .
• Tangents to a Circle with Questions and Solutions .
• Intersecting Secant and Tangent Theorem Questions with Solutions .
• Inscribed and Central Angles in Circles . Definitions and theorems related to inscribed and central angles in circles are discussed using examples and problems.
• Intersecting Chords Theorem Questions with Solutions.
• Intersecting Secant Theorem Questions with Solutions.
• Semicircle Thales Theorem with questions and solutions
• Central and Inscribed Angles - Interactive applet . The properties of central and inscribed angles intercepting a common arc in a circle are explored using an interactive geometry applet.
• Triangles . Definitions and properties of triangles in geometry.
• Area of Triangles Problems with Solutions . Use different formulas of the area of a triangle to calculate the areas of triangles and shapes.
• Simple Proofs of Pythagorean Theorem and Problems with Solutions .
• Altitudes, Medians and Angle Bisectors of a Triangle .
• Triangles, Bisectors and Circumcircles - interactive applet . The properties of perpendicular bisectors in triangles and circumcircles are explored interactively using a geometry Java applet.
• Quadrilaterals , properties and formulas.
• Kite Questions with Solutions .
• Angles in Geometry . Definitions and properties of angles in geometry including questions with solutions.
• Angles in Parallel Lines and Transversals . This tutorial is about the corresponding, interior and exterior angles formed when a transversal line intersects two parallel lines.
• Latitude and Longitude Coordinate System .
• Find the GPS Latitude and Longitude Using Google Map .
• Regular Polygons . Tutorial to develop useful formulas for area of regular polygons.

Other Geometry Topics

• Perpendicular Bisector Problems with Solutions .
• Table of Formulas for Geometry . A table of formulas for geometry, related to area and perimeter of triangles, rectangles, circles, sectors, and volume of sphere, cone, cylinder are presented.

Challenge Geometry Problems

• Two Tangent Circles and a Square - Problem With Solution . You are given the perimeter of a small circle to find the radius of a larger circle inscribed within a square.
• Kite Within a Square - Problem With Solution . A problem on finding the sine of the angle of a kite within a square.
• Solve Triangle Given Its Perimeter, Altitute and Angle - Problem With Solution .
• Solve Right Triangle Given Perimeter and Altitude - Problem With Solution .
• Triangle and Tangent Circle - Problem With Solution . A problem, on a triangle tangent at two points to a circle, is presented along with detailed solution.
• Three Tangent Circles - Problem With Solution . A problem, on three tangent circles, is presented along with solution.
• Equilateral Triangle Within a Square - Problem With Solution . A problem on the proof of an equilateral triangle within a square is presented along with detailed solution.
• Square Inscribed in Right Triangle - Problem With Solution . Find the side of a square inscribed in a right triangle given the sides of the triangle.

Polar Coordinates

• Plot Points in Polar Coordinates . An interactive tutorial on how to plot points given by their polar coordinates.
• Graphing Polar Equations . This is tutorial on graphing polar equations by hand, or sketching, to help you gain deep understanding of these equations. Several examples with detailed solutions are presented.
• Convert Polar to Rectangular Coordinates and Vice Versa . Problems, with detailed solutions, where polar coordinates are converted into rectangular coordinates and vice versa are presented.
• Convert Equation from Rectangular to Polar Form . Problems were equations in rectangular form are converted to polar form, using the relationship between polar and rectangular coordinates, are presented along with detailed solutions.
• Convert Equation from Polar to Rectangular Form . Equations in polar form are converted into rectangular form, using the relationship between polar and rectangular coordinates. Problems with detailed solutions are presented.

Geometric Transformations

• Reflection Across a Line . The properties of reflection of shapes across a line are explored using a geometry applet.
• Rotation of Geometric Shapes . The rotations of 2-D shapes are explored.

Geometric Calculators and Worksheets

• Online Geometry Calculators and Solvers : Several calculators to help in the calculations and solutions of geometry problems.
• Free Geometry Worksheets to Download

o Identify some critical steps of the process for solving practical geometry problems

o Apply geometry problem-solving techniques to practical situations

Geometry has a variety of real-life applications in everyday situations. In this article, we will learn to apply geometric principles and techniques to solve problems. The key to solving practical geometry problems is translation of the real-life situation into figures, measurements, and other information necessary to represent the situation conceptually. For instance, you already know how to calculate the area of a composite figure; if you were asked to determine how much floor space is available in a certain building with a composite shape, you would simply need to apply the same principles as you would use for calculating the area of a composite figure. Some measurements of the building might, of course, be required, but the same problem-solving techniques apply.

It behooves us to present a basic approach to solving practical geometry problems. This approach is similar to that for solving almost a word problem, but is geared slightly more toward the characteristics of geometry problems in particular.

1. Determine what you need to calculate to solve the problem. In some cases, you may need a length; in others, an area or angle measure. If you are conscious throughout the process of what you need to determine, you can save yourself a significant amount of time.

2. Draw a diagram. Sometimes a straightedge, compass, protractor, or some combination of these tools can be helpful. Even if you only use a rough sketch, however, making a visual representation of the problem can help you organize your thoughts and keep track of important information such as the relationship of line segments and angles as well as the measures thereof.

3. Record all appropriate measurements. If you are calculating an area, for instance, you may need to take measurements of certain lengths (alternatively, these may be provided to you). In either case, record them and mark them in some manner on your diagram.

4. Pay attention to units. Using units of square meters for a length or angle measure can be an embarrassing mistake! Keep careful track of the units you are using throughout the problem. If no units are given, simply use the generic term "units" in place of inches or meters, for example.

5. Divide the figure, if necessary, into manageable portions. If your diagram is a composite figure, it may help to divide the figure into bite-sized portions that you can handle.

6. Identify any appropriate geometric relationships. This step can greatly simplify the problem. Perhaps you can show two triangles to be congruent or similar, or perhaps you can identify congruent segments or angles. Use this step to fill in as much missing information in your diagram as you can.

7. Do the math. At this point, you need to apply what you've learned to analyze the figure and other data to solve the problem. You may, for example, need to apply the Pythagorean theorem, or you may need to calculate the perimeter of a figure. Whatever the details of the problem, you will need to apply your skills in geometry in an appropriate manner.

8. Check your results. Take a look at your answer in the context of your diagram-does your answer make sense? A result of millions of square meters for the area of a figure with dimensions in the range of a few meters should tell you that you've made an error at some point in your analysis.

Not every step of the approach outlined above will be needed in every problem. You must use your best judgment in determining what is necessary to solve the problem in a satisfactory and time-efficient manner. Also, you may not always think to use the exact progression of steps above; the outline is simply a way to describe a systematic approach to problem solving. The remainder of this article provides you the opportunity to test your geometry skills by way of several practice problems. Obviously, these problems do not require you to go out and make any measurements of lengths or angles, but keep in mind that problems you encounter in everyday life may require you to do so!

Practice Problem : The floor plan of a house is shown below. Determine the area covered by the house.

Solution : Let's first divide the diagram of the house into two rectangles and a trapezoid, since we can calculate the area of each of these figures. Using the properties of each figure, we can also fill in some of the unknown information.

Now, the area of the larger rectangle is the product of 40 feet and 20 feet, or 800 square feet. The area of the smaller rectangle is 25 feet times 6 feet, or 150 square feet. The area of the trapezoid is the following:

The height ( h ) is 6 feet, and the two bases ( b 1 and b 2 ) are 8 and 11 feet.

Adding all three areas gives us a total area of the house of 1,007 square feet.

Practice Problem : A hiker is walking up a steep hill. The slope of the hill between two trees is constant, and the base of one tree is 100 meters higher than the other. If the horizontal distance between the trees is 400 meters, how far must the hiker walk to get from one tree to the next?

Solution : Because this problem may be difficult to envision, a diagram is extremely helpful. Notice that the base of the trees differ in height by 100 meters--this is our vertical distance for the walk. The horizontal distance is 400 meters.

Note that we have shown the right angle because horizontal and vertical segments are perpendicular. We can now use the Pythagorean theorem to calculate the distance d the hiker must walk.

Thus, the hiker must walk about 412 meters. Note that although the hiker makes a significant (100 meter) change in elevation over this walk, the difference between the actual distance he walks and the horizontal distance is small--only about 12 meters.

Practice Problem : A homeowner has a rectangular fenced-in yard, and he wants to put mulch on his triangular gardens, as shown below. The inside border of each garden always meets the fence at the same angle. If a bag of mulch covers about 50 square feet, how many bags of mulch should the homeowner buy to cover his gardens?

Solution : We are told in the problem that the inside border of each garden meets the fence at the same angle in every case; thus, we can conclude (as shown below) that the triangles are all isosceles (and that the triangles with the same side lengths are congruent by the ASA condition). We can thus mark each side with an unknown variable x or y .

Recall that the fenced-in area is rectangular; thus the angle in each corner is 90°. We can then solve for x and y using the Pythagorean theorem. Notice first, however, that x and y are the height and base of their respective triangles.

Because the gardens include two of each triangle shape, the total garden area is simply the sum of x 2 and y 2 . (If you do not follow this point, simply use the triangle area formula in each case--you will get the same result.)

Thus, the homeowner needs six bags of mulch (for a total of 300 square feet) to cover his gardens. (Of course, we are assuming here that he must buy a whole number of bags.)

• Course Catalog
• Group Discounts
• Gift Certificates
• For Libraries
• CEU Verification
• Medical Terminology
• Accounting Course
• Writing Basics
• QuickBooks Training
• Proofreading Class
• Sensitivity Training
• Excel Certificate
• Teach Online
• Terms of Service
• Privacy Policy

Using Geometric Concepts and Properties to Solve Problems

Introduction.

Often, you will be asked to solve problems involving geometric relationships or other shapes. For real-world problems, those geometric relationships mostly involve measurable attributes, such as length, area, or volume.

Sometimes, those problems will involve the perimeter or circumference, or the area of a 2-dimensional figure.

For example, what is the distance around the track that is shown?  Or, what is the area of the portion of the field that is covered with grass?

You may also see problems that involve the volume or surface area of a 3-dimensional figure.  For example, what is the area of the roof of the building that is shown?

Another common type of geometric problem involves using proportional reasoning.

For example, an artist created a painting that needs to be reduced proportionally for the flyer advertising an art gallery opening. If the dimensions of the painting are reduced by a factor of 40%, what will be the dimensions of the image on the flyer?

In this resource, you will investigate ways to apply a problem-solving model to determine the solutions for geometric problems like these.

A basic problem solving model contains the following four steps:

Solving Problems Using Perimeter and Circumference

You may recall that the perimeter of an object is the distance around the edge of the object. If the object contains circles, then you may need to think about the circumference of a circle, which is the perimeter of the circle.

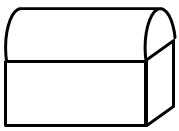
A tire on a passenger car has a diameter of 18 inches. When the tire has rotated 5 times, how far will the car have traveled?

Step 1 : Read, understand, and interpret the problem.

• What information is presented?
• What is the problem asking me to find?
• What information may be extra information that I do not need?

Step 2 : Make a plan.

• Draw a picture.
• Use a formula: Which formula do I need to use? (Hint: Look at your Mathematics Reference Materials)

Step 3 : Implement your plan.

• What formulas do I need?
• What information can I interpret from the diagram, table, or other given information?
• Solve the problem.

Step 4 : Evaluate your answer.

• Does my answer make sense?
• Did I answer the question that was asked?
• Are my units correct?

A cylindrical barrel with a diameter of 20 inches is used to hold fuel for a barbecue cook off. The chef rolls the barrel so that it completes 7 rotations. How many feet did the chef roll the barrel?

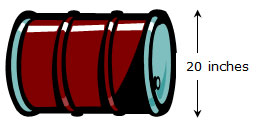
Solving Problems Using Area and Surface Area

You may also encounter real-world geometric problems that ask you to find the area of 2-dimensional figures or the surface area of 3-dimensional figures. The key to solving these problems is to look for ways to break the region into smaller figures of which you know how to find the area.

Mr. Elder wants to cover a wall in his kitchen with wallpaper. The wall is shown in the figure below.

If wallpaper costs $1.75 per square foot, how much will Mr. Elder spend on wallpaper to completely cover this wall, excluding sales tax?

To solve this problem, let's use the 4-step problem solving model.

Mrs. Nguyen wants to apply fertilizer to her front lawn. A bag of fertilizer that covers 1,000 square feet costs $18. How many bags of fertilizer will Mrs. Nguyen need to purchase?

Surface Area Problem

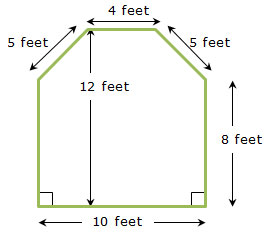
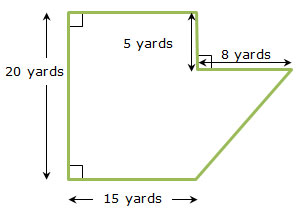
After a storm, the Serafina family needs to have their roof replaced. Their house is in the shape of a pentagonal prism with the dimensions shown in the diagram.

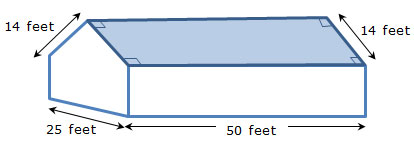
To match their new roof, Mrs. Serafina decided to have both pentagonal sides of their house covered in aluminum siding. Their house is in the shape of a pentagonal prism with the dimensions shown in the diagram.

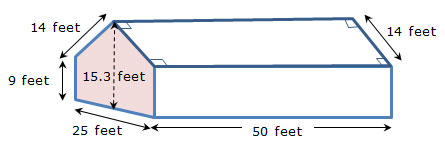
A contractor gave Mrs. Serafina an estimate based on a cost of $3.10 per square foot to complete the aluminum siding. How much will it cost the Serafina family to have the aluminum siding installed?

Solving Problems Using Proportionality

Proportional relationships are another important part of geometric problem solving.

A woodblock painting has dimensions of 60 centimeters by 79.5 centimeters. In order to fit on a flyer advertising the opening of a new art show, the image must be reduced by a scale factor of  1/25.

W hat will be the final dimensions of the image on the flyer?

Measuring Problem

For summer vacation, Jennifer and her family drove from their home in Inlandton to Beachville. Their car can drive 20 miles on one gallon of gasoline. Use the ruler to measure the distance that they drove to the nearest  1/4  inch, and then calculate the number of gallons of gasoline their car will use at this rate to drive from Inlandton to Beachville.

Practice #1

A blueprint for a rectangular tool shed has dimensions shown in the diagram below.

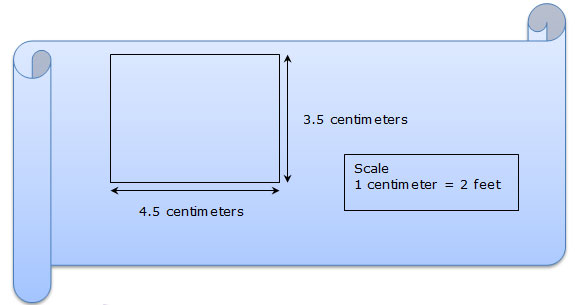
Todd is using this blueprint to build a tool shed, and he wants to surround the base of the tool shed with landscaping timbers as a border. How many feet of landscaping timbers will Todd need?

Practice #2

A scale model of a locomotive is shown. Use the ruler to measure the dimensions of the model to the nearest 1/4  inch, and then calculate the actual dimensions of the locomotive.

Scale : 1 inch = 5 feet

Solving geometric problems, such as those found in art and architecture, is an important skill. As with any mathematical problem, you can use the 4-step problem solving model to help you think through the important parts of the problem and be sure that you don't miss key information.

There are a lot of different applications of geometry to real-world problem solving. Some of the more common applications include the following:

What is the perimeter of the base of the cup, if the cup is in the shape of an octagonal prism?

The JP Morgan Chase Bank Tower in downtown Houston, Texas, is one of the tallest buildings west of the Mississippi River. It is in the shape of a pentagonal prism. If 40% of each face is covered with glass windows, what is the amount of surface area covered with glass?

The dimensions of Vincent van Gogh's Starry Night are 29 inches by 36 1 4 36\frac{1}{4} inches. If a print reduces these dimensions by a scale factor of 30%, what will be the dimensions of the print?

Copy and paste the link code above.

Related Items

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Introduction to Geometry
• Functions and Graphs
• 1. Introduction to Functions
• 2. Functions from Verbal Statements
• 3. Rectangular Coordinates
• 4. The Graph of a Function
• 4a. Domain and Range of a Function
• 4b. Domain and Range interactive applet
• 4c. Comparison calculator BMI - BAI
• 5. Graphing Using a Computer Algebra System
• 5a. Online graphing calculator (1): Plot your own graph (JSXGraph)
• 5b. Online graphing calculator (2): Plot your own graph (SVG)
• 6. Graphs of Functions Defined by Tables of Data
• 7. Continuous and Discontinuous Functions
• 8. Split Functions
• 9. Even and Odd Functions

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Online Math Solver

Solve your math problem step by step!

IntMath Forum

Get help with your math queries:

Geometrical Constructions in Geometry 

Geometrical constructions are a fundamental part of geometry and are used to solve a variety of problems. In this blog, we'll explore the essence of geometrical constructions, how they work, and why they are essential to understanding geometry. 

What is a Geometrical Construction? 

A geometrical construction is a problem-solving technique that uses geometric tools such as a straightedge and compass to construct figures with certain properties. The goal of this type of construction is to draw accurate figures based on given information. 

Constructions can be used for many different kinds of problems in geometry, including finding angles between lines, constructing triangles or circles with given angles or radii, and constructing other shapes with specified properties. By using geometrical constructions, you can solve problems more efficiently and accurately than if you were to use traditional methods like trial-and-error or guesswork. 

Why Are They Important? 

Geometric constructions are important because they teach students how to think critically about problems in geometry. Through the process of solving a geometrical construction problem, students learn how to identify relevant information and make deductions from it. This skill is essential for many fields outside of mathematics as well; by learning geometrical constructions, students are also developing skills like critical thinking and problem-solving that will serve them well in any field they pursue. 

Conclusion:

Geometric constructions are an integral part of geometry—and beyond! By learning these techniques, students can develop their critical thinking skills while also improving their understanding of the subject matter itself. Whether you’re studying geometry or any other field that involves problem-solving, it’s important to understand the essence of geometrical constructions and how they can be applied to various situations. With enough practice and perseverance, anyone can learn these valuable skills!

What is the importance of geometric constructions?

Geometric constructions are important because they teach students how to think critically about problems in geometry. Through the process of solving a geometrical construction problem, students learn how to identify relevant information and make deductions from it. This skill is essential for many fields outside of mathematics as well; by learning geometrical constructions, students are also developing skills like critical thinking and problem-solving that will serve them well in any field they pursue.

What do you understand by geometrical construction?

A geometrical construction is a problem-solving technique that uses geometric tools such as a straightedge and compass to construct figures with certain properties. The goal of this type of construction is to draw accurate figures based on given information. Constructions can be used for many different kinds of problems in geometry, including finding angles between lines, constructing triangles or circles with given angles or radii, and constructing other shapes with specified properties.

What important lessons are to be learned through geometric constructions?

By learning geometrical constructions, students are developing skills like critical thinking and problem-solving that will serve them well in any field they pursue. Additionally, it teaches them how to identify relevant information and make deductions from it, a skill that is essential for many fields outside of mathematics.

Problem Solver

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of GPT large language models to parse and generate natural language. This creates math problem solver thats more accurate than ChatGPT, more flexible than a calculator, and faster answers than a human tutor. Learn More.

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Hard Geometry Problems – Tackling Tough Challenges with Ease

Geometry problems often involve shapes, sizes, positions, and the properties of space. As I delve into the realm of geometry, it’s fascinating to explore the intricate challenges posed by harder problems in this field.

These problems test my understanding of concepts such as congruence, similarity, the Pythagorean Theorem, as well as area and perimeter calculations.

I find that working through these problems hones my analytical skills and enhances my spatial reasoning abilities.

Hard geometry problems usually cover a diverse array of topics, from basic triangle rules to complex geometric proofs.

Showcasing mastery in this domain often calls for a blend of creativity and meticulousness, especially as I encounter problems that push the boundaries of my knowledge. For example, proving that two or more shapes are congruent or similar or finding the area of intricate figures can be quite a brain teaser.

The journey through these challenges is not just about finding the right answers; it’s also about appreciating the beauty and precision of geometry itself. Are you ready to join me in unraveling the elegance and complexity of these geometrical puzzles?

Complex Geometry Problems

In my journey through mathematics , I’ve found that complex geometry problems often intimidate students preparing for standardized tests such as the ACT , GRE , and SAT . These problems can involve a variety of geometric figures, from triangles and circles to circular cylinders and squares .

When tackling triangles , I always pay attention to the isosceles and equilateral types. It’s crucial to remember that isosceles triangles have two sides of equal length, and the angles opposite these sides are equal. As for equilateral triangles , all three sides and angles are the same, with each angle measuring $\frac{\pi}{3}$ radians, or $60^\circ$.

Here’s a quick table summarizing triangle rules :

For circles , understanding the terminology is key. The diameter is twice the radius , and a chord that passes through the center of a circle forms a diameter . A semicircle is half of a circle, and when calculating area , I recall the formula $A = \pi r^2$, where $r$ is the radius .

If the problem involves a figure with both a triangle and a semicircle , I check if they share a side or a vertex . This often leads to interesting relationships between angles and sides which are essential to finding a solution .

Although these concepts might seem daunting at first, with practice, solving these types of geometry problems becomes a rewarding and enlightening act.

Solving Geometry Problems

When I tackle geometry problems , I think of them as intricate math puzzles . In my experience, practice is key to becoming proficient.

A reliable method I use involves several steps:

Understand the Problem : I carefully read the problem to grasp what’s being asked, especially the value we are trying to find, like the “value of ( x )”.

Draw It Out : I sketch the geometry figure, labeling known measurements and angles, which helps visualize and identify the ASA (Angle-Side-Angle) or other relevant theorems.

Apply Theorems : My familiarity with geometric principles, often refreshed by reading test prep books or resources from Stanford University , comes in handy.

Test Different Approaches : I try different problem-solving techniques, using tools from the Get 800 collection or insights from the MindYourDecisions channel.

Check the Work : I always verify my answers to avoid common mistakes.

Here’s a quick reference I’ve created that might be handy:

The practice doesn’t just involve solving problems from books or test prep books ; it also includes explaining concepts to others, which could be classmates or a teacher .

In my journey of learning and teaching, I’ve found that discussing the process openly in a friendly manner greatly reinforces understanding. As with all things, especially something as logical as geometry, maintaining persistent practice and a can-do attitude is essential in mastering challenging problems.

In grappling with hard geometry problems , I’ve encountered numerous challenges that have pushed my understanding to new heights.

From the intricate relationships between angles to the deep insights required for problem-solving, these problems offer a true test of mathematical skill. Mathematical contests often feature such problems to differentiate between good and exceptional problem solvers.

One thought that stands out is the value of persistence and logic. In facing problems about finding an unknown angle or solving for a particular length, the approach isn’t merely about applying formulas.

It requires a creative combination of geometry principles, sometimes integrating concepts borrowed from other areas of mathematics, such as algebra or trigonometry.

Reflecting on famous problems, like those I’ve come across from various online platforms, it becomes clear just how beautiful and complex geometry can be.

These problems often serve dual purposes, they are not just queries to be answered but lessons that deepen my appreciation and understanding of mathematics. The journey through tough geometry questions is not only about reaching the correct answer but also about appreciating the intricacies of the geometric world.

I encourage my readers to embrace these difficult problems with a sense of adventure. Remember, tackling a geometry problem is more than a test; it’s an opportunity to explore the elegance of mathematics.

Whether you solve a challenging problem on the first try or it takes numerous attempts, each effort enhances your mathematical intuition and prowess.

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

CHAPTER 3 Measurement, Perimeter, Area, and Volume

3.4 Solve Geometry Applications: Circles and Irregular Figures

Learning Objectives

By the end of this section, you will be able to:

• Use the properties of circles
• Find the area of irregular figures

In this section, we’ll continue working with geometry applications. We will add several new formulas to our collection of formulas. To help you as you do the examples and exercises in this section, we will show the Problem Solving Strategy for Geometry Applications here.

Problem Solving Strategy for Geometry Applications

• Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
• Identify what you are looking for.
• Name what you are looking for. Choose a variable to represent that quantity.
• Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

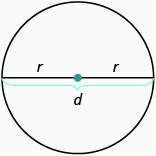
Use the Properties of Circles

 We’ll  refer to the properties of circles as we use them to solve applications.

Properties of Circles

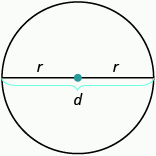
• 78.5 sq. in.

• 63.585 sq. ft

We will use this form of the circumference when we’re given the length of the diametre instead of the radius.

A circular table has a diametre of four feet. What is the circumference of the table?

Find the Area of Irregular Figures

So far, we have found area for rectangles, triangles, trapezoids, and circles. An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or more standard geometric shapes. To find the area of one of these irregular figures, we can split it into figures whose formulas we know and then add the areas of the figures.

Find the area of the shaded region.

The given figure is irregular, but we can break it into two rectangles. The area of the shaded region will be the sum of the areas of both rectangles.

Is there another way to split this figure into two rectangles? Try it, and make sure you get the same area.

Find the area of each shaded region:

28 sq. units

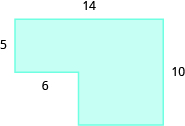
110 sq. units

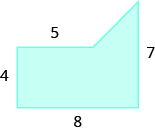
We can break this irregular figure into a triangle and rectangle. The area of the figure will be the sum of the areas of triangle and rectangle.

We need to find the base and height of the triangle.

Now we can add the areas to find the area of the irregular figure.

Find the area of each shaded region.

36.5 sq. units

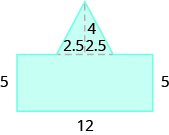
70 sq. units

We will break the figure into a rectangle and two semi-circles. The area of the figure will be the sum of the areas of the rectangle and the semicircles.

Find the area:

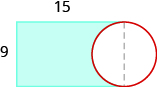
103.2 sq. units

38.24 sq. units

Access Additional Online Resources

• Circumference of a Circle
• Area of a Circle
• Area of an L-shaped polygon
• Area of an L-shaped polygon with Decimals
• Perimeter Involving a Rectangle and Circle
• Area Involving a Rectangle and Circle

Key Concepts

Practice Makes Perfect

In the following exercises, solve using the properties of circles.

In the following exercises, find the radius of the circle with given circumference.

In the following exercises, find the area of the irregular figure. Round your answers to the nearest hundredth.

In the following exercises, solve.

Everyday Math

Writing exercises, attributions.

This chapter has been adapted from “Solve Geometry Applications: Circles and Irregular Figures” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence . Adapted by Izabela Mazur. See the Copyright page for more information.

Introductory Algebra Copyright © 2021 by Izabela Mazur is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Solving 'geometric' problems - AQA Geometry problems

Geometric problems can involve finding the perimeter and area of shapes like triangles and quadrilaterals. Knowledge of shape properties is essential. A framework can be used to tackle these problems.

Part of Maths Problem solving

Geometry problems

Geometric problems often have diagrams provided that involve triangles, quadrilaterals and other polygons .

It is important to know properties of these shapes as questions will often involve knowing angle and length properties. For example, remember that each angle in an equilateral triangle is 60°.

When a problem involves lengths and angles, it may be easier to show any working out on the diagram. For example, you should label any angles calculated.

A problem solving framework can be used to tackle geometry problems.

This video can not be played

To play this video you need to enable JavaScript in your browser.

The six step framework is used to solve a geometric problem

More guides on this topic

• Problem solving introduction - AQA
• Solving 'number' problems - AQA
• Solving 'graphical' problems - AQA
• Solving 'algebraic' problems - AQA
• Solving 'statistical' problems - AQA

Related links

• Maths: Exam-style questions
• Personalise your Bitesize!
• Jobs that use Maths
• Skillswise: Maths
• Radio 4: Maths collection
• Save My Exams Subscription
• Pearson Education

Module 11: Geometry

Summary: solving problems with circles and irregular figures, key concepts.

• Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
• Identify what you are looking for.
• Name what you are looking for. Choose a variable to represent that quantity.
• Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

• [latex]d=2r[/latex]
• Circumference: [latex]C=2\pi r[/latex] or [latex]C=\pi d[/latex]
• Area: [latex]A=\pi {r}^{2}[/latex]
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.8: Solve Geometry Applications- Circles and Irregular Figures

• Last updated
• Save as PDF
• Page ID 5009

Learning Objectives

• Use the properties of circles
• Find the area of irregular figures

be prepared!

Before you get started, take this readiness quiz.

• Evaluate x 2 when x = 5. If you missed this problem, review Example 2.3.3 .
• Using 3.14 for \(\pi\), approximate the (a) circumference and (b) the area of a circle with radius 8 inches. If you missed this problem, review Example 5.6.12 .
• Simplify \(\dfrac{22}{7}\)(0.25) 2 and round to the nearest thousandth. If you missed this problem, review Example 5.5.9 .

In this section, we’ll continue working with geometry applications. We will add several new formulas to our collection of formulas. To help you as you do the examples and exercises in this section, we will show the Problem Solving Strategy for Geometry Applications here.

Problem Solving Strategy for Geometry Applications

Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.

Step 2. Identify what you are looking for.

Step 3. Name what you are looking for. Choose a variable to represent that quantity

Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.

Step 5. Solve the equation using good algebra techniques.

Step 6. Check the answer in the problem and make sure it makes sense.

Step 7. Answer the question with a complete sentence.

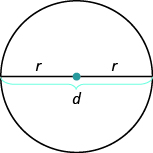
Use the Properties of Circles

Do you remember the properties of circles from Decimals and Fractions ? We’ll show them here again to refer to as we use them to solve applications.

Definition: Properties of Circles

• r is the length of the radius
• d is the length of the diameter
• Circumference is the perimeter of a circle. The formula for circumference is C = 2\(\pi\)r
• The formula for area of a circle is A = \(\pi\)r 2

Remember, that we approximate \(\pi\) with 3.14 or \(\dfrac{22}{7}\) depending on whether the radius of the circle is given as a decimal or a fraction. If you use the \(\pi\) key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the \(\pi\) key uses more than two decimal places.

Example \(\PageIndex{1}\):

A circular sandbox has a radius of 2.5 feet. Find the (a) circumference and (b) area of the sandbox.

Exercise \(\PageIndex{1}\):

A circular mirror has radius of 5 inches. Find the (a) circumference and (b) area of the mirror.

78.5 sq. in.

Exercise \(\PageIndex{2}\):

A circular spa has radius of 4.5 feet. Find the (a) circumference and (b) area of the spa.

63.585 sq. ft

We usually see the formula for circumference in terms of the radius r of the circle:

\[C = 2 \pi r\]

But since the diameter of a circle is two times the radius, we could write the formula for the circumference in terms of d.

\[\begin{split} C &= 2 \pi r \\ Using\; the\; commutative\; property,\; we\; get \qquad C &= \pi \cdot 2r \\ Then\; substituting\; d = 2r \qquad C &= \pi \cdot d \\ So \qquad C &= \pi d \end{split}\]

We will use this form of the circumference when we’re given the length of the diameter instead of the radius.

Example \(\PageIndex{2}\):

A circular table has a diameter of four feet. What is the circumference of the table?

Exercise \(\PageIndex{3}\):

Find the circumference of a circular fire pit whose diameter is 5.5 feet.

Exercise \(\PageIndex{4}\):

If the diameter of a circular trampoline is 12 feet, what is its circumference?

Example \(\PageIndex{3}\):

Find the diameter of a circle with a circumference of 47.1 centimeters.

Exercise \(\PageIndex{5}\):

Find the diameter of a circle with circumference of 94.2 centimeters.

Exercise \(\PageIndex{6}\):

Find the diameter of a circle with circumference of 345.4 feet.

Find the Area of Irregular Figures

So far, we have found area for rectangles, triangles, trapezoids, and circles. An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or more standard geometric shapes. To find the area of one of these irregular figures, we can split it into figures whose formulas we know and then add the areas of the figures.

Example \(\PageIndex{4}\):

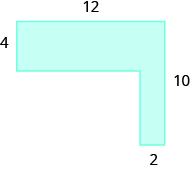
Find the area of the shaded region.

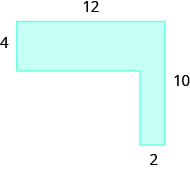
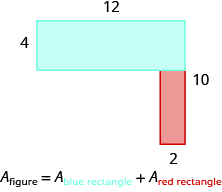
The given figure is irregular, but we can break it into two rectangles. The area of the shaded region will be the sum of the areas of both rectangles.

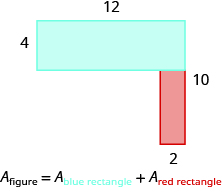
The blue rectangle has a width of 12 and a length of 4. The red rectangle has a width of 2, but its length is not labeled. The right side of the figure is the length of the red rectangle plus the length of the blue rectangle. Since the right side of the blue rectangle is 4 units long, the length of the red rectangle must be 6 units.

\[\begin{split} A_{figure} &= A_{\textcolor{blue}{rectangle}} + A_{\textcolor{red}{rectangle}} \\ A_{figure} &= \textcolor{blue}{bh} + \textcolor{red}{bh} \\ A_{figure} &= \textcolor{blue}{12 \cdot 4} + \textcolor{red}{2 \cdot 6} \\ A_{figure} &= \textcolor{blue}{48} + \textcolor{red}{12} \\ A_{figure} &= 60 \end{split}\]

The area of the figure is 60 square units.

Is there another way to split this figure into two rectangles? Try it, and make sure you get the same area.

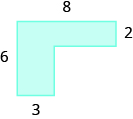
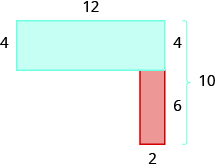
Exercise \(\PageIndex{7}\):

Find the area of each shaded region:

28 sq. units

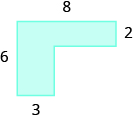
Exercise \(\PageIndex{8}\):

110 sq. units

Example \(\PageIndex{5}\):

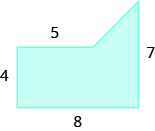
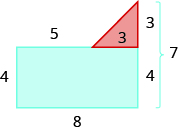
We can break this irregular figure into a triangle and rectangle. The area of the figure will be the sum of the areas of triangle and rectangle.

The rectangle has a length of 8 units and a width of 4 units.

We need to find the base and height of the triangle.

Since both sides of the rectangle are 4, the vertical side of the triangle is 3, which is 7 − 4. The length of the rectangle is 8, so the base of the triangle will be 3, which is 8 − 4.

Now we can add the areas to find the area of the irregular figure.

\[\begin{split} A_{figure} &= A_{\textcolor{blue}{rectangle}} + A_{\textcolor{red}{triangle}} \\ A_{figure} &= \textcolor{blue}{lw} + \dfrac{1}{2} \textcolor{red}{bh} \\ A_{figure} &= \textcolor{blue}{8 \cdot 4} + \dfrac{1}{2} \cdot \textcolor{red}{3 \cdot 3} \\ A_{figure} &= \textcolor{blue}{32} + \textcolor{red}{4.5} \\ A_{figure} &= 3.65\; sq.\; units \end{split}\]

The area of the figure is 36.5 square units.

Exercise \(\PageIndex{9}\):

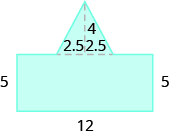
Find the area of each shaded region.

36.5 sq. units

Exercise \(\PageIndex{10}\):

70 sq. units

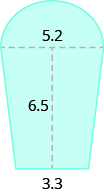
Example \(\PageIndex{6}\):

A high school track is shaped like a rectangle with a semi-circle (half a circle) on each end. The rectangle has length 105 meters and width 68 meters. Find the area enclosed by the track. Round your answer to the nearest hundredth.

We will break the figure into a rectangle and two semi-circles. The area of the figure will be the sum of the areas of the rectangle and the semicircles.

The rectangle has a length of 105 m and a width of 68 m. The semi-circles have a diameter of 68 m, so each has a radius of 34 m.

\[\begin{split} A_{figure} &= A_{\textcolor{blue}{rectangle}} + A_{\textcolor{red}{semicircles}} \\ A_{figure} &= \textcolor{blue}{bh} + \textcolor{red}{2\left(\dfrac{1}{2} \pi \cdot r^{2} \right)} \\ A_{figure} &\approx \textcolor{blue}{105 \cdot 68} + \textcolor{red}{2 \left(\dfrac{1}{2} \cdot 3.14 \cdot 34^{2}\right)} \\ A_{figure} &\approx \textcolor{blue}{7140} + \textcolor{red}{3629.84} \\ A_{figure} &\approx 10,769.84\; square\; meters \end{split}\]

Exercise \(\PageIndex{11}\):

Find the area:

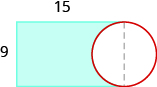
103.2 sq. units

Exercise \(\PageIndex{12}\):

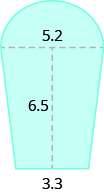
38.24 sq. units

ACCESS ADDITIONAL ONLINE RESOURCES

Circumference of a Circle

Area of a Circle

Area of an L-shaped polygon

Area of an L-shaped polygon with Decimals

Perimeter Involving a Rectangle and Circle

Area Involving a Rectangle and Circle

Practice Makes Perfect

In the following exercises, solve using the properties of circles.

• The lid of a paint bucket is a circle with radius 7 inches. Find the (a) circumference and (b) area of the lid.
• An extra-large pizza is a circle with radius 8 inches. Find the (a) circumference and (b) area of the pizza.
• A farm sprinkler spreads water in a circle with radius of 8.5 feet. Find the (a) circumference and (b) area of the watered circle.
• A circular rug has radius of 3.5 feet. Find the (a) circumference and (b) area of the rug.
• A reflecting pool is in the shape of a circle with diameter of 20 feet. What is the circumference of the pool?
• A turntable is a circle with diameter of 10 inches. What is the circumference of the turntable?
• A circular saw has a diameter of 12 inches. What is the circumference of the saw?
• A round coin has a diameter of 3 centimeters. What is the circumference of the coin?
• A barbecue grill is a circle with a diameter of 2.2 feet. What is the circumference of the grill?
• The top of a pie tin is a circle with a diameter of 9.5 inches. What is the circumference of the top?
• A circle has a circumference of 163.28 inches. Find the diameter.
• A circle has a circumference of 59.66 feet. Find the diameter.
• A circle has a circumference of 17.27 meters. Find the diameter.
• A circle has a circumference of 80.07 centimeters. Find the diameter.

In the following exercises, find the radius of the circle with given circumference.

• A circle has a circumference of 150.72 feet.
• A circle has a circumference of 251.2 centimeters.
• A circle has a circumference of 40.82 miles.
• A circle has a circumference of 78.5 inches.

In the following exercises, find the area of the irregular figure. Round your answers to the nearest hundredth.

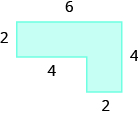
In the following exercises, solve.

• A city park covers one block plus parts of four more blocks, as shown. The block is a square with sides 250 feet long, and the triangles are isosceles right triangles. Find the area of the park.

• A gift box will be made from a rectangular piece of cardboard measuring 12 inches by 20 inches, with squares cut out of the corners of the sides, as shown. The sides of the squares are 3 inches. Find the area of the cardboard after the corners are cut out.

• Perry needs to put in a new lawn. His lot is a rectangle with a length of 120 feet and a width of 100 feet. The house is rectangular and measures 50 feet by 40 feet. His driveway is rectangular and measures 20 feet by 30 feet, as shown. Find the area of Perry’s lawn.

• Denise is planning to put a deck in her back yard. The deck will be a 20-ft by 12-ft rectangle with a semicircle of diameter 6 feet, as shown below. Find the area of the deck.

Everyday Math

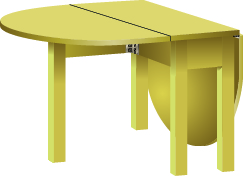
• Area of a Tabletop Yuki bought a drop-leaf kitchen table. The rectangular part of the table is a 1-ft by 3-ft rectangle with a semicircle at each end, as shown.(a) Find the area of the table with one leaf up. (b) Find the area of the table with both leaves up.

• Painting Leora wants to paint the nursery in her house. The nursery is an 8-ft by 10-ft rectangle, and the ceiling is 8 feet tall. There is a 3-ft by 6.5-ft door on one wall, a 3-ft by 6.5-ft closet door on another wall, and one 4-ft by 3.5-ft window on the third wall. The fourth wall has no doors or windows. If she will only paint the four walls, and not the ceiling or doors, how many square feet will she need to paint?

Writing Exercises

• Describe two different ways to find the area of this figure, and then show your work to make sure both ways give the same area.

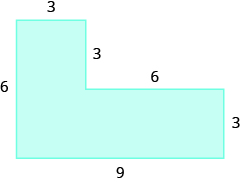
• A circle has a diameter of 14 feet. Find the area of the circle (a) using 3.14 for \(\pi\) (b) using \(\dfrac{22}{7}\) for \(\pi\). (c) Which calculation to do prefer? Why?

(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

(b) After looking at the checklist, do you think you are well prepared for the next section? Why or why not?

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/[email protected] ."

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Similarity

About this unit, definitions of similarity.

• Similar shapes & transformations (Opens a modal)
• Similarity & transformations 4 questions Practice

Introduction to triangle similarity

• Intro to triangle similarity (Opens a modal)
• Triangle similarity postulates/criteria (Opens a modal)
• Determining similar triangles (Opens a modal)
• Proving slope is constant using similarity (Opens a modal)
• Triangle similarity review (Opens a modal)
• Determine similar triangles: Angles 4 questions Practice
• Determine similar triangles: SSS 4 questions Practice

Solving similar triangles

• Solving similar triangles (Opens a modal)
• Solving similar triangles: same side plays different roles (Opens a modal)
• Solve similar triangles (basic) 4 questions Practice
• Solve similar triangles (advanced) 4 questions Practice

Angle bisector theorem

• Intro to angle bisector theorem (Opens a modal)
• Using the angle bisector theorem (Opens a modal)
• Solve triangles: angle bisector theorem 4 questions Practice

Solving problems with similar and congruent triangles

• Using similar & congruent triangles (Opens a modal)
• Challenging similarity problem (Opens a modal)
• Use similar triangles 4 questions Practice

Solving modeling problems with similar and congruent triangles

• Geometry word problem: the golden ratio (Opens a modal)
• Geometry word problem: Earth & Moon radii (Opens a modal)
• Geometry word problem: a perfect pool shot (Opens a modal)

• Directories

Search form

You are here.

• Summer 2024

MATH 125 BB: Calculus with Analytic Geometry II

•   News Feed
•   Alumni Update
•   Mailing List