solve algebraic equations with 2 variables

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Systems of Algebraic Equations Containing Two Variables

Last Updated: July 30, 2023 Fact Checked

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. There are 8 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,061,353 times.

In a "system of equations," you are asked to solve two or more equations at the same time. When these have two different variables in them, such as x and y, or a and b, it can be tricky at first glance to see how to solve them. [1] X Research source Fortunately, once you know what to do, all you need is basic algebra skills (and sometimes some knowledge of fractions) to solve the problem. If you are a visual learner or if your teacher requires it, learn how to graph the equations as well. Graphing can be useful to "see what's going on" or to check your work, but it can be slower than the other methods, and doesn't work well for all systems of equations.

Using the Substitution Method

• This method often uses fractions later on. You can try the elimination method below instead if you don't like fractions.

• 4x = 8 - 2y
• (4x)/4 = (8/4) - (2y/4)

• You know that x = 2 - ½y .
• Your second equation, that you haven't yet altered, is 5x + 3y = 9 .
• In the second equation, replace x with "2 - ½y": 5(2 - ½y) + 3y = 9 .

• 5(2 - ½y) + 3y = 9
• 10 – (5/2)y + 3y = 9
• 10 – (5/2)y + (6/2)y = 9 (If you don't understand this step, learn how to add fractions . This is often, but not always, necessary for this method.)
• 10 + ½y = 9

• You know that y = -2
• One of the original equations is 4x + 2y = 8 . (You can use either equation for this step.)
• Plug in -2 instead of y: 4x + 2(-2) = 8 .

• If you end up with an equation that has no variables and isn't true (for instance, 3 = 5), the problem has no solution . (If you graphed both of the equations, you'd see they were parallel and never intersect.)
• If you end up with an equation without variables that is true (such as 3 = 3), the problem has infinite solutions . The two equations are exactly equal to each other. (If you graphed the two equations, you'd see they were the same line.)

Using the Elimination Method

• You have the system of equations 3x - y = 3 and -x + 2y = 4 .
• Let's change the first equation so that the y variable will cancel out. (You can choose x instead, and you'll get the same answer in the end.)
• The - y on the first equation needs to cancel with the + 2y in the second equation. We can make this happen by multiplying - y by 2.
• Multiply both sides of the first equation by 2, like this: 2(3x - y)=2(3) , so 6x - 2y = 6 . Now the - 2y will cancel out with the +2y in the second equation.

• Your equations are 6x - 2y = 6 and -x + 2y = 4 .
• Combine the left sides: 6x - 2y - x + 2y = ?
• Combine the right sides: 6x - 2y - x + 2y = 6 + 4 .

• You have 6x - 2y - x + 2y = 6 + 4 .
• Group the x and y variables together: 6x - x - 2y + 2y = 6 + 4 .
• Simplify: 5x = 10
• Solve for x: (5x)/5 = 10/5 , so x = 2 .

• You know that x = 2 , and one of your original equations is 3x - y = 3 .
• Plug in 2 instead of x: 3(2) - y = 3 .
• Solve for y in the equation: 6 - y = 3
• 6 - y + y = 3 + y , so 6 = 3 + y

• If your combined equation has no variables and is not true (like 2 = 7), there is no solution that will work on both equations. (If you graph both equations, you'll see they're parallel and never cross.)
• If your combined equation has no variables and is true (like 0 = 0), there are infinite solutions . The two equations are actually identical. (If you graph them, you'll see that they're the same line.)

Graphing the Equations

• The basic idea is to graph both equations, and find the point where they intersect. The x and y values at this point will give us the value of x and the value of y in the system of equations.

• Your first equation is 2x + y = 5 . Change this to y = -2x + 5 .
• Your second equation is -3x + 6y = 0 . Change this to 6y = 3x + 0 , then simplify to y = ½x + 0 .
• If both equations are identical , the entire line will be an "intersection". Write infinite solutions .

• If you don't have graph paper, use a ruler to make sure the numbers are spaced precisely apart.
• If you are using large numbers or decimals, you may need to scale your graph differently. (For example, 10, 20, 30 or 0.1, 0.2, 0.3 instead of 1, 2, 3).

• In our examples from earlier, one line ( y = -2x + 5 ) intercepts the y-axis at 5 . The other ( y = ½x + 0 ) intercepts at 0 . (These are points (0,5) and (0,0) on the graph.)
• Use different colored pens or pencils if possible for the two lines.

• In our example, the line y = -2x + 5 has a slope of -2 . At x = 1, the line moves down 2 from the point at x = 0. Draw the line segment between (0,5) and (1,3).
• The line y = ½x + 0 has a slope of ½ . At x = 1, the line moves up ½ from the point at x=0. Draw the line segment between (0,0) and (1,½).
• If the lines have the same slope , the lines will never intersect, so there is no answer to the system of equations. Write no solution .

• If the lines are moving toward each other, keep plotting points in that direction.
• If the lines are moving away from each other, move back and plot points in the other direction, starting at x = -1.
• If the lines are nowhere near each other, try jumping ahead and plotting more distant points, such as at x = 10.

Practice Problems and Answers

Community Q&A

• You can check your work by plugging the answers back into the original equations. If the equations end up true (for instance, 3 = 3), your answer is correct. Thanks Helpful 3 Not Helpful 1
• In the elimination method, you will sometimes have to multiply one equation by a negative number in order to get a variable to cancel out. Thanks Helpful 1 Not Helpful 1

• These methods cannot be used if there is a variable raised to an exponent, such as x 2 . For more information on equations of this type, look up a guide to factoring quadratics with two variables. [11] X Research source Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ https://www.mathsisfun.com/definitions/system-of-equations.html
• ↑ https://calcworkshop.com/systems-equations/substitution-method/
• ↑ https://www.cuemath.com/algebra/substitution-method/
• ↑ https://tutorial.math.lamar.edu/Classes/Alg/SystemsTwoVrble.aspx
• ↑ http://www.purplemath.com/modules/systlin2.htm
• ↑ http://www.virtualnerd.com/algebra-2/linear-systems/graphing/solve-by-graphing/equations-solution-by-graphing
• ↑ https://www.khanacademy.org/math/algebra/multiplying-factoring-expression/factoring-quadratics-in-two-vari/v/factoring-quadratics-with-two-variables

About This Article

To solve systems of algebraic equations containing two variables, start by moving the variables to different sides of the equation. Then, divide both sides of the equation by one of the variables to solve for that variable. Next, take that number and plug it into the formula to solve for the other variable. Finally, take your answer and plug it into the original equation to solve for the other variable. To learn how to solve systems of algebraic equations using the elimination method, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Jan 8, 2018

Did this article help you?

Jul 24, 2017

Kaurovandu Uozondo

Apr 19, 2018

Nahid Shafreen Shareef

Feb 12, 2018

May 15, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

4.1 Solve Systems of Linear Equations with Two Variables

Learning objectives.

By the end of this section, you will be able to:

• Determine whether an ordered pair is a solution of a system of equations
• Solve a system of linear equations by graphing
• Solve a system of equations by substitution
• Solve a system of equations by elimination
• Choose the most convenient method to solve a system of linear equations

Be Prepared 4.1

Before you get started, take this readiness quiz.

For the equation y = 2 3 x − 4 , y = 2 3 x − 4 , ⓐ Is ( 6 , 0 ) ( 6 , 0 ) a solution? ⓑ Is ( −3 , −2 ) ( −3 , −2 ) a solution? If you missed this problem, review Example 3.2 .

Be Prepared 4.2

Find the slope and y -intercept of the line 3 x − y = 12 . 3 x − y = 12 . If you missed this problem, review Example 3.16 .

Be Prepared 4.3

Find the x- and y -intercepts of the line 2 x − 3 y = 12 . 2 x − 3 y = 12 . If you missed this problem, review Example 3.8 .

Determine Whether an Ordered Pair is a Solution of a System of Equations

In Solving Linear Equations , we learned how to solve linear equations with one variable. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations .

System of Linear Equations

When two or more linear equations are grouped together, they form a system of linear equations .

In this section, we will focus our work on systems of two linear equations in two unknowns. We will solve larger systems of equations later in this chapter.

An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

A linear equation in two variables, such as 2 x + y = 7 , 2 x + y = 7 , has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.

To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) ( x , y ) that make both equations true. These are called the solutions of a system of equations .

Solutions of a System of Equations

The solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ) . ( x , y ) .

To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.

Example 4.1

Determine whether the ordered pair is a solution to the system { x − y = −1 2 x − y = −5 . { x − y = −1 2 x − y = −5 .

ⓐ ( −2 , −1 ) ( −2 , −1 ) ⓑ ( −4 , −3 ) ( −4 , −3 )

Determine whether the ordered pair is a solution to the system { 3 x + y = 0 x + 2 y = −5 . { 3 x + y = 0 x + 2 y = −5 .

ⓐ ( 1 , −3 ) ( 1 , −3 ) ⓑ ( 0 , 0 ) ( 0 , 0 )

Determine whether the ordered pair is a solution to the system { x − 3 y = −8 − 3 x − y = 4 . { x − 3 y = −8 − 3 x − y = 4 .

ⓐ ( 2 , −2 ) ( 2 , −2 ) ⓑ ( −2 , 2 ) ( −2 , 2 )

Solve a System of Linear Equations by Graphing

In this section, we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.

The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.

Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end of the section you’ll decide which method was the most convenient way to solve this system.

Example 4.2

How to solve a system of equations by graphing.

Solve the system by graphing { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Solve the system by graphing: { x − 3 y = −3 x + y = 5 . { x − 3 y = −3 x + y = 5 .

Solve the system by graphing: { − x + y = 1 3 x + 2 y = 12 . { − x + y = 1 3 x + 2 y = 12 .

The steps to use to solve a system of linear equations by graphing are shown here.

Solve a system of linear equations by graphing.

• Step 1. Graph the first equation.
• Step 2. Graph the second equation on the same rectangular coordinate system.
• Step 3. Determine whether the lines intersect, are parallel, or are the same line.
• If the lines intersect, identify the point of intersection. This is the solution to the system.
• If the lines are parallel, the system has no solution.
• If the lines are the same, the system has an infinite number of solutions.
• Step 5. Check the solution in both equations.

In the next example, we’ll first re-write the equations into slope–intercept form as this will make it easy for us to quickly graph the lines.

Example 4.3

Solve the system by graphing: { 3 x + y = − 1 2 x + y = 0 . { 3 x + y = − 1 2 x + y = 0 .

We’ll solve both of these equations for y y so that we can easily graph them using their slopes and y -intercepts.

Solve the system by graphing: { − x + y = 1 2 x + y = 10 . { − x + y = 1 2 x + y = 10 .

Solve the system by graphing: { 2 x + y = 6 x + y = 1 . { 2 x + y = 6 x + y = 1 .

In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

Example 4.4

Solve the system by graphing: { y = 1 2 x − 3 x − 2 y = 4 . { y = 1 2 x − 3 x − 2 y = 4 .

Solve the system by graphing: { y = − 1 4 x + 2 x + 4 y = − 8 . { y = − 1 4 x + 2 x + 4 y = − 8 .

Solve the system by graphing: { y = 3 x − 1 6 x − 2 y = 6 . { y = 3 x − 1 6 x − 2 y = 6 .

Sometimes the equations in a system represent the same line. Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. There are infinitely many solutions to the system.

Example 4.5

Solve the system by graphing: { y = 2 x − 3 − 6 x + 3 y = − 9 . { y = 2 x − 3 − 6 x + 3 y = − 9 .

If you write the second equation in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.

Solve the system by graphing: { y = − 3 x − 6 6 x + 2 y = − 12 . { y = − 3 x − 6 6 x + 2 y = − 12 .

Try It 4.10

Solve the system by graphing: { y = 1 2 x − 4 2 x − 4 y = 16 . { y = 1 2 x − 4 2 x − 4 y = 16 .

When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident . Coincident lines have the same slope and same y- intercept.

Coincident Lines

Coincident lines have the same slope and same y- intercept.

The systems of equations in Example 4.2 and Example 4.3 each had two intersecting lines. Each system had one solution.

In Example 4.5 , the equations gave coincident lines, and so the system had infinitely many solutions.

The systems in those three examples had at least one solution. A system of equations that has at least one solution is called a consistent system.

A system with parallel lines, like Example 4.4 , has no solution. We call a system of equations like this inconsistent. It has no solution.

Consistent and Inconsistent Systems

A consistent system of equations is a system of equations with at least one solution.

An inconsistent system of equations is a system of equations with no solution.

We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent, they each have their own set of solutions. Intersecting lines and parallel lines are independent.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines.

Let’s sum this up by looking at the graphs of the three types of systems. See below and Table 4.1 .

Example 4.6

Without graphing, determine the number of solutions and then classify the system of equations.

ⓐ { y = 3 x − 1 6 x − 2 y = 12 { y = 3 x − 1 6 x − 2 y = 12 ⓑ { 2 x + y = − 3 x − 5 y = 5 { 2 x + y = − 3 x − 5 y = 5

ⓐ We will compare the slopes and intercepts of the two lines.

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

ⓑ We will compare the slope and intercepts of the two lines.

A system of equations whose graphs are intersect has 1 solution and is consistent and independent.

Try It 4.11

ⓐ { y = −2 x − 4 4 x + 2 y = 9 { y = −2 x − 4 4 x + 2 y = 9 ⓑ { 3 x + 2 y = 2 2 x + y = 1 { 3 x + 2 y = 2 2 x + y = 1

Try It 4.12

ⓐ { y = 1 3 x − 5 x − 3 y = 6 { y = 1 3 x − 5 x − 3 y = 6 ⓑ { x + 4 y = 12 − x + y = 3 { x + 4 y = 12 − x + y = 3

Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.

Solve a System of Equations by Substitution

We will now solve systems of linear equations by the substitution method.

We will use the same system we used first for graphing.

We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.

Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!

After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.

Example 4.7

How to solve a system of equations by substitution.

Solve the system by substitution: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Try It 4.13

Solve the system by substitution: { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 .

Try It 4.14

Solve the system by substitution: { 2 x + y = −1 4 x + 3 y = 3 . { 2 x + y = −1 4 x + 3 y = 3 .

Solve a system of equations by substitution.

• Step 1. Solve one of the equations for either variable.
• Step 2. Substitute the expression from Step 1 into the other equation.
• Step 3. Solve the resulting equation.
• Step 4. Substitute the solution in Step 3 into either of the original equations to find the other variable.
• Step 5. Write the solution as an ordered pair.
• Step 6. Check that the ordered pair is a solution to both original equations.

Be very careful with the signs in the next example.

Example 4.8

Solve the system by substitution: { 4 x + 2 y = 4 6 x − y = 8 . { 4 x + 2 y = 4 6 x − y = 8 .

We need to solve one equation for one variable. We will solve the first equation for y .

Try It 4.15

Solve the system by substitution: { x − 4 y = −4 − 3 x + 4 y = 0 . { x − 4 y = −4 − 3 x + 4 y = 0 .

Try It 4.16

Solve the system by substitution: { 4 x − y = 0 2 x − 3 y = 5 . { 4 x − y = 0 2 x − 3 y = 5 .

Solve a System of Equations by Elimination

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For any expressions a, b, c, and d .

To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.

Notice how that works when we add these two equations together:

The y ’s add to zero and we have one equation with one variable.

Let’s try another one:

This time we don’t see a variable that can be immediately eliminated if we add the equations.

But if we multiply the first equation by −2 , −2 , we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2 . −2 .

Then rewrite the system of equations.

Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.

Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.

Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.

Example 4.9

How to solve a system of equations by elimination.

Solve the system by elimination: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Try It 4.17

Solve the system by elimination: { 3 x + y = 5 2 x − 3 y = 7 . { 3 x + y = 5 2 x − 3 y = 7 .

Try It 4.18

Solve the system by elimination: { 4 x + y = − 5 − 2 x − 2 y = − 2 . { 4 x + y = − 5 − 2 x − 2 y = − 2 .

The steps are listed here for easy reference.

Solve a system of equations by elimination.

• Step 1. Write both equations in standard form. If any coefficients are fractions, clear them.
• Decide which variable you will eliminate.
• Multiply one or both equations so that the coefficients of that variable are opposites.
• Step 3. Add the equations resulting from Step 2 to eliminate one variable.
• Step 4. Solve for the remaining variable.
• Step 5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
• Step 6. Write the solution as an ordered pair.
• Step 7. Check that the ordered pair is a solution to both original equations.

Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.

Example 4.10

Solve the system by elimination: { 4 x − 3 y = 9 7 x + 2 y = −6 . { 4 x − 3 y = 9 7 x + 2 y = −6 .

In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by different constants to get the opposites.

Try It 4.19

Solve the system by elimination: { 3 x − 4 y = − 9 5 x + 3 y = 14 . { 3 x − 4 y = − 9 5 x + 3 y = 14 .

Try It 4.20

Solve each system by elimination: { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 .

When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by the LCD of all the fractions in the equation.

Example 4.11

Solve the system by elimination: { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 . { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 .

In this example, both equations have fractions. Our first step will be to multiply each equation by the LCD of all the fractions in the equation to clear the fractions.

Try It 4.21

Solve each system by elimination: { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 . { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 .

Try It 4.22

Solve each system by elimination: { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 . { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 .

When we solved the system by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.

The same is true using substitution or elimination. If the equation at the end of substitution or elimination is a true statement, we have a consistent but dependent system and the system of equations has infinitely many solutions. If the equation at the end of substitution or elimination is a false statement, we have an inconsistent system and the system of equations has no solution.

Example 4.12

Solve the system by elimination: { 3 x + 4 y = 12 y = 3 − 3 4 x . { 3 x + 4 y = 12 y = 3 − 3 4 x .

This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.

After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.

Try It 4.23

Solve the system by elimination: { 5 x − 3 y = 15 y = − 5 + 5 3 x . { 5 x − 3 y = 15 y = − 5 + 5 3 x .

Try It 4.24

Solve the system by elimination: { x + 2 y = 6 y = − 1 2 x + 3 . { x + 2 y = 6 y = − 1 2 x + 3 .

Choose the Most Convenient Method to Solve a System of Linear Equations

When you solve a system of linear equations in in an application, you will not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

Example 4.13

For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

ⓐ { 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32 ⓑ { 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1

Since both equations are in standard form, using elimination will be most convenient.

Since one equation is already solved for y , using substitution will be most convenient.

Try It 4.25

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

ⓐ { 4 x − 5 y = −32 3 x + 2 y = −1 { 4 x − 5 y = −32 3 x + 2 y = −1 ⓑ { x = 2 y − 1 3 x − 5 y = −7 { x = 2 y − 1 3 x − 5 y = −7

Try It 4.26

ⓐ { y = 2 x − 1 3 x − 4 y = − 6 { y = 2 x − 1 3 x − 4 y = − 6 ⓑ { 6 x − 2 y = 12 3 x + 7 y = −13 { 6 x − 2 y = 12 3 x + 7 y = −13

Section 4.1 Exercises

Practice makes perfect.

In the following exercises, determine if the following points are solutions to the given system of equations.

{ 2 x − 6 y = 0 3 x − 4 y = 5 { 2 x − 6 y = 0 3 x − 4 y = 5

ⓐ ( 3 , 1 ) ( 3 , 1 ) ⓑ ( −3 , 4 ) ( −3 , 4 )

{ − 3 x + y = 8 − x + 2 y = −9 { − 3 x + y = 8 − x + 2 y = −9

ⓐ ( −5 , −7 ) ( −5 , −7 ) ⓑ ( −5 , 7 ) ( −5 , 7 )

{ x + y = 2 y = 3 4 x { x + y = 2 y = 3 4 x

ⓐ ( 8 7 , 6 7 ) ( 8 7 , 6 7 ) ⓑ ( 1 , 3 4 ) ( 1 , 3 4 )

{ 2 x + 3 y = 6 y = 2 3 x + 2 { 2 x + 3 y = 6 y = 2 3 x + 2 ⓐ ( −6 , 2 ) ( −6 , 2 ) ⓑ ( −3 , 4 ) ( −3 , 4 )

In the following exercises, solve the following systems of equations by graphing.

{ 3 x + y = −3 2 x + 3 y = 5 { 3 x + y = −3 2 x + 3 y = 5

{ − x + y = 2 2 x + y = −4 { − x + y = 2 2 x + y = −4

{ y = x + 2 y = −2 x + 2 { y = x + 2 y = −2 x + 2

{ y = x − 2 y = −3 x + 2 { y = x − 2 y = −3 x + 2

{ y = 3 2 x + 1 y = − 1 2 x + 5 { y = 3 2 x + 1 y = − 1 2 x + 5

{ y = 2 3 x − 2 y = − 1 3 x − 5 { y = 2 3 x − 2 y = − 1 3 x − 5

{ x + y = −4 − x + 2 y = −2 { x + y = −4 − x + 2 y = −2

{ − x + 3 y = 3 x + 3 y = 3 { − x + 3 y = 3 x + 3 y = 3

{ − 2 x + 3 y = 3 x + 3 y = 12 { − 2 x + 3 y = 3 x + 3 y = 12

{ 2 x − y = 4 2 x + 3 y = 12 { 2 x − y = 4 2 x + 3 y = 12

{ x + 3 y = −6 y = − 4 3 x + 4 { x + 3 y = −6 y = − 4 3 x + 4

{ − x + 2 y = −6 y = − 1 2 x − 1 { − x + 2 y = −6 y = − 1 2 x − 1

{ − 2 x + 4 y = 4 y = 1 2 x { − 2 x + 4 y = 4 y = 1 2 x

{ 3 x + 5 y = 10 y = − 3 5 x + 1 { 3 x + 5 y = 10 y = − 3 5 x + 1

{ 4 x − 3 y = 8 8 x − 6 y = 14 { 4 x − 3 y = 8 8 x − 6 y = 14

{ x + 3 y = 4 − 2 x − 6 y = 3 { x + 3 y = 4 − 2 x − 6 y = 3

{ x = −3 y + 4 2 x + 6 y = 8 { x = −3 y + 4 2 x + 6 y = 8

{ 4 x = 3 y + 7 8 x − 6 y = 14 { 4 x = 3 y + 7 8 x − 6 y = 14

{ 2 x + y = 6 − 8 x − 4 y = −24 { 2 x + y = 6 − 8 x − 4 y = −24

{ 5 x + 2 y = 7 − 10 x − 4 y = −14 { 5 x + 2 y = 7 − 10 x − 4 y = −14

{ y = 2 3 x + 1 − 2 x + 3 y = 5 { y = 2 3 x + 1 − 2 x + 3 y = 5

{ y = 3 2 x + 1 2 x − 3 y = 7 { y = 3 2 x + 1 2 x − 3 y = 7

{ 5 x + 3 y = 4 2 x − 3 y = 5 { 5 x + 3 y = 4 2 x − 3 y = 5

{ y = − 1 2 x + 5 x + 2 y = 10 { y = − 1 2 x + 5 x + 2 y = 10

{ 5 x − 2 y = 10 y = 5 2 x − 5 { 5 x − 2 y = 10 y = 5 2 x − 5

In the following exercises, solve the systems of equations by substitution.

{ 2 x + y = −4 3 x − 2 y = −6 { 2 x + y = −4 3 x − 2 y = −6

{ 2 x + y = −2 3 x − y = 7 { 2 x + y = −2 3 x − y = 7

{ x − 2 y = −5 2 x − 3 y = −4 { x − 2 y = −5 2 x − 3 y = −4

{ x − 3 y = −9 2 x + 5 y = 4 { x − 3 y = −9 2 x + 5 y = 4

{ 5 x − 2 y = −6 y = 3 x + 3 { 5 x − 2 y = −6 y = 3 x + 3

{ − 2 x + 2 y = 6 y = −3 x + 1 { − 2 x + 2 y = 6 y = −3 x + 1

{ 2 x + 5 y = 1 y = 1 3 x − 2 { 2 x + 5 y = 1 y = 1 3 x − 2

{ 3 x + 4 y = 1 y = − 2 5 x + 2 { 3 x + 4 y = 1 y = − 2 5 x + 2

{ 2 x + y = 5 x − 2 y = −15 { 2 x + y = 5 x − 2 y = −15

{ 4 x + y = 10 x − 2 y = −20 { 4 x + y = 10 x − 2 y = −20

{ y = −2 x − 1 y = − 1 3 x + 4 { y = −2 x − 1 y = − 1 3 x + 4

{ y = x − 6 y = − 3 2 x + 4 { y = x − 6 y = − 3 2 x + 4

{ x = 2 y 4 x − 8 y = 0 { x = 2 y 4 x − 8 y = 0

{ 2 x − 16 y = 8 − x − 8 y = −4 { 2 x − 16 y = 8 − x − 8 y = −4

{ y = 7 8 x + 4 − 7 x + 8 y = 6 { y = 7 8 x + 4 − 7 x + 8 y = 6

{ y = − 2 3 x + 5 2 x + 3 y = 11 { y = − 2 3 x + 5 2 x + 3 y = 11

In the following exercises, solve the systems of equations by elimination.

{ 5 x + 2 y = 2 − 3 x − y = 0 { 5 x + 2 y = 2 − 3 x − y = 0

{ 6 x − 5 y = −1 2 x + y = 13 { 6 x − 5 y = −1 2 x + y = 13

{ 2 x − 5 y = 7 3 x − y = 17 { 2 x − 5 y = 7 3 x − y = 17

{ 5 x − 3 y = −1 2 x − y = 2 { 5 x − 3 y = −1 2 x − y = 2

{ 3 x − 5 y = −9 5 x + 2 y = 16 { 3 x − 5 y = −9 5 x + 2 y = 16

{ 4 x − 3 y = 3 2 x + 5 y = −31 { 4 x − 3 y = 3 2 x + 5 y = −31

{ 3 x + 8 y = −3 2 x + 5 y = −3 { 3 x + 8 y = −3 2 x + 5 y = −3

{ 11 x + 9 y = −5 7 x + 5 y = −1 { 11 x + 9 y = −5 7 x + 5 y = −1

{ 3 x + 8 y = 67 5 x + 3 y = 60 { 3 x + 8 y = 67 5 x + 3 y = 60

{ 2 x + 9 y = −4 3 x + 13 y = −7 { 2 x + 9 y = −4 3 x + 13 y = −7

{ 1 3 x − y = −3 x + 5 2 y = 2 { 1 3 x − y = −3 x + 5 2 y = 2

{ x + 1 2 y = 3 2 1 5 x − 1 5 y = 3 { x + 1 2 y = 3 2 1 5 x − 1 5 y = 3

{ x + 1 3 y = −1 1 3 x + 1 2 y = 1 { x + 1 3 y = −1 1 3 x + 1 2 y = 1

{ 1 3 x − y = −3 2 3 x + 5 2 y = 3 { 1 3 x − y = −3 2 3 x + 5 2 y = 3

{ 2 x + y = 3 6 x + 3 y = 9 { 2 x + y = 3 6 x + 3 y = 9

{ x − 4 y = −1 − 3 x + 12 y = 3 { x − 4 y = −1 − 3 x + 12 y = 3

{ − 3 x − y = 8 6 x + 2 y = −16 { − 3 x − y = 8 6 x + 2 y = −16

{ 4 x + 3 y = 2 20 x + 15 y = 10 { 4 x + 3 y = 2 20 x + 15 y = 10

In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.

ⓐ { 8 x − 15 y = −32 6 x + 3 y = −5 { 8 x − 15 y = −32 6 x + 3 y = −5 ⓑ { x = 4 y − 3 4 x − 2 y = −6 { x = 4 y − 3 4 x − 2 y = −6

ⓐ { y = 7 x − 5 3 x − 2 y = 16 { y = 7 x − 5 3 x − 2 y = 16 ⓑ { 12 x − 5 y = −42 3 x + 7 y = −15 { 12 x − 5 y = −42 3 x + 7 y = −15

ⓐ { y = 4 x + 9 5 x − 2 y = −21 { y = 4 x + 9 5 x − 2 y = −21 ⓑ { 9 x − 4 y = 24 3 x + 5 y = −14 { 9 x − 4 y = 24 3 x + 5 y = −14

ⓐ { 14 x − 15 y = −30 7 x + 2 y = 10 { 14 x − 15 y = −30 7 x + 2 y = 10 ⓑ { x = 9 y − 11 2 x − 7 y = −27 { x = 9 y − 11 2 x − 7 y = −27

Writing Exercises

In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.

Solve the system of equations by substitution and explain all your steps in words: { 3 x + y = 12 x = y − 8 . { 3 x + y = 12 x = y − 8 .

Solve the system of equations by elimination and explain all your steps in words: { 5 x + 4 y = 10 2 x = 3 y + 27 . { 5 x + 4 y = 10 2 x = 3 y + 27 .

Solve the system of equations { x + y = 10 x − y = 6 { x + y = 10 x − y = 6

ⓐ by graphing ⓑ by substitution ⓒ Which method do you prefer? Why?

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-1-solve-systems-of-linear-equations-with-two-variables

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Linear Equations in Two Variables

A linear equation in two variables is an equation in which two variables have the exponent 1. A system of equations with two variables has a unique solution, no solutions, or infinitely many solutions. A linear system of equations may have 'n' number of variables. An important thing to keep in mind while solving linear equations with n number of variables is that there must be n equations to solve and determine the value of variables.

Linear equations in two variables are the algebraic equations which are of the form (or can be converted to the form) y = mx + b, where m is the slope and b is the y-intercept . They are the equations of the first order. For example, y = 2x + 3 and 2y = 4x + 9 are two-variable linear equations.

What are Linear Equations in Two Variables?

The linear equations in two variables are the equations in which each of the two variables is of the highest order ( exponent ) of 1 and may have one, none, or infinitely many solutions. The standard form of a two-variable linear equation is ax + by + c = 0 where x and y are the two variables. The solutions can also be written in ordered pairs like (x, y). The graphical representation of the pairs of linear equations in two variables includes two straight lines which could be:

• intersecting lines
• parallel lines or
• coincident lines .

Forms of Linear Equations in Two Variables

A linear equation in two variables can be in different forms like standard form , intercept form and point-slope form . For example, the same equation 2x + 3y=9 can be represented in each of the forms like 2x + 3y - 9=0 (standard form), y = (-2/3)x + 3 ( slope-intercept form ), and y - 5/3 = -2/3(x + (-2)) (point-slope form). Look at the image given below showing all these three forms of representing linear equations in two variables with examples.

The system of equations means the collection of equations and they are also referred to as simultaneous linear equations . We will learn how to solve pair of linear equations in two variables using different methods.

Solving Pairs of Linear Equations in Two Variables

There are five methods to solve pairs of linear equations in two variables as shown below:

• Graphical Method
• Substitution Method
• Cross Multiplication Method
• Elimination Method

Determinant Method

Graphical method for solving linear equations in two variables.

The steps to solve linear equations in two variables graphically are given below:

• Step 1 : To solve a system of two equations in two variables graphically , we graph each equation. To know how, click here or follow steps 2 and 3 below.
• Step 2 : To graph an equation manually, first convert it to the form y = mx+b by solving the equation for y.
• Step 3 : Start putting the values of x as 0, 1, 2, and so on and find the corresponding values of y, or vice-versa.
• Step 4 : Identify the point where both lines meet.
• Step 5 : The point of intersection is the solution of the given system.

Example: Find the solution of the following system of equations graphically.

Solution: We will graph them and see whether they intersect at a point. As you can see below, both lines meet at (1, 2). Thus, the solution of the given system of linear equations is x=1 and y=2.

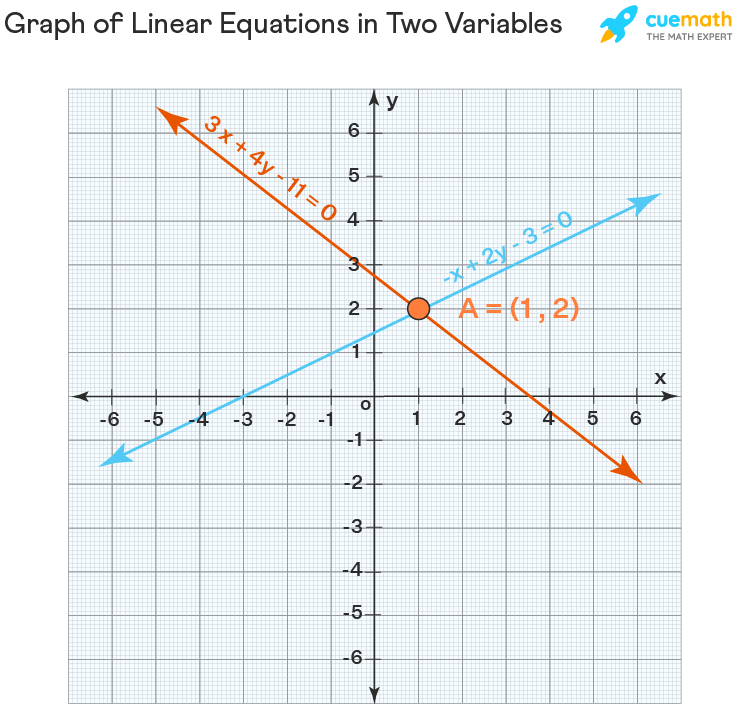
But both lines may not intersect always. Sometimes they may be parallel. In that case, the pairs of linear equations in two variables have no solution. In some other cases, both lines coincide with each other. In that case, each point on that line is a solution of the given system and hence the given system has an infinite number of solutions.

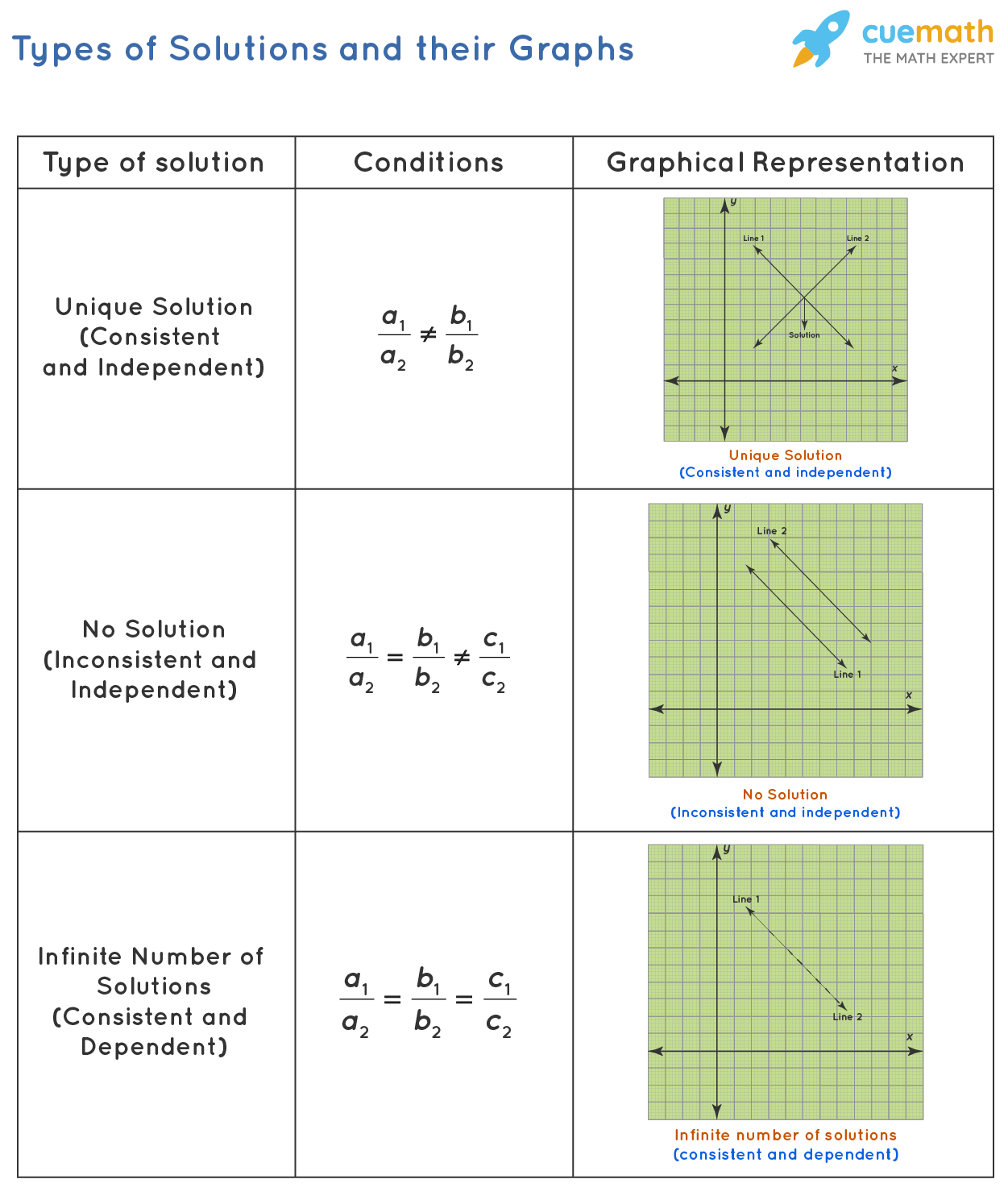
Consistent and Inconsistent System of Linear Equations:

• If the system has a solution, then it is said to be consistent;
• otherwise, it is said to be inconsistent.

Independent and Dependent System of Linear Equations:

• If the system has a unique solution, then it is independent.
• If it has an infinite number of solutions, then it is dependent. It means that one variable depends on the other.

Consider a system of two linear equations: a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0. Here we can understand when a linear system with two variables is consistent/inconsistent and independent/dependent.

Method of Substitution

To solve a system of two linear equations in two variables using the substitution method , we have to use the steps given below:

• Step 1: Solve one of the equations for one variable.
• Step 2: Substitute this in the other equation to get an equation in terms of a single variable.
• Step 3: Solve it for the variable.
• Step 4: Substitute it in any of the equations to get the value of another variable.

Example: Solve the following system of equations using the substitution method. x+2y-7=0 2x-5y+13=0

Solution: Let us solve the equation, x+2y-7=0 for y: x+2y-7=0 ⇒2y=7-x ⇒ y=(7-x)/2

Substitute this in the equation, 2x-5y+13=0:

2x-5y+13=0 ⇒ 2x-5((7-x)/2)+13=0 ⇒ 2x-(35/2)+(5x/2)+13=0 ⇒ 2x + (5x/2) = 35/2 - 13 ⇒ 9x/2 = 9/2 ⇒ x=1

Substitute x=1 this in the equation y=(7-x)/2:

y=(7-1)/2 = 3

Therefore, the solution of the given system is x=1 and y=3.

Consider a system of linear equations: a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0.

To solve this using the cross multiplication method , we first write the coefficients of each of x and y and constants as follows:

Here, the arrows indicate that those coefficients have to be multiplied. Now we write the following equation by cross-multiplying and subtracting the products. \(\dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}=\dfrac{y}{c_{1} a_{2}-c_{2} a_{1}}=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}}\)

From this equation, we get two equations:

\(\begin{align} \dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}} \\[0.2cm] \dfrac{y}{c_{1} a_{2}-c_{2} a_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}} \end{align}\)

Solving each of these for x and y, the solution of the given system is:

\(\begin{align} x&=\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\\[0.2cm] y&=\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}} \end{align}\)

Method of Elimination

To solve a system of linear equations in two variables using the elimination method , we will use the steps given below:

• Step 1: Arrange the equations in the standard form: ax+by+c=0 or ax+by=c.
• Step 2: Check if adding or subtracting the equations would result in the cancellation of a variable.
• Step 3: If not, multiply one or both equations by either the coefficient of x or y such that their addition or subtraction would result in the cancellation of any one of the variables.
• Step 4: Solve the resulting single variable equation.
• Step 5: Substitute it in any of the given equations to get the value of another variable.

Example: Solve the following system of equations using the elimination method. 2x+3y-11=0 3x+2y-9=0

Adding or subtracting these two equations would not result in the cancellation of any variable. Let us aim at the cancellation of x. The coefficients of x in both equations are 2 and 3. Their LCM is 6. We will make the coefficients of x in both equations 6 and -6 such that the x terms get canceled when we add the equations.

3 × (2x+3y-11=0) ⇒ 6x+9y-33=0 -2 × (3x+2y-9=0) ⇒ -6x-4y+18=0

Now we will add these two equations: 6x+9y-33=0 -6x-4y+18=0

On adding both the above equations we get, ⇒ 5y-15=0 ⇒ 5y=15 ⇒ y=3

Substitute this in one of the given two equations and solve the resultant variable for x. 2x+3y-11=0 ⇒ 2x+3(3)-11=0 ⇒ 2x+9-11=0 ⇒ 2x=2 ⇒ x=1

Therefore, the solution of the given system of equations is x=1 and y=3.

The determinant of a 2 × 2 matrix is obtained by cross-multiplying elements starting from the top left corner and subtracting the products.

Consider a system of linear equations in two variables: a 1 x + b 1 y = c 1 and a 2 x + b 2 y = c 2 . To solve them using the determinants method (which is also known as Crammer's Rule ), follow the steps given below:

• Step 1: We first find the determinant formed by the coefficients of x and y and label it Δ. Δ = \(\left|\begin{array}{ll}a_1 & b_1 \\a_2 & b_2\end{array}\right| = a_1 b_2 - a_2b_1\)
• Step 2: Then we find the determinant Δ x which is obtained by replacing the first column of Δ with constants. Δ x = \(\left|\begin{array}{ll}c_1 & b_1 \\c_2 & b_2\end{array}\right| = c_1 b_2 - c_2b_1\)
• Step 3: We then find the determinant Δ y which is obtained by replacing the second column of Δ with constants. Δ y = \(\left|\begin{array}{ll}a_1 & c_1 \\a_2 & c_2\end{array}\right| = a_1 c_2 - a_2c_1\)

Now, the solution of the given system of linear equations is obtained by the formulas:

• x = Δ x / Δ
• y = Δ y / Δ

Important Points on Linear Equations with Two Variables:

• A linear equation in two variables is of the form ax + by + c = 0, where x and y are variables; and a, b, and c are real numbers.
• A pair of linear equations are of the form a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0 and its solution is a pair of values (x, y) that satisfy both equations.
• To solve linear equations in two variables, we must have at least two equations.
• A linear equation in two variables has infinitely many solutions.

Tricks and Tips:

While solving the equations using either the substitution method or the elimination method:

• If we get an equation that is true (i.e., something like 0 = 0, -1 = -1, etc), then it means that the system has an infinite number of solutions.
• If we get an equation that is false (i.e., something like 0 = 2, 3 = -1, etc), then it means that the system has no solution.

☛Related Topics:

• Solving Linear Equations Calculator
• Equation Calculator
• System of Equations Calculator
• Linear Graph Calculator

Linear Equations in Two Variables Examples

Example 1: The sum of the digits of a two-digit number is 8. When the digits are reversed, the number is increased by 18. Find the number.

Solution: Let us assume that x and y are the tens digit and the ones digit of the required number. Then the number is 10x+y.

And the number when the digits are reversed is 10y+x.

The question says, "The sum of the digits of a two-digit number is 8".

So from this, we get a linear equation in two variables: x+y=8.

Also, when the digits are reversed, the number is increased by 18.

So, the equation is 10y+x =10x+y+18

⇒ 10(8-x)+x =10x+(8-x)+18 (by substituting the value of y) ⇒ 80-10x+x =10x+8-x+18 ⇒ 80-9x=9x+26 ⇒ 18x = 54 ⇒ x=3

Substituting x=3 in y=8-x, we get, ⇒ y = 8-3 = 5 ⇒ 10x+y=10(3)+5 =35 Answer: The required number is 35.

Example 2: Jake's piggy bank has 11 coins (only quarters or dimes) that have a total value of $1.85. How many dimes and quarters does the piggy bank has?

Solution: Let us assume that the number of dimes be x and the number of quarters be y in the piggy bank. Let us form linear equations in two variables based on the given information.

Since there are 11 coins in total, x+y=11 ⇒ y=11-x. We know that, 1 dime = 10 cents and 1 quarter = 25 cents. The total value of the money in the piggy bank is $1.85 (185 cents).

Thus we get the equation 10x + 25y = 185 ⇒ 10x + 25(11-x) = 185 (as y = 11-x) ⇒ 10x + 275 - 25x =185 ⇒ -15x +275 =185 ⇒ -15x=-90 ⇒ x = 6

Substitute this value of x in x+y=11. ⇒ y=11-6=5

Answer: Therefore, the number of dimes is 6 and the number of quarters is 5.

Example 3: In a river, a boat can travel 30 miles upstream in 2 hours. The same boat can travel 51 miles downstream in 3 hours. Find,

• What is the speed of the boat in still water?
• What is the speed of the current?

Solution: Let us assume that:

• the speed of the boat in still water = x miles per hour
• the speed of current = y miles per hour.

During upstream, the current pulls back the boat's speed and the speed of the boat upstream = (x-y). During downstream, the current's speed adds to the boat's speed and the speed of the boat downstream = (x+y).

Using the last two columns of the table, we can form a pair of linear equations in two variables: x-y=15 x+y=17

Adding both equations we get: 2x = 32 ⇒ x=16

Substitute x=16 in x+y=17 16+y= 17 y=1

Answer: Therefore, the speed of the boat is 16 miles per hour and the speed of the current is 1 mile per hour.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear Equations in Two Variables

go to slide go to slide

FAQs on Linear Equations in Two Variables

What is meant by linear equation in two variables.

A linear equation is an equation with degree 1. A linear equation in two variables is a type of linear equation in which there are 2 variables present. For example, 2x - y = 45, x+y =35, a-b = 45 etc.

How do you Identify Linear Equations in Two Variables?

We can identify a linear equation in two variables if it can be expressed in the form ax+by+ c = 0, consisting of two variables x and y and the highest degree of the given equation is 1.

Can You Solve a Pair of Linear Equations in Two Variables?

Yes, we can solve pair of linear equations in two variables using different methods and ensure there are two equations present in the given system of equations so as to obtain the values of variables. If there is one solution it means that the given lines are intersecting, if there is no solution possible, then it means that the given equations are of parallel lines. If there are infinitely many solutions possible, it means that the given equations are forming coincidental lines.

How to Graphically Represent a Pair of Linear Equations in Two Variables?

We can represent linear equations in two variables graphically using the steps given below:

• Step 1: A system of two equations in two variables can be solved graphically by graphing each equation by converting it to the form y=mx+b by solving the equation for y.
• Step 2: The points where both lines meet are identified.
• Step 3: The point of intersection is the solution of the given pair of linear equations in two variables.

How Does One Solve the System of Linear Equations in Two Variables?

We have different methods to solve the system of linear equations:

• Determinant or Matrix Method

How Many Solutions Does a Linear Equation with Two Variables Have?

Suppose we have a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0. The solutions of a linear equation with two variables are:

• One and unique if a 1 /a 2 ≠ b 1 /b 2
• None if a 1 /a 2 = b 1 /b 2 ≠ c 1 /c 2
• Infinitely many if a 1 /a 2 = b 1 /b 2 = c 1 /c 2

How is a Linear Inequality in Two Variables like a Linear Equation in Two Variables?

A linear inequality in two variables and a linear equation in two variables have the following things in common:

• The degree of a linear equation and linear inequality is always 1.
• Both of them can be solved graphically.
• The way to solve a linear inequality is the same as linear equations except that it is separated by an inequality symbol. But note that the inequality rules should be taken care of.

Chapter 6: Linear Equations in Two Variables

6.2: solving linear equations in two variables, learning objectives.

• Determine whether a given ordered pair is a solution of a given linear equation.
• Find solutions of a linear equation.
• Complete a table of solutions.
• Ordered pair solution : a solution written in the form [latex]\left (x,y\right )[/latex]

Finding Solutions of Linear Equations in Two Variables

When an equation has two variables, any solution will be an ordered pair with a value for each variable.

Solution to a Linear Equation in Two Variables

An ordered pair [latex]\left(x,y\right)[/latex] is a solution of the linear equation [latex]ax+by=c[/latex], if the equation is a true statement when the [latex]x[/latex]– and [latex]y[/latex]-values of the ordered pair are substituted into the equation.

Determine whether [latex](−2,4)[/latex] is a solution of the equation [latex]4y+5x=3[/latex].

Substitute [latex]x=−2[/latex] and [latex]y=4[/latex] into the equation:

[latex]\begin{array}{r}4y+5x=3\\4\left(4\right)+5\left(−2\right)=3\end{array}[/latex]

[latex]\begin{array}{r}16+\left(−10\right)=3\\6=3\end{array}[/latex]

The statement is not true, so [latex](−2,4)[/latex] is not a solution.

[latex](−2,4)[/latex] is not a solution of the equation [latex]4y+5x=3[/latex].

Determine which ordered pairs are solutions of the equation [latex]x+4y=8\text{:}[/latex]

1. [latex]\left(0,2\right)[/latex]

2. [latex]\left(2,-4\right)[/latex]

3. [latex]\left(-4,3\right)[/latex]

Substitute the [latex]x\text{- and }y\text{-values}[/latex] from each ordered pair into the equation and determine if the result is a true statement.

Determine which ordered pairs are solutions of the equation. [latex]y=5x - 1\text{:}[/latex]

1. [latex]\left(0,-1\right)[/latex]

2. [latex]\left(1,4\right)[/latex]

3. [latex]\left(-2,-7\right)[/latex]

Substitute the [latex]x\text{-}[/latex] and [latex]y\text{-values}[/latex] from each ordered pair into the equation and determine if it results in a true statement.

The video shows more examples of how to determine whether an ordered pair is a solution of a linear equation.

Complete a Table of Solutions

In the previous examples, we substituted the [latex]x\text{- and }y\text{-values}[/latex] of a given ordered pair to determine whether or not it was a solution of a given linear equation. But how do we find the ordered pairs if they are not given? One way is to choose a value for [latex]x[/latex] and then solve the equation for [latex]y[/latex]. Or, choose a value for [latex]y[/latex] and then solve for [latex]x[/latex].

Let’s consider the equation [latex]y=5x - 1[/latex]. The easiest value to choose for [latex]x[/latex] or [latex]y[/latex] is zero:

[latex]\begin{equation}\begin{aligned}y & =5x-1 \;\;\;\;\;\;\;\;\;\;\text{Substitute}\;x=0\\y & = 5(0)-1\\y & = -1\end{aligned}\end{equation}[/latex]      So, [latex]x=0,\;y=-1[/latex] is a solution, which as an ordered pair is [latex]\left (0,\,-1\right )[/latex].

[latex]\begin{equation}\begin{aligned}y & =5x-1 \;\;\;\;\;\;\;\;\;\text{Substitute}\;y=0\\0 & = 5x-1\;\;\;\;\;\;\;\;\;\text{Solve for}\;x\\1 & = 5x\\ \frac{1}{5} & =x\end{aligned}\end{equation}[/latex]      So, [latex]x=\frac{1}{5},\;y=0[/latex] is a solution, which as an ordered pair is [latex]\left (\frac{1}{5},\,0\right )[/latex].

We can continue to find more solutions by choosing different values of [latex]x[/latex] and [latex]y[/latex].

Suppose [latex]x=2[/latex]:

To find a third solution, we’ll let [latex]x=2[/latex] and solve for [latex]y[/latex].

We can write our solutions in a table:

We can find more solutions to the equation by substituting any value of [latex]x[/latex] or any value of [latex]y[/latex] and solving the resulting equation to get another ordered pair that is a solution. There are an infinite number of solutions for this equation.

Complete the table to find three solutions of the equation [latex]y=4x - 2\text{:}[/latex]

Substitute [latex]x=0,x=-1[/latex], and [latex]x=2[/latex] into [latex]y=4x - 2[/latex].

The results are summarized in the table.

Complete the table to find three solutions to the equation [latex]5x - 4y=20\text{:}[/latex]

To find a solution to a linear equation, we can choose any number we want to substitute into the equation for either [latex]x[/latex] or [latex]y[/latex]. We could choose [latex]1,100,-1,000, -\frac{4}{5}, 2.6[/latex], or any other value we want. But it’s a good idea to choose a number that’s easy to work with. We’ll usually choose [latex]0[/latex] as one of our values.

Find a solution to the equation [latex]3x+2y=6[/latex]

Find three solutions to the equation [latex]x - 4y=8[/latex].

So [latex]\left(0,-2\right),\left(8,0\right)[/latex], and [latex]\left(20,3\right)[/latex] are three solutions to the equation [latex]x - 4y=8[/latex].

Remember, there are an infinite number of solutions to each linear equation. Any ordered pair we find is a solution if it makes the equation true.

• Question ID 146941, 146929, 146928, 146927. Authored by : Lumen Learning. License : CC BY: Attribution
• Ex: Determine If An Ordered Pair is a Solution to a Linear Equation. Authored by : James Sousa (mathispower4u.com). Located at : https://youtu.be/pJtxugdFjEk . License : CC BY: Attribution
• Revised and adapted: Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Privacy Policy

A free service from Mattecentrum

Solving systems of equations in two variables

• System with two variables I
• System with two variables II
• System with two variables III

A system of a linear equation comprises two or more equations and one seeks a common solution to the equations. In a system of linear equations, each equation corresponds with a straight line corresponds and one seeks out the point where the two lines intersect.

Solve the following system of linear equations:

$$\left\{\begin{matrix} y=2x+4\\ y=3x+2\\ \end{matrix}\right.$$

Since we are seeking out the point of intersection, we may graph the equations:

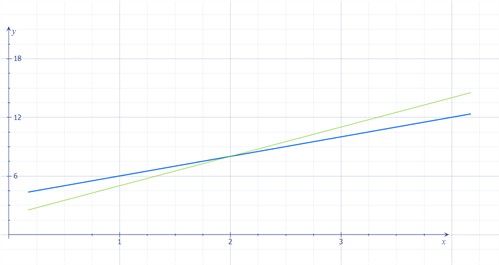
We see here that the lines intersect each other at the point x = 2, y = 8. This is our solution and we may refer to it as a graphic solution to the task.

But how does one reach a solution if the lines never intersect? One cannot, the system of equations have no solution.

One may also arrive at the correct answer with the help of the elimination method (also called the addition method or the linear combination method) or the substitution method.

When using the substitution method we use the fact that if two expressions y and x are of equal value x=y, then x may replace y or vice versa in another expression without changing the value of the expression.

Solve the systems of equations using the substitution method

We substitute the y in the top equation with the expression for the second equation:

$$\begin{array}{lcl} 2x+4 & = & 3x+2\\ 4-2 & = & 3x-2x\\ 2 & = & x\\ \end{array}$$

To determine the y -value, we may proceed by inserting our x -value in any of the equations. We select the first equation:

We plug in x=2 and get

$$y=2\cdot 2+4=8$$

We have thus arrived at precisely the same answer as in the graphic solution.

The elimination method requires us to add or subtract the equations in order to eliminate either x or y , often one may not proceed with the addition directly without first multiplying either the first or second equation by some value.

$$2x-2y=8$$

We now wish to add the two equations but it will not result in either x or y being eliminated. Therefore we must multiply the second equation by 2 on both sides and get:

$$2x+2y=2$$

Now we attempt to add our system of equations. We commence with the x -terms on the left, and the y -terms thereafter and finally with the numbers on the right side:

$$(2x+2x)+(-2y+2y)=8+2$$

The y -terms have now been eliminated and we now have an equation with only one variable:

$$x=\frac{10}{4}=2.5$$

Thereafter, in order to determine the y -value we insert x =2.5 in one of the equations. We select the first:

$$\begin{array}{lcl} 2\cdot 2.5-2y & = & 8\\ 5-8 & = & 2y\\ -3 & = & 2y\\ \frac{-3}{2} & = & y\\ y & = & -1.5\\ \end{array}$$

Video lesson

Solve the system of equations:

$$\left\{\begin{matrix} 2x-4y=0\\ -4x+4y=-4 \end{matrix}\right.$$

• Matrix properties
• Matrix operations
• Determinants
• Using matrices when solving system of equations
• Simplify expressions
• Polynomials
• Factoring polynomials
• Solving radical equations
• Complex numbers
• How to graph quadratic functions
• How to solve quadratic equations
• The Quadratic formula
• Standard deviation and normal distribution
• Distance between two points and the midpoint
• Equations of conic sections
• Basic knowledge of polynomial functions
• Remainder and factor theorems
• Roots and zeros
• Descartes' rule of sign
• Composition of functions
• Operate on rational expressions
• Exponential functions
• Logarithm and logarithm functions
• Logarithm property
• Arithmetic sequences and series
• Geometric sequences and series
• Binomial theorem
• Counting principle
• Permutations and combinations
• Probabilities
• Trigonometric functions
• Law of sines
• Law of cosines
• Circular functions
• Inverse functions
• Trigonometric identities
• Geometry Overview
• SAT Overview
• ACT Overview

How Do You Solve Two Equations with Two Variables?

Trying to solve two equations each with the same two unknown variables? Take one of the equations and solve it for one of the variables. Then plug that into the other equation and solve for the variable. Plug that value into either equation to get the value for the other variable. This tutorial will take you through this process of substitution step-by-step!

• substitution
• solve by substitution
• apply distributive property
• linear equation
• 2 equations 2 unknowns

Background Tutorials

Evaluating expressions.

What is a Variable?

You can't do algebra without working with variables, but variables can be confusing. If you've ever wondered what variables are, then this tutorial is for you!

Using the Distributive Property

How Do You Use the Distributive Property to Simplify an Expression?

In this tutorial you'll see how to apply the distributive property. Remember that this is important when you are trying to simplify an expression and get rid of parentheses!

Simplifying Expressions

How Do You Simplify an Expression?

Simplifying an algebraic expression is a fundamental part of solving math problems. Get some practice putting an expression in simplest form by following along with this tutorial.

Solving Two-Step Equations

How Do You Solve a Two-Step Equation?

Solving an equation for a variable? Perform the order of operations in reverse! Check it out in this tutorial.

Solving Systems by Graphing

How Do You Check Your Answer When You Have Two Equations?

Imagine you have two equations with two variables that you're trying to solve for, and someone hands you the answer. How do you know that the answer is right? After watching this tutorial you'll see exactly what it takes to check that the answer you have is correct for BOTH equations!

Further Exploration

Solving systems using substitution.

How Do You Solve a Word Problem Using Two Equations?

Sometimes word problems describe a system of equations, two equations each with two unknowns. Solving word problems like this one aren't so bad if you know what to do. Check it out with this tutorial!

Solving Systems Using Elimination

What Are the Ways You Can Solve a System of Linear Equations?

Knowing the definition of a system of equations is great, but you should also know how to solve them! This tutorial introduces you to the graphing method, substitution method, and elimination method for solving a system of equations. Take a look and learn them all!

• Terms of Use

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 4

• Two-variable linear equations intro
• Solutions to 2-variable equations
• Worked example: solutions to 2-variable equations
• Completing solutions to 2-variable equations

Complete solutions to 2-variable equations

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Online Systems of Equations Solver

Solve equations and systems of equations with wolfram|alpha, a powerful tool for finding solutions to systems of equations and constraints.

Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.

Learn more about:

• Systems of equations

Tips for entering queries

Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.

• solve y = 2x, y = x + 10
• solve system of equations {y = 2x, y = x + 10, 2x = 5y}
• y = x^2 - 2, y = 2 - x^2
• solve 4x - 3y + z = -10, 2x + y + 3z = 0, -x + 2y - 5z = 17
• solve system {x + 2y - z = 4, 2x + y + z = -2, z + 2y + z = 2}
• solve 4 = x^2 + y^2, 4 = (x - 2)^2 + (y - 2)^2
• x^2 + y^2 = 4, y = x
• View more examples

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

• Step-by-step solutions
• Wolfram Problem Generator

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 10^{1-x}=10^4
• \sqrt{3+x}=-2
• 6+11x+6x^2+x^3=0
• factor\:x^{2}-5x+6
• simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
• x+2y=2x-5,\:x-y=3
• How do you solve algebraic expressions?
• To solve an algebraic expression, simplify the expression by combining like terms, isolate the variable on one side of the equation by using inverse operations. Then, solve the equation by finding the value of the variable that makes the equation true.
• What are the basics of algebra?
• The basics of algebra are the commutative, associative, and distributive laws.
• What are the 3 rules of algebra?
• The basic rules of algebra are the commutative, associative, and distributive laws.
• What is the golden rule of algebra?
• The golden rule of algebra states Do unto one side of the equation what you do to others. Meaning, whatever operation is being used on one side of equation, the same will be used on the other side too.
• What are the 5 basic laws of algebra?
• The basic laws of algebra are the Commutative Law For Addition, Commutative Law For Multiplication, Associative Law For Addition, Associative Law For Multiplication, and the Distributive Law.

algebra-calculator

• High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables. In this blog post,...

Please add a message.

Message received. Thanks for the feedback.

Algebra › 2 equations, 2 unknowns

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.2: Solving Linear Systems with Two Variables

• Last updated
• Save as PDF
• Page ID 59867

Learning Objectives

• Solve linear systems using the substitution method.
• Solve linear systems using the elimination method.
• Identify the strengths and weaknesses of each method.

The Substitution Method

In this section, we review a completely algebraic technique for solving systems, the substitution method 11 . The idea is to solve one equation for one of the variables and substitute the result into the other equation. After performing this substitution step, we are left with a single equation with one variable, which can be solved using algebra.

Example \(\PageIndex{1}\):

Solve by substitution: \(\left\{ \begin{array} { l } { 2 x + y = - 3 } \\ { 3 x - 2 y = - 8 } \end{array} \right.\).

Solve for either variable in either equation. If you choose the first equation, you can isolate \(y\) in one step.

\(\begin{aligned} 2 x + y & = - 3 \\ y & = - 2 x - 3 \end{aligned}\)

Substitute the expression \(-2x-3\) for the variable \(y\) in the other equation.

\(3 x - 2 ( - \color{OliveGreen}{2 x - 3}\color{Black}{ )} = - 8\)

This leaves us with an equivalent equation with one variable, which can be solved using the techniques learned up to this point. Solve for the remaining variable.

\(\begin{aligned} 3 x - 2 ( \color{OliveGreen}{- 2 x - 3}\color{Black}{ )} & = - 8 \\ 3 x + 4 x + 6 & = - 8 \\ 7 x + 6 & = - 8 \\ 7 x & = - 14 \\ x & = - 2 \end{aligned}\)

Back substitute 12 to find the other coordinate. Substitute \(x = −2\) into either of the original equations or their equivalents. Typically, we use the equivalent equation that we found when isolating a variable in the first step.

\(\begin{aligned} y & = - 2 x - 3 \\ & = - 2 ( \color{OliveGreen}{- 2}\color{Black}{ )} - 3 \\ & = 4 - 3 \\ & = 1 \end{aligned}\)

Remember to present the solution as an ordered pair: \((−2, 1)\). Verify that these coordinates solve both equations of the original system:

The graph of this linear system follows:

The substitution method for solving systems is a completely algebraic method. Thus graphing the lines is not required.

\((-2, 1)\)

Example \(\PageIndex{2}\):

Solve by substitution: \(\left\{ \begin{array} { l } { 3 x - 5 y = 9 } \\ { 4 x + 2 y = - 1 } \end{array} \right.\).

It does not matter which variable we choose to isolate first. In this case, begin by solving for \(x\) in the first equation.

\(\begin{aligned} 3 x - 5 y & = 9 \\ 3 x & = 5 y + 9 \\ x & = \frac { 5 y + 9 } { 3 } \\ x & = \frac { 5 } { 3 } y + 3 \end{aligned}\)

\(\left\{ \begin{array} { c } { 3 x - 5 y = 9 \Longrightarrow \color{Cerulean}{x}\color{Black}{ =} \frac { 5 } { 3 } y + 3 } \\ { 4\color{Cerulean}{ x}\color{Black}{ +} 2 y = - 1 } \end{array} \right.\)

Next, substitute into the second equation and solve for \(y\).

\(\begin{aligned} 4 \left( \frac { 5 } { 3 } y + 3 \right) + 2 y & = - 1 \\ \frac { 20 } { 3 } y + 12 + 2 y & = - 1 \\ \frac { 26 } { 3 } y & = - 13 \\ y & = - 13 \left( \frac { 3 } { 26 } \right) \\ y & = - \frac { 3 } { 2 } \end{aligned}\)

Back substitute into the equation used in the substitution step:

\(\begin{aligned} x & = \frac { 5 } { 3 } y + 3 \\ & = \frac { 5 } { 3 } \left( \color{Cerulean}{- \frac { 3 } { 2 }} \right) + 3 \\ & = - \frac { 5 } { 2 } + 3 \\ & = \frac { 1 } { 2 } \end{aligned}\)

\(\left( \frac { 1 } { 2 } , - \frac { 3 } { 2 } \right)\)

Exercise \(\PageIndex{1}\)

Solve by substitution: \(\left\{ \begin{array} { l } { 5 x - 4 y = 3 } \\ { x + 2 y = 2 } \end{array} \right.\).

\(\left( 1 , \frac { 1 } { 2 } \right)\)

www.youtube.com/v/GzPhthhKeDA

As we know, not all linear systems have only one ordered pair solution. Next, we explore what happens when using the substitution method to solve a dependent system.

Example \(\PageIndex{3}\):

Solve by substitution: \(\left\{ \begin{array} { l } { - 5 x + y = - 1 } \\ { 10 x - 2 y = 2 } \end{array} \right.\).

Since the first equation has a term with coefficient \(1\), we choose to solve for that first.

\(\left\{ \begin{array} { l } { - 5 x + y = - 1 \quad \Rightarrow \quad \color{Cerulean}{y}\color{Black}{ =} 5 x - 1 } \\ { 10 x - 2\color{Cerulean}{ y}\color{Black}{ =} 2 } \end{array} \right.\)

Next, substitute this expression in for \(y\) in the second equation.

\(\begin{aligned} 10 x - 2 y & = 2 \\ 10 x - 2 ( \color{OliveGreen}{5 x - 1}\color{Black}{ )} & = 2 \\ 10 x - 10 x + 2 & = 2 \\ 2 & = 2\quad \color{Cerulean}{True} \end{aligned}\)

This process led to a true statement; hence the equation is an identity and any real number is a solution. This indicates that the system is dependent. The simultaneous solutions take the form \((x, mx + b)\), or in this case, \((x, 5x − 1)\), where \(x\) is any real number.

\(( x , 5 x - 1 )\)

To have a better understanding of the previous example, rewrite both equations in slope-intercept form and graph them on the same set of axes.

\(\left\{ \begin{array} { l } { - 5 x + y = - 1 } \\ { 10 x - 2 y = 2 } \end{array} \right. \Rightarrow \left\{ \begin{array} { l } { y = 5 x - 1 } \\ { y = 5 x - 1 } \end{array} \right.\)

We can see that both equations represent the same line, and thus the system is dependent. Now explore what happens when solving an inconsistent system using the substitution method.

Example \(\PageIndex{4}\):

Solve by substitution: \(\left\{ \begin{array} { l } { - 7 x + 3 y = 3 } \\ { 14 x - 6 y = - 16 } \end{array} \right.\).

Solve for \(y\) in the first equation.

\(\begin{aligned} - 7 x + 3 y & = 3 \\ - 7 x + 3 y & = 3 \\ 3 y & = 7 x + 3 \\ y & = \frac { 7 x + 3 } { 3 } \\ y & = \frac { 7 } { 3 } x + 1 \end{aligned}\)

\(\left\{ \begin{array} { l l } { - 7 x + 3 y = 3 } & { \Rightarrow \quad \color{Cerulean}{y}\color{Black}{ =} \frac { 7 } { 3 } x + 1 } \\ { 14 x - 6\color{Cerulean}{ y}\color{Black}{ =} - 16 } \end{array} \right. \)

Substitute into the second equation and solve.

\(\begin{aligned} 14 x - 6 y & = - 16 \\ 14x-6 \left( \color{OliveGreen}{\frac { 7 } { 3 } x + 1} \right) & = - 16 \\ 14x - \overset{\color{Cerulean}{2}}{\color{Black}{\cancel{6}}} \cdot \frac { 7 } { \underset{\color{Cerulean}{1}}{\cancel{3} }} x - 6 & = - 16 \\14 x - 14 x - 6 & = - 16 \\ - 6 &= - 16\quad\color{red}{False} \end{aligned}\)

Solving leads to a false statement. This indicates that the equation is a contradiction. There is no solution for \(x\) and hence no solution to the system.

\(\varnothing\)

A false statement indicates that the system is inconsistent, or in geometric terms, that the lines are parallel and do not intersect. To illustrate this, determine the slope-intercept form of each line and graph them on the same set of axes.

\(\left\{ \begin{array} { l l } { - 7 x + 3 y = 3 } \\ { 14 x - 6 y = - 16 } \end{array} \right. \Rightarrow \left\{ \begin{array} { l } { y = \frac { 7 } { 3 } x + 1 } \\ { y = \frac { 7 } { 3 } x + \frac { 8 } { 3 } } \end{array} \right.\)

In slope-intercept form, it is easy to see that the two lines have the same slope but different \(y\)-intercepts.

Exercise \(\PageIndex{2}\)

Solve by substitution: \(\left\{ \begin{array} { r } { 2 x - 5 y = 3 } \\ { 4 x - 10 y = 6 } \end{array} \right.\).

\(\left( x , \frac { 2 } { 5 } x - \frac { 3 } { 5 } \right)\)

www.youtube.com/v/JKX9M-L9Wow

The Elimination Method

In this section, the goal is to review another completely algebraic method for solving a system of linear equations called the elimination method 13 or addition method 14 . This method depends on the addition property of equations 15 : given algebraic expressions A, B, C, and D we have

\(\text{If} \:A = B \text { and } C = D , \text { then } A + C = B + D\)

We can add the equations together to eliminate the variable \(y\).

\(\begin{aligned} x \color{red}{+ y}\color{Black}{ =} 5 \\ \pm \frac { x \color{red}{- y} = 1 } { 2 x \:\:\:= \:\:\: 6 }\end{aligned}\)

This leaves us with a linear equation with one variable that can be easily solved:

\(\begin{aligned} 2 x & = 6 \\ x & = 3 \end{aligned}\)

At this point, we have the \(x\)-coordinate of the simultaneous solution, so all that is left to do is back substitute to find the corresponding \(y\)-value.

\(\begin{array} { r } { x + y = 5 } \\ { \color{OliveGreen}{3} \color{Black}{+} y = 5 } \\ { y = 2 } \end{array}\)

The solution to the system is \((3, 2)\). Of course, the variable is not always so easily eliminated. Typically, we have to find an equivalent system by applying the multiplication property of equality to one or both of the equations as a means to line up one of the variables to eliminate. The goal is to arrange that either the \(x\) terms or the \(y\) terms are opposites, so that when the equations are added, the terms eliminate.

Example \(\PageIndex{5}\):

Solve by elimination: \(\left\{ \begin{array} { l } { 5 x - 3 y = - 1 } \\ { 3 x + 2 y = 7 } \end{array} \right.\).

We choose to eliminate the terms with variable \(y\) because the coefficients have different signs. To do this, we first determine the least common multiple of the coefficients; in this case, the \(LCM(3, 2)\) is \(6\). Therefore, multiply both sides of both equations by the appropriate values to obtain coefficients of \(−6\) and \(6\). This results in the following equivalent system:

\(\left\{ \begin{array} { l l } { 5 x - 3 y = - 1 } & { \stackrel { x 2 } { \Rightarrow } } \\ { 3 x + 2 y = 7 } & { \stackrel { x3 } { \Rightarrow } } \end{array} \right. \left\{ \begin{array} { c } { 10 x - 6 y = - 2 } \\ { 9 x + 6 y = 21 } \end{array} \right.\)

The terms involving \(y\) are now lined up to eliminate. Add the equations together and solve for \(x\).

\(\begin{aligned} 10 x \color{red}{- 6 y} & \color{Black}{=} - 2 \\ + \quad 9 x \color{red}{+ 6 y} & \color{Black}{=} 21 \\ \hline 19 x & = 19 \\ x & = 1 \end{aligned}\)

Back substitute.

\(\begin{aligned} 3 x + 2 y & = 7 \\ 3 ( \color{OliveGreen}{1}\color{Black}{ )} + 2 y & = 7 \\ 3 + 2 y & = 7 \\ 2 y & = 4 \\ y & = 2 \end{aligned}\)

Therefore the simultaneous solution is \((1, 2)\). The check follows.

Sometimes linear systems are not given in standard form \(ax + by = c\). When this is the case, it is best to rearrange the equations before beginning the steps to solve by elimination. Also, we can eliminate either variable. The goal is to obtain a solution for one of the variables and then back substitute to find a solution for the other.

Example \(\PageIndex{6}\):

Solve by elimination: \(\left\{ \begin{aligned} 12 x + 5 y & = 11 \\ 3 x & = 4 y + 1 \end{aligned} \right.\).

First, rewrite the second equation in standard form.

\(\begin{aligned} 3 x & = 4 y + 1 \\ 3 x - 4 y & = 1 \end{aligned}\)

This results in an equivalent system in standard form, where like terms are aligned in columns.

\(\left\{ \begin{array} { c c } { 12 x + 5 y = 11 } \\ { 3 x = 4 y + 1 } \end{array} \right. \Rightarrow \left\{ \begin{array} { c } { 12 x + 5 y = 11 } \\ { 3 x - 4 y = 1 } \end{array} \right.\)

We can eliminate the term with variable \(x\) if we multiply the second equation by \(−4\).

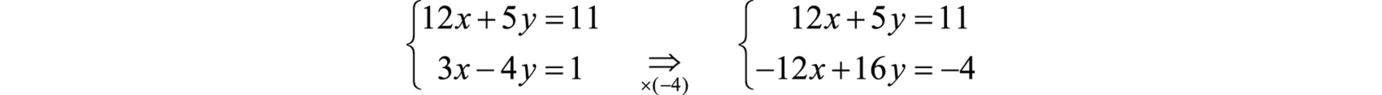
Next, we add the equations together,

\(\begin{aligned} \color{red}{12 x} \color{Black}{+5 y} & \color{Black}{=} 11 \\ + \quad \color{red}{-12x} \color{Black}{+ 16 y} & \color{Black}{=} -4 \\ \hline 21y & = 7 \\ y & = \frac{7}{21} = \frac{1}{3} \end{aligned}\)

\(\begin{array} { l } { 3 x = 4 y + 1 } \\ { 3 x = 4 \left( \color{OliveGreen}{\frac { 1 } { 3 }} \right) + 1 } \\ { 3 x = \frac { 4 } { 3 } + 1 } \\ { 3 x = \frac { 7 } { 3 } } \\ { x = \frac { 7 } { 3 } \cdot \frac { 1 } { 3 } } \\ { x = \frac { 7 } { 9 } } \end{array}\)

\(\left( \frac { 7 } { 9 } , \frac { 1 } { 3 } \right)\)

Exercise \(\PageIndex{3}\)

Solve by elimination: \(\left\{ \begin{array} { l } { 2 x + 5 y = 5 } \\ { 3 x + 2 y = - 9 } \end{array} \right.\).

\((-5, 3)\)

www.youtube.com/v/FX90hfggjbI

At this point, we explore what happens when solving dependent and inconsistent systems using the elimination method.

Example \(\PageIndex{7}\):

Solve by elimination: \(\left\{ \begin{array} { c } { 3 x - y = 7 } \\ { 6 x - 2 y = 14 } \end{array} \right.\).

To eliminate the variable \(x\), we could multiply the first equation by \(−2\).

Now adding the equations we have

\(\begin{aligned} -6 x + \color{red}{2 y} & \color{Black}{=} -14 \\ \pm \quad \color{black}{6x}- \color{red}{2 y} & \color{Black}{=} 14 \\ \hline 0 & = 0\quad\color{Cerulean}{True} \end{aligned}\)

A true statement indicates that this is a dependent system. The lines coincide, and we need \(y\) in terms of \(x\) to present the solution set in the form \((x, mx + b)\). Choose one of the original equations and solve for \(y\). Since the equations are equivalent, it does not matter which one we choose.

\(\begin{aligned} 3 x - y & = 7 \\ - y & = - 3 x + 7 \\ \color{Cerulean}{- 1}\color{Black}{ (} - y ) & = \color{Cerulean}{- 1}\color{Black}{ (} - 3 x + 7 ) \\ y & = 3 x - 7 \end{aligned}\)

\(( x , 3 x - 7 )\)

Exercise \(\PageIndex{4}\)

Solve by elimination: \(\left\{ \begin{array} { l } { 3 x + 15 y = - 15 } \\ { 2 x + 10 y = 30 } \end{array} \right.\).

No solution, \(\varnothing\)

www.youtube.com/v/E4B0lMLEliY

Given a linear system where the equations have fractional coefficients, it is usually best to clear the fractions before beginning the elimination method.

Example \(\PageIndex{8}\):

Solve: \(\left\{ \begin{array} { l } { - \frac { 1 } { 10 } x + \frac { 1 } { 2 } y = \frac { 4 } { 5 } } \\ { \frac { 1 } { 7 } x + \frac { 1 } { 3 } y = - \frac { 2 } { 21 } } \end{array} \right.\).

Recall that we can clear fractions by multiplying both sides of an equation by the least common multiple of the denominators (LCD). Take care to distribute and then simplify.

This results in an equivalent system where the equations have integer coefficients,

\(\left\{ \begin{array} { l l } { -\frac{1}{10} x + \frac{1}{2}y = \frac{4}{5} } & { \stackrel { x 10 } { \Rightarrow } } \\ { \frac{1}{7} x + \frac{1}{3} y = -\frac{2}{21} } & { \stackrel { x21 } { \Rightarrow } } \end{array} \right. \left\{ \begin{array} { c } { - x +5y = 8 } \\ { 3 x + 7 y = -2 } \end{array} \right.\)

Solve using the elimination method.

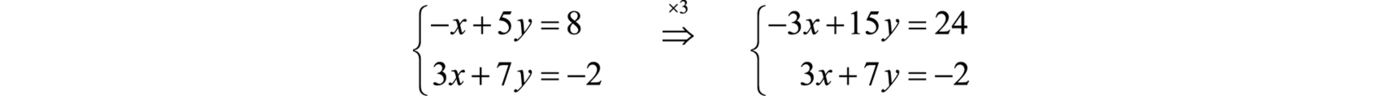
Figure \(\PageIndex{7}\)

\(\begin{aligned} \color{red}{-3 x} + \color{black}{15 y} & \color{Black}{=} 24 \\ \pm \quad \color{red}{3x}+ \color{black}{7 y} & \color{Black}{=} -2 \\ \hline 22y & = 22 \\ y&=1 \end{aligned}\)

\(\begin{aligned} 3 x + 7 y & = - 2 \\ 3 x + 7 ( \color{OliveGreen}{1}\color{Black}{ )} & = - 2 \\ 3 x + 7 & = - 2 \\ 3 x & = - 9 \\ x & = - 3 \end{aligned}\)

We can use a similar technique to clear decimals before solving.

Exercise \(\PageIndex{5}\)

Solve using elimination: \(\left\{ \begin{array} { l } { \frac { 1 } { 3 } x - \frac { 2 } { 3 } y = 3 } \\ { \frac { 1 } { 3 } x - \frac { 1 } { 2 } y = \frac { 8 } { 3 } } \end{array} \right.\).

\((5, -2)\)

www.youtube.com/v/ujlpeP7nakE

Summary of the Methods for Solving Linear Systems

We have reviewed three methods for solving linear systems of two equations with two variables. Each method is valid and can produce the same correct result. In this section, we summarize the strengths and weaknesses of each method.

The graphing method is useful for understanding what a system of equations is and what the solutions must look like. When the equations of a system are graphed on the same set of axes, we can see that the solution is the point where the graphs intersect. The graphing is made easy when the equations are in slope-intercept form. For example,

• \(\left\{ \begin{array} { l } { y = 5 x + 15 } \\ { y = - 5 x + 5 } \end{array} \right.\)

The simultaneous solution \((−1, 10)\) corresponds to the point of intersection. One drawback of this method is that it is very inaccurate. When the coordinates of the solution are not integers, the method is practically unusable. If we have a choice, we typically avoid this method in favor of the more accurate algebraic techniques.

The substitution method, on the other hand, is a completely algebraic method. It requires you to solve for one of the variables and substitute the result into the other equation. The resulting equation has one variable for which you can solve. This method is particularly useful when there is a variable within the system with coefficient of \(1\). For example,

\(\left\{ \begin{array} { l } { 10 x + y = 20 } \\ { 7 x + 5 y = 14 } \end{array} \right. \color{Cerulean}{Choose\: the\: substitution\: method.} \quad\)

In this case, it is easy to solve for \(y\) in the first equation and then substitute the result into the other equation. One drawback of this method is that it often leads to equivalent equations with fractional coefficients, which are tedious to work with. If there is not a coefficient of \(1\), then it usually is best to choose the elimination method.

The elimination method is a completely algebraic method which makes use of the addition property of equations. We multiply one or both of the equations to obtain equivalent equations where one of the variables is eliminated if we add them together. For example,

\(\left\{ \begin{array} { l } { 2 x - 3 y = 9 } \\ { 5 x - 8 y = - 16 } \end{array} \color{Cerulean}\:\:{Choose\: the\:elimination\: method.}\right. \quad\)

To eliminate the terms involving \(x\), we would multiply both sides of the first equation by \(5\) and both sides of the second equation by \(−2\). This results in an equivalent system where the variable \(x\) is eliminated when we add the equations together. Of course, there are other combinations of numbers that achieve the same result. We could even choose to eliminate the variable \(y\). No matter which variable is eliminated first, the solution will be the same. Note that the substitution method, in this case, would require tedious calculations with fractional coefficients. One weakness of the elimination method, as we will see later in our study of algebra, is that it does not always work for nonlinear systems.

Key Takeaways

• The substitution method requires that we solve for one of the variables and then substitute the result into the other equation. After performing the substitution step, the resulting equation has one variable and can be solved using the techniques learned up to this point.
• The elimination method is another completely algebraic method for solving a system of equations. Multiply one or both of the equations in a system by certain numbers to obtain an equivalent system where at least one variable in both equations have opposite coefficients. Adding these equivalent equations together eliminates that variable, and the resulting equation has one variable for which you can solve.
• It is a good practice to first rewrite the equations in standard form before beginning the elimination method.
• Solutions to systems of two linear equations with two variables, if they exist, are ordered pairs \((x, y)\).
• If the process of solving a system of equations leads to a false statement, then the system is inconsistent and there is no solution, \(Ø\).
• If the process of solving a system of equations leads to an identity, then the system is dependent and there are infinitely many solutions that can be expressed using the form \((x, mx + b)\).

Exercise \(\PageIndex{6}\)

Solve by substitution.

• \(\left\{ \begin{array} { l } { y = - 5 x + 1 } \\ { 4 x - 3 y = - 41 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x = 2 y - 3 } \\ { x + 3 y = - 8 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = x } \\ { 2 x + 3 y = 10 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = \frac { 1 } { 2 } x + \frac { 1 } { 3 } } \\ { x - 6 y = 4 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = 4 x + 1 } \\ { - 4 x + y = 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - 3 x + 5 } \\ { 3 x + y = 5 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = 2 x + 3 } \\ { 2 x - y = - 3 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = \frac { 2 } { 3 } x - 1 } \\ { 6 x - 9 y = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - 2 } \\ { - 2 x - y = - 6 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - \frac { 1 } { 5 } x + 3 } \\ { 7 x - 5 y = 9 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + y = 1 } \\ { 3 x - 5 y = 19 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x - y = 3 } \\ { - 2 x + 3 y = - 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x + y = 2 } \\ { 3 x - 2 y = 17 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x - 3 y = - 11 } \\ { 3 x + 5 y = - 5 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + 2 y = - 3 } \\ { 3 x - 4 y = - 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 5 x - y = 12 } \\ { 9 x - y = 10 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + 2 y = - 6 } \\ { - 4 x - 8 y = 24 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + 3 y = - 6 } \\ { - 2 x - 6 y = - 12 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 3 x + y = - 4 } \\ { 6 x - 2 y = - 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x - 5 y = - 10 } \\ { 2 x - 10 y = - 20 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 3 x - y = 9 } \\ { 4 x + 3 y = - 1 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x - y = 5 } \\ { 4 x + 2 y = - 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x - 5 y = 1 } \\ { 4 x + 10 y = 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 3 x - 7 y = - 3 } \\ { 6 x + 14 y = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 10 x - y = 3 } \\ { - 5 x + \frac { 1 } { 2 } y = 1 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - \frac { 1 } { 3 } x + \frac { 1 } { 6 } y = \frac { 2 } { 3 } } \\ { \frac { 1 } { 2 } x - \frac { 1 } { 3 } y = - \frac { 3 } { 2 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { 1 } { 3 } x + \frac { 2 } { 3 } y = 1 } \\ { \frac { 1 } { 4 } x - \frac { 1 } { 3 } y = - \frac { 1 } { 12 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { 1 } { 7 } x - y = \frac { 1 } { 2 } } \\ { \frac { 1 } { 4 } x + \frac { 1 } { 2 } y = 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - \frac { 3 } { 5 } x + \frac { 2 } { 5 } y = \frac { 1 } { 2 } } \\ { \frac { 1 } { 3 } x - \frac { 1 } { 12 } y = - \frac { 1 } { 3 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x = \frac { 2 } { 3 } y } \\ { x - \frac { 2 } { 3 } y = 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - \frac { 1 } { 2 } x + \frac { 1 } { 2 } y = \frac { 5 } { 8 } } \\ { \frac { 1 } { 4 } x + \frac { 1 } { 2 } y = \frac { 1 } { 4 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x - y = 0 } \\ { - x + 2 y = 3 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = 3 x } \\ { 2 x - 3 y = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 3 x + 4 y = 20 } \\ { 2 x + 8 y = 8 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 5 x - 3 y = - 1 } \\ { 3 x + 2 y = 7 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 3 x + 7 y = 2 } \\ { 2 x + 7 y = 1 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x = 5 } \\ { x = - 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = 4 } \\ { 5 y = 20 } \end{array} \right.\)

1. \((-2,11)\)

3. \((2,2)\)

5. \(\varnothing\)

7. \(( x , 2 x + 3 )\)

9. \(( 4 , - 2 )\)

11. \(( 3 , - 2 )\)

13. \(( 3 , - 4 )\)

15. \(\left( - \frac { 8 } { 5 } , - \frac { 7 } { 10 } \right)\)

17. \(\left( x , - \frac { 1 } { 2 } x - 3 \right)\)

19. \(\varnothing\)

21. \(( 2 , - 3 )\)

23. \(\left( \frac { 1 } { 2 } , 0 \right)\)

25. \(\varnothing\)

27. \(( 1,1 )\)

29. \(\left( - \frac { 11 } { 10 } , - \frac { 2 } { 5 } \right)\)

31. \(\left( - \frac { 1 } { 2 } , \frac { 3 } { 4 } \right)\)

33. \((0,0)\)

35. \((1, 2)\)

37. \(\varnothing\)

Exercise \(\PageIndex{7}\)

Solve by elimination.

• \(\left\{ \begin{array} { l } { 6 x + y = 3 } \\ { 3 x - y = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + y = 3 } \\ { 2 x - y = 9 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x - y = - 6 } \\ { 5 x + y = - 18 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + 3 y = 5 } \\ { - x - 2 y = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - x + 4 y = 4 } \\ { x - y = - 7 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - x + y = 2 } \\ { x - y = - 3 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 3 x - y = - 2 } \\ { 6 x + 4 y = 2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 5 x + 2 y = - 3 } \\ { 10 x - y = 4 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 2 x + 14 y = 28 } \\ { x - 7 y = 21 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 2 x + y = 4 } \\ { 12 x - 6 y = - 24 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + 8 y = 3 } \\ { 3 x + 12 y = 6 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x - 3 y = 15 } \\ { 4 x + 10 y = 14 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 4 x + 3 y = - 10 } \\ { 3 x - 9 y = 15 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 4 x - 5 y = - 3 } \\ { 8 x + 3 y = - 15 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 2 x + 7 y = 56 } \\ { 4 x - 2 y = - 112 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 9 x - 15 y = - 15 } \\ { 3 x + 5 y = - 10 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 6 x - 7 y = 4 } \\ { 2 x + 6 y = - 7 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 4 x + 2 y = 4 } \\ { - 5 x - 3 y = - 7 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 7 x + 3 y = 9 } \\ { 2 x + 5 y = - 14 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 9 x - 3 y = 3 } \\ { 7 x + 2 y = - 15 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 5 x - 3 y = - 7 } \\ { - 7 x + 6 y = 11 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x + 9 y = 8 } \\ { 3 x + 7 y = - 1 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x + 2 y = 5 } \\ { 3 x + 3 y = - 5 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 3 x + 6 y = - 12 } \\ { 2 x - 4 y = 8 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 25 x + 15 y = - 1 } \\ { 15 x + 10 y = - 1 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x - 3 y = 2 } \\ { 18 x - 12 y = 5 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - 2 x - 3 } \\ { - 3 x - 2 y = 4 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 28 x + 6 y = 9 } \\ { 6 y = 4 x - 15 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 x - 3 y = 9 } \\ { 5 x - 8 y = - 16 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x - \frac { 1 } { 3 } y = \frac { 1 } { 6 } } \\ { \frac { 5 } { 2 } x + y = \frac { 7 } { 2 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { 1 } { 4 } x - \frac { 1 } { 9 } y = 1 } \\ { x + y = \frac { 3 } { 4 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x - \frac { 1 } { 4 } y = \frac { 1 } { 3 } } \\ { \frac { 1 } { 4 } x + \frac { 1 } { 2 } y = - \frac { 19 } { 6 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - \frac { 14 } { 3 } x + 2 y = 4 } \\ { - \frac { 1 } { 3 } x + \frac { 1 } { 7 } y = \frac { 4 } { 21 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 0.025 x + 0.1 y = 0.5 } \\ { 0.11 x + 0.04 y = - 0.2 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 1.3 x + 0.1 y = 0.35 } \\ { 0.5 x + y = - 2.75 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + y = 5 } \\ { 0.02 x + 0.03 y = 0.125 } \end{array} \right.\)

1. \(\left( \frac { 1 } { 3 } , 1 \right)\)

3. \((-4,2)\)

5. \((-8,-1)\)

7. \(\left( - \frac { 1 } { 3 } , 1 \right)\)

9. \(\varnothing\)

11. \(\left( 1 , \frac { 1 } { 4 } \right)\)

13. \((-1,-2)\)

15. \((-28,0)\)

17. \(\left( - \frac { 1 } { 2 } , - 1 \right)\)

19. \((1,2)\)

21. \((-1,-4)\)

23. \((-5,2)\)

25. \(\left( x , \frac { 1 } { 2 } x - 2 \right)\)

27. \(\left( - \frac { 3 } { 10 } , - \frac { 13 } { 15 } \right)\)

29. \(\left( \frac { 3 } { 4 } , - 2 \right)\)

31. \((120,77)\)

33. \(\left( 3 , - \frac { 9 } { 4 } \right)\)

35. \(\varnothing\)

37. \(( 0.5 , - 3 )\)

Exercise \(\PageIndex{8}\)

Solve using any method.

• \(\left\{ \begin{array} { l } { 6 x = 12 y + 7 } \\ { 6 x + 24 y + 5 = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = 2 x - 3 } \\ { 3 x + y = 12 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { x + 3 y = - 5 } \\ { y = \frac { 1 } { 3 } x + 5 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = 1 } \\ { x = - 4 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = \frac { 1 } { 2 } } \\ { x + 9 = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = x } \\ { - x + y = 1 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = 5 x } \\ { y = - 10 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - \frac { 3 } { 2 } x + 1 } \\ { - 2 y + 2 = 3 x } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 7 y = - 2 x - 1 } \\ { 7 x = 2 y + 23 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 5 x + 9 y - 14 = 0 } \\ { 3 x + 2 y - 5 = 0 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - \frac { 5 } { 16 } x + 10 } \\ { y = \frac { 5 } { 16 } x - 10 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - \frac { 6 } { 5 } x + 12 } \\ { x = 6 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 ( x - 3 ) + y = 0 } \\ { 3 ( 2 x + y - 1 ) = 15 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 3 - 2 ( x - y ) = - 3 } \\ { 4 x - 3 ( y + 1 ) = 8 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 2 ( x + 1 ) = 3 ( 2 y - 1 ) - 21 } \\ { 3 ( x + 2 ) = 1 - ( 3 y - 2 ) } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { x } { 2 } - \frac { y } { 3 } = - 7 } \\ { \frac { x } { 3 } - \frac { y } { 2 } = - 8 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - \frac { 1 } { 7 } x + y = - \frac { 2 } { 3 } } \\ { - \frac { 1 } { 14 } x + \frac { 1 } { 2 } y = \frac { 1 } { 3 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { x } { 4 } - \frac { y } { 2 } = \frac { 3 } { 4 } } \\ { \frac { x } { 3 } + \frac { y } { 6 } = \frac { 1 } { 6 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { y = - \frac { 5 } { 3 } x + \frac { 1 } { 2 } } \\ { \frac { 1 } { 3 } x + \frac { 1 } { 5 } y = \frac { 1 } { 10 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { \frac { 1 } { 15 } x - \frac { 1 } { 12 } y = \frac { 1 } { 3 } } \\ { - \frac { 3 } { 10 } x + \frac { 3 } { 8 } y = - \frac { 3 } { 2 } } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 0.2 x - 0.05 y = 0.43 } \\ { 0.3 x + 0.1 y = - 0.3 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 0.1 x + 0.3 y = 0.3 } \\ { 0.05 x - 0.5 y = - 0.63 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { 0.15 x - 0.25 y = - 0.3 } \\ { - 0.75 x + 1.25 y = - 4 } \end{array} \right.\)
• \(\left\{ \begin{array} { l } { - 0.15 x + 1.25 y = 0.4 } \\ { - 0.03 x + 0.25 y = 0.08 } \end{array} \right.\)

1. \(\left( \frac { 1 } { 2 } , - \frac { 1 } { 3 } \right)\)

3. \(\left( - 10 , \frac { 5 } { 3 } \right)\)

5. \(\left( - 9 , \frac { 1 } { 2 } \right)\)

7. \(( - 2 , - 10 )\)

9. \(( 3 , - 1 )\)

11. \(( 32,0 )\)

13. \(( x , - 2 x + 6 )\)

15. \(( - 4,3 )\)

17. \(\varnothing\)

19. \(\left( x - \frac { 5 } { 3 } x + \frac { 1 } { 2 } \right)\)

21. \(( 0.8 , - 5.4 )\)

23. \(\varnothing\)

Exercise \(\PageIndex{9}\)

• Explain to a beginning algebra student how to choose a method for solving a system of two linear equations. Also, explain what solutions look like and why.
• Make up your own linear system with two variables and solve it using all three methods. Explain which method was preferable in your exercise.

1. Answer may vary

11 A means of solving a linear system by solving for one of the variables and substituting the result into the other equation.

12 Once a value is found for a variable, substitute it back into one of the original equations, or its equivalent, to determine the corresponding value of the other variable.

13 A means of solving a system by adding equivalent equations in such a way as to eliminate a variable.

14 Often used when referring to the elimination method for solving systems.

15 If \(A, B, C\), and \(D\) are algebraic expressions, where \(A = B\) and \(C = D\), then \(A + C = B + D\).