how to solve a logarithmic equation

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics
• Exponents and Logarithms

How to Solve Logarithms

Last Updated: March 17, 2024 Fact Checked

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 251,762 times.

Logarithms might be intimidating, but solving a logarithm is much simpler once you realize that logarithms are just another way to write out exponential equations. Once you rewrite the logarithm into a more familiar form, you should be able to solve it as you would solve any standard exponential equation.

Before You Begin: Learn to Express a Logarithmic Equation Exponentially [1] X Research source [2] X Research source

• If and only if: b y = x
• b does not equal 1
• In the same equation, y is the exponent and x is the exponential expression that the logarithm is set equal to.

• Example: 1024 = ?

• This could also be written as: 4 5

• Example: 4 5 = 1024

Method One: Solve for X

• log 3 ( x + 5) + 6 - 6 = 10 - 6
• log 3 ( x + 5) = 4

• Comparing this equation to the definition [ y = log b (x) ], you can conclude that: y = 4; b = 3; x = x + 5
• Rewrite the equation so that: b y = x
• 3 4 = x + 5

• 3 * 3 * 3 * 3 = x + 5
• 81 - 5 = x + 5 - 5

• Example: x = 76

Method Two: Solve for X Using the Logarithmic Product Rule [3] X Research source [4] X Research source

• log b (m * n) = log b (m) + log b (n)

• log 4 (x + 6) + log 4 (x) = 2 - log 4 (x) + log 4 (x)
• log 4 (x + 6) + log 4 (x) = 2

• log 4 [(x + 6) * x] = 2
• log 4 (x 2 + 6x) = 2

• Comparing this equation to the definition [ y = log b (x) ], you can conclude that: y = 2; b = 4 ; x = x 2 + 6x
• 4 2 = x 2 + 6x

• 4 * 4 = x 2 + 6x
• 16 = x 2 + 6x
• 16 - 16 = x 2 + 6x - 16
• 0 = x 2 + 6x - 16
• 0 = (x - 2) * (x + 8)
• x = 2; x = -8

• Example: x = 2
• Note that you cannot have a negative solution for a logarithm, so you can discard x - 8 as a solution.

Method Three: Solve for X Using the Logarithmic Quotient Rule [5] X Research source

• log b (m / n) = log b (m) - log b (n)

• log 3 (x + 6) - log 3 (x - 2) = 2 + log 3 (x - 2) - log 3 (x - 2)
• log 3 (x + 6) - log 3 (x - 2) = 2

• log 3 [(x + 6) / (x - 2)] = 2

• Comparing this equation to the definition [ y = log b (x) ], you can conclude that: y = 2; b = 3; x = (x + 6) / (x - 2)
• 3 2 = (x + 6) / (x - 2)

• 3 * 3 = (x + 6) / (x - 2)
• 9 = (x + 6) / (x - 2)
• 9 * (x - 2) = [(x + 6) / (x - 2)] * (x - 2)
• 9x - 18 = x + 6
• 9x - x - 18 + 18 = x - x + 6 + 18
• 8x / 8 = 24 / 8

• Example: x = 3

Community Q&A

You Might Also Like

• ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut43_logfun.htm#logdef
• ↑ https://www.mathsisfun.com/algebra/logarithms.html
• ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut46_logeq.htm
• ↑ https://www.youtube.com/watch?v=fnhFneOz6n8
• ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut44_logprop.htm

About This Article

To solve a logarithm, start by identifying the base, which is "b" in the equation, the exponent, which is "y," and the exponential expression, which is "x." Then, move the exponential expression to one side of the equation, and apply the exponent to the base by multiplying the base by itself the number of times indicated in the exponent. Finally, rewrite your final answer as an exponential expression. To learn how to solve for "x" in a logarithm, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Nov 13, 2023

Did this article help you?

May 1, 2019

Ayush Shukla

Mar 26, 2023

May 19, 2017

Aishat Mujitaba

Apr 29, 2018

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

Module 12: Exponential and Logarithmic Equations and Models

Logarithmic equations, learning outcomes.

• Solve a logarithmic equation algebraically.
• Solve a logarithmic equation graphically.
• Use the one-to-one property of logarithms to solve a logarithmic equation.
• Solve a radioactive decay problem.

We have already seen that every logarithmic equation [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex] is equal to the exponential equation [latex]{b}^{y}=x[/latex]. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation [latex]{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3[/latex]. To solve this equation, we can use rules of logarithms to rewrite the left side as a single log and then apply the definition of logs to solve for [latex]x[/latex]:

[latex]\begin{array}{l}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3\hfill & \hfill \\ \text{ }{\mathrm{log}}_{2}\left(2\left(3x - 5\right)\right)=3\hfill & \text{Apply the product rule of logarithms}.\hfill \\ \text{ }{\mathrm{log}}_{2}\left(6x - 10\right)=3\hfill & \text{Distribute}.\hfill \\ \text{ }{2}^{3}=6x - 10\hfill & \text{Convert to exponential form}.\hfill \\ \text{ }8=6x - 10\hfill & \text{Calculate }{2}^{3}.\hfill \\ \text{ }18=6x\hfill & \text{Add 10 to both sides}.\hfill \\ \text{ }x=3\hfill & \text{Divide both sides by 6}.\hfill \end{array}[/latex]

A General Note: Using the Definition of a Logarithm to Solve Logarithmic Equations

For any algebraic expression S and real numbers b and c , where [latex]b>0,\text{ }b\ne 1[/latex],

[latex]{\mathrm{log}}_{b}\left(S\right)=c\text{ if and only if }{b}^{c}=S[/latex]

Example: Using Algebra to Solve a Logarithmic Equation

Solve [latex]2\mathrm{ln}x+3=7[/latex].

[latex]\begin{array}{l}2\mathrm{ln}x+3=7\hfill & \hfill \\ \text{}2\mathrm{ln}x=4\hfill & \text{Subtract 3 from both sides}.\hfill \\ \text{}\mathrm{ln}x=2\hfill & \text{Divide both sides by 2}.\hfill \\ \text{}x={e}^{2}\hfill & \text{Rewrite in exponential form}.\hfill \end{array}[/latex]

Solve [latex]6+\mathrm{ln}x=10[/latex].

[latex]x={e}^{4}[/latex]

Example: Using Algebra Before and After Using the Definition of the Natural Logarithm

Solve [latex]2\mathrm{ln}\left(6x\right)=7[/latex].

[latex]\begin{array}{l}2\mathrm{ln}\left(6x\right)=7\hfill & \hfill \\ \text{}\mathrm{ln}\left(6x\right)=\frac{7}{2}\hfill & \text{Divide both sides by 2}.\hfill \\ \text{}6x={e}^{\left(\frac{7}{2}\right)}\hfill & \text{Use the definition of }\mathrm{ln}.\hfill \\ \text{}x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}\hfill & \text{Divide both sides by 6}.\hfill \end{array}[/latex]

Solve [latex]2\mathrm{ln}\left(x+1\right)=10[/latex].

[latex]x={e}^{5}-1[/latex]

Example: Using a Graph to Understand the Solution to a Logarithmic Equation

Solve [latex]\mathrm{ln}x=3[/latex].

[latex]\begin{array}{l}\mathrm{ln}x=3\hfill & \hfill \\ x={e}^{3}\hfill & \text{Use the definition of }\mathrm{ln}\text{.}\hfill \end{array}[/latex]

Below is a graph of the equation. On the graph the x -coordinate of the point where the two graphs intersect is close to 20. In other words [latex]{e}^{3}\approx 20[/latex]. A calculator gives a better approximation: [latex]{e}^{3}\approx 20.0855[/latex].

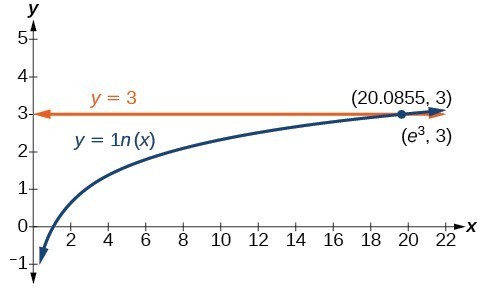
The graphs of [latex]y=\mathrm{ln}x[/latex] and y = 3 cross at the point [latex]\left(e^3,3\right)[/latex] which is approximately (20.0855, 3).

Use a graphing calculator to estimate the approximate solution to the logarithmic equation [latex]{2}^{x}=1000[/latex] to 2 decimal places.

[latex]x\approx 9.97[/latex]

Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers x  > 0, S  > 0, T  > 0 and any positive real number b , where [latex]b\ne 1[/latex],

[latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex]

For example,

[latex]\text{If }{\mathrm{log}}_{2}\left(x - 1\right)={\mathrm{log}}_{2}\left(8\right),\text{then }x - 1=8[/latex]

So if [latex]x - 1=8[/latex], then we can solve for x  and we get x  = 9. To check, we can substitute x  = 9 into the original equation: [latex]{\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3[/latex]. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.

For example, consider the equation [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex]. To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm and then apply the one-to-one property to solve for x :

[latex]\begin{array}{l}\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{3x - 2}{2}\right)=\mathrm{log}\left(x+4\right)\hfill & \text{Apply the quotient rule of logarithms}.\hfill \\ \text{}\frac{3x - 2}{2}=x+4\hfill & \text{Apply the one-to-one property}.\hfill \\ \text{}3x - 2=2x+8\hfill & \text{Multiply both sides of the equation by }2.\hfill \\ \text{}x=10\hfill & \text{Subtract 2}x\text{ and add 2}.\hfill \end{array}[/latex]

To check the result, substitute x  = 10 into [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex].

[latex]\begin{array}{l}\mathrm{log}\left(3\left(10\right)-2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(\left(10\right)+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(28\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(14\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{28}{2}\right)=\mathrm{log}\left(14\right)\hfill & \text{The solution checks}.\hfill \end{array}[/latex]

A General Note: Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

For any algebraic expressions S and T and any positive real number b , where [latex]b\ne 1[/latex],

Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.

How To: Given an equation containing logarithms, solve it using the one-to-one property

• Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation is of the form [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T[/latex].
• Use the one-to-one property to set the arguments equal to each other.
• Solve the resulting equation, S =  T , for the unknown.

Example: Solving an Equation Using the One-to-One Property of Logarithms

Solve [latex]\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)[/latex].

[latex]\begin{array}{l}\text{ }\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)\hfill & \hfill \\ \text{ }{x}^{2}=2x+3\hfill & \text{Use the one-to-one property of the logarithm}.\hfill \\ \text{ }{x}^{2}-2x - 3=0\hfill & \text{Get zero on one side before factoring}.\hfill \\ \left(x - 3\right)\left(x+1\right)=0\hfill & \text{Factor using FOIL}.\hfill \\ \text{ }x - 3=0\text{ or }x+1=0\hfill & \text{If a product is zero, one of the factors must be zero}.\hfill \\ \text{ }x=3\text{ or }x=-1\hfill & \text{Solve for }x.\hfill \end{array}[/latex]

Analysis of the Solution

There are two solutions: x  = 3 or x  = –1. The solution x  = –1 is negative, but it checks when substituted into the original equation because the argument of the logarithm function is still positive.

Solve [latex]\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}1[/latex].

[latex]x=1[/latex] or [latex]x=–1[/latex]

Contribute!

Improve this page Learn More

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Question ID 14406. Authored by : Sousa, James. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Question ID 122911. Authored by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL

Forgot password? New user? Sign up

Existing user? Log in

Solving Logarithmic Equations

Already have an account? Log in here.

Equations involving logarithms and unknown variables can often be solved by employing the definition of the logarithm, as well as several of its basic properties :

\( \log_x(a) + \log_x(b) = \log_x(ab) \)

\(\log_x(a) - \log_x(b) = \log_x\big(\frac ab\big) \)

\(a\log_x(b) = \log_x(b^a) \)

\(\log_x(a) = \frac{\log_y(a)}{\log_y(x)} = \frac1{\log_a(x)}\) for any positive real number \(y \)

\(x^{\log_x(a)} = a\).

Common mistakes to watch out for include

\(\log_x(a) \cdot \log_x(b) \neq \log_x(ab) \)

\(\frac{\log_x(a)}{\log_x(b)} \neq \log_x\big(\frac{a}{b}\big)\).

The general strategy is to consolidate the logarithms using these properties, and then to take both sides of the equation to the appropriate power in order to eliminate the logarithms if possible.

Solving Logarithmic Equations - Basic

Solving logarithmic equations - intermediate.

For many equations with logarithms, solving them is simply a matter of using the definition of \( \log x \) to eliminate logarithms from the equation and convert it into a polynomial or exponential equation.

Find \( x \) if \( \log_2(3x+1) = 4 \). By the definition of the logarithm, \[\begin{align} 3x+1 &= 2^4 \\&= 16 \\ 3x &= 15 \\ x &= 5.\ _\square \end{align}\]

Another way to view this solution is that we took \( 2 \) to the power of the left side and got \( 3x+1 \), and took \( 2 \) to the power of the right side and got \( 2^4 = 16 \). More complicated logarithmic equations are often simplified by exponentiating both sides.

If \(\log_{8}m + \log_{8}\frac{1}{6}=\frac{2}{3}\), then what is \(m?\)

Other equations can be simplified using other properties of logarithms. One difficulty that arises is that eliminating logarithms and solving the resulting equation can introduce spurious solutions. These solutions violate the principle that the argument of the log function must always be positive. It is generally wise to check solutions by plugging them into the original equation and making sure that both sides are defined.

Find all \( x\) such that \( \log_3(x-12) +\log_3(x-6) = 3. \) Simplify the given equation as follows: \[\begin{align} \log_3(x-12) + \log_3(x-6) &=3 \\ \log_3\big((x-12)(x-6)\big) &= 3\\ (x-12)(x-6) &= 27 \\ x^2-18x-45 &=0\\ (x-15)(x-3) &= 0. \end{align}\] This produces two potential solutions \( x=3, x=15\). But note that \( x = 3 \) is not an actual solution, as \( \log_3(3-12) \) is undefined. The only actual solution is \( x=15 \). \(_\square\)

The step in the solution above that was not reversible was the first one: although \( (x-12)(x-6)\) is positive if \( x =3\), \( x-12 \) and \( x-6\) are not themselves positive.

Find all real solutions \(x\) to

\[3\log_2(x) - 1 = \log_2\left(\frac32 x-1\right).\]

Enter your answer as the sum of all such \( x \).

More complicated logarithmic equations often involve more than one base. It can help to introduce unknowns to solve for the logarithms first. Another useful identity is \( \log_x(y) = \frac{\log_z(y)}{\log_z(x)} \), especially since \( z\) can be chosen to be whatever simplifies the problem.

Suppose \( a,b\) are positive real numbers such that \[\log_a(10)+\log_b(100) = \log_{ab}(1000000).\] Show that \( a = b \) or \( a^2=b \). Rewrite this as \[\frac{\log(10)}{\log(a)} + \frac{\log(100)}{\log(b)} = \frac{\log(1000000)}{\log(ab)},\] where the logs are all to the base \( 10 \). This simplifies to \[\frac1{\log(a)}+\frac2{\log(b)} = \frac6{\log(ab)}.\] Let \( m = \log(a) \) and \( n = \log(b) \). Then \(\log(ab) = m+n\), so \[\begin{align} \frac1{m}+\frac2{n} &= \frac6{m+n} \\ n+2m &= \frac{6mn}{m+n} \\ (2m+n)(m+n) &= 6mn \\ 2m^2+3mn+n^2 &= 6mn \\ 2m^2-3mn+n^2 &= 0 \\ (2m-n)(m-n) &= 0. \end{align}\] So \( m=n\) or \( 2m=n\). In the first case, \( \log(a)=\log(b) \), so \( a=b\). In the second case, \( 2\log(a) = \log(b) \), so \( \log(a^2)=\log(b) \), so \(a^2=b \). \(_\square \)

The sum of all (positive) solutions of the equation

\[\log_{16}x +\log _x 16=\log_{512} x + \log_x {512}\]

can be written as \( \frac{a}{b} \), where \(a\) and \(b\) are coprime positive integers. What are the last three digits of \(a+b\)?

Equations involving exponents can often be simplified by taking logarithms:

Solve for \( x \) if \[\left( \frac{x}2 \right)^{\log_2(x)} = 8x.\] Take \(\log_2\) of both sides: \[\begin{align} \log_2\left(\left(\frac{x}2 \right)^{\log_2(x)}\right) &= \log_2(8x) \\ \log_2(x)\log_2\left(\frac x2\right) &= \log_2(x)+3 \\ \log_2(x)\big(\log_2(x)-1\big) &= \log_2(x)+3, \end{align}\] and substituting \( y = \log_2(x) \) turns this into \( y(y-1)=y+3\), or \( y^2-2y-3 = 0 \). So \( y = 3 \) or \( y = -1 \), which leads to \( x = 8 \) or \( x = \frac 12 \). \(_\square\)

What is the sum of all possible real values of \(x\) that satisfies the equation \(x^{\log_{5} x} = \frac{x^3}{25}?\)

Logarithms can also make computation easier in certain practical situations. For example, logarithms with base \(10\) give information about the number of decimal digits in a number.

Given that \[\begin{align} \log_{10}(2) &= 0.3010299\ldots \\ \log_{10}(3) &= 0.4771212\ldots \\ \log_{10}(7) &= 0.8450980\ldots, \end{align}\] which is bigger, \( 12^{50} \) or \( 7^{64} \)? How many decimal digits do these two numbers have? Compute \[\begin{align} \log_{10}\big(2^{100}3^{50}\big) &= 100\log_{10}(2)+50\log_{10}(3) \\ &= 30.10299\ldots + 23.85656\ldots \\ &= 53.9595\ldots \\\\ \log_{10}\big(7^{64}\big) &= 64\log_{10}(7) \\ &= 64(0.8450980\ldots) \\ &= 54.0862\ldots. \end{align}\] So \( 7^{64} \) is bigger. The number of decimal digits of \( x \) is \( \lfloor \log_{10}(x) \rfloor +1 \), so \( 2^{100}3^{50} \) has \( 54 \) digits and \( 7^{64} \) has \( 55 \) digits. \(_\square\)

Note that this is much easier than multiplying the numbers and comparing them directly. For applications that require large numbers (such as RSA encryption ), this is very important.

Find the number of digits in \(\Large 9^{9^{2}}\).

Note : You may use the fact that \(\log_{10} 3 = 0.4771\) correct up to 4 decimal places.

Problem Loading...

Note Loading...

Set Loading...

The Ultimate Guide to Solving Logarithmic Equations in Algebra

• The Albert Team
• Last Updated On: March 1, 2022

Equations containing variables in logarithmic expressions are called logarithmic equations (sometimes shortened as “log equations”). Solving logarithmic equations can be easy and entertaining if you are aware of the principal methods and different scenarios. Here, we’ll provide a comprehensive guide on the most efficient methods to solve log equations.

Type 1 Logarithmic Equations

The simplest logarithmic equations are equations of the form

where the base of the logarithm, b, is a positive number, b ≠ 1. For any real value of the variable x, this equation has a single solution:

For example, the log equation

only has one solution:

Consider logarithmic equations of the form

This can be simplified by using the change of base formula for logarithms:

This results in

can be written in the following form:

This has the solution

Type 2 Logarithmic Equations

Consider a slightly more complicated logarithmic equation:

Here, again, the base of the logarithm, b, is a positive number, b ≠ 1, and f(x) is some elementary algebraic function. This equation can be solved by introducing a new variable, t = f(x), defined as

Thus, we can write the following general solution for this equation:

Let’s illustrate this idea with examples.

Say we want to solve the following logarithmic equation:

We substitute the following variable:

This turns the equation into a standard form:

Thus, we have a quadratic equation for the variable x:

We can easily determine the roots of this quadratic equation, which are also the solutions of the original logarithmic equation:

Consider the following log equation:

This can be solved after applying the change of base formula:

We must also substitute a new variable:

For the variable t, we have

This results in t = 10. Thus, we obtain

Both roots of this algebraic equation are solutions to the original logarithmic equation:

This method also works if f(x) is a logarithmic function by itself. For example, consider the equation

As usual, we can introduce a new variable t, according to the following equation:

Then, t is a solution to the simple log equation

which can be solved easily:

The variable x also becomes the solution to a simple log equation:

Finally, we can find the solution:

Type 3 Logarithmic Equations

Next, we will investigate how to solve log equations of the form

where f(x) and h(x) are some elementary algebraic functions, and b is a positive number, b ≠ 1. This log equation is equivalent to the algebraic equation

We should also remember that the domain of any logarithmic function is nonnegative, real numbers. Thus, among all the solutions to the equation f(x) = h(x), we should only select solutions that satisfy one of the following conditions:

This guarantees that the logarithmic functions are well-defined.

As an example, let us consider the equation

Among all the roots of this equation, which can be defined as

Only those that satisfy the condition

can be solutions of the original logarithmic equation. Hence, roots x 1 and x 2 should be rejected, and the only solution is

If we take into account that

We can rewrite this log equation as

Applying the method described for this type of logarithmic equation, we obtain

This equation is equivalent to

This has a single solution:

Obviously, this solution satisfies the condition x > 0.

The method we are now investigating only requires a slight modification if the logarithmic expressions on both sides of the log equation have different bases:

where both a and b are positive numbers, a ≠ 1 and b ≠1. We can rewrite the left-hand side of this equation in the form

Thus, we have

Then, the log equation in question is again equivalent to the following algebraic equation:

Pay attention to the fact that both of the following conditions must be satisfied in this case:

To illustrate, consider the log equation

Using the change of base formula, we have

Thus, we can write

This results in the following algebraic equation:

Further, remember that both initial logarithmic functions are defined only in the region

Thus, between the two roots of the quadratic equation

only x = 2 is a solution to the original log equation.  

Type 4 Logarithmic Equations

A more challenging class of logarithmic equations are equations of the form

where b is a positive number, b ≠ 1, and

These are some algebraic functions (some of them can be constant numbers).

Solving logarithmic equations of this type is equivalent to solving the following system of algebraic equations:

For example, consider the following log equation:

As we have just discussed, to solve this logarithmic equation, we have to solve

Among the two roots of the quadratic equation,

only the second one satisfies the above inequalities. Thus, the only solution of the given logarithmic equation is

Based on our general consideration that solving this logarithmic equation is equivalent to solving a mixed system of algebraic equations,

These, in turn, are equivalent to the system

Both roots of the quadratic equation,

satisfy the inequality x > 1/3. Thus, both roots are solutions of the logarithmic equation.

Consider the following equation:

This belongs to the same class of logarithmic equations. It is not difficult to observe that it can be written in the form

This equation is equivalent to a mixed system of algebraic equations:

The quadratic equation can be written in the form

This has two roots:

We can easily verify that the first root, x 1 = – 1, does not satisfy the inequality 2 x + 1 > 0, while the second root, x 2 = 1/2, satisfies both inequalities. Thus,

This is the only solution to the logarithmic equation in question.

If we encounter a problem with fractions of logarithms, most likely, the log equation can be transformed into the same standard form. For example, if we need to solve

First, we note that

This is the range for which the variable x is valid. Next, rewrite the equation in the form

Thus, the logarithmic equation under investigation becomes an algebraic equation:

This can be solved easily:

Finally, the only root satisfying the condition x > 0 is

Type 5 Logarithmic Equations

Finally, we will learn how to solve logarithmic equations of the form

Here, h(x) is some logarithmic function and F(u) is an elementary algebraic function. In this case, we can introduce a new variable t = h(x) and solve:

be the n real numbers that are solutions to the algebraic equation F(t) = 0. Then, to solve the original logarithmic equation, we have to find solutions to the following system of n algebraic equations:

Using the fact that

we can write this log equation in the following form:

For the auxiliary variable

we obtain a simple algebraic equation:

This has the following roots:

Thus, we have to solve two logarithmic equations:

This is quite an easy task. The corresponding solutions are

These are both in the range of validity for the logarithmic function, x > 0.

Consider another logarithmic equation:

we can rewrite this equation in the form

Now, we introduce a new variable:

This is the solution of the equation

After some simple algebraic transformations, we obtain

Thus, we have to solve the following log equations:

The obvious solutions are

Although this log equation seems quite different from those we have considered so far, we will now show how it can be solved using the same methods.

First, since the base of a logarithm can only be a positive number not equal to unity, the domain of validity for the variable x can be expressed as

Now, we can use a change of base formula for logarithms to express log x 3 in terms of log 3 x:

Analogously, we can write

The original logarithmic equation now transforms into an equation of standard form:

This can be solved by the following substitution:

The equation in terms of the variable t takes the form:

We can easily find the corresponding roots:

Thus, we have two log equations:

These are extremely easy to solve, yielding the following results:

Both solutions are in the valid range for the variable x.

Hopefully, this review article has improved your understanding of how to solve logarithmic equations in algebra. If you work through the wide range of examples presented here, you will be prepared to solve logarithmic equations of any difficulty. Best of luck!

Looking for Algebra practice?

Kickstart your Algebra prep with Albert. Start your Algebra exam prep today .

Interested in a school license?​

Popular posts.

AP® Score Calculators

Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides

The ultimate review guides for AP® subjects to help you plan and structure your prep.

Core Subject Review Guides

Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator

See how scores on each section impacts your overall SAT® score

ACT® Score Calculator

See how scores on each section impacts your overall ACT® score

Grammar Review Hub

Comprehensive review of grammar skills

AP® Posters

Download updated posters summarizing the main topics and structure for each AP® exam.

Interested in a school license?

Bring Albert to your school and empower all teachers with the world's best question bank for: ➜ SAT® & ACT® ➜ AP® ➜ ELA, Math, Science, & Social Studies aligned to state standards ➜ State assessments Options for teachers, schools, and districts.

How To Solve Logarithmic Equations

Step By Step Video and practice Problems

more interesting facts

How To Solve Logarithmic Equations Video

What is the general strategy for solving log equations?

Answer: As the video above points out, there are two main types of logarithmic equations. Before you to decide how to solve an equation, you must determine whether the equation

• A) has a logarithm on one side and a number on the other
• B) whether it has logarithms on both sides

Example 1 Logarithm on one side and a number on the other

$$ log_4 x + log_4 8 = 3 $$

Step 1 Rewrite log side as single logarithm

$$ log_4 8x = 3 $$

Step 2 Rewrite as exponential equation

$$ 4^ 3 = 8x $$

Step 3 Solve the exponential equation

64 = 8x 8 = x

Example 2 Logarithm on both sides

Step 1 use the rules of logarithms to rewrite the left side and the right side of the equation to a single logarithm

Step 2 "cancel" the log

Step 3 solve the expression

Let's look at a specific ex $$ log_5 x + log_2 3 = log_5 6 $$

Step 1 rewrite both sides as single logs

$$ log_5 x + log_5 2 = log_5 6 \\ log_5 2x = log_5 6 $$

Step 2 "cancel" logs

$$ \color{Red}{ \cancel {log_5}} 2x = \color{Red}{ \cancel {log_5}} 6 \\ 2x = 6 $$

Step 2 Solve expression

Practice Problems

Solve the following equation: $ log_3 5 + log_3 x = log_3 15 $

Follow the steps for solving logarithmic equations with logs on both sides

rewrite both sides as single logs

$$ log_3 5x = log_3 15 $$

"cancel" logs

$$ \color{Red}{ \cancel{log_3}} 5x = \color{Red}{ \cancel{log_3}} 15 \\ 5x=15 $$

Solve expression

Solve the equation below: $ log_3 9 + log_3 x = 4 $

Follow the steps for solving logarithmic equations with a log on one side

Rewrite log side as single logarithm

$$ log_3 9x = 4$$

Rewrite as exponential equation

$$ 3^4 = 9x $$

Solve exponential equation

81 = 9 x 9 = x

Solve the following equation: $ 2log_3 5 + log_3 x = 3log_3 $

Follow the steps on how to solve equations with logs on both sides

rewrite both sides as single logs<

$ log_3 5^2 + log_3 x = log_3 5^3 \\ log_3 25 +log_3 x = log_3 125 \\ log_3 25x = log_3 125 $

$ \color{Red}{ \cancel{log_3}} 25x = \color{Red}{ \cancel{log_3}} 125 \\ 25x = 125 $

Solve the equation below: $ 2 log_2 4 + log_2 x = 5 $

$ 2 log_2 4 + log_2 x = 5 \\ log_2 4^2 = log_2 x = 5 \\ log_2 16 + log_2 x = 5 \\ log_2 16x = 5 $

32 =16x 2 = x

Solve the following equation: $ 2 log_3 5 + log_3 x = 3 log_3 5 $

$ log_3 5^2 + log_3 x + log_3 5^3 \\ log_3 25x + log_3 125 $

log 3 25x = log 3 5 3

$ \color{Red}{ \cancel{log_3}} 25x + \color{Red}{ \cancel{log_3}} 125 \\ 25x=125 $

$ \frac{25x}{25} = \frac{125}{25} \\ $

Solve the following equation: $2 log_3 7 - log_3 2x = log_3 98$

$ 2 log_3 7 - log_3 2x = log_3 98 \\ log_3 7^2 - log_3 2x = log_3 98 \\ log_3 49 - log_3 2x = log_3 98 \\ log_3 \frac{49}{2x} = log_3 98 $

$ \color{Red}{ \cancel{log_3}} \frac{49}{2x} = \color{Red}{ \cancel{log_3}} 98 \\ \frac{49}{2x} = 98 $

$ 49 = 196x \\ \frac{49}{196} = x \\ x = 49 $

Solve the following equation: $ 2 log_11 5 + log_11 x + log_11 2 = log_11 150 $

You know the deal. Just follow the steps for solving logarithmic equations with logs on both sides

rewrite as single logs

$ 2 log_11 5 + log_11 x + log_11 2 = log_11 150 \\ log_11 5^2 + log_11 2x = log_11 150 \\ log_11 25 + log_11 2x = log_11 150 \\ log_11 50x= log_11 150 $

2log 11 5 + log 11 x+ log 11 2 = log 11 150

$ \color{Red}{ \cancel{log_1}} 50x = \color{Red}{ \cancel{log_11}} 150 \\ 50x = 150 $

Ultimate Math Solver (Free)

Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com and around the web

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Solving Logarithmic Equations – Explanation & Examples

JUMP TO TOPIC

How to solve equations with logarithms on one side?

How to solve equations with logarithms on both sides of the equation, practice questions, solving logarithmic equations – explanation & examples.

Before we can get into solving logarithmic equations, let’s first familiarize ourselves with the following rules of logarithms :

• The product rule:

The product rule states that the sum of two logarithms is equal to the product of the logarithms.  The first law is represented as;

⟹ log b (x) + log b (y) = log b (xy)

• The quotient rule:

The difference of two logarithms x and y is equal to the ratio of the logarithms.

⟹ log b (x) – log b (y) = log (x/y)

• The power rule:

⟹ log b (x) n = n log b (x)

• Change of base rule.

⟹ log b x = (log a x) / (log a b)

• Identity rule

The logarithm of any positive number to the same base of that number is always 1. b 1 =b ⟹ log b (b)=1.

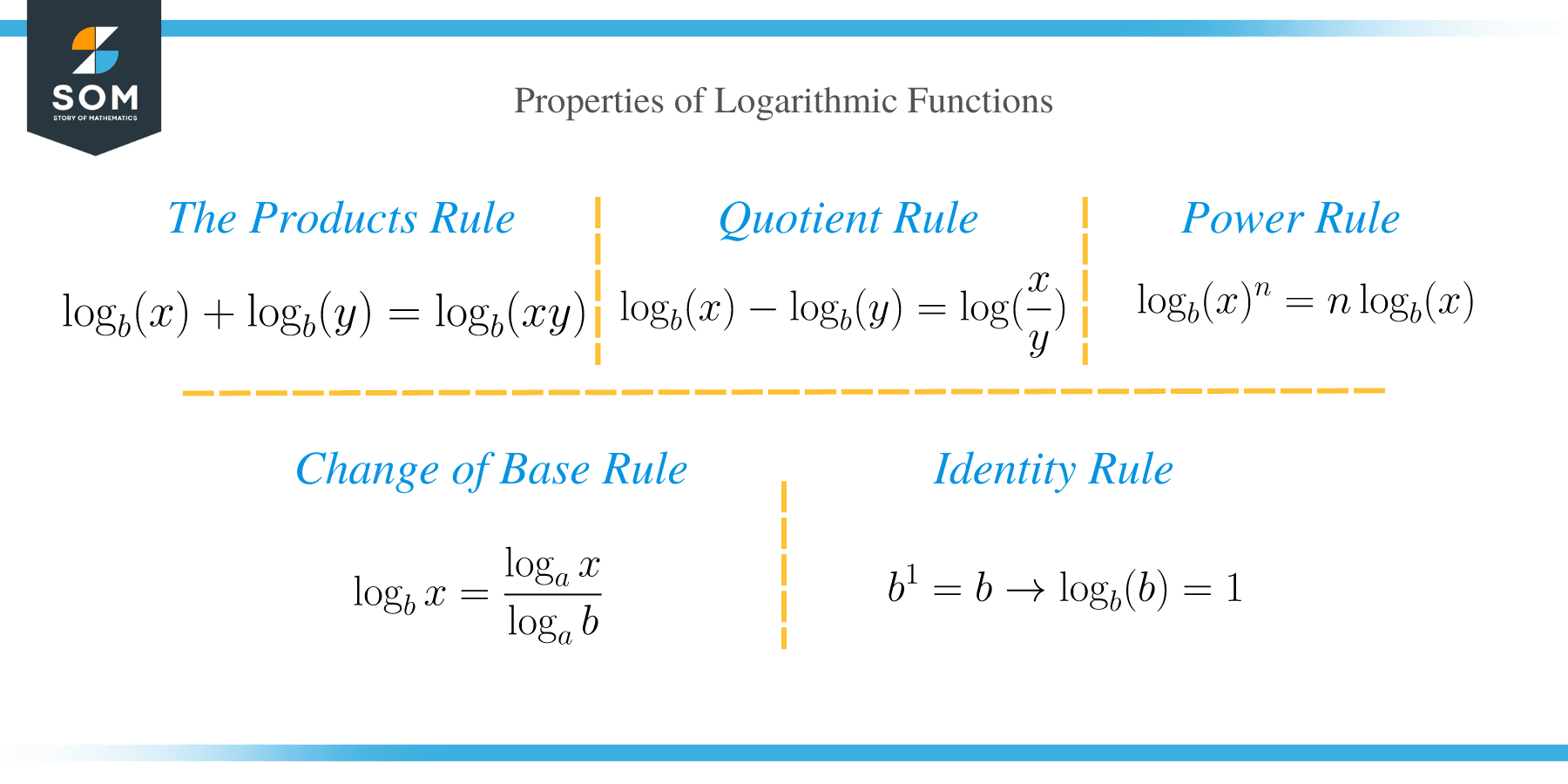
How to Solve Logarithmic Equations?

An equation containing variables in the exponents is knowns as an exponential equation. In contrast, an equation that involves the logarithm of an expression containing a variable is referred to as a logarithmic equation.

The purpose of solving a logarithmic equation is to find the value of the unknown variable.

In this article, we will learn how to solve the general two types of logarithmic equations, namely:

• Equations containing logarithms on one side of the equation.
• Equations with logarithms on opposite sides of the equal to sign.

Equations with logarithms on one side take log b M = n ⇒ M = b n .

To solve this type of equations, here are the steps:

• Simplify the logarithmic equations by applying the appropriate laws of logarithms.
• Rewrite the logarithmic equation in exponential form.
• Now simplify the exponent and solve for the variable.
• Verify your answer by substituting it back in the logarithmic equation. You should note that the acceptable answer of a logarithmic equation only produces a positive argument.

Solve log 2 (5x + 7) = 5

Rewrite the equation to exponential form

logs 2 (5x + 7) = 5 ⇒ 2 5 = 5x + 7

⇒ 32 = 5x + 7

⇒ 5x = 32 – 7

Divide both sides by 5 to get

Solve for x in log (5x -11) = 2

Since the base of this equation is not given, we therefore assume the base of 10.

Now change the write the logarithm in exponential form.

⇒ 10 2 = 5x – 11

⇒ 100 = 5x -11

Hence, x = 111/5 is the answer.

Solve log 10 (2x + 1) = 3

Rewrite the equation in exponential form

log 10  (2x + 1) = 3n⇒ 2x + 1 = 10 3

⇒ 2x + 1 = 1000

On dividing both sides by 2, we get;

Verify your answer by substituting it in the original logarithmic equation;

⇒ log 10  (2 x 499.5 + 1) = log 10  (1000) = 3 since 10 3  = 1000

Evaluate ln (4x -1) = 3

Rewrite the equation in exponential form as;

ln (4x -1) = 3 ⇒ 4x – 3 =e 3

But as you know, e = 2.718281828

4x – 3 = (2.718281828) 3 = 20.085537

x = 5.271384

Solve the logarithmic equation log 2 (x +1) – log 2 (x – 4) = 3

First simplify the logarithms by applying the quotient rule as shown below.

log 2 (x +1) – log 2 (x – 4) = 3 ⇒ log 2 [(x + 1)/ (x – 4)] = 3

Now, rewrite the equation in exponential form

⇒2 3 = [(x + 1)/ (x – 4)]

⇒ 8 = [(x + 1)/ (x – 4)]

Cross multiply the equation

⇒ [(x + 1) = 8(x – 4)]

⇒ x + 1 = 8x -32

7x = 33 …… (Collecting the like terms)

Solve for x if log 4 (x) + log 4 (x -12) = 3

Simplify the logarithm by using the product rule as follows;

log 4 (x) + log 4 (x -12) = 3 ⇒ log 4 [(x) (x – 12)] = 3

⇒ log 4 (x 2 – 12x) = 3

Convert the equation in exponential form.

⇒ 4 3 = x 2 – 12x

⇒ 64 = x 2 – 12x

Since this is a quadratic equation, we therefore solve by factoring.

x 2 -12x – 64 ⇒ (x + 4) (x – 16) = 0

x = -4 or 16

When x = -4 is substituted in the original equation, we get a negative answer which is imaginary. Therefore, 16 is the only acceptable solution.

The equations with logarithms on both sides of the equal to sign take log M = log N, which is the same as M = N.

The procedure of solving equations with logarithms on both sides of the equal sign.

• If the logarithms have are a common base, simplify the problem and then rewrite it without logarithms.
• Simplify by collecting like terms and solve for the variable in the equation.
• Check your answer by plugging it back in the original equation. Remember that, an acceptable answer will produce a positive argument.

Solve log 6 (2x – 4) + log 6 ( 4) = log 6 (40)

First, simplify the logarithms.

log 6 (2x – 4) + log 6 (4) = log 6 (40) ⇒ log 6 [4(2x – 4)] = log 6 (40)

Now drop the logarithms

⇒ [4(2x – 4)] = (40)

⇒ 8x – 16 = 40

⇒ 8x = 40 + 16

Solve the logarithmic equation: log 7 (x – 2) + log 7 (x + 3) = log 7 14

Simplify the equation by applying the product rule.

Log 7 [(x – 2) (x + 3)] = log 7 14

Drop the logarithms.

⇒ [(x – 2) (x + 3)] = 14

Distribute the FOIL to get;

⇒ x 2 – x – 6 = 14

⇒ x 2 – x – 20 = 0

⇒ (x + 4) (x – 5) = 0

x = -4 or x = 5

when x = -5 and x = 5 are substituted in the original equation, they give a negative and positive argument respectively. Therefor, x = 5 is the only acceptable solution.

Solve log 3  x + log 3  (x + 3) = log 3  (2x + 6)

Given the equation; log 3  (x 2  + 3x) = log 3  (2x + 6), drop the logarithms to get; ⇒ x 2  + 3x = 2x + 6 ⇒ x 2  + 3x – 2x – 6 = 0 x 2  + x – 6 = 0……………… (Quadratic equation) Factor the quadratic equation to get;

(x – 2) (x + 3) = 0 x = 2 and x = -3

By verifying both values of x, we get x = 2 to be the correct answer.

Solve log 5  (30x – 10) – 2 = log 5  (x + 6)

log 5  (30x – 10) – 2 = log 5  (x + 6)

This equation can be rewritten as;

⇒ log 5  (30x – 10) –  log 5  (x + 6) = 2

Simplify the logarithms

log 5  [(30x – 10)/ (x + 6)] = 2

Rewrite logarithm in exponential form.

⇒ 5 2 = [(30x – 10)/ (x + 6)]

⇒ 25 = [(30x – 10)/ (x + 6)]

On cross multiplying, we get;

⇒ 30x – 10 = 25 (x + 6)

⇒ 30x – 10 = 25x + 150

⇒ 30x – 25x = 150 + 10

Previous Lesson  |  Main Page | Next Lesson

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Logarithmic Equations? (+FREE Worksheet!)

In this blog post, you will learn how to solve Logarithmic Equations using the properties of logarithms in a few easy steps.

Related Topics

• How to Solve Natural Logarithms Problems
• How to Evaluate Logarithms
• Logarithms Properties

Step-by-step guide to solving logarithmic equations

• Convert the logarithmic equation to an exponential equation when it’s possible. (If no base is indicated, the base of the logarithm is \(10\))
• Condense logarithms if you have more than one log on one side of the equation.
• Plug the answers back into the original equation and check if the solution works.

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Logarithmic equations – example 1:.

Find the value of the variables in each equation. \(\log_{4}{(20-x^2)}=2\)

Use log rule: \(\log_{b}{x}=\log_{b}{y}\), then: \(x=y\)

\(2=\log_{4}{4^2},\log_{4}{(20-x^2)}=\log_{4}{4^2}=\log_{4}{16}\)

then: \(20-x^2=16→20-16=x^2→x^2=4→x=2\) or \(x=-2\)

Logarithmic Equations – Example 2:

Find the value of the variables in each equation. \(log⁡(2x+2)=log⁡(4x-6)\)

When the logs have the same base: \(f(x)=g(x)\),then: \(ln(f(x))=ln(g(x))\),

\(log⁡(2x+2)=log⁡(4x-6)→2x+2=4x-6→2x+2-4x+6=0\)

\(2x+2-4x+6=0→-2x+8=0→-2x=-8→x=\frac{-8}{-2}=4\)

Logarithmic Equations – Example 3:

Find the value of the variables in each equation. \(\log_{2}{(25-x^2)}=2\)

\(2=\log_{2}{2^2},\log_{2}{(25-x^2)}=\log_{2}{2^2}=\log_{2}{4}\)

Then: \(25-x^2=4→25-4=x^2→x^2=21 →x=\sqrt{21} \) or \(-\sqrt{21}\)

Logarithmic Equations – Example 4:

Find the value of the variables in each equation. \(log⁡(8x+3)=log⁡(2x-6)\)

\(log⁡(8x+3)=log⁡(2x-6)→8x+3=2x-6→8x+3-2x+6=0\)

\(6x+9=0→6x=-9→x=\frac{-9}{6}=-\frac{3}{2}\) Logarithms of negative numbers are not defined. Therefore, there is no solution for this equation.

Exercises for Logarithmic Equations

The Best Math Book to Help You Ace the Math Test

Algebra I for Beginners The Ultimate Step by Step Guide to Acing Algebra I

Find the value of the variables in each equation..

• \(\color{blue}{log⁡(x+5)=2}\)
• \(\color{blue}{log x-log 4=3}\)
• \(\color{blue}{log x+log 2=4}\)
• \(\color{blue}{log 10+log x=1}\)
• \(\color{blue}{log x+log 8=log 48}\)
• \(\color{blue}{-3\log_{3}{(x-2)}=-12}\)
• \(\color{blue}{log 6x=log (x+5)}\)
• \(\color{blue}{log (4k-5)=log (2k-1)}\)
• \(\color{blue}{95}\)
• \(\color{blue}{4000}\)
• \(\color{blue}{5000}\)
• \(\color{blue}{1}\)
• \(\color{blue}{6}\)
• \(\color{blue}{83}\)
• \(\color{blue}{2}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 5 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• Geometry Puzzle – Challenge 59
• Finding Derivatives Made Easy! Derivative of A Chain of Functions
• Top 10 Algebra 2 Textbooks in 2024 (Expert Recommendations)
• How to Multiply Three or More Mixed Numbers, Fractions & Whole Numbers?
• 5th Grade NHSAS Math Worksheets: FREE & Printable
• Top 10 Accuplacer Math Prep Books (Our 2023 Favorite Picks)
• How to Apply Trigonometry: Practical Uses and Insights into Engineering and Astronomy
• Why Do Most Students Struggle with Math?
• Area of a Parallelogram
• 10 Most Common 5th Grade FSA Math Questions

What people say about "How to Solve Logarithmic Equations? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra for beginners the ultimate step by step guide to preparing for the pre-algebra test, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \log _2(x+1)=\log _3(27)
• \ln (x+2)-\ln (x+1)=1
• \ln (x)+\ln (x-1)=\ln (3x+12)
• 4+\log _3(7x)=10
• \ln (10)-\ln (7-x)=\ln (x)
• \log _2(x^2-6x)=3+\log _2(1-x)
• How do you calculate logarithmic equations?
• To solve a logarithmic equations use the esxponents rules to isolate logarithmic expressions with the same base. Set the arguments equal to each other, solve the equation and check your answer.
• What is logarithm equation?
• A logarithmic equation is an equation that involves the logarithm of an expression containing a varaible.
• What are the 3 types of logarithms?
• The three types of logarithms are common logarithms (base 10), natural logarithms (base e), and logarithms with an arbitrary base.
• Is log10 and log the same?
• When there's no base on the log it means the common logarithm which is log base 10.
• What is the inverse of log in math?
• The inverse of a log function is an exponantial.

logarithmic-equation-calculator

• High School Math Solutions – Logarithmic Equation Calculator Logarithmic equations are equations involving logarithms. In this segment we will cover equations with logarithms...

Please add a message.

Message received. Thanks for the feedback.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Log Equations from the Definition

Using the Definition Using Exponentials Calculators & Etc.

The first type of logarithmic equation has two logs , each having the same base, which have been set equal to each other. We solve this sort of equation by setting the insides (that is, setting the "arguments") of the logarithmic expressions equal to each other. For example:

Solve log 2 ( x ) = log 2 (14) .

The logarithms on either side of the equation have the same base;namely, a base of 2 . The only way these two log expressions can be equal is for their arguments to be equal. In other words, the log expressions being equal says that the arguments must be equal, so I can create the following equation:

Content Continues Below

MathHelp.com

Advanced Log Equations

And that's all there is to solving this equation. My solution is:

Solve log b ( x 2 ) = log b (2 x − 1) .

The base of these logarithmic terms is unknown, being indicated by the letter b . But that's okay. I only need them bases to be the same. What those bases actually are doesn't matter for this sort of equation. Because the bases of the logs are the same, then I know that the insides of the logs must be equal. I'll use this to create my equation:

x 2 = 2 x − 1

Then I can solve the log equation by solving this quadratic equation :

x 2 − 2 x + 1 = 0

( x − 1)( x − 1) = 0

Then my solution is:

Logarithms cannot have non-positive arguments (that is, arguments which are negative or zero), but quadratics and other equations can have negative solutions. When we convert a log equation to a different type of equation by equating the insides of the logs, we may be "creating" solutions that didn't previously exist. Because of this, it is generally a good idea to check the solutions you get for log equations.

To check my solution for the exercise above, I'll plug my solution value of x = 1 into each side of the equation, and see if I get the same value for each side:

the left-hand side:

log b ( x 2 ) = log b (1 2 ) = log b (1) = 0

the right-hand side:

log b (2 x − 1) = log b (2(1) − 1) = log b (2 − 1) = log b (1) = 0

The fact that each side of the original equation evaluated to the same value (in this case, to the value of zero) proves that my solution is correct.

It should be noted that the particular value of the base of the log was irrelevant here. Each log in the equation had the same base, and each side of the log equation ended up with the value, so the solution "checks".

Solve log b ( x 2 − 30) = log b ( x ) .

Since the logs have the same base, I can set the arguments equal and solve:

x 2 − 30 = x

x 2 − x − 30 = 0

( x − 6)( x + 5) = 0

x = 6, − 5

Since I cannot have a negative inside a logarithm, the quadratic-equation solution " x = −5 " can not be a valid solution to the original logarithmic equation (in particular, this negative value won't work in the right-hand side of the original equation).

Solve 2log b ( x ) = log b (4) + log b ( x − 1) .

All of these logs have the same base, but I can't solve yet, because I don't yet have the equation in the form "log(of something) equals log(of something else)". So first I'll have to apply some log rules to condense the log expression on the right-hand side of the equation and to move the multiplier on the left-hand side to inside that log:

2log b ( x ) = log b (4) + log b ( x − 1)

log b ( x 2 ) = log b ((4)( x − 1))

log b ( x 2 ) = log b (4 x − 4)

Now that I've rearranged the original equation to put it in the proper "log(of something) equals log(of something else)" form, I can equate the logs' arguments and solve the resulting equation:

x 2 = 4 x − 4

x 2 − 4 x + 4 = 0

( x − 2)( x − 2) = 0

Solve ln( e x ) = ln( e 3 ) + ln( e 5 ) .

Advertisement

To solve this, I need to remember the defintion of logarithms. Logarithms are powers. Specifically, " log b ( a ) " is the power that, when put on the base " b ", gives me " a ". In this case, the base of the log is e . The argument of " ln( e x ) " is " e x ". That is, " ln( e x ) " is "the power that, when put on e , gives you e x .

What power do I have to put on e to get e x ? Why, x , of course! So:

ln( e x ) = x

ln( e 3 ) = 3

ln( e 5 ) = 5

So the given equation simplifies quite nicely:

ln( e x ) = ln( e 3 ) + ln( e 5 )

Some students like to think of the statement " log b (b x ) =  x " as a "cancellation" of some sort. Technically, that isn't a correct statement. But this type of expression often proves quite confusing. If thinking of this as a "cancellation" helps you to keep things straight in your mind, then please go right ahead. Just don't use that lingo in class, or your instructor might get a bit tetchy.

Note: The above equation could also have been solved by using log rules:

ln( e x ) = ln[( e 3 )( e 5 )]

ln( e x ) = ln( e 3 + 5 )

ln( e x ) = ln( e 8 )

Comparing the arguments, I get:

These log equations were fairly simple to solve, because of their form; namely, "log(of something) equals log(of something else)". But if a given log equation is not in this form, and cannot be rearranged to be put into this form, then we'll have to bring exponentials into the mix...

URL: https://www.purplemath.com/modules/solvelog.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

OpenAlgebra.com

• Videos & Interactives
• Algebra Worksheets

Solving Logarithmic Equations

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.6: Solve Exponential and Logarithmic Equations

• Last updated
• Save as PDF
• Page ID 114263

Learning Objectives

By the end of this section, you will be able to:

• Solve logarithmic equations using the properties of logarithms
• Solve exponential equations using logarithms
• Use exponential models in applications

Be Prepared 10.13

Before you get started, take this readiness quiz.

Solve: x 2 = 16 . x 2 = 16 . If you missed this problem, review Example 6.46.

Be Prepared 10.14

Solve: x 2 − 5 x + 6 = 0 . x 2 − 5 x + 6 = 0 . If you missed this problem, review Example 6.45.

Be Prepared 10.15

Solve: x ( x + 6 ) = 2 x + 5 . x ( x + 6 ) = 2 x + 5 . If you missed this problem, review Example 6.47.

Solve Logarithmic Equations Using the Properties of Logarithms

In the section on logarithmic functions, we solved some equations by rewriting the equation in exponential form. Now that we have the properties of logarithms, we have additional methods we can use to solve logarithmic equations.

If our equation has two logarithms we can use a property that says that if log a M = log a N log a M = log a N then it is true that M = N . M = N . This is the One-to-One Property of Logarithmic Equations .

One-to-One Property of Logarithmic Equations

For M > 0 , N > 0 , a > 0 , M > 0 , N > 0 , a > 0 , and a ≠ 1 a ≠ 1 is any real number:

If log a M = log a N , then M = N . If log a M = log a N , then M = N .

To use this property, we must be certain that both sides of the equation are written with the same base.

Remember that logarithms are defined only for positive real numbers. Check your results in the original equation. You may have obtained a result that gives a logarithm of zero or a negative number.

Example 10.38

Solve: 2 log 5 x = log 5 81 . 2 log 5 x = log 5 81 .

Try It 10.75

Solve: 2 log 3 x = log 3 36 2 log 3 x = log 3 36

Try It 10.76

Solve: 3 log x = log 64 3 log x = log 64

Another strategy to use to solve logarithmic equations is to condense sums or differences into a single logarithm.

Example 10.39

Solve: log 3 x + log 3 ( x − 8 ) = 2 . log 3 x + log 3 ( x − 8 ) = 2 .

Try It 10.77

Solve: log 2 x + log 2 ( x − 2 ) = 3 log 2 x + log 2 ( x − 2 ) = 3

Try It 10.78

Solve: log 2 x + log 2 ( x − 6 ) = 4 log 2 x + log 2 ( x − 6 ) = 4

When there are logarithms on both sides, we condense each side into a single logarithm. Remember to use the Power Property as needed.

Example 10.40

Solve: log 4 ( x + 6 ) − log 4 ( 2 x + 5 ) = − log 4 x . log 4 ( x + 6 ) − log 4 ( 2 x + 5 ) = − log 4 x .

Try It 10.79

Solve: log ( x + 2 ) − log ( 4 x + 3 ) = − log x . log ( x + 2 ) − log ( 4 x + 3 ) = − log x .

Try It 10.80

Solve: log ( x − 2 ) − log ( 4 x + 16 ) = log 1 x . log ( x − 2 ) − log ( 4 x + 16 ) = log 1 x .

Solve Exponential Equations Using Logarithms

In the section on exponential functions, we solved some equations by writing both sides of the equation with the same base. Next we wrote a new equation by setting the exponents equal.

It is not always possible or convenient to write the expressions with the same base. In that case we often take the common logarithm or natural logarithm of both sides once the exponential is isolated.

Example 10.41

Solve 5 x = 11 . 5 x = 11 . Find the exact answer and then approximate it to three decimal places.

Try It 10.81

Solve 7 x = 43 . 7 x = 43 . Find the exact answer and then approximate it to three decimal places.

Try It 10.82

Solve 8 x = 98 . 8 x = 98 . Find the exact answer and then approximate it to three decimal places.

When we take the logarithm of both sides we will get the same result whether we use the common or the natural logarithm (try using the natural log in the last example. Did you get the same result?) When the exponential has base e , we use the natural logarithm.

Example 10.42

Solve 3 e x + 2 = 24 . 3 e x + 2 = 24 . Find the exact answer and then approximate it to three decimal places.

Try It 10.83

Solve 2 e x − 2 = 18 . 2 e x − 2 = 18 . Find the exact answer and then approximate it to three decimal places.

Try It 10.84

Solve 5 e 2 x = 25 . 5 e 2 x = 25 . Find the exact answer and then approximate it to three decimal places.

Use Exponential Models in Applications

In previous sections we were able to solve some applications that were modeled with exponential equations. Now that we have so many more options to solve these equations, we are able to solve more applications.

We will again use the Compound Interest Formulas and so we list them here for reference.

Compound Interest

For a principal, P , invested at an interest rate, r , for t years, the new balance, A is:

A = P ( 1 + r n ) n t when compounded n times a year. A = P e r t when compounded continuously. A = P ( 1 + r n ) n t when compounded n times a year. A = P e r t when compounded continuously.

Example 10.43

Jermael’s parents put $10,000 in investments for his college expenses on his first birthday. They hope the investments will be worth $50,000 when he turns 18. If the interest compounds continuously, approximately what rate of growth will they need to achieve their goal?

Try It 10.85

Hector invests $ 10,000 $ 10,000 at age 21. He hopes the investments will be worth $ 150,000 $ 150,000 when he turns 50. If the interest compounds continuously, approximately what rate of growth will he need to achieve his goal?

Try It 10.86

Rachel invests $ 15,000 $ 15,000 at age 25. She hopes the investments will be worth $ 90,000 $ 90,000 when she turns 40. If the interest compounds continuously, approximately what rate of growth will she need to achieve her goal?

We have seen that growth and decay are modeled by exponential functions. For growth and decay we use the formula A = A 0 e k t . A = A 0 e k t . Exponential growth has a positive rate of growth or growth constant, k k , and exponential decay has a negative rate of growth or decay constant, k .

Exponential Growth and Decay

For an original amount, A 0 , A 0 , that grows or decays at a rate, k , for a certain time, t , the final amount, A , is:

A = A 0 e k t A = A 0 e k t

We can now solve applications that give us enough information to determine the rate of growth. We can then use that rate of growth to predict other situations.

Example 10.44

Researchers recorded that a certain bacteria population grew from 100 to 300 in 3 hours. At this rate of growth, how many bacteria will there be 24 hours from the start of the experiment?

This problem requires two main steps. First we must find the unknown rate, k . Then we use that value of k to help us find the unknown number of bacteria.

Try It 10.87

Researchers recorded that a certain bacteria population grew from 100 to 500 in 6 hours. At this rate of growth, how many bacteria will there be 24 hours from the start of the experiment?

Try It 10.88

Researchers recorded that a certain bacteria population declined from 700,000 to 400,000 in 5 hours after the administration of medication. At this rate of decay, how many bacteria will there be 24 hours from the start of the experiment?

Radioactive substances decay or decompose according to the exponential decay formula. The amount of time it takes for the substance to decay to half of its original amount is called the half-life of the substance.

Similar to the previous example, we can use the given information to determine the constant of decay, and then use that constant to answer other questions.

Example 10.45

The half-life of radium-226 is 1,590 years. How much of a 100 mg sample will be left in 500 years?

This problem requires two main steps. First we must find the decay constant k . If we start with 100-mg, at the half-life there will be 50-mg remaining. We will use this information to find k . Then we use that value of k to help us find the amount of sample that will be left in 500 years.

Try It 10.89

The half-life of magnesium-27 is 9.45 minutes. How much of a 10-mg sample will be left in 6 minutes?

Try It 10.90

The half-life of radioactive iodine is 60 days. How much of a 50-mg sample will be left in 40 days?

Access these online resources for additional instruction and practice with solving exponential and logarithmic equations.

• Solving Logarithmic Equations
• Solving Logarithm Equations
• Finding the rate or time in a word problem on exponential growth or decay

Section 10.5 Exercises

Practice makes perfect.

In the following exercises, solve for x .

log 4 64 = 2 log 4 x log 4 64 = 2 log 4 x

log 49 = 2 log x log 49 = 2 log x

3 log 3 x = log 3 27 3 log 3 x = log 3 27

3 log 6 x = log 6 64 3 log 6 x = log 6 64

log 5 ( 4 x − 2 ) = log 5 10 log 5 ( 4 x − 2 ) = log 5 10

log 3 ( x 2 + 3 ) = log 3 4 x log 3 ( x 2 + 3 ) = log 3 4 x

log 3 x + log 3 x = 2 log 3 x + log 3 x = 2

log 4 x + log 4 x = 3 log 4 x + log 4 x = 3

log 2 x + log 2 ( x − 3 ) = 2 log 2 x + log 2 ( x − 3 ) = 2

log 3 x + log 3 ( x + 6 ) = 3 log 3 x + log 3 ( x + 6 ) = 3

log x + log ( x + 3 ) = 1 log x + log ( x + 3 ) = 1

log x + log ( x − 15 ) = 2 log x + log ( x − 15 ) = 2

log ( x + 4 ) − log ( 5 x + 12 ) = − log x log ( x + 4 ) − log ( 5 x + 12 ) = − log x

log ( x − 1 ) − log ( x + 3 ) = log 1 x log ( x − 1 ) − log ( x + 3 ) = log 1 x

log 5 ( x + 3 ) + log 5 ( x − 6 ) = log 5 10 log 5 ( x + 3 ) + log 5 ( x − 6 ) = log 5 10

log 5 ( x + 1 ) + log 5 ( x − 5 ) = log 5 7 log 5 ( x + 1 ) + log 5 ( x − 5 ) = log 5 7

log 3 ( 2 x − 1 ) = log 3 ( x + 3 ) + log 3 3 log 3 ( 2 x − 1 ) = log 3 ( x + 3 ) + log 3 3

log ( 5 x + 1 ) = log ( x + 3 ) + log 2 log ( 5 x + 1 ) = log ( x + 3 ) + log 2

In the following exercises, solve each exponential equation. Find the exact answer and then approximate it to three decimal places.

3 x = 89 3 x = 89

2 x = 74 2 x = 74

5 x = 110 5 x = 110

4 x = 112 4 x = 112

e x = 16 e x = 16

e x = 8 e x = 8

( 1 2 ) x = 6 ( 1 2 ) x = 6

( 1 3 ) x = 8 ( 1 3 ) x = 8

4 e x + 1 = 16 4 e x + 1 = 16

3 e x + 2 = 9 3 e x + 2 = 9

6 e 2 x = 24 6 e 2 x = 24

2 e 3 x = 32 2 e 3 x = 32

1 4 e x = 3 1 4 e x = 3

1 3 e x = 2 1 3 e x = 2

e x + 1 + 2 = 16 e x + 1 + 2 = 16

e x − 1 + 4 = 12 e x − 1 + 4 = 12

In the following exercises, solve each equation.

3 3 x + 1 = 81 3 3 x + 1 = 81

6 4 x − 17 = 216 6 4 x − 17 = 216

e x 2 e 14 = e 5 x e x 2 e 14 = e 5 x

e x 2 e x = e 20 e x 2 e x = e 20

log a 64 = 2 log a 64 = 2

log a 81 = 4 log a 81 = 4

ln x = −8 ln x = −8

ln x = 9 ln x = 9

log 5 ( 3 x − 8 ) = 2 log 5 ( 3 x − 8 ) = 2

log 4 ( 7 x + 15 ) = 3 log 4 ( 7 x + 15 ) = 3

ln e 5 x = 30 ln e 5 x = 30

ln e 6 x = 18 ln e 6 x = 18

3 log x = log 125 3 log x = log 125

7 log 3 x = log 3 128 7 log 3 x = log 3 128

log 6 x + log 6 ( x − 5 ) = log 6 24 log 6 x + log 6 ( x − 5 ) = log 6 24

log 9 x + log 9 ( x − 4 ) = log 9 12 log 9 x + log 9 ( x − 4 ) = log 9 12

log 2 ( x + 2 ) − log 2 ( 2 x + 9 ) = − log 2 x log 2 ( x + 2 ) − log 2 ( 2 x + 9 ) = − log 2 x

log 6 ( x + 1 ) − log 6 ( 4 x + 10 ) = log 6 1 x log 6 ( x + 1 ) − log 6 ( 4 x + 10 ) = log 6 1 x

In the following exercises, solve for x , giving an exact answer as well as an approximation to three decimal places.

6 x = 91 6 x = 91

( 1 2 ) x = 10 ( 1 2 ) x = 10

7 e x − 3 = 35 7 e x − 3 = 35

8 e x + 5 = 56 8 e x + 5 = 56

In the following exercises, solve.

Sung Lee invests $ 5,000 $ 5,000 at age 18. He hopes the investments will be worth $ 10,000 $ 10,000 when he turns 25. If the interest compounds continuously, approximately what rate of growth will he need to achieve his goal? Is that a reasonable expectation?

Alice invests $ 15,000 $ 15,000 at age 30 from the signing bonus of her new job. She hopes the investments will be worth $ 30,000 $ 30,000 when she turns 40. If the interest compounds continuously, approximately what rate of growth will she need to achieve her goal?

Coralee invests $ 5,000 $ 5,000 in an account that compounds interest monthly and earns 7 % . 7 % . How long will it take for her money to double?

Simone invests $ 8,000 $ 8,000 in an account that compounds interest quarterly and earns 5 % . 5 % . How long will it take for his money to double?

Researchers recorded that a certain bacteria population declined from 100,000 to 100 in 24 hours. At this rate of decay, how many bacteria will there be in 16 hours?

Researchers recorded that a certain bacteria population declined from 800,000 to 500,000 in 6 hours after the administration of medication. At this rate of decay, how many bacteria will there be in 24 hours?

A virus takes 6 days to double its original population ( A = 2 A 0 ) . ( A = 2 A 0 ) . How long will it take to triple its population?

A bacteria doubles its original population in 24 hours ( A = 2 A 0 ) . ( A = 2 A 0 ) . How big will its population be in 72 hours?

Carbon-14 is used for archeological carbon dating. Its half-life is 5,730 years. How much of a 100-gram sample of Carbon-14 will be left in 1000 years?

Radioactive technetium-99m is often used in diagnostic medicine as it has a relatively short half-life but lasts long enough to get the needed testing done on the patient. If its half-life is 6 hours, how much of the radioactive material form a 0.5 ml injection will be in the body in 24 hours?

Writing Exercises

Explain the method you would use to solve these equations: 3 x + 1 = 81 , 3 x + 1 = 81 , 3 x + 1 = 75 . 3 x + 1 = 75 . Does your method require logarithms for both equations? Why or why not?

What is the difference between the equation for exponential growth versus the equation for exponential decay?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

• calculators
• Logarithmic Equations

Logarithmic Equations Calculator

Get detailed solutions to your math problems with our logarithmic equations step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems.

Solved example of logarithmic equations

Apply the formula: $a\log_{b}\left(x\right)$$=\log_{b}\left(x^a\right)$

The difference of two logarithms of equal base $b$ is equal to the logarithm of the quotient: $\log_b(x)-\log_b(y)=\log_b\left(\frac{x}{y}\right)$

Take the variable outside of the logarithm

Any expression (except $0$ and $\infty$) to the power of $0$ is equal to $1$

Simplifying the logarithm

Multiply both sides of the equation by $x+6$

Move everything to the left hand side of the equation

Factor the trinomial $x^2-x-6$ finding two numbers that multiply to form $-6$ and added form $-1$

Break the equation in $2$ factors and set each equal to zero, to obtain

Solve the equation ($1$)

We need to isolate the dependent variable $x$, we can do that by simultaneously subtracting $2$ from both sides of the equation

 Intermediate steps

Canceling terms on both sides

$x+0=x$, where $x$ is any expression

Solve the equation ($2$)

We need to isolate the dependent variable $x$, we can do that by simultaneously subtracting $-3$ from both sides of the equation

Combining all solutions, the $2$ solutions of the equation are

Verify that the solutions obtained are valid in the initial equation

The valid solutions to the logarithmic equation are the ones that, when replaced in the original equation, don't result in any logarithm of negative numbers or zero, since in those cases the logarithm does not exist

 Final Answer

Struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Related Calculators

 popular problems.