how to solve trig equations by factoring

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.6: Solving Trigonometric Equations

• Last updated
• Save as PDF
• Page ID 114045

Learning Objectives

In this section, you will:

• Solve linear trigonometric equations in sine and cosine.
• Solve equations involving a single trigonometric function.
• Solve trigonometric equations using a calculator.
• Solve trigonometric equations that are quadratic in form.
• Solve trigonometric equations using fundamental identities.
• Solve trigonometric equations with multiple angles.
• Solve right triangle problems.

Figure 1 Egyptian pyramids standing near a modern city. (credit: Oisin Mulvihill)

Thales of Miletus (circa 625–547 BC) is known as the founder of geometry. The legend is that he calculated the height of the Great Pyramid of Giza in Egypt using the theory of similar triangles , which he developed by measuring the shadow of his staff. Based on proportions, this theory has applications in a number of areas, including fractal geometry, engineering, and architecture. Often, the angle of elevation and the angle of depression are found using similar triangles.

In earlier sections of this chapter, we looked at trigonometric identities. Identities are true for all values in the domain of the variable. In this section, we begin our study of trigonometric equations to study real-world scenarios such as the finding the dimensions of the pyramids.

Solving Linear Trigonometric Equations in Sine and Cosine

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is 2π.2π. In other words, every 2π2π units, the y- values repeat. If we need to find all possible solutions, then we must add 2πk,2πk, where kk is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is 2π:2π:

sinθ=sin(θ±2kπ)sinθ=sin(θ±2kπ)

There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.

Solving a Linear Trigonometric Equation Involving the Cosine Function

Find all possible exact solutions for the equation cosθ=12.cosθ=12.

Solving a Linear Equation Involving the Sine Function

Find all possible exact solutions for the equation sint=12.sint=12.

Given a trigonometric equation, solve using algebra .

• Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
• Substitute the trigonometric expression with a single variable, such as xx or u.u.
• Solve the equation the same way an algebraic equation would be solved.
• Substitute the trigonometric expression back in for the variable in the resulting expressions.
• Solve for the angle.

Solve the Trigonometric Equation in Linear Form

Solve the equation exactly: 2cosθ−3=−5,0≤θ<2π.2cosθ−3=−5,0≤θ<2π.

Solve exactly the following linear equation on the interval [0,2π):2sinx+1=0.[0,2π):2sinx+1=0.

Solving Equations Involving a Single Trigonometric Function

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle (see Figure 2 ). We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is π,π, not 2π.2π. Further, the domain of tangent is all real numbers with the exception of odd integer multiples of π2,π2, unless, of course, a problem places its own restrictions on the domain.

Solving a Problem Involving a Single Trigonometric Function

Solve the problem exactly: 2sin2θ−1=0,0≤θ<2π.2sin2θ−1=0,0≤θ<2π.

Solving a Trigonometric Equation Involving Cosecant

Solve the following equation exactly: cscθ=−2,0≤θ<4π.cscθ=−2,0≤θ<4π.

As sinθ=−12,sinθ=−12, notice that all four solutions are in the third and fourth quadrants.

Solving an Equation Involving Tangent

Solve the equation exactly: tan(θ−π2)=1,0≤θ<2π.tan(θ−π2)=1,0≤θ<2π.

Find all solutions for tanx=3–√.tanx=3.

Identify all Solutions to the Equation Involving Tangent

Identify all exact solutions to the equation 2(tanx+3)=5+tanx,0≤x<2π.2(tanx+3)=5+tanx,0≤x<2π.

Solve Trigonometric Equations Using a Calculator

Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.

Using a Calculator to Solve a Trigonometric Equation Involving Sine

Use a calculator to solve the equation sinθ=0.8,sinθ=0.8, where θθ is in radians.

Note that a calculator will only return an angle in quadrants I or IV for the sine function, since that is the range of the inverse sine. The other angle is obtained by using π−θ.π−θ.

Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation secθ=−4,secθ=−4, giving your answer in radians.

Solve cosθ=−0.2.cosθ=−0.2.

Solving Trigonometric Equations in Quadratic Form

Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as xx or u.u. If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.

Solving a Trigonometric Equation in Quadratic Form

Solve the equation exactly: cos2θ+3cosθ−1=0,0≤θ<2π.cos2θ+3cosθ−1=0,0≤θ<2π.

Solving a Trigonometric Equation in Quadratic Form by Factoring

Solve the equation exactly: 2sin2θ−5sinθ+3=0,0≤θ≤2π.2sin2θ−5sinθ+3=0,0≤θ≤2π.

Make sure to check all solutions on the given domain as some factors have no solution.

Solve sin2θ=2cosθ+2,0≤θ≤2π.sin2θ=2cosθ+2,0≤θ≤2π. [Hint: Make a substitution to express the equation only in terms of cosine.]

Solving a Trigonometric Equation Using Algebra

Solve exactly:

2sin2θ+sinθ=0;0≤θ<2π2sin2θ+sinθ=0;0≤θ<2π

We can see the solutions on the graph in Figure 3 . On the interval 0≤θ<2π,0≤θ<2π, the graph crosses the x- axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

We can verify the solutions on the unit circle in Figure 2 as well.

Solving a Trigonometric Equation Quadratic in Form

Solve the equation quadratic in form exactly: 2sin2θ−3sinθ+1=0,0≤θ<2π.2sin2θ−3sinθ+1=0,0≤θ<2π.

Solve the quadratic equation 2cos2θ+cosθ=0.2cos2θ+cosθ=0.

Solving Trigonometric Equations Using Fundamental Identities

While algebra can be used to solve a number of trigonometric equations, we can also use the fundamental identities because they make solving equations simpler. Remember that the techniques we use for solving are not the same as those for verifying identities. The basic rules of algebra apply here, as opposed to rewriting one side of the identity to match the other side. In the next example, we use two identities to simplify the equation.

Use Identities to Solve an Equation

Use identities to solve exactly the trigonometric equation over the interval 0≤x<2π.0≤x<2π.

cosxcos(2x)+sinxsin(2x)=3–√2cosxcos(2x)+sinxsin(2x)=32

Solving the Equation Using a Double-Angle Formula

Solve the equation exactly using a double-angle formula: cos(2θ)=cosθ.cos(2θ)=cosθ.

Solving an Equation Using an Identity

Solve the equation exactly using an identity: 3cosθ+3=2sin2θ,0≤θ<2π.3cosθ+3=2sin2θ,0≤θ<2π.

Solving Trigonometric Equations with Multiple Angles

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as sin(2x)sin(2x) or cos(3x).cos(3x). When confronted with these equations, recall that y=sin(2x)y=sin(2x) is a horizontal compression by a factor of 2 of the function y=sinx.y=sinx. On an interval of 2π,2π, we can graph two periods of y=sin(2x),y=sin(2x), as opposed to one cycle of y=sinx.y=sinx. This compression of the graph leads us to believe there may be twice as many x -intercepts or solutions to sin(2x)=0sin(2x)=0 compared to sinx=0.sinx=0. This information will help us solve the equation.

Solving a Multiple Angle Trigonometric Equation

Solve exactly: cos(2x)=12cos(2x)=12 on [0,2π).[ 0,2π ).

Solving Right Triangle Problems

We can now use all of the methods we have learned to solve problems that involve applying the properties of right triangles and the Pythagorean Theorem. We begin with the familiar Pythagorean Theorem, a2+b2=c2,a2+b2=c2, and model an equation to fit a situation.

Using the Pythagorean Theorem to Model an Equation

Use the Pythagorean Theorem, and the properties of right triangles to model an equation that fits the problem.

One of the cables that anchors the center of the London Eye Ferris wheel to the ground must be replaced. The center of the Ferris wheel is 69.5 meters above the ground, and the second anchor on the ground is 23 meters from the base of the Ferris wheel. Approximately how long is the cable, and what is the angle of elevation (from ground up to the center of the Ferris wheel)? See Figure 4 .

Using the Pythagorean Theorem to Model an Abstract Problem

OSHA safety regulations require that the base of a ladder be placed 1 foot from the wall for every 4 feet of ladder length. Find the angle that a ladder of any length forms with the ground and the height at which the ladder touches the wall.

Access these online resources for additional instruction and practice with solving trigonometric equations.

• Solving Trigonometric Equations I
• Solving Trigonometric Equations II
• Solving Trigonometric Equations III
• Solving Trigonometric Equations IV
• Solving Trigonometric Equations V
• Solving Trigonometric Equations VI

7.5 Section Exercises

Will there always be solutions to trigonometric function equations? If not, describe an equation that would not have a solution. Explain why or why not.

When solving a trigonometric equation involving more than one trig function, do we always want to try to rewrite the equation so it is expressed in terms of one trigonometric function? Why or why not?

When solving linear trig equations in terms of only sine or cosine, how do we know whether there will be solutions?

For the following exercises, find all solutions exactly on the interval 0≤θ<2π.0≤θ<2π.

2sinθ=−2–√2sinθ=−2

2sinθ=3–√2sinθ=3

2cosθ=12cosθ=1

2cosθ=−2–√2cosθ=−2

tanθ=−1tanθ=−1

tanx=1tanx=1

cotx+1=0cotx+1=0

4sin2x−2=04sin2x−2=0

csc2x−4=0csc2x−4=0

For the following exercises, solve exactly on [0,2π).[0,2π).

2cosθ=2–√2cosθ=2

2cosθ=−12cosθ=−1

2sinθ=−12sinθ=−1

2sinθ=−3–√2sinθ=−3

2sin(3θ)=12sin(3θ)=1

2sin(2θ)=3–√2sin(2θ)=3

2cos(3θ)=−2–√2cos(3θ)=−2

cos(2θ)=−3√2cos(2θ)=−32

2sin(πθ)=12sin(πθ)=1

2cos(π5θ)=3–√2cos(π5θ)=3

For the following exercises, find all exact solutions on [0,2π).[ 0,2π ).

sec(x)sin(x)−2sin(x)=0sec(x)sin(x)−2sin(x)=0

tan(x)−2sin(x)tan(x)=0tan(x)−2sin(x)tan(x)=0

2cos2t+cos(t)=12cos2t+cos(t)=1

2tan2(t)=3sec(t)2tan2(t)=3sec(t)

2sin(x)cos(x)−sin(x)+2cos(x)−1=02sin(x)cos(x)−sin(x)+2cos(x)−1=0

cos2θ=12cos2θ=12

sec2x=1sec2x=1

tan2(x)=−1+2tan(−x)tan2(x)=−1+2tan(−x)

8sin2(x)+6sin(x)+1=08sin2(x)+6sin(x)+1=0

tan5(x)=tan(x)tan5(x)=tan(x)

For the following exercises, solve with the methods shown in this section exactly on the interval [0,2π).[0,2π).

sin(3x)cos(6x)−cos(3x)sin(6x)=−0.9sin(3x)cos(6x)−cos(3x)sin(6x)=−0.9

sin(6x)cos(11x)−cos(6x)sin(11x)=−0.1sin(6x)cos(11x)−cos(6x)sin(11x)=−0.1

cos(2x)cosx+sin(2x)sinx=1cos(2x)cosx+sin(2x)sinx=1

6sin(2t)+9sint=06sin(2t)+9sint=0

9cos(2θ)=9cos2θ−49cos(2θ)=9cos2θ−4

sin(2t)=costsin(2t)=cost

cos(2t)=sintcos(2t)=sint

cos(6x)−cos(3x)=0cos(6x)−cos(3x)=0

For the following exercises, solve exactly on the interval [0,2π).[ 0,2π ). Use the quadratic formula if the equations do not factor.

tan2x−3–√tanx=0tan2x−3tanx=0

sin2x+sinx−2=0sin2x+sinx−2=0

sin2x−2sinx−4=0sin2x−2sinx−4=0

5cos2x+3cosx−1=05cos2x+3cosx−1=0

3cos2x−2cosx−2=03cos2x−2cosx−2=0

5sin2x+2sinx−1=05sin2x+2sinx−1=0

tan2x+5tanx−1=0tan2x+5tanx−1=0

cot2x=−cotxcot2x=−cotx

−tan2x−tanx−2=0−tan2x−tanx−2=0

For the following exercises, find exact solutions on the interval [0,2π).[0,2π). Look for opportunities to use trigonometric identities.

sin2x−cos2x−sinx=0sin2x−cos2x−sinx=0

sin2x+cos2x=0sin2x+cos2x=0

sin(2x)−sinx=0sin(2x)−sinx=0

cos(2x)−cosx=0cos(2x)−cosx=0

2tanx2−sec2x−sin2x=cos2x2tanx2−sec2x−sin2x=cos2x

1−cos(2x)=1+cos(2x)1−cos(2x)=1+cos(2x)

sec2x=7sec2x=7

10sinxcosx=6cosx10sinxcosx=6cosx

−3sint=15costsint−3sint=15costsint

4cos2x−4=15cosx4cos2x−4=15cosx

8sin2x+6sinx+1=08sin2x+6sinx+1=0

8cos2θ=3−2cosθ8cos2θ=3−2cosθ

6cos2x+7sinx−8=06cos2x+7sinx−8=0

12sin2t+cost−6=012sin2t+cost−6=0

tanx=3sinxtanx=3sinx

cos3t=costcos3t=cost

For the following exercises, algebraically determine all solutions of the trigonometric equation exactly, then verify the results by graphing the equation and finding the zeros.

6sin2x−5sinx+1=06sin2x−5sinx+1=0

8cos2x−2cosx−1=08cos2x−2cosx−1=0

100tan2x+20tanx−3=0100tan2x+20tanx−3=0

2cos2x−cosx+15=02cos2x−cosx+15=0

20sin2x−27sinx+7=020sin2x−27sinx+7=0

2tan2x+7tanx+6=02tan2x+7tanx+6=0

130tan2x+69tanx−130=0130tan2x+69tanx−130=0

For the following exercises, use a calculator to find all solutions to four decimal places.

sinx=0.27sinx=0.27

sinx=−0.55sinx=−0.55

tanx=−0.34tanx=−0.34

cosx=0.71cosx=0.71

For the following exercises, solve the equations algebraically, and then use a calculator to find the values on the interval [0,2π).[0,2π). Round to four decimal places.

tan2x+3tanx−3=0tan2x+3tanx−3=0

6tan2x+13tanx=−66tan2x+13tanx=−6

tan2x−secx=1tan2x−secx=1

sin2x−2cos2x=0sin2x−2cos2x=0

2tan2x+9tanx−6=02tan2x+9tanx−6=0

4sin2x+sin(2x)secx−3=04sin2x+sin(2x)secx−3=0

For the following exercises, find all solutions exactly to the equations on the interval [0,2π).[0,2π).

csc2x−3cscx−4=0csc2x−3cscx−4=0

sin2x−cos2x−1=0sin2x−cos2x−1=0

sin2x(1−sin2x)+cos2x(1−sin2x)=0sin2x(1−sin2x)+cos2x(1−sin2x)=0

3sec2x+2+sin2x−tan2x+cos2x=03sec2x+2+sin2x−tan2x+cos2x=0

sin2x−1+2cos(2x)−cos2x=1sin2x−1+2cos(2x)−cos2x=1

tan2x−1−sec3xcosx=0tan2x−1−sec3xcosx=0

sin(2x)sec2x=0sin(2x)sec2x=0

sin(2x)2csc2x=0sin(2x)2csc2x=0

2cos2x−sin2x−cosx−5=02cos2x−sin2x−cosx−5=0

1sec2x+2+sin2x+4cos2x=41sec2x+2+sin2x+4cos2x=4

Real-World Applications

An airplane has only enough gas to fly to a city 200 miles northeast of its current location. If the pilot knows that the city is 25 miles north, how many degrees north of east should the airplane fly?

If a loading ramp is placed next to a truck, at a height of 4 feet, and the ramp is 15 feet long, what angle does the ramp make with the ground?

If a loading ramp is placed next to a truck, at a height of 2 feet, and the ramp is 20 feet long, what angle does the ramp make with the ground?

A woman is watching a launched rocket currently 11 miles in altitude. If she is standing 4 miles from the launch pad, at what angle is she looking up from horizontal?

An astronaut is in a launched rocket currently 15 miles in altitude. If a man is standing 2 miles from the launch pad, at what angle is she looking down at him from horizontal? (Hint: this is called the angle of depression.)

A woman is standing 8 meters away from a 10-meter tall building. At what angle is she looking to the top of the building?

A man is standing 10 meters away from a 6-meter tall building. Someone at the top of the building is looking down at him. At what angle is the person looking at him?

A 20-foot tall building has a shadow that is 55 feet long. What is the angle of elevation of the sun?

A 90-foot tall building has a shadow that is 2 feet long. What is the angle of elevation of the sun?

A spotlight on the ground 3 meters from a 2-meter tall man casts a 6 meter shadow on a wall 6 meters from the man. At what angle is the light?

A spotlight on the ground 3 feet from a 5-foot tall woman casts a 15-foot tall shadow on a wall 6 feet from the woman. At what angle is the light?

For the following exercises, find a solution to the word problem algebraically. Then use a calculator to verify the result. Round the answer to the nearest tenth of a degree.

A person does a handstand with his feet touching a wall and his hands 1.5 feet away from the wall. If the person is 6 feet tall, what angle do his feet make with the wall?

A person does a handstand with her feet touching a wall and her hands 3 feet away from the wall. If the person is 5 feet tall, what angle do her feet make with the wall?

A 23-foot ladder is positioned next to a house. If the ladder slips at 7 feet from the house when there is not enough traction, what angle should the ladder make with the ground to avoid slipping?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.2.8: Trigonometric Equations Using Factoring

• Last updated
• Save as PDF
• Page ID 14832

Factoring and the Quadratic Formula.

Solving trig equations is an important process in mathematics. Quite often you'll see powers of trigonometric functions and be asked to solve for the values of the variable which make the equation true. For example, suppose you were given the trig equation

\(2\sin x \cos x=\cos x\)

Trigonometric Equations Using Factoring

You have no doubt had experience with factoring. You have probably factored equations when looking for the possible values of some variable, such as "\(x\)". It might interest you to find out that you can use the same factoring method for more than just a variable that is a number. You can factor trigonometric equations to find the possible values the function can take to satisfy an equation.

Algebraic skills like factoring and substitution that are used to solve various equations are very useful when solving trigonometric equations . As with algebraic expressions, one must be careful to avoid dividing by zero during these maneuvers.

Solving for Unknown Values

1. Solve \(2\sin^2 x−3\sin x+1=0\) for \(0<x \leq 2\pi\).

\(\begin{aligned} \qquad \qquad \quad x^2 \sin^2 x−3\sin x+1&=0 \qquad \text{Factor this like a quadratic equation} \\ \qquad \qquad \quad (2\sin x−1)(\sin x−1)&=0 \end{aligned} \\ \begin{aligned} & \downarrow & \searrow& \\ 2\sin x−1&=0 &\text{or} \quad \sin x−1&=0 \\ 2\sin x&=1 & \sin x&=1 \\ \sin x&=\dfrac{1}{2} & x&=\dfrac{\pi}{2} \\ x=\dfrac{\pi}{6} \text{ and } x&=\dfrac{5\pi}{6} & & \end{aligned} \)

2. Solve \(2 \tan x \sin x+2\sin x=\tan x+1\) for all values of \(x\).

Pull out \(\sin x\)

There is a common factor of \((\tan x+1)\)

Think of the \(−(\tan x+1)\) as \((−1)(\tan x+1)\), which is why there is a \(−1\) behind the \(2 \sin x\).

3. Solve \(2\sin^2 x+3\sin x−2=0\) for all \(x\), \([0,\pi ]\).

\(\begin{aligned} \qquad \quad 2 \sin ^{2} x+3 \sin x-2&=0 \rightarrow \text { Factor like a quadratic }\\ \qquad \quad (2 \sin x-1)(\sin x+2)&=0 \end{aligned} \\ \begin{aligned} \swarrow&& \qquad \searrow &\\ 2 \sin x-1 &=0 & \sin x+2&=0 \\ \sin x&=\dfrac{1}{2} & \sin x&=-2 \end{aligned}\) \(x=\dfrac{\pi}{6} \text { and } x=\dfrac{5 \pi}{6} \text { There is no solution because the range of } \sin x \text { is }[-1,1] \text { . }\)

Some trigonometric equations have no solutions. This means that there is no replacement for the variable that will result in a true expression.

Example \(\PageIndex{1}\)

Earlier, you were asked to solve this:

\(2 \sin x \cos x=\cos x\)

Subtract \(\cos x\) from both sides and factor it out of the equation:

\(\begin{aligned} 2\sin x \cos x−\cos x&=0 \\ \cos x(2\sin x−1)&=0 \end{aligned}\)

Now set each factor equal to zero and solve. The first is \(\cos x\):

\(\begin{aligned} \cos x&=0 \\ x&=\dfrac{\pi}{2},\; \dfrac{3\pi }{2}\end{aligned}\)

And now for the other term:

\(\begin{aligned} 2 \sin x−1&=0 \\ \sin x&=\dfrac{1}{2} \\ x&=\dfrac{\pi}{6},\; \dfrac{5\pi}{6}\end{aligned}\)

Example \(\PageIndex{2}\)

Solve the trigonometric equation \(4 \sin x \cos x+2\cos x−2\sin x−1=0\) such that \(0\leq x<2\pi\).

Use factoring by grouping.

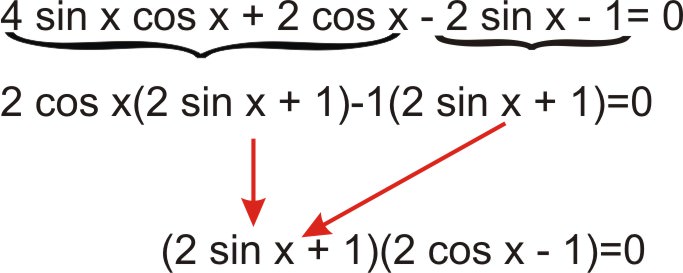
\(\begin{aligned} 2 \sin x+1&=0 & \text { or } \qquad 2 \cos x-1&=0 \\ 2 \sin x&=-1 & 2 \cos x&=1 \\ \sin x&=-\dfrac{1}{2} & \cos x&=\dfrac{1}{2} \\ x&=\dfrac{7 \pi}{6},\; \dfrac{11 \pi}{6} & x&=\dfrac{\pi}{3},\; \dfrac{5 \pi}{3} \end{aligned}\)

Example \(\PageIndex{3}\)

Solve \(\tan^2 x=3\tan x\) for \(x\) over \([0,\pi ]\).

\(\begin{aligned} \tan ^{2} x &=3 \tan x & & &\\ \tan ^{2} x-3 \tan x &=0 & & &\\ \tan x(\tan x-3) &=0 & & &\\ \tan x &=0 \qquad \text { or } \quad &\tan x&=3 \\ x &=0, \pi & x&=1.25 \end{aligned}\)

Example \(\PageIndex{4}\)

Find all the solutions for the trigonometric equation \(2 \sin^2\dfrac{x}{4}−3\cos \dfrac{x}{4}=0\) over the interval \([0,2\pi )\).

\(2\sin^2 \dfrac{x}{4}−3\cos \dfrac{x}{4}=0\)

\(\begin{array}{c} &\qquad \qquad \quad 2\left(1-\cos ^{2} \dfrac{x}{4}\right)-3 \cos \dfrac{x}{4}=0 \\ & \qquad \qquad \quad 2-2 \cos ^{2} \dfrac{x}{4}-3 \cos \dfrac{x}{4}=0 \\ & \qquad \qquad \quad 2 \cos ^{2} \dfrac{x}{4}+3 \cos \dfrac{x}{4}-2=0 \\ &\qquad \qquad \quad \left(2 \cos \dfrac{x}{4}-1\right)\left(\cos \dfrac{x}{4}+2\right)=0 \end{array} \\ \begin{aligned} &\swarrow & \searrow &\\ 2 \cos \dfrac{x}{4}-1&=0 &\text { or } \quad \cos \dfrac{x}{4}+2&=0 \\ 2 \cos \dfrac{x}{4}&=1 & \cos \dfrac{x}{4}&=-2 \\ \cos \dfrac{x}{4}&=\dfrac{1}{2} & & \\ \dfrac{x}{4}=\dfrac{\pi}{3} \quad \text { or } \quad& \dfrac{5 \pi}{3} && \\ x=\dfrac{4 \pi}{3} \quad \text { or }\quad& \dfrac{20 \pi}{3} && \end{aligned}\)

\(\dfrac{20\pi}{3}\) is eliminated as a solution because it is outside of the range and \(\cos x^4=−2\) will not generate any solutions because \(−2\) is outside of the range of cosine. Therefore, the only solution is \(\dfrac{4\pi}{3}\).

Solve each equation for \(x\) over the interval \([0,2\pi )\).

• \(\cos^2 (x)+2 \cos(x)+1=0\)
• \(1−2\sin (x)+\sin^2 (x)=0\)
• \(2\cos (x) \sin (x)−\cos(x)=0\)
• \(\sin (x) \tan^2 (x)−\sin (x) =0\)
• \(\sec^2 (x)=4\)
• \(\sin^2 (x)−2\sin (x) =0\)
• \(3\sin (x) =2\cos^2 (x)\)
• \(2\sin^2 (x)+3\sin (x) =2\)
• \(\tan(x) \sin^2 (x)=\tan(x)\)
• \(2\sin^2 (x)+\sin (x) =1\)
• \(2\cos(x)\tan(x)−\tan (x)=0\)
• \(\sin^2 (x)+\sin (x) =2\)
• \(\tan(x)(2 \cos^2 (x)+3\cos(x)−2)=0\)
• \(\sin^2 (x)+1=2\sin (x)\)
• \(2\cos^2 (x)−3\cos (x)=2\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 3.4.

Additional Resources

Video: Example: Solve a Trig Equation by Factoring

Practice: Trigonometric Equations Using Factoring

Solving Trigonometric Equations using Factoring

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Trigonometry : Factoring Trigonometric Equations

Study concepts, example questions & explanations for trigonometry, all trigonometry resources, example questions, example question #1 : factoring trigonometric equations.

Example Question #171 : Trigonometry

1, 2, and 3

Our first choice is valid.

Therefore, our third answer choice is not correct, meaning only 1 is correct.

Find the zeros of the above equation in the interval

Therefore, 

Example Question #4 : Factoring Trigonometric Equations

Factor the expression

This last expression can be written as :

This shows the required result.

Example Question #5 : Factoring Trigonometric Equations

Factor the following expression:

We know that we can write

This is the result that we need.

Example Question #6 : Factoring Trigonometric Equations

We accept that :

What is a simple expression of

First we see that :

We know that :

We can't factor this expression.

Note first that:

We therefore have :

Example Question #8 : Factoring Trigonometric Equations

Factor the following expression

We cannot factor the above expression.

This shows that we cannot factor the above expression.

Example Question #9 : Factoring Trigonometric Equations

We first note that we have:

Example Question #10 : Factoring Trigonometric Equations

Find a simple expression for the following :

First of all we know that :

we have then:

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Trigonometric equations and identities

About this unit.

In this unit, you'll explore the power and beauty of trigonometric equations and identities, which allow you to express and relate different aspects of triangles, circles, and waves. You'll learn how to use trigonometric functions, their inverses, and various identities to solve and check equations and inequalities, and to model and analyze problems involving periodic motion, sound, light, and more.

Inverse trigonometric functions

• Intro to arcsine (Opens a modal)
• Intro to arctangent (Opens a modal)
• Intro to arccosine (Opens a modal)
• Restricting domains of functions to make them invertible (Opens a modal)
• Domain & range of inverse tangent function (Opens a modal)
• Using inverse trig functions with a calculator (Opens a modal)
• Inverse trigonometric functions review (Opens a modal)
• Trigonometric equations and identities: FAQ (Opens a modal)
• Evaluate inverse trig functions Get 3 of 4 questions to level up!

Sinusoidal equations

• Solving sinusoidal equations of the form sin(x)=d (Opens a modal)
• Cosine equation algebraic solution set (Opens a modal)
• Cosine equation solution set in an interval (Opens a modal)
• Sine equation algebraic solution set (Opens a modal)
• Solving cos(θ)=1 and cos(θ)=-1 (Opens a modal)
• Solve sinusoidal equations (basic) Get 3 of 4 questions to level up!
• Solve sinusoidal equations Get 3 of 4 questions to level up!

Sinusoidal models

• Interpreting solutions of trigonometric equations (Opens a modal)
• Trig word problem: solving for temperature (Opens a modal)
• Trigonometric equations review (Opens a modal)
• Interpret solutions of trigonometric equations in context Get 3 of 4 questions to level up!
• Sinusoidal models word problems Get 3 of 4 questions to level up!

Angle addition identities

• Trig angle addition identities (Opens a modal)
• Using the cosine angle addition identity (Opens a modal)
• Using the cosine double-angle identity (Opens a modal)
• Proof of the sine angle addition identity (Opens a modal)
• Proof of the cosine angle addition identity (Opens a modal)
• Proof of the tangent angle sum and difference identities (Opens a modal)
• Using the trig angle addition identities Get 3 of 4 questions to level up!

Using trigonometric identities

• Finding trig values using angle addition identities (Opens a modal)
• Using the tangent angle addition identity (Opens a modal)
• Using trig angle addition identities: finding side lengths (Opens a modal)
• Using trig angle addition identities: manipulating expressions (Opens a modal)
• Using trigonometric identities (Opens a modal)
• Trig identity reference (Opens a modal)
• Find trig values using angle addition identities Get 3 of 4 questions to level up!

Challenging trigonometry problems

• Trig challenge problem: area of a triangle (Opens a modal)
• Trig challenge problem: area of a hexagon (Opens a modal)
• Trig challenge problem: cosine of angle-sum (Opens a modal)
• Trig challenge problem: arithmetic progression (Opens a modal)
• Trig challenge problem: maximum value (Opens a modal)
• Trig challenge problem: multiple constraints (Opens a modal)
• Trig challenge problem: system of equations (Opens a modal)

Precalculus

Trigonometry, solving trigonometric equations by factoring.

In many cases, the left side of the trigonometric equation

can be factored. If f ( x ) can be represented as

then the solution of the original equation will be all the roots of the equations

which belong to the domain of the original equation f ( x ) = 0 .

Factoring can be done in various ways: by the grouping method, using short multiplication formulas, etc.

For quadratic expressions , the following factoring formula is true:

where \(x_1\) and \(x_2\) are the roots of the equation

For example, the trigonometric equation

contains a quadratic expression whose roots are \({\frac{1}{2}}\) and \(1.\) In this case, this equation is represented in the form

As you can see, the problem is reduced to solving two basic trigonometric equations :

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Pythagorean
• Angle Sum/Difference
• Double Angle
• Multiple Angle
• Negative Angle
• Sum to Product
• Product to Sum
• Proving Identities
• Trigonometric Equations
• Trig Inequalities
• Evaluate Functions
• Conversions

Most Used Actions

Number line.

• \sin (x)+\sin (\frac{x}{2})=0,\:0\le \:x\le \:2\pi
• \cos (x)-\sin (x)=0
• \sin (4\theta)-\frac{\sqrt{3}}{2}=0,\:\forall 0\le\theta<2\pi
• 2\sin ^2(x)+3=7\sin (x),\:x\in[0,\:2\pi ]
• 3\tan ^3(A)-\tan (A)=0,\:A\in \:[0,\:360]
• 2\cos ^2(x)-\sqrt{3}\cos (x)=0,\:0^{\circ \:}\lt x\lt 360^{\circ \:}
• What is tangent equal to?
• The tangent function (tan), is a trigonometric function that relates the ratio of the length of the side opposite a given angle in a right-angled triangle to the length of the side adjacent to that angle.
• How to solve trigonometric equations step-by-step?
• To solve a trigonometric simplify the equation using trigonometric identities. Then, write the equation in a standard form, and isolate the variable using algebraic manipulation to solve for the variable. Use inverse trigonometric functions to find the solutions, and check for extraneous solutions.
• What is a basic trigonometric equation?
• A basic trigonometric equation has the form sin(x)=a, cos(x)=a, tan(x)=a, cot(x)=a
• How to convert radians to degrees?
• The formula to convert radians to degrees: degrees = radians * 180 / π
• What is cotangent equal to?
• The cotangent function (cot(x)), is the reciprocal of the tangent function.cot(x) = cos(x) / sin(x)

trigonometric-equation-calculator

• High School Math Solutions – Trigonometry Calculator, Trig Equations In a previous post, we learned about trig evaluation. It is important that topic is mastered before continuing...

Please add a message.

Message received. Thanks for the feedback.

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

How do you solve trigonometric equations by factoring?

Hence, the solutions are #theta=pi/6, {5pi}/6, {3pi}/2# .

I hope that this was helpful.

Related questions

• How do you find all solutions trigonometric equations?
• How do you express trigonometric expressions in simplest form?
• How do you solve trigonometric equations by the quadratic formula?
• How do you use the fundamental identities to solve trigonometric equations?
• What are other methods for solving equations that can be adapted to solving trigonometric equations?
• How do you solve #\sin^2 x - 2 \sin x - 3 = 0# over the interval #[0,2pi]#?
• How do you find all the solutions for #2 \sin^2 \frac{x}{4}-3 \cos \frac{x}{4} = 0# over the...
• How do you solve #\cos^2 x = \frac{1}{16} # over the interval #[0,2pi]#?
• How do you solve for x in #3sin2x=cos2x# for the interval #0 ≤ x < 2π#
• How do you solve #2cos x+3= sin2x# on the interval [0,2π]?

Impact of this question