problems for solving inequalities

Solving Inequalities

Sometimes we need to solve Inequalities like these:

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

We call that "solved".

Example: x + 2 > 12

Subtract 2 from both sides:

x + 2 − 2 > 12 − 2

x > 10

How to Solve

Solving inequalities is very like solving equations , we do most of the same things ...

... but we must also pay attention to the direction of the inequality .

Some things can change the direction !

< becomes >

> becomes <

≤ becomes ≥

≥ becomes ≤

Safe Things To Do

These things do not affect the direction of the inequality:

• Add (or subtract) a number from both sides
• Multiply (or divide) both sides by a positive number
• Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

But these things do change the direction of the inequality ("<" becomes ">" for example):

• Multiply (or divide) both sides by a negative number
• Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality :

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra ), like this:

Example: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 − 3 < 7 − 3    

And that is our solution: x < 4

In other words, x can be any value less than 4.

What did we do?

And that works well for adding and subtracting , because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5

If we subtract 5 from both sides, we get:

12 − 5 < x + 5 − 5    

That is a solution!

But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

Do you see how the inequality sign still "points at" the smaller value (7) ?

And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

Multiplying or Dividing by a Value

Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying ).

But we need to be a bit more careful (as you will see).

Positive Values

Everything is fine if we want to multiply or divide by a positive number :

Example: 3y < 15

If we divide both sides by 3 we get:

3y /3 < 15 /3

And that is our solution: y < 5

Negative Values

Well, just look at the number line!

For example, from 3 to 7 is an increase , but from −3 to −7 is a decrease.

See how the inequality sign reverses (from < to >) ?

Let us try an example:

Example: −2y < −8

Let us divide both sides by −2 ... and reverse the inequality !

−2y < −8

−2y /−2 > −8 /−2

And that is the correct solution: y > 4

(Note that I reversed the inequality on the same line I divided by the negative number.)

So, just remember:

When multiplying or dividing by a negative number, reverse the inequality

Multiplying or Dividing by Variables

Here is another (tricky!) example:

Example: bx < 3b

It seems easy just to divide both sides by b , which gives us:

... but wait ... if b is negative we need to reverse the inequality like this:

But we don't know if b is positive or negative, so we can't answer this one !

To help you understand, imagine replacing b with 1 or −1 in the example of bx < 3b :

• if b is 1 , then the answer is x < 3
• but if b is −1 , then we are solving −x < −3 , and the answer is x > 3

The answer could be x < 3 or x > 3 and we can't choose because we don't know b .

Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).

A Bigger Example

Example: x−3 2 < −5.

First, let us clear out the "/2" by multiplying both sides by 2.

Because we are multiplying by a positive number, the inequalities will not change.

x−3 2 ×2 < −5  ×2  

x−3 < −10

Now add 3 to both sides:

x−3 + 3 < −10 + 3    

And that is our solution: x < −7

Two Inequalities At Once!

How do we solve something with two inequalities at once?

Example: −2 < 6−2x 3 < 4

First, let us clear out the "/3" by multiplying each part by 3.

Because we are multiplying by a positive number, the inequalities don't change:

−6 < 6−2x < 12

−12 < −2x < 6

Now divide each part by 2 (a positive number, so again the inequalities don't change):

−6 < −x < 3

Now multiply each part by −1. Because we are multiplying by a negative number, the inequalities change direction .

6 > x > −3

And that is the solution!

But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):

−3 < x < 6

• Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own.
• Multiplying or dividing both sides by a negative number
• Don't multiply or divide by a variable (unless you know it is always positive or always negative)

How to Solve Inequalities—Step-by-Step Examples and Tutorial

September 13, 2023 by Anthony Persico

How to Solve Inequalities Explained

Step-by-step guide: how to solve an inequality equation.

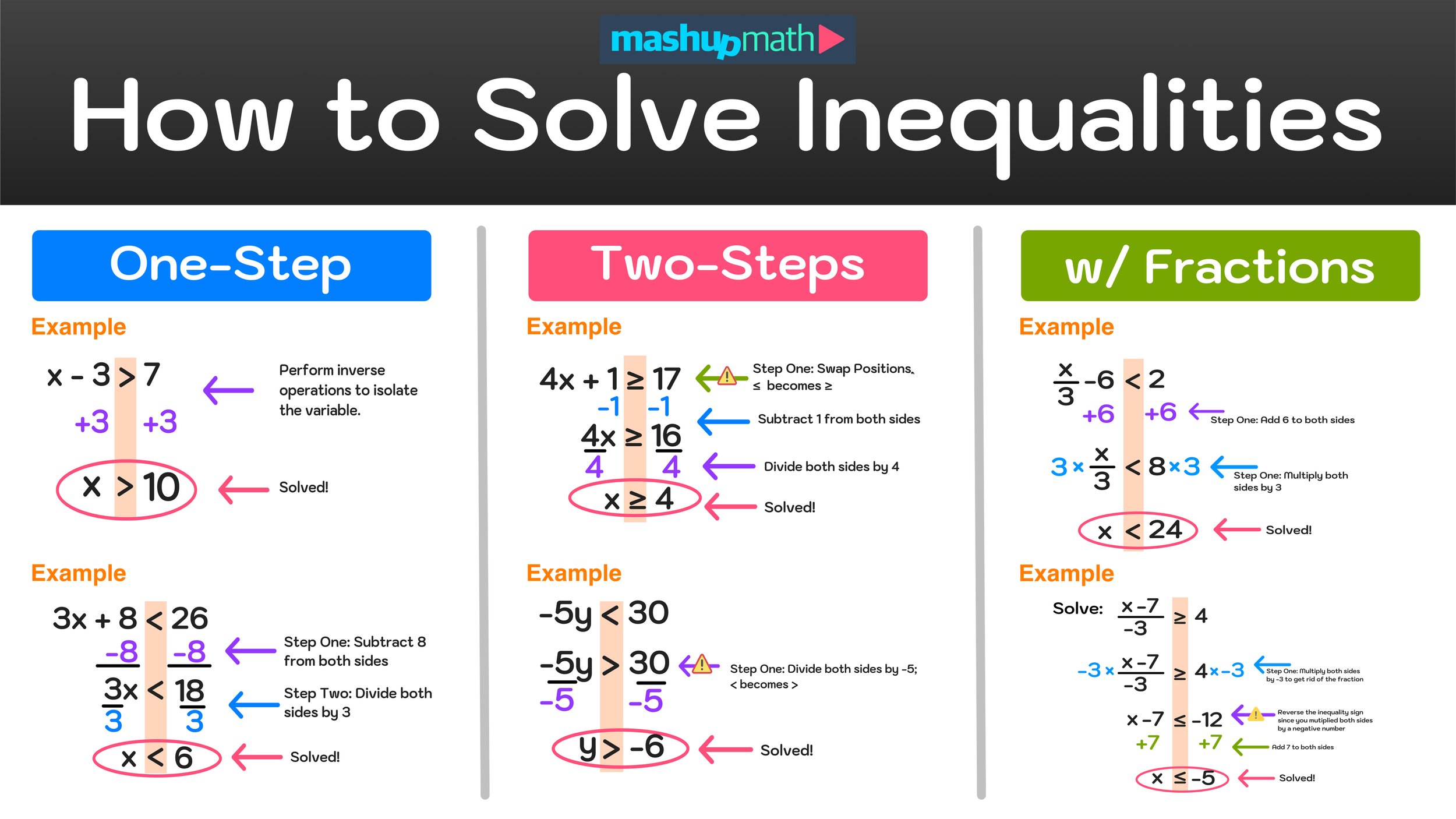
Free Step-by-Step Guide: How to solve inequalities and inequality equations

In math, an inequality is a symbol that is used to represent the relationship between two values or expressions that are not necessarily equal to each other. There are four types of inequality symbols:

> : greater than

< : less than

≥ : greater than or equal to

≤ : less than or equal to

Understanding how to solve inequalities is an important math skill that all students will need to be successful in algebra and beyond. To acquire this skill, you will have to build upon your knowledge of solving equations and extend that understanding to solving inequalities.

This free Step-by-Step Guide on How to Solve Inequalities covers the following:

What is an inequality?

How to Solve Inequalities Example #1 (basic)

How to Solve Inequalities Example #2 (basic)

When do inequality signs reverse direction?

How to Solve Inequalities Example #3 (complex)

How to Solve Inequalities Example #4 (complex)

How to Solve Inequalities with Fractions: Example #5

How to Solve Inequalities with Fractions: Example #6

How to Solve Inequalities Extra Practice: Example #7

How to Solve Inequalities Extra Practice: Example #8

Free Solving Inequalities Worksheet (w/ Answers)

While learning how to solve an inequality is a little trickier than learning how to solve an equation, you can easily learn how to solve inequalities by working through this guide. By working through the step-by-step practice problems below, you will gain plenty of helpful practice with solving inequalities, which will put you on the path of being able to solve any inequality with ease.

While you are probably eager to dive into a few practice problems, let’s start off with a quick review of a few key vocabulary terms that you should deeply understand before you begin learning how to solve an inequality.

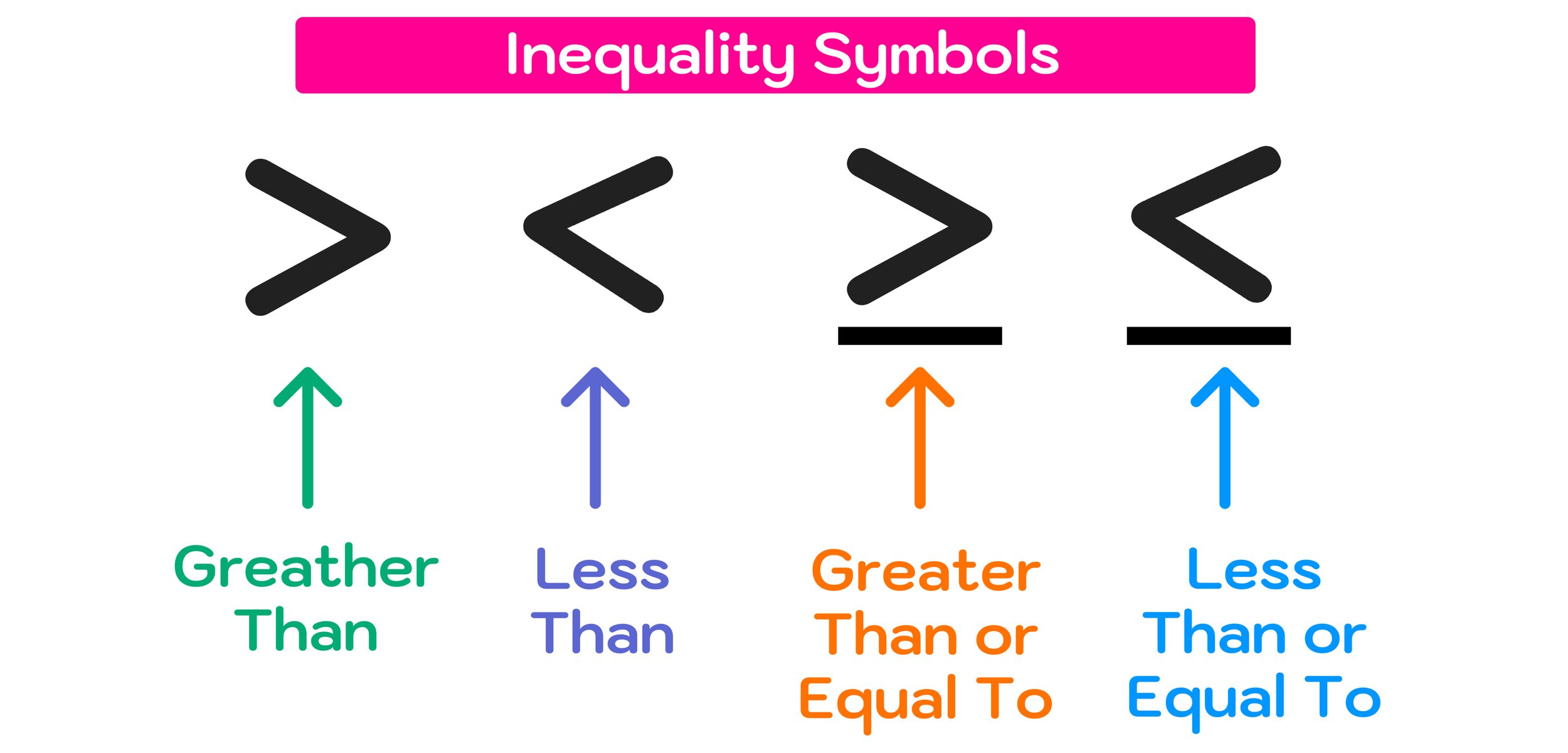
Figure 01: There are four types of inequality symbols: > : greater than, < : less than, ≥ : greater than or equal to, and ≤ : less than or equal to.

As said earlier, in math, an inequality is a relationship between two values or expressions that are not equal to each other. Because the values or expressions are not equal to each other, we have to use an inequality sign instead of an equals (=) sign.

You already know that there are four types of inequalities: > : greater than, < : less than, ≥ : greater than or equal to, and ≤ : less than or equal to (these four types of inequalities are illustrated in Figure 01 above).

Basic inequalities do not need to be solved since the variable is already by itself.

For example, consider the inequalities x>7 and y ≤-3 .

These inequalities can be thought of as solved because the variables are already on their own. These “solved” inequalities are illustrated in Figure 02 below.

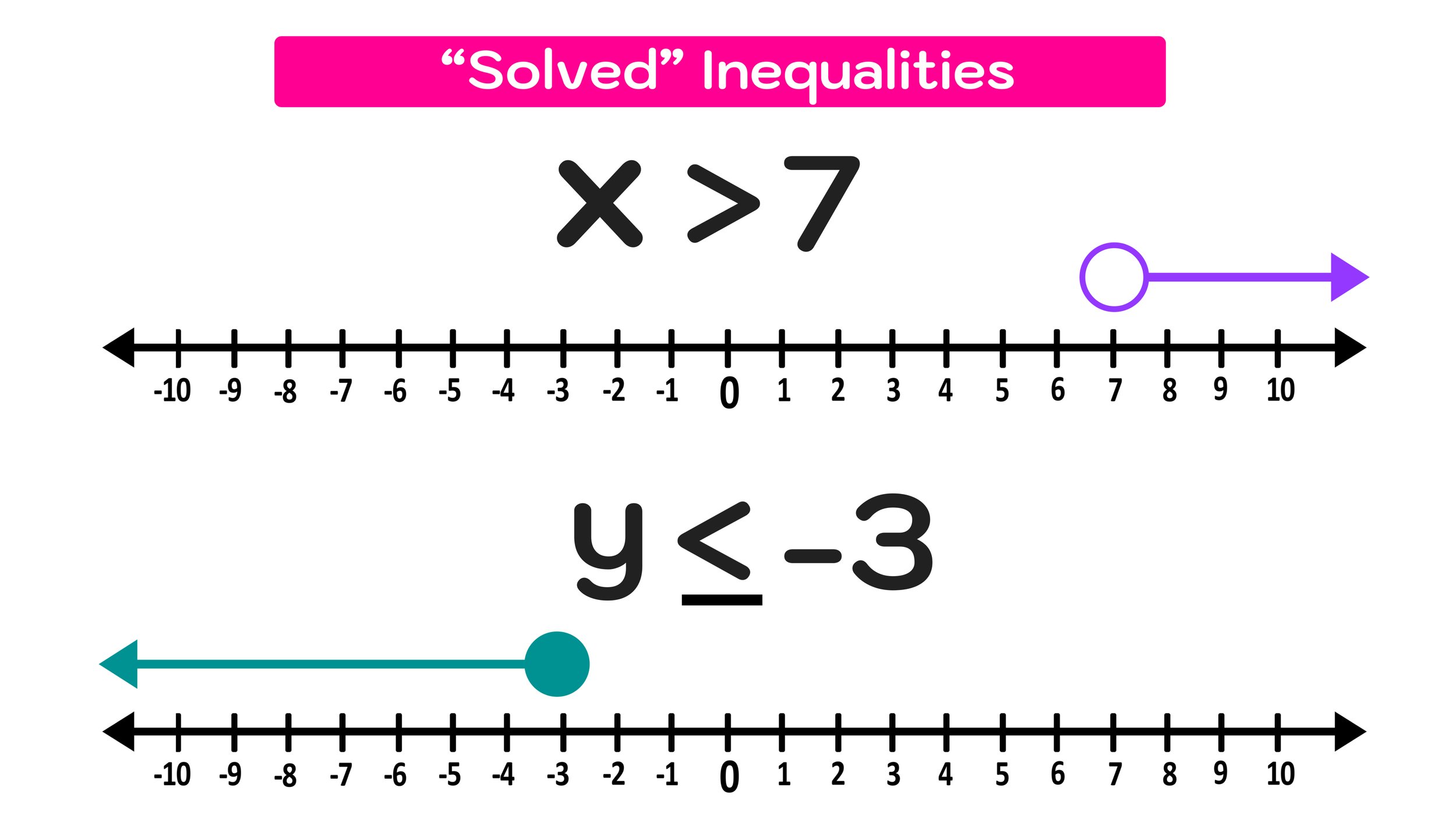
Figure 02: How to solve inequalities. What do solved inequalities look like?

But, what if we had an inequality that looked like this: x - 3 > 7

Since the variable, x, is not by itself, this inequality still needs to be solved, and the remainder of this guide will show you exactly how to do that.

Now that you are familiar with the key vocabulary terms, it’s time to look at a few examples.

How to Solve Inequalities Example #1

Example: x - 3 > 7

Just as you would solve an equation, to solve an inequality, you must use inverse operations to isolate the variable, which, in this example, is x.

You can isolate x easily by adding 3 to both sides of the inequality sign as follows:

x - 3 > 7

x -3 + 3 > 7 +3

Now the inequality is solved! The answer is x>10. The step-by-step procedure to solving this first example is illustrated in Figure 03 below.

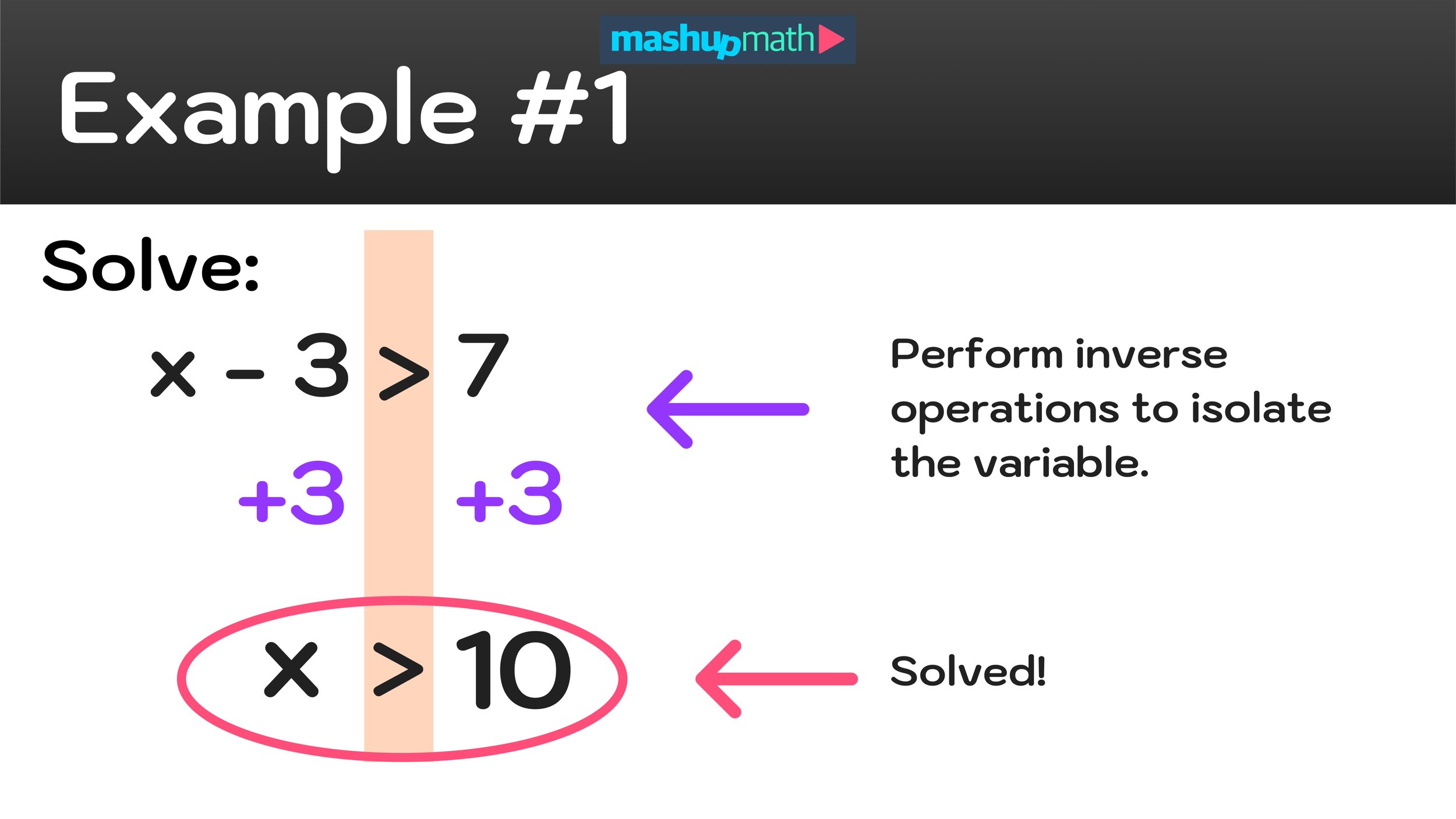
Figure 03: How to solve an inequality: x-3>7

This first example of how to solve inequalities was relatively simple and only took one step to solve. Now, let’s move onto solving a slightly more difficult inequality.

How to Solve Inequalities Example #2

Example: 3x + 8 < 26

Again, to solve the inequality you have to isolate the variable x by performing inverse operations as follows:

3x + 8 < 26

3x - 8 < 26 - 8

3x/3 < 18/3

Solving this example required two steps (step one: subtract 8 from both sides; step two: divide both sides by 3). The result is the solved inequality x<6.

The step-by-step procedure to solving example #2 is illustrated in Figure 04 below.

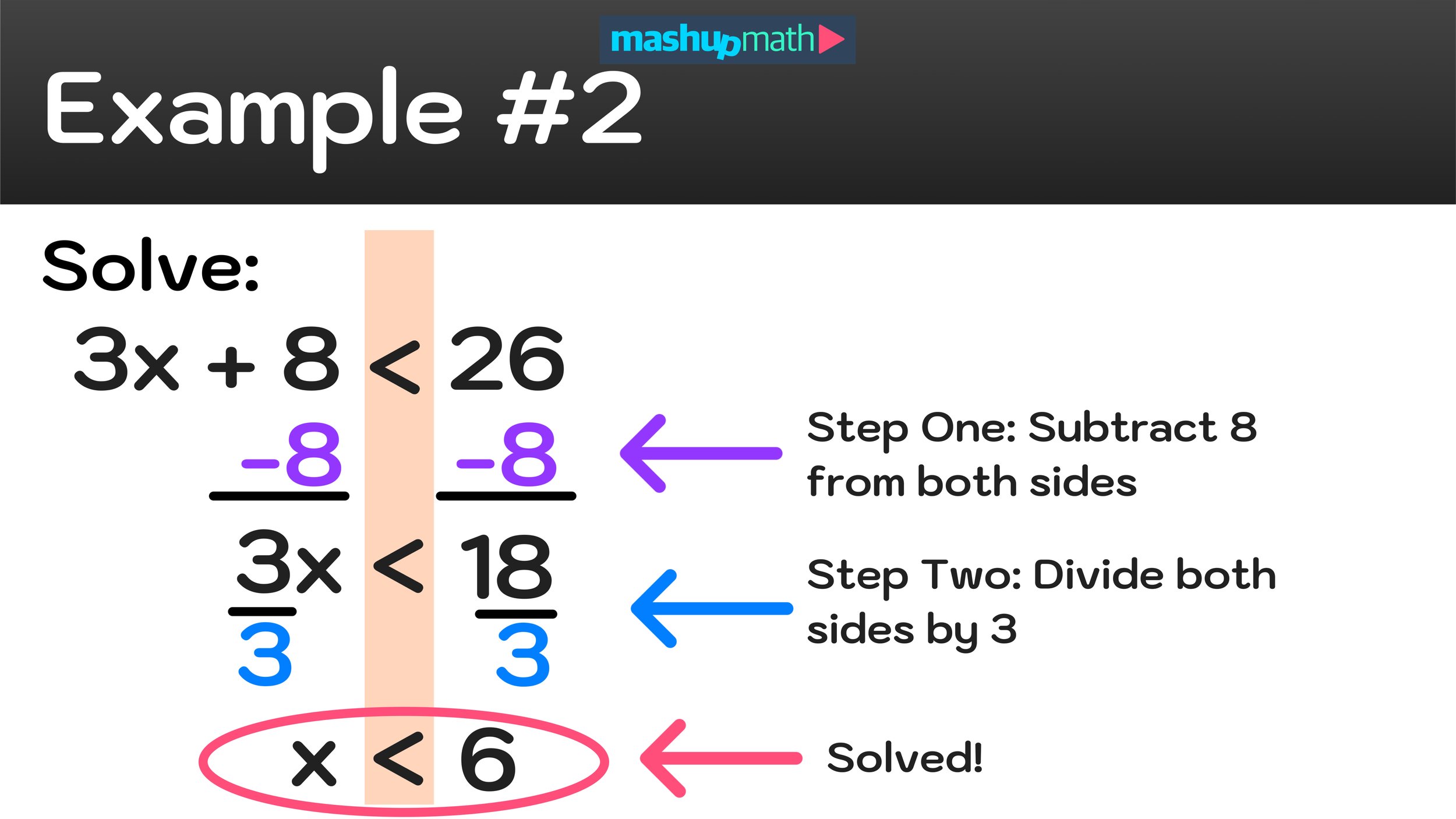
Figure 04: How to solve an inequality: 3x+8<26

When Do Inequality Signs Reverse Directions?

The first two examples of solving inequalities are considered basic and they can both be solved in two steps or less.

However, more complex inequalities can include instances when the inequality sign will reverse direction in one of the following ways:

> becomes <

< becomes >

≥ becomes ≤

≤ becomes ≥

So, when do you have to worry about reversing the direction of an inequality sign?

Let’s start by listing all of the instances when you are safe and do not have to change the direction of the inequality sign.

Whenever you add or subtract a number from both sides of the inequality

Whenever you multiply or divide both sides of the inequality by a positive number

Both of these cases occurred in examples #1 and #2, which is why we did not have to change the direction of the inequality sign.

However, you do have to change the direction of the inequality sign under these instances:

🔄 Whenever you swap the position of the left side of the inequality with the right side of the inequality

🔄 Whenever you multiply or divide both sides of the inequality by a negative number

These rules are illustrated in Figure 05 below.

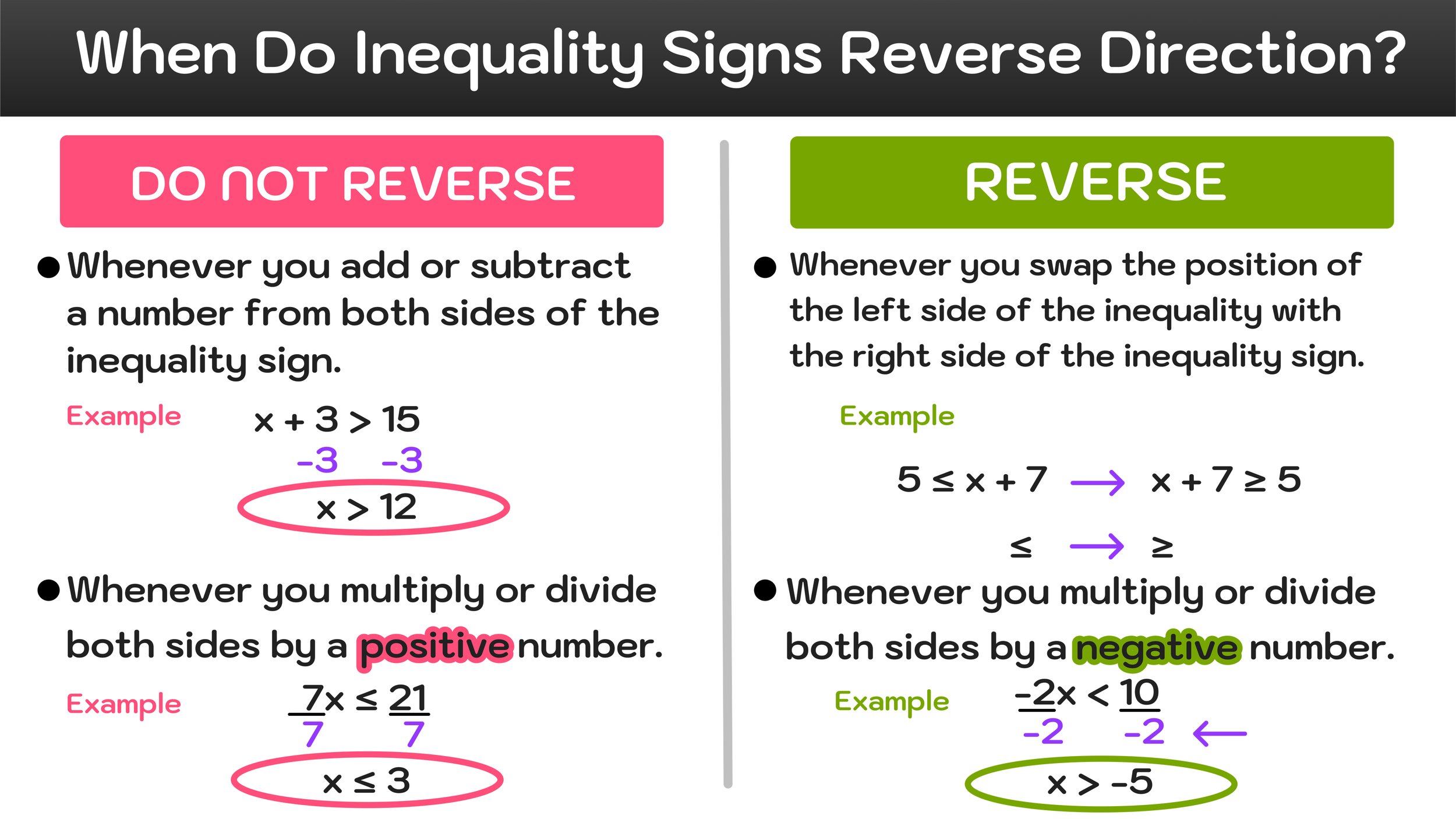
Figure 05: When do inequality signs reverse direction?

Now, let’s take a look at a few examples of solving inequalities where you will have to reverse the direction of the inequality sign.

How to Solve Inequalities Example #3

Example: 17 ≤ 4x + 1

This example is a bit different because the variable, x, is on the right side of the equal sign and we typically express solved inequalities with the variable on the left.

You can still solve this problem the same way that you solved example #2, but first you must swap the left side of the inequality with the right side. However, remember that swapping the position of the left side and the right side requires you to also reverse the direction of the inequality as follows:

17 ≤ 4x + 1 ➙ 4x + 1 ≥ 17

⚠️ Notice that the ≤ reversed position to become ≥ !

Now, you can solve 4x + 1 ≥ 17 as follows:

4x + 1 ≥ 17

4x + 1 -1 ≥ 17 -1

4x/4 ≥ 16/4

The inequality has been solved and the final result is x ≥ 4.

The steps for solving example #3 are detailed in Figure 06 below.

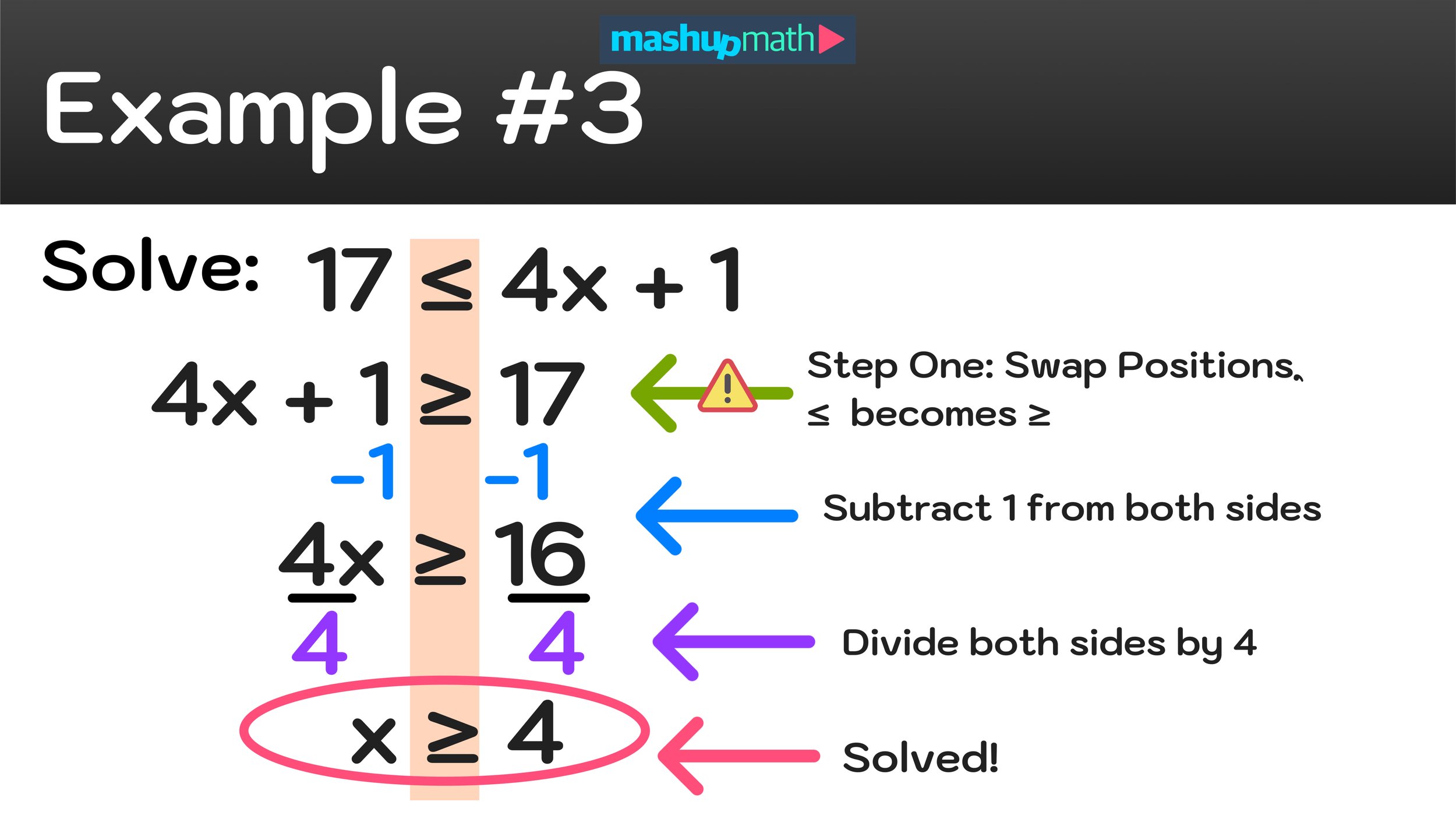
Figure 06: How to solve an inequality when the variable is on the right.

Now that we have covered the first instance of when you have to reverse the direction of an inequality sign, let’s see an example of the second instance—Whenever you multiply or divide both sides of the inequality by a negative number.

How to Solve Inequalities Example #4

Example: -5y < 30

Solving this inequality will require only step to isolate the variable, y, on the left side of the inequality. However, since that one step involves multiplying or dividing by a negative number, you must also reverse the direction of the inequality sign as follows:

-5y < 30

-5y/-5 > 30/-5 (⚠️ since you divided by a negative , < becomes >)

The inequality has been solved and the final result is y > -6.

The steps for solving example #4 are detailed in Figure 07 below.

Figure 07: How to solve an inequality when you have to multiply or divide both sides by a negative number.

How to Solve Inequalities with Fractions

Now that you have some more experience with solving inequalities and you know when you have to reverse the direction of the inequality sign, let’s take a look at two more complex examples that involve fractions.

How to Solve Inequalities with Fractions Example #5

Example: x/3 - 6 < 2

When it comes to solving inequalities with fractions, the same strategy as the previous examples will apply. To solve, you have to use inverse operations to isolate the variable on the left side of the equation.

And, if you have to swap the positions of the left and right sides of the inequality or if you multiply or divide both sides by a negative number, then you will have to reverse the direction of the inequality sign.

You can solve this inequality as follows:

x/3 - 6 < 2

x/3 -6 +6 < 2 + 6

3 x (x/3) < 3 x (8)

The inequality has been solved and the final result is x < 24 .

* Note that this example did not require you to reverse the direction of the inequality sign since you did not have to swap positions or multiply/divide by a negative number.

The step-by-step process for solving example #5 is shown in Figure 08 below.

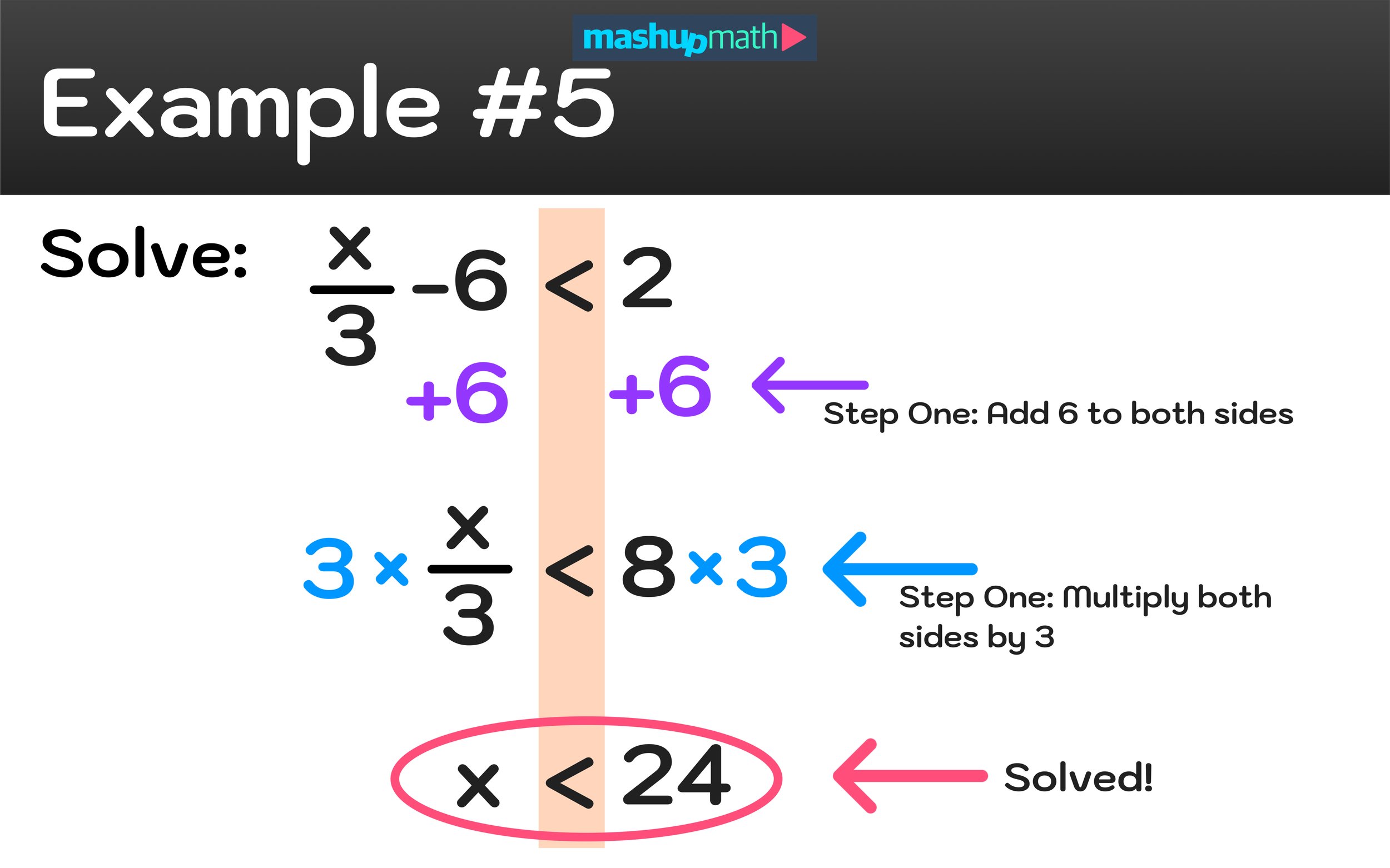
Figure 08: Solving Inequalities with Fractions Example #5

How to Solve Inequalities with Fractions Example #6

Example: (x-7)/-3 ≥ 4

This next example is the most complex one we have seen so far, but our strategy of using inverse operations to isolate the variable remains the same.

(x-7)/-3 ≥ 4

(x-7)/-3 x -3 ≥ 4 x -3 (multiply both sides by -3 to get rid of the fraction)

x-7 ≤ -12 (⚠️ because you multiplied both sides by a negative, ≥ becomes ≤)

x-7 +6 ≤ -12 +7

The inequality has been solved and the final result is x ≤ -5 .

⚠️ Note that we did have to reverse the inequality sign from ≥ to ≤ because we multiplied both sides by negative 3.

The step-by-step process for solving example #5 is shown in Figure 09 below.

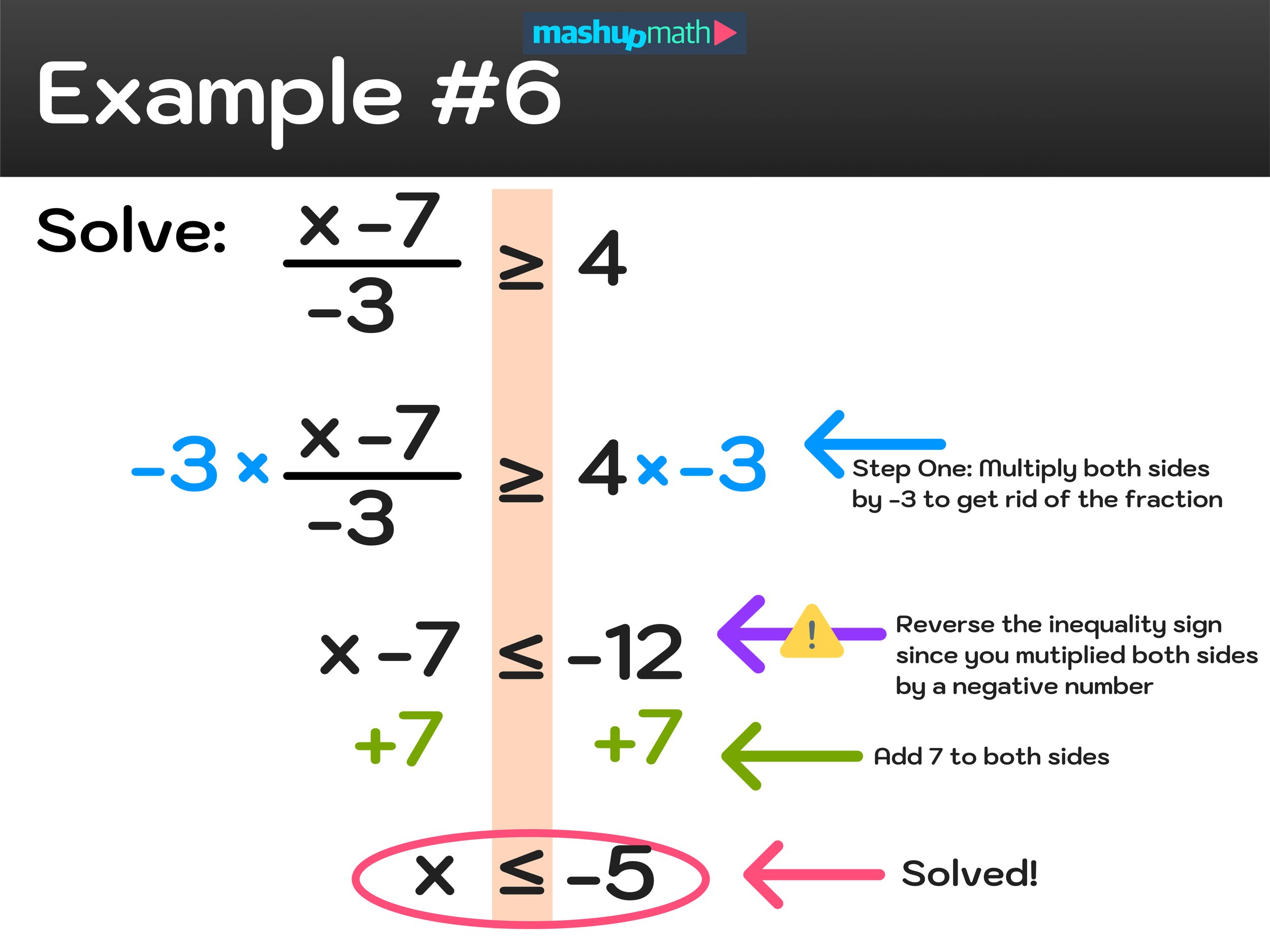
Figure 09: Figure 08: Solving Inequalities with Fractions Example #6

As we enter the last section of this step-by-step guide to solving inequalities, let’s take a look at two more multi-step examples. If you can solve these next two problems using the previously discussed strategies, then you will be able to solve almost any problem related to solving inequalities.

How to Solve Inequalities with Fractions Example #7

Example: -6 > (7y-5)/9

This example will require a few steps in order to isolate the variable x, but we can still used inverse operations to solve as follows:

-6 > (7y-5)/9 ➙ (7y-5)/9 < -6

⚠️ Notice that the variable, y, is on the right side of the inequality sign, so we will start by reversing the positions of the left side and the right side, which also means that we have to reverse the direction of the inequality sign.

(7y-5)/9 < -6

(7y-5)/9 x 9 < -6 x 9

7y-5 < -54

7y -5 +5 < -54 + 5

7y < -49

7y ÷ 7 < -49 ÷ 7

The inequality has been solved and the final result is y < -7 .

Note that we did not have to reverse the inequality sign because the number that we multiplied both sides of the equation by was a positive 9.

The step-by-step process for solving example #7 is shown in Figure 10 below.

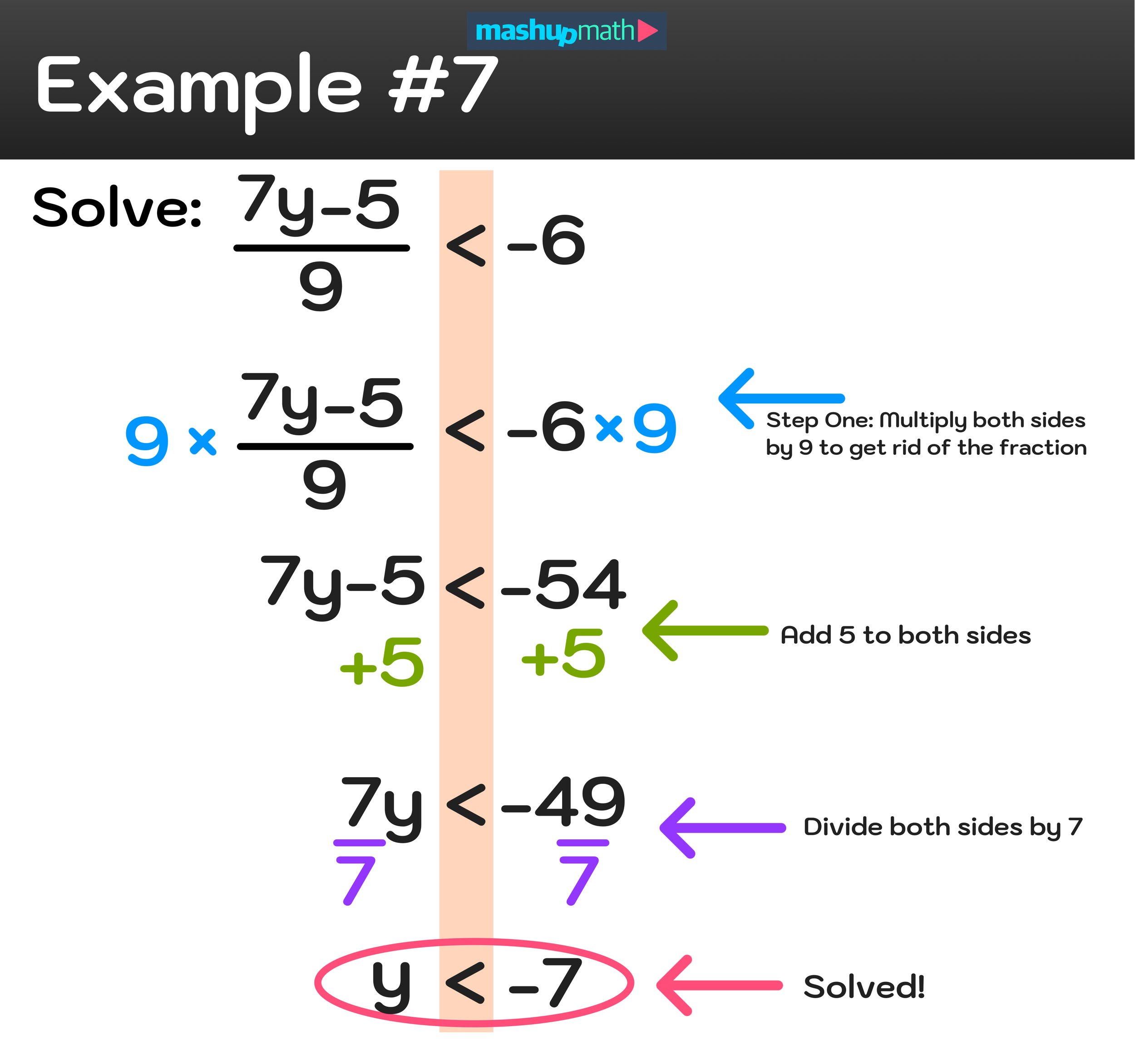
Figure 10: Solving Inequalities with Fractions Example #7

How to Solve Inequalities with Fractions Example #8

Are you ready for one final example of how how to solve inequalities with fractions? This one is a little tricky, but you have all of the tools that you need to solve it as long as you take it step-by-step.

Example: -5x - 6 ≤ (x+17)/-2

The first thing that you are probably noticing is that there are x’s on both sides of the inequality sign. Since the goal is to isolate x on the left side of the inequality, you will have to use inverse operations to get x by itself.

Let’s start by getting rid of the fraction on the right side of the inequality by multiplying both sides by -2.

-2(-5x - 6) ≤ (x+17)/-2(-2)

To solve the right side of the inequality, you will have to use the distributive property to multiply both terms (-5x-6) by -2.

10x + 12 ≥ x+17 ⚠️

⚠️ And because we just multiplied both sides by a negative number, we had to reverse the direction of the inequality sign, so ≤ became ≥

Now we can continue solving this inequality by using inverse operations:

10x + 12 ≥ x+17

10x + 12 -12 ≥ x +17 -12 (move the constants to the right side)

10x ≥ x + 5

10x -x ≥ x -x +5 (move the variables to the left side)

9x ÷ 9 ≥ 5 ÷ 9 (isolate x)

The inequality has been solved and the final result is x ≥ 5/9 .

Note that it’s totally fine for our final result to be a fraction.

The step-by-step process for solving example #8 is shown in Figure 11 below.

Figure 10: Solving Inequalities with Fractions Example #8

Are you looking for some extra independent practice on how to solve inequalities and how to solve inequalities with fractions?

You can use the link below to download a free solving inequalities worksheet pdf file that includes a complete answer key. We recommend that you work through each problem on your own keeping this guide close by as a reference.

▶ Download your free Solving Inequalities Worksheet (One-Step) PDF

▶ Download your free Solving Inequalities Worksheet (Two-Steps) PDF

Preview: Solving Inequalities Worksheet PDF

While you work through the practice problems, keep the lesson summary main points below in mind.

Conclusion: How to Solve Inequalities

Like equations, inequalities can be solved by using inverse operations to isolate a variable on the left side of the inequality.

Solving an inequality by adding/subtracting numbers on both sides of the inequality or by multiplying/dividing both sides by a positive number does not result in a reversal of the inequality sign.

⚠️ On the other hand, swapping the positions of the left and right sides of an inequality or multiplying/dividing both sides by a negative number requires you to reverse the position of the inequality sign such that: > becomes <, < becomes > , ≥ becomes ≤ , and ≤ becomes ≥

When solving inequalities with fractions or inequalities with variables on both sides, the process of using inverse operations to isolate the variable and solve remains the same, albeit with a few more steps involved.

Keep Learning:

Free Guide: How to Solve Compound Inequalities in 3 Easy Steps

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

In order to access this I need to be confident with:

Solving inequalities

Here you will learn about solving inequalities, including how to solve linear inequalities, identify integers in the solution set, and represent solutions on a number line.

Students will first learn about solving simple inequalities as part of expressions and equations in 6th grade math and expand that knowledge in 7th grade math.

What is solving inequalities?

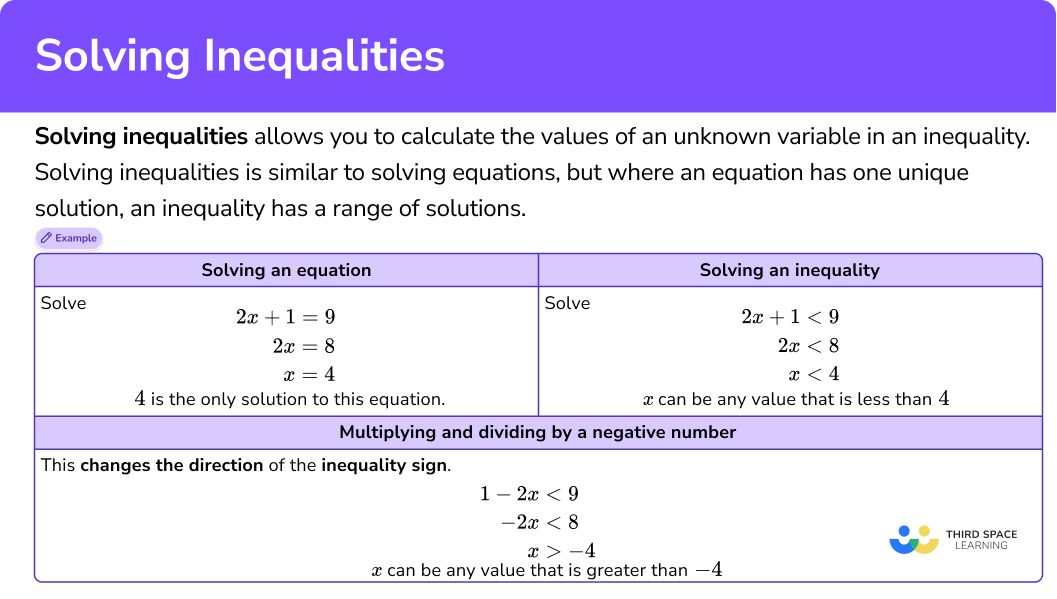
Solving inequalities allows you to calculate the values of an unknown variable in an inequality.

Solving inequalities is similar to solving equations, but where an equation has one unique solution, an inequality has a range of solutions.

In order to solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.

For example,

Common Core State Standards

How does this relate to 6th grade and 7th grade math?

• Grade 6 – Expressions and Equations (6.EE.B.8) Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
• Grade 7 – Expressions and Equations (7.EE.4b) Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid \$50 per week plus \$3 per sale. This week you want your pay to be at least \$100. Write an inequality for the number of sales you need to make, and describe the solutions.

How to solve inequalities

In order to solve inequalities:

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.

Write your solution with the inequality symbol.

[FREE] Solving Inequalities Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of solving inequalities. 15 questions with answers to identify areas of strength and support!

Solving linear inequalities examples

Example 1: solving linear inequalities.

4 x+6<26

In this case you are subtracting 6 from both sides.

\begin{aligned} 4x+6&<26\\ 4x&<20 \end{aligned}

This leaves 4x on the left side of the inequality sign and 20 on the right side.

2 Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.

In this case you need to divide both sides by 4.

\begin{aligned} 4x&<20\\ x&<5 \end{aligned}

This leaves x on the left side of the inequality sign and 5 on the right side.

3 Write your solution with the inequality symbol.

Any value less than 5 satisfies the inequality.

Example 2: solving linear inequalities

5x-4 \geq 26

In this case you need to add 4 to both sides.

\begin{aligned} 5x-4&\geq26\\ 5x&\geq30 \end{aligned}

This leaves 5x on the left side of the inequality sign and 30 on the right side.

In this case you need to divide both sides by 5.

\begin{aligned} 5x&\geq30\\ x&\geq6 \end{aligned}

This leaves x on the left side of the inequality sign and 6 on the right side.

Any value greater than or equal to 6 satisfies the inequality.

Example 3: solving linear inequalities with parentheses

3(x-4)\leq12

Let’s start by expanding the parentheses.

3x-12\leq12

Then you need to add 12 to both sides.

\begin{aligned} 3x-12&\leq12\\ 3x&\leq24 \end{aligned}

This leaves 3x on the left side of the inequality sign and 24 on the right side.

In this case you need to divide both sides by 3.

\begin{aligned} 3x&\leq24\\ x&\leq8 \end{aligned}

This leaves x on the left side of the inequality sign and 8 on the right side.

Any value less than or equal to 8 satisfies the inequality.

Example 4: solving linear inequalities with unknowns on both sides

5x-6 > 2x + 15

In this case you need to subtract 2x from both sides.

\begin{aligned} 5x-6&>2x+15\\ 3x-6&>15 \end{aligned}

This leaves 3x-6 on the left side of the inequality sign and 15 on the right side.

Rearrange the inequality so that \textbf{‘x’} s are on one side of the inequality sign and numbers on the other.

In this case you need to add 6 to both sides.

\begin{aligned} 3x-6&>15\\ 3x&>21 \end{aligned}

This leaves 3x on the left side of the inequality sign and 21 on the right side.

\begin{aligned} 3x&>21\\ x&>7 \end{aligned}

This leaves x on the left side of the inequality sign and 7 on the right side.

Any value greater than 7 satisfies the inequality.

Example 5: solving linear inequalities with fractions

\cfrac{x+3}{5}<2

Rearrange the inequality to eliminate the denominator.

In this case you need to multiply both sides by 5.

\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10 \end{aligned}

In this case you need to subtract 3 from both sides.

\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10\\ x&<7 \end{aligned}

Any value less than 7 satisfies the inequality.

Example 6: solving linear inequalities with non-integer solutions

In this case you need to subtract 6 from both sides.

\begin{aligned} 6x+1&\geq4\\ 6x&\geq3 \end{aligned}

In this case you need to divide both sides by 6.

\begin{aligned} 6x+1&\geq4\\ 6x&\geq3\\ x&\geq\cfrac{3}{6} \end{aligned}

This can be simplified to \, \cfrac{1}{2} \, or the decimal equivalent.

x\geq\cfrac{1}{2}

Any value greater than or equal to \, \cfrac{1}{2} \, satisfies the inequality.

Example 7: solving linear inequalities and representing solutions on a number line

Represent the solution on a number line:

2x-7 < 5

In this case you need to add 7 to both sides.

\begin{aligned} 2x-7&<5\\ 2x&<12 \end{aligned}

In this case you need to divide both sides by 2.

\begin{aligned} 2x-7& <5\\ 2x& <12\\ x& < 6 \end{aligned}

Represent your solution on a number line.

Any value less than 6 satisfies the inequality. An open circle is required at 6 and the values lower than 6 indicated with an arrow.

Example 8: solving linear inequalities with negative x coefficients

In this case you need to subtract 1 from both sides.

\begin{aligned} 1-2x & <7 \\ -2x & <6 \end{aligned}

In this case you need to divide both sides by negative 2.

6 \div-2=-3

Change the direction of the inequality sign.

Because you divided by a negative number, you also need to change the direction of the inequality sign.

\begin{aligned} 1-2x & <7 \\ -2x & <6 \\ x &>-3 \end{aligned}

Example 9: solving linear inequalities and listing integer values that satisfy the inequality

List the integer values that satisfy:

3 < x+1\leq8

In this case you need to subtract 1 from each part.

\begin{aligned} 3&<x+1\leq8\\ 2&<x\leq7\\ \end{aligned}

List the integer values satisfied by the inequality.

2<x\leq7

2 is not included in the solution set. 7 is included in the solution set. The integers that satisfy this inequality are:

3, 4, 5, 6, 7

Example 10: solving linear inequalities and listing integer values that satisfy the inequality

7\leq4x\leq20

In this case you need to divide each part by 4.

\begin{aligned} 7\leq \, & 4x\leq20\\ \cfrac{7}{4}\leq & \; x \leq5 \end{aligned}

\cfrac{7}{4} \leq x \leq 5

\cfrac{7}{4} \, is included in the solution set but it is not an integer.

The first integer higher is 2.

5 is also included in the solution set.

The integers that satisfy this inequality are:

Example 11: solving linear inequalities and representing the solution on a number line

-3<2x+5\leq7

In this case you need to subtract 5 from each part.

\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2 \end{aligned}

Rearrange the inequality so that \textbf{‘x’} is isolated. In this case you need to divide each part by \bf{2} .

\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2\\ -4<x&\leq1 \end{aligned}

Represent the solution set on a the number line

-4<x\leq1

-4 is not included in the solution set so requires an open circle. 1 is included in the solution set so requires a closed circle.

Put a solid line between the circles to indicate all the values that satisfy the solution set.

Teaching tips for solving inequalities

• Students should master solving simple inequalities (one-step inequalities) before moving on to two-step inequalities (or multi-step inequalities).
• Foster student engagement by practicing solving inequalities through classroom games such as BINGO rather than daily worksheets.
• Student practice problems should have a variety of inequalities such as inequalities with fractions, negative numbers, and parentheses. (see examples above)

Easy mistakes to make

• Solutions as inequalities Not including the inequality symbol in the solution is a common mistake. An inequality has a range of values that satisfy it rather than a unique solution so the inequality symbol is essential. For example, when solving x + 3 < 7 giving a solution of 4 or x = 4 is incorrect, the answer must be written as an inequality x < 4 .
• Balancing inequalities Errors can be made with solving equations and inequalities by not applying inverse operations or not balancing the inequalities. Work should be shown step-by-step with the inverse operations applied to both sides of the inequality. For example, when solving x + 3 < 7 , adding 3 to both sides rather than subtracting 3 from both sides.

Related inequalities lessons

• Inequalities
• Linear inequalities
• Inequalities on a number line
• Graphic inequalities
• Quadratic inequalities
• Greater than sign
• Less than sign

Practice solving inequalities questions

3x+7 < 31

\begin{aligned} 3x+7&<31\\ 3x&<24\\ x&<8 \end{aligned}

\begin{aligned} 4x-3&\geq25\\ 4x&\geq28\\ x&\geq7 \end{aligned}

2(x-5)\leq8

\begin{aligned} 2(x-5)&\leq8\\ 2x-10&\leq8\\ 2x&\leq18\\ x&\leq9 \end{aligned}

6x-5 > 4x + 1

\begin{aligned} 6x-5&>4x+1\\ 2x-5&>1\\ 2x&>6\\ x&>3 \end{aligned}

\cfrac{x-4}{2}>6

\begin{aligned} \cfrac{x-4}{2}&>6\\ x-4&>12\\ x&>16 \end{aligned}

\begin{aligned} 8x+1&\geq3\\ 8x&\geq2\\ x&\geq\cfrac{2}{8}\\ x&\geq\cfrac{1}{4} \end{aligned}

7. Represent the solution on a number line.

5x-2 < 28

\begin{aligned} 5x-2&<28\\ 5x&<30\\ x&<6 \end{aligned}

An open circle is required and all values less than 6 indicated.

2-3x > 14

\begin{aligned} 2-3x &>14 \\ -3x &>12 \\ x &< -4 \end{aligned}

Change the direction of the inequality sign as you have divided by a negative number.

9. List the integer values that satisfy:

2<x+3\leq5

\begin{aligned} 2<x&+3\leq5\\ -1< \, &x\leq2 \end{aligned}

-1 is not included in the solution set as is greater than -1.

2 is included in the solution set as x is less than or equal to 2.

10. List the integer values that satisfy:

4\leq3x\leq21

\begin{aligned} 4\leq3&x\leq21\\ \cfrac{4}{3} \, \leq \, &x\leq7 \end{aligned}

The first integer greater than \, \cfrac{4}{3} \, is 2.

7 is included in the solution set as x is less than or equal to 7.

11. List the integer values that satisfy:

-4<3x+2\leq5

\begin{aligned} -4<3x&+2\leq5\\ -6<3&x\leq3\\ -2< \, &x\leq1 \end{aligned}

-2 is not included in the solution set as x is greater than -2.

1 is included in the solution set as x is less than or equal to 1.

Solving inequalities FAQs

Solving inequalities is where you calculate the values that an unknown variable can be in an inequality.

To solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.

The next lessons are

• Types of graphs
• Math formulas
• Coordinate plane

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.5: Solve Inequalities

• Last updated
• Save as PDF
• Page ID 51443

Learning Objectives

Represent inequalities on a number line, represent inequalities using interval notation.

• Use the addition and multiplication properties to solve algebraic inequalities and express their solutions graphically and with interval notation
• Solve inequalities that contain absolute value
• Combine properties of inequality to isolate variables, solve algebraic inequalities, and express their solutions graphically
• Simplify and solve algebraic inequalities using the distributive property to clear parentheses and fractions

First, let’s define some important terminology. An inequality is a mathematical statement that compares two expressions using the ideas of greater than or less than. Special symbols are used in these statements. When you read an inequality, read it from left to right—just like reading text on a page. In algebra, inequalities are used to describe large sets of solutions. Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite amount of numbers, we have developed some ways to describe very large lists in succinct ways.

The first way you are probably familiar with—the basic inequality. For example:

• \({x}\lt{9}\) or try to list all the possible numbers that are less than 9? (hopefully, your answer is no)

Note how placing the variable on the left or right of the inequality sign can change whether you are looking for greater than or less than.

For example:

• \(x\lt5\) means all the real numbers that are less than 5, whereas;
• \(x\gt{5}\) note how the inequality is still pointing the same direction relative to x. This statement represents all the real numbers that are greater than 5, which is easier to interpret than 5 is less than x.

The second way is with a graph using the number line:

And the third way is with an interval.

We will explore the second and third ways in depth in this section. Again, those three ways to write solutions to inequalities are:

• an inequality
• an interval

Inequality Signs

The box below shows the symbol, meaning, and an example for each inequality sign. Sometimes it’s easy to get tangled up in inequalities, just remember to read them from left to right.

The inequality \({y}<{x}\). The sides of any inequality can be switched as long as the inequality symbol between them is also reversed.

Graphing an Inequality

Inequalities can also be graphed on a number line. Below are three examples of inequalities and their graphs. Graphs are a very helpful way to visualize information – especially when that information represents an infinite list of numbers!

\(x\leq -4\). This translates to all the real numbers on a number line that are less than or equal to 4.

\({x}\geq{-3}\). This translates to all the real numbers on the number line that are greater than or equal to -3.

Each of these graphs begins with a circle—either an open or closed (shaded) circle. This point is often called the end point of the solution. A closed, or shaded, circle is used to represent the inequalities greater than or equal to \(\displaystyle \left(\leq\right)\). The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution.

The graph then extends endlessly in one direction. This is shown by a line with an arrow at the end. For example, notice that for the graph of \(−3\), represented with a closed circle since the inequality is greater than or equal to \(−3\). The arrow at the end indicates that the solutions continue infinitely.

Graph the inequality \(x\ge 4\) [reveal-answer q=”797241″]Show Solution[/reveal-answer] [hidden-answer a=”797241″]

We can use a number line as shown. Because the values for x include 4, we place a solid dot on the number line at 4.

[/hidden-answer]

This video shows an example of how to draw the graph of an inequality.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

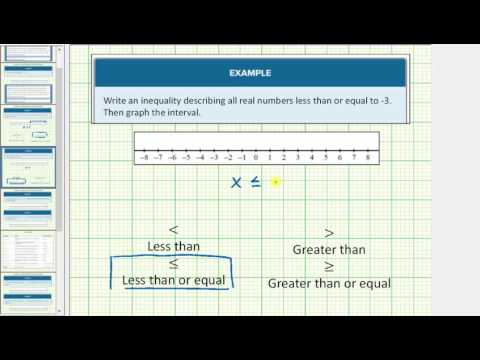
Write an inequality describing all the real numbers on the number line that are less than 2, then draw the corresponding graph. [reveal-answer q=”867890″]Show Solution[/reveal-answer] [hidden-answer a=”867890″]

We need to start from the left and work right, so we start from negative infinity and end at \(-2\).

Inequality: \(x<2\)

To draw the graph, place an open dot on the number line first, then draw a line extending to the left. Draw an arrow at the leftmost point of the line to indicate that it continues for infinity.

The following video shows how to write an inequality mathematically when it is given in words. We will then graph it.

Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. With this convention, sets are built with parentheses or brackets, each having a distinct meaning. The solutions to \(\left[4,\infty \right)\). This method is widely used and will be present in other math courses you may take.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval , or a set of numbers in which a solution falls, are \(-2\) and \(-2\), but not including \(\left(-1,0\right)\), all real numbers between, but not including \(0\); and \(1\). The table below outlines the possibilities. Remember to read inequalities from left to right, just like text.

The table below describes all the possible inequalities that can occur and how to write them using interval notation, where a and b are real numbers.

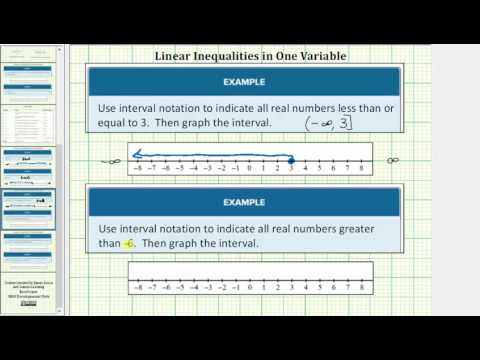
Describe the inequality \(x\ge 4\) using interval notation [reveal-answer q=”817362″]Show Solution[/reveal-answer] [hidden-answer a=”817362″]

The solutions to \(\left[4,\infty \right)\).

Note the use of a bracket on the left because 4 is included in the solution set.

In the following video we show another example of using interval notation to describe an inequality.

Use interval notation to indicate all real numbers greater than or equal to \(-2\). [reveal-answer q=”961990″]Show Solution[/reveal-answer] [hidden-answer a=”961990″]

Use a bracket on the left of \(\left[-2,\infty \right)\). The bracket indicates that \(-2\) to infinity.

In the following video we show another example of translating words into an inequality and writing it in interval notation, as well as drawing the graph.

Think About It

In the previous examples you were given an inequality or a description of one with words and asked to draw the corresponding graph and write the interval. In this example you are given an interval and asked to write the inequality and draw the graph.

Given \(\left(-\infty,10\right)\), write the associated inequality and draw the graph.

In the box below, write down whether you think it will be easier to draw the graph first or write the inequality first.

[practice-area rows=”1″][/practice-area] [reveal-answer q=”15120″]Show Solution[/reveal-answer]

[hidden-answer a=”15120″]

We will draw the graph first.

The interval reads “all real numbers less than 10,” so we will start by placing an open dot on 10 and drawing a line to the left with an arrow indicating the solution continues to negative infinity.

To write the inequality, we will use < since the parentheses indicate that 10 is not included. \(x<10\)

In the following video, you will see examples of how to draw a graph given an inequality in interval notation.

And finally, one last video that shows how to write inequalities using a graph, with interval notation and as an inequality.

Solve Single-Step Inequalities

Solve inequalities with addition and subtraction.

You can solve most inequalities using inverse operations as you did for solving equations. This is because when you add or subtract the same value from both sides of an inequality, you have maintained the inequality. These properties are outlined in the box below.

Addition and Subtraction Properties of Inequality

If \(a+c>b+c\).

If \(a−c>b−c\).

Because inequalities have multiple possible solutions, representing the solutions graphically provides a helpful visual of the situation, as we saw in the last section. The example below shows the steps to solve and graph an inequality and express the solution using interval notation.

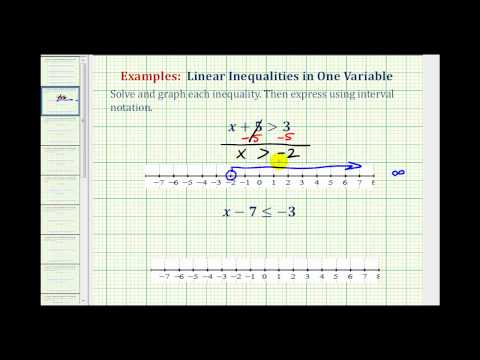
Solve for x.

\({x}+3\lt{5}\)

[reveal-answer q=”952771″]Show Solution[/reveal-answer] [hidden-answer a=”952771″]

It is helpful to think of this inequality as asking you to find all the values for x , including negative numbers, such that when you add three you will get a number less than 5.

\(\displaystyle \begin{array}{l}x+3<\,\,\,\,5\\\underline{\,\,\,\,\,-3\,\,\,\,-3}\\x\,\,\,\,\,\,\,\,<\,\,\,\,2\,\,\end{array}\)

Isolate the variable by subtracting 3 from both sides of the inequality.

Interval: \(\left(-\infty, 2\right)\)

The line represents all the numbers to which you can add 3 and get a number that is less than 5. There’s a lot of numbers that solve this inequality!

Just as you can check the solution to an equation, you can check a solution to an inequality. First, you check the end point by substituting it in the related equation. Then you check to see if the inequality is correct by substituting any other solution to see if it is one of the solutions. Because there are multiple solutions, it is a good practice to check more than one of the possible solutions. This can also help you check that your graph is correct.

The example below shows how you could check that \(x+3<5\) .

Check that \(x+3<5\).

[reveal-answer q=”811564″]Show Solution[/reveal-answer] [hidden-answer a=”811564″]

Substitute the end point 2 into the related equation, \(x+3=5\).

\(\begin{array}{r}x+3=5 \\ 2+3=5 \\ 5=5\end{array}\)

Pick a value less than 2, such as 0, to check into the inequality. (This value will be on the shaded part of the graph.)

\(\displaystyle \begin{array}{r}x+3<5 \\ 0+3<5 \\ 3<5\end{array}\)

\(x+3<5\).[/hidden-answer]

The following examples show inequality problems that include operations with negative numbers. The graph of the solution to the inequality is also shown. Remember to check the solution. This is a good habit to build!

Solve for x : \(x-10\leq-12\) [reveal-answer q=”815894″]Show Solution[/reveal-answer] [hidden-answer a=”815894″]

Isolate the variable by adding 10 to both sides of the inequality.

\(\displaystyle \begin{array}{r}x-10\le -12\\\underline{\,\,\,+10\,\,\,\,\,+10}\\x\,\,\,\,\,\,\,\,\,\,\le \,\,\,-2\end{array}\)

Check the solution to \(x-10\leq -12\) [reveal-answer q=”268062″]Show Solution[/reveal-answer] [hidden-answer a=”268062″]

Substitute the end point \(x-10=−12\)

\(\displaystyle \begin{array}{r}x-10=-12\,\,\,\\\text{Does}\,\,\,-2-10=-12?\\-12=-12\,\,\,\end{array}\)

Pick a value less than \(−5\), to check in the inequality. (This value will be on the shaded part of the graph.)

\(\displaystyle \begin{array}{r}x-10\le -12\,\,\,\\\text{ }\,\text{ Is}\,\,-5-10\le -12?\\-15\le -12\,\,\,\\\text{It}\,\text{checks!}\end{array}\)

\(x-10\leq -12\)

Solve for a . \(a-17>-17\) [reveal-answer q=”343031″]Show Solution[/reveal-answer] [hidden-answer a=”343031″]

Isolate the variable by adding 17 to both sides of the inequality.

\(\displaystyle \begin{array}{r}a-17>-17\\\underline{\,\,\,+17\,\,\,\,\,+17}\\a\,\,\,\,\,\,\,\,\,\,\,>\,\,\,\,\,\,0\end{array}\)

Inequality: \(\displaystyle a\,\,>\,0\)

Interval: \(\left(0,\infty\right)\) Note how we use parentheses on the left to show that the solution does not include 0.

Graph: Note the open circle to show that the solution does not include 0.

Check the solution to \(a-17>-17\) [reveal-answer q=”653357″]Show Solution[/reveal-answer] [hidden-answer a=”653357″]

Is \(a-17>-17\)?

Substitute the end point 0 into the related equation.

\(\displaystyle \begin{array}{r}a-17=-17\,\,\,\\\text{Does}\,\,\,0-17=-17?\\-17=-17\,\,\,\end{array}\)

Pick a value greater than 0, such as 20, to check in the inequality. (This value will be on the shaded part of the graph.)

\(\displaystyle \begin{array}{r}a-17>-17\,\,\,\\\text{Is }\,\,20-17>-17?\\3>-17\,\,\,\\\\\text{It checks!}\,\,\,\,\end{array}\)

\(a-17>-17\)

The previous examples showed you how to solve a one-step inequality with the variable on the left hand side. The following video provides examples of how to solve the same type of inequality.

What would you do if the variable were on the right side of the inequality? In the following example, you will see how to handle this scenario.

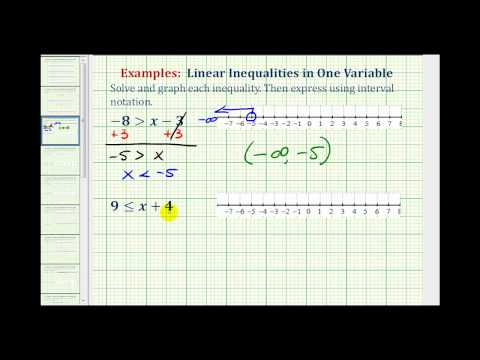
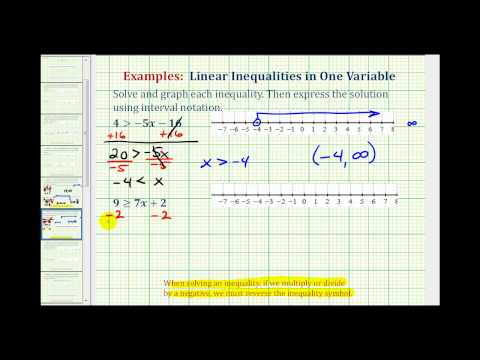
Solve for x : \(4\geq{x}+5\) [reveal-answer q=”815893″]Show Solution[/reveal-answer] [hidden-answer a=”815893″]

\(\displaystyle \begin{array}{r}4\geq{x}+5 \\\underline{\,\,\,-5\,\,\,\,\,-5}\\-1\,\,\,\,\,\,\,\,\,\,\ge \,\,\,x\end{array}\)

Rewrite the inequality with the variable on the left – this makes writing the interval and drawing the graph easier.

\(x\le{-1}\)

Note how the the pointy part of the inequality is still directed at the variable, so instead of reading as negative one is greater or equal to x, it now reads as x is less than or equal to negative one.

Check the solution to \(4\geq{x}+5\) [reveal-answer q=”568062″]Show Solution[/reveal-answer] [hidden-answer a=”568062″]

Substitute the end point \(4=x+5\)

\(\displaystyle \begin{array}{r}4=x+5\,\,\,\\\text{Does}\,\,\,4=-1+5?\\-1=-1\,\,\,\end{array}\)

\(\displaystyle \begin{array}{r}4\geq{-5}+5\,\,\,\\\text{ }\,\text{ Is}\,\,4\ge 0?\\\text{It}\,\text{checks!}\end{array}\)

\(4\geq{x}+5\) [/hidden-answer]

The following video show examples of solving inequalities with the variable on the right side.

Solve inequalities with multiplication and division

Solving an inequality with a variable that has a coefficient other than 1 usually involves multiplication or division. The steps are like solving one-step equations involving multiplication or division EXCEPT for the inequality sign. Let’s look at what happens to the inequality when you multiply or divide each side by the same number.

Multiplication and Division Properties of Inequality

Keep in mind that you only change the sign when you are multiplying and dividing by a negative number. If you add or subtract by a negative number, the inequality stays the same.

Solve for x. \(3x>12\)

[reveal-answer q=”691711″]Show Solution[/reveal-answer] [hidden-answer a=”691711″]Divide both sides by 3 to isolate the variable.

\(\displaystyle \begin{array}{r}\underline{3x}>\underline{12}\\3\,\,\,\,\,\,\,\,\,\,\,\,3\\x>4\,\,\,\end{array}\)

Check your solution by first checking the end point 4, and then checking another solution for the inequality.

\(\begin{array}{r}3\cdot4=12\\12=12\\3\cdot10>12\\30>12\\\text{It checks!}\end{array}\)

Inequality: \(\displaystyle x>4\)

Interval: \(\left(4,\infty\right)\)

There was no need to make any changes to the inequality sign because both sides of the inequality were divided by positive 3. In the next example, there is division by a negative number, so there is an additional step in the solution!

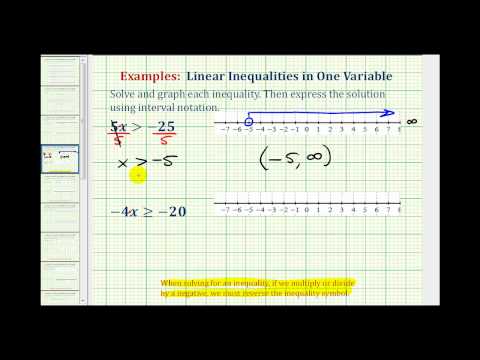
Solve for x . \(−2x>6\)

[reveal-answer q=”604033″]Show Solution[/reveal-answer] [hidden-answer a=”604033″]Divide each side of the inequality by \(−2\) to isolate the variable, and change the direction of the inequality sign because of the division by a negative number.

\(\displaystyle \begin{array}{r}\underline{-2x}<\underline{\,6\,}\\-2\,\,\,\,-2\,\\x<-3\end{array}\)

Check your solution by first checking the end point \(−3\), and then checking another solution for the inequality.

\(\begin{array}{r}-2\left(-3\right)=6 \\6=6\\ -2\left(-6\right)>6 \\ 12>6\end{array}\)

Inequality: \(\displaystyle x<-3\)

Interval: \(\left(-\infty, -3\right)\)

Graph: \(−2\), the inequality symbol was switched from > to <. [/hidden-answer]

The following video shows examples of solving one step inequalities using the multiplication property of equality where the variable is on the left hand side.

Before you read the solution to the next example, think about what properties of inequalities you may need to use to solve the inequality. What is different about this example from the previous one? Write your ideas in the box below.

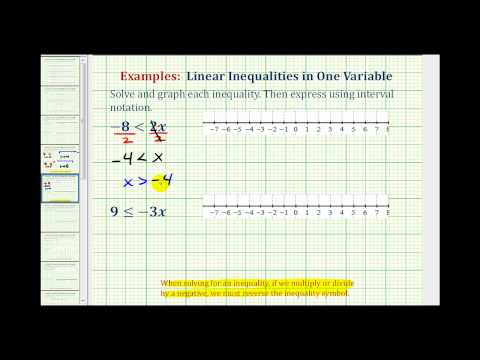
Solve for x . \(-\frac{1}{2}>-12x\)

[practice-area rows=”1″][/practice-area] [reveal-answer q=”811465″]Show Solution[/reveal-answer] [hidden-answer a=”811465″]

This inequality has the variable on the right hand side, which is different from the previous examples. Start the solution process as before, and at the end, you can move the variable to the left to write the final solution.

Divide both sides by \(-12\) to isolate the variable. Since you are dividing by a negative number, you need to change the direction of the inequality sign.

\(\displaystyle\begin{array}{l}-\frac{1}{2}\gt{-12x}\\\\\frac{-\frac{1}{2}}{-12}\gt\frac{-12x}{-12}\\\end{array}\)

Dividing a fraction by an integer requires you to multiply by the reciprocal, and the reciprocal of \(\frac{1}{-12}\)

\(\displaystyle\begin{array}{r}\left(-\frac{1}{12}\right)\left(-\frac{1}{2}\right)\lt\frac{-12x}{-12}\,\,\\\\ \frac{1}{24}\lt\frac{\cancel{-12}x}{\cancel{-12}}\\\\ \frac{1}{24}\lt{x}\,\,\,\,\,\,\,\,\,\,\end{array}\)

Inequality: \(x\gt\frac{1}{24}\). Writing the inequality with the variable on the left requires a little thinking, but helps you write the interval and draw the graph correctly.

Interval: \(\left(\frac{1}{24},\infty\right)\)

The following video gives examples of how to solve an inequality with the multiplication property of equality where the variable is on the right hand side.

Combine properties of inequality to solve algebraic inequalities

A popular strategy for solving equations, isolating the variable, also applies to solving inequalities. By adding, subtracting, multiplying and/or dividing, you can rewrite the inequality so that the variable is on one side and everything else is on the other. As with one-step inequalities, the solutions to multi-step inequalities can be graphed on a number line.

Solve for p . \(4p+5<29\)

[reveal-answer q=”211828″]Show Solution[/reveal-answer] [hidden-answer a=”211828″]

Begin to isolate the variable by subtracting 5 from both sides of the inequality.

\(\displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\,\,\,\,\,\,-5\,\,\,\,\,-5}\\4p\,\,\,\,\,\,\,\,\,<\,\,24\,\,\end{array}\)

Divide both sides of the inequality by 4 to express the variable with a coefficient of 1.

\(\begin{array}{l}\underline{4p}\,<\,\,\underline{24}\,\,\\\,4\,\,\,\,<\,\,4\\\,\,\,\,\,p<6\end{array}\)

Inequality: \(p<6\)

Interval: \(\left(-\infty,6\right)\)

Graph: Note the open circle at the end point 6 to show that solutions to the inequality do not include 6. The values where p is less than 6 are found all along the number line to the left of 6.

Check the solution. [reveal-answer q=”291597″]Show Solution[/reveal-answer] [hidden-answer a=”291597″]

Check the end point 6 in the related equation.

\(\displaystyle \begin{array}{r}4p+5=29\,\,\,\\\text{Does}\,\,\,4(6)+5=29?\\24+5=29\,\,\,\\29=29\,\,\,\\\text{Yes!}\,\,\,\,\,\,\end{array}\)

Try another value to check the inequality. Let’s use \(p=0\).

\(\displaystyle \begin{array}{r}4p+5<29\,\,\,\\\text{Is}\,\,\,4(0)+5<29?\\0+5<29\,\,\,\\5<29\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}\)

\(4p+5<29\)

Solve for x : \(3x–7\ge 41\) [reveal-answer q=”238157″]Show Solution[/reveal-answer] [hidden-answer a=”238157″]

Begin to isolate the variable by adding 7 to both sides of the inequality, then divide both sides of the inequality by 3 to express the variable with a coefficient of 1.

\(\displaystyle \begin{array}{l}3x-7\ge 41\\\underline{\,\,\,\,\,\,\,+7\,\,\,\,+7}\\\frac{3x}{3}\,\,\,\,\,\,\,\,\ge \frac{48}{3}\\\,\,\,\,\,\,\,\,\,\,x\ge 16\end{array}\)

Inequality: \(x\ge 16\)

Interval: \(\left[16,\infty\right)\)

Check the solution. [reveal-answer q=”437341″]Show Solution[/reveal-answer]

[hidden-answer a=”437341″]

First, check the end point 16 in the related equation.

\(\displaystyle \begin{array}{r}3x-7=41\,\,\,\\\text{Does}\,\,\,3(16)-7=41?\\48-7=41\,\,\,\\41=41\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}\)

Then, try another value to check the inequality. Let’s use \(x = 20\).

\(\displaystyle \begin{array}{r}\,\,\,\,3x-7\ge 41\,\,\,\\\text{Is}\,\,\,\,\,3(20)-7\ge 41?\\60-7\ge 41\,\,\,\\53\ge 41\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}\)

When solving multi-step equations, pay attention to situations in which you multiply or divide by a negative number. In these cases, you must reverse the inequality sign.

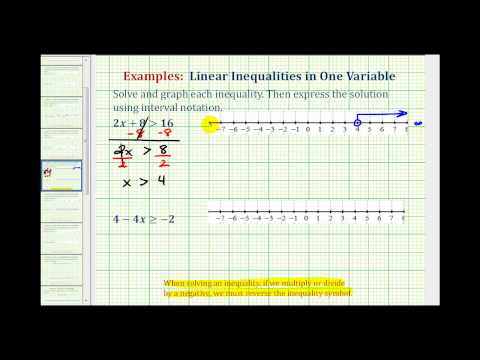
Solve for p . \(−58>14−6p\)

[reveal-answer q=”424351″]Show Solution[/reveal-answer] [hidden-answer a=”424351″]

Note how the variable is on the right hand side of the inequality, the method for solving does not change in this case.

Begin to isolate the variable by subtracting 14 from both sides of the inequality.

\(\displaystyle \begin{array}{l}−58\,\,>14−6p\\\underline{\,\,\,\,\,\,\,\,\,\,\,\,-14\,\,\,\,\,\,\,-14}\\-72\,\,\,\,\,\,\,\,\,\,\,>-6p\end{array}\)

Divide both sides of the inequality by \(−6\) to express the variable with a coefficient of 1. Dividing by a negative number results in reversing the inequality sign.

\(\begin{array}{l}\underline{-72}>\underline{-6p}\\-6\,\,\,\,\,\,\,\,\,\,-6\\\,\,\,\,\,\,12\lt{p}\end{array}\)

We can also write this as \(p>12\). Notice how the inequality sign is still opening up toward the variable p.

Inequality: \(\left(12,\infty\right)\) Graph: The graph of the inequality p > 12 has an open circle at 12 with an arrow stretching to the right.

Check the solution. [reveal-answer q=”500309″]Show Solution[/reveal-answer] [hidden-answer a=”500309″]

First, check the end point 12 in the related equation.

\(\begin{array}{r}-58=14-6p\\-58=14-6\left(12\right)\\-58=14-72\\-58=-58\end{array}\)

Then, try another value to check the inequality. Try 100.

\(\begin{array}{r}-58>14-6p\\-58>14-6\left(100\right)\\-58>14-600\\-58>-586\end{array}\)

In the following video, you will see an example of solving a linear inequality with the variable on the left side of the inequality, and an example of switching the direction of the inequality after dividing by a negative number.

In the following video, you will see an example of solving a linear inequality with the variable on the right side of the inequality, and an example of switching the direction of the inequality after dividing by a negative number.

Simplify and solve algebraic inequalities using the distributive property

As with equations, the distributive property can be applied to simplify expressions that are part of an inequality. Once the parentheses have been cleared, solving the inequality will be straightforward.

Solve for x . \(2\left(3x–5\right)\leq 4x+6\)

[reveal-answer q=”587737″]Show Solution[/reveal-answer] [hidden-answer a=”587737″]

Distribute to clear the parentheses.

\(\displaystyle \begin{array}{r}\,2(3x-5)\leq 4x+6\\\,\,\,\,6x-10\leq 4x+6\end{array}\)

Subtract 4 x from both sides to get the variable term on one side only.

\(\begin{array}{r}6x-10\le 4x+6\\\underline{-4x\,\,\,\,\,\,\,\,\,\,\,\,\,\,-4x}\,\,\,\,\,\,\,\,\,\\\,\,\,2x-10\,\,\leq \,\,\,\,\,\,\,\,\,\,\,\,6\end{array}\)

Add 10 to both sides to isolate the variable.

\(\begin{array}{r}\\\,\,\,2x-10\,\,\le \,\,\,\,\,\,\,\,6\,\,\,\\\underline{\,\,\,\,\,\,+10\,\,\,\,\,\,\,\,\,+10}\\\,\,\,2x\,\,\,\,\,\,\,\,\,\,\,\le \,\,\,\,\,16\,\,\,\end{array}\)

Divide both sides by 2 to express the variable with a coefficient of 1.

\(\begin{array}{r}\underline{2x}\le \,\,\,\underline{16}\\\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\le \,\,\,\,\,8\end{array}\)

Inequality: \(\left(-\infty,8\right]\) Graph: The graph of this solution set includes 8 and everything left of 8 on the number line.

Check the solution. [reveal-answer q=”808701″]Show Solution[/reveal-answer] [hidden-answer a=”808701″]

First, check the end point 8 in the related equation.

\(\displaystyle \begin{array}{r}2(3x-5)=4x+6\,\,\,\,\,\,\\2(3\,\cdot \,8-5)=4\,\cdot \,8+6\\\,\,\,\,\,\,\,\,\,\,\,2(24-5)=32+6\,\,\,\,\,\,\\2(19)=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\38=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)

Then, choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 0.

\(\displaystyle \begin{array}{l}2(3\,\cdot \,0-5)\le 4\,\cdot \,0+6?\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2(-5)\le 6\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-10\le 6\,\,\end{array}\)

\(\left(-\infty,8\right]\)

In the following video, you are given an example of how to solve a multi-step inequality that requires using the distributive property.

In the next example, you are given an inequality with a term that looks complicated. If you pause and think about how to use the order of operations to solve the inequality, it will hopefully seem like a straightforward problem. Use the textbox to write down what you think is the best first step to take.

Solve for a. \(\displaystyle\frac ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/01:_Solving_Equations_and_Inequalities/1.05:_Solve_Inequalities), /content/body/div[7]/div/div/div[3]/div/p[2]/span[1], line 1, column 2 6{<2}\)

[practice-area rows=”1″][/practice-area]

[reveal-answer q=”701072″]Show Solution[/reveal-answer]

[hidden-answer a=”701072″]

Clear the fraction by multiplying both sides of the equation by 6.

\(\displaystyle \begin{array}{r}\frac ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/01:_Solving_Equations_and_Inequalities/1.05:_Solve_Inequalities), /content/body/div[7]/div/div/div[3]/div/p[7]/span[1], line 1, column 2 6{<2}\,\,\,\,\,\,\,\,\\\\6\,\cdot \,\frac{2a-4}{6}<2\,\cdot \,6\\\\{2a-4}<12\,\,\,\,\,\,\end{array}\)

Add 4 to both sides to isolate the variable.

\(\displaystyle \begin{array}{r}2a-4<12\\\underline{\,\,\,+4\,\,\,\,+4}\\2a<16\end{array}\)

\(\displaystyle \begin{array}{c}\frac{2a}{2}<\,\frac{16}{2}\\\\a<8\end{array}\)

Inequality: \(a<8\)

Interval: \(\left(-\infty,8\right)\)

Check the solution. [reveal-answer q=”905072″]Show Solution[/reveal-answer]

[hidden-answer a=”905072″] First, check the end point 8 in the related equation.

\(\displaystyle \begin{array}{r}\frac{2a-4}{6}=2\,\,\,\,\\\\\text{Does}\,\,\,\frac{2(8)-4}{6}=2?\\\\\frac{16-4}{6}=2\,\,\,\,\\\\\frac{12}{6}=2\,\,\,\,\\\\2=2\,\,\,\,\\\\\text{Yes!}\,\,\,\,\,\end{array}\)

Then choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 5.

\(\displaystyle \begin{array}{r}\text{Is}\,\,\,\frac{2(5)-4}{6}<2?\\\\\frac{10-4}{6}<2\,\,\,\\\\\,\,\,\,\frac{6}{6}<2\,\,\,\\\\1<2\,\,\,\\\\\text{Yes!}\,\,\,\,\,\end{array}\)

Solving inequalities is very similar to solving equations, except you have to reverse the inequality symbols when you multiply or divide both sides of an inequality by a negative number. There are three ways to represent solutions to inequalities: an interval, a graph, and an inequality. Because there is usually more than one solution to an inequality, when you check your answer you should check the end point and one other value to check the direction of the inequality.

Inequalities can have a range of answers. The solutions are often graphed on a number line in order to visualize all of the solutions. Multi-step inequalities are solved using the same processes that work for solving equations with one exception. When you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol. The inequality symbols stay the same whenever you add or subtract either positive or negative numbers to both sides of the inequality.

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Graph Linear Inequalities in One Variable (Basic). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/-kiAeGbSe5c . License : CC BY: Attribution
• Given Interval in Words, Graph and Give Inequality. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/E_ZWNVNEvOg . License : CC BY: Attribution
• Given an Inequality, Graph and Give Interval Notation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/BKhDzNKjVBc . License : CC BY: Attribution
• Given Interval in Words, Graph and Give Interval Notation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/OYkQ-McI2qg . License : CC BY: Attribution
• Given Interval Notation, Graph and Give Inequality. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/lkhILNEPbfk . License : CC BY: Attribution
• Screenshot: Cecilia Venn Diagram. Authored by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Internet Privacy. Authored by : Lumen Learning. License : CC BY: Attribution
• Solutions to Basic OR Compound Inequalities. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/nKarzhZOFIk . License : CC BY: Attribution
• Solutions to Basic AND Compound Inequalities. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/LP3fsZNjJkc . License : CC BY: Attribution
• Unit 10: Solving Equations and Inequalities, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License : CC BY: Attribution
• Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Left Side). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/1Z22Xh66VFM . License : CC BY: Attribution
• Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Right Side). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/RBonYKvTCLU . License : CC BY: Attribution
• Ex: Solve One Step Linear Inequality by Dividing (Variable Left). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/IajiD3R7U-0 . License : CC BY: Attribution
• Ex: Solve One Step Linear Inequality by Dividing (Variable Right). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/s9fJOnVTHhs . License : CC BY: Attribution
• Ex: Graph Basic Inequalities and Express Using Interval Notation. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/X0xrHKgbDT0 . License : CC BY: Attribution
• College Algebra. Authored by : Jay Abramson, et al.. Located at : courses.candelalearning.com/collegealgebra1xmaster/. License : CC BY: Attribution
• Ex: Graph Basic Inequalities and Express Using Interval Notation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/X0xrHKgbDT0 . License : CC BY: Attribution
• Ex: Solve a Two Step Linear Inequality (Variable Left). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/RB9wvIogoEM . License : CC BY: Attribution
• Ex: Solve a Two Step Linear Inequality (Variable Right). Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/9D2g_FaNBkY . License : CC BY: Attribution
• Ex: Solve a Linear Inequality Requiring Multiple Steps (One Var). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/vjZ3rQFVkh8 . License : Public Domain: No Known Copyright
• Ex: Solve a Compound Inequality Involving OR (Union). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/oRlJ8G7trR8 . License : CC BY: Attribution
• Ex 1: Solve and Graph Basic Absolute Value inequalities. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/0cXxATY2S-k . License : CC BY: Attribution
• Ex 2: Solve and Graph Absolute Value inequalities Mathispower4u . Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/d-hUviSkmqE . License : CC BY: Attribution
• Ex 3: Solve and Graph Absolute Value inequalitie. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/ttUaRf-GzpM . License : CC BY: Attribution
• Ex 4: Solve and Graph Absolute Value inequalities (Requires Isolating Abs. Value). Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/5jRUuiMUxWQ . License : CC BY: Attribution
• College Algebra. Authored by : Jay Abramson, et. al. Located at : courses.candelalearning.com/collegealgebra1xmaster/. License : CC BY: Attribution

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 6

Two-step inequalities.

• Two-step inequality word problem: apples
• Two-step inequality word problem: R&B
• Two-step inequality word problems
• (Choice A)   A
• (Choice B)   B
• (Choice C)   C
• (Choice D)   D

Inequalities

In Mathematics, equations are not always about being balanced on both sides with an 'equal to' symbol. Sometimes it can be about 'not an equal to' relationship like something is greater than the other or less than. In mathematics, inequality refers to a relationship that makes a non-equal comparison between two numbers or other mathematical expressions. These mathematical expressions come under algebra and are called inequalities.

Let us learn the rules of inequalities, and how to solve and graph them.

What is an Inequality?

Inequalities  are the mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.

Olivia is selected in the 12U Softball. How old is Olivia? You don't know the age of Olivia, because it doesn't say "equals". But you do know her age should be less than or equal to 12, so it can be written as Olivia's Age ≤ 12. This is a practical scenario related to inequalities.

Inequality Meaning

The meaning of inequality is to say that two things are NOT equal. One of the things may be less than, greater than, less than or equal to, or greater than or equal to the other things.

• p ≠ q means that p is not equal to q
• p < q means that p is less than q
• p > q means that p is greater than q
• p ≤ q means that p is less than or equal to q
• p ≥ q means that p is greater than or equal to q

There are different types of inequalities. Some of the important inequalities are:

• Polynomial inequalities
• Absolute value inequalities
• Rational inequalities

Rules of Inequalities

The rules of inequalities are special. Here are some listed with inequalities examples.

Inequalities Rule 1

When inequalities are linked up you can jump over the middle inequality.

• If, p < q and q < d, then p < d
• If, p > q and q > d, then p > d

Example: If Oggy is older than Mia and Mia is older than Cherry, then Oggy must be older than Cherry.

Inequalities Rule 2

Swapping of numbers p and q results in:

• If, p > q, then q < p
• If, p < q, then q > p

Example: Oggy is older than Mia, so Mia is younger than Oggy.

Inequalities Rule 3

Adding the number d to both sides of inequality: If p < q, then p + d < q + d

Example: Oggy has less money than Mia. If both Oggy and Mia get $5 more, then Oggy will still have less money than Mia.

• If p < q, then p − d < q − d
• If p > q, then p + d > q + d, and
• If p > q, then p − d > q − d

So, the addition and subtraction of the same value to both p and q will not change the inequality.

Inequalities Rule 4

If you multiply numbers p and q by a positive number , there is no change in inequality. If you multiply both p and q by a negative number , the inequality swaps: p<q becomes q<p after multiplying by (-2)

Here are the rules:

• If p < q, and d is positive, then pd < qd
• If p < q, and d is negative, then pd > qd (inequality swaps)

Positive case example: Oggy's score of 5 is lower than Mia's score of 9 (p < q). If Oggy and Mia double their scores '×2', Oggy's score will still be lower than Mia's score, 2p < 2q. If the scores turn minuses, then scores will be −p > −q.

Inequalities Rule 5

Putting minuses in front of p and q changes the direction of the inequality.

• If p < q then −p > −q
• If p > q, then −p < −q
• It is the same as multiplying by (-1) and changes direction.

Inequalities Rule 6

Taking the reciprocal 1/value of both p and q changes the direction of the inequality. When p and q are both positive or both negative:

• If, p < q, then 1/p > 1/q
• If p > q, then 1/p < 1/q

Inequalities Rule 7

A square of a number is always greater than or equal to zero p 2  ≥ 0.

Example: (4) 2 = 16, (−4) 2 = 16, (0) 2 = 0

Inequalities Rule 8

Taking a square root will not change the inequality. If p ≤ q, then √p ≤ √q (for p, q ≥ 0).

Example: p=2, q=7 2 ≤ 7, then √2 ≤ √7

The rules of inequalities are summarized in the following table.

Solving Inequalities

Here are the steps for  solving inequalities :

• Step - 1: Write the inequality as an equation.
• Step - 2: Solve the equation for one or more values.
• Step - 3: Represent all the values on the number line.
• Step - 4: Also, represent all excluded values on the number line using open circles.
• Step - 5: Identify the intervals.
• Step - 6: Take a random number from each interval, substitute it in the inequality and check whether the inequality is satisfied.
• Step - 7: Intervals that are satisfied are the solutions.

But for solving simple inequalities (linear), we usually apply algebraic operations like addition , subtraction , multiplication , and division . Consider the following example:

2x + 3 > 3x + 4

Subtracting 3x and 3 from both sides,

2x - 3x > 4 - 3

Multiplying both sides by -1,

Notice that we have changed the ">" symbol into "<" symbol. Why? This is because we have multiplied both sides of the inequality by a negative number. The process of solving inequalities mentioned above works for a simple linear inequality. But to solve any other complex inequality, we have to use the following process.

Let us use this procedure to solve inequalities of different types.

Graphing Inequalities

While graphing inequalities , we have to keep the following things in mind.

• If the endpoint is included (i.e., in case of ≤ or ≥) use a closed circle.
• If the endpoint is NOT included (i.e., in case of < or >), use an open circle.
• Use open circle at either ∞ or -∞.
• Draw a line from the endpoint that extends to the right side if the variable is greater than the number.
• Draw a line from the endpoint that extends to the left side if the variable is lesser than the number.

Writing Inequalities in Interval Notation

While writing the solution of an inequality in the interval notation , we have to keep the following things in mind.

• If the endpoint is included (i.e., in case of ≤ or ≥) use the closed brackets '[' or ']'
• If the endpoint is not included (i.e., in case of < or >), use the open brackets '(' or ')'
• Use always open bracket at either ∞ or -∞.

Here are some examples to understand the same:

Graphing Inequalities with Two Variables

For graphing  inequalities with two variables , you will have to plot the "equals" line and then, shade the appropriate area. There are three steps:

• Write the equation such as "y" is on the left and everything else on the right.
• Plot the "y=" line (draw a solid line for y≤ or y≥, and a dashed line for y< or y>)
• Shade the region above the line for a "greater than" (y> or y≥) or below the line for a "less than" (y< or y≤).

Let us try some example: This is a graph of a linear inequality: y ≤ x + 4

You can see, y = x + 4 line and the shaded area (in yellow) is where y is less than or equal to x + 4. Let us now see how to solve different types of inequalities and how to graph the solution in each case.

Solving Polynomial Inequalities

The polynomial inequalities are inequalities that can be expressed as a polynomial on one side and 0 on the other side of the inequality. There are different types of polynomial inequalities but the important ones are:

• Linear Inequalities
• Quadratic Inequalities

Solving Linear Inequalities

A linear inequality is an inequality that can be expressed with a linear expression on one side and a 0 on the other side. Solving linear inequalities is as same as solving linear equations , but just the rules of solving inequalities (that was explained before) should be taken care of. Let us see some examples.

Solving One Step Inequalities

Consider an inequality 2x < 6 (which is a linear inequality with one variable ). To solve this, just one step is sufficient which is dividing both sides by 2. Then we get x < 3. Therefore, the solution of the inequality is x < 3 (or) (-∞, 3).

Solving Two Step Inequalities

Consider an inequality -2x + 3 > 6. To solve this, we need two steps . The first step is subtracting 3 from both sides, which gives -2x > 3. Then we need to divide both sides by -2 and it results in x < -3/2 (note that we have changed the sign of the inequality). So the solution of the inequality is x < -3/2 (or) (-∞, -3/2).

Solving Compound Inequalities

Compound inequalities refer to the set of inequalities with either "and" or "or" in between them. For solving inequalities, in this case, just solve each inequality independently and then find the final solution according to the following rules:

• The final solution is the intersection of the solutions of the independent inequalities if we have "and" between them.
• The final solution is the union of the solutions of the independent inequalities if we have "or" between them.

Example: Solve the compound inequality 2x + 3 < -5 and x + 6 < 3.

By first inequality: 2x + 3 < -5 2x < -8 x < -4

By second inequality, x + 6 < 3 x < -3

Since we have "and" between them, we have to find the intersection of the sets x < -4 and x < -3. A number line may be helpful in this case. Then the final solution is:

x < -3 (or) (-∞, -3).

Solving Quadratic Inequalities

A quadratic inequality involves a quadratic expression in it. Here is the process of solving quadratic inequalities . The process is explained with an example where we are going to solve the inequality x 2 - 4x - 5 ≥ 0.

• Step 1: Write the inequality as equation. x 2 - 4x - 5 = 0
• Step 2: Solve the equation. Here we can use any process of solving quadratic equations . Then (x - 5) (x + 1) = 0 x = 5; x = -1.

• Step 5: The inequalities with "true" from the above table are solutions. Therefore, the solutions of the quadratic inequality x 2 - 4x - 5 ≥ 0 is (-∞, -1] U [5, ∞).

We can use the same process for solving cubic inequalities, biquadratic inequalities, etc.

Solving Absolute Value Inequalities

An absolute value inequality includes an algebraic expression inside the absolute value sign. Here is the process of solving absolute value inequalities where the process is explained with an example of solving an absolute value inequality |x + 3| ≤ 2. If you want to learn different methods of solving absolute value inequalities, click here .

• Step 1: Consider the absolute value inequality as equation. |x + 3| = 2
• Step 2: Solve the equation. x + 3 = ±2 x + 3 = 2; x + 3 = -2 x = -1; x = -5

• Step 5: The intervals that satisfied the inequality are the solution intervals. Therefore, the solution of the absolute value inequality |x + 3| ≤ 2 is [-5, -1].

Solving Rational Inequalities

Rational inequalities are inequalities that involve rational expressions (fractions with variables). To solve the rational inequalities (inequalities with fractions), we just use the same procedure as other inequalities but we have to take care of the excluded points . For example, while solving the rational inequality (x + 2) / (x - 2) < 3, we should note that the rational expression (x + 2) / (x - 2) is NOT defined at x = 2 (set the denominator x - 2 = 0 ⇒x = 2). Let us solve this inequality step by step.

• Step 1: Consider the inequality as the equation. (x + 2) / (x - 2) = 3
• Step 2: Solve the equation. x + 2 = 3(x - 2) x + 2 = 3x - 6 2x = 8 x = 4

• Step 5: The intervals that have come up with "true" in Step 4 are the solutions. Therefore, the solution of the rational inequality (x + 2) / (x - 2) < 3 is (-∞, 2) U (4, ∞).

Important Notes on Inequalities:

Here are the notes about inequalities:

• If we have strictly less than or strictly greater than symbol, then we never get any closed interval in the solution.
• We always get open intervals at ∞ or -∞ symbols because they are NOT numbers to include.
• Write open intervals always at excluded values when solving rational inequalities.
• Excluded values should be taken care of only in case of rational inequalities.

☛  Related Topics:

• Linear Inequalities Calculator
• Triangle Inequality Theorem Calculator
• Rational Inequalities Calculator

Inequalities Examples

Example 1: Using the techniques of solving inequalities, solve: -19 < 3x + 2 ≤ 17 and write the answer in the interval notation.

Given that -19 < 3x + 2 ≤ 17.

This is a compound inequality.

Subtracting 2 from all sides,

-21 < 3x ≤ 15

Dividing all sides by 3,

-7 < x ≤ 5

Answer: The solution is (-7, 5].

Example 2: While solving inequalities, explain why each of the following statements is incorrect. Also, correct them. a) 2x < 5 ⇒ x > 5/2 b) x > 3 ⇒ x ∈ [3, ∞) c) -x > -7 ⇒ x > 7.

a) 2x < 5. Here, when we divide both sides by 2, which is a positive number, the sign does not change. So the correct inequality is x < 5/2.

b) x > 3. It does not include an equal to symbol. So 3 should NOT be included in the interval. So the correct interval is (3, ∞).

c) -x > -7. When we divide both sides by -1, a negative number, the sign should change. So the correct inequality is x < 7.

Answer: The corrected ones are a) x < 5/2; b) x ∈ (3, ∞); c) x < 7.

Example 3: Solve the inequality x 2 - 7x + 10 < 0.

First, solve the equation x 2 - 7x + 10 = 0.

(x - 2) (x - 5) = 0.

x = 2, x = 5.

If we represent these numbers on the number line, we get the following intervals: (-∞, 2), (2, 5), and (5, ∞).

Let us take some random numbers from each interval to test the given quadratic inequality.

Therefore, the only interval that satisfies the inequality is (2, 5).

Answer: The solution is (2, 5).

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Inequalities

go to slide go to slide

FAQs on Inequalities

What are inequalities in math.

When two or more algebraic expressions are compared using the symbols <, > ≤, or ≥, then they form an inequality. They   are the mathematical expressions in which both sides are not equal.

How Do you Solve Inequalities On A Number Line?

To plot an inequality in math, such as x>3, on a number line,

• Step 1: Draw a circle over the number (e.g., 3).
• Step 2: Check if the sign includes equal to (≥ or ≤) or not. If equal to sign is there along with > or <, then fill in the circle otherwise leave the circle unfilled.
• Step 3: On the number line, extend the line from 3(after encircling it) to show it is greater than or equal to 3.

How to Calculate Inequalities in Math?

To  calculate inequalities :

• just make it an equation
• mark the zeros  on the number line to get intervals
• test the intervals by taking any one number from it against the inequality.

Explain the Process of Solving Inequalities Graphically.

Solving inequalities graphically is possible when we have a system of two inequalities in two variables. In this case, we consider both inequalities as two linear equations and graph them. Then we get two lines. Shade the upper/lower portion of each of the lines that satisfies the inequality. The common portion of both shaded regions is the solution region.

What is the Difference Between Equations and Inequalities?

Here are the differences between equations and inequalities.

What Happens When you Square An Inequality?

A square of a number is always greater than or equal to zero p 2  ≥ 0. Example: (4) 2 = 16, (−4) 2 = 16, (0) 2 = 0

What are the Steps to Calculate Inequalities with Fractions?

Calculating inequalities with fractions is just like solving any other inequality. One easy way of solving such inequalities is to multiply every term on both sides by the LCD of all denominators so that all fractions become integers . For example, to solve (1/2) x + 1 > (3/4) x + 2, multiply both sides by 4. Then we get 2x + 4 > 3x + 8 ⇒ -x > 4 ⇒ x < -4.

What are the Steps for Solving Inequalities with Variables on Both Sides?

When an inequality has a variable on both sides, we have to try to isolate the variable. But in this process, flip the inequality sign whenever we are dividing or multiplying both sides by a negative number. Here is an example. 3x - 7 < 5x - 11 ⇒ -2x < -4 ⇒ x > 2.

How Do you Find the Range of Inequality?

You can find the range of values of x, by solving the inequality by considering it as a normal linear equation.

What Are the 5 Inequality Symbols?

The 5 inequality symbols are less than (<), greater than (>), less than or equal (≤), greater than or equal (≥), and the not equal symbol (≠).

How Do you Tell If It's An Inequality?

Equations and inequalities are mathematical sentences formed by relating two expressions to each other. In an equation, the two expressions are supposed to be equal and shown by the symbol =. Whereas in inequality, the two expressions are not necessarily equal and are indicated by the symbols: >, <, ≤ or ≥.

How to Graph the Solution After Solving Inequalities?

After solving inequalities, we can graph the solution keeping the following things in mind.

• Use an open circle at the number if it is not included and use a closed circle if it is included.
• Draw a line to the right side of the number in case of '>' and to the left side of the number in case of '<'.

• Practice Problems
• Assignment Problems
• Show all Solutions/Steps/ etc.
• Hide all Solutions/Steps/ etc.
• Complex Numbers
• Solutions and Solution Sets
• Preliminaries
• Graphing and Functions
• Calculus II
• Calculus III
• Differential Equations
• Algebra & Trig Review
• Common Math Errors
• Complex Number Primer
• How To Study Math
• Cheat Sheets & Tables
• MathJax Help and Configuration
• Notes Downloads
• Complete Book
• Practice Problems Downloads
• Complete Book - Problems Only
• Complete Book - Solutions
• Assignment Problems Downloads
• Other Items
• Get URL's for Download Items
• Print Page in Current Form (Default)
• Show all Solutions/Steps and Print Page
• Hide all Solutions/Steps and Print Page

Chapter 2 : Solving Equations and Inequalities

Here are a set of practice problems for the Solving Equations and Inequalities chapter of the Algebra notes.

• If you’d like a pdf document containing the solutions the download tab above contains links to pdf’s containing the solutions for the full book, chapter and section. At this time, I do not offer pdf’s for solutions to individual problems.
• If you’d like to view the solutions on the web go to the problem set web page, click the solution link for any problem and it will take you to the solution to that problem.

Note that some sections will have more problems than others and some will have more or less of a variety of problems. Most sections should have a range of difficulty levels in the problems although this will vary from section to section.

Here is a list of all the sections for which practice problems have been written as well as a brief description of the material covered in the notes for that particular section.

Solutions and Solution Sets – In this section we introduce some of the basic notation and ideas involved in solving equations and inequalities. We define solutions for equations and inequalities and solution sets.

Linear Equations – In this section we give a process for solving linear equations, including equations with rational expressions, and we illustrate the process with several examples. In addition, we discuss a subtlety involved in solving equations that students often overlook.

Applications of Linear Equations – In this section we discuss a process for solving applications in general although we will focus only on linear equations here. We will work applications in pricing, distance/rate problems, work rate problems and mixing problems.

Equations With More Than One Variable – In this section we will look at solving equations with more than one variable in them. These equations will have multiple variables in them and we will be asked to solve the equation for one of the variables. This is something that we will be asked to do on a fairly regular basis.

Quadratic Equations, Part I – In this section we will start looking at solving quadratic equations. Specifically, we will concentrate on solving quadratic equations by factoring and the square root property in this section.

Quadratic Equations, Part II – In this section we will continue solving quadratic equations. We will use completing the square to solve quadratic equations in this section and use that to derive the quadratic formula. The quadratic formula is a quick way that will allow us to quickly solve any quadratic equation.

Quadratic Equations : A Summary – In this section we will summarize the topics from the last two sections. We will give a procedure for determining which method to use in solving quadratic equations and we will define the discriminant which will allow us to quickly determine what kind of solutions we will get from solving a quadratic equation.

Applications of Quadratic Equations – In this section we will revisit some of the applications we saw in the linear application section, only this time they will involve solving a quadratic equation. Included are examples in distance/rate problems and work rate problems.

Equations Reducible to Quadratic Form – Not all equations are in what we generally consider quadratic equations. However, some equations, with a proper substitution can be turned into a quadratic equation. These types of equations are called quadratic in form. In this section we will solve this type of equation.

Equations with Radicals – In this section we will discuss how to solve equations with square roots in them. As we will see we will need to be very careful with the potential solutions we get as the process used in solving these equations can lead to values that are not, in fact, solutions to the equation.

Linear Inequalities – In this section we will start solving inequalities. We will concentrate on solving linear inequalities in this section (both single and double inequalities). We will also introduce interval notation.

Polynomial Inequalities – In this section we will continue solving inequalities. However, in this section we move away from linear inequalities and move on to solving inequalities that involve polynomials of degree at least 2.

Rational Inequalities – We continue solving inequalities in this section. We now will solve inequalities that involve rational expressions, although as we’ll see the process here is pretty much identical to the process used when solving inequalities with polynomials.

Absolute Value Equations – In this section we will give a geometric as well as a mathematical definition of absolute value. We will then proceed to solve equations that involve an absolute value. We will also work an example that involved two absolute values.

Absolute Value Inequalities – In this final section of the Solving chapter we will solve inequalities that involve absolute value. As we will see the process for solving inequalities with a \(<\) (i.e. a less than) is very different from solving an inequality with a \(>\) (i.e. greater than).