survival case control study kaplan meier

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 01 September 2022

Epidemiology

Standardised survival probabilities: a useful and informative tool for reporting regression models for survival data

• Elisavet Syriopoulou   ORCID: orcid.org/0000-0002-5749-4094 1 ,
• Tove Wästerlid 2 , 3 ,
• Paul C. Lambert 1 , 4 &
• Therese M.-L. Andersson   ORCID: orcid.org/0000-0001-8644-9041 1  

British Journal of Cancer volume  127 ,  pages 1808–1815 ( 2022 ) Cite this article

6654 Accesses

4 Citations

5 Altmetric

Metrics details

• Cancer epidemiology
• Cancer models

When interested in studying the effect of a treatment (or other exposure) on a time-to-event outcome, the most popular approach is to estimate survival probabilities using the Kaplan–Meier estimator. In the presence of confounding, regression models are fitted, and results are often summarised as hazard ratios. However, despite their broad use, hazard ratios are frequently misinterpreted as relative risks instead of relative rates.

We discuss measures for summarising the analysis from a regression model that overcome some of the limitations associated with hazard ratios. Such measures are the standardised survival probabilities for treated and untreated: survival probabilities if everyone in the population received treatment and if everyone did not. The difference between treatment arms can be calculated to provide a measure for the treatment effect.

Using publicly available data on breast cancer, we demonstrated the usefulness of standardised survival probabilities for comparing the experience between treated and untreated after adjusting for confounding. We also showed that additional important research questions can be addressed by standardising among subgroups of the total population.

Standardised survival probabilities are a useful way to report the treatment effect while adjusting for confounding and have an informative interpretation in terms of risk.

Similar content being viewed by others

SpatialData: an open and universal data framework for spatial omics

Luca Marconato, Giovanni Palla, … Oliver Stegle

A single-cell atlas enables mapping of homeostatic cellular shifts in the adult human breast

Austin D. Reed, Sara Pensa, … Walid T. Khaled

Best practices for single-cell analysis across modalities

Lukas Heumos, Anna C. Schaar, … Fabian J. Theis

When analysing time-to-event data (or survival data) from epidemiological cohort studies in which a specific treatment (or exposure) is under study, it is often of interest to compare survival probabilities between treated and untreated patients. It is important to note that the term survival probabilities does not necessarily refer to being alive or not. Instead, it refers to being event-free. For instance, when time to relapse or death (whichever occurred first) is under study, survival probabilities refer to the probability of being alive without having a relapse (this is often referred to as relapse-free survival). Survival probabilities can also be interpreted as the proportion of individuals who are event-free at this time. When there are competing events, the survival probabilities can under some assumptions be interpreted as the probability of being event-free (or the proportion of individuals who are event-free) in the absence of competing events. We will not discuss these assumptions here as they are out of the scope of this paper, but we instead refer the reader to other related literature [ 1 ]. Survival probabilities can be compared using the Kaplan–Meier estimator [ 2 ]. However, since confounding variables might drive part of the observed differences in survival probabilities, researchers often adjust for these potential confounder variables by fitting regression models, such as the Cox proportional hazards model [ 3 , 4 ]. A common practice after fitting regression models is to summarise differences between treatment or exposure groups using adjusted hazard ratios. The hazard ratio for treatment is defined as the ratio of the hazard rates for the treated and untreated.

Despite the popularity and broad use of hazard ratios, these are often misinterpreted as relative risks. Several authors have stressed the difference between hazard ratios and relative risks previously, but their interpretation remains loose to this day [ 5 , 6 , 7 , 8 ]. A measure that has a more intuitive and easier interpretation than hazard ratios and may be more relevant in several applications is the survival probability. The survival probability at a specific time is the probability that an individual did not have the event until that specified time. The Kaplan–Meier method is a crude, i.e. unadjusted, measure of the survival probability at a specified time. The survival probabilities under different treatment arms or exposure groups can be compared by calculating their difference and can provide a measure for estimating the association between treatment (or other exposure) and a specified outcome. An appealing feature of using survival probabilities is that their complement (1 minus survival probabilities) can be interpreted as the risk of experiencing the event by a specific time, which is often the quantity of interest. In fact, the popularity of Kaplan–Meier estimates as a crude measure in various studies, even though the potential for confounding is known, highlights the importance of presenting data in terms of survival probabilities as this is easier to interpret than hazard rates.

However, there are methods to obtain survival curves that are similar to Kaplan–Meier estimates, but adjusted for potential confounders. After fitting a regression model including various confounding variables, estimates of adjusted survival probabilities by treatment arms can be obtained and presented graphically. These are called adjusted survival curves and are similar to a Kaplan–Meier curve but have been adjusted for potential confounders. Typically, after fitting a regression model, adjusted survival curves by treatment status are estimated by setting all other variables to the mean value of the population [ 9 ]. However, the average values of confounding variables may be implausible and with no useful meaning for the cohort in the study. Instead, a more appropriate way to graphically report regression models may be to estimate adjusted survival curves using standardisation (so-called standardised survival curves). To do this, the individual-specific survival probabilities across all patients in the study population are estimated and averaged to obtain the standardised survival estimates (i.e. by applying regression standardisation) [ 10 , 11 ]. In this way, we obtain estimates of the survival probabilities under the observed covariate pattern of the overall study population.

In this paper, we will discuss how we can summarise and present the analysis of a regression model in a useful way using standardised survival probabilities. This will be presented using plain language and with a practical focus. We will use publicly available data on breast cancer patients to demonstrate the different measures that can be estimated, including survival probabilities after fitting regression models with various confounders. We will also provide Stata code in the supplementary material to encourage the use of standardised survival probabilities in practice.

Introducing the illustrative example

For the remainder of the paper, we will use an example on breast cancer to illustrate the concepts. This dataset has been used in several applications and is publicly available at http://www.stata-press.com/data/fpsaus.html [ 12 , 13 ]. The dataset consists of 2982 primary breast cancer patients included in the Rotterdam tumour bank. The exposure of interest is hormonal therapy, and in the remainder of the paper, we will refer to a comparison of treatment groups even though these could also be exposure groups. The methods discussed are applicable to any other exposure that might be of interest (e.g., stage, deprivation status). The outcome of interest in our example is time to relapse or death (measured as time from primary surgery to relapse or death, whichever occurred first, and is also known as relapse-free survival). However, the methods discussed are applicable to any time-to-event outcome (e.g., overall survival, metastasis-free survival). Data include information on several factors, including age at surgery, tumour size, differentiation grade, number of positive nodes and progesterone level. More details on the data can be found in Table  1 .

Exploring differences in survival probabilities between treatment groups with the Kaplan–Meier estimator

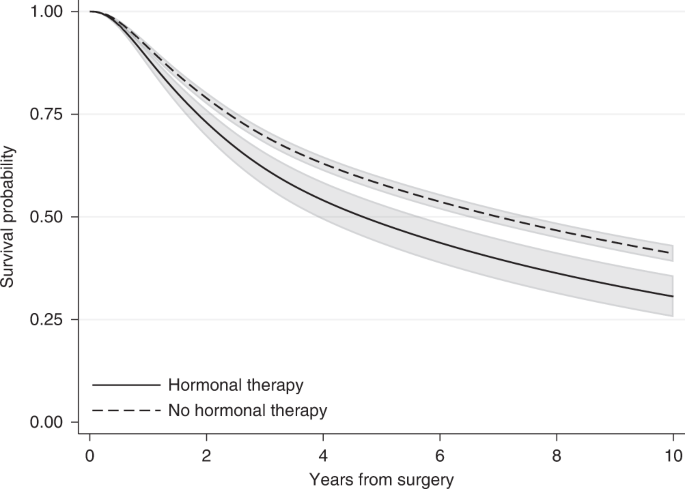
To explore whether treatment affects a time-to-event outcome, the survival probabilities under different treatment arms are frequently compared using the Kaplan–Meier estimator [ 2 , 3 ]. For instance, Fig.  1 shows the Kaplan–Meier survival probabilities for the outcome of relapse-free survival for the breast cancer patients who received hormonal therapy or not in the example dataset. The event of interest in this example is death or relapse (whichever occurs first). Here, survival probabilities are interpreted in terms of not only being alive but also having no relapse.

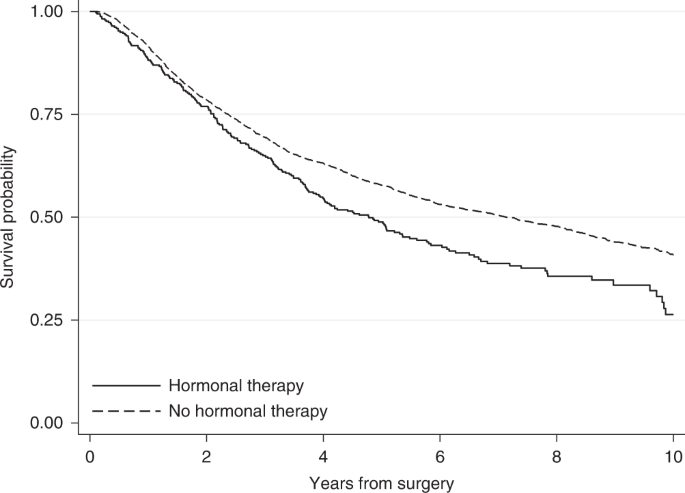
Kaplan–Meier survival probabilities for the event of relapse-free survival by treatment group for breast cancer patients.

Based on the Kaplan–Meier curves, hormonal therapy seems to have an adverse effect on breast cancer patients. Ten years after surgery, the survival probability for relapse-free survival (i.e. the probability of being alive with no relapse) for those who received hormonal therapy is 0.26, while those who did not receive hormonal therapy had a higher probability of 0.41. This can also be interpreted in terms of proportions: 26% of those who received hormonal therapy and 41% of those who did not receive hormonal therapy were alive with no relapse 10 years after surgery. However, these crude Kaplan–Meier estimates do not adjust for the fact that patients who received hormonal therapy were older (median age of 62 years versus 53 years in the no hormonal therapy group), had a higher number of positive nodes and that there was a larger proportion of patients with a tumour above 50 mm among those who received hormonal therapy (Table  1 ). These imbalances between treatment groups might drive part of the differences in probabilities of relapse-free survival and so it is important to consider these factors in the analysis.

Adjusting for multiple covariates at once can be done by estimating the Kaplan–Meier curves within subgroups of the population. If many potential factors are of interest this would require calculation of multiple Kaplan–Meier estimates, and for continuous covariates it would be possible only after categorisation. When there are several confounding variables, it may not be feasible to estimate Kaplan–Meier estimates within each subgroup, due to potentially low number of individuals within each strata. Also, it becomes difficult to summarise the results when the survival probability within each strata has to be reported. An additional limitation is that although there are ways to evaluate whether differences in the two survival curves are statistically significant (e.g using the log-rank test), an estimate of the magnitude of the difference between the groups is not provided [ 14 ]. An alternative and more popular way to explore differences in survival probabilities between treatment groups, while accounting for several covariates, is to fit regression models.

Estimating hazard ratios using regression models

The most commonly applied statistical regression model when studying time-to-event outcomes is Cox’s proportional hazards model [ 15 ]. Other regression models are also available with some (e.g. so-called flexible parametric survival models) having advantages in terms of modelling time-dependent effects (i.e. relaxing the assumption of proportional hazards) and also in terms of predictions [ 12 ]. For the analysis of the breast cancer data, we will use flexible parametric survival models. However, in principle, any survival model could be fitted, including the Cox model. As the main focus of this paper is to describe different ways of summarising the results of a regression model and not the model itself, we skip details on flexible parametric survival models but more information on these can be found elsewhere [ 12 , 16 ].

After fitting a survival model the analysis is often summarised using the hazard ratio (HR) which is the ratio of the event rates in the two groups we want to compare. The hazard rate of a particular group is the rate of individuals who experience the event under study over a short period of time, provided that the individuals have not experienced the event yet. For instance, by fitting a flexible parametric survival model to the breast cancer data including only hormonal therapy in the model, we obtain a HR equal to 1.33 (95% CI: 1.15–1.54). This is in agreement with the findings of the Kaplan–Meier estimator about an adverse effect of hormonal therapy, but also provides an estimate of the size of the difference between treatment groups, i.e. the hazard rate of patients who received hormonal therapy is 33% higher than the hazard rate of those who did not receive hormonal therapy. However, this model does not take into consideration the imbalances we see between treatment groups in Table  1 . After fitting a flexible parametric model for hormonal therapy adjusting for age at surgery, the number of positive nodes, progesterone level, differentiation grade and tumour size and relaxing the proportionality assumption for tumour grade and the number of positive nodes, we obtain a HR suggestive of a protective treatment effect and equal to 0.76 (95% CI: 0.65–0.89) i.e. the hazard rate of those who received hormonal therapy is 24% (=1–0.76) lower than the hazard rate of those who did not receive hormonal therapy.

Many authors have previously argued about limitations related to the use of HRs. Despite the wide use of HRs to estimate the treatment effect, the interpretation of HRs remains challenging as HRs are often misinterpreted as relative risks [ 5 , 7 ]. By definition the HR compares the rate of experiencing the event among treated and the rate of experiencing the event among untreated. This is different from the relative risk of experiencing the event by a specific time. The relative risk is the ratio of the probability of experiencing the event by a specific time for the treated to the probability for the untreated. In contrast to HR, the relative risk is always a function of time. For instance, the HR estimated for breast cancer patients after fitting a flexible parametric model that included only hormonal therapy and no confounding variables (unadjusted) was equal to 1.33 and remained constant during follow-up. However, the relative risk of having the event (relapse or death) is different and varies with time. The risk for treated and untreated can be obtained as 1 minus the survival probability estimates of Fig.  2 , which shows the survival probabilities estimated from the same flexible parametric model that includes only hormonal therapy. These are similar to the Kaplan–Meier curves of Fig.  1 but are obtained from a regression model. As we can see in Fig.  2 , both survival probabilities are close to each other early on, with values close to 1 since not many patients had relapsed or died in either treatment group, i.e. the risk of experiencing the event is close to 0 and the relative risk is ~1. One year after surgery, the risk of having the event for those who received hormonal therapy is 0.11 (=1–0.89) and for those who did not receive hormonal therapy 0.09 (=1–0.91), resulting in a relative risk of 1.22 (=0.11/0.09). Similarly, ten years after surgery the risk is equal to 0.69 (=1–0.31) for those who received hormonal therapy and 0.59 (=1–0.41) for those who did not receive it, resulting in a relative risk equal to 1.17 (=0.69/0.59). If we had allowed more follow-up time, the relative risk would approach 1 again later on, as the survival curves would eventually reach 0 both for treated and untreated (as all deaths will be realised eventually). However, this would not be the case when the event of interest is death due to a specific cause or when the event of interest is not death. As we can see by this example, the relative risk is highly dependent on the time of interest and its value differed from the HR estimate. HRs should be interpreted as relative rates and not relative risks. However, it is important to note that even though the HR estimate will be different to the relative risk value, the direction of the hazard ratio will be the same as the direction of the relative risk if the proportional hazards assumption is valid [ 5 ]. For example, a HR below 1 that corresponds to a lower hazard rate under treatment is also suggestive of a lower relative risk under treatment.

Estimates are obtained after fitting a flexible parametric survival model including only hormonal therapy.

Another challenge with HRs is that studies often report a single HR estimate for the whole study follow-up. This was also the case in our example above. Thus, we assumed that the HR remains constant over time i.e. proportional hazards for treatment. However, this is often an unrealistic assumption and the HR will vary over time [ 17 ]. For instance, the effect of age might vary with time or the effect of a treatment may lose effectiveness over time. Thus, when the proportionality assumption is not valid, reporting a single hazard ratio is non-informative and can be very misleading. Several methods are available to obtain time-dependent HRs, but these are often overlooked. Moreover, the HR is a relative measure; although a HR lower than 1 suggests a protective effect of treatment and a HR higher than 1 suggest an adverse effect, HRs provide no information on the absolute effect or whether this effect is clinically meaningful. Statistically significant HRs indicate that there is a statistical significant difference between treatment groups, but the corresponding difference in survival probabilities might be very small and not important from a clinical point of view. Assessing the treatment effect by examining absolute measures such as the difference in survival probabilities at fixed time points can be more informative than relative measures [ 18 ]. Finally, HRs are estimated based on individuals who have survived up to a particular time. As time increases, the characteristics of individuals who are still in follow-up in each treatment group might differ, resulting in an imbalanced comparison between treatment groups. This is often referred to as built-in selection bias of hazard ratios [ 6 , 19 ]. For instance, when an effective treatment is under study, as time increases there will be more patients with worse prognosis characteristics (e.g. older patients or patients with comorbidities) still alive among the treated group in comparison to the placebo group. This will be the case even if we have sufficiently adjusted for confounding and there are no imbalances between the treatment groups at the start of follow-up, due to emerging differences in characteristics between treated and untreated survivors with time. The selection bias of hazard ratios cannot be addressed even after appropriately modelling time-varying covariates and allowing for time-dependent covariate effects.

Adjusted survival curves using the mean covariate method

A more informative way to summarise the treatment effect is to use adjusted survival probabilities. As mentioned earlier for the Kaplan–Meier estimator, the survival probability at a specific time corresponds to the probability of being event-free at a particular time after the beginning of follow-up (e.g., 5 years after surgery). Even though rarely reported, estimating survival probabilities after fitting a regression model is no more difficult than HRs and it can be obtained using standard statistical software. In a modelling context, when multiple covariates are included in the regression model, adjusted survival probabilities are often estimated using the average covariate value for the adjusting covariates. For the breast cancer example, after fitting the same flexible parametric survival model described earlier for the HR (with hormonal therapy as the treatment of interest and adjusting for various variables), 10 years after surgery the relapse-free survival probability (i.e. the probability of being alive with no relapse) was 0.48 (95% CI: 0.43–0.54) for those who received hormonal therapy and 0.39 (95% CI: 0.36–0.41) for those who did not receive it (Fig.  3 ). This can also be interpreted in terms of proportions: 48% of those who received hormonal therapy and 39% of those who did not receive hormonal therapy were alive without having a relapse 10 years after surgery. To obtain these estimates, we set all adjusting variables to their mean value, except the treatment that is first set to treated and then untreated, and an adjusted survival curve is estimated for each treatment arm. So, our estimates correspond to the survival probability of an “average” individual if this “average” individual received hormonal therapy and an “average” individual who did not receive hormonal therapy. Thus, a caveat with “naively” adjusted survival curves is the need to calculate an “average” for included variables. For continuous variables, such as age at surgery, the “average” individual in terms of the mean value might be easy to interpret. However, for categorical variables, such as tumour size, it is not clear what an average individual is [ 9 ]. The average value for a binary variable such as sex taking values 1 for females and 0 for males corresponds for instance to the proportion of individuals who were females (e.g. if 40% of the individual were females it will be equal to 0.4) and has no meaning on an individual level (as it does not correspond to either females or males). Also, for continuous variables, even though it is more straightforward to think about the mean value, this might still not be relevant to our study population. Imagine for example, a disease that is more common among individuals younger than 25 years old and older than 60 years old. In this example, the average age at diagnosis might not even correspond to a plausible patient profile. A way to overcome this is to obtain adjusted survival curves at fixed values for the adjusting variables but in this way the survival curves will still be restricted to a specific covariate pattern.

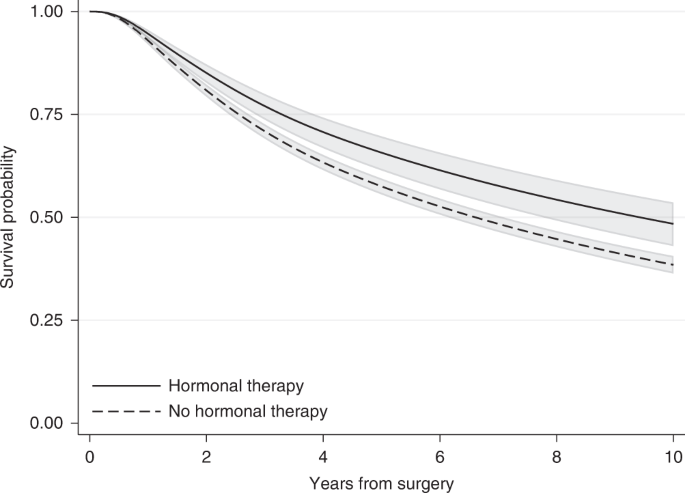
95% confidence intervals are also provided.

Standardised survival curves

Another way to overcome the need to estimate adjusted survival probabilities for an “average” individual but still obtain adjusted survival probabilities that can be presented graphically is to apply regression standardisation and thus obtain so-called standardised survival curves (also known as marginal survival curves) [ 10 , 11 , 20 , 21 ]. To do this, a regression model is fitted as in the previous examples. Based on this model, the standardised survival curve under treatment is obtained by first estimating individual-specific survival probabilities for every individual in the study population given the individual’s covariate pattern and if they received the treatment. It is important to note that “under treatment” is used here to be explicit about the fact that the covariate value used for the survival estimates for some individuals will be different from their observed value. We do not simply calculate an average over those who received treatment and an average over those who did not receive the treatment: this would result on comparing two groups with very different covariate distributions. For the standardised survival estimates under treatment, no change is made on the treatment covariate for those who were treated but the covariate value for those not treated is changed to treated. Then, the individual-specific survival probabilities are averaged to obtain the standardised survival probability under treatment. Similarly, the standardised survival curve under no treatment is estimated by averaging the individual-specific survival probabilities for each individual given the individuals covariate pattern but this time if everyone was untreated. For this, no change is made in the treatment covariate for those who were untreated but the covariate value for the treated is changed to untreated.

Note that for a study population of N individuals, N estimates of individual-specific survival probabilities are obtained and then averaged to obtain the standardised survival curve in the whole population under each treatment arm. This is different to the approach described in the previous section where only one survival curve is estimated for each treatment arm based on the average values of the adjusting covariates. With standardisation, instead of using an “average individual,” the empirical (i.e. observed) covariate distribution of the population is used for the estimate. Standardised survival estimates under treatment and no treatment can thus be interpreted as the average survival probabilities if everyone in the study population was treated or if everyone in the study population was untreated. Since the distribution of all other adjusting covariates are the same in the two standardised probabilities, fairer comparisons between treated and untreated can be made. An alternative interpretation for standardised survival estimates would be the proportion of individuals in the observed population that would survive if everyone was treated and the proportion of individuals in the observed population that would survive if no one was treated.

In the breast cancer example, we can obtain the standardised survival curve under hormonal therapy as the average of the individual-specific survival probability estimates for the event of relapse-free survival if each individual received hormonal therapy over all individuals in the cohort. Similarly, the standardised survival curve under no hormonal therapy can be obtained by averaging across the individual-specific survival probability estimates if each individual did not receive hormonal therapy. Figure  4a shows the standardised survival curves under hormonal therapy and under no hormonal therapy. Ten years after surgery, the standardised survival probabilities are 0.48 (95% CI: 0.43–0.53) under hormonal therapy and 0.39 (95% CI: 0.37–0.41) under no hormonal therapy. Note that these standardised estimates are very close to the adjusted survival curves for an “average” individual (Fig.  3 ), but this will not always be the case. For instance, at 5 years since surgery, the standardised survival estimates are 0.63 (95% CI: 0.60–0.67) under hormonal therapy and 0.56 (95% CI: 0.54–0.58) under no hormonal therapy (Fig.  4a ), while the adjusted survival probabilities for the “average” individual are higher: they are 0.66 (95% CI: 0.61–0.70) under hormonal therapy and 0.58 (95% CI: 0.56–0.59) under no hormonal therapy (Fig.  3 ). Estimates at 1, 5 and 10 years after surgery are also shown in Supplementary Table  S1 .

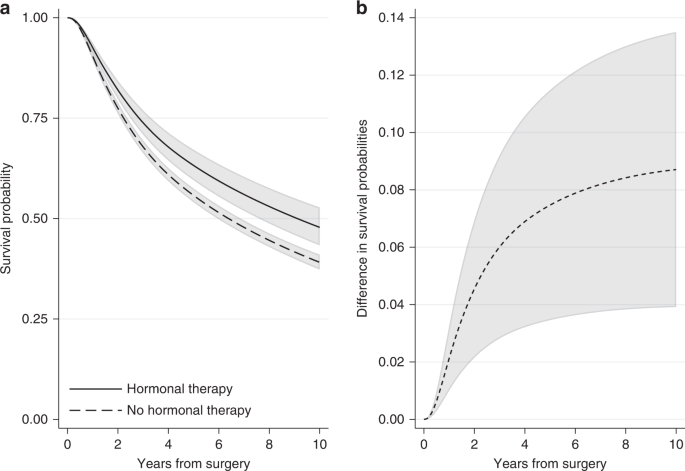
a Standardised survival probabilities for the event of relapse-free survival by treatment group and b the difference in standardised survival probabilities for the event of relapse-free survival under hormonal therapy and under no hormonal therapy, with 95% confidence intervals. Standardisation is performed by using the empirical covariate distribution of the total breast cancer population.

A comparison of the survival probabilities for different treatment groups can be performed by calculating the difference in the standardised survival probabilities under treatment and under no treatment. By applying the empirical covariate distribution in the survival estimates for both treatment groups, a fairer comparison between treated and not treated is obtained. The difference in standardised survival probabilities is a comparison of the probability of being event-free if all individuals had received treatment versus if they had not. An advantage of quantifying the treatment effect in terms of survival probabilities is that this can now be interpreted as risk (e.g., difference in risk of experiencing the event by a specific time under treatment in comparison to no treatment). Moreover, if the variables we had adjusted for are sufficient and there are no unmeasured confounders, the difference in standardised survival probabilities is an estimate of the causal effect of treatment on survival outcome [ 11 ]. This assumption is particularly important and its validity requires subject matter knowledge. Figure  4b shows the difference in standardised relapse-free survival probabilities under hormonal therapy and no hormonal therapy for the breast cancer population. The difference is increasing with time and ten years after surgery it is equal to 0.09 (95% CI: 0.04–0.14). Similarly, we can say that the proportion of being alive with no relapse under hormonal therapy is 9 percentage points larger than the proportion under no hormonal therapy.

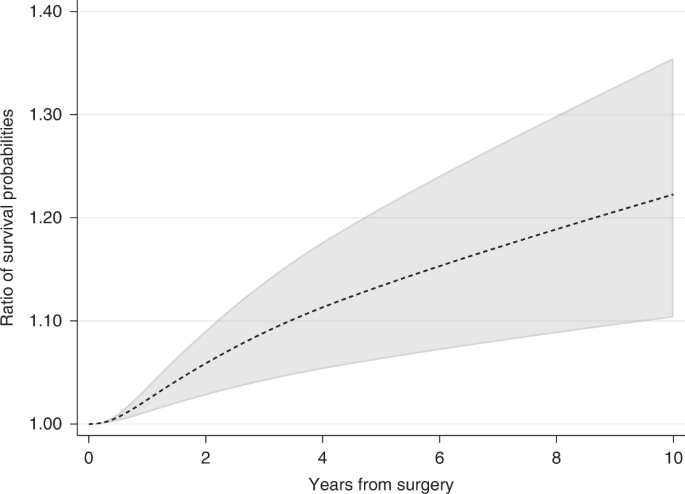
The ratio in survival probabilities can also be calculated if a relative measure is of interest. For instance, 10 years after surgery the ratio in survival probabilities for the event of relapse-free survival under hormonal therapy compared to no hormonal therapy is equal to 1.22 (95% CI: 1.10–1.36) (Fig.  5 ). However, absolute measures are often better for understanding if differences between groups are clinically meaningful. For example, if 60% of treated patients are event-free at 5 years compared to 40% for untreated, the absolute difference in proportion of event-free patients is 20 percentage points, equal to a ratio of proportions of 1.5 at 5 years. In a different study population, with a 5-year proportion of being event-free of 15% for treated and 10% for untreated, the ratio in proportions is also equal to 1.5, whereas the absolute difference is only 5 percentage points.

Standardising within a subset of the study population

In the previous section, standardisation was performed using the empirical covariate distribution in the whole population, i.e., we estimated the average survival probability for the whole population if everyone was treated compared to if no one was treated. However, in some situations it may be more relevant to apply the empirical covariate distribution of a subset of the total study population, such as the covariate distribution among the treated. This would, for example, be the case when evaluating the impact of an intervention (e.g., a new treatment or a nutritional diet) in the population who actually received the intervention as opposed to evaluating the effect of the intervention in the total population (including patients to whom the intervention was never allocated). For instance, how large was the improvement in the probability of being alive with no relapse for the breast cancer patients who received hormonal therapy? Similarly, if the interest is to assess the potential impact of an intervention on a population who have not yet received it, it would be more relevant to apply the empirical distribution among the untreated. For instance, what would the improvement be in the probability of being alive and having no relapse if the untreated group had hormonal therapy? As was also the case when we standardised over the whole group, we need to assume that the treatment effect would be the same in this group (untreated). Such research questions are of high importance from a public health view and for policymakers. Providing estimates of the standardised survival probabilities within a subset of the total population is easily done by restricting the population on which we standardise to the subset of interest. Once again, we use the same population to obtain estimates under treatment and under no treatment. However, this time only the covariate distribution of a specific subset is used for the standardisation. For instance, by applying the empirical covariate distribution of breast cancer patients who received hormonal therapy (i.e. restricting our estimates only to those who received hormonal treatment), the 10-year standardised relapse-free survival probability is equal to 0.32 (95% CI: 0.28–0.37) under hormonal therapy and 0.24 (95% CI: 0.22–0.26) under no hormonal therapy. This results in a difference in 10-year standardised survival probabilities of 0.08 (95% CI: 0.04–0.13) within the treated group (Fig.  6 ). The standardised survival probabilities within the treated group is lower than the survival within the total population (Fig.  3 ). This is expected as the patients who had hormonal therapy were older, had a higher number of positive nodes, and there was a larger proportion of tumours above 50 mm in comparison to patients who did not receive hormonal therapy (Table  1 ).

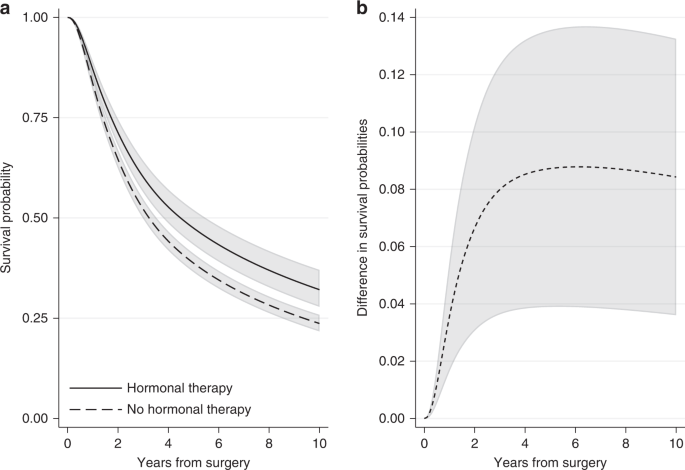
a Standardised survival probabilities for the event of relapse-free survival among patients who received treatment by treatment group and b the difference in standardised survival probabilities for the event of relapse-free survival under hormonal therapy and under no hormonal therapy, with 95% confidence intervals.

When estimating the effect of a treatment (or exposure) on a time-to-event outcome, it is important to consider potential imbalances in the groups of comparison and as far as possible adjust the statistical analysis for confounding variables. This can be done by fitting regression models. In this article, we have reviewed different ways to do this and provided illustrative examples of how regression models can be depicted graphically. We showed that absolute values for differences in standardised survival can be obtained by estimating standardised survival probabilities for each treatment arm. The association between treatment and the outcome of interest can then be quantified by calculating the difference in standardised survival probabilities by treatment status.

Currently, HRs are commonly reported as the main measure after fitting regression models to time-to-event data, i.e. a relative rather than absolute value for the effect of treatment (or exposure). In comparison, the difference in standardised survival probabilities provide an estimate of the absolute risk with/without treatment (or exposure) and are thus in general more informative than the HR. Comparing the effect of treatment on survival using absolute rather than relative measures makes it easier to understand whether treatment results in clinically meaningful improvements in survival. Moreover, survival probabilities have a less challenging interpretation in comparison to hazard ratios. Often HRs are misinterpreted as relative risks. However, the HR is simply calculated as the ratio of hazard rates and corresponds to relative rates. In contrast, the survival probability estimates the probability of not experiencing the event by a specific time and its complement (1 minus survival probability) can be interpreted as the risk. Further, HR estimates are affected by built-in selection bias, as HRs are conditional on individuals that have not yet experienced the event, which is not the case with survival probabilities [ 6 , 19 ]. Finally, the effect of treatment is often reported as a single HR for the whole study duration assuming that the treatment effect remains constant during follow-up. For many settings, this is not a realistic assumption and time-dependent HRs can communicate the experience of patients more accurately (e.g., by plotting the time-dependent hazard ratio of age across time since diagnosis). The difference in standardised survival probabilities provides a summary of the treatment effect using a single measure for each time of interest even after fitting complex models with various time-dependent effects and interactions. If the covariates we have adjusted for in the analysis are sufficient for confounding control, then the difference in standardised survival probabilities can be interpreted as the population causal effect [ 11 ]. It is important to note, though that this interpretation relies on the validity of the unmeasured confounding assumption (which is based on subject matter knowledge) and requires careful consideration, as often it is not possible to adjust for all relevant confounders. Adjusting for sufficient confounders is important also when hazard ratios are of interest and is not specific only to standardised survival curves. In practice, sensitivity analyses to modelling assumption are recommend as a way of assessing their impact on the estimates of interest. Moreover, in this paper, we focus on examples with no competing events, however, the interpretation of the standardised survival probabilities is less straightforward in the presence of competing events. If the competing events are conditionally independent, standardised cause-specific survival curves can be obtained after fitting cause-specific regression models. Otherwise, standardised cumulative incidence functions for the event of interest in the presence of competing events can be obtained instead, and these are discussed in detail elsewhere [ 22 ].

Compared to adjusted survival curves using the mean covariate method, standardised survival probabilities are obtained by averaging the conditional survival estimates of all individuals in the study population. In this way, the empirical covariate distribution is applied and the standardised estimates correspond to the estimates for the observed covariate distribution in the overall population instead of setting the adjusting covariates to a fixed and potentially meaningless value (e.g., mean observed value), as when obtaining “naively” adjusted survival curves. Standardising to a subset of the population can also be done by restricting the estimates to a particular subset (e.g. treated) and this help us address important clinical questions regarding the potential impact of interventions on individuals who did not receive the intervention yet or the impact of an intervention on individuals who actually received the intervention. Standardised survival estimates, as well as confidence intervals, can easily be obtained using standard existing software. A code example is provided in the supplementary material, with the standard errors obtained using the delta-method [ 23 , 24 ]. In our analysis, we fitted a flexible parametric survival model that can incorporate complex effects easily. However, standardised survival curves can, in principle, be obtained after fitting any survival model and have also been implemented in R for the Cox model [ 11 ]. Finally, even though in this paper our focus was on using regression standardisation to obtain standardised survival probabilities, marginal probabilities can also be estimated using other approaches not presented in the paper, such as inverse probability weights [ 25 ]. In the inverse probability weighting approach, instead of adjusting for covariates in the survival model, each individual is given a weight based on the probability of receiving their own treatment conditional on their observed covariate pattern. These weights are obtained from fitting a regression model with the treatment as the outcome, for example using logistic regression for a binary treatment.

Our illustrative example included only baselines covariates (i.e. covariates measured at start of follow-up). However, time-varying covariates may be of interest. In principle, standardised survival curves can also be obtained when the treatment under study is time-varying by estimating the survival curve under a scenario were individuals are “always treated” and the scenario “never treated”. However, careful consideration is required to determine whether this comparison is relevant for the question under study. Obtaining standardised curves is though more straightforward when other covariates included in the model are time-varying. This is because when comparing survival curves under different treatment arms, we only need to set the other adjusting covariates to the same values for both estimated curves to compare the same population. However, the interpretation is in terms of the covariate distribution at the start of follow-up/baseline.

The difference in standardised survival probabilities under different treatment arms is a valuable and informative measure to summarise the effect of treatment while adjusting for several confounding variables. Its estimation is no more complex than frequently reported measures, such as HRs, and so we highly encourage its use as an additional measure for reporting the results of a time-to-event analysis.

Data availability

The authors use publicly available data on breast cancer patients to demonstrate the different measures. Data can be downloaded from http://www.stata-press.com/data/fpsaus.html . The authors also provide Stata code in the supplementary material.

Putter H, Fiocco M, Geskus R. Tutorial in biostatistics: competing risks and multi-state models. Stat Med. 2007;26:2389–430.

Article   CAS   PubMed   Google Scholar  

Kaplan E, Meier P. Nonparametric estimation from incomplete observations. J Am Stat Assoc. 1958;53:457–81.

Article   Google Scholar  

Collett D. Modelling survival data in medical research, 3rd edition. Chapman: Hall/CRC; 2014.

Royston P, Parmar M. Flexible parametric proportional-hazards and proportional-odds models for censored survival data, with application to prognostic modelling and estimation of treatment effects. Stat Med. 2002;21:2175–97.

Article   PubMed   Google Scholar  

Sutradhar R, Austin PC. Relative rates not relative risks: addressing a widespread misinterpretation of hazard ratios. Ann Epidemiol. 2018;28:54–7.

Hernán M. The hazards of hazard ratios. Epidemiology. 2010;21:13–5.

Article   PubMed   PubMed Central   Google Scholar  

De Neve J, Gerds TA. On the interpretation of the hazard ratio in cox regression. Biometrical J. 2020;62:742–50.

Sedgwick P. Hazards and hazard ratios. BMJ. 2012;345:e5980.

Nieto F, Coresh J. Adjusting survival curves for confounders: a review and a new method. Am J Epidemiol. 1996;143:1059–68.

Rothman K, Greenland S, Lash T. Modern epidemiology, 3rd edition. Philadelphia: Lippincott Williams & Wilkins; 2008.

Sjölander A. Regression standardization with the r package stdReg. Eur J Epidemiol. 2016;31:563–74.

Royston P, Lambert P. Flexible parametric survival analysis in stata: beyond the cox model. College Station, TX: Stata Press; 2011.

Royston P, Altman D. External validation of a Cox prognostic model: principles and methods. BMC Med Res Methodol. 2013;13:1–15.

Clark T, Bradburn M, Love S, Altman D. Survival analysis part i: basic concepts and first analyses. Br J Cancer. 2003;89:232–8.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Cox DR. Regression models and life-tables. J R Stat Soc Ser B (Methodol). 1972;34:187–220.

Google Scholar  

Syriopoulou E, Mozumder SI, Rutherford MJ, Lambert PC. Robustness of individual and marginal model-based estimates: a sensitivity analysis of flexible parametric models. Cancer Epidemiol. 2019;58:17–24.

Bellera C, MacGrogan G, Debled M, Tunon de Lara C, Brouste V, Mathoulin-Pélissier S. Variables with time-varying effects and the cox model: some statistical concepts illustrated with a prognostic factor study in breast cancer. BMC Med Res Methodol. 2010;10:1–12.

Vandenbroucke J, Elm Evon, Altman D, Gøtzsche P, Mulrow C, Pocock S, et al. Strengthening the reporting of observational studies in epidemiology (STROBE): explanation and elaboration. PLoS Med. 2007;4:e297.

Aalen O, Cook R, Røysland K. Does cox analysis of a randomized survival study yield a causal treatment effect? Lifetime Data Anal. 2015;21:579–93.

Hu Z, Peter Gale R, Zhang M. Direct adjusted survival and cumulative incidence curves for observational studies. Bone Marrow Transpl. 2020;55:583–43.

Chang I-M, Gelman R, Pagano M. Corrected group prognostic curves and summary statistics. J Chronic Dis. 1982;35:669–74.

Syriopoulou E, Mozumder SI, Rutherford MJ, Lambert PC. Estimating causal effects in the presence of competing events using regression standardisation with the Stata command standsurv. BMC Med Res Methodol. 2022;22:226.

Cox C. Delta Method. In Encyclopedia of Biostatistics (eds Armitage P, Colton, T) 2005. https://doi.org/10.1002/0470011815.b2a15029 .

Lambert PC, Royston P. Further development of flexible parametric models for survival analysis. Stata J. 2009;9:265–90.

Cole S, Hernán M. Adjusted survival curves with inverse probability weights. Computer Methods Prog Biomedicine. 2004;75:45–9.

Download references

ES and TMLA were supported by the Swedish Cancer Society (grant number: 19 0102), the Swedish Research Council (grant numbers: 2019–01965, 2019–00227), and The Strategic Research Area in Epidemiology and Biostatistics (SFOepi) at Karolinska Institutet. TW was supported by Region Stockholm (clinical postdoctoral appointment). PCL was supported by the Swedish Cancer Society (Cancerfonden) (grant number 2018/744) and the Swedish Research Council (Vetenskapsrådet) (grant number 2017–01591). Open access funding provided by Karolinska Institute.

Author information

Authors and affiliations.

Department of Medical Epidemiology and Biostatistics, Karolinska Institutet, Stockholm, Sweden

Elisavet Syriopoulou, Paul C. Lambert & Therese M.-L. Andersson

Clinical Epidemiology Division, Department of Medicine Solna, Karolinska Institutet, Stockholm, Sweden

Tove Wästerlid

Department of Hematology, Karolinska University Hospital, Stockholm, Sweden

Biostatistics Research Group, Department of Health Sciences, University of Leicester, Leicester, UK

Paul C. Lambert

You can also search for this author in PubMed   Google Scholar

Contributions

ES and TMLA conceived and designed the study. ES performed the analysis with input from TMLA. ES drafted the manuscript. All authors substantially contributed to the interpretation of results, critically revised the manuscript and approved the final manuscript.

Corresponding author

Correspondence to Elisavet Syriopoulou .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Ethics approval and consent to participate

Not applicable.

Consent to publish

Additional information.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplemental code, supplemental table s1, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Syriopoulou, E., Wästerlid, T., Lambert, P.C. et al. Standardised survival probabilities: a useful and informative tool for reporting regression models for survival data. Br J Cancer 127 , 1808–1815 (2022). https://doi.org/10.1038/s41416-022-01949-6

Download citation

Received : 20 December 2021

Revised : 03 August 2022

Accepted : 04 August 2022

Published : 01 September 2022

Issue Date : 09 November 2022

DOI : https://doi.org/10.1038/s41416-022-01949-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

12. Survival analysis

• The times are most unlikely to be Normally distributed.
• We cannot afford to wait until events have happened to all the subjects, for example until all are dead. Some patients might have left the study early – they are lost to follow up . Thus the only information we have about some patients is that they were still alive at the last follow up. These are termed censored observations

Kaplan-Meier survival curve

Survival analysis I: the Kaplan-Meier method

Affiliation.

• 1 ERA-EDTA Registry, Department of Medical Informatics, Academic Medical Center, University of Amsterdam, The Netherlands. [email protected]
• PMID: 21677442
• DOI: 10.1159/000324758

The Kaplan-Meier (KM) method is used to analyze 'time-to-event' data. The outcome in KM analysis often includes all-cause mortality, but could also include other outcomes such as the occurrence of a cardiovascular event. The purpose of this article is to explain the basic concepts of the KM method, to provide some guidance regarding the presentation of the KM results and to discuss some important limitations of this method. To do this, we use a clinical example derived from the nephrology literature.

Copyright © 2011 S. Karger AG, Basel.

Publication types

• Comparative Study
• Randomized Controlled Trial
• Research Support, Non-U.S. Gov't
• Follow-Up Studies
• Kaplan-Meier Estimate*
• Kidney Failure, Chronic / mortality*
• Survival Analysis

Kaplan-Meier Survival Analysis

There are many situations in which you would want to examine the distribution of times between two events, such as length of employment (time between being hired and leaving the company). However, this kind of data usually includes some censored cases. Censored cases are cases for which the second event isn't recorded (for example, people still working for the company at the end of the study). The Kaplan-Meier procedure is a method of estimating time-to-event models in the presence of censored cases. The Kaplan-Meier model is based on estimating conditional probabilities at each time point when an event occurs and taking the product limit of those probabilities to estimate the survival rate at each point in time.

Example. Does a new treatment for AIDS have any therapeutic benefit in extending life? You could conduct a study using two groups of AIDS patients, one receiving traditional therapy and the other receiving the experimental treatment. Constructing a Kaplan-Meier model from the data would allow you to compare overall survival rates between the two groups to determine whether the experimental treatment is an improvement over the traditional therapy. You can also plot the survival or hazard functions and compare them visually for more detailed information.

Statistics. Survival table, including time, status, cumulative survival and standard error, cumulative events, and number remaining; and mean and median survival time, with standard error and 95% confidence interval. Plots: survival, hazard, log survival, and one minus survival.

The Kaplan-Meier procedure is available only if you have installed the Advanced Analyze option.

Kaplan-Meier Data Considerations

Data. The time variable should be continuous, the status variable can be categorical or continuous, and the factor and strata variables should be categorical.

Assumptions. Probabilities for the event of interest should depend only on time after the initial event--they are assumed to be stable with respect to absolute time. That is, cases that enter the study at different times (for example, patients who begin treatment at different times) should behave similarly. There should also be no systematic differences between censored and uncensored cases. If, for example, many of the censored cases are patients with more serious conditions, your results may be biased.

Related procedures. The Kaplan-Meier procedure uses a method of calculating life tables that estimates the survival or hazard function at the time of each event. The Life Tables procedure uses an actuarial approach to survival analysis that relies on partitioning the observation period into smaller time intervals and may be useful for dealing with large samples. If you have variables that you suspect are related to survival time or variables that you want to control for (covariates), use the Cox Regression procedure. If your covariates can have different values at different points in time for the same case, use Cox Regression with Time-Dependent Covariates.

Obtaining a Kaplan-Meier Survival Analysis

This feature requires Custom Tables and Advanced Statistics .

Analyze > Survival > Kaplan-Meier...

• Select a time variable.
• Select a status variable to identify cases for which the terminal event has occurred. This variable can be numeric or short string . Then click Define Event.

Optionally, you can select a factor variable to examine group differences. You can also select a strata variable, which will produce separate analyses for each level (stratum) of the variable.

This procedure pastes KM command syntax.

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

The Ultimate Guide to Survival Analysis

Get all of your Survival Analysis questions answered here

What is Survival Analysis? 

Survival Analysis is a field of statistical tools used to assess the time until an event occurs. As the name implies, this “event” could be death (of humans with a particular disease process, crops or plants under certain conditions, animals, etc.), but it also could be any number of alternatives (the failure of a structural beam or engineering component, the reoccurrence of a disease process, etc.).

For the rest of this article, we’ll look at a fabricated example about the survival rate of domesticated dogs on different diets.

Want to save this for later? Click here to download the eBook

What is survival analysis used for?

Survival analysis is used to describe or predict the survival (or failure) characteristics of a particular population. Often, the researcher is interested in how various treatments or predictor variables affect survival.

Research questions range from general lifespan questions about a population, such as:

• What are the lifespan characteristics of a particular species?
• In a particular setting, such as a country, how long do people live? How does the survival rate change for different age groups such as infants, children, adults, and the elderly?
• In a manufactured product, such as a structural beam, at what load weight do over 1% or 5% of the units fail?

Survival analysis also provides tools to incorporate covariates and other predictors. Some example research questions in this case are:

• How do various factors and covariates (e.g., genetics, diet, exercise, smoking, etc.) affect lifespan?
• Of patients diagnosed with a particular form of cancer, how do various medical treatments affect lifespan, prognosis, or likelihood of remission?
• How do manufacturing processes (e.g., temperature, time, material composition, etc.) affect the failure rate of a product (such as a structural beam)?

See the different uses for Survival Analysis in Prism

What is a survival curve?

A survival curve plots the survival function, which is defined as the probability that the event of interest hasn’t occurred by (and including) each time point. 

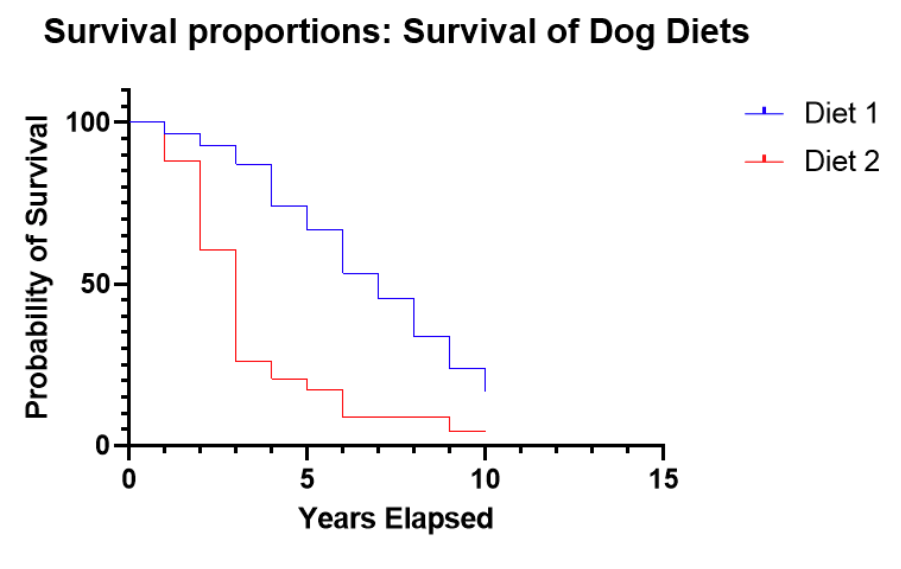
Survival curve or Kaplan-Meier curve interpretation

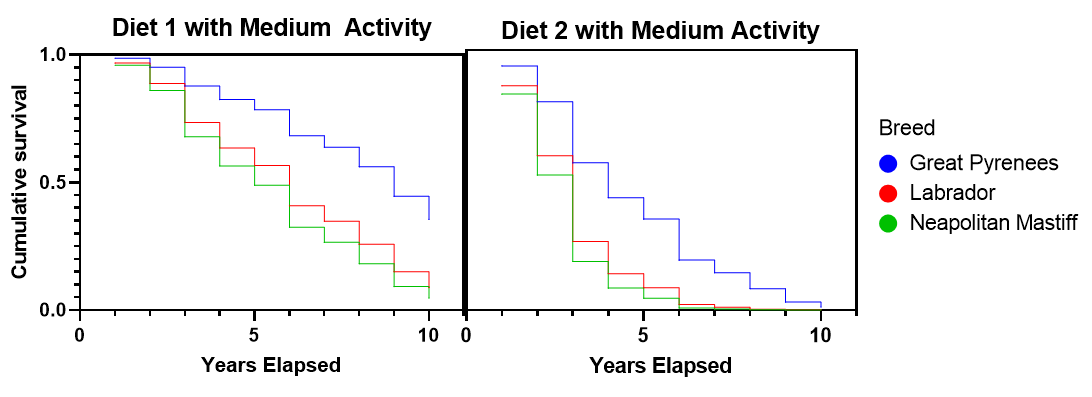
With our simulated data, this graph indicates that for Diet 2, after 3 years, 70% of the dogs remain, but after 4 years, only about 25% of dogs on Diet 2 survived. This is strikingly different from Diet 1, which still has 90% surviving after 4 years.

Because the survival curves after 10 years elapsed to have a greater than 0 probability, this plot shows that some values were censored, meaning that some dogs were still alive at the conclusion of the study. With the censored observations, we can’t know for how long they will survive. 

In practice, censoring is a very common occurrence. A study is designed and funded for a particular amount of time, with the intention of observing the event of interest, but that might not be the case. Also, dogs, in this case, might come into the study after the study has been running for seven years, so they are only observed for a maximum of three years in this case.

In the discrete case, the survival function at time t , S(t), is  S(t) = probability of surviving after (not including) time t

Mathematically, the survival function is 1 - the cumulative distribution function (CDF), or:

S(t) = 1  - F(t) = 1 - Pr {T ≤ t}

This means that in the discrete case, the probability density function (PDF) is the probability of the event occurring at time t .

What is a hazard function?

Hazard functions depict the instantaneous rate of death (or failure) given that an individual has survived up to that time. They are rarely plotted on their own or estimated directly in survival analysis. Instead, they are used behind the scenes in several prominent situations. The most common of these is comparing the ratio of hazards between, say treatment and a control group. Additionally, the hazard function forms the backbone of the calculations and assumptions underlying the very popular Cox proportional hazards model, but even in that situation, the actual hazard functions aren’t of much interest.

Intuitively, hazard functions give you a sense of the risk of the event occurring for an individual at a current point in time. In our demo example, we only recorded data annually, so our data are discrete. This makes the interpretation a little more challenging. Instead of an instantaneous rate of death, we have something close to (but not exactly) an annual rate of death, which we call a “hazard.”

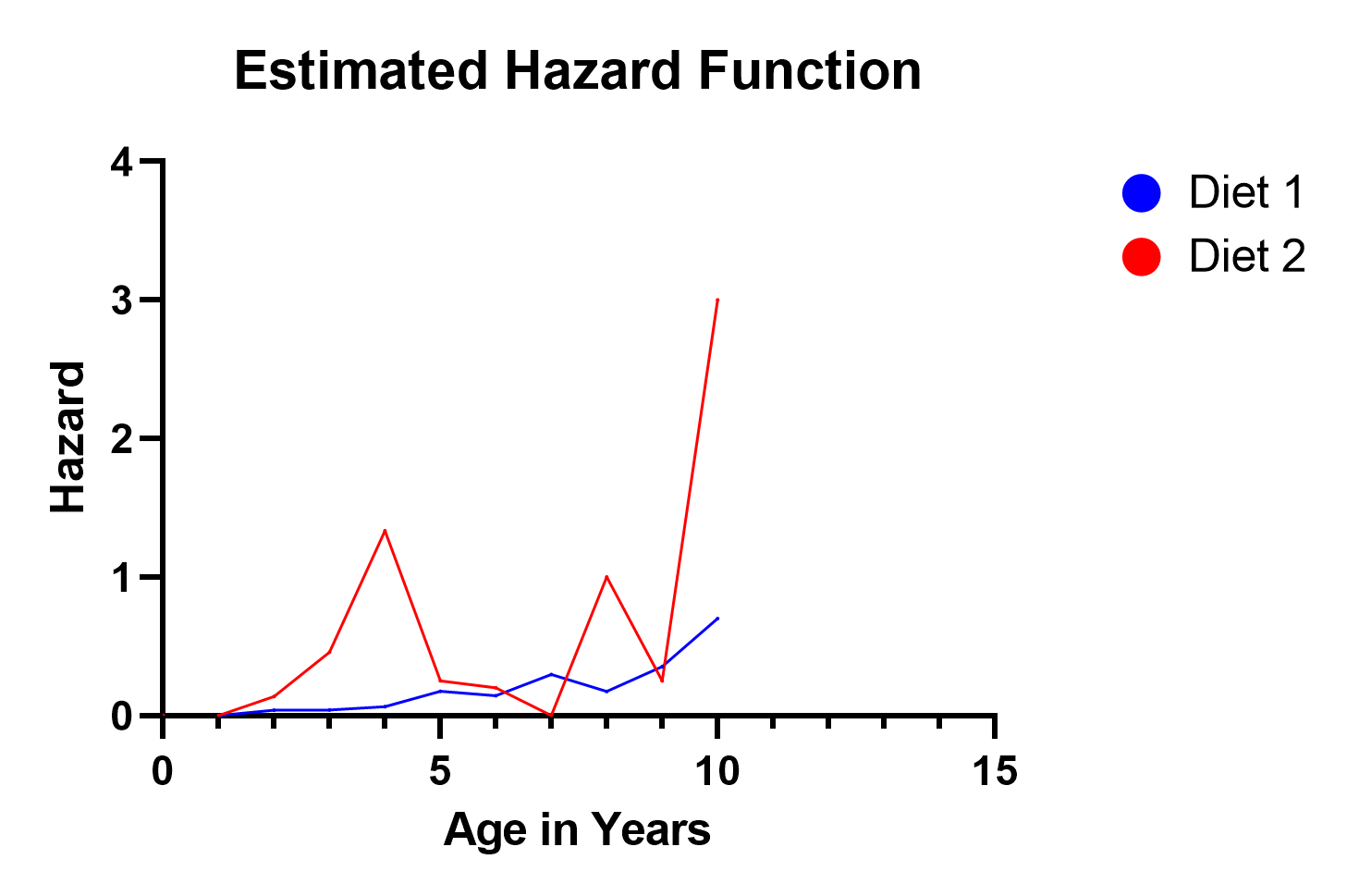
In our example, notice the hazard function for Diet 2 spikes in three locations (ages 4, 8, and 10). This reflects the fact that on the survival curve, more dogs died after 4 years elapsed than remained after 4 years. So clearly, that was a highly hazardous year, and the estimated hazard function value of 1.3 reflects this. Similar situations occurred at years 8 and 10. Even though not nearly as many dogs were surviving at that time, the proportion of dogs that died in years 8 and 10 was relatively large.

In the discrete case, the hazard at time t , h ( t ), is: 

How do I choose a model for survival analysis?

The two most common survival analysis techniques are the Kaplan-Meier method and Cox proportional hazard model.

Both of these require that your data are a sample of independent observations from some “population of interest.” With our example, this means the domesticated dogs are randomly sampled and don’t have confounding effects and relationships with other dogs in the study (such as being from the same litter, breeder, kennel, etc.).

The Kaplan-Meier method is intuitive and nonparametric and therefore requires few assumptions. However, besides a treatment variable (control, treatment 1, treatment 2, …), it cannot easily incorporate additional variables and predictors into the model.

The Cox proportional hazard model , on the other hand, easily incorporates predictor variables, but it is more esoteric. The model has been around for decades, is tried and true, and continues to perform well compared to other alternatives.

What is The Kaplan-Meier method?

The Kaplan-Meier method is the most intuitive model for performing a survival analysis with some added bells and whistles for statistical rigor.

With our example data about domestic dogs on two different diets, we recorded the diet and the year of death of each dog in the study. If we wanted to get an idea of survival rates and probabilities, the most straightforward way to do that would be to just count up how many dogs on each diet died each year. We can also easily aggregate the data to calculate the number of dogs still alive at each time point.

In a nutshell, that’s the basis of the Kaplan-Meier method. It’s called a nonparametric method because there are no distributional assumptions about the data. It’s just a fancy way of tabulating and discussing the results.

If this sounds too simple, you are correct. This perspective oversimplifies Kaplan-Meier, but not by a lot. For example, if some observations in the study don’t experience the event of interest before the study ends, those values need to be represented appropriately in the calculations.

Additionally, statisticians have worked out a mathematical theory that justifies the Kaplan-Meier estimate as being a reasonable choice. Although not all that important in practice (besides giving statisticians like us a job), this provides credence for the method. For example, the Kaplan-Meier estimator for the survival curve is asymptotically unbiased, meaning that as the sample size goes to infinity, the estimator converges on the true value.

When is the Kaplan-Meier method appropriate?

The Kaplan-Meier method is appropriate when you have a fairly simple survival analysis that doesn’t have covariates or other predictor variables. A common example is studying treatment versus control groups. In our simulated data set for this article, we record the survival rate of dogs on two different diets, which is also appropriate here.

However, we have additional (simulated) data about the breed of dogs and their level of activity. Those are likely interesting and important confounding factors in the survival of dogs. We don’t have a way of including them in the analysis with Kaplan-Meier, but we can with the Cox proportional hazards model below.

How do I perform a Kaplan-Meier analysis?

Analyzing Kaplan-Meier can be very simple. All that is needed is the information over time of how long the observational unit or subject was in the study, which group (e.g., treatment, control, etc.) it was in, and whether or not the event occurred or was censored (the event didn’t occur before the end of the study).

See how Prism makes it easy to perform a Kaplan-Meier analysis.

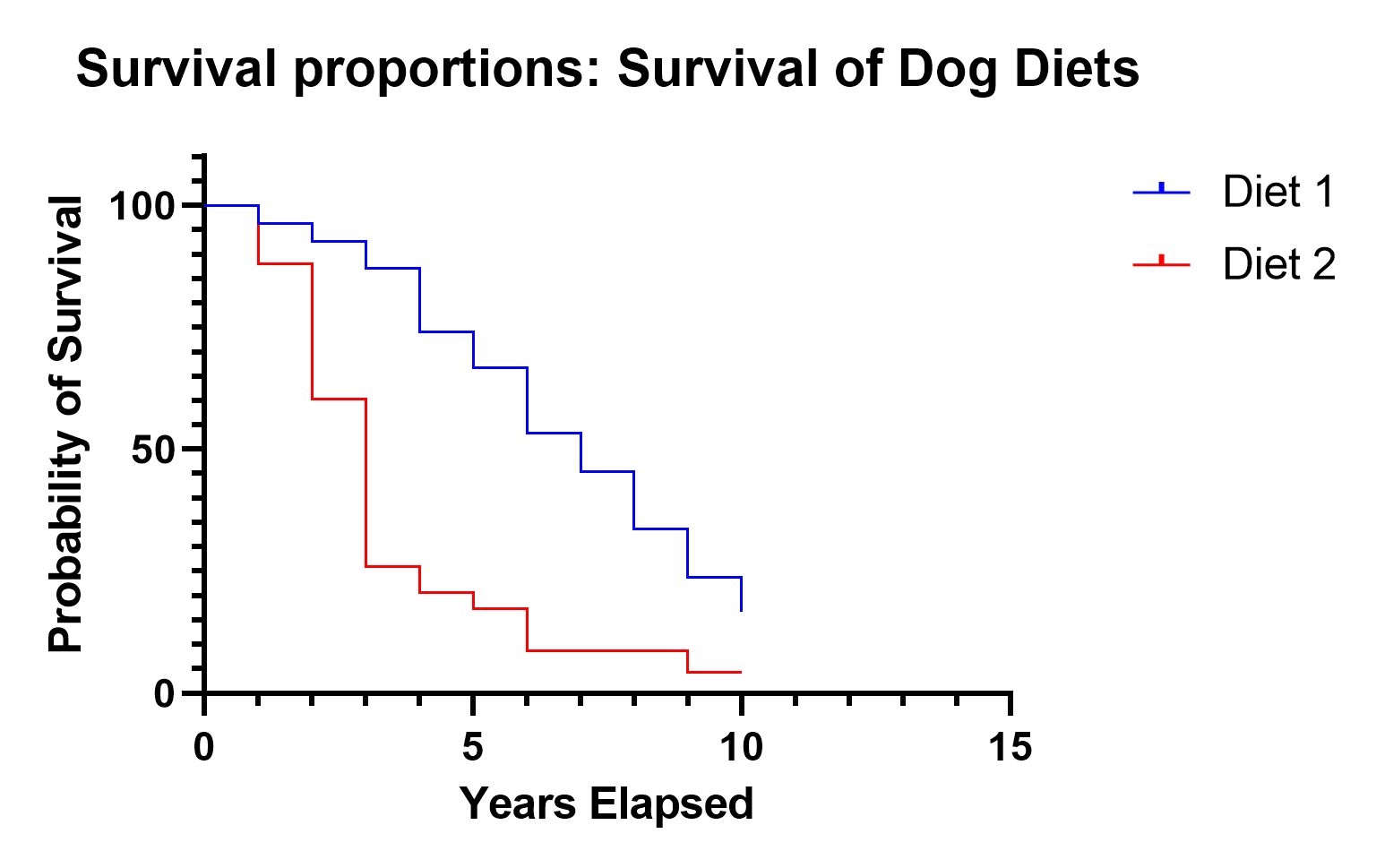
The Kaplan-Meier Curve is an estimate for the survival curve, which is a graphical representation of the proportion of observations that have not experienced the event of interest at each time point.

What is the Cox proportional hazards model?

The industry standard for survival analysis is the Cox proportional hazards model (also called the Cox regression model ). To this day, when a new survival model is proposed, researchers compare their model to this one. 

It is a robust model, meaning that it works well even if some of the model assumptions are violated. That’s a good thing because the assumptions are difficult to validate empirically, let alone understand.

Rather than modeling the survival curve, which is the approach taken by the Kaplan-Meier method, the Cox model estimates the hazard function. In general, hazard functions are more stable and thus easier to model than survival curves. They depict the hazard, i.e. the instantaneous rate of death (or failure) given that an individual has survived up to that time.

What is the Cox regression model?

It’s just a more ambiguous name for the Cox proportional hazards model.

What are the Cox regression model assumptions?

The prominent assumption with Cox proportional hazards model is that, not surprisingly, the hazard functions are proportional. David Cox noticed that by enforcing that “simple” constraint on the form of the hazard model, a lot of difficult math and unstable optimization can be avoided.

This constraint (that the hazards functions are proportional) also provides an easy way to add in additional variables (covariates) to the model. With our simulated example of dogs on different diets, we can now include the additional information of breed (Great Pyrenees, Labrador, Neapolitan Mastiff) and activity level (Low, Medium, High).

What is the Cox regression model used for?

Because of a clever constraint and the ease at which predictor variables can be added to the model, the Cox proportional hazards model can ascertain hazards and make predictions on data with multiple predictor (covariate) variables. For example, with our simulated data, we could determine the estimated hazard or survival rate of a specific age, breed, and activity level, such as a Great Pyrenees that’s been in the study for three years with a medium activity level.

How do I fit a Cox proportional hazard model?

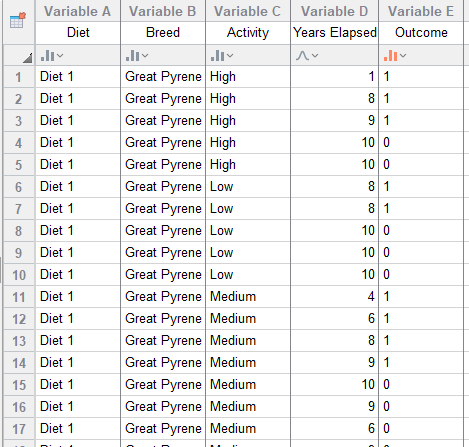
To fit a Cox proportional hazard model, you need to specify the data including time elapsed, outcome (whether that observational unit died or was censored), and any other variables (covariates). In our simulated example data, we are looking at the survival rate of dogs on two different diets, and we include Breed and Activity as additional variables.

Learn how Prism makes it easy to perform Cox Regression.

How do you write a Cox proportional hazard model?

Mathematically, the primary Cox model assumption is that the hazard function, h ( t ), can be written:

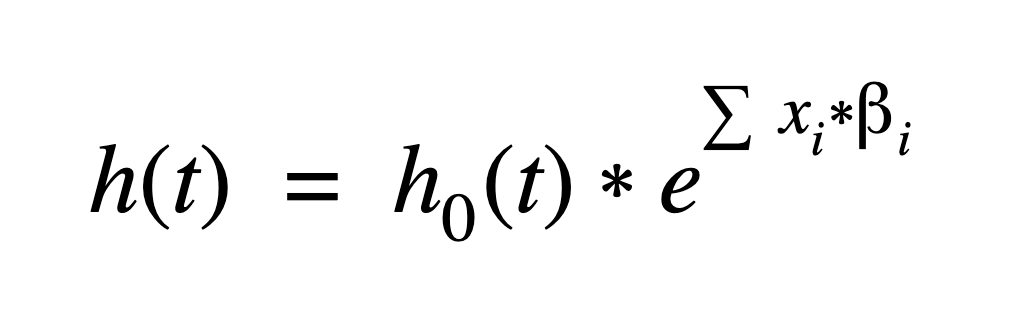
Where i=1pxi*i is a linear combination (a sum) of p predictor (covariate) variables times a regression coefficient. The coefficients and baseline hazard function, h 0( t ),  are estimated using the data.

Another way of saying that the hazard functions are proportional is that the predictor variables’ effects on the hazard function are multiplicative. That’s a major assumption that is difficult to assess.

Unless we include interaction terms (such as activity by breed), this assumes, in our example, that activity level has the same effect on the hazard regardless of how long the dog has been in the study, what breed the dog is, or what diet it is on. 

Interaction terms can be included, but greatly complicate interpretation, and introduce multicollinearity, which makes the estimates unstable. As with many statistical models, George Box’s quip that, “All models are wrong but some are useful,” applies here.

The baseline hazard function, h0( t ), is key to David Cox’s formulation of the hazard function because that value gets canceled out when taking a ratio of two different hazards (say for Diet 1 vs Diet 2 in our example).

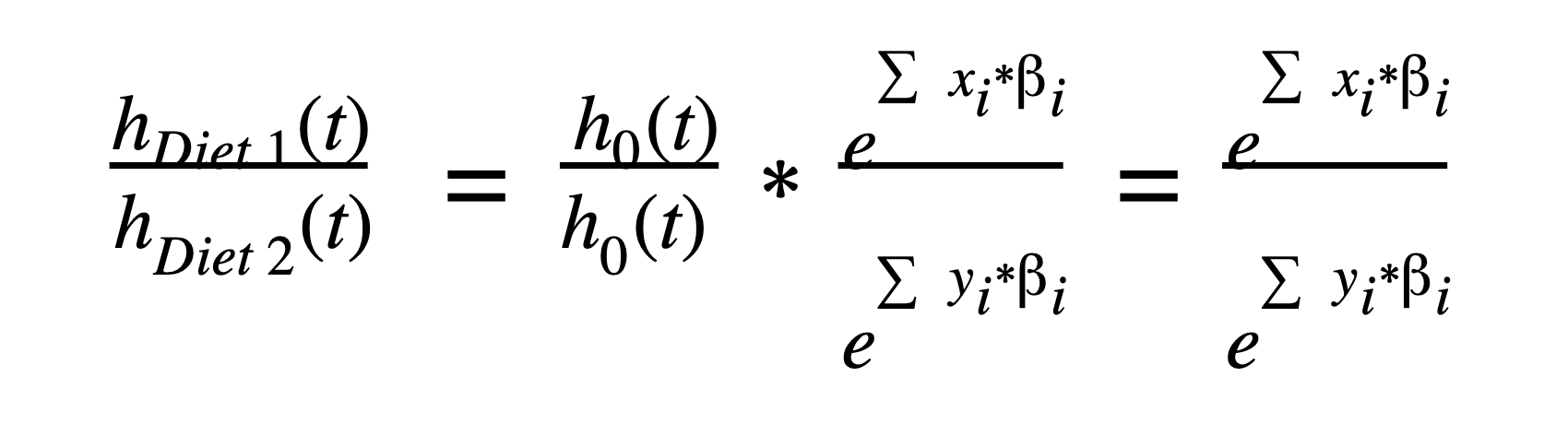
How do you interpret Cox proportional hazards?

Although there are nuances, there are two main options for reporting the results of the Cox proportional hazards model: numerically or graphically.

Numerical results

The most informative part of the numerical results are in the parameter estimates (and hazard ratios). If you are familiar with linear and logistic regression, the interpretation of the numerical results only requires a slight adjustment. The following estimates provide the guts of the information that is needed to understand how each predictor variable affects the hazard functions.

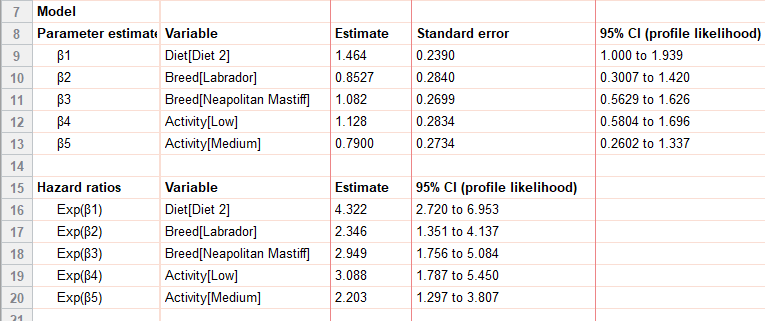
Mathematically, these parameter estimates are used to calculate the hazard function at different values (or levels) of the covariates using the equation:

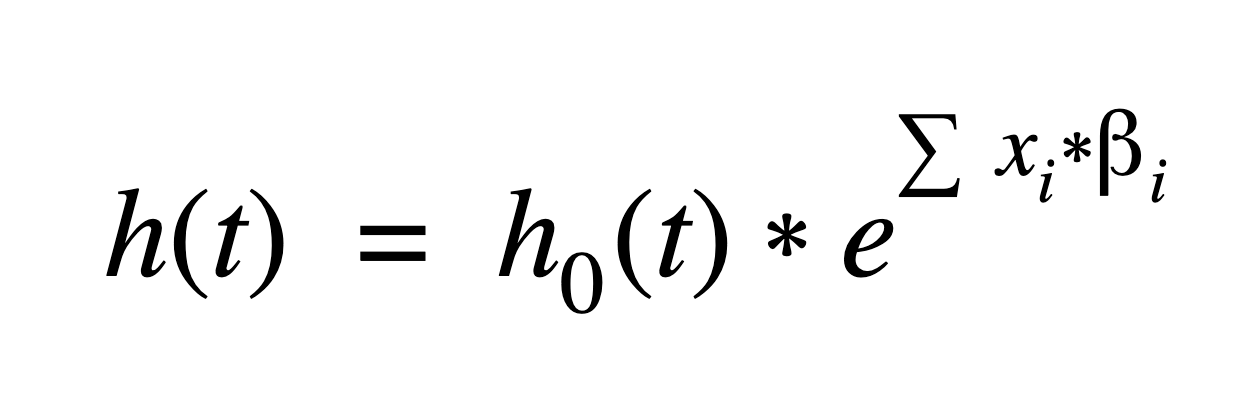
The Cox model uses the data to find the maximum likelihood estimators for the regression (β) coefficients in the hazard function. Each variable in the model (in our example, these are Diet, Breed, and Activity) has its own regression coefficient and estimate. Categorical variables in the model use reference level coding . 

It’s necessary to have a baseline reference with Cox regression models because all of the interpretation is based on calculating proportional hazard functions to the baseline, h 0( t ).

For our example, the primary question of interest is: Do the two different diets have a significant effect on the survival of dogs? From the parameter estimates and hazard ratio, we can see they do, and, in fact, have quite a drastic difference. In particular (regardless of breed or activity level) dogs on Diet 2 had a 4.322 times higher hazard than dogs on Diet 1, with a 95% confidence interval of (2.720 to 6.953). Because the 95% CI does not include 1, we can also say that this coefficient is statistically significant (p<0.05).

The value we reported above is the hazard ratio, which is just e [ˆβ1] in this case.

What is a hazard ratio?

The hazard ratio is used for interpreting the results of a Cox proportional hazards model and is the multiplicative effect of a variable on the baseline hazard function. For continuous predictor variables, this is the multiplicative effect of a 1-unit change in the predictor (e.g., if weight was a predictor and was measured in kilograms, it would be the multiplicative effect per kilogram). For categorical variables, it is the multiplicative effect that results from that level of the predictor (e.g., Diet 2).

Graphical results

The main graphs for interpretation of the Cox regression model are the cumulative survival functions for specific values of the predictor variables.

There are a number of interesting graphics to look at with our simulated data. For example, the two plots below show the drastic differences between the survival rates of Diet 1 and Diet 2. Here we fixed the activity level at medium and show the differences between breeds by color. Notice the much steeper decline of Diet 2, which indicates a much lower survival rate. Because there aren’t any interaction terms in the model, these survival curves don’t cross. Our data was simulated to behave nicely, and interaction terms weren’t needed. Note that these survival rates per breed are completely fictitious!

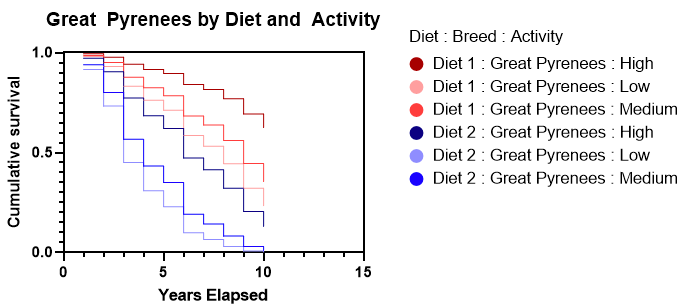
A second graphical example looks at the effect of diet and activity level within a single breed (Great Pyrenees). Again, this clearly shows that Diet 1 has a much higher survival rate. It also shows that as the activity level increases, the survival rate increases. Diet 2 is so much worse than Diet 1, that even at a low activity level on Diet 1 there is a higher survival rate than a high activity level on Diet 2.

See how to graph your Survival Analysis results in Prism.

Advantages of Cox proportional hazards model vs logistic regression

The Cox proportional hazards model and a logistic regression model are used for different purposes; they aren’t actually comparable. The Cox proportional hazards model is a tool for survival analysis and measures the time until an event occurs. It is used to compare survival (or failure) rates across different experimental or observational variables. In our example, we look at simulated data on the survival of domesticated dogs on two different diets. We also record information on breed and activity level.

Logistic regression, on the other hand, is a tool for predicting a binary response such as success/failure, present/absent, yes/no. Logistic regression also uses predictor variables, but it’s to ascertain whether or not the event occurs for a specific observational unit. In its standard form, there is no element of time involved in the predictions. You could, for example, use logistic regression to predict whether a student passes a class based on some predictor variables (previous exam scores, age, head circumference, etc.).

Perform Your Own Survival Analysis

Now it’s time to execute your own Survival Analysis according to your specific needs.  Start your 30 day free trial of Prism   and get access to:

• A step-by-step guide on how to perform Survival Analysis
• Sample data to save you time
• More tips on how Prism can help your research

More than a million scientists in 110 countries rely on Prism to help share their research with the world. With Prism, in a matter of minutes, you learn how to go from entering data to performing statistical analyses and generating high-quality graphs. Start your 30 day trial today or learn more about Survival Analysis in Prism .

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Survival analysis.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: May 22, 2023 .

• Definition/Introduction

Survival analysis is widely used in evidence-based medicine to examine the time-to-event series. [1]  Often used for survival/death events, time-to-event series can illustrate time to any dichotomous event. [2]  Examples: the number of days before treatment allows an individual to go into remission; or the severity grade of disease and the hours in the hospital before being released. Using this method, one can compare patients and/or groups of patients. [1]  Relationships between more than one group can use Kaplan-Meier estimations and log-rank tests, which are both nonparametric. Researchers interested in quantifying the effect of the comparison(s) can use Cox proportional hazard models. [2]  Survival analysis techniques were first used for medical studies but have expanded to a variety of other disciplines including financial services and engineering. [1]

• Issues of Concern

Due to the frequency of utilization of survival analysis in medical literature, healthcare providers must understand common concepts and analyses associated with these techniques, including Kaplan-Meier, log-rank tests, and Cox proportional hazards models.

Survival analysis is used with a binary or dichotomous outcome of interest. [1]  Typically, multiple groups are compared, for example, a group may have treatment A, and another group may have treatment B. The survival function is the probability of surviving (or not experiencing an event) up to a specified time point, whereas hazard rate is the rate of occurrence for the event within a given period. [3]  To determine survival time, one must know the time of the original event at origin and the time of the final event. [4]  Truncation helps in determining a sample for survival analysis to limit bias; researchers should not choose subjects they know will likely (or not) experience an event in order to support their hypotheses. [3]

Censoring is an important topic in survival analysis. Censored subjects never experienced the outcome of interest during the study specified timeframe. Whether or not an individual is censored should not be associated with whether or not the event occurred. [1]  Left censoring occurs when an individual experienced the event before origin; right censoring occurs when an individual did not experience the event during the specified timeframe (occurred after, or unsure if and when the incident occurred). [3]  Essentially, censoring means that the outcome of interest for that subject cannot be determined based on the study. [5]  Survival analysis examines the time before an individual or group experiences the event or outcome of interest or until censored. [1]  Ignoring or excluding censored subjects would bias the results. [3]  While some study facets remain out of the control of the researchers, recruiting subjects into the study that have characteristics suggesting better study retention can limit censoring.

Life Tables

Life tables (also known as actuarial life tables) differ from other methods of survival analysis in that the observation outputs categorize into distinct time events. [6] [7]  Life tables present outputs that show whether the case occurred, whether the individual was censored, and the time to that event. [8]  When examining a life table, one can determine the proportion of patients experiencing an event (e.g., dying) during which interval the outcome occurred. Life tables can also denote which individuals were censored and which were not (experienced the event in the timeframe). Within these life tables, one should assume no changes in experiencing an event at different intervals. For example, if patients with breast cancer received a second drug halfway through the treatment, they may be less likely to experience the event of dying, thus potentially invalidating results. Life tables remain useful, but in 1958, Kaplan and Meier proposed a new method that removed the pre-fixed time interval requirement. With their method, the events/outcomes of interests are assessable as they happen regardless of specific time point intervals. [6]

  Kaplan-Meier Method

One of the most frequently used methods of survival analysis is the Kaplan-Meier (KM) approach. The KM method estimates the likelihood of survival. [9]  This approach often utilizes a KM survival curve to represent the survival function. [3]  Similar to life tables, the KM curves assume that those censored would have had similar outcomes, and those recruited later in the study have the same probabilities as those recruited earlier. [10]  The KM plots a survival curve, which often reports median survival time(s), a reliable estimate if the majority of the observations are uncensored. [7]  One can calculate confidence intervals (CIs) for KM probabilities and plot CIs in the survival curves to provide a range of possible values for the population based on the sample. [3]  The curve itself does not provide information on whether or not the difference between the groups is significant. To do this, one can use the log-rank test. [1]

The log-rank test is a non-parametric test that compares two or more groups’ survival distributions. [5]  This test, which assumes censoring is unrelated to prognosis, examines the null hypothesis (that there are no differences in distribution between the groups). [5]  In other words, researchers can determine if curves between two different groups were statistically significant, i.e., if the event rate in one group is consistently higher than the other over time. [6] [7]  Log-rank tests are utilized when a data set has censored observations; if one has no censored cases, the Wilcoxon rank-sum test can compare survival times. [11] [7]  Researchers reporting log-rank tests should specify the entire distribution being tested, not a specific timeframe. [3]  The log-rank test itself is limited in the sense that it cannot determine an estimate of the difference between groups, whereas a Cox proportional hazard model can. [3]

Cox Proportional Hazard Model

The Cox proportional hazards model is a semiparametric regression model that allows researchers to examine the effects of multiple variables on survival curves. [7]  Semiparametric means that the method does not require a specific distribution of the survival function; however, it does assume a relationship between the covariates and outcome. [3]  The output of the Cox model is presented in hazard ratios (HR).

Hazard, or the hazard function, refers to the chances of an event/outcome to occur within a unit of time, assuming that the subject has survived up to that time. [7] [5]  The hazard ratio (HR) represents the ratio of the two different treatment groups. [3]  As the value above 1 increases, the risk increases for the event associated with that variable. As HR decreases below 1, the risk decreases. Cox proportional hazards model investigates relationships of predictors in these analyses and develops HRs. [2]

An important assumption made by the Cox model is that the proportional hazards between the variables remain steady over time. Cox hazard models allow researchers to adjust for confounders and to form relative risk (RR) for individuals to experience an event based on risk factors. [1] [7]

• Clinical Significance

Software is available to compute KM survival curves, log-rank tests, and hazard regressions. This article covers the three most commonly used survival analyses in the medical literature; however, others exist. [5]  By having a foundational understanding of the commonly used survival analyses addressed here, healthcare providers can properly assess survival analysis methods in literature to make evidence-based decisions in practice or their own clinical studies.

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Survival Analysis. [Updated 2023 May 22]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas. [Cochrane Database Syst Rev. 2022] Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas. Crider K, Williams J, Qi YP, Gutman J, Yeung L, Mai C, Finkelstain J, Mehta S, Pons-Duran C, Menéndez C, et al. Cochrane Database Syst Rev. 2022 Feb 1; 2(2022). Epub 2022 Feb 1.
• Biostatistics Series Module 9: Survival Analysis. [Indian J Dermatol. 2017] Biostatistics Series Module 9: Survival Analysis. Hazra A, Gogtay N. Indian J Dermatol. 2017 May-Jun; 62(3):251-257.
• Survival analysis: Part I - analysis of time-to-event. [Korean J Anesthesiol. 2018] Survival analysis: Part I - analysis of time-to-event. In J, Lee DK. Korean J Anesthesiol. 2018 Jun; 71(3):182-191. Epub 2018 May 17.
• Review Survival Analysis and Interpretation of Time-to-Event Data: The Tortoise and the Hare. [Anesth Analg. 2018] Review Survival Analysis and Interpretation of Time-to-Event Data: The Tortoise and the Hare. Schober P, Vetter TR. Anesth Analg. 2018 Sep; 127(3):792-798.
• Review Admission avoidance hospital at home. [Cochrane Database Syst Rev. 2008] Review Admission avoidance hospital at home. Shepperd S, Doll H, Angus RM, Clarke MJ, Iliffe S, Kalra L, Ricauda NA, Wilson AD. Cochrane Database Syst Rev. 2008 Oct 8; (4):CD007491. Epub 2008 Oct 8.

Recent Activity

• Survival Analysis - StatPearls Survival Analysis - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers