using four equations to solve a problem is called a four order system

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Systems of equations

About this unit, intro to systems of equations.

• Systems of equations: trolls, tolls (1 of 2) (Opens a modal)
• Systems of equations: trolls, tolls (2 of 2) (Opens a modal)
• Testing a solution to a system of equations (Opens a modal)
• Solutions of systems of equations Get 3 of 4 questions to level up!

Systems of equations with graphing

• Systems of equations with graphing (Opens a modal)
• Systems of equations with graphing: y=7/5x-5 & y=3/5x-1 (Opens a modal)
• Systems of equations with graphing: 5x+3y=7 & 3x-2y=8 (Opens a modal)
• Systems of equations with graphing: chores (Opens a modal)
• Systems of equations with graphing: exact & approximate solutions (Opens a modal)
• Systems of equations with graphing Get 3 of 4 questions to level up!

Solving systems with substitution

• Systems of equations with substitution: 2y=x+7 & x=y-4 (Opens a modal)
• Systems of equations with substitution (Opens a modal)
• Systems of equations with substitution: y=4x-17.5 & y+2x=6.5 (Opens a modal)
• Systems of equations with substitution: -3x-4y=-2 & y=2x-5 (Opens a modal)
• Systems of equations with substitution: 9x+3y=15 & y-x=5 (Opens a modal)
• Systems of equations with substitution: y=-5x+8 & 10x+2y=-2 (Opens a modal)
• Systems of equations with substitution: y=-1/4x+100 & y=-1/4x+120 (Opens a modal)
• Substitution method review (systems of equations) (Opens a modal)
• Systems of equations with substitution Get 3 of 4 questions to level up!

Number of solutions to systems of equations

• Systems of equations number of solutions: fruit prices (1 of 2) (Opens a modal)
• Systems of equations number of solutions: fruit prices (2 of 2) (Opens a modal)
• Solutions to systems of equations: dependent vs. independent (Opens a modal)
• Number of solutions to a system of equations (Opens a modal)
• Number of solutions to a system of equations graphically (Opens a modal)
• Number of solutions to a system of equations algebraically (Opens a modal)
• How many solutions does a system of linear equations have if there are at least two? (Opens a modal)
• Number of solutions to system of equations review (Opens a modal)
• Number of solutions to a system of equations graphically Get 3 of 4 questions to level up!
• Number of solutions to a system of equations algebraically Get 3 of 4 questions to level up!

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}

step-by-step

system of 4 equations solver

• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.6: Solve Systems of Equations Using Matrices

• Last updated
• Save as PDF
• Page ID 5142

Learning Objectives

By the end of this section, you will be able to:

• Write the augmented matrix for a system of equations
• Use row operations on a matrix
• Solve systems of equations using matrices

Before you get started, take this readiness quiz.

• Solve: \(3(x+2)+4=4(2x−1)+9\). If you missed this problem, review [link] .
• Solve: \(0.25p+0.25(x+4)=5.20\). If you missed this problem, review [link] .
• Evaluate when \(x=−2\) and \(y=3:2x^2−xy+3y^2\). If you missed this problem, review [link] .

Write the Augmented Matrix for a System of Equations

Solving a system of equations can be a tedious operation where a simple mistake can wreak havoc on finding the solution. An alternative method which uses the basic procedures of elimination but with notation that is simpler is available. The method involves using a matrix . A matrix is a rectangular array of numbers arranged in rows and columns.

A matrix is a rectangular array of numbers arranged in rows and columns.

A matrix with m rows and n columns has order \(m\times n\). The matrix on the left below has 2 rows and 3 columns and so it has order \(2\times 3\). We say it is a 2 by 3 matrix.

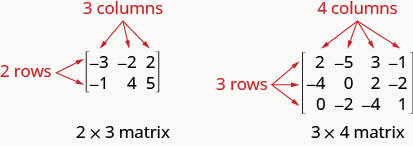
Each number in the matrix is called an element or entry in the matrix.

We will use a matrix to represent a system of linear equations. We write each equation in standard form and the coefficients of the variables and the constant of each equation becomes a row in the matrix. Each column then would be the coefficients of one of the variables in the system or the constants. A vertical line replaces the equal signs. We call the resulting matrix the augmented matrix for the system of equations.

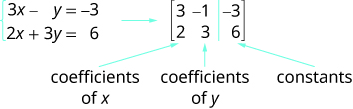
Notice the first column is made up of all the coefficients of x , the second column is the all the coefficients of y , and the third column is all the constants.

Example \(\PageIndex{1}\)

ⓐ \(\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right. \) ⓑ \( \left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. \)

ⓐ The second equation is not in standard form. We rewrite the second equation in standard form.

\[\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber\]

We replace the second equation with its standard form. In the augmented matrix, the first equation gives us the first row and the second equation gives us the second row. The vertical line replaces the equal signs.

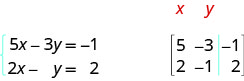
ⓑ All three equations are in standard form. In the augmented matrix the first equation gives us the first row, the second equation gives us the second row, and the third equation gives us the third row. The vertical line replaces the equal signs.

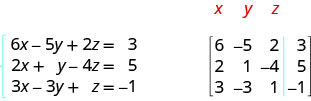
Example \(\PageIndex{2}\)

Write each system of linear equations as an augmented matrix:

ⓐ \(\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right. \) ⓑ \(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)

ⓐ \(\left[ \begin{matrix} 3 &8 &-3 \\ 2 &5 &−3 \end{matrix} \right] \)

ⓑ \(\left[ \begin{matrix} 2 &3 &1 &−5 \\ −1 &3 &3 &4 \\ 2 &8 &7 &−3 \end{matrix} \right] \)

Example \(\PageIndex{3}\)

ⓐ \(\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right. \) ⓑ \(\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. \)

ⓐ \(\left[ \begin{matrix} 11 &9 &−5 \\ 7 &5 &−1 \end{matrix} \right] \) ⓑ \(\left[ \begin{matrix} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{matrix} \right] \)

It is important as we solve systems of equations using matrices to be able to go back and forth between the system and the matrix. The next example asks us to take the information in the matrix and write the system of equations.

Example \(\PageIndex{4}\)

Write the system of equations that corresponds to the augmented matrix:

\(\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right] \).

We remember that each row corresponds to an equation and that each entry is a coefficient of a variable or the constant. The vertical line replaces the equal sign. Since this matrix is a \(4\times 3\), we know it will translate into a system of three equations with three variables.

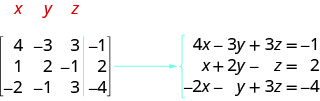
Example \(\PageIndex{5}\)

Write the system of equations that corresponds to the augmented matrix: \(\left[ \begin{matrix} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{matrix} \right] \).

\(\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.\)

Example \(\PageIndex{6}\)

Write the system of equations that corresponds to the augmented matrix: \(\left[ \begin{matrix} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{matrix} \right] \).

\(\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.\)

Use Row Operations on a Matrix

Once a system of equations is in its augmented matrix form, we will perform operations on the rows that will lead us to the solution.

To solve by elimination, it doesn’t matter which order we place the equations in the system. Similarly, in the matrix we can interchange the rows.

When we solve by elimination, we often multiply one of the equations by a constant. Since each row represents an equation, and we can multiply each side of an equation by a constant, similarly we can multiply each entry in a row by any real number except 0.

In elimination, we often add a multiple of one row to another row. In the matrix we can replace a row with its sum with a multiple of another row.

These actions are called row operations and will help us use the matrix to solve a system of equations.

ROW OPERATIONS

In a matrix, the following operations can be performed on any row and the resulting matrix will be equivalent to the original matrix.

• Interchange any two rows.
• Multiply a row by any real number except 0.
• Add a nonzero multiple of one row to another row.

Performing these operations is easy to do but all the arithmetic can result in a mistake. If we use a system to record the row operation in each step, it is much easier to go back and check our work.

We use capital letters with subscripts to represent each row. We then show the operation to the left of the new matrix. To show interchanging a row:

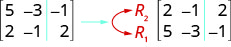
To multiply row 2 by \(−3\):

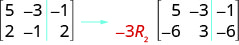
To multiply row 2 by \(−3\) and add it to row 1:

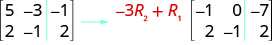
Example \(\PageIndex{7}\)

Perform the indicated operations on the augmented matrix:

ⓐ Interchange rows 2 and 3.

ⓑ Multiply row 2 by 5.

ⓒ Multiply row 3 by −2−2 and add to row 1.

\( \left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right] \)

ⓐ We interchange rows 2 and 3.

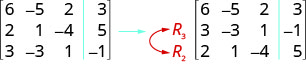
ⓑ We multiply row 2 by 5.

ⓒ We multiply row 3 by \(−2\) and add to row 1.

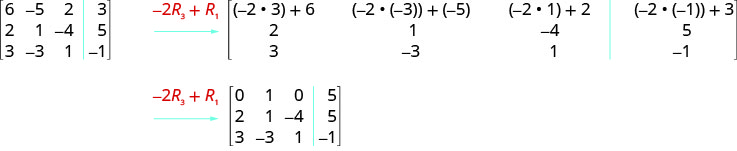
Example \(\PageIndex{8}\)

ⓐ Interchange rows 1 and 3.

ⓑ Multiply row 3 by 3.

ⓒ Multiply row 3 by 2 and add to row 2.

\( \left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right] \)

ⓐ \( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right] \)

ⓑ \( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right] \)

ⓒ \( \left[ \begin{matrix} -2 &3 &0 &2 & \\ 3 &4 &-13 &-16 &-8 \\ 15 &-6 &-6 &-6 & \end{matrix} \right] \)

Example \(\PageIndex{9}\)

ⓐ Interchange rows 1 and 2,

ⓑ Multiply row 1 by 2,

ⓒ Multiply row 2 by 3 and add to row 1.

\( \left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right] \)

ⓐ \( \left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \) ⓑ \( \left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \) ⓒ \( \left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \)

Now that we have practiced the row operations, we will look at an augmented matrix and figure out what operation we will use to reach a goal. This is exactly what we did when we did elimination. We decided what number to multiply a row by in order that a variable would be eliminated when we added the rows together.

Given this system, what would you do to eliminate x ?

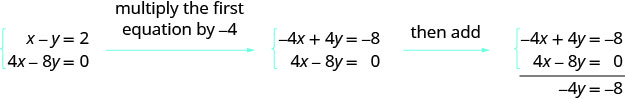
This next example essentially does the same thing, but to the matrix.

Example \(\PageIndex{10}\)

Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: \( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right] \)

To make the 4 a 0, we could multiply row 1 by \(−4\) and then add it to row 2.

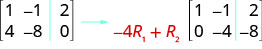
Example \(\PageIndex{11}\)

Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: \( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right] \)

\( \left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right] \)

Example \(\PageIndex{12}\)

Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: \( \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right] \)

\( \left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right] \)

Solve Systems of Equations Using Matrices

To solve a system of equations using matrices, we transform the augmented matrix into a matrix in row-echelon form using row operations. For a consistent and independent system of equations, its augmented matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.

ROW-ECHELON FORM

For a consistent and independent system of equations, its augmented matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.

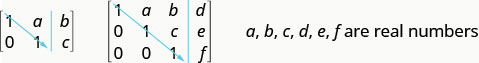
Once we get the augmented matrix into row-echelon form, we can write the equivalent system of equations and read the value of at least one variable. We then substitute this value in another equation to continue to solve for the other variables. This process is illustrated in the next example.

How to Solve a System of Equations Using a Matrix

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 3x+4y=5 \\ x+2y=1 \end{array} \right. \)

Example \(\PageIndex{14}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)

The solution is \((4,−1)\).

Example \(\PageIndex{15}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right. \)

The solution is \((−2,0)\).

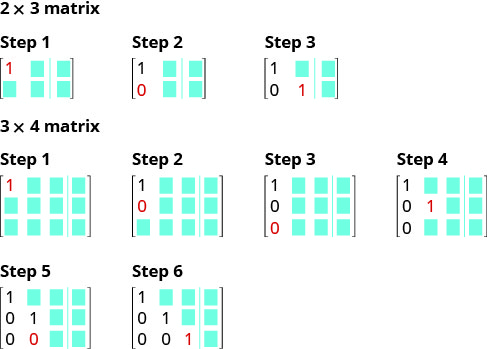
The steps are summarized here.

SOLVE A SYSTEM OF EQUATIONS USING MATRICES.

• Write the augmented matrix for the system of equations.
• Using row operations get the entry in row 1, column 1 to be 1.
• Using row operations, get zeros in column 1 below the 1.
• Using row operations, get the entry in row 2, column 2 to be 1.
• Continue the process until the matrix is in row-echelon form.
• Write the corresponding system of equations.
• Use substitution to find the remaining variables.
• Write the solution as an ordered pair or triple.
• Check that the solution makes the original equations true.

Here is a visual to show the order for getting the 1’s and 0’s in the proper position for row-echelon form.

We use the same procedure when the system of equations has three equations.

Example \(\PageIndex{16}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. \)

Example \(\PageIndex{17}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)

\((6,−1,−3)\)

Example \(\PageIndex{18}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right. \)

\((5,7,4)\)

So far our work with matrices has only been with systems that are consistent and independent, which means they have exactly one solution. Let’s now look at what happens when we use a matrix for a dependent or inconsistent system.

Example \(\PageIndex{19}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x+y+3z=0 \\ x+3y+5z=0 \\ 2x+4z=1 \end{array} \right. \)

Example \(\PageIndex{20}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. \)

no solution

Example \(\PageIndex{21}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right. \)

The last system was inconsistent and so had no solutions. The next example is dependent and has infinitely many solutions.

Example \(\PageIndex{22}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. \)

Example \(\PageIndex{23}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)

infinitely many solutions \((x,y,z)\), where \(x=z−3;\space y=3;\space z\) is any real number.

Example \(\PageIndex{24}\)

Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)

infinitely many solutions \((x,y,z)\), where \(x=5z−2;\space y=4z−3;\space z\) is any real number.

Access this online resource for additional instruction and practice with Gaussian Elimination.

• Gaussian Elimination

Key Concepts

• Interchange any two rows
• Multiply a row by any real number except 0
• Add a nonzero multiple of one row to another row

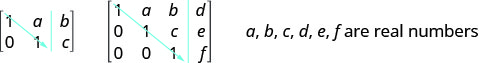
4.5 Solve Systems of Equations Using Matrices

Learning objectives.

By the end of this section, you will be able to:

• Write the augmented matrix for a system of equations
• Use row operations on a matrix
• Solve systems of equations using matrices

Be Prepared 4.13

Before you get started, take this readiness quiz.

Solve: 3 ( x + 2 ) + 4 = 4 ( 2 x − 1 ) + 9 . 3 ( x + 2 ) + 4 = 4 ( 2 x − 1 ) + 9 . If you missed this problem, review Example 2.2 .

Be Prepared 4.14

Solve: 0.25 p + 0.25 ( p + 4 ) = 5.20 . 0.25 p + 0.25 ( p + 4 ) = 5.20 . If you missed this problem, review Example 2.13 .

Be Prepared 4.15

Evaluate when x = −2 x = −2 and y = 3 : 2 x 2 − x y + 3 y 2 . y = 3 : 2 x 2 − x y + 3 y 2 . If you missed this problem, review Example 1.21 .

Write the Augmented Matrix for a System of Equations

Solving a system of equations can be a tedious operation where a simple mistake can wreak havoc on finding the solution. An alternative method which uses the basic procedures of elimination but with notation that is simpler is available. The method involves using a matrix . A matrix is a rectangular array of numbers arranged in rows and columns.

A matrix is a rectangular array of numbers arranged in rows and columns.

A matrix with m rows and n columns has order m × n . m × n . The matrix on the left below has 2 rows and 3 columns and so it has order 2 × 3 . 2 × 3 . We say it is a 2 by 3 matrix.

Each number in the matrix is called an element or entry in the matrix.

We will use a matrix to represent a system of linear equations. We write each equation in standard form and the coefficients of the variables and the constant of each equation becomes a row in the matrix. Each column then would be the coefficients of one of the variables in the system or the constants. A vertical line replaces the equal signs. We call the resulting matrix the augmented matrix for the system of equations.

Notice the first column is made up of all the coefficients of x , the second column is the all the coefficients of y , and the third column is all the constants.

Example 4.37

Write each system of linear equations as an augmented matrix:

ⓐ { 5 x − 3 y = −1 y = 2 x − 2 { 5 x − 3 y = −1 y = 2 x − 2 ⓑ { 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1 { 6 x − 5 y + 2 z = 3 2 x + y − 4 z = 5 3 x − 3 y + z = −1

ⓐ The second equation is not in standard form. We rewrite the second equation in standard form.

We replace the second equation with its standard form. In the augmented matrix, the first equation gives us the first row and the second equation gives us the second row. The vertical line replaces the equal signs.

ⓑ All three equations are in standard form. In the augmented matrix the first equation gives us the first row, the second equation gives us the second row, and the third equation gives us the third row. The vertical line replaces the equal signs.

Try It 4.73

ⓐ { 3 x + 8 y = −3 2 x = −5 y − 3 { 3 x + 8 y = −3 2 x = −5 y − 3 ⓑ { 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3 { 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3

Try It 4.74

ⓐ { 11 x = −9 y − 5 7 x + 5 y = −1 { 11 x = −9 y − 5 7 x + 5 y = −1 ⓑ { 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7 { 5 x − 3 y + 2 z = −5 2 x − y − z = 4 3 x − 2 y + 2 z = −7

It is important as we solve systems of equations using matrices to be able to go back and forth between the system and the matrix. The next example asks us to take the information in the matrix and write the system of equations.

Example 4.38

Write the system of equations that corresponds to the augmented matrix:

[ 4 −3 3 1 2 −1 −2 −1 3 | −1 2 −4 ] . [ 4 −3 3 1 2 −1 −2 −1 3 | −1 2 −4 ] .

We remember that each row corresponds to an equation and that each entry is a coefficient of a variable or the constant. The vertical line replaces the equal sign. Since this matrix is a 4 × 3 4 × 3 , we know it will translate into a system of three equations with three variables.

Try It 4.75

Write the system of equations that corresponds to the augmented matrix: [ 1 −1 2 3 2 1 −2 1 4 −1 2 0 ] . [ 1 −1 2 3 2 1 −2 1 4 −1 2 0 ] .

Try It 4.76

Write the system of equations that corresponds to the augmented matrix: [ 1 1 1 4 2 3 −1 8 1 1 −1 3 ] . [ 1 1 1 4 2 3 −1 8 1 1 −1 3 ] .

Use Row Operations on a Matrix

Once a system of equations is in its augmented matrix form, we will perform operations on the rows that will lead us to the solution.

To solve by elimination, it doesn’t matter which order we place the equations in the system. Similarly, in the matrix we can interchange the rows.

When we solve by elimination, we often multiply one of the equations by a constant. Since each row represents an equation, and we can multiply each side of an equation by a constant, similarly we can multiply each entry in a row by any real number except 0.

In elimination, we often add a multiple of one row to another row. In the matrix we can replace a row with its sum with a multiple of another row.

These actions are called row operations and will help us use the matrix to solve a system of equations.

Row Operations

In a matrix, the following operations can be performed on any row and the resulting matrix will be equivalent to the original matrix.

• Interchange any two rows.
• Multiply a row by any real number except 0.
• Add a nonzero multiple of one row to another row.

Performing these operations is easy to do but all the arithmetic can result in a mistake. If we use a system to record the row operation in each step, it is much easier to go back and check our work.

We use capital letters with subscripts to represent each row. We then show the operation to the left of the new matrix. To show interchanging a row:

To multiply row 2 by −3 −3 :

To multiply row 2 by −3 −3 and add it to row 1:

Example 4.39

Perform the indicated operations on the augmented matrix:

ⓐ Interchange rows 2 and 3.

ⓑ Multiply row 2 by 5.

ⓒ Multiply row 3 by −2 −2 and add to row 1.

ⓐ We interchange rows 2 and 3.

ⓑ We multiply row 2 by 5.

ⓒ We multiply row 3 by −2 −2 and add to row 1.

Try It 4.77

Perform the indicated operations sequentially on the augmented matrix:

ⓐ Interchange rows 1 and 3.

ⓑ Multiply row 3 by 3.

ⓒ Multiply row 3 by 2 and add to row 2.

[ 5 −2 −2 4 −1 −4 −2 3 0 | −2 4 −1 ] [ 5 −2 −2 4 −1 −4 −2 3 0 | −2 4 −1 ]

Try It 4.78

ⓐ Interchange rows 1 and 2,

ⓑ Multiply row 1 by 2,

ⓒ Multiply row 2 by 3 and add to row 1.

[ 2 −3 −2 4 1 −3 5 0 4 | −4 2 −1 ] [ 2 −3 −2 4 1 −3 5 0 4 | −4 2 −1 ]

Now that we have practiced the row operations, we will look at an augmented matrix and figure out what operation we will use to reach a goal. This is exactly what we did when we did elimination. We decided what number to multiply a row by in order that a variable would be eliminated when we added the rows together.

Given this system, what would you do to eliminate x ?

This next example essentially does the same thing, but to the matrix.

Example 4.40

Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: [ 1 −1 4 −8 | 2 0 ] . [ 1 −1 4 −8 | 2 0 ] .

To make the 4 a 0, we could multiply row 1 by −4 −4 and then add it to row 2.

Try It 4.79

Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: [ 1 −1 3 −6 | 2 2 ] . [ 1 −1 3 −6 | 2 2 ] .

Try It 4.80

Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: [ 1 −1 −2 −3 | 3 2 ] . [ 1 −1 −2 −3 | 3 2 ] .

Solve Systems of Equations Using Matrices

To solve a system of equations using matrices, we transform the augmented matrix into a matrix in row-echelon form using row operations. For a consistent and independent system of equations, its augmented matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.

Row-Echelon Form

For a consistent and independent system of equations, its augmented matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.

Once we get the augmented matrix into row-echelon form, we can write the equivalent system of equations and read the value of at least one variable. We then substitute this value in another equation to continue to solve for the other variables. This process is illustrated in the next example.

Example 4.41

How to solve a system of equations using a matrix.

Solve the system of equations using a matrix: { 3 x + 4 y = 5 x + 2 y = 1 . { 3 x + 4 y = 5 x + 2 y = 1 .

Try It 4.81

Solve the system of equations using a matrix: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Try It 4.82

Solve the system of equations using a matrix: { 2 x + y = −4 x − y = −2 . { 2 x + y = −4 x − y = −2 .

The steps are summarized here.

Solve a system of equations using matrices.

• Step 1. Write the augmented matrix for the system of equations.
• Step 2. Using row operations get the entry in row 1, column 1 to be 1.
• Step 3. Using row operations, get zeros in column 1 below the 1.
• Step 4. Using row operations, get the entry in row 2, column 2 to be 1.
• Step 5. Continue the process until the matrix is in row-echelon form.
• Step 6. Write the corresponding system of equations.
• Step 7. Use substitution to find the remaining variables.
• Step 8. Write the solution as an ordered pair or triple.
• Step 9. Check that the solution makes the original equations true.

Here is a visual to show the order for getting the 1’s and 0’s in the proper position for row-echelon form.

We use the same procedure when the system of equations has three equations.

Example 4.42

Solve the system of equations using a matrix: { 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1 . { 3 x + 8 y + 2 z = −5 2 x + 5 y − 3 z = 0 x + 2 y − 2 z = −1 .

Try It 4.83

Solve the system of equations using a matrix: { 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3 . { 2 x − 5 y + 3 z = 8 3 x − y + 4 z = 7 x + 3 y + 2 z = −3 .

Try It 4.84

Solve the system of equations using a matrix: { −3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1 . { −3 x + y + z = −4 − x + 2 y − 2 z = 1 2 x − y − z = −1 .

So far our work with matrices has only been with systems that are consistent and independent, which means they have exactly one solution. Let’s now look at what happens when we use a matrix for a dependent or inconsistent system.

Example 4.43

Solve the system of equations using a matrix: { x + y + 3 z = 0 x + 3 y + 5 z = 0 2 x + 4 z = 1 . { x + y + 3 z = 0 x + 3 y + 5 z = 0 2 x + 4 z = 1 .

Try It 4.85

Solve the system of equations using a matrix: { x − 2 y + 2 z = 1 −2 x + y − z = 2 x − y + z = 5 . { x − 2 y + 2 z = 1 −2 x + y − z = 2 x − y + z = 5 .

Try It 4.86

Solve the system of equations using a matrix: { 3 x + 4 y − 3 z = −2 2 x + 3 y − z = −12 x + y − 2 z = 6 . { 3 x + 4 y − 3 z = −2 2 x + 3 y − z = −12 x + y − 2 z = 6 .

The last system was inconsistent and so had no solutions. The next example is dependent and has infinitely many solutions.

Example 4.44

Solve the system of equations using a matrix: { x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7 . { x − 2 y + 3 z = 1 x + y − 3 z = 7 3 x − 4 y + 5 z = 7 .

Try It 4.87

Solve the system of equations using a matrix: { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 . { x + y − z = 0 2 x + 4 y − 2 z = 6 3 x + 6 y − 3 z = 9 .

Try It 4.88

Solve the system of equations using a matrix: { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 . { x − y − z = 1 − x + 2 y − 3 z = −4 3 x − 2 y − 7 z = 0 .

Access this online resource for additional instruction and practice with Gaussian Elimination.

• Gaussian Elimination

Section 4.5 Exercises

Practice makes perfect.

In the following exercises, write each system of linear equations as an augmented matrix.

ⓐ { 3 x − y = −1 2 y = 2 x + 5 { 3 x − y = −1 2 y = 2 x + 5 ⓑ { 4 x + 3 y = −2 x − 2 y − 3 z = 7 2 x − y + 2 z = −6 { 4 x + 3 y = −2 x − 2 y − 3 z = 7 2 x − y + 2 z = −6

ⓐ { 2 x + 4 y = −5 3 x − 2 y = 2 { 2 x + 4 y = −5 3 x − 2 y = 2 ⓑ { 3 x − 2 y − z = −2 −2 x + y = 5 5 x + 4 y + z = −1 { 3 x − 2 y − z = −2 −2 x + y = 5 5 x + 4 y + z = −1

ⓐ { 3 x − y = −4 2 x = y + 2 { 3 x − y = −4 2 x = y + 2 ⓑ { x − 3 y − 4 z = −2 4 x + 2 y + 2 z = 5 2 x − 5 y + 7 z = −8 { x − 3 y − 4 z = −2 4 x + 2 y + 2 z = 5 2 x − 5 y + 7 z = −8

ⓐ { 2 x − 5 y = −3 4 x = 3 y − 1 { 2 x − 5 y = −3 4 x = 3 y − 1 ⓑ { 4 x + 3 y − 2 z = −3 −2 x + y − 3 z = 4 − x − 4 y + 5 z = −2 { 4 x + 3 y − 2 z = −3 −2 x + y − 3 z = 4 − x − 4 y + 5 z = −2

Write the system of equations that corresponds to the augmented matrix.

[ 2 −1 1 −3 | 4 2 ] [ 2 −1 1 −3 | 4 2 ]

[ 2 −4 3 −3 | −2 −1 ] [ 2 −4 3 −3 | −2 −1 ]

[ 1 0 −3 1 −2 0 0 −1 2 | −1 −2 3 ] [ 1 0 −3 1 −2 0 0 −1 2 | −1 −2 3 ]

[ 2 −2 0 0 2 −1 3 0 −1 | −1 2 −2 ] [ 2 −2 0 0 2 −1 3 0 −1 | −1 2 −2 ]

In the following exercises, perform the indicated operations on the augmented matrices.

[ 6 −4 3 −2 | 3 1 ] [ 6 −4 3 −2 | 3 1 ]

ⓐ Interchange rows 1 and 2

ⓑ Multiply row 2 by 3

ⓒ Multiply row 2 by −2 −2 and add row 1 to it.

[ 4 −6 3 2 | −3 1 ] [ 4 −6 3 2 | −3 1 ]

ⓑ Multiply row 1 by 4

ⓒ Multiply row 2 by 3 and add row 1 to it.

[ 4 −12 −8 4 −2 −3 −6 2 −1 | 16 −1 −1 ] [ 4 −12 −8 4 −2 −3 −6 2 −1 | 16 −1 −1 ]

ⓐ Interchange rows 2 and 3

ⓒ Multiply row 2 by −2 −2 and add to row 3.

[ 6 −5 2 2 1 −4 3 −3 1 | 3 5 −1 ] [ 6 −5 2 2 1 −4 3 −3 1 | 3 5 −1 ]

ⓑ Multiply row 2 by 5

Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: [ 1 2 −3 −4 | 5 −1 ] . [ 1 2 −3 −4 | 5 −1 ] .

Perform the needed row operations that will get the first entry in both row 2 and row 3 to be zero in the augmented matrix: [ 1 −2 3 3 −1 −2 2 −3 −4 | −4 5 −1 ] . [ 1 −2 3 3 −1 −2 2 −3 −4 | −4 5 −1 ] .

In the following exercises, solve each system of equations using a matrix.

{ 2 x + y = 2 x − y = −2 { 2 x + y = 2 x − y = −2

{ 3 x + y = 2 x − y = 2 { 3 x + y = 2 x − y = 2

{ − x + 2 y = −2 x + y = −4 { − x + 2 y = −2 x + y = −4

{ −2 x + 3 y = 3 x + 3 y = 12 { −2 x + 3 y = 3 x + 3 y = 12

{ 2 x − 3 y + z = 19 −3 x + y − 2 z = −15 x + y + z = 0 { 2 x − 3 y + z = 19 −3 x + y − 2 z = −15 x + y + z = 0

{ 2 x − y + 3 z = −3 − x + 2 y − z = 10 x + y + z = 5 { 2 x − y + 3 z = −3 − x + 2 y − z = 10 x + y + z = 5

{ 2 x − 6 y + z = 3 3 x + 2 y − 3 z = 2 2 x + 3 y − 2 z = 3 { 2 x − 6 y + z = 3 3 x + 2 y − 3 z = 2 2 x + 3 y − 2 z = 3

{ 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7 { 4 x − 3 y + z = 7 2 x − 5 y − 4 z = 3 3 x − 2 y − 2 z = −7

{ x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3 { x + 2 z = 0 4 y + 3 z = −2 2 x − 5 y = 3

{ 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3 { 2 x + 5 y = 4 3 y − z = 3 4 x + 3 z = −3

{ 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1 { 2 y + 3 z = −1 5 x + 3 y = −6 7 x + z = 1

{ 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8 { 3 x − z = −3 5 y + 2 z = −6 4 x + 3 y = −8

{ 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20 { 2 x + 3 y + z = 12 x + y + z = 9 3 x + 4 y + 2 z = 20

{ x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1 { x + 2 y + 6 z = 5 − x + y − 2 z = 3 x − 4 y − 2 z = 1

{ x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2 { x + 2 y − 3 z = −1 x − 3 y + z = 1 2 x − y − 2 z = 2

{ 4 x − 3 y + 2 z = 0 −2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6 { 4 x − 3 y + 2 z = 0 −2 x + 3 y − 7 z = 1 2 x − 2 y + 3 z = 6

{ x − y + 2 z = −4 2 x + y + 3 z = 2 −3 x + 3 y − 6 z = 12 { x − y + 2 z = −4 2 x + y + 3 z = 2 −3 x + 3 y − 6 z = 12

{ − x − 3 y + 2 z = 14 − x + 2 y − 3 z = −4 3 x + y − 2 z = 6 { − x − 3 y + 2 z = 14 − x + 2 y − 3 z = −4 3 x + y − 2 z = 6

{ x + y − 3 z = −1 y − z = 0 − x + 2 y = 1 { x + y − 3 z = −1 y − z = 0 − x + 2 y = 1

{ x + 2 y + z = 4 x + y − 2 z = 3 −2 x − 3 y + z = −7 { x + 2 y + z = 4 x + y − 2 z = 3 −2 x − 3 y + z = −7

Writing Exercises

Solve the system of equations { x + y = 10 x − y = 6 { x + y = 10 x − y = 6 ⓐ by graphing and ⓑ by substitution. ⓒ Which method do you prefer? Why?

Solve the system of equations { 3 x + y = 12 x = y − 8 { 3 x + y = 12 x = y − 8 by substitution and explain all your steps in words.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-5-solve-systems-of-equations-using-matrices

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.