were you able to solve the problem with the given formula

Game Central

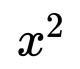
Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

Equation Solver

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

How to solve your equation, solving equations video lessons.

• Solving Simple Equations

Need more problem types? Try MathPapa Algebra Calculator

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.3: Solve Quadratic Equations Using the Quadratic Formula

• Last updated
• Save as PDF
• Page ID 79535

Learning Objectives

By the end of this section, you will be able to:

• Solve quadratic equations using the quadratic formula
• Use the discriminant to predict the number of solutions of a quadratic equation
• Identify the most appropriate method to use to solve a quadratic equation

Be Prepared

Before you get started, take this readiness quiz.

• Simplify: \(\frac{−20−5}{10}\). If you missed this problem, review [link] .
• Simplify: \(4+\sqrt{121}\). If you missed this problem, review [link] .
• Simplify: \(\sqrt{128}\). If you missed this problem, review [link] .

When we solved quadratic equations in the last section by completing the square, we took the same steps every time. By the end of the exercise set, you may have been wondering ‘isn’t there an easier way to do this?’ The answer is ‘yes.’ In this section, we will derive and use a formula to find the solution of a quadratic equation.

We have already seen how to solve a formula for a specific variable ‘in general’ so that we would do the algebraic steps only once and then use the new formula to find the value of the specific variable. Now, we will go through the steps of completing the square in general to solve a quadratic equation for x . It may be helpful to look at one of the examples at the end of the last section where we solved an equation of the form\( ax^2+bx+c=0\) as you read through the algebraic steps below, so you see them with numbers as well as ‘in general.’

This last equation is the Quadratic Formula.

Definition: QUADRATIC FORMULA

The solutions to a quadratic equation of the form \(ax^2+bx+c=0\), \(a\ge 0\) are given by the formula:

\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)

To use the Quadratic Formula, we substitute the values of a, b, and c into the expression on the right side of the formula. Then, we do all the math to simplify the expression. The result gives the solution(s) to the quadratic equation.

How to Solve a Quadratic Equation Using the Quadratic Formula

Example \(\PageIndex{1}\)

Solve \(2x^2+9x−5=0\) by using the Quadratic Formula.

Example \(\PageIndex{2}\)

Solve \(3y^2−5y+2=0\) by using the Quadratic Formula.

\(y=\frac{2}{3}\), \(y=1\)

Example \(\PageIndex{3}\)

Solve \(4z^2+2z−6=0\) by using the Quadratic Formula.

\(z=−\frac{3}{2}\), \(z=1\) ​​​​​

Definition: SOLVE A QUADRATIC EQUATION USING THE QUADRATIC FORMULA

• Write the Quadratic Formula in standard form. Identify the aa, bb, and cc values.
• Write the Quadratic Formula. Then substitute in the values of a, b, and c.
• Check the solutions.

If you say the formula as you write it in each problem, you’ll have it memorized in no time. And remember, the Quadratic Formula is an equation. Be sure you start with ‘\(x=\)’.

Example \(\PageIndex{4}\)

Solve \(x^2−6x+5=0\) by using the Quadratic Formula.

Example \(\PageIndex{5}\)

Solve \(a^2−2a−15=0\) by using the Quadratic Formula.

\(a=−3\), \(a=5\)

Example \(\PageIndex{6}\)

Solve \(b^2+10b+24=0\) by using the Quadratic Formula.

\(b=−6\), \(b=−4\)

When we solved quadratic equations by using the Square Root Property, we sometimes got answers that had radicals. That can happen, too, when using the Quadratic Formula. If we get a radical as a solution, the final answer must have the radical in its simplified form.

Example \(\PageIndex{7}\)

Solve \(4y^2−5y−3=0\) by using the Quadratic Formula.

We can use the Quadratic Formula to solve for the variable in a quadratic equation, whether or not it is named ‘ x ’.

Example \(\PageIndex{8}\)

Solve \(2p^2+8p+5=0\) by using the Quadratic Formula.

\(p=\frac{−4\pm\sqrt{6}}{2}\)

Example \(\PageIndex{9}\)

Solve \(5q^2−11q+3=0\) by using the Quadratic Formula.

\(q=\frac{11\pm\sqrt{61}}{10}\)

Example \(\PageIndex{10}\)

Solve \(2x^2+10x+11=0\) by using the Quadratic Formula.

Example \(\PageIndex{11}\)

Solve \(3m^2+12m+7=0\) by using the Quadratic Formula.

\(m=\frac{−6\pm\sqrt{15}}{3}\)

Example \(\PageIndex{12}\)

Solve \(5n^2+4n−4=0\) by using the Quadratic Formula.

\(n=\frac{−2\pm2\sqrt{6}}{5}\)

We cannot take the square root of a negative number. So, when we substitute a, b, and c into the Quadratic Formula, if the quantity inside the radical is negative, the quadratic equation has no real solution. We will see this in the next example.

Example \(\PageIndex{13}\)

Solve \(3p^2+2p+9=0\) by using the Quadratic Formula.

Example \(\PageIndex{14}\)

Solve \(4a^2−3a+8=0\) by using the Quadratic Formula.

no real solution

Exeample \(\PageIndex{15}\)

Solve \(5b^2+2b+4=0\) by using the Quadratic Formula.

The quadratic equations we have solved so far in this section were all written in standard form, \(ax^2+bx+c=0\). Sometimes, we will need to do some algebra to get the equation into standard form before we can use the Quadratic Formula.

Example \(\PageIndex{16}\)

Solve \(x(x+6)+4=0\) by using the Quadratic Formula.

Example \(\PageIndex{17}\)

Solve \(x(x+2)−5=0\) by using the Quadratic Formula.

\(x=−1\pm\sqrt{6}\)

Example \(\PageIndex{18}\)

Solve \(y(3y−1)−2=0\) by using the Quadratic Formula.

\(y=−\frac{2}{3}\), \(y=1\)

When we solved linear equations, if an equation had too many fractions we ‘cleared the fractions’ by multiplying both sides of the equation by the LCD. This gave us an equivalent equation—without fractions—to solve. We can use the same strategy with quadratic equations.

Example \(\PageIndex{19}\)

Solve \(\frac{1}{2}u^2+\frac{2}{3}u=\frac{1}{3}\) by using the Quadratic Formula.

Example \(\PageIndex{20}\)

Solve \(\frac{1}{4}c^2−\frac{1}{3}c=\frac{1}{12}\) by using the Quadratic Formula.

\(c=\frac{2\pm\sqrt{7}}{3}\)

Example \(\PageIndex{21}\)

Solve \(\frac{1}{9}d^2−\frac{1}{2}d=−\frac{1}{2}\) by using the Quadratic Formula.

\(d=\frac{3}{2}\), \(d=3\)

Think about the equation \((x−3)^2=0\). We know from the Zero Products Principle that this equation has only one solution: \(x=3\).

We will see in the next example how using the Quadratic Formula to solve an equation with a perfect square also gives just one solution.

Example \(\PageIndex{22}\)

Solve \(4x^2−20x=−25\) by using the Quadratic Formula.

Did you recognize that \(4x^2−20x+25\) is a perfect square?

Example \(\PageIndex{23}\)

Solve \(r^2+10r+25=0\) by using the Quadratic Formula.

\(r=−5\)​​​​​​

Example \(\PageIndex{24}\)

Solve \(25t^2−40t=−16\) by using the Quadratic Formula.

\(t=\frac{4}{5}\)

Use the Discriminant to Predict the Number of Solutions of a Quadratic Equation

When we solved the quadratic equations in the previous examples, sometimes we got two solutions, sometimes one solution, sometimes no real solutions. Is there a way to predict the number of solutions to a quadratic equation without actually solving the equation?

Yes, the quantity inside the radical of the Quadratic Formula makes it easy for us to determine the number of solutions. This quantity is called the discriminant .

Definition: DISCRIMINANT

In the Quadratic Formula\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\), the quantity \(b^2−4ac\) is called the discriminant .

Let’s look at the discriminant of the equations in Example , Example , and Example , and the number of solutions to those quadratic equations.

When the discriminant is positive \(x=\frac{−b\pm\sqrt{+}}{2a}\) the quadratic equation has two solutions .

When the discriminant is zero \(x=\frac{−b\pm\sqrt{0}}{2a}\) the quadratic equation has one solution .

When the discriminant is negative \(x=\frac{−b\pm\sqrt{−}}{2a}\) the quadratic equation has no real solutions .

Definition:USE THE DISCRIMINANT, \(b^2−4ac\), TO DETERMINE THE NUMBER OF SolutionS OF A QUADRATIC EQUATION

For a quadratic equation of the form \(ax^2+bx+c=0\), \(a \ge 0\),

• if \(b^2−4ac>0\), the equation has two solutions.
• if \(b^2−4ac=0\), the equation has one solution.
• if \(b^2−4ac<0\), the equation has no real solutions.

Example \(\PageIndex{25}\)

Determine the number of solutions to each quadratic equation:

• \(2v^2−3v+6=0\)
• \(3x^2+7x−9=0\)
• \(5n^2+n+4=0\)
• \(9y^2−6y+1=0\)

Example \(\PageIndex{26}\)

• \(8m^2−3m+6=0\)
• \(5z^2+6z−2=0\)
• \(9w^2+24w+16=0\)
• \(9u^2−2u+4=0\)
• no real solutions

Example \(\PageIndex{27}\)

​​​​​​​Determine the number of solutions to each quadratic equation:

• \( b^2+7b−13=0\)
• \(5a^2−6a+10=0\)
• \(4r^2−20r+25=0\)
• \(7t^2−11t+3=0\)

Identify the Most Appropriate Method to Use to Solve a Quadratic Equation

We have used four methods to solve quadratic equations:

• Square Root Property
• Completing the Square
• Quadratic Formula

You can solve any quadratic equation by using the Quadratic Formula, but that is not always the easiest method to use.

Definition: IDENTIFY THE MOST APPROPRIATE METHOD TO SOLVE A QUADRATIC EQUATION.

• Try Factoring first. If the quadratic factors easily, this method is very quick.
• Try the Square Root Property next. If the equation fits the form \(ax^2=k\) or \(a(x−h)^2=k\), it can easily be solved by using the Square Root Property.
• Use the Quadratic Formula . Any quadratic equation can be solved by using the Quadratic Formula.

​​​​​​What about the method of completing the square? Most people find that method cumbersome and prefer not to use it. We needed to include it in this chapter because we completed the square in general to derive the Quadratic Formula. You will also use the process of completing the square in other areas of algebra.

Example \(\PageIndex{28}\)

Identify the most appropriate method to use to solve each quadratic equation:

• \(5z^2=17\)
• \(4x^2−12x+9=0\)
• \(8u^2+6u=11\)

1. \(5z^2=17\)

Since the equation is in the \(ax^2=k\), the most appropriate method is to use the Square Root Property.

2. \(4x^2−12x+9=0\)

We recognize that the left side of the equation is a perfect square trinomial, and so Factoring will be the most appropriate method.

3. \(8u^2+6u=11\)

Put the equation in standard form. \(8u^2+6u−11=0\)

While our first thought may be to try Factoring, thinking about all the possibilities for trial and error leads us to choose the Quadratic Formula as the most appropriate method.

Example \(\PageIndex{29}\)

• \(x^2+6x+8=0\)
• \((n−3)^2=16\)
• \(5p^2−6p=9\)

Example \(\PageIndex{30}\)

• \(8a^2+3a−9=0\)
• \(4b^2+4b+1=0\)
• \(5c2=125\)

​​​​​​​ Access these online resources for additional instruction and practice with using the Quadratic Formula:

• Solving Quadratic Equations: Solving with the Quadratic Formula
• How to solve a quadratic equation in standard form using the Quadratic Formula (example)
• Solving Quadratic Equations using the Quadratic Formula—Example 3
• Solve Quadratic Equations using Quadratic Formula

Key Concepts

• Write the quadratic formula in standard form. Identify the a, b, c values.
• Write the quadratic formula. Then substitute in the values of a, b, c.
• if \(b^2−4ac>0\), the equation has 2 solutions.
• if \(b^2−4ac=0\), the equation has 1 solution.
• Try Factoring first. If the quadratic factors easily this method is very quick.
• Use the Quadratic Formula. Any other quadratic equation is best solved by using the Quadratic Formula.

• Try for free

Problem Solving: Use a Formula

What Is It?

Using a Formula is a problem-solving strategy that students can use to find answers to math problems involving geometry , percents , measurement , or algebra. To solve these problems, students must choose the appropriate formula and substitute data in the correct places of a formula. The following problem would be best solved using a formula:

If it is 46 degrees Celsius, how many degrees Fahrenheit is it?

Students can use the formula F = 1.8C + 32 to find the solution.

Why Is It Important?

Using a Formula is a problem-solving strategy that can be used for problems that involve converting units or measuring geometric objects. Also, real-world problems such as tipping in a restaurant, finding the price of a sale item, and buying enough paint for a room all involve using formulas.

How Can You Make It Happen?

Introduce a problem to students that requires them to use a formula to solve the problem. For example:

A rectangle has an area of 40 square meters. If the perimeter of the rectangle is 26 meters, what are the length and the width of the rectangle?

Understand the Problem

Demonstrate that the first step to solving the problem is understanding it. This involves identifying the key pieces of information needed to find the answer. This may require students to read the problem several times or put the problem into their own words. Here are a few formulas that students can use to solve this problem:

A = L x W 40 = L x W

2W + 2L = P 2W + 2L = 26

(Note: L and W can be interchanged in this problem.)

Choose a Strategy

The strategy of Using a Formula can be used in situations where measurements are required to find the solution.

Solve the Problem

I know 40 is a product of 2 and 20, 4 and 10, or 5 and 8.

I looked at the possible answers that would fit the formula for the area of the rectangle. Then I put the numbers into the formula for the perimeter. The numbers 5 and 8 are the two numbers that work for both formulas.

Read the problem again to be sure the question was answered.

I found the length and width of the rectangle, 5 meters and 8 meters.

Check the math to be sure it is correct.

A = L x W 40 = L x W 40 = 8 x 5 P = 2L + 2W 26 = 2L + 2W 26 + 2(8) + 2(5)

Determine if the best strategy was chosen for this problem, or if there was another way to solve the problem.

Using a formula was a good strategy to use for this problem.

The last step is explaining how you found the answer. Demonstrate how to write a paragraph describing the steps taken and how decisions were made throughout the process.

Students should explain their answer and the process they went through to solve it. It is important for students to talk or write about their thinking.

I knew the formula for area and perimeter, so I wrote down the formulas. A = L x W P = 2L + 2W I added the information I knew, which was the area and perimeter of this rectangle. 40 = L x W 26 = 2L + 2W Then I wrote down the numbers that could be the length and width if the area is 40 square meters. I know 40 is a product of 2 and 20, 4 and 10, or 5 and 8. I took those possible numbers and used them with the formula for perimeter. The numbers that did not also fit into this formula, I eliminated. I eliminated 2 and 20 as well as 4 and 10, since those numbers did not work in the perimeter formula. I was left with the numbers 8 and 5. Since they are interchangeable in this problem, I assigned the width as 5 meters and the length as 8 meters.

Guided Practice

Have students try to solve the following problem using the strategy of Using a Formula.

In an isosceles triangle, the unequal side measures half the length of one of the two equal sides. What is the perimeter if the length of the unequal side is 5 cm? What is the length of the sides if the perimeter is 80 cm?

Have students work in pairs, in groups, or individually to solve this problem. They should be able to tell or write about how they found the answer and justify their reasoning.

How Can You Stretch Students' Thinking?

Math problems requiring formulas can be simple, with few criteria needed to solve them, or they can be multidimensional, requiring charts or tables to organize students' thinking. Including more than one formula in a problem, or having multiple correct answers to a problem will help stretch this strategy.

Featured High School Resources

Related Resources

About the author.

TeacherVision Editorial Staff

The TeacherVision editorial team is comprised of teachers, experts, and content professionals dedicated to bringing you the most accurate and relevant information in the teaching space.

2.3 Models and Applications

Learning objectives.

In this section, you will:

• Set up a linear equation to solve a real-world application.
• Use a formula to solve a real-world application.

Neka is hoping to get an A in his college algebra class. He has scores of 75, 82, 95, 91, and 94 on his first five tests. Only the final exam remains, and the maximum number of points that can be earned is 100. Is it possible for Neka to end the course with an A? A simple linear equation will give Neka his answer.

Many real-world applications can be modeled by linear equations. For example, a cell phone package may include a monthly service fee plus a charge per minute of talk-time; it costs a widget manufacturer a certain amount to produce x widgets per month plus monthly operating charges; a car rental company charges a daily fee plus an amount per mile driven. These are examples of applications we come across every day that are modeled by linear equations. In this section, we will set up and use linear equations to solve such problems.

Setting up a Linear Equation to Solve a Real-World Application

To set up or model a linear equation to fit a real-world application, we must first determine the known quantities and define the unknown quantity as a variable. Then, we begin to interpret the words as mathematical expressions using mathematical symbols. Let us use the car rental example above. In this case, a known cost, such as $0.10/mi, is multiplied by an unknown quantity, the number of miles driven. Therefore, we can write 0.10 x . 0.10 x . This expression represents a variable cost because it changes according to the number of miles driven.

If a quantity is independent of a variable, we usually just add or subtract it, according to the problem. As these amounts do not change, we call them fixed costs. Consider a car rental agency that charges $0.10/mi plus a daily fee of $50. We can use these quantities to model an equation that can be used to find the daily car rental cost C . C .

When dealing with real-world applications, there are certain expressions that we can translate directly into math. Table 1 lists some common verbal expressions and their equivalent mathematical expressions.

Given a real-world problem, model a linear equation to fit it.

• Identify known quantities.
• Assign a variable to represent the unknown quantity.
• If there is more than one unknown quantity, find a way to write the second unknown in terms of the first.
• Write an equation interpreting the words as mathematical operations.
• Solve the equation. Be sure the solution can be explained in words, including the units of measure.

Modeling a Linear Equation to Solve an Unknown Number Problem

Find a linear equation to solve for the following unknown quantities: One number exceeds another number by 17 17 and their sum is 31. 31. Find the two numbers.

Let x x equal the first number. Then, as the second number exceeds the first by 17, we can write the second number as x + 17. x + 17. The sum of the two numbers is 31. We usually interpret the word is as an equal sign.

The two numbers are 7 7 and 24. 24.

Find a linear equation to solve for the following unknown quantities: One number is three more than twice another number. If the sum of the two numbers is 36 , 36 , find the numbers.

Setting Up a Linear Equation to Solve a Real-World Application

There are two cell phone companies that offer different packages. Company A charges a monthly service fee of $34 plus $.05/min talk-time. Company B charges a monthly service fee of $40 plus $.04/min talk-time.

• ⓐ Write a linear equation that models the packages offered by both companies.
• ⓑ If the average number of minutes used each month is 1,160, which company offers the better plan?
• ⓒ If the average number of minutes used each month is 420, which company offers the better plan?
• ⓓ How many minutes of talk-time would yield equal monthly statements from both companies?
• ⓐ The model for Company A can be written as A = 0.05 x + 34. A = 0.05 x + 34. This includes the variable cost of 0.05 x 0.05 x plus the monthly service charge of $34. Company B ’s package charges a higher monthly fee of $40, but a lower variable cost of 0.04 x . 0.04 x . Company B ’s model can be written as B = 0.04 x + $ 40. B = 0.04 x + $ 40.

If the average number of minutes used each month is 1,160, we have the following:

So, Company B offers the lower monthly cost of $86.40 as compared with the $92 monthly cost offered by Company A when the average number of minutes used each month is 1,160.

If the average number of minutes used each month is 420, we have the following:

If the average number of minutes used each month is 420, then Company A offers a lower monthly cost of $55 compared to Company B ’s monthly cost of $56.80.

To answer the question of how many talk-time minutes would yield the same bill from both companies, we should think about the problem in terms of ( x , y ) ( x , y ) coordinates: At what point are both the x- value and the y- value equal? We can find this point by setting the equations equal to each other and solving for x.

Check the x- value in each equation.

Therefore, a monthly average of 600 talk-time minutes renders the plans equal. See Figure 2

Find a linear equation to model this real-world application: It costs ABC electronics company $2.50 per unit to produce a part used in a popular brand of desktop computers. The company has monthly operating expenses of $350 for utilities and $3,300 for salaries. What are the company’s monthly expenses?

Using a Formula to Solve a Real-World Application

Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Typically, these problems involve two equations representing two trips, two investments, two areas, and so on. Examples of formulas include the area of a rectangular region, A = L W ; A = L W ; the perimeter of a rectangle, P = 2 L + 2 W ; P = 2 L + 2 W ; and the volume of a rectangular solid, V = L W H . V = L W H . When there are two unknowns, we find a way to write one in terms of the other because we can solve for only one variable at a time.

Solving an Application Using a Formula

It takes Andrew 30 min to drive to work in the morning. He drives home using the same route, but it takes 10 min longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?

This is a distance problem, so we can use the formula d = r t , d = r t , where distance equals rate multiplied by time. Note that when rate is given in mi/h, time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution.

First, we identify the known and unknown quantities. Andrew’s morning drive to work takes 30 min, or 1 2 1 2 h at rate r . r . His drive home takes 40 min, or 2 3 2 3 h, and his speed averages 10 mi/h less than the morning drive. Both trips cover distance d . d . A table, such as Table 2 , is often helpful for keeping track of information in these types of problems.

Write two equations, one for each trip.

As both equations equal the same distance, we set them equal to each other and solve for r .

We have solved for the rate of speed to work, 40 mph. Substituting 40 into the rate on the return trip yields 30 mi/h. Now we can answer the question. Substitute the rate back into either equation and solve for d.

The distance between home and work is 20 mi.

Note that we could have cleared the fractions in the equation by multiplying both sides of the equation by the LCD to solve for r . r .

On Saturday morning, it took Jennifer 3.6 h to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer 4 h to return home. Her speed was 5 mi/h slower on Sunday than on Saturday. What was her speed on Sunday?

Solving a Perimeter Problem

The perimeter of a rectangular outdoor patio is 54 54 ft. The length is 3 3 ft greater than the width. What are the dimensions of the patio?

The perimeter formula is standard: P = 2 L + 2 W . P = 2 L + 2 W . We have two unknown quantities, length and width. However, we can write the length in terms of the width as L = W + 3. L = W + 3. Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides as in Figure 3 .

Now we can solve for the width and then calculate the length.

The dimensions are L = 15 L = 15 ft and W = 12 W = 12 ft.

Find the dimensions of a rectangle given that the perimeter is 110 110 cm and the length is 1 cm more than twice the width.

Solving an Area Problem

The perimeter of a tablet of graph paper is 48 in. The length is 6 6 in. more than the width. Find the area of the graph paper.

The standard formula for area is A = L W ; A = L W ; however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one.

We know that the length is 6 in. more than the width, so we can write length as L = W + 6. L = W + 6. Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.

Now, we find the area given the dimensions of L = 15 L = 15 in. and W = 9 W = 9 in.

The area is 135 135 in. 2 .

A game room has a perimeter of 70 ft. The length is five more than twice the width. How many ft 2 of new carpeting should be ordered?

Solving a Volume Problem

Find the dimensions of a shipping box given that the length is twice the width, the height is 8 8 inches, and the volume is 1,600 in. 3 .

The formula for the volume of a box is given as V = L W H , V = L W H , the product of length, width, and height. We are given that L = 2 W , L = 2 W , and H = 8. H = 8. The volume is 1,600 1,600 cubic inches.

The dimensions are L = 20 L = 20 in., W = 10 W = 10 in., and H = 8 H = 8 in.

Note that the square root of W 2 W 2 would result in a positive and a negative value. However, because we are describing width, we can use only the positive result.

Access these online resources for additional instruction and practice with models and applications of linear equations.

• Problem solving using linear equations
• Problem solving using equations
• Finding the dimensions of area given the perimeter
• Find the distance between the cities using the distance = rate * time formula
• Linear equation application (Write a cost equation)

2.3 Section Exercises

To set up a model linear equation to fit real-world applications, what should always be the first step?

Use your own words to describe this equation where n is a number: 5 ( n + 3 ) = 2 n 5 ( n + 3 ) = 2 n

If the total amount of money you had to invest was $2,000 and you deposit x x amount in one investment, how can you represent the remaining amount?

If a carpenter sawed a 10-ft board into two sections and one section was n n ft long, how long would the other section be in terms of n n ?

If Bill was traveling v v mi/h, how would you represent Daemon’s speed if he was traveling 10 mi/h faster?

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^4-5x^2+4=0
• \sqrt{x-1}-x=-7
• \left|3x+1\right|=4
• \log _2(x+1)=\log _3(27)
• 3^x=9^{x+5}
• What is the completing square method?
• Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
• What is the golden rule for solving equations?
• The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
• How do you simplify equations?
• To simplify equations, combine like terms, remove parethesis, use the order of operations.
• How do you solve linear equations?
• To solve a linear equation, get the variable on one side of the equation by using inverse operations.

equation-calculator

• High School Math Solutions – Exponential Equation Calculator Solving exponential equations is pretty straightforward; there are basically two techniques: <ul> If the exponents...

Please add a message.

Message received. Thanks for the feedback.

Quadratic Formula Calculator

Enter the equation you want to solve using the quadratic formula.

The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions.

Quadratic Formula : x = − b ± b 2 − 4 a c 2 a

Click the blue arrow to submit. Choose "Solve Using the Quadratic Formula" from the topic selector and click to see the result in our Algebra Calculator !

Solve Using the Quadratic Formula Apply the Quadratic Formula

Popular Problems

Solve Using the Quadratic Formula x 2 + 5 x + 6 = 0 Solve Using the Quadratic Formula x 2 - 9 = 0 Solve Using the Quadratic Formula 5 x 2 - 7 x - 3 = 0 Apply the Quadratic Formula x 2 - 14 x + 49 Apply the Quadratic Formula x 2 - 18 x - 4

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Chapter 1: Solving Equations and Inequalities

Problem solving, learning objectives.

• Translate words into algebraic expressions and equations
• Define a process for solving word problems
• Apply the steps for solving word problems to distance, rate, and time problems
• Apply the steps for solving word problems to interest rate problems
• Evaluate a formula using substitution
• Rearrange formulas to isolate specific variables
• Identify an unknown given a formula
• Apply the steps for solving word problems to geometry problems
• Use the formula for converting between Fahrenheit and Celsius

Define a Process for Problem Solving

Word problems can be tricky. Often it takes a bit of practice to convert an English sentence into a mathematical sentence, which is one of the first steps to solving word problems. In the table below, words or phrases commonly associated with mathematical operators are categorized. Word problems often contain these or similar words, so it’s good to see what mathematical operators are associated with them.

Some examples follow:

• [latex]x\text{ is }5[/latex]  becomes [latex]x=5[/latex]
• Three more than a number becomes [latex]x+3[/latex]
• Four less than a number becomes [latex]x-4[/latex]
• Double the cost becomes [latex]2\cdot\text{ cost }[/latex]
• Groceries and gas together for the week cost $250 means [latex]\text{ groceries }+\text{ gas }=250[/latex]
• The difference of 9 and a number becomes [latex]9-x[/latex]. Notice how 9 is first in the sentence and the expression

Let’s practice translating a few more English phrases into algebraic expressions.

Translate the table into algebraic expressions:

In this example video, we show how to translate more words into mathematical expressions.

The power of algebra is how it can help you model real situations in order to answer questions about them.

Here are some steps to translate problem situations into algebraic equations you can solve. Not every word problem fits perfectly into these steps, but they will help you get started.

• Read and understand the problem.
• Determine the constants and variables in the problem.
• Translate words into algebraic expressions and equations.
• Write an equation to represent the problem.
• Solve the equation.
• Check and interpret your answer. Sometimes writing a sentence helps.

Twenty-eight less than five times a certain number is 232. What is the number?

Following the steps provided:

• Read and understand: we are looking for a number.
• Constants and variables: 28 and 232 are constants, “a certain number” is our variable because we don’t know its value, and we are asked to find it. We will call it x.
• Translate:  five times a certain number translates to [latex]5x[/latex] Twenty-eight less than five times a certain number translates to [latex]5x-28[/latex] because subtraction is built backward. is 232 translates to [latex]=232[/latex] because “is” is associated with equals.
• Write an equation:  [latex]5x-28=232[/latex]

[latex]\begin{array}{r}5x-28=232\\5x=260\\x=52\,\,\,\end{array}[/latex]

[latex]\begin{array}{r}5\left(52\right)-28=232\\5\left(52\right)=260\\260=260\end{array}[/latex].

In the video that follows, we show another example of how to translate a sentence into a mathematical expression using a problem solving method.

Another type of number problem involves consecutive numbers. Consecutive numbers are numbers that come one after the other, such as 3, 4, 5. If we are looking for several consecutive numbers it is important to first identify what they look like with variables before we set up the equation.

For example, let’s say I want to know the next consecutive integer after 4. In mathematical terms, we would add 1 to 4 to get 5. We can generalize this idea as follows: the consecutive integer of any number, x , is [latex]x+1[/latex]. If we continue this pattern we can define any number of consecutive integers from any starting point. The following table shows how to describe four consecutive integers using algebraic notation.

We apply the idea of consecutive integers to solving a word problem in the following example.

The sum of three consecutive integers is 93. What are the integers?

• Read and understand:  We are looking for three numbers, and we know they are consecutive integers.
• Constants and Variables:  93 is a constant. The first integer we will call x . Second: [latex]x+1[/latex] Third: [latex]x+2[/latex]
• Translate:  The sum of three consecutive integers translates to [latex]x+\left(x+1\right)+\left(x+2\right)[/latex], based on how we defined the first, second, and third integers. Notice how we placed parentheses around the second and third integers. This is just to make each integer more distinct. is 93 translates to [latex]=93[/latex] because is is associated with equals.
• Write an equation:  [latex]x+\left(x+1\right)+\left(x+2\right)=93[/latex]

[latex]x+x+1+x+2=93[/latex]

Combine like terms, simplify, and solve.

[latex]\begin{array}{r}x+x+1+x+2=93\\3x+3 = 93\\\underline{-3\,\,\,\,\,-3}\\3x=90\\\frac{3x}{3}=\frac{90}{3}\\x=30\end{array}[/latex]

• Check and Interpret: Okay, we have found a value for x . We were asked to find the value of three consecutive integers, so we need to do a couple more steps. Remember how we defined our variables: The first integer we will call [latex]x[/latex], [latex]x=30[/latex] Second: [latex]x+1[/latex] so [latex]30+1=31[/latex] Third: [latex]x+2[/latex] so [latex]30+2=32[/latex] The three consecutive integers whose sum is [latex]93[/latex] are [latex]30\text{, }31\text{, and }32[/latex]

There is often a well-known formula or relationship that applies to a word problem. For example, if you were to plan a road trip, you would want to know how long it would take you to reach your destination. [latex]d=rt[/latex] is a well-known relationship that associates distance traveled, the rate at which you travel, and how long the travel takes.

Distance, Rate, and Time

If you know two of the quantities in the relationship [latex]d=rt[/latex], you can easily find the third using methods for solving linear equations. For example, if you know that you will be traveling on a road with a speed limit of [latex]30\frac{\text{ miles }}{\text{ hour }}[/latex] for 2 hours, you can find the distance you would travel by multiplying rate times time or [latex]\left(30\frac{\text{ miles }}{\text{ hour }}\right)\left(2\text{ hours }\right)=60\text{ miles }[/latex].

We can generalize this idea depending on what information we are given and what we are looking for. For example, if we need to find time, we could solve the [latex]d=rt[/latex] equation for t using division:

[latex]d=rt\\\frac{d}{r}=t[/latex]

Likewise, if we want to find rate, we can isolate r using division:

[latex]d=rt\\\frac{d}{t}=r[/latex]

In the following examples you will see how this formula is applied to answer questions about ultra marathon running.

Ultra marathon running (defined as anything longer than 26.2 miles) is becoming very popular among women even though it remains a male-dominated niche sport. Ann Trason has broken twenty world records in her career. One such record was the American River 50-mile Endurance Run which begins in Sacramento, California, and ends in Auburn, California. [1] In 1993 Trason finished the run with a time of 6:09:08.  The men’s record for the same course was set in 1994 by Tom Johnson who finished the course with a time of 5:33:21. [2]

In the next examples we will use the [latex]d=rt[/latex] formula to answer the following questions about the two runners.

What was each runner’s rate for their record-setting runs?

By the time Johnson had finished, how many more miles did Trason have to run?

How much further could Johnson have run if he had run as long as Trason?

What was each runner’s time for running one mile?

To make answering the questions easier, we will round the two runners’ times to 6 hours and 5.5 hours.

Read and Understand:  We are looking for rate and we know distance and time, so we can use the idea: [latex]d=rt\\\frac{d}{t}=r[/latex]

Define and Translate: Because there are two runners, making a table to organize this information helps. Note how we keep units to help us keep track of what how all the terms are related to each other.

Write and Solve:

Trason’s rate:

[latex]\begin{array}{c}d=rt\\\\50\text{ miles }=\text{r}\left(6\text{ hours }\right)\\\frac{50\text{ miles }}{6\text{ hours }}=\frac{8.33\text{ miles }}{\text{ hour }}\end{array}[/latex].

(rounded to two decimal places)

Johnson’s rate:

[latex]\begin{array}{c}d=rt\\\\,\,\,\,\,\,\,50\text{ miles }=\text{r}\left(5.5\text{ hours }\right)\\\frac{50\text{ miles }}{6\text{ hours }}=\frac{9.1\text{ miles }}{\text{ hour }}\end{array}[/latex]

Check and Interpret:

We can fill in our table with this information.

Now that we know each runner’s rate we can answer the second question.

Here is the table we created for reference:

Read and Understand:  We are looking for how many miles Trason still had on the trail when Johnson had finished after 5.5 hours. This is a distance, and we know rate and time.

Define and Translate:  We can use the formula [latex]d=rt[/latex] again. This time the unknown is d , and the time Trason had run is 5.5 hours.

[latex]\begin{array}{l}d=rt\\\\d=8.33\frac{\text{ miles }}{\text{ hour }}\left(5.5\text{ hours }\right)\\\\d=45.82\text{ miles }\end{array}[/latex].

Have we answered the question? We were asked to find how many more miles she had to run after 5.5 hours.  What we have found is how long she had run after 5.5 hours. We need to subtract [latex]d=45.82\text{ miles }[/latex] from the total distance of the course.

[latex]50\text{ miles }-45.82\text{ miles }=1.48\text{ miles }[/latex]

The third question is similar to the second. Now that we know each runner’s rate, we can answer questions about individual distances or times.

Read and Understand:  The word further implies we are looking for a distance.

Define and Translate:  We can use the formula [latex]d=rt[/latex] again. This time the unknown is d , the time is 6 hours, and Johnson’s rate is [latex]9.1\frac{\text{ miles }}{\text{ hour }}[/latex]

[latex]\begin{array}{l}d=rt\\\\d=9.1\frac{\text{ miles }}{\text{ hour }}\left(6\text{ hours }\right)\\\\d=54.6\text{ miles }\end{array}[/latex].

Have we answered the question? We were asked to find how many more miles Johnson would have run if he had run at his rate of [latex]9.1\frac{\text{ miles }}{\text{ hour }}[/latex] for 6 hours.

Johnson would have run 54.6 miles, so that’s 4.6 more miles than than he ran for the race.

Now we will tackle the last question where we are asked to find a time for each runner.

Read and Understand:  we are looking for time, and this time our distance has changed from 50 miles to 1 mile, so we can use

Define and Translate: we can use the formula [latex]d=rt[/latex] again. This time the unknown is t , the distance is 1 mile, and we know each runner’s rate. It may help to create a new table:

We will need to divide to isolate time.

[latex]\begin{array}{c}d=rt\\\\1\text{ mile }=8.33\frac{\text{ miles }}{\text{ hour }}\left(t\text{ hours }\right)\\\\\frac{1\text{ mile }}{\frac{8.33\text{ miles }}{\text{ hour }}}=t\text{ hours }\\\\0.12\text{ hours }=t\end{array}[/latex].

0.12 hours is about 7.2 minutes, so Trason’s time for running one mile was about 7.2 minutes. WOW! She did that for 6 hours!

[latex]\begin{array}{c}d=rt\\\\1\text{ mile }=9.1\frac{\text{ miles }}{\text{ hour }}\left(t\text{ hours }\right)\\\\\frac{1\text{ mile }}{\frac{9.1\text{ miles }}{\text{ hour }}}=t\text{ hours }\\\\0.11\text{ hours }=t\end{array}[/latex].

0.11 hours is about 6.6 minutes, so Johnson’s time for running one mile was about 6.6 minutes. WOW! He did that for 5.5 hours!

Have we answered the question? We were asked to find how long it took each runner to run one mile given the rate at which they ran the whole 50-mile course.  Yes, we answered our question.

Trason’s mile time was [latex]7.2\frac{\text{minutes}}{\text{mile}}[/latex] and Johnsons’ mile time was [latex]6.6\frac{\text{minutes}}{\text{mile}}[/latex]

In the following video, we show another example of answering many rate questions given distance and time.

Simple Interest

In order to entice customers to invest their money, many banks will offer interest-bearing accounts. The accounts work like this: a customer deposits a certain amount of money (called the Principal, or P ), which then grows slowly according to the interest rate ( R , measured in percent) and the length of time ( T , usually measured in months) that the money stays in the account. The amount earned over time is called the interest ( I ), which is then given to the customer.

The simplest way to calculate interest earned on an account is through the formula [latex]\displaystyle I=P\,\cdot \,R\,\cdot \,T[/latex].

If we know any of the three amounts related to this equation, we can find the fourth. For example, if we want to find the time it will take to accrue a specific amount of interest, we can solve for T using division:

[latex]\displaystyle\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,I=P\,\cdot \,R\,\cdot \,T\\\\ \frac{I}{{P}\,\cdot \,R}=\frac{P\cdot\,R\,\cdot \,T}{\,P\,\cdot \,R}\\\\\,\,\,\,\,\,\,\,\,\,\,{T}=\frac{I}{\,R\,\cdot \,T}\end{array}[/latex]

Below is a table showing the result of solving for each individual variable in the formula.

In the next examples, we will show how to substitute given values into the simple interest formula, and decipher which variable to solve for.

If a customer deposits a principal of $2000 at a monthly rate of 0.7%, what is the total amount that she has after 24 months?

Substitute in the values given for the Principal, Rate, and Time.

[latex]\displaystyle\begin{array}{l}I=P\,\cdot \,R\,\cdot \,T\\I=2000\cdot 0.7\%\cdot 24\end{array}[/latex]

Rewrite 0.7% as the decimal 0.007, then multiply.

[latex]\begin{array}{l}I=2000\cdot 0.007\cdot 24\\I=336\end{array}[/latex]

Add the interest and the original principal amount to get the total amount in her account.

[latex] \displaystyle 2000+336=2336[/latex]

She has $2336 after 24 months.

The following video shows another example of finding an account balance after a given amount of time, principal invested, and a rate.

In the following example you will see why it is important to make sure the units of the interest rate match the units of time when using the simple interest formula.

Alex invests $600 at 3.25% monthly interest for 3 years. What amount of interest has Alex earned?

Read and Understand: The question asks for an amount, so we can substitute what we are given into the simple interest formula [latex]I=P\,\cdot \,R\,\cdot \,T[/latex]

Define and Translate:  we know P, R, and T so we can use substitution. R  = 0.0325, P = $600, and T = 3 years. We have to be careful! R is in months, and T is in years.  We need to change T into months because we can’t change the rate—it is set by the bank.

[latex]{T}=3\text{ years }\cdot12\frac{\text{ months }}{ year }=36\text{ months }[/latex]

Substitute the given values into the formula.

[latex]\begin{array}{l} I=P\,\cdot \,R\,\cdot \,T\\\\I=600\,\cdot \,0.035\,\cdot \,36\\\\{I}=756\end{array}[/latex]

We were asked what amount Alex earned, which is the amount provided by the formula. In the previous example we were asked the total amount in the account, which included the principal and interest earned.

Alex has earned $756.

After 10 years, Jodi’s account balance has earned $1080 in interest. The rate on the account is 0.09% monthly. What was the original amount she invested in the account?

Read and Understand: The question asks for the original amount invested, the principal. We are given a length of time in years, and an interest rate in months, and the amount of interest earned.

Define and Translate:  we know I = $1080, R = 0.009, and T = 10 years so we can use [latex]{P}=\frac{I}{{R}\,\cdot \,T}[/latex]

We also need to make sure the units on the interest rate and the length of time match, and they do not. We need to change time into months again.

[latex]{T}=10\text{ years }\cdot12\frac{\text{ months }}{ year }=120\text{ months }[/latex]

Substitute the given values into the formula

[latex]\begin{array}{l}{P}=\frac{I}{{R}\,\cdot \,T}\\\\{P}=\frac{1080}{{0.009}\,\cdot \,120}\\\\{P}=\frac{1080}{1.08}=1000\end{array}[/latex]

We were asked to find the principal given the amount of interest earned on an account.  If we substitute P = $1000 into the formula [latex]I=P\,\cdot \,R\,\cdot \,T[/latex] we get

[latex]I=1000\,\cdot \,0.009\,\cdot \,120\\I=1080[/latex]

Our solution checks out. Jodi invested $1000.

Further Applications of Linear Equations

Formulas come up in many different areas of life. We have seen the formula that relates distance, rate, and time and the formula for simple interest on an investment. In this section we will look further at formulas and see examples of formulas for dimensions of geometric shapes as well as the formula for converting temperature between Fahrenheit and Celsius.

There are many geometric shapes that have been well studied over the years. We know quite a bit about circles, rectangles, and triangles. Mathematicians have proven many formulas that describe the dimensions of geometric shapes including area, perimeter, surface area, and volume.

Perimeter is the distance around an object. For example, consider a rectangle with a length of 8 and a width of 3. There are two lengths and two widths in a rectangle (opposite sides), so we add [latex]8+8+3+3=22[/latex]. Since there are two lengths and two widths in a rectangle, you may find the perimeter of a rectangle using the formula [latex]{P}=2\left({L}\right)+2\left({W}\right)[/latex] where

In the following example, we will use the problem-solving method we developed to find an unknown width using the formula for the perimeter of a rectangle. By substituting the dimensions we know into the formula, we will be able to isolate the unknown width and find our solution.

You want to make another garden box the same size as the one you already have. You write down the dimensions of the box and go to the lumber store to buy some boards. When you get there you realize you didn’t write down the width dimension—only the perimeter and length. You want the exact dimensions so you can have the store cut the lumber for you.

Here is what you have written down:

Perimeter = 16.4 feet Length = 4.7 feet

Can you find the dimensions you need to have your boards cut at the lumber store? If so, how many boards do you need and what lengths should they be?

Read and Understand:  We know perimeter = 16.4 feet and length = 4.7 feet, and we want to find width.

Define and Translate:

Define the known and unknown dimensions:

First we will substitute the dimensions we know into the formula for perimeter:

[latex]\begin{array}{l}\,\,\,\,\,P=2{W}+2{L}\\\\16.4=2\left(w\right)+2\left(4.7\right)\end{array}[/latex]

Then we will isolate w to find the unknown width.

[latex]\begin{array}{l}16.4=2\left(w\right)+2\left(4.7\right)\\16.4=2{w}+9.4\\\underline{-9.4\,\,\,\,\,\,\,\,\,\,\,\,\,-9.4}\\\,\,\,\,\,\,\,7=2\left(w\right)\\\,\,\,\,\,\,\,\frac{7}{2}=\frac{2\left(w\right)}{2}\\\,\,\,\,3.5=w\end{array}[/latex]

Write the width as a decimal to make cutting the boards easier and replace the units on the measurement, or you won’t get the right size of board!

If we replace the width we found, [latex]w=3.5\text{ feet }[/latex] into the formula for perimeter with the dimensions we wrote down, we can check our work:

[latex]\begin{array}{l}\,\,\,\,\,{P}=2\left({L}\right)+2\left({W}\right)\\\\{16.4}=2\left({4.7}\right)+2\left({3.5}\right)\\\\{16.4}=9.4+7\\\\{16.4}=16.4\end{array}[/latex]

Our calculation for width checks out. We need to ask for 2 boards cut to 3.5 feet and 2 boards cut to 4.7 feet so we can make the new garden box.

This video shows a similar garden box problem.

We could have isolated the w in the formula for perimeter before we solved the equation, and if we were going to use the formula many times, it could save a lot of time. The next example shows how to isolate a variable in a formula before substituting known dimensions or values into the formula.

Isolate the term containing the variable, w, from the formula for the perimeter of a rectangle :  

[latex]{P}=2\left({L}\right)+2\left({W}\right)[/latex].

First, isolate the term with  w by subtracting 2 l from both sides of the equation.

[latex] \displaystyle \begin{array}{l}\,\,\,\,\,\,\,\,\,\,p\,=\,\,\,\,2l+2w\\\underline{\,\,\,\,\,-2l\,\,\,\,\,-2l\,\,\,\,\,\,\,\,\,\,\,}\\p-2l=\,\,\,\,\,\,\,\,\,\,\,\,\,2w\end{array}[/latex]

Next, clear the coefficient of w by dividing both sides of the equation by 2.

[latex]\displaystyle \begin{array}{l}\underline{p-2l}=\underline{2w}\\\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\\ \,\,\,\frac{p-2l}{2}\,\,=\,\,w\\\,\,\,\,\,\,\,\,\,\,\,w=\frac{p-2l}{2}\end{array}[/latex]

You can rewrite the equation so the isolated variable is on the left side.

[latex]w=\frac{p-2l}{2}[/latex]

The area of a triangle is given by [latex] A=\frac{1}{2}bh[/latex] where

A = area b = the length of the base h = the height of the triangle

Remember that when two variables or a number and a variable are sitting next to each other without a mathematical operator between them, you can assume they are being multiplied. This can seem frustrating, but you can think of it like mathematical slang. Over the years, people who use math frequently have just made that shortcut enough that it has been adopted as convention.

In the next example we will use the formula for area of a triangle to find a missing dimension, as well as use substitution to solve for the base of a triangle given the area and height.

Find the base ( b) of a triangle with an area ( A ) of 20 square feet and a height ( h) of 8 feet.

Use the formula for the area of a triangle, [latex] {A}=\frac{{1}}{{2}}{bh}[/latex] .

Substitute the given lengths into the formula and solve for  b.

[latex]\displaystyle \begin{array}{l}\,\,A=\frac{1}{2}bh\\\\20=\frac{1}{2}b\cdot 8\\\\20=\frac{8}{2}b\\\\20=4b\\\\\frac{20}{4}=\frac{4b}{4}\\\\ \,\,\,5=b\end{array}[/latex]

The base of the triangle measures 5 feet.

We can rewrite the formula in terms of b or h as we did with perimeter previously. This probably seems abstract, but it can help you develop your equation-solving skills, as well as help you get more comfortable with working with all kinds of variables, not just x .

Use the multiplication and division properties of equality to isolate the variable b .

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,A=\frac{1}{2}bh\\\\\left(2\right)A=\left(2\right)\frac{1}{2}bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\frac{2A}{h}=\frac{bh}{h}\\\\\,\,\,\,\,\,\,\,\frac{2A}{h}=\frac{b\cancel{h}}{\cancel{h}}\end{array}[/latex]

Write the equation with the desired variable on the left-hand side as a matter of convention:

Use the multiplication and division properties of equality to isolate the variable h .

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,A=\frac{1}{2}bh\\\\\left(2\right)A=\left(2\right)\frac{1}{2}bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\frac{2A}{b}=\frac{bh}{b}\\\\\,\,\,\,\,\,\,\,\frac{2A}{b}=\frac{h\cancel{b}}{\cancel{b}}\end{array}[/latex]

Temperature

Let’s look at another formula that includes parentheses and fractions, the formula for converting from the Fahrenheit temperature scale to the Celsius scale.

[latex]C=\left(F-32\right)\cdot \frac{5}{9}[/latex]

Given a temperature of [latex]12^{\circ}{C}[/latex], find the equivalent in [latex]{}^{\circ}{F}[/latex].

Substitute the given temperature in[latex]{}^{\circ}{C}[/latex] into the conversion formula:

[latex]12=\left(F-32\right)\cdot \frac{5}{9}[/latex]

Isolate the variable F to obtain the equivalent temperature.

[latex]\begin{array}{r}12=\left(F-32\right)\cdot \frac{5}{9}\\\\\left(\frac{9}{5}\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\\left(\frac{108}{5}\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\21.6=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+32}\,\,\,\,\,\,\,\,\,\,\,\,\\\\53.6={}^{\circ}{F}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

As with the other formulas we have worked with, we could have isolated the variable F first, then substituted in the given temperature in Celsius.

Solve the formula shown below for converting from the Fahrenheit scale to the Celsius scale for F.

To isolate the variable F, it would be best to clear the fraction involving F first. Multiply both sides of the equation by [latex] \displaystyle \frac{9}{5}[/latex].

[latex]\begin{array}{l}\\\,\,\,\,\left(\frac{9}{5}\right)C=\left(F-32\right)\left(\frac{5}{9}\right)\left(\frac{9}{5}\right)\\\\\,\,\,\,\,\,\,\,\,\,\,\,\frac{9}{5}C=F-32\end{array}[/latex]

Add 32 to both sides.

[latex]\begin{array}{l}\frac{9}{5}\,C+32=F-32+32\\\\\frac{9}{5}\,C+32=F\end{array}[/latex]

[latex]F=\frac{9}{5}C+32[/latex]

Think About It

Express the formula for the surface area of a cylinder, [latex]s=2\pi rh+2\pi r^{2}[/latex], in terms of the height, h .

In this example, the variable h is buried pretty deeply in the formula for surface area of a cylinder. Using the order of operations, it can be isolated. Before you look at the solution, use the box below to write down what you think is the best first step to take to isolate h .

[latex]\begin{array}{r}S\,\,=2\pi rh+2\pi r^{2} \\ \underline{-2\pi r^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,-2\pi r^{2}}\\S-2\pi r^{2}\,\,\,\,=\,\,\,\,2\pi rh\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Next, isolate the variable h by dividing both sides of the equation by [latex]2\pi r[/latex].

[latex]\begin{array}{r}\frac{S-2\pi r^{2}}{2\pi r}=\frac{2\pi rh}{2\pi r} \\\\ \frac{S-2\pi r^{2}}{2\pi r}=h\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

• "Ann Trason." Wikipedia. Accessed May 05, 2016. https://en.wikipedia.org/wiki/Ann_Trason . ↵
•  "American River 50 Mile Endurance Run." Wikipedia. Accessed May 05, 2016. https://en.wikipedia.org/wiki/American_River_50_Mile_Endurance_Run . ↵
• Writing Algebraic Expressions. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/uD_V5t-6Kzs . License : CC BY: Attribution
• Write and Solve a Linear Equations to Solve a Number Problem (1). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/izIIqOztUyI . License : CC BY: Attribution
• Write and Solve a Linear Equations to Solve a Number Problem (Consecutive Integers). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/S5HZy3jKodg . License : CC BY: Attribution
• Screenshot: Ann Trason Trail Running. Authored by : Lumen Learning. License : CC BY: Attribution
• Problem Solving Using Distance, Rate, Time (Running). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/3WLp5mY1FhU . License : CC BY: Attribution
• Simple Interest - Determine Account Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/XkGgEEMR_00 . License : CC BY: Attribution
• Simple Interest - Determine Interest Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/mRV5ljj32Rg . License : CC BY: Attribution
• Simple Interest - Determine Principal Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/vbMqN6lVoOM . License : CC BY: Attribution
• Find the Width of a Rectangle Given the Perimeter / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/jlxPgKQfhQs . License : CC BY: Attribution
• Find the Base of a Triangle Given Area / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/VQZQvJ3rXYg . License : CC BY: Attribution
• Convert Celsius to Fahrenheit / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/DRydX8V-JwY . License : CC BY: Attribution
• Ann Trason. Provided by : Wikipedia. Located at : https://en.wikipedia.org/wiki/Ann_Trason . License : CC BY-SA: Attribution-ShareAlike
• American River 50 Mile Endurance Run. Provided by : Wikipedia. Located at : https://en.wikipedia.org/wiki/American_River_50_Mile_Endurance_Run . License : CC BY-SA: Attribution-ShareAlike

• Daily Games
• Strategy and Puzzles
• Vocabulary Games
• Junior Edition Games
• All problems
• High School Math
• MAML Problems
• Calculus Problems
• Loony Physics
• Pro Problems
• Getting Started
• Pro Control Panel
• Virtual Classroom
• Play My Favorites
• Select My Favorites

Using Formulas to Solve Word Problems

Students sometimes think, "Oh no! Formulas! I hate formulas!" But really, formulas are designed to make life easier for you. Because if you didn't have a formula to use, you'd have to do a lot more work to get an answer. Formulas can help us do a wider range of problems. Here are a few formulas, with explanations:

The perimeter of a square is 4 times the length of a side.

P = 2W + 2L

The perimeter of a rectangle is twice the width plus twice the length.

F = 1.8C + 32

The temperature in Fahrenheit is 1.8 times the temperature in Celsius, plus 32.

Distance traveled is the rate (speed) times the amount of time traveled.

A = 1/2(bh)

The area of a triangle is one half the base times the height.

The circumference of circle is two times pi times the radius.

A + B + C = 180

The sum of the measures of the angles in a triangle is 180 degrees.

Here are some sample problems. These problems use the formulas shown above.

If the perimeter of a square is 48 units, what is the length of a side?

Solution #1

P = 4s, so 48 = 4s, and the answer is s = 12

A car travels 400 miles in 5 hours. How fast is it driving?

Solution #2

d = rt, so 400 = 5r, so r = 80

Blogs on This Site