hard maths problem solving questions

These Are the 10 Hardest Math Problems Ever Solved

They’re guaranteed to make your head spin.

On the surface, it seems easy. Can you think of the integers for x, y, and z so that x³+y³+z³=8? Sure. One answer is x = 1, y = -1, and z = 2. But what about the integers for x, y, and z so that x³+y³+z³=42?

That turned out to be much harder—as in, no one was able to solve for those integers for 65 years until a supercomputer finally came up with the solution to 42. (For the record: x = -80538738812075974, y = 80435758145817515, and z = 12602123297335631. Obviously.)

That’s the beauty of math : There’s always an answer for everything, even if takes years, decades, or even centuries to find it. So here are nine more brutally difficult math problems that once seemed impossible, until mathematicians found a breakthrough.

• This Math Trivia Question Is Going Viral Because the Answer Is Completely Wrong
• To Create His Geometric Artwork, M.C. Escher Had to Learn Math the Hard Way
• Fourier Transforms: The Math That Made Color TV Possible

The Poincaré Conjecture

In 2000, the Clay Mathematics Institute , a non-profit dedicated to “increasing and disseminating mathematical knowledge,” asked the world to solve seven math problems and offered $1,000,000 to anybody who could crack even one. Today, they’re all still unsolved, except for the Poincaré conjecture.

Henri Poincaré was a French mathematician who, around the turn of the 20th century, did foundational work in what we now call topology. Here’s the idea: Topologists want mathematical tools for distinguishing abstract shapes. For shapes in 3D space, like a ball or a donut, it wasn’t very hard to classify them all . In some significant sense, a ball is the simplest of these shapes.

Poincaré then went up to 4-dimensional stuff, and asked an equivalent question. After some revisions and developments, the conjecture took the form of “Every simply-connected, closed 3-manifold is homeomorphic to S^3,” which essentially says “the simplest 4D shape is the 4D equivalent of a sphere.”

Still with us?

A century later, in 2003, a Russian mathematician named Grigori Perelman posted a proof of Poincaré’s conjecture on the modern open math forum arXiv. Perelman’s proof had some small gaps, and drew directly from research by American mathematician Richard Hamilton. It was groundbreaking, yet modest.

After the math world spent a few years verifying the details of Perelman’s work, the awards began . Perelman was offered the million-dollar Millennium Prize, as well as the Fields Medal, often called the Nobel Prize of Math. Perelman rejected both. He said his work was for the benefit of mathematics, not personal gain, and also that Hamilton, who laid the foundations for his proof, was at least as deserving of the prizes.

Fermat’s Last Theorem

Pierre de Fermat was a 17th-century French lawyer and mathematician. Math was apparently more of a hobby for Fermat, and so one of history’s greatest math minds communicated many of his theorems through casual correspondence. He made claims without proving them, leaving them to be proven by other mathematicians decades, or even centuries, later. The most challenging of these has become known as Fermat’s Last Theorem.

It’s a simple one to write. There are many trios of integers (x,y,z) that satisfy x²+y²=z². These are known as the Pythagorean Triples, like (3,4,5) and (5,12,13). Now, do any trios (x,y,z) satisfy x³+y³=z³? The answer is no, and that’s Fermat’s Last Theorem.

Fermat famously wrote the Last Theorem by hand in the margin of a textbook, along with the comment that he had a proof, but could not fit it in the margin. For centuries, the math world has been left wondering if Fermat really had a valid proof in mind.

Flash forward 330 years after Fermat’s death to 1995, when British mathematician Sir Andrew Wiles finally cracked one of history’s oldest open problems . For his efforts, Wiles was knighted by Queen Elizabeth II and was awarded a unique honorary plaque in lieu of the Fields Medal, since he was just above the official age cutoff to receive a Fields Medal.

Wiles managed to combine new research in very different branches of math in order to solve Fermat’s classic number theory question. One of these topics, Elliptic Curves, was completely undiscovered in Fermat’s time, leading many to believe Fermat never really had a proof of his Last Theorem.

The Classification of Finite Simple Groups

From solving Rubik’s Cube to proving a fact about body-swapping on Futurama , abstract algebra has a wide range of applications. Algebraic groups are sets that follow a few basic properties, like having an “identity element,” which works like adding 0.

Groups can be finite or infinite, and if you want to know what groups of a particular size n look like, it can get very complicated depending on your choice of n .

If n is 2 or 3, there’s only one way that group can look. When n hits 4, there are two possibilities. Naturally, mathematicians wanted a comprehensive list of all possible groups for any given size.

The complete list took decades to finish conclusively, because of the difficulties in being sure that it was indeed complete. It’s one thing to describe what infinitely many groups look like, but it’s even harder to be sure the list covers everything. Arguably the greatest mathematical project of the 20th century, the classification of finite simple groups was orchestrated by Harvard mathematician Daniel Gorenstein, who in 1972 laid out the immensely complicated plan.

By 1985, the work was nearly done, but spanned so many pages and publications that it was unthinkable for one person to peer review. Part by part, the many facets of the proof were eventually checked and the completeness of the classification was confirmed.

By the 1990s, the proof was widely accepted. Subsequent efforts were made to streamline the titanic proof to more manageable levels, and that project is still ongoing today .

The Four Color Theorem

This one is as easy to state as it is hard to prove.

Grab any map and four crayons. It’s possible to color each state (or country) on the map, following one rule: No states that share a border get the same color.

The fact that any map can be colored with five colors—the Five Color Theorem —was proven in the 19th century. But getting that down to four took until 1976.

Two mathematicians at the University of Illinois, Urbana-Champaign, Kenneth Appel and Wolfgang Hakan, found a way to reduce the proof to a large, finite number of cases . With computer assistance, they exhaustively checked the nearly 2,000 cases, and ended up with an unprecedented style of proof.

Arguably controversial since it was partially conceived in the mind of a machine, Appel and Hakan’s proof was eventually accepted by most mathematicians. It has since become far more common for proofs to have computer-verified parts, but Appel and Hakan blazed the trail.

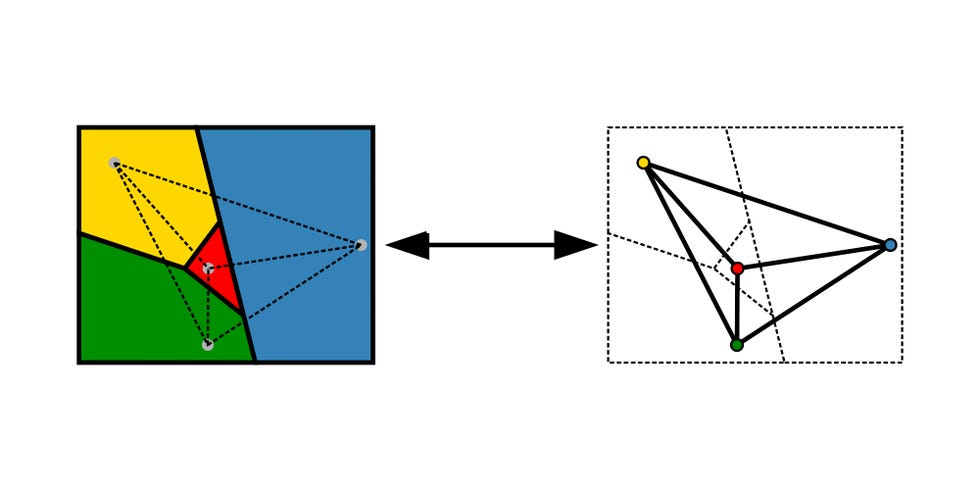
(The Independence of) The Continuum Hypothesis

In the late 19th century, a German mathematician named Georg Cantor blew everyone’s minds by figuring out that infinities come in different sizes, called cardinalities. He proved the foundational theorems about cardinality, which modern day math majors tend to learn in their Discrete Math classes.

Cantor proved that the set of real numbers is larger than the set of natural numbers, which we write as |ℝ|>|ℕ|. It was easy to establish that the size of the natural numbers, |ℕ|, is the first infinite size; no infinite set is smaller than ℕ.

Now, the real numbers are larger, but are they the second infinite size? This turned out to be a much harder question, known as The Continuum Hypothesis (CH) .

If CH is true, then |ℝ| is the second infinite size, and no infinite sets are smaller than ℝ, yet larger than ℕ. And if CH is false, then there is at least one size in between.

So what’s the answer? This is where things take a turn.

CH has been proven independent, relative to the baseline axioms of math. It can be true, and no logical contradictions follow, but it can also be false, and no logical contradictions will follow.

It’s a weird state of affairs, but not completely uncommon in modern math. You may have heard of the Axiom of Choice, another independent statement. The proof of this outcome spanned decades and, naturally, split into two major parts: the proof that CH is consistent, and the proof that the negation of CH is consistent.

The first half is thanks to Kurt Gödel, the legendary Austro-Hungarian logician. His 1938 mathematical construction, known as Gödel’s Constructible Universe , proved CH compatible with the baseline axioms, and is still a cornerstone of Set Theory classes. The second half was pursued for two more decades until Paul Cohen, a mathematician at Stanford, solved it by inventing an entire method of proof in Model Theory known as “forcing.”

Gödel’s and Cohen’s halves of the proof each take a graduate level of Set Theory to approach, so it’s no wonder this unique story has been esoteric outside mathematical circles.

Gödel’s Incompleteness Theorems

Gödel’s work in mathematical logic was totally next-level. On top of proving stuff, Gödel also liked to prove whether or not it was possible to prove stuff . His Incompleteness Theorems are often misunderstood, so here’s a perfect chance to clarify them.

Gödel’s First Incompleteness Theorem says that, in any proof language, there are always unprovable statements. There’s always something that’s true, that you can’t prove true. It’s possible to understand a (non-mathematically rigorous) version of Gödel’s argument, with some careful thinking. So buckle up, here it is: Consider the statement, “This statement cannot be proven true.”

Think through every case to see why this is an example of a true, but unprovable statement. If it’s false, then what it says is false, so then it can be proven true, which is contradictory, so this case is impossible. On the other extreme, if it did have a proof, then that proof would prove it true … making it true that it has no proof, which is contradictory, killing this case. So we’re logically left with the case that the statement is true, but has no proof. Yeah, our heads are spinning, too.

But follow that nearly-but-not-quite-paradoxical trick, and you’ve illustrated that Gödel’s First Incompleteness Theorem holds.

Gödel’s Second Incompleteness Theorem is similarly weird. It says that mathematical “formal systems” can’t prove themselves consistent. A consistent system is one that won’t give you any logical contradictions.

Here’s how you can think of that. Imagine Amanda and Bob each have a set of mathematical axioms—baseline math rules—in mind. If Amanda can use her axioms to prove that Bob’s axiom system is free of contradictions, then it’s impossible for Bob to use his axioms to prove Amanda’s system doesn’t yield contradictions.

So when mathematicians debate the best choices for the essential axioms of mathematics (it’s much more common than you might imagine) it’s crucial to be aware of this phenomenon.

The Prime Number Theorem

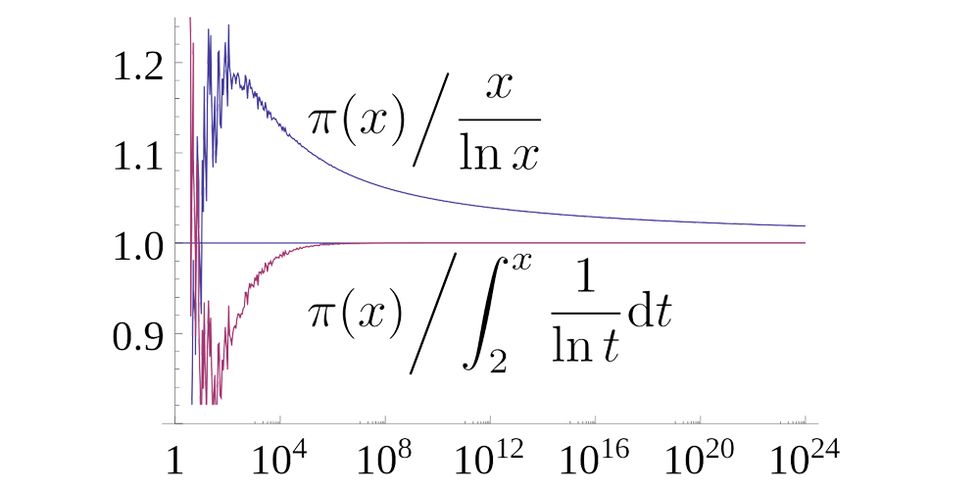
There are plenty of theorems about prime numbers . One of the simplest facts—that there are infinitely many prime numbers—can even be adorably fit into haiku form .

The Prime Number Theorem is more subtle; it describes the distribution of prime numbers along the number line. More precisely, it says that, given a natural number N, the number of primes below N is approximately N/log(N) ... with the usual statistical subtleties to the word “approximately” there.

Drawing on mid-19th-century ideas, two mathematicians, Jacques Hadamard and Charles Jean de la Vallée Poussin, independently proved the Prime Number Theorem in 1898. Since then, the proof has been a popular target for rewrites, enjoying many cosmetic revisions and simplifications. But the impact of the theorem has only grown.

The usefulness of the Prime Number Theorem is huge. Modern computer programs that deal with prime numbers rely on it. It’s fundamental to primality testing methods, and all the cryptology that goes with that.

Solving Polynomials by Radicals

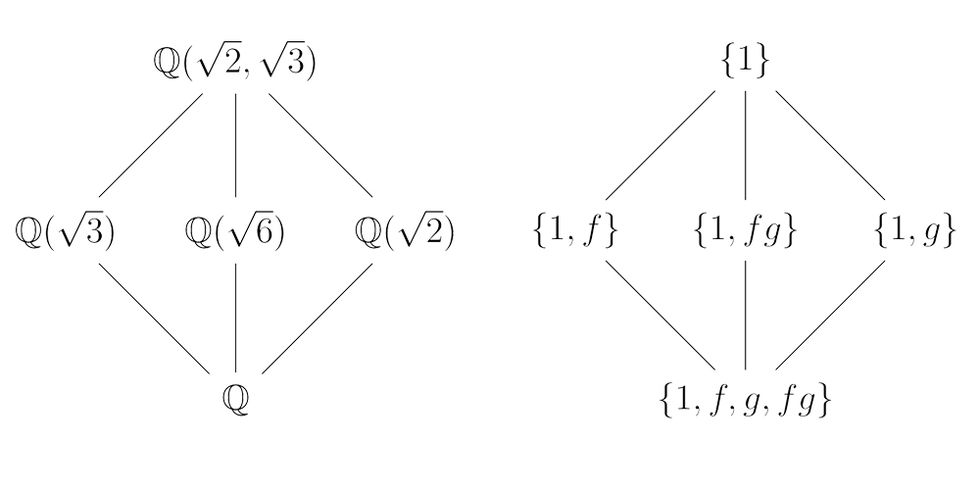
Remember the quadratic formula ? Given ax²+bx+c=0, the solution is x=(-b±√(b^2-4ac))/(2a), which may have felt arduous to memorize in high school, but you have to admit is a conveniently closed-form solution.

Now, if we go up to ax³+bx²+cx+d=0, a closed form for “x=” is possible to find, although it’s much bulkier than the quadratic version. It’s also possible, yet ugly, to do this for degree 4 polynomials ax⁴+bx³+cx²+dx+f=0.

The goal of doing this for polynomials of any degree was noted as early as the 15th century. But from degree 5 on, a closed form is not possible. Writing the forms when they’re possible is one thing, but how did mathematicians prove it’s not possible from 5 up?

The world was only starting to comprehend the brilliance of French mathematician Evariste Galois when he died at the age of 20 in 1832. His life included months spent in prison, where he was punished for his political activism, writing ingenious, yet unrefined mathematics to scholars, and it ended in a fatal duel.

Galois’ ideas took decades after his death to be fully understood, but eventually they developed into an entire theory now called Galois Theory . A major theorem in this theory gives exact conditions for when a polynomial can be “solved by radicals,” meaning it has a closed form like the quadratic formula. All polynomials up to degree 4 satisfy these conditions, but starting at degree 5, some don’t, and so there’s no general form for a solution for any degree higher than 4.

Trisecting an Angle

To finish, let’s go way back in history.

The Ancient Greeks wondered about constructing lines and shapes in various ratios, using the tools of an unmarked compass and straightedge . If someone draws an angle on some paper in front of you, and gives you an unmarked ruler, a basic compass, and a pen, it’s possible for you to draw the line that cuts that angle exactly in half. It’s a quick four steps, nicely illustrated like this , and the Greeks knew it two millennia ago.

What eluded them was cutting an angle in thirds. It stayed elusive for literally 15 centuries, with hundreds of attempts in vain to find a construction. It turns out such a construction is impossible.

Modern math students learn the angle trisection problem—and how to prove it’s not possible—in their Galois Theory classes. But, given the aforementioned period of time it took the math world to process Galois’ work, the first proof of the problem was due to another French mathematician, Pierre Wantzel . He published his work in 1837, 16 years after the death of Galois, but nine years before most of Galois’ work was published.

Either way, their insights are similar, casting the construction question into one about properties of certain representative polynomials. Many other ancient construction questions became approachable with these methods, closing off some of the oldest open math questions in history.

So if you ever time-travel to ancient Greece, you can tell them their attempts at the angle trisection problem are futile.

Dave Linkletter is a Ph.D. candidate in Pure Mathematics at the University of Nevada, Las Vegas. His research is in Large Cardinal Set Theory. He also teaches undergrad classes, and enjoys breaking down popular math topics for wide audiences.

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Pop Mech Pro .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

Inside the Final Minutes of a Horrible Train Wreck

This Is the Most Lethal Submarine in the Sea

Build a DIY Eclipse Viewer in Minutes

Navy Helicopters Have Morphed Into Drone Killers

J Allen Hynek: The Man Who Made Us Watch the Skies

Army: The Days of Towed Artillery Are Over

The Right Way to Prune a Tree

Simplified Furniture Refinishing

How to Stripe a Lawn

The US Army Has Deployed Lasers to a Combat Zone

How Vacuum Energy Could Help Us Reach Light Speed

Choose Your Test

Sat / act prep online guides and tips, the 15 hardest sat math questions ever.

Want to test yourself against the most difficult SAT math questions? Want to know what makes these questions so difficult and how best to solve them? If you're ready to really sink your teeth into the SAT math section and have your sights set on that perfect score, then this is the guide for you.

We've put together what we believe to be the 15 most difficult questions for the current SAT , with strategies and answer explanations for each. These are all hard SAT Math questions from College Board SAT practice tests, which means understanding them is one of the best ways to study for those of you aiming for perfection.

Image: Sonia Sevilla /Wikimedia

Brief Overview of SAT Math

The third and fourth sections of the SAT will always be math sections . The first math subsection (labeled "3") does not allow you to use a calculator, while the second math subsection (labeled as "4") does allow the use of a calculator. Don't worry too much about the no-calculator section, though: if you're not allowed to use a calculator on a question, it means you don't need a calculator to answer it.

Each math subsection is arranged in order of ascending difficulty (where the longer it takes to solve a problem and the fewer people who answer it correctly, the more difficult it is). On each subsection, question 1 will be "easy" and question 15 will be considered "difficult." However, the ascending difficulty resets from easy to hard on the grid-ins.

Hence, multiple choice questions are arranged in increasing difficulty (questions 1 and 2 will be the easiest, questions 14 and 15 will be the hardest), but the difficulty level resets for the grid-in section (meaning questions 16 and 17 will again be "easy" and questions 19 and 20 will be very difficult).

With very few exceptions, then, the most difficult SAT math problems will be clustered at the end of the multiple choice segments or the second half of the grid-in questions. In addition to their placement on the test, though, these questions also share a few other commonalities. In a minute, we'll look at example questions and how to solve them, then analyze them to figure out what these types of questions have in common.

But First: Should You Be Focusing on the Hardest Math Questions Right Now?

If you're just getting started in your study prep (or if you've simply skipped this first, crucial step), definitely stop and take a full practice test to gauge your current scoring level. Check out our guide to all the free SAT practice tests available online and then sit down to take a test all at once.

The absolute best way to assess your current level is to simply take the SAT practice test as if it were real , keeping strict timing and working straight through with only the allowed breaks (we know—probably not your favorite way to spend a Saturday). Once you've got a good idea of your current level and percentile ranking, you can set milestones and goals for your ultimate SAT Math score.

If you're currently scoring in the 200-400 or the 400-600 range on SAT Math, your best bet is first to check out our guide to improving your math score to be consistently at or over a 600 before you start in trying to tackle the most difficult math problems on the test.

If, however, you're already scoring above a 600 on the Math section and want to test your mettle for the real SAT, then definitely proceed to the rest of this guide. If you're aiming for perfect (or close to) , then you'll need to know what the most difficult SAT math questions look like and how to solve them. And luckily, that's exactly what we'll do.

WARNING: Since there are a limited number of official SAT practice tests , you may want to wait to read this article until you've attempted all or most of the first four official practice tests (since most of the questions below were taken from those tests). If you're worried about spoiling those tests, stop reading this guide now; come back and read it when you've completed them.

Now let's get to our list of questions (whoo)!

Image: Niytx /DeviantArt

The 15 Hardest SAT Math Questions

Now that you're sure you should be attempting these questions, let's dive right in! We've curated 15 of the most difficult SAT Math questions for you to try below, along with walkthroughs of how to get the answer (if you're stumped).

No Calculator SAT Math Questions

$$C=5/9(F-32)$$

The equation above shows how temperature $F$, measured in degrees Fahrenheit, relates to a temperature $C$, measured in degrees Celsius. Based on the equation, which of the following must be true?

• A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of $5/9$ degree Celsius.
• A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
• A temperature increase of $5/9$ degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.

A) I only B) II only C) III only D) I and II only

ANSWER EXPLANATION: Think of the equation as an equation for a line

where in this case

$$C= {5}/{9} (F−32)$$

$$C={5}/{9}F −{5}/{9}(32)$$

You can see the slope of the graph is ${5}/{9}$, which means that for an increase of 1 degree Fahrenheit, the increase is ${5}/{9}$ of 1 degree Celsius.

$$C= {5}/{9} (F)$$

$$C= {5}/{9} (1)= {5}/{9}$$

Therefore, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of ${9}/{5}$ degrees Fahrenheit.

$$1= {5}/{9} (F)$$

$$(F)={9}/{5}$$

Since ${9}/{5}$ = 1.8, statement II is true.

The only answer that has both statement I and statement II as true is D , but if you have time and want to be absolutely thorough, you can also check to see if statement III (an increase of ${5}/{9}$ degree Fahrenheit is equal to a temperature increase of 1 degree Celsius) is true:

$$C= {5}/{9} ({5}/{9})$$

$$C= {25} /{81} (\which \is ≠ 1)$$

An increase of $5/9$ degree Fahrenheit leads to an increase of ${25}/{81}$, not 1 degree, Celsius, and so Statement III is not true.

The final answer is D.

The equation ${24x^2 + 25x -47}/{ax-2} = -8x-3-{53/{ax-2}}$ is true for all values of $x≠2/a$, where $a$ is a constant.

What is the value of $a$?

A) -16 B) -3 C) 3 D) 16

ANSWER EXPLANATION: There are two ways to solve this question. The faster way is to multiply each side of the given equation by $ax-2$ (so you can get rid of the fraction). When you multiply each side by $ax-2$, you should have:

$$24x^2 + 25x - 47 = (-8x-3)(ax-2) - 53$$

You should then multiply $(-8x-3)$ and $(ax-2)$ using FOIL.

$$24x^2 + 25x - 47 = -8ax^2 - 3ax +16x + 6 - 53$$

Then, reduce on the right side of the equation

$$24x^2 + 25x - 47 = -8ax^2 - 3ax +16x - 47$$

Since the coefficients of the $x^2$-term have to be equal on both sides of the equation, $−8a = 24$, or $a = −3$.

The other option which is longer and more tedious is to attempt to plug in all of the answer choices for a and see which answer choice makes both sides of the equation equal. Again, this is the longer option, and I do not recommend it for the actual SAT as it will waste too much time.

The final answer is B.

If $3x-y = 12$, what is the value of ${8^x}/{2^y}$?

A) $2^{12}$ B) $4^4$ C) $8^2$ D) The value cannot be determined from the information given.

ANSWER EXPLANATION: One approach is to express

$${8^x}/{2^y}$$

so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting $2^3$ for 8 in the numerator of ${8^x}/{2^y}$ gives

$${(2^3)^x}/{2^y}$$

which can be rewritten

$${2^3x}/{2^y}$$

Since the numerator and denominator of have a common base, this expression can be rewritten as $2^(3x−y)$. In the question, it states that $3x − y = 12$, so one can substitute 12 for the exponent, $3x − y$, which means that

$${8^x}/{2^y}= 2^12$$

The final answer is A.

Points A and B lie on a circle with radius 1, and arc ${AB}↖⌢$ has a length of $π/3$. What fraction of the circumference of the circle is the length of arc ${AB}↖⌢$?

ANSWER EXPLANATION: To figure out the answer to this question, you'll first need to know the formula for finding the circumference of a circle.

The circumference, $C$, of a circle is $C = 2πr$, where $r$ is the radius of the circle. For the given circle with a radius of 1, the circumference is $C = 2(π)(1)$, or $C = 2π$.

To find what fraction of the circumference the length of ${AB}↖⌢$ is, divide the length of the arc by the circumference, which gives $π/3 ÷ 2π$. This division can be represented by $π/3 * {1/2}π = 1/6$.

The fraction $1/6$ can also be rewritten as $0.166$ or $0.167$.

The final answer is $1/6$, $0.166$, or $0.167$.

$${8-i}/{3-2i}$$

If the expression above is rewritten in the form $a+bi$, where $a$ and $b$ are real numbers, what is the value of $a$? (Note: $i=√{-1}$)

ANSWER EXPLANATION: To rewrite ${8-i}/{3-2i}$ in the standard form $a + bi$, you need to multiply the numerator and denominator of ${8-i}/{3-2i}$ by the conjugate, $3 + 2i$. This equals

$$({8-i}/{3-2i})({3+2i}/{3+2i})={24+16i-3+(-i)(2i)}/{(3^2)-(2i)^2}$$

Since $i^2=-1$, this last fraction can be reduced simplified to

$$ {24+16i-3i+2}/{9-(-4)}={26+13i}/{13}$$

which simplifies further to $2 + i$. Therefore, when ${8-i}/{3-2i}$ is rewritten in the standard form a + bi, the value of a is 2.

In triangle $ABC$, the measure of $∠B$ is 90°, $BC=16$, and $AC$=20. Triangle $DEF$ is similar to triangle $ABC$, where vertices $D$, $E$, and $F$ correspond to vertices $A$, $B$, and $C$, respectively, and each side of triangle $DEF$ is $1/3$ the length of the corresponding side of triangle $ABC$. What is the value of $sinF$?

ANSWER EXPLANATION: Triangle ABC is a right triangle with its right angle at B. Therefore, $\ov {AC}$ is the hypotenuse of right triangle ABC, and $\ov {AB}$ and $\ov {BC}$ are the legs of right triangle ABC. According to the Pythagorean theorem,

$$AB =√{20^2-16^2}=√{400-256}=√{144}=12$$

Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of $\angle ∠ {F}$ equals the measure of $\angle ∠ {C}$. Therefore, $sin F = sin C$. From the side lengths of triangle ABC,

$$sinF ={\opposite \side}/{\hypotenuse}={AB}/{AC}={12}/{20}={3}/{5}$$

Therefore, $sinF ={3}/{5}$.

The final answer is ${3}/{5}$ or 0.6.

Calculator-Allowed SAT Math Questions

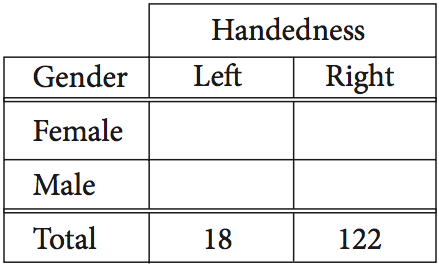
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. if there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)

A) 0.410 B) 0.357 C) 0.333 D) 0.250

ANSWER EXPLANATION: In order to solve this problem, you should create two equations using two variables ($x$ and $y$) and the information you're given. Let $x$ be the number of left-handed female students and let $y$ be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be $5x$ and the number of right-handed male students will be $9y$. Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:

$$x + y = 18$$

$$5x + 9y = 122$$

When you solve this system of equations, you get $x = 10$ and $y = 8$. Thus, 5*10, or 50, of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is ${50}/{122}$, which to the nearest thousandth is 0.410.

Questions 8 & 9

Use the following information for both question 7 and question 8.

If shoppers enter a store at an average rate of $r$ shoppers per minute and each stays in the store for average time of $T$ minutes, the average number of shoppers in the store, $N$, at any one time is given by the formula $N=rT$. This relationship is known as Little's law.

The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little's law to estimate that there are 45 shoppers in the store at any time.

Little's law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?

ANSWER EXPLANATION: Since the question states that Little's law can be applied to any single part of the store (for example, just the checkout line), then the average number of shoppers, $N$, in the checkout line at any time is $N = rT$, where $r$ is the number of shoppers entering the checkout line per minute and $T$ is the average number of minutes each shopper spends in the checkout line.

Since 84 shoppers per hour make a purchase, 84 shoppers per hour enter the checkout line. However, this needs to be converted to the number of shoppers per minute (in order to be used with $T = 5$). Since there are 60 minutes in one hour, the rate is ${84 \shoppers \per \hour}/{60 \minutes} = 1.4$ shoppers per minute. Using the given formula with $r = 1.4$ and $T = 5$ yields

$$N = rt = (1.4)(5) = 7$$

Therefore, the average number of shoppers, $N$, in the checkout line at any time during business hours is 7.

The final answer is 7.

The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)

ANSWER EXPLANATION: According to the original information given, the estimated average number of shoppers in the original store at any time (N) is 45. In the question, it states that, in the new store, the manager estimates that an average of 90 shoppers per hour (60 minutes) enter the store, which is equivalent to 1.5 shoppers per minute (r). The manager also estimates that each shopper stays in the store for an average of 12 minutes (T). Thus, by Little's law, there are, on average, $N = rT = (1.5)(12) = 18$ shoppers in the new store at any time. This is

$${45-18}/{45} * 100 = 60$$

percent less than the average number of shoppers in the original store at any time.

The final answer is 60.

Question 10

In the $xy$-plane, the point $(p,r)$ lies on the line with equation $y=x+b$, where $b$ is a constant. The point with coordinates $(2p, 5r)$ lies on the line with equation $y=2x+b$. If $p≠0$, what is the value of $r/p$?

ANSWER EXPLANATION: Since the point $(p,r)$ lies on the line with equation $y=x+b$, the point must satisfy the equation. Substituting $p$ for $x$ and $r$ for $y$ in the equation $y=x+b$ gives $r=p+b$, or $\bi b$ = $\bi r-\bi p$.

Similarly, since the point $(2p,5r)$ lies on the line with the equation $y=2x+b$, the point must satisfy the equation. Substituting $2p$ for $x$ and $5r$ for $y$ in the equation $y=2x+b$ gives:

$5r=2(2p)+b$

$\bi b$ = $\bo 5 \bi r-\bo 4\bi p$.

Next, we can set the two equations equal to $b$ equal to each other and simplify:

$b=r-p=5r-4p$

Finally, to find $r/p$, we need to divide both sides of the equation by $p$ and by $4$:

The correct answer is B , $3/4$.

If you picked choices A and D, you may have incorrectly formed your answer out of the coefficients in the point $(2p, 5r)$. If you picked Choice C, you may have confused $r$ and $p$.

Note that while this is in the calculator section of the SAT, you absolutely do not need your calculator to solve it!

Question 11

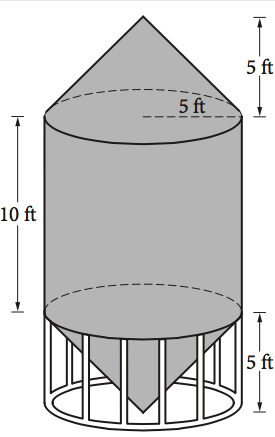
A) 261.8 B) 785.4 C) 916.3 D) 1047.2

ANSWER EXPLANATION: The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed (a cylinder and two cones). The silo is made up of a cylinder (with height 10 feet and base radius 5 feet) and two cones (each with height 5 ft and base radius 5 ft). The formulas given at the beginning of the SAT Math section:

Volume of a Cone

$$V={1}/{3}πr^2h$$

Volume of a Cylinder

$$V=πr^2h$$

can be used to determine the total volume of the silo. Since the two cones have identical dimensions, the total volume, in cubic feet, of the silo is given by

$$V_{silo}=π(5^2)(10)+(2)({1}/{3})π(5^2)(5)=({4}/{3})(250)π$$

which is approximately equal to 1,047.2 cubic feet.

Question 12

If $x$ is the average (arithmetic mean) of $m$ and $9$, $y$ is the average of $2m$ and $15$, and $z$ is the average of $3m$ and $18$, what is the average of $x$, $y$, and $z$ in terms of $m$?

A) $m+6$ B) $m+7$ C) $2m+14$ D) $3m + 21$

ANSWER EXPLANATION: Since the average (arithmetic mean) of two numbers is equal to the sum of the two numbers divided by 2, the equations $x={m+9}/{2}$, $y={2m+15}/{2}$, $z={3m+18}/{2}$are true. The average of $x$, $y$, and $z$ is given by ${x + y + z}/{3}$. Substituting the expressions in m for each variable ($x$, $y$, $z$) gives

$$[{m+9}/{2}+{2m+15}/{2}+{3m+18}/{2}]/3$$

This fraction can be simplified to $m + 7$.

Question 13

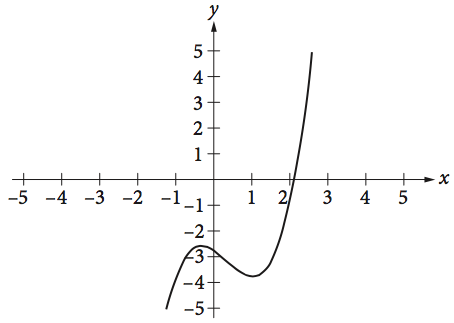
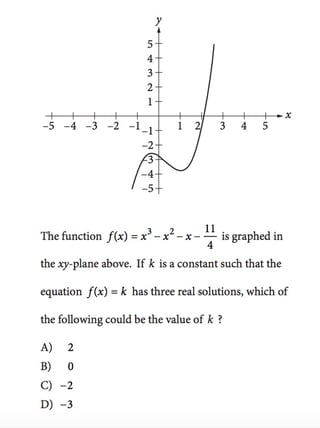
The function $f(x)=x^3-x^2-x-{11/4}$ is graphed in the $xy$-plane above. If $k$ is a constant such that the equation $f(x)=k$ has three real solutions, which of the following could be the value of $k$?

ANSWER EXPLANATION: The equation $f(x) = k$ gives the solutions to the system of equations

$$y = f(x) = x^3-x^2-x-{11}/{4}$$

A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the $xy$-plane.

The graph of $y = k$ is a horizontal line that contains the point $(0, k)$ and intersects the graph of the cubic equation three times (since it has three real solutions). Given the graph, the only horizontal line that would intersect the cubic equation three times is the line with the equation $y = −3$, or $f(x) = −3$. Therefore, $k$ is $-3$.

Question 14

$$q={1/2}nv^2$$

The dynamic pressure $q$ generated by a fluid moving with velocity $v$ can be found using the formula above, where $n$ is the constant density of the fluid. An aeronautical engineer users the formula to find the dynamic pressure of a fluid moving with velocity $v$ and the same fluid moving with velocity 1.5$v$. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?

ANSWER EXPLANATION: To solve this problem, you need to set up to equations with variables. Let $q_1$ be the dynamic pressure of the slower fluid moving with velocity $v_1$, and let $q_2$ be the dynamic pressure of the faster fluid moving with velocity $v_2$. Then

$$v_2 =1.5v_1$$

Given the equation $q = {1}/{2}nv^2$, substituting the dynamic pressure and velocity of the faster fluid gives $q_2 = {1}/{2}n(v_2)^2$. Since $v_2 =1.5v_1$, the expression $1.5v_1$ can be substituted for $v_2$ in this equation, giving $q_2 = {1}/{2}n(1.5v_1)^2$. By squaring $1.5$, you can rewrite the previous equation as

$$q_2 = (2.25)({1}/{2})n(v_1)^2 = (2.25)q_1$$

Therefore, the ratio of the dynamic pressure of the faster fluid is

$${q2}/{q1} = {2.25 q_1}/{q_1}= 2.25$$

The final answer is 2.25 or 9/4.

Question 15

For a polynomial $p(x)$, the value of $p(3)$ is $-2$. Which of the following must be true about $p(x)$?

A) $x-5$ is a factor of $p(x)$. B) $x-2$ is a factor of $p(x)$. C) $x+2$ is a factor of $p(x)$. D) The remainder when $p(x)$ is divided by $x-3$ is $-2$.

ANSWER EXPLANATION: If the polynomial $p(x)$ is divided by a polynomial of the form $x+k$ (which accounts for all of the possible answer choices in this question), the result can be written as

$${p(x)}/{x+k}=q(x)+{r}/{x+k}$$

where $q(x)$ is a polynomial and $r$ is the remainder. Since $x + k$ is a degree-1 polynomial (meaning it only includes $x^1$ and no higher exponents), the remainder is a real number.

Therefore, $p(x)$ can be rewritten as $p(x) = (x + k)q(x) + r$, where $r$ is a real number.

The question states that $p(3) = -2$, so it must be true that

$$-2 = p(3) = (3 + k)q(3) + r$$

Now we can plug in all the possible answers. If the answer is A, B, or C, $r$ will be $0$, while if the answer is D, $r$ will be $-2$.

A. $-2 = p(3) = (3 + (-5))q(3) + 0$ $-2=(3-5)q(3)$ $-2=(-2)q(3)$

This could be true, but only if $q(3)=1$

B. $-2 = p(3) = (3 + (-2))q(3) + 0$ $-2 = (3-2)q(3)$ $-2 = (-1)q(3)$

This could be true, but only if $q(3)=2$

C. $-2 = p(3) = (3 + 2)q(3) + 0$ $-2 = (5)q(3)$

This could be true, but only if $q(3)={-2}/{5}$

D. $-2 = p(3) = (3 + (-3))q(3) + (-2)$ $-2 = (3 - 3)q(3) + (-2)$ $-2 = (0)q(3) + (-2)$

This will always be true no matter what $q(3)$ is.

Of the answer choices, the only one that must be true about $p(x)$ is D, that the remainder when $p(x)$ is divided by $x-3$ is -2.

Want to improve your SAT score by 160 points? We've written a guide about the top 5 strategies you must be using to have a shot at improving your score. Download it for free now:

You deserve all the naps after running through those questions.

What Do the Hardest SAT Math Questions Have in Common?

It's important to understand what makes these hard questions "hard." By doing so, you'll be able to both understand and solve similar questions when you see them on test day, as well as have a better strategy for identifying and correcting your previous SAT math errors.

In this section, we'll look at what these questions have in common and give examples of each type. Some of the reasons why the hardest math questions are the hardest math questions is because they:

#1: Test Several Mathematical Concepts at Once

Here, we must deal with imaginary numbers and fractions all at once.

Secret to success: Think of what applicable math you could use to solve the problem, do one step at a time, and try each technique until you find one that works!

#2: Involve a Lot of Steps

Remember: the more steps you need to take, the easier to mess up somewhere along the line!

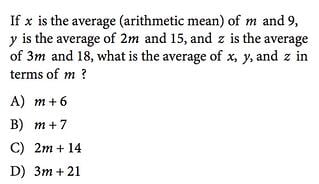
We must solve this problem in steps (doing several averages) to unlock the rest of the answers in a domino effect. This can get confusing, especially if you're stressed or running out of time.

Secret to success: Take it slow, take it step by step, and double-check your work so you don't make mistakes!

#3: Test Concepts That You Have Limited Familiarity With

For example, many students are less familiar with functions than they are with fractions and percentages, so most function questions are considered "high difficulty" problems.

If you don't know your way around functions , this would be a tricky problem.

Secret to success: Review math concepts that you don't have as much familiarity with such as functions . We suggest using our great free SAT Math review guides .

#4: Are Worded in Unusual or Convoluted Ways

It can be difficult to figure out exactly what some questions are asking , much less figure out how to solve them. This is especially true when the question is located at the end of the section, and you are running out of time.

Because this question provides so much information without a diagram, it can be difficult to puzzle through in the limited time allowed.

Secret to success: Take your time, analyze what is being asked of you, and draw a diagram if it's helpful to you.

#5: Use Many Different Variables

With so many different variables in play, it is quite easy to get confused.

Secret to success: Take your time, analyze what is being asked of you, and consider if plugging in numbers is a good strategy to solve the problem (it wouldn't be for the question above, but would be for many other SAT variable questions).

The Take-Aways

The SAT is a marathon and the better prepared you are for it, the better you'll feel on test day. Knowing how to handle the hardest questions the test can throw at you will make taking the real SAT seem a lot less daunting.

If you felt that these questions were easy, make sure not underestimate the effect of adrenaline and fatigue on your ability to solve problems. As you continue to study, always adhere to the proper timing guidelines and try to take full tests whenever possible. This is the best way to recreate the actual testing environment so that you can prepare for the real deal.

If you felt these questions were challenging, be sure to strengthen your math knowledge by checking out our individual math topic guides for the SAT . There, you'll see more detailed explanations of the topics in question as well as more detailed answer breakdowns.

What's Next?

Felt that these questions were harder than you were expecting? Take a look at all the topics covered in the SAT math section and then note which sections were particular difficulty for you. Next, take a gander at our individual math guides to help you shore up any of those weak areas.

Running out of time on the SAT math section? Our guide will help you beat the clock and maximize your score .

Aiming for a perfect score? Check out our guide on how to get a perfect 800 on the SAT math section , written by a perfect-scorer.

Want to improve your SAT score by 160 points?

Check out our best-in-class online SAT prep classes . We guarantee your money back if you don't improve your SAT score by 160 points or more.

Our classes are entirely online, and they're taught by SAT experts . If you liked this article, you'll love our classes. Along with expert-led classes, you'll get personalized homework with thousands of practice problems organized by individual skills so you learn most effectively. We'll also give you a step-by-step, custom program to follow so you'll never be confused about what to study next.

Try it risk-free today:

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Student and Parent Forum

Our new student and parent forum, at ExpertHub.PrepScholar.com , allow you to interact with your peers and the PrepScholar staff. See how other students and parents are navigating high school, college, and the college admissions process. Ask questions; get answers.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents