how can you solve real world problems using the triangle proportionality theorems

Triangle Proportionality Theorem: Statement, Proof, Examples

What is the triangle proportionality theorem, proof of the triangle proportionality theorem, converse of the triangle proportionality theorem, solved examples on triangle proportionality theorem, practice problems on triangle proportionality theorem, frequently asked questions on triangle proportionality theorem.

Triangle proportionality theorem is also known as “basic proportionality theorem” or “Thales theorem,” or “side-splitter theorem.” It was proposed by a famous Greek mathematician Thales. 

The theorem is helpful in understanding the concept of similar triangles.

The triangle proportionality theorem uses a line drawn parallel to one side of a triangle to determine the proportions of the other two sides. 

If you draw a line parallel to any one side of a triangle that intersects the other two sides of the triangle in two distinct points, then the line divides the other two sides in the same ratio.

Triangle Proportionality Theorem: Statement

The triangle proportionality theorem states that if a line parallel to one side of a triangle intersects the other two sides at different points, then it divides the remaining two sides proportionally. 

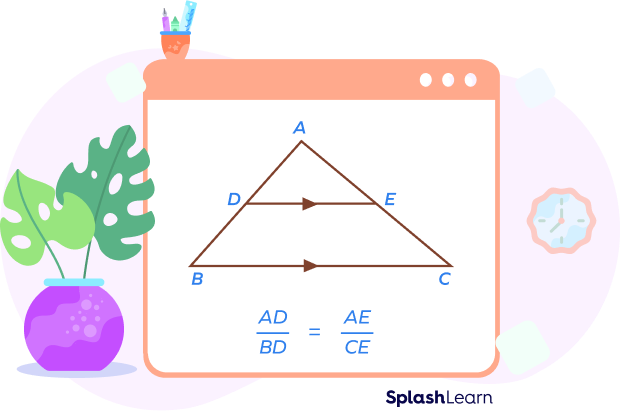
Here, the line DE is parallel to the side BC. It intersects sides AB and AC at two distinct points, D and E. 

According to the triangle proportionality theorem, a ratio of AD to DB is equal to the ratio of CE to AE.

Hence, $\frac{AD}{BD} = \frac{AE}{CE}$

Related Worksheets

Given: In $\Delta ABC$, the line segment DE is drawn parallel to the side BC.

To prove: $\frac{AD}{BD} = \frac{AE}{CE}$

Construction: Join the vertex B to the point E. Join the vertex C to the point D. 

Draw $EG\; \bot \;AB$ and $DF\; \bot \;AC$ as shown in the given figure.

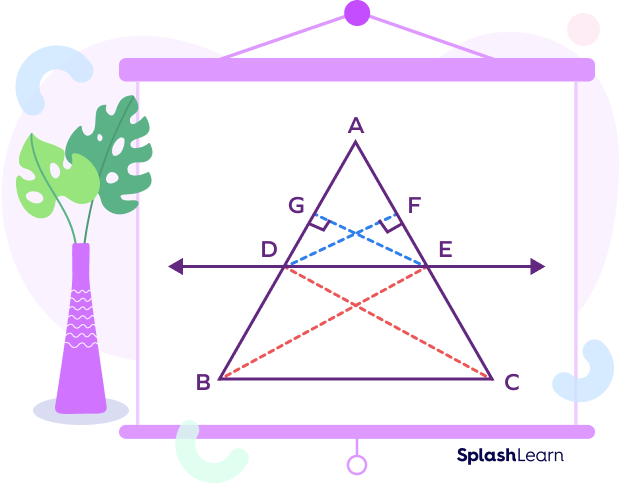
In $\Delta ADE$ and $\Delta BDE$,

$\frac{(Area\; of\;  \Delta ADE)}{(Area\; of\;  \Delta BDE)} = \frac{\frac{1}{2} \times AD \times EG}{\frac{1}{2} \times BD \times EG}$ (Both the triangles have the same height EG.)

$\frac{(Area\; of\; \Delta ADE)}{(Area\; of\; \Delta BDE)} = \frac{AD}{BD}$ …(1)

Now In $\Delta CDE$ and  $\Delta ADE$,

$\frac{(Area\; of\; \Delta ADE)}{(Area\; of\; \Delta CDE)} = \frac{\frac{1}{2} \times AE \times DF}{\frac{1}{2} \times CE \times DF}$ (Both the triangles have the same height DF.)

$\frac{(Area\; of\; \Delta ADE)}{(Area\; of\; \Delta CDE)} = \frac{AE}{CE}$ …(2)

$\Delta BDE$ and $\Delta CDE$ are lying between the same parallel lines DE and BC.

Triangles having the same base and lying between the same parallels are equal in area.

$\therefore\; Area\; of\; \Delta BDE = Area\; of\; \Delta CDE$ 

Using this result in equation (1) and (2), we get left sides equal.

$\frac{(Area\; of\; ADE)} {(Area\; of\; BDE)} = \frac{(Area\; of\; ADE)} {(Area\; of\; CDE)}$

Thus, from equation (1) and (2), we get

$\frac{AD}{BD} = \frac{AE}{CE}$

Hence, proved.

If a line segment divides any two sides of a triangle proportionally (in the same ratio), then the line is parallel to the third side of the triangle.

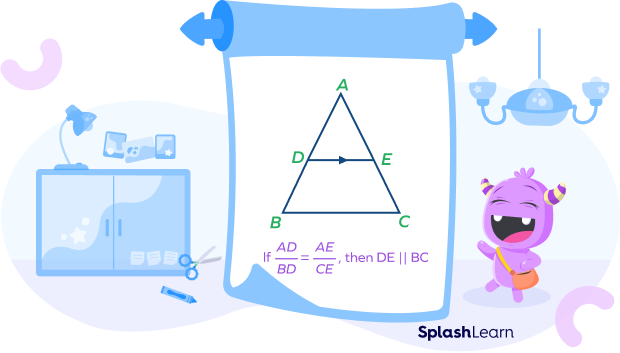
Here, if the line segment DE divides sides AB and AC in equal proportion, i.e., $\frac{AD}{BD} = \frac{AE}{CE}$, then 

by the converse of the triangle proportionality theorem, we can say that the line DE must be parallel to BC or $DE\; || \;BC$.

Proof of the Converse of the Triangle Proportionality Theorem

Given: In ΔABC, the line segment DE divides the sides AB and AC in equal proportion. ADBD=AECE.

To prove: DE || BC

Construction: Let us assume DE is not parallel to BC. So draw another line DF, which is parallel to BC.

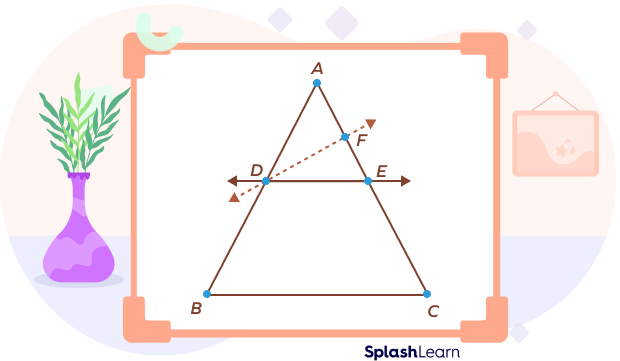
Now, we have to show that points E and F are identical or that DE and DF represent the same lines.

According to the Basic Proportionality theorem, 

$\frac{AD}{BD} = \frac{AF}{CF}$ … (1)

Also, $\frac{AD}{BD} = \frac{AE}{CE}$ (given) … (2)

From equation (1) and (2), we get

$\frac{AF}{CF} = \frac{AE}{CE}$

Adding 1 on both sides, we get

$\frac{AF}{CF} + 1 = \frac{AE}{CE} + 1$

$\frac{AF + CF}{CF} = \frac{AE + CE}{CE}$

$\frac{AC}{CF} = \frac{AC}{CE}$

$\therefore\; CF = CE$

Therefore, from the above statement, we can conclude that the points E and F are the same points. So, DE and DF represent the same lines.

Hence, $DE\; || \;BC$. 

Thus, it proves the converse of the basic proportionality theorem.

Facts about Triangle Proportionality Theorem

• The well-known Greek mathematician Thales proposed the basic proportionality theorem, which is why it is also known as the Thales theorem.
• In daily life, the triangle proportionality theorem has applications in the construction of houses, bridges, towers, etc.

In this article, we have learned about the triangle proportionality and converse of triangle proportionality theorem with statement, proof, applications, facts. Let’s solve a few examples.

• In the figure given below ST || QR, find the ratio PT : TR.

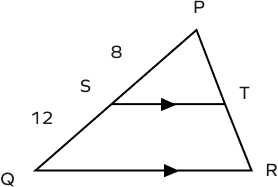
$PS = 8,\; SQ = 12$

$ST\; || \;QR$

According to the triangle proportionality theorem, the ratio of PS to SQ is equal to the ratio of PT to TR.

$\frac{PS}{SQ} = \frac{PT}{TR}$

$\frac{8}{12} = \frac{PT}{TR}$

$\Rightarrow \frac{2}{3} = \frac{PT}{TR}$

$\Rightarrow PT\;:\;TR =2\;:\;3$

• Check whether the line PQ is parallel to the BC or not.

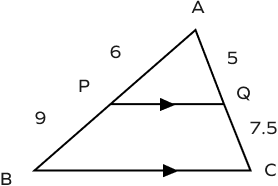
$AP = 6,\; BP = 9,\; AQ = 5,$ and $CQ = 7.5$

$\frac{AP}{BP} = \frac{6}{9} = \frac{2}{3}$

$\frac{AQ}{CQ} = \frac{5}{7.5} = \frac{2}{3}$

Since, $\frac{AP}{BP} = \frac{AQ}{CQ}$

Hence, by the converse of triangle proportionality theorem, the line PQ is parallel to the BC.

• In the figure given below $DE\; || \;BC$ , find the value of “x.”

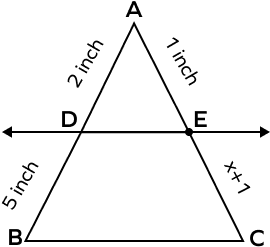
Given, $DE\; || \;BC,\; AD = 2$ in, $BD = 5$ in, $AE = 1$ in, and $CE = x + 1$

According to the triangle proportionality theorem, 

$\Rightarrow \frac{2}{5} = \frac{1}{x + 1}$

$\Rightarrow 2x + 2 = 5$

$\Rightarrow 2x = 3$

$\Rightarrow x = \frac{3}{2} = 1.5$ in

Hence, the value of x is 1.5 inches.

• In the figure given below, $PQ\; || \;BC$ , find the value of x.

Given, $PQ\; || \;BC,\; AP = 2,\; BP = x \;−\; 1,\; AQ = 3,$ and $CQ = x + 1$

$\frac{AP}{BP} = \frac{AQ}{CQ}$

$\Rightarrow \frac{2}{x \;-\;1} = \frac{3}{x\;+\;1}$

$\Rightarrow 2(x\;+\;1) = 3(x\;-\;1)$

$\Rightarrow 2x\;+\;2 = 3x\;-\;3$

$3x\;-\;2x = 3+2$

Hence, the value of x is 5.

Attend this quiz & Test your knowledge

In the figure below $DE\; || \;BC$. By the triangle proportionality theorem, we can write $\frac{AE}{EC}=$ ?

Which of the following is correct for the figure below?

Which of the following is the triangle proportionality theorem’s condition such that the equation $\frac{AP}{PB} = \frac{AQ}{QC}$ becomes true?

What are the uses of the triangle proportionality theorem?

In daily life, it is used in the construction of houses, bridges, towers, etc., where precision and proportions are important.

What is the other name of the triangle proportionality theorem?

The triangle proportionality theorem is also known as the Thales theorem or basic proportionality theorem.

What is the formula of the triangle proportionality theorem?

In any $\Delta ABC$ where line segment DE is drawn parallel to the side BC of $\Delta ABC,\; \frac{AD}{BD} = \frac{AE}{CE}$.

What is the converse of the triangle proportionality theorem?

If a line segment divides any two sides of a triangle in equal proportion, then the line is parallel to the third side of the triangle.

What is the basic proportionality theorem?

The basic proportionality theorem (B.P.T.) states that if a line is drawn parallel to one side of a triangle and is cutting the other two sides, then it divides the other two sides in equal proportion.

It is also known as the Thales theorem.

RELATED POSTS

• Corresponding Angles – Definition, Theorem, Types, Examples
• Lattice Multiplication – Definition, Method, Examples, Facts, FAQs
• X Intercept – Definition, Formula, Graph, Examples
• Negative Slope: Definition, Graph, Solved Examples, Facts
• Comparing and Ordering Numbers: Definition with Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free