how to problem solve in math

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Math Problems

Last Updated: May 16, 2023 Fact Checked

This article was co-authored by Daron Cam . Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary's College. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 588,717 times.

Although math problems may be solved in different ways, there is a general method of visualizing, approaching and solving math problems that may help you to solve even the most difficult problem. Using these strategies can also help you to improve your math skills overall. Keep reading to learn about some of these math problem solving strategies.

Understanding the Problem

• Draw a Venn diagram. A Venn diagram shows the relationships among the numbers in your problem. Venn diagrams can be especially helpful with word problems.
• Draw a graph or chart.
• Arrange the components of the problem on a line.
• Draw simple shapes to represent more complex features of the problem.

Developing a Plan

Solving the Problem

Expert Q&A

• Seek help from your teacher or a math tutor if you get stuck or if you have tried multiple strategies without success. Your teacher or a math tutor may be able to easily identify what is wrong and help you to understand how to correct it. Thanks Helpful 1 Not Helpful 1
• Keep practicing sums and diagrams. Go through the concept your class notes regularly. Write down your understanding of the methods and utilize it. Thanks Helpful 2 Not Helpful 0

You Might Also Like

• ↑ Daron Cam. Math Tutor. Expert Interview. 29 May 2020.
• ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
• ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
• ↑ https://math.berkeley.edu/~gmelvin/polya.pdf

About This Article

To solve a math problem, try rewriting the problem in your own words so it's easier to solve. You can also make a drawing of the problem to help you figure out what it's asking you to do. If you're still completely stuck, try solving a different problem that's similar but easier and then use the same steps to solve the harder problem. Even if you can't figure out how to solve it, try to make an educated guess instead of leaving the question blank. To learn how to come up with a solid plan to use to help you solve a math problem, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Thakgalo Mokalapa

Feb 16, 2018

Did this article help you?

Offor Chukwuemeka

May 17, 2018

Jan 21, 2017

May 3, 2018

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Don’t miss out! Sign up for

wikiHow’s newsletter

Problem Solving in Mathematics

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.

Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures

Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.

Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.

Look for Clue Words

Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.

Common clue words for addition  problems:

Common clue words for  subtraction  problems:

• How much more

Common clue words for multiplication problems:

Common clue words for division problems:

Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.

Read the Problem Carefully

This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:

• Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
• What did you need to do in that instance?
• What facts are you given about this problem?
• What facts do you still need to find out about this problem?

Develop a Plan and Review Your Work

Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:

• Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
• If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.

If it seems like you’ve solved the problem, ask yourself the following:

• Does your solution seem probable?
• Does it answer the initial question?
• Did you answer using the language in the question?
• Did you answer using the same units?

If you feel confident that the answer is “yes” to all questions, consider your problem solved.

Tips and Hints

Some key questions to consider as you approach the problem may be:

• What are the keywords in the problem?
• Do I need a data visual, such as a diagram, list, table, chart, or graph?
• Is there a formula or equation that I'll need? If so, which one?
• Will I need to use a calculator? Is there a pattern I can use or follow?

Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.

• 2nd Grade Math Word Problems
• The Horse Problem: A Math Challenge
• 2020-21 Common Application Essay Option 4—Solving a Problem
• How to Use Math Journals in Class
• The Frayer Model for Math
• Algorithms in Mathematics and Beyond
• "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
• Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
• Critical Thinking Definition, Skills, and Examples
• Graphic Organizers in Math
• College Interview Tips: "Tell Me About a Challenge You Overcame"
• Christmas Word Problem Worksheets
• Solving Problems Involving Distance, Rate, and Time
• Innovative Ways to Teach Math
• Study Tips for Math Homework and Math Tests
• 7 Steps to Math Success

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

A Guide to Problem Solving

When confronted with a problem, in which the solution is not clear, you need to be a skilled problem-solver to know how to proceed. When you look at STEP problems for the first time, it may seem like this problem-solving skill is out of your reach, but like any skill, you can improve your problem-solving with practice. How do I become a better problem-solver? First and foremost, the best way to become better at problem-solving is to try solving lots of problems! If you are preparing for STEP, it makes sense that some of these problems should be STEP questions, but to start off with it's worth spending time looking at problems from other sources. This collection of NRICH problems  is designed for younger students, but it's very worthwhile having a go at a few to practise the problem-solving technique in a context where the mathematics should be straightforward to you. Then as you become a more confident problem-solver you can try more past STEP questions. One student who worked with NRICH said: "From personal experience, I was disastrous at STEP to start with. Yet as I persisted with it for a long time it eventually started to click - 'it' referring to being able to solve problems much more easily. This happens because your brain starts to recognise that problems fall into various categories and you subconsciously remember successes and pitfalls of previous 'similar' problems." A Problem-solving Heuristic for STEP Below you will find some questions you can ask yourself while you are solving a problem. The questions are divided into four phases, based loosely on those found in George Pólya's 1945 book "How to Solve It". Understanding the problem

• What area of mathematics is this?
• What exactly am I being asked to do?
• What do I know?
• What do I need to find out?
• What am I uncertain about?
• Can I put the problem into my own words?

Devising a plan

• Work out the first few steps before leaping in!
• Have I seen something like it before?
• Is there a diagram I could draw to help?
• Is there another way of representing?
• Would it be useful to try some suitable numbers first?
• Is there some notation that will help?

Carrying out the plan STUCK!

• Try special cases or a simpler problem
• Work backwards
• Guess and check
• Be systematic
• Work towards subgoals
• Imagine your way through the problem
• Has the plan failed? Know when it's time to abandon the plan and move on.

Looking back

• Have I answered the question?
• Sanity check for sense and consistency
• Check the problem has been fully solved
• Read through the solution and check the flow of the logic.

Throughout the problem solving process it's important to keep an eye on how you're feeling and making sure you're in control:

• Am I getting stressed?
• Is my plan working?
• Am I spending too long on this?
• Could I move on to something else and come back to this later?
• Am I focussing on the problem?
• Is my work becoming chaotic, do I need to slow down, go back and tidy up?
• Do I need to STOP, PEN DOWN, THINK?

Finally, don't forget that STEP questions are designed to take at least 30-45 minutes to solve, and to start with they will take you longer than that. As a last resort, read the solution, but not until you have spent a long time just thinking about the problem, making notes, trying things out and looking at resources that can help you. If you do end up reading the solution, then come back to the same problem a few days or weeks later to have another go at it.

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

• What do you know?
• What do you need to know?
• Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

• Identify - What is the question?
• Plan - What strategy will I use to solve the problem?
• Solve - Carry out your plan.
• Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square.   18 + 2 = 20   If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square   61 + (3 x 7) = 82   If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Appendix A: Applications

Apply a problem-solving strategy to basic word problems, learning outcomes.

• Practice mindfulness with your attitude about word problems
• Apply a general problem-solving strategy to solve word problems

 Approach Word Problems with a Positive Attitude

The world is full of word problems. How much money do I need to fill the car with gas? How much should I tip the server at a restaurant? How many socks should I pack for vacation? How big a turkey do I need to buy for Thanksgiving dinner, and what time do I need to put it in the oven? If my sister and I buy our mother a present, how much will each of us pay?

Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student in the cartoon below?

Negative thoughts about word problems can be barriers to success.

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.

Start with a fresh slate and begin to think positive thoughts like the student in the cartoon below. Read the positive thoughts and say them out loud.

When it comes to word problems, a positive attitude is a big step toward success.

If we take control and believe we can be successful, we will be able to master word problems.

Think of something that you can do now but couldn’t do three years ago. Whether it’s driving a car, snowboarding, cooking a gourmet meal, or speaking a new language, you have been able to learn and master a new skill. Word problems are no different. Even if you have struggled with word problems in the past, you have acquired many new math skills that will help you succeed now!

Use a Problem-Solving Strategy for Word Problems

In earlier chapters, you translated word phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. Since then you’ve increased your math vocabulary as you learned about more algebraic procedures, and you’ve had more practice translating from words into algebra.

You have also translated word sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. You had to restate the situation in one sentence, assign a variable, and then write an equation to solve. This method works as long as the situation is familiar to you and the math is not too complicated.

Now we’ll develop a strategy you can use to solve any word problem. This strategy will help you become successful with word problems. We’ll demonstrate the strategy as we solve the following problem.

Pete bought a shirt on sale for $[latex]18[/latex], which is one-half the original price. What was the original price of the shirt?

Solution: Step 1. Read the problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the Internet.

• In this problem, do you understand what is being discussed? Do you understand every word?

Step 2. Identify what you are looking for. It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!

• In this problem, the words “what was the original price of the shirt” tell you what you are looking for: the original price of the shirt.

Step 3. Name what you are looking for. Choose a variable to represent that quantity. You can use any letter for the variable, but it may help to choose one that helps you remember what it represents.

• Let [latex]p=[/latex] the original price of the shirt

Step 4. Translate into an equation. It may help to first restate the problem in one sentence, with all the important information. Then translate the sentence into an equation.

Step 6. Check the answer in the problem and make sure it makes sense.

• We found that [latex]p=36[/latex], which means the original price was [latex]\text{\$36}[/latex]. Does [latex]\text{\$36}[/latex] make sense in the problem? Yes, because [latex]18[/latex] is one-half of [latex]36[/latex], and the shirt was on sale at half the original price.

Step 7. Answer the question with a complete sentence.

• The problem asked “What was the original price of the shirt?” The answer to the question is: “The original price of the shirt was [latex]\text{\$36}[/latex].”

If this were a homework exercise, our work might look like this:

We list the steps we took to solve the previous example.

Problem-Solving Strategy

• Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the internet.
• Identify what you are looking for.
• Name what you are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to first restate the problem in one sentence before translating.
• Solve the equation using good algebra techniques.
• Check the answer in the problem. Make sure it makes sense.
• Answer the question with a complete sentence.

For a review of how to translate algebraic statements into words, watch the following video.

Let’s use this approach with another example.

Yash brought apples and bananas to a picnic. The number of apples was three more than twice the number of bananas. Yash brought [latex]11[/latex] apples to the picnic. How many bananas did he bring?

In the next example, we will apply our Problem-Solving Strategy to applications of percent.

Nga’s car insurance premium increased by [latex]\text{\$60}[/latex], which was [latex]\text{8%}[/latex] of the original cost. What was the original cost of the premium?

• Write Algebraic Expressions from Statements: Form ax+b and a(x+b). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/Hub7ku7UHT4 . License : CC BY: Attribution
• Question ID 142694, 142722, 142735, 142761. Authored by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License, CC-BY + GPL
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

• Prodigy Math
• Prodigy English

From our blog

• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Game Portal

How to Solve Math Problems Faster: 15 Techniques to Show Students

Written by Marcus Guido

• Teaching Strategies

“Test time. No calculators.”

You’ll intimidate many students by saying this, but teaching techniques to solve math problems with ease and speed can make it less daunting.

This can also  make math more rewarding . Instead of relying on calculators, students learn strategies that can improve their concentration and estimation skills while building number sense. And, while there are educators who  oppose math “tricks”  for valid reasons, proponents point to benefits such as increased confidence to handle difficult problems.

Here are 15 techniques to show students,  helping them solve math problems faster:

Addition and Subtraction

1. two-step addition.

Many students struggle when learning to add integers of three digits or higher together, but changing the process’s steps can make it easier.

The first step is to  add what’s easy.  The second step is to  add the rest.

Let’s say students must find the sum of 393 and 89. They should quickly see that adding 7 onto 393 will equal 400 — an easier number to work with. To balance the equation, they can then subtract 7 from 89.

Broken down, the process is:

• (393 + 7) + (89 – 7)

With this fast technique, big numbers won’t look as scary now.

2. Two-Step Subtraction

There’s a similar method for subtraction.

Remove what’s easy. Then remove what’s left.

Suppose students must find the difference of 567 and 153. Most will feel that 500 is a simpler number than 567. So, they just have to take away 67 from the minuend — 567 — and the subtrahend — 153 — before solving the equation.

Here’s the process:

• (567 – 67) – (153 – 67)

Instead of two complex numbers, students will only have to tackle one.

3. Subtracting from 1,000

You can  give students confidence  to handle four-digit integers with this fast technique.

To subtract a number from 1,000, subtract that number’s first two digits from 9. Then, subtract the final digit from 10.

Let’s say students must solve 1,000 – 438.  Here are the steps:

This also applies to 10,000, 100,000 and other integers that follow this pattern.

Multiplication and Division

4. doubling and halving.

When students have to multiply two integers, they can speed up the process when one is an even number. They just need to  halve the even number and double the other number.

Students can stop the process when they can no longer halve the even integer, or when the equation becomes manageable.

Using 33 x 48 as an example,  here’s the process:

The only prerequisite is understanding the 2 times table.

5. Multiplying by Powers of 2

This tactic is a speedy variation of doubling and halving.

It simplifies multiplication if a number in the equation is a power of 2, meaning it works for 2, 4, 8, 16 and so on.

Here’s what to do:  For each power of 2 that makes up that number, double the other number.

For example, 9 x 16 is the same thing as 9 x (2 x 2 x 2 x 2) or 9 x 24. Students can therefore double 9 four times to reach the answer:

Unlike doubling and halving, this technique demands an understanding of exponents along with a strong command of the 2 times table.

6. Multiplying by 9

For most students, multiplying by 9 — or 99, 999 and any number that follows this pattern — is difficult compared with multiplying by a power of 10.

But there’s an easy tactic to solve this issue, and  it has two parts.

First, students round up the 9  to 10. Second, after solving the new equation, they subtract the number they just multiplied by 10 from the answer.

For example, 67 x 9 will lead to the same answer as 67 x 10 – 67. Following the order of operations will give a result of 603. Similarly, 67 x 99 is the same as 67 x 100 – 67.

Despite more steps, altering the equation this way is usually faster.

7. Multiplying by 11

There’s an easier way for multiplying two-digit integers by 11.

Let’s say students must find the product of 11 x 34.

The idea is to put a space between the digits, making it 3_4. Then, add the two digits together and put the sum in the space.

The answer is 374.

What happens if the sum is two digits? Students would put the second digit in the space and add 1 to the digit to the left of the space.  For example:

It’s multiplication without having to multiply.

8. Multiplying Even Numbers by 5

This technique only requires basic division skills.

There are two steps,  and 5 x 6 serves as an example. First, divide the number being multiplied by 5 — which is 6 — in half. Second, add 0 to the right of number.

The result is 30, which is the correct answer.

It’s an ideal, easy technique for students mastering the 5 times table.

9. Multiplying Odd Numbers by 5

This is another time-saving tactic that works well when teaching students the 5 times table.

This one has three steps,  which 5 x 7 exemplifies.

First, subtract 1 from the number being multiplied by 5, making it an even number. Second, cut that number in half — from 6 to 3 in this instance. Third, add 5 to the right of the number.

The answer is 35.

Who needs a calculator?

10. Squaring a Two-Digit Number that Ends with 1

Squaring a high two-digit number can be tedious, but there’s a shortcut if 1 is the second digit.

There are four steps to this shortcut,  which 812 exemplifies:

• Subtract 1 from the integer: 81 – 1 = 80
• Square the integer, which is now an easier number: 80 x 80 = 6,400
• Add the integer with the resulting square twice: 6,400 + 80 + 80 = 6,560
• Add 1: 6,560 + 1 = 6,561

This work-around eliminates the difficulty surrounding the second digit, allowing students to work with multiples of 10.

11. Squaring a Two-Digit Numbers that Ends with 5

Squaring numbers ending in 5 is easier, as there are  only two parts of the process.

First, students will always make 25 the product’s last digits.

Second, to determine the product’s first digits, students must multiply the number’s first digit — 9, for example — by the integer that’s one higher — 10, in this case.

So, students would solve 952 by designating 25 as the last two digits. They would then multiply 9 x 10 to receive 90. Putting these numbers together, the  result is 9,025.

Just like that, a hard problem becomes easy multiplication for many students.

12. Calculating Percentages

Cross-multiplication is an  important skill  to develop, but there’s an easier way to calculate percentages.

For example, if students want to know what 65% of 175 is, they can multiply the numbers together and move the decimal place two digits to the left.

The result is 113.75, which is indeed the correct answer.

This shortcut is a useful timesaver on tests and quizzes.

13. Balancing Averages

To determine the average among a set of numbers, students can balance them instead of using a complex formula.

Suppose a student wants to volunteer for an average of 10 hours a week over a period of four weeks. In the first three weeks, the student worked for 10, 12 and 14 hours.

To determine the number of hours required in the fourth week, the student must  add how much he or she surpassed or missed the target average  in the other weeks:

• 14 hours – 10 hours = 4 hours
• 12 – 10 = 2
• 10 – 10 = 0
• 4 hours + 2 hours + 0 hours = 6 hours

To learn the number of hours for the final week, the student must  subtract the sum from the target average:

• 10 hours – 6 hours = 4 hours

With practice, this method may not even require pencil and paper. That’s how easy it is. 

Word Problems

14. identifying buzzwords.

Students who struggle to translate  word problems  into equations will benefit from learning how to spot buzzwords — phrases that indicate specific actions.

This isn’t a trick. It’s a tactic.

Teach students to look for these buzzwords,  and what skill they align with in most contexts:

Be sure to include buzzwords that typically appear in their textbooks (or other classroom  math books ), as well as ones you use on tests and assignments.

As a result, they should have an  easier time processing word problems .

15. Creating Sub-Questions

For complex word problems, show students how to dissect the question by answering three specific sub-questions.

Each student should ask him or herself:

• What am I looking for?  — Students should read the question over and over, looking for buzzwords and identifying important details.
• What information do I need?  — Students should determine which facts, figures and variables they need to solve the question. For example, if they determine the question is rooted in subtraction, they need the minuend and subtrahend.
• What information do I have?  — Students should be able to create the core equation using the information in the word problem, after determining which details are important.

These sub-questions help students avoid overload.

Instead of writing and analyzing each detail of the question, they’ll be able to identify key information. If you identify students who are struggling with these, you can use  peer learning  as needed.  

For more fresh approaches to teaching math in your classroom, consider treating your students to a range of  fun math activities .

Final Thoughts About these Ways to Solve Math Problems Faster

Showing these 15 techniques to students can give them the  confidence to tackle tough questions .

They’re also  mental math  exercises, helping them build skills related to focus, logic and critical thinking.

A rewarding class equals an  engaging class . That’s an easy equation to remember.

> Create or log into your teacher account on Prodigy  — a free, adaptive math game that adjusts content to accommodate player trouble spots and learning speeds. Aligned to US and Canadian curricula, it’s loved by more than 500,000 teachers and 15 million students.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Praxis Core Math

Course: praxis core math   >   unit 1.

• Algebraic properties | Lesson
• Algebraic properties | Worked example
• Solution procedures | Lesson
• Solution procedures | Worked example
• Equivalent expressions | Lesson
• Equivalent expressions | Worked example
• Creating expressions and equations | Lesson
• Creating expressions and equations | Worked example

Algebraic word problems | Lesson

• Algebraic word problems | Worked example
• Linear equations | Lesson
• Linear equations | Worked example
• Quadratic equations | Lesson
• Quadratic equations | Worked example

What are algebraic word problems?

What skills are needed.

• Translating sentences to equations
• Solving linear equations with one variable
• Evaluating algebraic expressions
• Solving problems using Venn diagrams

How do we solve algebraic word problems?

• Define a variable.
• Write an equation using the variable.
• Solve the equation.
• If the variable is not the answer to the word problem, use the variable to calculate the answer.

What's a Venn diagram?

• 7 + 10 − 13 = 4 ‍   brought both food and drinks.
• 7 − 4 = 3 ‍   brought only food.
• 10 − 4 = 6 ‍   brought only drinks.
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  
• (Choice A)   $ 4 ‍   A $ 4 ‍  
• (Choice B)   $ 5 ‍   B $ 5 ‍  
• (Choice C)   $ 9 ‍   C $ 9 ‍  
• (Choice D)   $ 14 ‍   D $ 14 ‍  
• (Choice E)   $ 20 ‍   E $ 20 ‍  
• (Choice A)   10 ‍   A 10 ‍  
• (Choice B)   12 ‍   B 12 ‍  
• (Choice C)   24 ‍   C 24 ‍  
• (Choice D)   30 ‍   D 30 ‍  
• (Choice E)   32 ‍   E 32 ‍  
• (Choice A)   4 ‍   A 4 ‍  
• (Choice B)   10 ‍   B 10 ‍  
• (Choice C)   14 ‍   C 14 ‍  
• (Choice D)   18 ‍   D 18 ‍  
• (Choice E)   22 ‍   E 22 ‍  

Things to remember

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• For a new problem, you will need to begin a new live expert session.
• You can contact support with any questions regarding your current subscription.
• You will be able to enter math problems once our session is over.
• I am only able to help with one math problem per session. Which problem would you like to work on?
• Does that make sense?
• I am currently working on this problem.
• Are you still there?
• It appears we may have a connection issue. I will end the session - please reconnect if you still need assistance.
• Let me take a look...
• Can you please send an image of the problem you are seeing in your book or homework?
• If you click on "Tap to view steps..." you will see the steps are now numbered. Which step # do you have a question on?
• Please make sure you are in the correct subject. To change subjects, please exit out of this live expert session and select the appropriate subject from the menu located in the upper left corner of the Mathway screen.
• What are you trying to do with this input?
• While we cover a very wide range of problems, we are currently unable to assist with this specific problem. I spoke with my team and we will make note of this for future training. Is there a different problem you would like further assistance with?
• Mathway currently does not support this subject. We are more than happy to answer any math specific question you may have about this problem.
• Mathway currently does not support Ask an Expert Live in Chemistry. If this is what you were looking for, please contact support.
• Mathway currently only computes linear regressions.
• We are here to assist you with your math questions. You will need to get assistance from your school if you are having problems entering the answers into your online assignment.
• Have a great day!
• Hope that helps!
• You're welcome!
• Per our terms of use, Mathway's live experts will not knowingly provide solutions to students while they are taking a test or quiz.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.6: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 132869

• Michelle Manes
• University of Hawaii

Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solve them), you learn strategies and techniques that can be useful. But no single strategy works every time.

How to Solve It

George Pólya was a great champion in the field of teaching  effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, How to Solve it . Pólya died at the age 98 in 1985. [1]

George Pólya, circa 1973

• Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 ( http://creativecommons.org/licenses/by/2.0 )], via Wikimedia Commons ↵

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

• First, you have to understand the problem.
• After understanding, then make a plan.
• Carry out the plan.
• Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:

• What if the picture was different?
• What if the numbers were simpler?
• What if I just made up some numbers?

You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.

This brings us to the most important problem solving strategy of all:

A Problem Solving Strategy: Try Something!

If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.

Note that being "good at mathematics" is not about doing things right the first time. It is about figuring things out. Practice being okay with having done something incorrectly. Try to avoid using an eraser and just lightly cross out incorrect work (do not black out the entire thing). This way if it turns out that you did something useful, you still have that work to reference! If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.

Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what was left after paying Brianna. Finally, Alex saw David and gave him 1/2 of the remaining money. Who got the most money from Alex?

Think/Pair/Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.

A Problem Solving Strategy: Draw a Picture

Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?

Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?

After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.

A Problem Solving Strategy: Make Up Numbers

Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!

Try this: Assume (that is, pretend) Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person.

Or try working backward: suppose Alex has some specific amount left at the end, say $10. Since he gave David half of what he had before seeing David, that means he had $20 before running into David. Now, work backwards and figure out how much each person got.

Watch the solution only after you tried this strategy for yourself.

If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!

(Squares on a Chess Board)

How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)

Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?

Most people want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. Instead of asking the teacher, “Is this right?”, you should be ready to justify it and say, “Here’s my answer, and here is how I got it.”

A Problem Solving Strategy: Try a Simpler Problem

Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said, “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?

The ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).

A Problem Solving Strategy: Work Systematically

If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.

For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:

A Problem Solving Strategy: Use Manipulatives to Help You Investigate

Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!

For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.

A Problem Solving Strategy: Look for and Explain Patterns

Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.

If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:

• Describe all of the patterns you see in the table. If possible, actually describe these to a friend.
• Explain and justify any of the patterns you see (if possible, actually do this with a friend). If you don't have a partner to work with, imagine they asked you, "How can you be sure the patterns will continue?"
• Expand this to find what calculation(s) you would perform to find the total number of squares on a 100 × 100 chess board.

(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)

(Broken Clock)

This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)

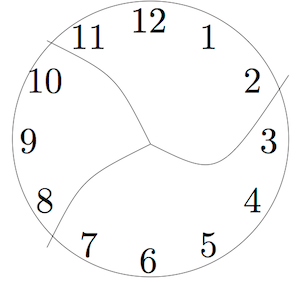
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2).

Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What progress have you made?

A Problem Solving Strategy: Find the Math, Remove the Context

Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.

In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:

• What is the sum of all the numbers on the clock’s face?
• Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
• How do I know when I am done? When should I stop looking?

Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.

A Problem Solving Strategy: Check Your Assumptions

When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?

In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:

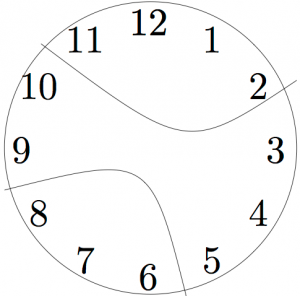
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• Our Mission

3 Simple Strategies to Improve Students’ Problem-Solving Skills

These strategies are designed to make sure students have a good understanding of problems before attempting to solve them.

Research provides a striking revelation about problem solvers. The best problem solvers approach problems much differently than novices. For instance, one meta-study showed that when experts evaluate graphs , they tend to spend less time on tasks and answer choices and more time on evaluating the axes’ labels and the relationships of variables within the graphs. In other words, they spend more time up front making sense of the data before moving to addressing the task.

While slower in solving problems, experts use this additional up-front time to more efficiently and effectively solve the problem. In one study, researchers found that experts were much better at “information extraction” or pulling the information they needed to solve the problem later in the problem than novices. This was due to the fact that they started a problem-solving process by evaluating specific assumptions within problems, asking predictive questions, and then comparing and contrasting their predictions with results. For example, expert problem solvers look at the problem context and ask a number of questions:

• What do we know about the context of the problem?
• What assumptions are underlying the problem? What’s the story here?
• What qualitative and quantitative information is pertinent?
• What might the problem context be telling us? What questions arise from the information we are reading or reviewing?
• What are important trends and patterns?

As such, expert problem solvers don’t jump to the presented problem or rush to solutions. They invest the time necessary to make sense of the problem.

Now, think about your own students: Do they immediately jump to the question, or do they take time to understand the problem context? Do they identify the relevant variables, look for patterns, and then focus on the specific tasks?

If your students are struggling to develop the habit of sense-making in a problem- solving context, this is a perfect time to incorporate a few short and sharp strategies to support them.

3 Ways to Improve Student Problem-Solving

1. Slow reveal graphs: The brilliant strategy crafted by K–8 math specialist Jenna Laib and her colleagues provides teachers with an opportunity to gradually display complex graphical information and build students’ questioning, sense-making, and evaluating predictions.

For instance, in one third-grade class, students are given a bar graph without any labels or identifying information except for bars emerging from a horizontal line on the bottom of the slide. Over time, students learn about the categories on the x -axis (types of animals) and the quantities specified on the y -axis (number of baby teeth).

The graphs and the topics range in complexity from studying the standard deviation of temperatures in Antarctica to the use of scatterplots to compare working hours across OECD (Organization for Economic Cooperation and Development) countries. The website offers a number of graphs on Google Slides and suggests questions that teachers may ask students. Furthermore, this site allows teachers to search by type of graph (e.g., scatterplot) or topic (e.g., social justice).

2. Three reads: The three-reads strategy tasks students with evaluating a word problem in three different ways . First, students encounter a problem without having access to the question—for instance, “There are 20 kangaroos on the grassland. Three hop away.” Students are expected to discuss the context of the problem without emphasizing the quantities. For instance, a student may say, “We know that there are a total amount of kangaroos, and the total shrinks because some kangaroos hop away.”

Next, students discuss the important quantities and what questions may be generated. Finally, students receive and address the actual problem. Here they can both evaluate how close their predicted questions were from the actual questions and solve the actual problem.

To get started, consider using the numberless word problems on educator Brian Bushart’s site . For those teaching high school, consider using your own textbook word problems for this activity. Simply create three slides to present to students that include context (e.g., on the first slide state, “A salesman sold twice as much pears in the afternoon as in the morning”). The second slide would include quantities (e.g., “He sold 360 kilograms of pears”), and the third slide would include the actual question (e.g., “How many kilograms did he sell in the morning and how many in the afternoon?”). One additional suggestion for teams to consider is to have students solve the questions they generated before revealing the actual question.

3. Three-Act Tasks: Originally created by Dan Meyer, three-act tasks follow the three acts of a story . The first act is typically called the “setup,” followed by the “confrontation” and then the “resolution.”

This storyline process can be used in mathematics in which students encounter a contextual problem (e.g., a pool is being filled with soda). Here students work to identify the important aspects of the problem. During the second act, students build knowledge and skill to solve the problem (e.g., they learn how to calculate the volume of particular spaces). Finally, students solve the problem and evaluate their answers (e.g., how close were their calculations to the actual specifications of the pool and the amount of liquid that filled it).

Often, teachers add a fourth act (i.e., “the sequel”), in which students encounter a similar problem but in a different context (e.g., they have to estimate the volume of a lava lamp). There are also a number of elementary examples that have been developed by math teachers including GFletchy , which offers pre-kindergarten to middle school activities including counting squares , peas in a pod , and shark bait .

Students need to learn how to slow down and think through a problem context. The aforementioned strategies are quick ways teachers can begin to support students in developing the habits needed to effectively and efficiently tackle complex problem-solving.

March 12, 2024

The Simplest Math Problem Could Be Unsolvable

The Collatz conjecture has plagued mathematicians for decades—so much so that professors warn their students away from it

By Manon Bischoff

Mathematicians have been hoping for a flash of insight to solve the Collatz conjecture.

James Brey/Getty Images

At first glance, the problem seems ridiculously simple. And yet experts have been searching for a solution in vain for decades. According to mathematician Jeffrey Lagarias, number theorist Shizuo Kakutani told him that during the cold war, “for about a month everybody at Yale [University] worked on it, with no result. A similar phenomenon happened when I mentioned it at the University of Chicago. A joke was made that this problem was part of a conspiracy to slow down mathematical research in the U.S.”

The Collatz conjecture—the vexing puzzle Kakutani described—is one of those supposedly simple problems that people tend to get lost in. For this reason, experienced professors often warn their ambitious students not to get bogged down in it and lose sight of their actual research.

The conjecture itself can be formulated so simply that even primary school students understand it. Take a natural number. If it is odd, multiply it by 3 and add 1; if it is even, divide it by 2. Proceed in the same way with the result x : if x is odd, you calculate 3 x + 1; otherwise calculate x / 2. Repeat these instructions as many times as possible, and, according to the conjecture, you will always end up with the number 1.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example: If you start with 5, you have to calculate 5 x 3 + 1, which results in 16. Because 16 is an even number, you have to halve it, which gives you 8. Then 8 / 2 = 4, which, when divided by 2, is 2—and 2 / 2 = 1. The process of iterative calculation brings you to the end after five steps.

Of course, you can also continue calculating with 1, which gives you 4, then 2 and then 1 again. The calculation rule leads you into an inescapable loop. Therefore 1 is seen as the end point of the procedure.

Following iterative calculations, you can begin with any of the numbers above and will ultimately reach 1.

Credit: Keenan Pepper/Public domain via Wikimedia Commons

It’s really fun to go through the iterative calculation rule for different numbers and look at the resulting sequences. If you start with 6: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1. Or 42: 42 → 21 → 64 → 32 → 16 → 8 → 4 → 2 → 1. No matter which number you start with, you always seem to end up with 1. There are some numbers, such as 27, where it takes quite a long time (27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → ...), but so far the result has always been 1. (Admittedly, you have to be patient with the starting number 27, which requires 111 steps.)

But strangely there is still no mathematical proof that the Collatz conjecture is true. And that absence has mystified mathematicians for years.

The origin of the Collatz conjecture is uncertain, which is why this hypothesis is known by many different names. Experts speak of the Syracuse problem, the Ulam problem, the 3 n + 1 conjecture, the Hasse algorithm or the Kakutani problem.

German mathematician Lothar Collatz became interested in iterative functions during his mathematics studies and investigated them. In the early 1930s he also published specialist articles on the subject , but the explicit calculation rule for the problem named after him was not among them. In the 1950s and 1960s the Collatz conjecture finally gained notoriety when mathematicians Helmut Hasse and Shizuo Kakutani, among others, disseminated it to various universities, including Syracuse University.

Like a siren song, this seemingly simple conjecture captivated the experts. For decades they have been looking for proof that after repeating the Collatz procedure a finite number of times, you end up with 1. The reason for this persistence is not just the simplicity of the problem: the Collatz conjecture is related to other important questions in mathematics. For example, such iterative functions appear in dynamic systems, such as models that describe the orbits of planets. The conjecture is also related to the Riemann conjecture, one of the oldest problems in number theory.

Empirical Evidence for the Collatz Conjecture

In 2019 and 2020 researchers checked all numbers below 2 68 , or about 3 x 10 20 numbers in the sequence, in a collaborative computer science project . All numbers in that set fulfill the Collatz conjecture as initial values. But that doesn’t mean that there isn’t an outlier somewhere. There could be a starting value that, after repeated Collatz procedures, yields ever larger values that eventually rise to infinity. This scenario seems unlikely, however, if the problem is examined statistically.

An odd number n is increased to 3 n + 1 after the first step of the iteration, but the result is inevitably even and is therefore halved in the following step. In half of all cases, the halving produces an odd number, which must therefore be increased to 3 n + 1 again, whereupon an even result is obtained again. If the result of the second step is even again, however, you have to divide the new number by 2 twice in every fourth case. In every eighth case, you must divide it by 2 three times, and so on.

In order to evaluate the long-term behavior of this sequence of numbers , Lagarias calculated the geometric mean from these considerations in 1985 and obtained the following result: ( 3 / 2 ) 1/2 x ( 3 ⁄ 4 ) 1/4 x ( 3 ⁄ 8 ) 1/8 · ... = 3 ⁄ 4 . This shows that the sequence elements shrink by an average factor of 3 ⁄ 4 at each step of the iterative calculation rule. It is therefore extremely unlikely that there is a starting value that grows to infinity as a result of the procedure.

There could be a starting value, however, that ends in a loop that is not 4 → 2 → 1. That loop could include significantly more numbers, such that 1 would never be reached.

Such “nontrivial” loops can be found, for example, if you also allow negative integers for the Collatz conjecture: in this case, the iterative calculation rule can end not only at –2 → –1 → –2 → ... but also at –5 → –14 → –7 → –20 → –10 → –5 → ... or –17 → –50 → ... → –17 →.... If we restrict ourselves to natural numbers, no nontrivial loops are known to date—which does not mean that they do not exist. Experts have now been able to show that such a loop in the Collatz problem, however, would have to consist of at least 186 billion numbers .

The length of the Collatz sequences for all numbers from 1 to 9,999 varies greatly.

Credit: Cirne/Public domain via Wikimedia Commons

Even if that sounds unlikely, it doesn’t have to be. In mathematics there are many examples where certain laws only break down after many iterations are considered. For instance,the prime number theorem overestimates the number of primes for only about 10 316 numbers. After that point, the prime number set underestimates the actual number of primes.

Something similar could occur with the Collatz conjecture: perhaps there is a huge number hidden deep in the number line that breaks the pattern observed so far.

A Proof for Almost All Numbers

Mathematicians have been searching for a conclusive proof for decades. The greatest progress was made in 2019 by Fields Medalist Terence Tao of the University of California, Los Angeles, when he proved that almost all starting values of natural numbers eventually end up at a value close to 1.

“Almost all” has a precise mathematical meaning: if you randomly select a natural number as a starting value, it has a 100 percent probability of ending up at 1. ( A zero-probability event, however, is not necessarily an impossible one .) That’s “about as close as one can get to the Collatz conjecture without actually solving it,” Tao said in a talk he gave in 2020 . Unfortunately, Tao’s method cannot generalize to all figures because it is based on statistical considerations.

All other approaches have led to a dead end as well. Perhaps that means the Collatz conjecture is wrong. “Maybe we should be spending more energy looking for counterexamples than we’re currently spending,” said mathematician Alex Kontorovich of Rutgers University in a video on the Veritasium YouTube channel .

Perhaps the Collatz conjecture will be determined true or false in the coming years. But there is another possibility: perhaps it truly is a problem that cannot be proven with available mathematical tools. In fact, in 1987 the late mathematician John Horton Conway investigated a generalization of the Collatz conjecture and found that iterative functions have properties that are unprovable. Perhaps this also applies to the Collatz conjecture. As simple as it may seem, it could be doomed to remain unsolved forever.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

Netflix's hit sci-fi series '3 Body Problem' is based on a real math problem that is so complex it's impossible to solve

• The three-body problem is a centuries-old physics question that puzzled Isaac Newton .
• It describes the orbits of three bodies, like planets or stars, trapped in each other's gravity.
• The problem is unsolvable and led to the development of chaos theory.

While Netflix's "3 Body Problem" is a science-fiction show, its name comes from a real math problem that's puzzled scientists since the late 1600s.

In physics, the three-body problem refers to the motion of three bodies trapped in each other's gravitational grip — like a three-star system.

It might sound simple enough, but once you dig into the mathematics, the orbital paths of each object get complicated very quickly.

Two-body vs. three- and multi-body systems

A simpler version is a two-body system like binary stars. Two-body systems have periodic orbits, meaning they are mathematically predictable because they follow the same trajectory over and over. So, if you have the stars' initial positions and velocities, you can calculate where they've been or will be in space far into the past and future.

However, "throwing in a third body that's close enough to interact leads to chaos," Shane Ross, an aerospace and ocean engineering professor at Virginia Tech, told Business Insider. In fact, it's nearly impossible to precisely predict the orbital paths of any system with three bodies or more.

While two orbiting planets might look like a ven diagram with ovular paths overlapping, the paths of three bodies interacting often resemble tangled spaghetti. Their trajectories usually aren't as stable as systems with only two bodies.

All that uncertainty makes what's known as the three-body problem largely unsolvable, Ross said. But there are certain exceptions.

The three-body problem is over 300 years old

The three-body problem dates back to Isaac Newton , who published his "Principia" in 1687.

In the book, the mathematician noted that the planets move in elliptical orbits around the sun. Yet the gravitational pull from Jupiter seemed to affect Saturn's orbital path.

Related stories

The three-body problem didn't just affect distant planets. Trying to understand the variations in the moon's movements caused Newton literal headaches, he complained.

But Newton never fully figured out the three-body problem. And it remained a mathematical mystery for nearly 200 years.

In 1889, a Swedish journal awarded mathematician Henri Poincaré a gold medal and 2,500 Swedish crowns, roughly half a year's salary for a professor at the time, for his essay about the three-body problem that outlined the basis for an entirely new mathematical theory called chaos theory .

According to chaos theory, when there is uncertainty about a system's initial conditions, like an object's mass or velocity, that uncertainty ripples out, making the future more and more unpredictable.

Think of it like taking a wrong turn on a trip. If you make a left instead of a right at the end of your journey, you're probably closer to your destination than if you made the mistake at the very beginning.

Can you solve the three-body problem?

Cracking the three-body problem would help scientists chart the movements of meteors and planets, including Earth, into the extremely far future. Even comparatively small movements of our planet could have large impacts on our climate, Ross said.

Though the three-body problem is considered mathematically unsolvable, there are solutions to specific scenarios. In fact, there are a few that mathematicians have found.

For example, three bodies could stably orbit in a figure eight or equally spaced around a ring. Both are possible depending on the initial positions and velocities of the bodies.

One way researchers look for solutions is with " restricted " three-body problems, where two main bodies (like the sun and Earth) interact and a third object with much smaller mass (like the moon) offers less gravitational interference. In this case, the three-body problem looks a lot like a two-body problem since the sun and Earth comprise the majority of mass in the system.

However, if you're looking at a three-star system, like the one in Netflix's show "3 Body Problem," that's a lot more complicated.

Computers can also run simulations far more efficiently than humans, though due to the inherent uncertainties, the results are typically approximate orbits instead of exact.

Finding solutions to three-body problems is also essential to space travel, Ross said. For his work, he inputs data about the Earth, moon, and spacecraft into a computer. "We can build up a whole library of possible trajectories," he said, "and that gives us an idea of the types of motion that are possible."

• Main content

Easy Finger Math Tricks to Help Kids Solve Problems

While using your fingers isn't the fastest way to recall a multiplication fact while doing a problem, finger math tricks can help kids figure out how to answer the problem at hand — and as they work on their math, they will eventually learn all the facts by repetition.

Note that before your child can understand other finger tricks, they must be able to count by 2s, 5s, and 10s and multiply by 2s, 3s, and 4s.

Quick Finger Math Tricks for Threes and Fours

The tricks for multiplying by threes and fours are really a matter of counting out the answer on your fingers. As your children count out the answer repeatedly, they'll memorize it and then be able to move on to larger numbers.

Multiplying by Three

Did you realize that all of your fingers have three segments? Therefore, you can figure out anything from 3 x 1 to 3 x 10 by counting the segments on each finger. To start:

• Hold up the number of fingers you're going to multiply by 3. For example, if the problem is 3 x 4 — hold up four fingers.
• Count each segment on each finger you're holding up, and you should come up with 12 — which is the correct answer.

Multiplying by Four

Multiplying by four is the same as multiplying by two — twice. To start:

• Hold up the number of fingers to correspond with the number you are multiplying by four. For example, if you are multiplying 4 x 6 — hold up six fingers.
• Count each finger by two, moving from left to right. Then count each finger again, continuing to count by twos, until you've counted every finger twice.

Helpful Hack To keep track of the fingers you've counted twice, sometimes it's easier to put your finger down as you count the first time, and back up as you count the second time.

Finger Math Tricks for Multiplying by 6, 7, 8, and 9

While numbers one through five are easy for most kids to remember, six and up often pose a problem. This handy trick will make it a little easier to work those problems out.

Multiplying 6, 7, 8, and 9 by Hand

To begin, assign each finger a number. For example, your thumbs represent 6, your index fingers each represent 7, etc. This will remain the same throughout the finger math hack.

Your left hand will represent the first number that you are multiplying and your right hand will represent the second number you are multiplying. In this example, we are multiplying 7 x 8. 

To Determine the Part of Your Answer:

• On your left hand, put down the finger that represents the number you are multiplying as well as any fingers whose number value is less than this figure. In this example, you are multiplying 7 x 8, so the left hand will represent 7. You will drop your index finger (number 7) and your thumb (number 6).
• Similarly, the right hand will represent eight, so you will drop down your middle finger (number 8), your index finger (number 7), and your thumb (number 6).
• Now, just multiply the fingers that are still pointed upwards. In this case, you will have three fingers on your left hand and two on your right, so you will multiply 3 x 2 to get 6. This is the first part of your answer!

To Determine the Second Part of Your Answer:

• Keeping your fingers in the same positions, count how many fingers are folded down. In the 7 x 8 example, you should have five fingers folded. 
• You will count each of these in quantities of ten. So, 10, 20, 30, 40, 50.
• 50 is your answer.

To Determine Your Final Answer:

• Add your two numbers together. In this example, you would add 6 + 50, which gives you 56!

Another Finger Math Trick Just for Nine

There is a trick that works separately, just for multiplying by the number nine.

• To start, hold up all ten fingers, with your palms facing you.
• Assign each finger a number, starting with your left-hand thumb and ending with your right-hand thumb. The left-hand thumb will be one, the left-hand index finger will be two, and so on until you reach the number 10 for your right-hand thumb.
• To tackle a problem, put down the corresponding finger of the number you're multiplying by nine. For example, if you are multiplying 9 x 8, you'd put down the eighth finger (which will be on your right hand).
• Count all the fingers to the left of the finger you have folded down. This will give you 7. This is the first digit of your answer.
• Count all the fingers to the right of the finger you have folded down. This will give you 2. This is the second digit of your answer.
• Put the numbers together! Your answer is 72.

Finger Multiplication Tricks Can Make Math Easy and Fun

While the hope is that your kids will eventually memorize their multiplication charts , using some quick hand tricks for multiplication and letting them count things out on their fingers is not a bad way to learn. It keeps frustration at bay since the answer is always a fingertip away, and the repetition of having to figure it out will help cement those facts into their brains.

Help | Advanced Search

Computer Science > Computation and Language

Title: large language models are unconscious of unreasonability in math problems.

Abstract: Large language models (LLMs) demonstrate substantial capabilities in solving math problems. However, they tend to produce hallucinations when given questions containing unreasonable errors. In this paper, we study the behavior of LLMs when faced with unreasonable math problems and further explore their potential to address these problems. First, we construct the Unreasonable Math Problem (UMP) benchmark to examine the error detection ability of LLMs. Experiments show that LLMs are able to detect unreasonable errors, but still fail in generating non-hallucinatory content. In order to improve their ability of error detection and correction, we further design a strategic prompt template called Critical Calculation and Conclusion(CCC). With CCC, LLMs can better self-evaluate and detect unreasonable errors in math questions, making them more reliable and safe in practical application scenarios.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Ai Math Solver & Scanner 4+

Learn math, step-by-step, hhh technologies llc, designed for ipad.

• 4.6 • 8 Ratings
• Offers In-App Purchases

Screenshots

Description.

Introducing "AI Math Solver" - your ultimate academic sidekick! Say goodbye to math headaches and hello to instant solutions at your fingertips. Why Choose AI Math Solver? - Instant Math Magic: Snap a pic of any math problem, and watch our AI work its magic with lightning-fast solutions! - All-Subject AI Chat: Stuck on science or tangled up in literature? No worries! Our AI chat is here to give you personalized guidance whenever you need it. - Learning, Simplified: We're not just about answers; we're all about making complex concepts easy to understand! - Super Easy to Use: Our app is designed to be super intuitive and fun for learners of all ages! Key Features: - Snap & Solve: Snap a pic of any problem, and our AI will crack it in seconds! - Live Chat Help: Get instant explanations and study tips through interactive chat! - Covers Everything: From math mysteries to literary puzzles, we've got every subject covered! Your Ultimate Study Buddy: - Always Improving: We're constantly updating with the latest AI advancements and feedback from users like you! - Perfect for Everyone: Whether you're a student, teacher, or just curious, our app is tailor-made for all learners! Don't let homework stress you out any longer. With "AI Math Solver" by your side, acing assignments has never been easier! Download now and unleash your academic superpowers! Privacy Policy: https://www.hhhtechnologies.com/privacy-policy Terms of Use: https://www.hhhtechnologies.com/terms-and-conditions

Version 1.4

Just a few bug fixes!

Ratings and Reviews

App privacy.

The developer, HHH Technologies LLC , indicated that the app’s privacy practices may include handling of data as described below. For more information, see the developer’s privacy policy .

Data Not Collected

The developer does not collect any data from this app.

Privacy practices may vary, for example, based on the features you use or your age. Learn More

Information

• Weekly Access $6.99
• Lifetime Access $39.99
• Yearly Access $39.99
• App Support
• Privacy Policy

More By This Developer

QR Scanner & Generator Pro

You Might Also Like

Pi - Math AI Solver

Math Solver: Homework AI Tutor

Edu AI - AI Homework Helper

AI Homework Helper－Math Solver

Math AI : Tutor & Math Helper

AI Math Solver Homework Help