how to solve trig equations on a calculator

Game Central

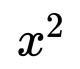
Related Concepts

Trig Calculator

The sine and cosine trigonometric functions, tan, cot, sec, and csc, calculated from trig identities., trigonometry in a right triangle, other trigonometric calculators.

Welcome to this trigonometric calculator, a trig tool created to:

• Calculate any trigonometric function by inputting the angle at which you want to evaluate it; and
• Solve for the sides or angles of right triangles by using trigonometry.

Keep reading this article to learn more about trigonometric functions and the trig identities that relate them.

Trig functions are functions that take an angle as the argument. We define these functions by using the angle of a right triangle that is inserted in a unitary circle . Then, we relate that angle to the sides of such a triangle.

As the right triangle is circumscribed in a unit circle, the length of its hypotenuse equals the circle's radius (which equals one unit).

Sine and cosine are the fundamental trigonometric functions arising from the previous diagram:

• The sine of theta ( sin θ ) is the hypotenuse's vertical projection (green line); and
• The cosine of theta ( cos θ ) is the hypotenuse's horizontal projection (blue line).

We can rotate the radial line through the four quadrants and obtain the values of the trig functions from 0 to 360 degrees , as in the diagram below:

• For example, for an angle that leads to the second quadrant (90-180°), the cosine will be negative as the horizontal projection of the hypotenuse will point to the left. That's the case of 135°, whose cosine (horizontal projection, or x coordinate) equals -√2/2.
• For the third quadrant (180-270°), the cosine and the sine of the angles lying on it will be negative.
• For the fourth quadrant angles (270-360)°, the cosines will be positive and the sines negative.

Beyond 360 degrees

The previous behavior repeats cyclically, so trigonometric functions are not limited to 360°. We can keep rotating counterclockwise, and once we reach 360 degrees, the sine and cosine functions start to repeat the same behavior. As a consequence, we can relate the functions at different angles with the following trig identities for any n integer:

• sin(θ + 2πn) = sin(θ) ;
• cos(θ + 2πn) = cos(θ); and

For example a trig function at 90° (π/2) will be mathematically the same as at 450° (5π/2), as 5π/2 = π/2 + 2π.

Negative angles

Negative angles imply the same way to calculate sine and cosine (vertical and horizontal projections, respectively), with the difference that angular rotation occurs in the clockwise direction. For example, a trigonometric function at 270° is the same as at -90°, as their radial lines are the same (you can check it with this calculator)

Once you know the value of sine and cosine, you can use the following trigonometric identities to obtain the values of the other four functions:

Tangent is the sine-to-cosine ratio

tan(α) = sin(α)/cos(α)

Cosecant is the reciprocal of the sine

csc(α) = 1/sin(α)

Secant is the reciprocal of the cosine

sec(α) = 1/cos(α)

Cotangent is the reciprocal of the tangent

cot(α) = 1/tan(α)

From the previous analysis, we can obtain some valuable formulas that relate the angle of a right triangle to its sides. Of course, this doesn't limit to unit circles, so we can use it for hypotenuses of any length.

We relate the angle of the right triangle to its sides in the following way:

sin(α) = opposite/hypotenuse

cos(α) = adjacent/hypotenuse

tan(α) = opposite/adjacent

Remember that cotangent, secant, and cosecant are the inverse of the previous functions:

csc(α) = 1/sin(α) = hypotenuse/opposite

sec(α) = 1/cos(α) = hypotenuse/adjacent

cot(α) = 1/tan(α) = adjacent/opposite

You also can apply the previous formulas for the other acute angle ( β ), but consider that the legs of the triangle will switch: the adjacent will now be the hypotenuse and vice versa.

If you like this calculator, you may find these other tools interesting:

• Trigonometry calculator ;
• Cosine triangle calculator ;
• Sine triangle calculator ;
• Trig triangle calculator ;
• Right triangle trigonometry calculator ;
• Sine cosine tangent calculator ;
• Tangent ratio calculator ; and
• Tangent angle calculator .

How do I solve a 45-90-45 degree triangle by trig formulas?

If one leg of a 45 45 90 triangle is equal to a , then:

• The second leg also equals a ;
• The hypotenuse equals a √2 (from the hypotenuse formula c = √( a ² + a ²) = a √2 );
• The area is A = a ²/2 ; and
• The perimeter equals a (2 + √2) (the sum of the two sides plus the hypotenuse).

What are the values of the 6 trig functions at 90 degrees?

The values of the 6 trig functions for 90 degrees (π/2) are the following ones:

• sin(90°) = 1;
• cos(90°) = 0;
• tan(90°)= undefined;
• cot(90°) = 0;
• sec(90°) = undefined; and
• csc(90°) = 1.

Expanded form

Plastic footprint, social media time alternatives.

• Biology (99)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (508)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

• calculators
• Trigonometric Equations

Trigonometric Equations Calculator

Get detailed solutions to your math problems with our trigonometric equations step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems.

Solved example of trigonometric equations

The reciprocal sine function is cosecant: $\frac{1}{\csc(x)}=\sin(x)$

Move everything to the left hand side of the equation

Combining like terms $8\sin\left(x\right)$ and $-4\sin\left(x\right)$

Factor the polynomial $4\sin\left(x\right)-2$ by it's greatest common factor (GCF): $2$

Divide both sides of the equation by $2$

Simplifying the quotients

Divide $0$ by $2$

 Intermediate steps

We need to isolate the dependent variable $x$, we can do that by simultaneously subtracting $-1$ from both sides of the equation

$x+0=x$, where $x$ is any expression

Multiply $-1$ times $-1$

Divide $1$ by $2$

The angles where the function $\sin\left(x\right)$ is $\frac{1}{2}$ are

The angles expressed in radians in the same order are equal to

 Final Answer

Struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Popular problems

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Solving Trigonometric Equations

• Last updated
• Save as PDF
• Page ID 61251

Learning Objectives

• Use the fundamental identities to solve trigonometric equations.
• Express trigonometric expressions in simplest form.
• Solve trigonometric equations by factoring.
• Solve trigonometric equations by using the Quadratic Formula.

Thales of Miletus (circa 625–547 BC) is known as the founder of geometry. The legend is that he calculated the height of the Great Pyramid of Giza in Egypt using the theory of similar triangles , which he developed by measuring the shadow of his staff. Based on proportions, this theory has applications in a number of areas, including fractal geometry, engineering, and architecture. Often, the angle of elevation and the angle of depression are found using similar triangles.

In earlier sections of this chapter, we looked at trigonometric identities. Identities are true for all values in the domain of the variable. In this section, we begin our study of trigonometric equations to study real-world scenarios such as the finding the dimensions of the pyramids.

Solving Linear Trigonometric Equations in Sine and Cosine

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is \(2\pi\). In other words, every \(2\pi\) units, the y- values repeat. If we need to find all possible solutions, then we must add \(2\pi k\),where \(k\) is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is \(2\pi\):

\[\sin \theta=\sin(\theta \pm 2k\pi)\]

There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.

Example \(\PageIndex{1A}\): Solving a Linear Trigonometric Equation Involving the Cosine Function

Find all possible exact solutions for the equation \(\cos \theta=\dfrac{1}{2}\).

From the unit circle, we know that

\[ \begin{align*} \cos \theta &=\dfrac{1}{2} \\[4pt] \theta &=\dfrac{\pi}{3},\space \dfrac{5\pi}{3} \end{align*}\]

These are the solutions in the interval \([ 0,2\pi ]\). All possible solutions are given by

\[\theta=\dfrac{\pi}{3} \pm 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} \pm 2k\pi \nonumber\]

where \(k\) is an integer.

Example \(\PageIndex{1B}\): Solving a Linear Equation Involving the Sine Function

Find all possible exact solutions for the equation \(\sin t=\dfrac{1}{2}\).

Solving for all possible values of \(t\) means that solutions include angles beyond the period of \(2\pi\). From the section on Sum and Difference Identities, we can see that the solutions are \(t=\dfrac{\pi}{6}\) and \(t=\dfrac{5\pi}{6}\). But the problem is asking for all possible values that solve the equation. Therefore, the answer is

\[t=\dfrac{\pi}{6}\pm 2\pi k \quad \text{and} \quad t=\dfrac{5\pi}{6}\pm 2\pi k \nonumber\]

How to: Given a trigonometric equation, solve using algebra

• Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
• Substitute the trigonometric expression with a single variable, such as \(x\) or \(u\).
• Solve the equation the same way an algebraic equation would be solved.
• Substitute the trigonometric expression back in for the variable in the resulting expressions.
• Solve for the angle.

Example \(\PageIndex{2}\): Solve the Linear Trigonometric Equation

Solve the equation exactly: \(2 \cos \theta−3=−5\), \(0≤\theta<2\pi\).

Use algebraic techniques to solve the equation.

\[\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}\]

Exercise \(\PageIndex{1}\)

Solve exactly the following linear equation on the interval \([0,2\pi)\): \(2 \sin x+1=0\).

\(x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}\)

Solving Equations Involving a Single Trigonometric Function

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle (see [link]). We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is \(\pi\),not \(2\pi\). Further, the domain of tangent is all real numbers with the exception of odd integer multiples of \(\dfrac{\pi}{2}\),unless, of course, a problem places its own restrictions on the domain.

Example \(\PageIndex{3A}\): Solving a Trignometric Equation Involving Sine

Solve the problem exactly: \(2 {\sin}^2 \theta−1=0\), \(0≤\theta<2\pi\).

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate \(\sin \theta\). Then we will find the angles.

\[\begin{align*} 2 {\sin}^2 \theta-1&= 0\\ 2 {\sin}^2 \theta&= 1\\ {\sin}^2 \theta&= \dfrac{1}{2}\\ \sqrt{ {\sin}^2 \theta }&= \pm \sqrt{ \dfrac{1}{2} }\\ \sin \theta&= \pm \dfrac{1}{\sqrt{2}}\\ &= \pm \dfrac{\sqrt{2}}{2}\\ \theta&= \dfrac{\pi}{4}, \space \dfrac{3\pi}{4},\space \dfrac{5\pi}{4}, \space \dfrac{7\pi}{4} \end{align*}\]

As \(\sin \theta=−\dfrac{1}{2}\), notice that all four solutions are in the third and fourth quadrants.

Example \(\PageIndex{3B}\): Solving a Trigonometric Equation Involving Cosecant

Solve the following equation exactly: \(\csc \theta=−2\), \(0≤\theta<4\pi\).

We want all values of \(\theta\) for which \(\csc \theta=−2\) over the interval \(0≤\theta<4\pi\).

\[\begin{align*} \csc \theta&= -2\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6},\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6} \end{align*}\]

Example \(\PageIndex{3C}\): Solving an Equation Involving Tangent

Solve the equation exactly: \(\tan\left(\theta−\dfrac{\pi}{2}\right)=1\), \(0≤\theta<2\pi\).

Recall that the tangent function has a period of \(\pi\). On the interval \([ 0,\pi )\),and at the angle of \(\dfrac{\pi}{4}\),the tangent has a value of \(1\). However, the angle we want is \(\left(\theta−\dfrac{\pi}{2}\right)\). Thus, if \(\tan\left(\dfrac{\pi}{4}\right)=1\),then

\[\begin{align*} \theta-\dfrac{\pi}{2}&= \dfrac{\pi}{4}\\ \theta&= \dfrac{3\pi}{4} \pm k\pi \end{align*}\]

Over the interval \([ 0,2\pi )\),we have two solutions:

\(\theta=\dfrac{3\pi}{4}\) and \(\theta=\dfrac{3\pi}{4}+\pi=\dfrac{7\pi}{4}\)

Exercise \(\PageIndex{2}\)

Find all solutions for \(\tan x=\sqrt{3}\).

\(\dfrac{\pi}{3}\pm \pi k\)

Example \(\PageIndex{4}\): Identify all Solutions to the Equation Involving Tangent

Identify all exact solutions to the equation \(2(\tan x+3)=5+\tan x\), \(0≤x<2\pi\).

We can solve this equation using only algebra. Isolate the expression \(\tan x\) on the left side of the equals sign.

There are two angles on the unit circle that have a tangent value of \(−1\): \(\theta=\dfrac{3\pi}{4}\) and \(\theta=\dfrac{7\pi}{4}\).

Solve Trigonometric Equations Using a Calculator

Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.

Example \(\PageIndex{5A}\): Using a Calculator to Solve a Trigonometric Equation Involving Sine

Use a calculator to solve the equation \(\sin \theta=0.8\),where \(\theta\) is in radians.

Make sure mode is set to radians. To find \(\theta\), use the inverse sine function. On most calculators, you will need to push the 2 ND button and then the SIN button to bring up the \({\sin}^{−1}\) function. What is shown on the screen is \({\sin}^{−1}\).The calculator is ready for the input within the parentheses. For this problem, we enter \({\sin}^{−1}(0.8)\), and press ENTER. Thus, to four decimals places,

\({\sin}^{−1}(0.8)≈0.9273\)

The solution is

\(\theta≈0.9273\pm 2\pi k\)

The angle measurement in degrees is

\[\begin{align*} \theta&\approx 53.1^{\circ}\\ \theta&\approx 180^{\circ}-53.1^{\circ}\\ &\approx 126.9^{\circ} \end{align*}\]

Note that a calculator will only return an angle in quadrants I or IV for the sine function since that is the range of the inverse sine. The other angle is obtained by using \(\pi−\theta\).

Example \(\PageIndex{5B}\): Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation \( \sec θ=−4, \) giving your answer in radians.

We can begin with some algebra.

\[\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}\]

Check that the MODE is in radians. Now use the inverse cosine function

\[\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right)&\approx 1.8235\\ \theta&\approx 1.8235+2\pi k \end{align*}\]

Since \(\dfrac{\pi}{2}≈1.57\) and \(\pi≈3.14\),\(1.8235\) is between these two numbers, thus \(\theta≈1.8235\) is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine. See Figure \(\PageIndex{2}\).

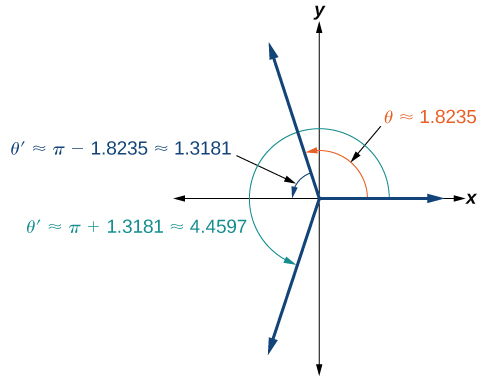
So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is \(\theta '≈\pi−1.8235≈1.3181\). The other solution in quadrant III is \(\theta '≈\pi+1.3181≈4.4597\).

The solutions are \(\theta≈1.8235\pm 2\pi k\) and \(\theta≈4.4597\pm 2\pi k\).

Exercise \(\PageIndex{3}\)

Solve \(\cos \theta=−0.2\).

\(\theta≈1.7722\pm 2\pi k\) and \(\theta≈4.5110\pm 2\pi k\)

Solving Trigonometric Equations in Quadratic Form

Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as \(x\) or \(u\). If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.

Example \(\PageIndex{6A}\): Solving a Trigonometric Equation in Quadratic Form

Solve the equation exactly: \({\cos}^2 \theta+3 \cos \theta−1=0\), \(0≤\theta<2\pi\).

We begin by using substitution and replacing \(\cos \theta\) with \(x\). It is not necessary to use substitution, but it may make the problem easier to solve visually. Let \(\cos \theta=x\). We have

\(x^2+3x−1=0\)

The equation cannot be factored, so we will use the quadratic formula: \(x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\).

\[\begin{align*} x&= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2}\\ &= \dfrac{-3\pm \sqrt{13}}{2}\end{align*}\]

Replace \(x\) with \(\cos \theta \) and solve.

\[\begin{align*} \cos \theta&= \dfrac{-3\pm \sqrt{13}}{2}\\ \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \end{align*}\]

Note that only the + sign is used. This is because we get an error when we solve \(\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)\) on a calculator, since the domain of the inverse cosine function is \([ −1,1 ]\). However, there is a second solution:

\[\begin{align*} \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 1.26 \end{align*}\]

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

\[\begin{align*} \theta&= 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 5.02 \end{align*}\]

Example \(\PageIndex{6B}\): Solving a Trigonometric Equation in Quadratic Form by Factoring

Solve the equation exactly: \(2 {\sin}^2 \theta−5 \sin \theta+3=0\), \(0≤\theta≤2\pi\).

Using grouping, this quadratic can be factored. Either make the real substitution, \(\sin \theta=u\),or imagine it, as we factor:

\[\begin{align*} 2 {\sin}^2 \theta-5 \sin \theta+3&= 0\\ (2 \sin \theta-3)(\sin \theta-1)&= 0 \qquad \text {Now set each factor equal to zero.}\\ 2 \sin \theta-3&= 0\\ 2 \sin \theta&= 3\\ \sin \theta&= \dfrac{3}{2}\\ \sin \theta-1&= 0\\ \sin \theta&= 1 \end{align*}\]

Next solve for \(\theta\): \(\sin \theta≠\dfrac{3}{2}\), as the range of the sine function is \([ −1,1 ]\). However, \(\sin \theta=1\), giving the solution \(\theta=\dfrac{\pi}{2}\).

Make sure to check all solutions on the given domain as some factors have no solution.

Exercise \(\PageIndex{4}\)

Solve \({\sin}^2 \theta=2 \cos \theta+2\), \(0≤\theta≤2\pi\). [Hint: Make a substitution to express the equation only in terms of cosine.]

\(\cos \theta=−1\), \(\theta=\pi\)

Example \(\PageIndex{7A}\): Solving a Trigonometric Equation Using Algebra

Solve exactly: \(2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi\)

This problem should appear familiar as it is similar to a quadratic. Let \(\sin \theta=x\). The equation becomes \(2x^2+x=0\). We begin by factoring:

\[\begin{align*} 2x^2+x&= 0\\ x(2x+1)&= 0\qquad \text {Set each factor equal to zero.}\\ x&= 0\\ 2x+1&= 0\\ x&= -\dfrac{1}{2} \end{align*}\] Then, substitute back into the equation the original expression \(\sin \theta \) for \(x\). Thus, \[\begin{align*} \sin \theta&= 0\\ \theta&= 0,\pi\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}\]

The solutions within the domain \(0≤\theta<2\pi\) are \(\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}\).

If we prefer not to substitute, we can solve the equation by following the same pattern of factoring and setting each factor equal to zero.

\[\begin{align*} {\sin}^2 \theta+\sin \theta&= 0\\ \sin \theta(2\sin \theta+1)&= 0\\ \sin \theta&= 0\\ \theta&= 0,\pi\\ 2 \sin \theta+1&= 0\\ 2\sin \theta&= -1\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}\]

We can see the solutions on the graph in Figure \(\PageIndex{3}\). On the interval \(0≤\theta<2\pi\),the graph crosses the \(x\) - axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

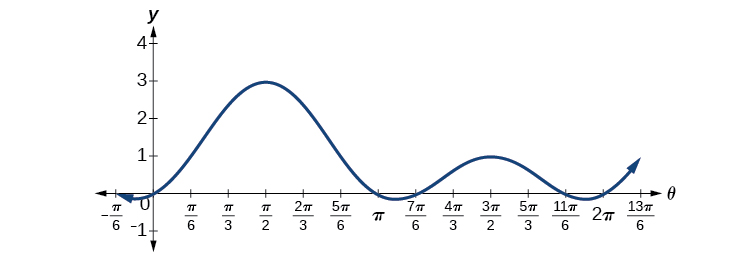
We can verify the solutions on the unit circle in via the result in the section on Sum and Difference Identities as well.

Example \(\PageIndex{7B}\): Solving a Trigonometric Equation Quadratic in Form

Solve the equation quadratic in form exactly: \(2 {\sin}^2 \theta−3 \sin \theta+1=0\), \(0≤\theta<2\pi\).

We can factor using grouping. Solution values of \(\theta\) can be found on the unit circle.

\[\begin{align*} (2 \sin \theta-1)(\sin \theta-1)&= 0\\ 2 \sin \theta-1&= 0\\ \sin \theta&= \dfrac{1}{2}\\ \theta&= \dfrac{\pi}{6}, \dfrac{5\pi}{6}\\ \sin \theta&= 1\\ \theta&= \dfrac{\pi}{2} \end{align*}\]

Exercise \(\PageIndex{5}\)

Solve the quadratic equation \(2{\cos}^2 \theta+\cos \theta=0\).

\(\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}\)

Solving Trigonometric Equations Using Fundamental Identities

While algebra can be used to solve a number of trigonometric equations, we can also use the fundamental identities because they make solving equations simpler. Remember that the techniques we use for solving are not the same as those for verifying identities. The basic rules of algebra apply here, as opposed to rewriting one side of the identity to match the other side. In the next example, we use two identities to simplify the equation.

Example \(\PageIndex{8}\): Solving an Equation Using an Identity

Solve the equation exactly using an identity: \(3 \cos \theta+3=2 {\sin}^2 \theta\), \(0≤\theta<2\pi\).

If we rewrite the right side, we can write the equation in terms of cosine:

\[\begin{align*} 3 \cos \theta+3&= 2 {\sin}^2 \theta\\ 3 \cos \theta+3&= 2(1-{\cos}^2 \theta)\\ 3 \cos \theta+3&= 2-2{\cos}^2 \theta\\ 2 {\cos}^2 \theta+3 \cos \theta+1&= 0\\ (2 \cos \theta+1)(\cos \theta+1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{2\pi}{3},\space \dfrac{4\pi}{3}\\ \cos \theta+1&= 0\\ \cos \theta&= -1\\ \theta&= \pi\\ \end{align*}\]

Our solutions are \(\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi\).

Solving Trigonometric Equations with Multiple Angles

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as \(\sin(2x)\) or \(\cos(3x)\). When confronted with these equations, recall that \(y=\sin(2x)\) is a horizontal compression by a factor of 2 of the function \(y=\sin x\). On an interval of \(2\pi\),we can graph two periods of \(y=\sin(2x)\),as opposed to one cycle of \(y=\sin x\). This compression of the graph leads us to believe there may be twice as many x -intercepts or solutions to \(\sin(2x)=0\) compared to \(\sin x=0\). This information will help us solve the equation.

Example \(\PageIndex{9}\): Solving a Multiple Angle Trigonometric Equation

Solve exactly: \(\cos(2x)=\dfrac{1}{2}\) on \([ 0,2\pi )\).

We can see that this equation is the standard equation with a multiple of an angle. If \(\cos(\alpha)=\dfrac{1}{2}\),we know \(\alpha\) is in quadrants I and IV. While \(\theta={\cos}^{−1} \dfrac{1}{2}\) will only yield solutions in quadrants I and II, we recognize that the solutions to the equation \(\cos \theta=\dfrac{1}{2}\) will be in quadrants I and IV.

Therefore, the possible angles are \(\theta=\dfrac{\pi}{3}\) and \(\theta=\dfrac{5\pi}{3}\). So, \(2x=\dfrac{\pi}{3}\) or \(2x=\dfrac{5\pi}{3}\), which means that \(x=\dfrac{\pi}{6}\) or \(x=\dfrac{5\pi}{6}\). Does this make sense? Yes, because \(\cos\left(2\left(\dfrac{\pi}{6}\right)\right)=\cos\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}\).

Are there any other possible answers? Let us return to our first step.

In quadrant I, \(2x=\dfrac{\pi}{3}\), so \(x=\dfrac{\pi}{6}\) as noted. Let us revolve around the circle again:

\[\begin{align*} 2x&= \dfrac{\pi}{3}+2\pi\\ &= \dfrac{\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{7\pi}{3}\\ x&= \dfrac{7\pi}{6}\\ \text {One more rotation yields}\\ 2x&= \dfrac{\pi}{3}+4\pi\\ &= \dfrac{\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{13\pi}{3}\\ \end{align*}\]

\(x=\dfrac{13\pi}{6}>2\pi\), so this value for \(x\) is larger than \(2\pi\), so it is not a solution on \([ 0,2\pi )\).

In quadrant IV, \(2x=\dfrac{5\pi}{3}\), so \(x=\dfrac{5\pi}{6}\) as noted. Let us revolve around the circle again:

\[\begin{align*} 2x&= \dfrac{5\pi}{3}+2\pi\\ &= \dfrac{5\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{11\pi}{3} \end{align*}\]

so \(x=\dfrac{11\pi}{6}\).

One more rotation yields

\[\begin{align*} 2x&= \dfrac{5\pi}{3}+4\pi\\ &= \dfrac{5\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{17\pi}{3} \end{align*}\]

\(x=\dfrac{17\pi}{6}>2\pi\),so this value for \(x\) is larger than \(2\pi\),so it is not a solution on \([ 0,2\pi )\)  .

Our solutions are \(x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}\), and \(\dfrac{11\pi}{6}\). Note that whenever we solve a problem in the form of \(sin(nx)=c\), we must go around the unit circle \(n\) times.

Key Concepts

• When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution. See Example \(\PageIndex{1}\), Example \(\PageIndex{2}\), and Example \(\PageIndex{3}\).
• Equations involving a single trigonometric function can be solved or verified using the unit circle. See Example \(\PageIndex{4}\), Example \(\PageIndex{5}\), and Example \(\PageIndex{6}\), and Example \(\PageIndex{7}\).
• We can also solve trigonometric equations using a graphing calculator. See Example \(\PageIndex{8}\) and Example \(\PageIndex{9}\).
• Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc. See Example \(\PageIndex{10}\), Example \(\PageIndex{11}\), Example \(\PageIndex{12}\), and Example \(\PageIndex{13}\).
• We can also use the identities to solve trigonometric equation. See Example \(\PageIndex{14}\), Example \(\PageIndex{15}\), and Example \(\PageIndex{16}\).
• We can use substitution to solve a multiple-angle trigonometric equation, which is a compression of a standard trigonometric function. We will need to take the compression into account and verify that we have found all solutions on the given interval. See Example \(\PageIndex{17}\).
• Real-world scenarios can be modeled and solved using the Pythagorean Theorem and trigonometric functions. See Example \(\PageIndex{18}\).

Contributors and Attributions

Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a  Creative Commons Attribution License 4.0  license. Download for free at  https://openstax.org/details/books/precalculus .

Wolfram|Alpha Widgets Overview Tour Gallery Sign In

Share this page.

• StumbleUpon
• Google Buzz

Output Type

Output width, output height.

To embed this widget in a post, install the Wolfram|Alpha Widget Shortcode Plugin and copy and paste the shortcode above into the HTML source.

To embed a widget in your blog's sidebar, install the Wolfram|Alpha Widget Sidebar Plugin , and copy and paste the Widget ID below into the "id" field:

Save to My Widgets

Build a new widget.

We appreciate your interest in Wolfram|Alpha and will be in touch soon.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Trigonometric equations and identities

About this unit, inverse trigonometric functions.

• Intro to arcsine (Opens a modal)
• Intro to arctangent (Opens a modal)
• Intro to arccosine (Opens a modal)
• Restricting domains of functions to make them invertible (Opens a modal)
• Domain & range of inverse tangent function (Opens a modal)
• Using inverse trig functions with a calculator (Opens a modal)
• Inverse trigonometric functions review (Opens a modal)
• Trigonometric equations and identities: FAQ (Opens a modal)
• Evaluate inverse trig functions Get 3 of 4 questions to level up!

Sinusoidal equations

• Solving sinusoidal equations of the form sin(x)=d (Opens a modal)
• Cosine equation algebraic solution set (Opens a modal)
• Cosine equation solution set in an interval (Opens a modal)
• Sine equation algebraic solution set (Opens a modal)
• Solving cos(θ)=1 and cos(θ)=-1 (Opens a modal)
• Solve sinusoidal equations (basic) Get 3 of 4 questions to level up!
• Solve sinusoidal equations Get 3 of 4 questions to level up!

Sinusoidal models

• Interpreting solutions of trigonometric equations (Opens a modal)
• Trig word problem: solving for temperature (Opens a modal)
• Trigonometric equations review (Opens a modal)
• Interpret solutions of trigonometric equations in context Get 3 of 4 questions to level up!
• Sinusoidal models word problems Get 3 of 4 questions to level up!

Angle addition identities

• Trig angle addition identities (Opens a modal)
• Using the cosine angle addition identity (Opens a modal)
• Using the cosine double-angle identity (Opens a modal)
• Proof of the sine angle addition identity (Opens a modal)
• Proof of the cosine angle addition identity (Opens a modal)
• Proof of the tangent angle sum and difference identities (Opens a modal)
• Using the trig angle addition identities Get 3 of 4 questions to level up!

Using trigonometric identities

• Finding trig values using angle addition identities (Opens a modal)
• Using the tangent angle addition identity (Opens a modal)
• Using trig angle addition identities: finding side lengths (Opens a modal)
• Using trig angle addition identities: manipulating expressions (Opens a modal)
• Using trigonometric identities (Opens a modal)
• Trig identity reference (Opens a modal)
• Find trig values using angle addition identities Get 3 of 4 questions to level up!

Challenging trigonometry problems

• Trig challenge problem: area of a triangle (Opens a modal)
• Trig challenge problem: area of a hexagon (Opens a modal)
• Trig challenge problem: cosine of angle-sum (Opens a modal)
• Trig challenge problem: arithmetic progression (Opens a modal)
• Trig challenge problem: maximum value (Opens a modal)
• Trig challenge problem: multiple constraints (Opens a modal)
• Trig challenge problem: system of equations (Opens a modal)

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Trigonometry Calculators
• Trigonometric Equations Solver

Trigonometric equation solver

This calculator can solve basic trigonometric equations such as: $\color{blue}{ \sin(x) = \frac{1}{2} }$ or $ \color{blue}{ \sqrt{2} \cos\left(-\frac{3x}{4}\right) - 1 = 0 } $.

The calculator will find exact or approximate solutions on custom range. Solution can be expressed either in radians or degrees.

sin cos tan cot ( · x ) =

Most popular calculators

• Factoring Polynomials
• Solving equations
• Rationalize Denominator
• Arithmetic sequences

Polynomial Calculators

• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Expand & Simplify
• Generate From Roots

Rational Expressions

• Simplify Expression
• Multiplication / Division
• Addition / Subtraction

Radical Expressions

• Simplifying

Solving Equations

• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps

Quadratic Equation

• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism

Complex Numbers

• Modulus, inverse, polar form

Systems of equations

• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition

Calculus Calculators

• Limit Calculator
• Derivative Calculator
• Integral Calculator

Sequences & Series

• Arithmetic Sequences
• Geometric Sequences
• Find n th Term

Analytic Geometry

• Distance and Midpoint
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection

Trigonometry

• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex

Statistics and probability

• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression

Financial Calculators

• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator

Other Calculators

• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Solve equation $ \sin(2x)=\frac{\sqrt{3}}{2} ~~ \text{for} ~~ 0 \leq x \leq 360^\circ $.

Find all solutions of the equation $ \cos \left( \frac{3x}{2} \right) = -\frac{\sqrt{2}}{2}$. Express the results in degrees.

Find exact solutions of the equation $ \tan \left( -\frac{4x}{3} \right) = 0.4$. Express the results in radians.

Solve $ 2\sin \left( x \right) + \sqrt{2}= 0 ~~ \text{for} ~~ -180^\circ \leq x \leq 180^\circ $. Express the results in degrees.

Related Calculators

Was this calculator helpful?

Please tell me how can I make this better.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Trigonometric Equation Calculator

Instructions: Use calculator to solve trigonometric equations you provide, showing all the steps. Please type in the trigonometric equation you want to carry out in the box below.

ABout this Trigonometric Equation Calculator

This calculator will allow you to solve trig equations, showing all the steps of the way. All you need to do is to provide a valid trigonometric equation, with an unknown (x). It could be something simple as 'sin(x) = 1/2', or something more complex like 'sin^2(x) = cos(x) + tan(x)'.

Once you are done typing your equation, just go ahead and click on "Solve" to get all the details of the processes of finding the solutions, if solutions can be found.

Trigonometric properties and rules almost always allow to reduce most trig equations into simpler ones, so this type of equation is one type that often times lead to solutions, but it can be extremely cumbersome at times.

What is a trigonometric Equation?

A trigonometric equation, in the simplest possible terms, is a math equation where the unknown x is inside of a trigonometric expression.

For example, the following expression is a trigonometric eqn:

Why? Simply because x appears inside of trig expression sine. Or for example:

Now, these two are trig eqns, but the difference between the two is that for the first one, x appears ONLY inside of sine, whereas in the second one x appears inside of a trig function (tangent), but it also appears outside. This will usually make it difficult (or impossible) to solve the equation.

How to solve trigonometric equations

• Step 1: Make sure you are dealing with a trigonometric equation. Non-trigonometric equations will likely require a different approach
• Step 2: Make sure that the unknown x is inside of the trigonometric expression , but x does not appear outside a trig expression. If that is the case, it is likely you won't be able to solve the equation with elementary methods
• Step 3: Conduct an appropriate substitution, by first expressing all the trig functions present in the equation into one type (typically sine), and then use a substitution involving sine
• Step 4: With a little luck and if you did the correct substitution, you have reduced the original trigonometric equation into a polynomial equation to solve .

One of the key trig rules you need to use the ability to express all trigonometric functions in terms of any fixed trigonometric function. For example, we can write cosine in terms of sine:

Trigonometric Substitutions

Using trigonometric identities and substitutions is your way to go in this case. For example, suppose you want to solve this:

So we know this is a trig equation, and we know we can write cosine in terms of sine, so we do this:

Now what? Well, we can use the substitution: \(u = \sin x\), so the equation above becomes:

which is a rational equation , which by using simple algebraic manipulation means that we need to solve a polynomial equation in order to solve the original trig equation.

Application of trigonometry

• Step 1: All things mechanical: In manufacturing mechanical parts, circles and trigonometry play a crucial role
• Step 2: Analysis of periodic functions: Many phenomena are tightly related to periodicity, the point at which trigonometry comes to play
• Step 3: Advanced math: Mathematicians love their Fourier Series and Transform, which play a crucial role in spectral analysis

Circles and all their symmetry are so really important in real life, and trigonometry is the language by which we can quantify circles and its relationships. Solving trigonometric equations is at the center of math.

Why would you solve trigonometric equations

Trigonometric equations carry lots of value in practice especially in Engineering. Notable properties such as the period and frequency open a full spectrum of applications.

Circular structures play a crucial role in everything mechanical that we use today. Circles are synonymous of trigonometry, and trigonometric equations are at the center of it.

Example: Solving simple trig equations

Solve: \(\sin(x) = \frac{1}{2}\)

We need to solve the following given trigonometric equation equation:

The following is obtained:

By direct application of the properties of the inverse trigonometric function \( \arcsin(\cdot)\), as well as the properties of the trigonometric function \( \sin\left(x\right)\), we obtain that

Therefore, solving for \(x\) for the given equation leads to the solutions \(x=\frac{5}{6}\pi{}+2\pi{}K_1,\,\,x=\frac{1}{6}\pi{}+2\pi{}K_2\), for \(K_1, K_2\) arbitrary integer constants.

More equation calculators

Our trigonometric equation with steps will come in handy when dealing with equations with specific structure. If you are unsure of the type of equation you are dealing with, you can use our general equation solver , which will figure out the structure of the given equation, and will find a suitable approach.

The main difficulty with solving equations that are not linear equation or polynomial equation is that there is not a specific route to follow, nor there is any guarantee you will find solutions.

Usually, the strategy consists of simplifying expressions as much as possible, and after doing that, it is usually nowhere land, where you need to try whatever feels suitable.

Naturally, the idea is to try to reduce the equation to a simpler equation, by using some kind of substitution and a multi-step process, where you first find solutions of an auxiliary solution, which gives you CANDIDATES to the original equation. You would like to solve a linear equation , or even a quadratic equation , but perhaps the reduction you get will be a bit less generous.

Related Calculators

log in to your account

Reset password.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics
• Trigonometry

How to Easily Solve Trigonometric Equations

Last Updated: February 1, 2023 Fact Checked

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 17 people, some anonymous, worked to edit and improve it over time. There are 10 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 258,598 times. Learn more...

Did you get homework from your teacher that was about solving Trigonometric equations? Did you maybe not pay full attention in class during the lesson on Trigonometric questions? Do you even know what "Trigonometric" means? If you answered yes to these questions, then you don't need to worry because this wikiHow will teach you how to solve Trigonometric equations.

• To solve a trig equation, transform it into one or many basic trig equations. Solving trig equations finally results in solving 4 types of basic trig equations.

• There are 4 types of basic trig equations:
• sin x = a ; cos x = a
• tan x = a ; cot x = a
• Solving basic trig equations proceeds by studying the various positions of the arc x on the trig circle, and by using trig conversion table (or calculator ). To fully know how to solve these basic trig equations, and similar, see book titled :"Trigonometry: Solving trig equations and inequalities" (Amazon E-book 2010).
• Example 1. Solve sin x = 0.866. The conversion table (or calculator) gives the answer: x = Pi/3. The trig circle gives another arc (2Pi/3) that has the same sin value (0.866). The trig circle also gives an infinity of answers that are called extended answers.
• x1 = Pi/3 + 2k.Pi, and x2 = 2Pi/3. (Answers within period (0, 2Pi))
• x1 = Pi/3 + 2k Pi, and x2 = 2Pi/3 + 2k Pi. (Extended answers).
• Example 2. Solve: cos x = -1/2. Calculators give x = 2 Pi/3. The trig circle gives another x = -2Pi/3.
• x1 = 2Pi/3 + 2k.Pi, and x2 = - 2Pi/3. (Answers within period (0, 2Pi))
• x1 = 2Pi/3 + 2k Pi, and x2 = -2Pi/3 + 2k.Pi. (Extended answers)
• Example 3. Solve: tan (x - Pi/4) = 0.
• x = Pi/4 ; (Answer)
• x = Pi/4 + k Pi; ( Extended answer)
• Example 4. Solve cot 2x = 1.732. Calculators and the trig circle give
• x = Pi/12 ; (Answer)
• x = Pi/12 + k Pi ; (Extended answers)

• To transform a given trig equation into basic trig ones, use common algebraic transformations ( factoring , common factor , polynomial identities...), definitions and properties of trig functions, and trig identities. There are about 31, among them the last 14 trig identities, from 19 to 31, are called Transformation Identities, since they are used in the transformation of trig equations. [4] X Research source See book mentioned above.
• Example 5: The trig equation: sin x + sin 2x + sin 3x = 0 can be transformed, using trig identities, into a product of basic trig equations: 4cos x*sin (3x/2)*cos (x/2) = 0. The basic trig equations to be solved are: cos x = 0 ; sin (3x/2) = 0 ; and cos (x/2) = 0.

• Before learning solving trig equations, you must know how to quickly find the arcs whose trig functions are known. Conversion values of arcs (or angles) are given by trig tables or calculators. [6] X Research source
• Example: After solving, get cos x = 0.732. Calculators give the solution arc x = 42.95 degree. The trig unit circle will give other solution arcs that have the same cos value.

• You can graph to illustrate the solution arcs on the trig unit circle. The terminal points of these solution arcs constitute regular polygons on the trig circle. For examples:
• The terminal points of the solution arcs x = Pi/3 + k.Pi/2 constitute a square on the trig unit circle.
• The solution arcs x = Pi/4 + k.Pi/3 are represented by the vertexes of a regular hexagon on the trig unit circle.

• A. Approach 1.
• Transform the given trig equation into a product in the form: f(x).g(x) = 0 or f(x).g(x).h(x) = 0, in which f(x), g(x) and h(x) are basic trig equations.
• Example 6. Solve: 2cos x + sin 2x = 0. (0 < x < 2Pi)
• Solution. Replace in the equation sin 2x by using the identity: sin 2x = 2*sin x*cos x.
• cos x + 2*sin x*cos x = 2cos x*( sin x + 1) = 0. Next, solve the 2 basic trig functions: cos x = 0, and (sin x + 1) = 0.
• Example 7. Solve: cos x + cos 2x + cos 3x = 0. (0 < x < 2Pi)
• Solution: Transform it to a product, using trig identities: cos 2x(2cos x + 1 ) = 0. Next, solve the 2 basic trig equations: cos 2x = 0, and (2cos x + 1) = 0.
• Example 8. Solve: sin x - sin 3x = cos 2x. (0 < x < 2Pi)
• B. Approach 2.
• Transform the given trig equation into a trig equation having only one unique trig function as variable. There are a few tips on how to select the appropriate variable. The common variables to select are: sin x = t; cos x = t; cos 2x = t, tan x = t and tan (x/2) = t.
• Example 9. Solve: 3sin^2 x - 2cos^2 x = 4sin x + 7 (0 < x < 2Pi).
• Solution. Replace in the equation (cos^2 x) by (1 - sin^2 x), then simplify the equation:
• 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Call sin x = t. The equation becomes: 5t^2 - 4t - 9 = 0. This is a quadratic equation that has 2 real roots: t1 = -1 and t2 = 9/5. The second t2 is rejected since > 1. Next, solve: t = sin = -1 --> x = 3Pi/2.
• Example 10. Solve: tan x + 2 tan^2 x = cot x + 2.
• Solution. Call tan x = t. Transform the given equation into an equation with t as variable: (2t + 1)(t^2 - 1) = 0. Solve for t from this product, then solve the basic trig equation tan x = t for x.

• There are a few special types of trig equations that require some specific transformations. Examples:
• a*sin x+ b*cos x = c ; a(sin x + cos x) + b*cos x*sin x = c ;
• a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0

• The function f(x) = sin x has 2Pi as period.
• The function f(x) = tan x has Pi as period.
• The function f(x) = sin 2x has Pi as period.
• The function f(x) = cos (x/2) has 4Pi as period.
• If the period is specified in the problem/test, you have to only find the solution arc(s) x within this period.
• NOTE: Solving trig equation is a tricky work that often leads to errors and mistakes. Therefore, answers should be carefully checked. After solving, you can check the answers by using a graphing calculator to directly graph the given trig equation R(x) = 0. The answers (real roots) will be given in decimals. For example, Pi is given by the value 3.14
• ↑ https://www.khanacademy.org/math/geometry/hs-geo-trig/hs-geo-solve-for-a-side/a/unknown-side-in-right-triangle-w-trig
• ↑ https://www.purplemath.com/modules/solvtrig.htm
• ↑ https://www.shelovesmath.com/algebra/advanced-algebra/parent-graphs-and-transformations/#GenericTransformationsofFunctions
• ↑ https://www.khanacademy.org/math/precalculus/trig-equations-and-identities-precalc/using-trig-identities-precalc/v/examples-using-pythagorean-identities-to-simplify-trigonometric-expressions
• ↑ https://www.khanacademy.org/math/precalculus/trig-equations-and-identities-precalc/inverse-trig-functions-precalc/v/inverse-trig-functions-arcsin
• ↑ https://www.mathopenref.com/arcsin.html
• ↑ https://courses.lumenlearning.com/precalculus/chapter/unit-circle-sine-and-cosine-functions/
• ↑ https://mathbitsnotebook.com/Algebra2/TrigConcepts/TCEquationsMore.html
• ↑ https://www.analyzemath.com/trigonometry/properties.html
• ↑ https://www.youtube.com/watch?v=8Z60_yXX4xA

Community Q&A

You Might Also Like

About This Article

• Send fan mail to authors

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

• For a new problem, you will need to begin a new live expert session.
• You can contact support with any questions regarding your current subscription.
• You will be able to enter math problems once our session is over.
• I am only able to help with one math problem per session. Which problem would you like to work on?
• Does that make sense?
• I am currently working on this problem.
• Are you still there?
• It appears we may have a connection issue. I will end the session - please reconnect if you still need assistance.
• Let me take a look...
• Can you please send an image of the problem you are seeing in your book or homework?
• If you click on "Tap to view steps..." you will see the steps are now numbered. Which step # do you have a question on?
• Please make sure you are in the correct subject. To change subjects, please exit out of this live expert session and select the appropriate subject from the menu located in the upper left corner of the Mathway screen.
• What are you trying to do with this input?
• While we cover a very wide range of problems, we are currently unable to assist with this specific problem. I spoke with my team and we will make note of this for future training. Is there a different problem you would like further assistance with?
• Mathway currently does not support this subject. We are more than happy to answer any math specific question you may have about this problem.
• Mathway currently does not support Ask an Expert Live in Chemistry. If this is what you were looking for, please contact support.
• Mathway currently only computes linear regressions.
• We are here to assist you with your math questions. You will need to get assistance from your school if you are having problems entering the answers into your online assignment.
• Have a great day!
• Hope that helps!
• You're welcome!
• Per our terms of use, Mathway's live experts will not knowingly provide solutions to students while they are taking a test or quiz.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Trigonometric equations online calculator

The general form of trigonometric equation is

f ( trig ( x ) ) = 0

where - some arbitrary function, trig ( x ) - some trigonometric function.

As a rule, to solve trigonometric equation one need to transform it to the simplier form which has a known solution. The transformation can be done by using different trigonometric formulas .

For example, consider the solution of trigonometric equation

By using the cosine double angle formula, transform this equation to the simplier one:

The received equation is the very simple and has known solution. Our online calculator, build on Wolfram Alpha system is able to solve more complex trigonometric equations with step by step solution.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Pythagorean
• Angle Sum/Difference
• Double Angle
• Multiple Angle
• Negative Angle
• Sum to Product
• Product to Sum
• Proving Identities
• Trigonometric Equations
• Trig Inequalities
• Evaluate Functions
• Conversions

Most Used Actions

Number line.

• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• prove\:\cot(2x)=\frac{1-\tan^2(x)}{2\tan(x)}
• prove\:\csc(2x)=\frac{\sec(x)}{2\sin(x)}
• prove\:\frac{\sin(3x)+\sin(7x)}{\cos(3x)-\cos(7x)}=\cot(2x)
• prove\:\frac{\csc(\theta)+\cot(\theta)}{\tan(\theta)+\sin(\theta)}=\cot(\theta)\csc(\theta)
• prove\:\cot(x)+\tan(x)=\sec(x)\csc(x)

trigonometric-identity-proving-calculator

• High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification. Trig identities are very similar to this concept. An identity...

Please add a message.

Message received. Thanks for the feedback.

Triangle Calculator

Please provide 3 values including at least one side to the following 6 fields, and click the "Calculate" button. When radians are selected as the angle unit, it can take values such as pi/2, pi/4, etc.

A triangle is a polygon that has three vertices. A vertex is a point where two or more curves, lines, or edges meet; in the case of a triangle, the three vertices are joined by three line segments called edges. A triangle is usually referred to by its vertices. Hence, a triangle with vertices a, b, and c is typically denoted as Δabc. Furthermore, triangles tend to be described based on the length of their sides, as well as their internal angles. For example, a triangle in which all three sides have equal lengths is called an equilateral triangle while a triangle in which two sides have equal lengths is called isosceles. When none of the sides of a triangle have equal lengths, it is referred to as scalene, as depicted below.

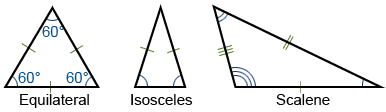
Tick marks on the edge of a triangle are a common notation that reflects the length of the side, where the same number of ticks means equal length. Similar notation exists for the internal angles of a triangle, denoted by differing numbers of concentric arcs located at the triangle's vertices. As can be seen from the triangles above, the length and internal angles of a triangle are directly related, so it makes sense that an equilateral triangle has three equal internal angles, and three equal length sides. Note that the triangle provided in the calculator is not shown to scale; while it looks equilateral (and has angle markings that typically would be read as equal), it is not necessarily equilateral and is simply a representation of a triangle. When actual values are entered, the calculator output will reflect what the shape of the input triangle should look like.

Triangles classified based on their internal angles fall into two categories: right or oblique. A right triangle is a triangle in which one of the angles is 90°, and is denoted by two line segments forming a square at the vertex constituting the right angle. The longest edge of a right triangle, which is the edge opposite the right angle, is called the hypotenuse. Any triangle that is not a right triangle is classified as an oblique triangle and can either be obtuse or acute. In an obtuse triangle, one of the angles of the triangle is greater than 90°, while in an acute triangle, all of the angles are less than 90°, as shown below.

Triangle facts, theorems, and laws

• It is not possible for a triangle to have more than one vertex with internal angle greater than or equal to 90°, or it would no longer be a triangle.
• The interior angles of a triangle always add up to 180° while the exterior angles of a triangle are equal to the sum of the two interior angles that are not adjacent to it. Another way to calculate the exterior angle of a triangle is to subtract the angle of the vertex of interest from 180°.
• The sum of the lengths of any two sides of a triangle is always larger than the length of the third side

a 2 + b 2 = c 2

EX: Given a = 3, c = 5, find b:

3 2 + b 2 = 5 2 9 + b 2 = 25 b 2 = 16 b = 4

• Law of sines: the ratio of the length of a side of a triangle to the sine of its opposite angle is constant. Using the law of sines makes it possible to find unknown angles and sides of a triangle given enough information. Where sides a, b, c, and angles A, B, C are as depicted in the above calculator, the law of sines can be written as shown below. Thus, if b, B and C are known, it is possible to find c by relating b/sin(B) and c/sin(C). Note that there exist cases when a triangle meets certain conditions, where two different triangle configurations are possible given the same set of data.
• Given the lengths of all three sides of any triangle, each angle can be calculated using the following equation. Refer to the triangle above, assuming that a, b, and c are known values.

Area of a Triangle

There are multiple different equations for calculating the area of a triangle, dependent on what information is known. Likely the most commonly known equation for calculating the area of a triangle involves its base, b , and height, h . The "base" refers to any side of the triangle where the height is represented by the length of the line segment drawn from the vertex opposite the base, to a point on the base that forms a perpendicular.

Another method for calculating the area of a triangle uses Heron's formula. Unlike the previous equations, Heron's formula does not require an arbitrary choice of a side as a base, or a vertex as an origin. However, it does require that the lengths of the three sides are known. Again, in reference to the triangle provided in the calculator, if a = 3, b = 4, and c = 5:

Median, inradius, and circumradius

The median of a triangle is defined as the length of a line segment that extends from a vertex of the triangle to the midpoint of the opposing side. A triangle can have three medians, all of which will intersect at the centroid (the arithmetic mean position of all the points in the triangle) of the triangle. Refer to the figure provided below for clarification.

The medians of the triangle are represented by the line segments m a , m b , and m c . The length of each median can be calculated as follows:

Where a, b, and c represent the length of the side of the triangle as shown in the figure above.

As an example, given that a=2, b=3, and c=4, the median m a can be calculated as follows:

The inradius is the radius of the largest circle that will fit inside the given polygon, in this case, a triangle. The inradius is perpendicular to each side of the polygon. In a triangle, the inradius can be determined by constructing two angle bisectors to determine the incenter of the triangle. The inradius is the perpendicular distance between the incenter and one of the sides of the triangle. Any side of the triangle can be used as long as the perpendicular distance between the side and the incenter is determined, since the incenter, by definition, is equidistant from each side of the triangle.

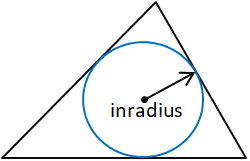
For the purposes of this calculator, the inradius is calculated using the area (Area) and semiperimeter (s) of the triangle along with the following formulas:

where a, b, and c are the sides of the triangle

Circumradius

The circumradius is defined as the radius of a circle that passes through all the vertices of a polygon, in this case, a triangle. The center of this circle, where all the perpendicular bisectors of each side of the triangle meet, is the circumcenter of the triangle, and is the point from which the circumradius is measured. The circumcenter of the triangle does not necessarily have to be within the triangle. It is worth noting that all triangles have a circumcircle (circle that passes through each vertex), and therefore a circumradius.

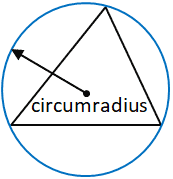
For the purposes of this calculator, the circumradius is calculated using the following formula:

Where a is a side of the triangle, and A is the angle opposite of side a

Although side a and angle A are being used, any of the sides and their respective opposite angles can be used in the formula.