word problems on system of linear equations in two variables

WORD PROBLEMS INVOLVING LINEAR EQUATIONS IN TWO VARIABLES

Problem 1 :

Raman’s age is three times he sum of the ages of his two sons. After 5 years his age will be twice the sum of the ages of his two sons. Find the age of Raman

Let x be Raman's age and y be the sum of ages of his two sons.

x  =  3y  -----(1)

After 5 years :

Raman's age  =  x + 5

The sum of the ages of his two sons  =  y + 5 + 5  

  =  y + 10

x + 5  =  2(y + 10)

x + 5  =  2y + 20

x - 2y  =  20 - 5

x - 2y  =  15 --------(2)

By applying the value of x in (2), we get

3y - 2y  =  15

y  =  15

x  =  3(15)

x  =  45

So, Raman is 45 years old.

Problem 2 :

The middle digit of a number between 100 and 1000 is zero and the sum of the other digit is 13. If the digits are reversed, the number so formed exceeds the original number by 495. Find the number

The required number will be in the form X 0 Y

Middle digit  =  0

x + y  =  13 -------(1)

Y 0 X  =  X0Y + 495

100y + x  =  100x + 1y + 495

x - 100x + 100y - y  =  495

 -99x + 99y  =  495

-x + y  =  5 -------(2)

x  =  y - 5

By applying the value of x in (1), we get

y - 5  + y  =  13

2y  =  13+5

2y  =  18

y  =  9

When y  =  9,

x  =  9 - 5

x  =  4

So, the required number is 409.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

How to Find a Limit Using a Table

Apr 09, 24 08:44 PM

Evaluating Logarithms Worksheet

Apr 09, 24 09:30 AM

Evaluating Logarithmic Expressions Worksheet

Apr 09, 24 02:01 AM

4.2 Solve Applications with Systems of Equations

Learning objectives.

By the end of this section, you will be able to:

• Solve direct translation applications
• Solve geometry applications

Solve uniform motion applications

Be prepared 4.4.

Before you get started, take this readiness quiz.

The sum of twice a number and nine is 31. Find the number. If you missed this problem, review Example 2.15 .

Be Prepared 4.5

Twins Jon and Ron together earned $96,000 last year. Ron earned $8000 more than three times what Jon earned. How much did each of the twins earn? If you missed this problem, review Example 2.19 .

Be Prepared 4.6

An express train and a local train leave Pittsburgh to travel to Washington, D.C. The express train can make the trip in four hours and the local train takes five hours for the trip. The speed of the express train is 12 miles per hour faster than the speed of the local train. Find the speed of both trains. If you missed this problem, review Example 2.43 .

Solve Direct Translation Applications

Systems of linear equations are very useful for solving applications. Some people find setting up word problems with two variables easier than setting them up with just one variable. To solve an application, we’ll first translate the words into a system of linear equations. Then we will decide the most convenient method to use, and then solve the system.

Solve applications with systems of equations.

• Step 1. Read the problem. Make sure all the words and ideas are understood.
• Step 2. Identify what we are looking for.
• Step 3. Name what we are looking for. Choose variables to represent those quantities.
• Step 4. Translate into a system of equations.
• Step 5. Solve the system of equations using good algebra techniques.
• Step 6. Check the answer in the problem and make sure it makes sense.
• Step 7. Answer the question with a complete sentence.

We solved number problems with one variable earlier. Let’s see how differently it works using two variables.

Example 4.14

The sum of two numbers is zero. One number is nine less than the other. Find the numbers.

Try It 4.27

The sum of two numbers is 10. One number is 4 less than the other. Find the numbers.

Try It 4.28

The sum of two numbers is −6 . −6 . One number is 10 less than the other. Find the numbers.

Example 4.15

Heather has been offered two options for her salary as a trainer at the gym. Option A would pay her $25,000 plus $15 for each training session. Option B would pay her $ 10,000 + $ 40 $ 10,000 + $ 40 for each training session. How many training sessions would make the salary options equal?

Try It 4.29

Geraldine has been offered positions by two insurance companies. The first company pays a salary of $12,000 plus a commission of $100 for each policy sold. The second pays a salary of $20,000 plus a commission of $50 for each policy sold. How many policies would need to be sold to make the total pay the same?

Try It 4.30

Kenneth currently sells suits for company A at a salary of $22,000 plus a $10 commission for each suit sold. Company B offers him a position with a salary of $28,000 plus a $4 commission for each suit sold. How many suits would Kenneth need to sell for the options to be equal?

As you solve each application, remember to analyze which method of solving the system of equations would be most convenient.

Example 4.16

Translate to a system of equations and then solve:

When Jenna spent 10 minutes on the elliptical trainer and then did circuit training for 20 minutes, her fitness app says she burned 278 calories. When she spent 20 minutes on the elliptical trainer and 30 minutes circuit training she burned 473 calories. How many calories does she burn for each minute on the elliptical trainer? How many calories for each minute of circuit training?

Try It 4.31

Mark went to the gym and did 40 minutes of Bikram hot yoga and 10 minutes of jumping jacks. He burned 510 calories. The next time he went to the gym, he did 30 minutes of Bikram hot yoga and 20 minutes of jumping jacks burning 470 calories. How many calories were burned for each minute of yoga? How many calories were burned for each minute of jumping jacks?

Try It 4.32

Erin spent 30 minutes on the rowing machine and 20 minutes lifting weights at the gym and burned 430 calories. During her next visit to the gym she spent 50 minutes on the rowing machine and 10 minutes lifting weights and burned 600 calories. How many calories did she burn for each minutes on the rowing machine? How many calories did she burn for each minute of weight lifting?

Solve Geometry Applications

We will now solve geometry applications using systems of linear equations. We will need to add complementary angles and supplementary angles to our list some properties of angles.

The measures of two complementary angles add to 90 degrees. The measures of two supplementary angles add to 180 degrees.

Complementary and Supplementary Angles

Two angles are complementary if the sum of the measures of their angles is 90 degrees.

Two angles are supplementary if the sum of the measures of their angles is 180 degrees.

If two angles are complementary, we say that one angle is the complement of the other.

If two angles are supplementary, we say that one angle is the supplement of the other.

Example 4.17

Translate to a system of equations and then solve.

The difference of two complementary angles is 26 degrees. Find the measures of the angles.

Try It 4.33

The difference of two complementary angles is 20 degrees. Find the measures of the angles.

Try It 4.34

The difference of two complementary angles is 80 degrees. Find the measures of the angles.

In the next example, we remember that the measures of supplementary angles add to 180.

Example 4.18

Two angles are supplementary. The measure of the larger angle is twelve degrees less than five times the measure of the smaller angle. Find the measures of both angles.

Try It 4.35

Two angles are supplementary. The measure of the larger angle is 12 degrees more than three times the smaller angle. Find the measures of the angles.

Try It 4.36

Two angles are supplementary. The measure of the larger angle is 18 less than twice the measure of the smaller angle. Find the measures of the angles.

Recall that the angles of a triangle add up to 180 degrees. A right triangle has one angle that is 90 degrees. What does that tell us about the other two angles? In the next example we will be finding the measures of the other two angles.

Example 4.19

The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle. Find the measures of both angles.

We will draw and label a figure.

Try It 4.37

The measure of one of the small angles of a right triangle is 2 more than 3 times the measure of the other small angle. Find the measure of both angles.

Try It 4.38

The measure of one of the small angles of a right triangle is 18 less than twice the measure of the other small angle. Find the measure of both angles.

Often it is helpful when solving geometry applications to draw a picture to visualize the situation.

Example 4.20

Randall has 125 feet of fencing to enclose the part of his backyard adjacent to his house. He will only need to fence around three sides, because the fourth side will be the wall of the house. He wants the length of the fenced yard (parallel to the house wall) to be 5 feet more than four times as long as the width. Find the length and the width.

Try It 4.39

Mario wants to put a fence around the pool in his backyard. Since one side is adjacent to the house, he will only need to fence three sides. There are two long sides and the one shorter side is parallel to the house. He needs 155 feet of fencing to enclose the pool. The length of the long side is 10 feet less than twice the width. Find the length and width of the pool area to be enclosed.

Try It 4.40

Alexis wants to build a rectangular dog run in her yard adjacent to her neighbor’s fence. She will use 136 feet of fencing to completely enclose the rectangular dog run. The length of the dog run along the neighbor’s fence will be 16 feet less than twice the width. Find the length and width of the dog run.

We used a table to organize the information in uniform motion problems when we introduced them earlier. We’ll continue using the table here. The basic equation was D = r t D = r t where D is the distance traveled, r is the rate, and t is the time.

Our first example of a uniform motion application will be for a situation similar to some we have already seen, but now we can use two variables and two equations.

Example 4.21

Joni left St. Louis on the interstate, driving west towards Denver at a speed of 65 miles per hour. Half an hour later, Kelly left St. Louis on the same route as Joni, driving 78 miles per hour. How long will it take Kelly to catch up to Joni?

A diagram is useful in helping us visualize the situation.

Identify and name what we are looking for. A chart will help us organize the data. We know the rates of both Joni and Kelly, and so we enter them in the chart. We are looking for the length of time Kelly, k , and Joni, j , will each drive.

Since D = r · t D = r · t we can fill in the Distance column.

Translate into a system of equations.

To make the system of equations, we must recognize that Kelly and Joni will drive the same distance. So,

Also, since Kelly left later, her time will be 1 2 1 2 hour less than Joni’s time. So,

Try It 4.41

Mitchell left Detroit on the interstate driving south towards Orlando at a speed of 60 miles per hour. Clark left Detroit 1 hour later traveling at a speed of 75 miles per hour, following the same route as Mitchell. How long will it take Clark to catch Mitchell?

Try It 4.42

Charlie left his mother’s house traveling at an average speed of 36 miles per hour. His sister Sally left 15 minutes ( 1 4 hour ) ( 1 4 hour ) later traveling the same route at an average speed of 42 miles per hour. How long before Sally catches up to Charlie?

Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.

Let’s take a look at a boat travelling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.

The images below show how a river current affects the speed at which a boat is actually travelling. We’ll call the speed of the boat in still water b and the speed of the river current c .

The boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is b + c . b + c .

Now, the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is b − c . b − c .

We’ll put some numbers to this situation in the next example.

Example 4.22

A river cruise ship sailed 60 miles downstream for 4 hours and then took 5 hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.

Try It 4.43

A Mississippi river boat cruise sailed 120 miles upstream for 12 hours and then took 10 hours to return to the dock. Find the speed of the river boat in still water and the speed of the river current.

Try It 4.44

Jason paddled his canoe 24 miles upstream for 4 hours. It took him 3 hours to paddle back. Find the speed of the canoe in still water and the speed of the river current.

Wind currents affect airplane speeds in the same way as water currents affect boat speeds. We’ll see this in the next example. A wind current in the same direction as the plane is flying is called a tailwind . A wind current blowing against the direction of the plane is called a headwind .

Example 4.23

A private jet can fly 1,095 miles in three hours with a tailwind but only 987 miles in three hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Try It 4.45

A small jet can fly 1,325 miles in 5 hours with a tailwind but only 1,035 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Try It 4.46

A commercial jet can fly 1,728 miles in 4 hours with a tailwind but only 1,536 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Access this online resource for additional instruction and practice with systems of equations.

• Systems of Equations

Section 4.2 Exercises

Practice makes perfect.

Direct Translation Applications

In the following exercises, translate to a system of equations and solve.

The sum of two number is 15. One number is 3 less than the other. Find the numbers.

The sum of two number is 30. One number is 4 less than the other. Find the numbers.

The sum of two number is −16. One number is 20 less than the other. Find the numbers.

The sum of two number is −26 . −26 . One number is 12 less than the other. Find the numbers.

The sum of two numbers is 65. Their difference is 25. Find the numbers.

The sum of two numbers is 37. Their difference is 9. Find the numbers.

The sum of two numbers is −27 . −27 . Their difference is −59 . −59 . Find the numbers.

The sum of two numbers is −45 . −45 . Their difference is −89 . −89 . Find the numbers.

Maxim has been offered positions by two car companies. The first company pays a salary of $10,000 plus a commission of $1000 for each car sold. The second pays a salary of $20,000 plus a commission of $500 for each car sold. How many cars would need to be sold to make the total pay the same?

Jackie has been offered positions by two cable companies. The first company pays a salary of $14,000 plus a commission of $100 for each cable package sold. The second pays a salary of $20,000 plus a commission of $25 for each cable package sold. How many cable packages would need to be sold to make the total pay the same?

Amara currently sells televisions for company A at a salary of $17,000 plus a $100 commission for each television she sells. Company B offers her a position with a salary of $29,000 plus a $20 commission for each television she sells. How many televisions would Amara need to sell for the options to be equal?

Mitchell currently sells stoves for company A at a salary of $12,000 plus a $150 commission for each stove he sells. Company B offers him a position with a salary of $24,000 plus a $50 commission for each stove he sells. How many stoves would Mitchell need to sell for the options to be equal?

Two containers of gasoline hold a total of fifty gallons. The big container can hold ten gallons less than twice the small container. How many gallons does each container hold?

June needs 48 gallons of punch for a party and has two different coolers to carry it in. The bigger cooler is five times as large as the smaller cooler. How many gallons can each cooler hold?

Shelly spent 10 minutes jogging and 20 minutes cycling and burned 300 calories. The next day, Shelly swapped times, doing 20 minutes of jogging and 10 minutes of cycling and burned the same number of calories. How many calories were burned for each minute of jogging and how many for each minute of cycling?

Drew burned 1800 calories Friday playing one hour of basketball and canoeing for two hours. Saturday he spent two hours playing basketball and three hours canoeing and burned 3200 calories. How many calories did he burn per hour when playing basketball? How many calories did he burn per hour when canoeing?

Troy and Lisa were shopping for school supplies. Each purchased different quantities of the same notebook and thumb drive. Troy bought four notebooks and five thumb drives for $116. Lisa bought two notebooks and three thumb dives for $68. Find the cost of each notebook and each thumb drive.

Nancy bought seven pounds of oranges and three pounds of bananas for $17. Her husband later bought three pounds of oranges and six pounds of bananas for $12. What was the cost per pound of the oranges and the bananas?

Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?

Peter is buying office supplies. He is able to buy 3 packages of paper and 4 staplers for $40 or he is able to buy 5 packages of paper and 6 staplers for $62. How much does a package of paper cost? How much does a stapler cost?

The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?

The total number of calories in 2 hot dogs and 3 cups of cottage cheese is 960 calories. The total number of calories in 5 hot dogs and 2 cups of cottage cheese is 1190 calories. How many calories are in a hot dog? How many calories are in a cup of cottage cheese?

Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water as juice. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?

Owen is making lemonade from concentrate. The number of quarts of water he needs is 4 times the number of quarts of concentrate. How many quarts of water and how many quarts of concentrate does Owen need to make 100 quarts of lemonade?

The difference of two complementary angles is 55 degrees. Find the measures of the angles.

The difference of two complementary angles is 17 degrees. Find the measures of the angles.

Two angles are complementary. The measure of the larger angle is twelve less than twice the measure of the smaller angle. Find the measures of both angles.

Two angles are complementary. The measure of the larger angle is ten more than four times the measure of the smaller angle. Find the measures of both angles.

The difference of two supplementary angles is 8 degrees. Find the measures of the angles.

The difference of two supplementary angles is 88 degrees. Find the measures of the angles.

Two angles are supplementary. The measure of the larger angle is four more than three times the measure of the smaller angle. Find the measures of both angles.

Two angles are supplementary. The measure of the larger angle is five less than four times the measure of the smaller angle. Find the measures of both angles.

The measure of one of the small angles of a right triangle is 14 more than 3 times the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 26 more than 3 times the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 15 less than twice the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles.

Wayne is hanging a string of lights 45 feet long around the three sides of his patio, which is adjacent to his house. The length of his patio, the side along the house, is five feet longer than twice its width. Find the length and width of the patio.

Darrin is hanging 200 feet of Christmas garland on the three sides of fencing that enclose his front yard. The length is five feet less than three times the width. Find the length and width of the fencing.

A frame around a family portrait has a perimeter of 90 inches. The length is fifteen less than twice the width. Find the length and width of the frame.

The perimeter of a toddler play area is 100 feet. The length is ten more than three times the width. Find the length and width of the play area.

Solve Uniform Motion Applications

Sarah left Minneapolis heading east on the interstate at a speed of 60 mph. Her sister followed her on the same route, leaving two hours later and driving at a rate of 70 mph. How long will it take for Sarah’s sister to catch up to Sarah?

College roommates John and David were driving home to the same town for the holidays. John drove 55 mph, and David, who left an hour later, drove 60 mph. How long will it take for David to catch up to John?

At the end of spring break, Lucy left the beach and drove back towards home, driving at a rate of 40 mph. Lucy’s friend left the beach for home 30 minutes (half an hour) later, and drove 50 mph. How long did it take Lucy’s friend to catch up to Lucy?

Felecia left her home to visit her daughter driving 45 mph. Her husband waited for the dog sitter to arrive and left home twenty minutes (1/3 hour) later. He drove 55 mph to catch up to Felecia. How long before he reaches her?

The Jones family took a 12-mile canoe ride down the Indian River in two hours. After lunch, the return trip back up the river took three hours. Find the rate of the canoe in still water and the rate of the current.

A motor boat travels 60 miles down a river in three hours but takes five hours to return upstream. Find the rate of the boat in still water and the rate of the current.

A motor boat traveled 18 miles down a river in two hours but going back upstream, it took 4.5 4.5 hours due to the current. Find the rate of the motor boat in still water and the rate of the current.

A river cruise boat sailed 80 miles down the Mississippi River for four hours. It took five hours to return. Find the rate of the cruise boat in still water and the rate of the current.

A small jet can fly 1072 miles in 4 hours with a tailwind but only 848 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

A small jet can fly 1435 miles in 5 hours with a tailwind but only 1,215 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

A commercial jet can fly 868 miles in 2 hours with a tailwind but only 792 miles in 2 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

A commercial jet can fly 1,320 miles in 3 hours with a tailwind but only 1170 miles in 3 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Writing Exercises

Write an application problem similar to Example 4.14 . Then translate to a system of equations and solve it.

Write a uniform motion problem similar to Example 4.15 that relates to where you live with your friends or family members. Then translate to a system of equations and solve it.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-2-solve-applications-with-systems-of-equations

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Systems of Linear Equations Word Problems - Practice - Expii

Systems of linear equations word problems - practice, explanations (3).

(Videos) Set up Word Problems Using a System

by mathman1024

This video by mathman1024 works through word problems with systems of equations.

The general guideline to follow when doing these word problems is:

• Define your variables . Since this is a system, there will be two or more variables.
• Write your equations. Again, since this is a system, there will be two or more equations. This is also the tricky part which will be focused on in the videos.
• Solve the system. This can be done using the elimination method , substitution method , or graphing .
• State your answer.

The first problem that he goes over in the video is, " The sum of two numbers is 79, and their difference is 23. What are the two numbers? "

We want to write algebraic expressions for this system.

Step one is defining the variables. The question asks for two numbers so we can see that these are the variables. Let x=one numbery=the other number The first sentence is, " The sum of two numbers is 79. " Since sum means addition , we write, x+y=79 The next part states, " The difference of those two numbers is 23. " Since difference means subtraction, we write, x−y=23 And now we have our system of equations: {x+y=79x−y=23. This can be solved with substitution but you might notice it would be easier with elimination. x+y=79+x−y=232x+0y=1022x=1022x2=1022x=51 Finally, plug this back in to either equation to find the y value. (51)+y=7951−51+y=79−51y=28 The solution to this word problem's system of equations is (51,28).

The next problem is a little trickier. It isn't as obvious how to set up the equations. It says, " A minor league ballpark attracts 88 fans and draws in $553 in revenue from ticket sales. A child's ticket costs $4 and an adult's ticket is $7. How many of each type of ticket were sold? "

First, we define our variables. The problem asks for how many of each type of ticket. Since there are two types of tickets we can write, Let C=# of childrenA=# of adults The first snippet is, " A minor league ballpark attracts 88 fans ". We know there's a total of 88 fans which are made up of children and adults. So we can write, C+A=88 Next we have, " and draws in $553 in revenue from ticket sales. A child's ticket costs $4 and an adult's ticket is $7. " So we have to factor in the money. We see that we get $4 from each child and we get $7 from each adult. Total, we have $553. So we can write, 4C+7A=553 Now we have the system: {C+A=884C+7A=553. This can be solved by either elimination or substitution. For this one, I personally would choose substitution, but either works.

Let's solve the first equation for C. C+A=88C+A−A=88−AC=88−A Plug this back into the other equation to solve for A. 4(88−A)+7A=553352−4A+7A=553352+3A=553352−352+3A=553−3523A=2013A3=2013A=67 Finally, plug this back into either equation to solve for C. C=88−(67)C=21 Our solution is (21,67).

Remember, the best way to double check your answer to either of these example problems is to plug in your solved coordinates back into the original equations.

Related Lessons

As with most word problems, the most effective approach to take is translation. The goal is to take written information and translate into a new language: math equations.

Let's work through an example to see how this translation works.

Image by Clker-Free-Vector-Images via Pixabay ( CC0 )

The key to translating a word problem is to identify the given information. Here's what we know from reading the problem:

• Cupcakes cost $2
• Pies cost $7.50
• William bought 20 items
• Total cost (pies + cupcakes) = $73

We can get two equations from this information.

First, we know that, all together, William bought 20 items. If we say that the number of cupcakes is C and the number of pies is P, we can write the equation:

Systems of Linear Equations: Word Problems

Sometimes, it is helpful to translate a word problem into a system of linear equations and solve the system. After translating words to math, isolate one variable in one equation, then use its corresponding expression to solve for the other variable in the other equation. Finally, solve for the first variable! Here is a graphic with an example.

Image source: By Caroline Kulczycky

Systems of Equations (Word Problems)

These lessons, with videos, examples and step-by-step solutions help Grade 8 students learn how to analyze and solve pairs of simultaneous linear equations.

Related Pages Systems of Equations - Graphical Method Solving Equations Common Core for Grade 8 Common Core for Mathematics More Math Lessons for Grade 8

A. Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.

B. Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection.  For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6 .

C. Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair.

Common Core: 8.EE.8c

Suggested Learning Targets

• I can identify the solution(s) to a system of two linear equations in two variables as the point(s) of intersection of their graphs.
• I can describe the point(s) of intersection between two lines as the points that satisfy both equations simultaneously.
• I can define “inspection.”
• I can solve a system of two equations (linear) in two unknowns algebraically.
• I can identify cases in which a system of two equations in two unknowns has no solution.
• I can identify cases in which a system of two equations in two unknowns has an infinite number of solutions.
• I can solve simple cases of systems of two linear equations in two variables by inspection.
• I can estimate the point(s) of intersection for a system of two equations in two unknowns by graphing the equations.
• I can represent real-world and mathematical problems leading to two linear equations in two variables.

Systems of equations word problem (coins)

Example: A man has 14 coins in his pocket, all of which are dimes and quarters. If the total value of his change is $2.75, how many dimes and how many quarters does he have?

Word problem using system of equations (investment-interest)

Example: A woman invests a total of $20,000 in two accounts, one paying 5% and another paying 8% simple interest per year. Her annual interest is $1,180. How much did she invest in each rate?

Systems of Equations Word Problems

Example: The sum of two numbers is 16. One number is 4 less than 3 times the other. Find the numbers.

Systems of Equations (word problems)

Example: Two times a number plus ten times a second number is twenty. Thirty times the second number plus three times the first number is 45. What are the two numbers?

Systems of Equations-Word Problems

How to solve a word problem involving a system of 2 equations with 2 variables?

Example: Three coffees and two muffins cost a total of 7 dollars. Two coffees and four muffins cost a total of 8 dollars. What is the individual price for a single coffee and a single muffin?

How to translate words or word problems into a systems of equations?

Example: A coin collection is made up of 34 coins comprised of nickels and dimes. The total value of the collection is $1.90. How many dimes and nickels made up this collections?

Systems of Equations - word problems Examples of setting up word (or application) problems solved by a system of equations.

Example: For some reason, in our math class, there are 14 more boys than there are girls. If a total of 32 students are in the class, how many boys and how many girls are there?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Module 5: Systems of Linear Equations

5.2 – applications of systems of linear equations, learning objectives.

• Specify what the variables in a cost/ revenue system of linear equations represent
• Determine and apply an appropriate method for solving the system

(5.2.2) – Solve value problems with a system of linear equations

(5.2.3) – solve mixture problems with a system of linear equations, (5.2.4) – solve uniform motion problems with a system of linear equations.

A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How can the company determine if it is making a profit with its new line? How many skateboards must be produced and sold before a profit is possible?

(credit: Thomas Sørenes)

(5.2.1) – Solve cost and revenue problems

Using what we have learned about systems of equations, we can return to the skateboard manufacturing problem at the beginning of the section. The skateboard manufacturer’s revenue function is the function used to calculate the amount of money that comes into the business. It can be represented by the equation [latex]R=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price. The revenue function is shown in orange in the graph below.

The cost function is the function used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost function is shown in blue in the graph below. The [latex]x[/latex] -axis represents quantity in hundreds of units. The y -axis represents either cost or revenue in hundreds of dollars.

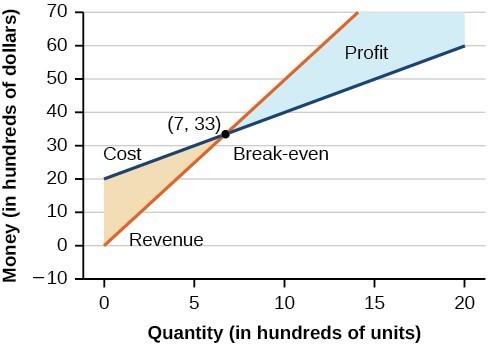
The point at which the two lines intersect is called the break-even point . We can see from the graph that if 700 units are produced, the cost is $3,300 and the revenue is also $3,300. In other words, the company breaks even if they produce and sell 700 units. They neither make money nor lose money.

The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss. The profit function is the revenue function minus the cost function, written as [latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex]. Clearly, knowing the quantity for which the cost equals the revenue is of great importance to businesses.

A business wants to manufacture bike frames. Before they start production, they need to make sure they can make a profit with the materials and labor force they have. Their accountant has given them a cost equation of [latex]y=0.85x+35,000[/latex] and a revenue equation of [latex]y=1.55x[/latex]:

• Interpret x and y for the cost equation
• Interpret x and y for the revenue equation

Cost: [latex]y=0.85x+35,000[/latex]

Revenue:[latex]y=1.55x[/latex]

The cost equation represents money leaving the company, namely how much it costs to produce a given number of bike frames. If we use the skateboard example as a model, x would represent the number of frames produced (instead of skateboards) and y would represent the amount of money it would cost to produce them (the same as the skateboard problem).

The revenue equation represents money coming into the company, so in this context x still represents the number of bike frames manufactured, and y now represents the amount of money made from selling them.  Let’s organize this information in a table:

Example: Finding the Break-Even Point and the Profit Function Using Substitution

Given the cost function [latex]C\left(x\right)=0.85x+35,000[/latex] and the revenue function [latex]R\left(x\right)=1.55x[/latex], find the break-even point and the profit function.

Write the system of equations using [latex]y[/latex] to replace function notation.

[latex]\begin{array}{l}\begin{array}{l}\\ y=0.85x+35,000\end{array}\hfill \\ y=1.55x\hfill \end{array}[/latex]

Substitute the expression [latex]0.85x+35,000[/latex] from the first equation into the second equation and solve for [latex]x[/latex].

[latex]\begin{array}{c}0.85x+35,000=1.55x\\ 35,000=0.7x\\ 50,000=x\end{array}[/latex]

Then, we substitute [latex]x=50,000[/latex] into either the cost function or the revenue function. [latex]1.55\left(50,000\right)=77,500[/latex]

The break-even point is [latex]\left(50,000,77,500\right)[/latex].

The profit function is found using the formula [latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex].

[latex]\begin{array}{l}P\left(x\right)=1.55x-\left(0.85x+35,000\right)\hfill \\ \text{ }=0.7x - 35,000\hfill \end{array}[/latex]

The profit function is [latex]P\left(x\right)=0.7x - 35,000[/latex].

Analysis of the Solution

The cost to produce 50,000 units is $77,500, and the revenue from the sales of 50,000 units is also $77,500. To make a profit, the business must produce and sell more than 50,000 units.

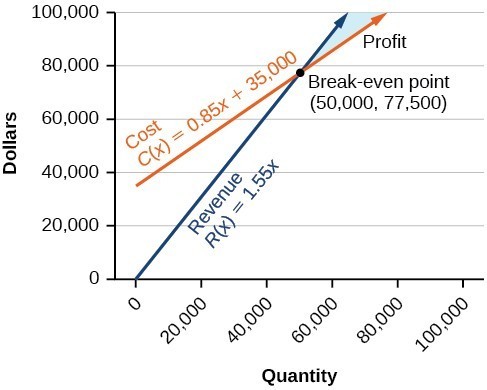
We see from the graph below that the profit function has a negative value until [latex]x=50,000[/latex], when the graph crosses the x -axis. Then, the graph emerges into positive y -values and continues on this path as the profit function is a straight line. This illustrates that the break-even point for businesses occurs when the profit function is 0. The area to the left of the break-even point represents operating at a loss.

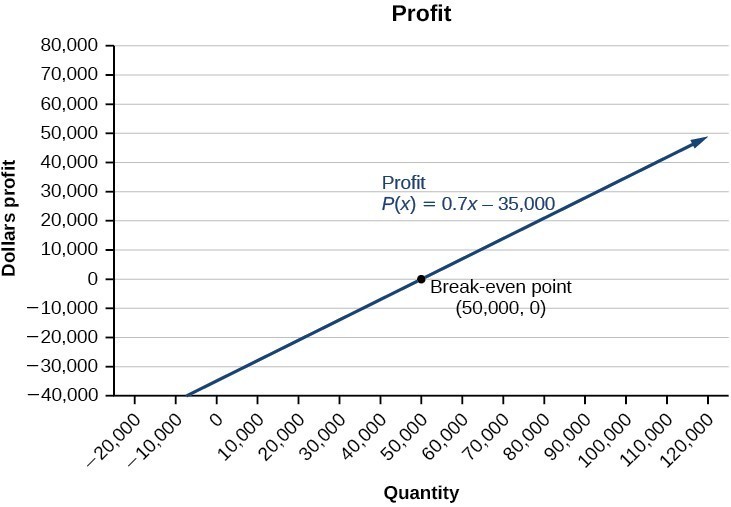
It is rare to be given equations that neatly model behaviors that you encounter in business, rather, you will probably be faced with a situation for which you know key information as in the example above. Below, we summarize three key factors that will help guide you in translating a situation into a system.

How To: Given a situation that represents a system of linear equations, write the system of equations and identify the solution.

1) Identify unknown quantities in a problem represent them with variables.

2) Write a system of equations which models the problem’s conditions.

3) Solve the system.

4) Check proposed solution.

Now let’s practice putting these key factors to work. In the next example, we determine how many different types of tickets are sold given information about the total revenue and amount of tickets sold to an event.

Example: Writing and Solving a System of Equations in Two Variables

The cost of a ticket to the circus is $25.00 for children and $50.00 for adults. On a certain day, attendance at the circus is 2,000 and the total gate revenue is $70,000. How many children and how many adults bought tickets?

Let c = the number of children and a = the number of adults in attendance.

The total number of people is [latex]2,000[/latex]. We can use this to write an equation for the number of people at the circus that day.

[latex]c+a=2,000[/latex]

The revenue from all children can be found by multiplying $25.00 by the number of children, [latex]25c[/latex]. The revenue from all adults can be found by multiplying $50.00 by the number of adults, [latex]50a[/latex]. The total revenue is $70,000. We can use this to write an equation for the revenue.

[latex]25c+50a=70,000[/latex]

We now have a system of linear equations in two variables.

[latex]\begin{array}{c}c+a=2,000\\ 25c+50a=70,000\end{array}[/latex]

In the first equation, the coefficient of both variables is 1. We can quickly solve the first equation for either [latex]c[/latex] or [latex]a[/latex]. We will solve for [latex]a[/latex].

[latex]\begin{array}{c}c+a=2,000\\ a=2,000-c\end{array}[/latex]

Substitute the expression [latex]2,000-c[/latex] in the second equation for [latex]a[/latex] and solve for [latex]c[/latex].

[latex]\begin{array}{l} 25c+50\left(2,000-c\right)=70,000\hfill \\ 25c+100,000 - 50c=70,000\hfill \\ \text{ }-25c=-30,000\hfill \\ \text{ }c=1,200\hfill \end{array}[/latex]

Substitute [latex]c=1,200[/latex] into the first equation to solve for [latex]a[/latex].

[latex]\begin{array}{l}1,200+a=2,000\hfill \\ \text{ }\text{}a=800\hfill \end{array}[/latex]

We find that [latex]1,200[/latex] children and [latex]800[/latex] adults bought tickets to the circus that day.

In this video example we show how to set up a system of linear equations that represents the total cost for admission to a museum.

Meal tickets at the circus cost $4.00 for children and $12.00 for adults. If 1,650 meal tickets were bought for a total of $14,200, how many children and how many adults bought meal tickets?

700 children, 950 adults

Sometimes, a system can inform a decision.  In our next example, we help answer the question, “Which truck rental company will give the best value?”

Example: Building a System of Linear Models to Choose a Truck Rental Company

Jamal is choosing between two truck-rental companies. The first, Keep on Trucking, Inc., charges an up-front fee of $20, then 59 cents a mile. The second, Move It Your Way, charges an up-front fee of $16, then 63 cents a mile. [1] When will Keep on Trucking, Inc. be the better choice for Jamal?

The two important quantities in this problem are the cost and the number of miles driven. Because we have two companies to consider, we will define two functions.

A linear function is of the form [latex]f\left(x\right)=mx+b[/latex]. Using the rates of change and initial charges, we can write the equations

[latex]\begin{array}{l}K\left(d\right)=0.59d+20\\ M\left(d\right)=0.63d+16\end{array}[/latex]

Using these equations, we can determine when Keep on Trucking, Inc., will be the better choice. Because all we have to make that decision from is the costs, we are looking for when Move It Your Way, will cost less, or when [latex]K\left(d\right)<M\left(d\right)[/latex]. The solution pathway will lead us to find the equations for the two functions, find the intersection, and then see where the [latex]K\left(d\right)[/latex] function is smaller.

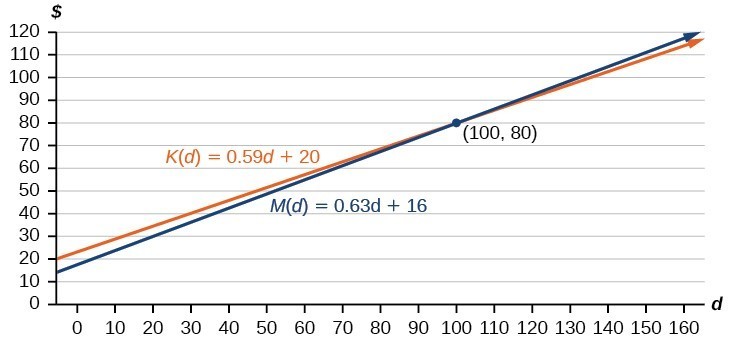
These graphs are sketched above, with K ( d ) in blue.

To find the intersection, we set the equations equal and solve:

[latex]\begin{array}{l}K\left(d\right)=M\left(d\right)\hfill \\ 0.59d+20=0.63d+16\hfill \\ 4=0.04d\hfill \\ 100=d\hfill \\ d=100\hfill \end{array}[/latex]

This tells us that the cost from the two companies will be the same if 100 miles are driven. Either by looking at the graph, or noting that [latex]K\left(d\right)[/latex] is growing at a slower rate, we can conclude that Keep on Trucking, Inc. will be the cheaper price when more than 100 miles are driven, that is [latex]d>100[/latex].

One application of systems of equations are mixture problems. Mixture problems are ones where two different solutions are mixed together resulting in a new final solution.  A solution is a mixture of two or more different substances like water and salt or vinegar and oil.  Most biochemical reactions occur in liquid solutions, making them important for doctors, nurses, and researchers to understand.  There are many other disciplines that use solutions as well.

The concentration or strength of a liquid solution is often described  as a percentage.  This number comes from the ratio of how much mass is in a specific volume of liquid.  For example if you have 50 grams of salt in a 100mL of water you have a 50% salt solution based on the following ratio:

[latex]\frac{50\text{ grams }}{100\text{ mL }}=0.50\frac{\text{ grams }}{\text{ mL }}=50\text{ % }[/latex]

Solutions used for most purposes typically come in pre-made concentrations from manufacturers, so if you need a custom concentration, you would need to mix two different strengths.  In this section, we will practice writing equations that represent the outcome from mixing two different concentrations of solutions.

We will use the following table to help us solve mixture problems:

To demonstrate why the table is helpful in solving for unknown amounts or concentrations of a solution, consider two solutions that are mixed together, one is 120mL of a 9% solution, and the other is 75mL of a 23% solution. If we mix both of these solutions together we will have a new volume and a new mass of solute and with those we can find a new concentration.

First, find the total mass of solids for each solution by multiplying the volume by the concentration.

Next we add the new volumes and new masses.

Now we have used mathematical operations to describe the result of mixing two different solutions. We know the new volume, concentration and mass of solute in the new solution.  In the following examples, you will see that we can use the table to find an unknown final volume or concentration. These problems can have either one or two variables. We will start with one variable problems, then move to two variable problems.

A chemist has 70 mL of a 50% methane solution. How much of an 80% solution must she add so the final solution is 60% methane?

Let’s use the problem solving process outlined in Module 1 to help us work through a solution to the problem.

Read and Understand:  We are looking for a new amount – in this case a volume –  based on the words “how much”.  We know two starting  concentrations and the final concentration, as well as one volume.

Define and Translate:  Solution 1 is the 70 mL of 50% methane and solution 2 is the unknown amount with 80% methane.  We can call our unknown amount x.

Write and Solve:   Set up the mixture table. Remember that concentrations are written as decimals before we can perform mathematical operations on them.

Multiply amount by concentration to get total, be sure to distribute on the last row: [latex]\left(70 + x\right)0.6[/latex]Add the entries in the amount column to get final amount. The concentration for this amount is 0.6 because we want the final solution to be 60% methane.

Add the total mass for solution 1 and solution 2 to get the total mass for the 60% solution. This is our equation for finding the unknown volume.

[latex]35+0.8x=42+0.6x[/latex]

[latex]\begin{array}{c}35+0.8x=42+0.6x\\\underline{-0.6x}\,\,\,\,\,\,\,\underline{-0.6x}\\35+0.2x=42\\\end{array}[/latex]

Subtract 35 from both sides

[latex]\begin{array}{c}35+0.2x=42\\\underline{-35}\,\,\,\,\,\,\,\underline{-35}\\0.2x=7\end{array}[/latex]

Divide both sides by 0.2

[latex]\begin{array}{c}0.2x=7\\\frac{0.2x}{0.2}=\frac{7}{0.2}\end{array}[/latex] [latex]x=35[/latex]

35mL must be added to the original 70 mL to gain a solution with a concentration of 60%

The above problem illustrates how we can use the mixture table to define an equation to solve for an unknown volume. In the next example we will start with two known concentrations and use a system of equations to find two starting volumes necessary to achieve a specified final concentration.

A farmer has two types of milk, one that is 24% butterfat and another which is 18% butterfat. How much of each should he use to end up with 42 gallons of 20% butterfat?

Read and Understand:  We are asked to find two starting volumes of milk whose concentrations of butterfat are both known. We also know the final volume is 42 gallons. There are two unknowns in this problem.

Define and Translate:  We will call the unknown volume of the  24% solution x, and the unknown volume of the 18% solution y.

Write and Solve:  Fill in the table with the information we know.

Find the total mass by multiplying the amount of each solution by the concentration. The total mass of the final solution comes from

When you sum the amount column you get one equation: [latex]x+ y = 42[/latex] When you sum the total column you get a second equation: [latex]0.24x + 0.18y = 8.4[/latex]

Use elimination to find a value for [latex]x[/latex], and [latex]y[/latex].

Multiply the first equation by [latex]-0.18[/latex]

[latex]\begin{array}{cc}-0.18(x+y) &= (42)(-0.18) \\ -0.18x-0.18y &= -7.56 \end{array}[/latex]

Now our system of equations looks like this:

[latex]\begin{array}{cc} -0.18x-0.18y &= -7.56\\0.24x + 0.18y &= 8.4 \end{array}[/latex]

Adding the two equations together to eliminate the y terms gives this equation:

[latex]0.06x = 8.4[/latex]

Divide by 0.06 on each side:

[latex]x = 14[/latex]

Now substitute the value for x into one of the equations in order to solve for y.

[latex]\begin{array}{cc} (14) + y &= 42\\ y &= 28 \end{array}[/latex]

This can be interpreted as 14 gallons of 24% butterfat milk added to 28 gallons of 18% butterfat milk will give 42 gallons of 20% butterfat milk.

In the following video you will be given an example of how to solve a mixture problem without using a table, and interpret the results.

Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.

Let’s take a look at a boat travelling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.

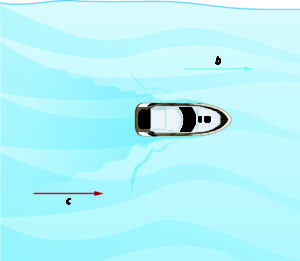
The images below show how a river current affects the speed at which a boat is actually travelling. We’ll call the speed of the boat in still water [latex]b[/latex] and the speed of the river current [latex]c[/latex].

The boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is [latex]b+c[/latex].

Now, the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is [latex]b-c[/latex].

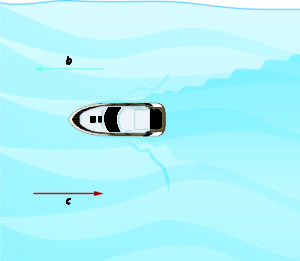
We’ll put some numbers to this situation in the next example.

Translate to a system of equations and then solve.

A river cruise ship sailed 60 miles downstream for 4 hours and then took 5 hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.

Read the problem: This is a uniform motion problem and a picture will help us visualize the situation.

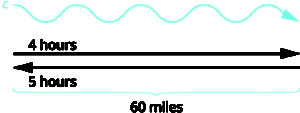
Identify  what we are looking for: We are looking for the speed of the ship in still water and the speed of the current.

Name  what we are looking for:

Let [latex]s=[/latex] the rate of the ship in still water.

Let [latex]c=[/latex] the rate of the current.

A chart will help us organize the information. The ship goes downstream and then upstream. Going downstream, the current helps the ship and so the ship’s actual rate is [latex]s+c[/latex]. Going upstream, the current slows the ship and so the actual rate is [latex]s-c[/latex]. Downstream it takes 4 hours. Upstream it takes 5 hours. Each way the distance is 60 miles.

Translate  into a system of equations. Since rate times time is distance, we can write the system of equations.

 [latex]\begin{array}{c}4(s+c)=60 \\ 5(s-c) = 60\end{array}[/latex]

Solve  the system of equations. Distribute to put both equations in standard form, then solve by elimination.

 [latex]\begin{array}{c}4s+4c=60 \\ 5s-5c = 60\end{array}[/latex]

Multiply the top equation by 5 and the bottom equation by 4. Add the equations, then solve for [latex]s[/latex].

[latex]\begin{array}{cc}20s+20c &= 300 \\ 20s-20c &= 240 \\ \hline \\ 40s &= 540 \\ s &= 13.5 \end{array}[/latex]

Substitute [latex]s=13.5[/latex] into one of the original equations.

[latex]\begin{array}{cc}4(s+c) &= 60 \\ 4(13.5+c) &= 60 \\ 54 + 4c &= 60 \\ 4c &= 6 \\ c &= 1.5 \end{array}[/latex]

Check  the answer in the problem. The downstream rate would be:

[latex]13.5+1.5 = 15[/latex] mph

In 4 hours the ship would travel:

[latex]15 \cdot 4 = 60[/latex] miles.

The upstream rate would be

[latex]13.5 - 1.5 = 12[/latex] mph.

In 5 hours the ship would travel

[latex]12\cdot 5[/latex] miles.

Answer  the question. The rate of the ship is 13.5 mph and the rate of the current is 1.5 mph.

In the next video, we present another example of a uniform motion problem which can be solved with a system of linear equations.

• Rates retrieved Aug 2, 2010 from http://www.budgettruck.com and http://www.uhaul.com/ ↵
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Solving Systems of Equations using Elimination. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/ova8GSmPV4o . License : CC BY: Attribution
• Question ID 115164, 115120, 115110. Authored by : Shabazian, Roy. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Beginning and Intermediate Algebra. Authored by : Wallace, Tyler. Located at : http://www.wallace.ccfaculty.org/book/book.html . License : CC BY: Attribution
• Question ID 29699. Authored by : McClure, Caren. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 23774. Authored by : Roy Shahbazian. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 8589. Authored by : Greg Harbaugh. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Question ID 2239. Authored by : Morales, Lawrence. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Ex: System of Equations Application - Mixture Problem.. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning.. Located at : https://youtu.be/4s5MCqphpKo. . License : CC BY: Attribution
• Beginning and Intermediate Algebra Textbook. . Authored by : Tyler Wallace. Located at : . License : CC BY: Attribution
• Ex: System of Equations Application - Plane and Wind problem. Authored by : James Sousa (Mathispower4u.com). Located at : https://www.youtube.com/watch?v=OuxMYTqDhxw . License : CC BY: Attribution
• Intermediate Algebra . Authored by : Lynn Marecek et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution

Linear Equations in Two Variables Questions

Linear equations in two variables questions presented here cover a variety of questions asked regarding linear equations in two variables with solutions and proper explanations. By practising these questions students will develop problem-solving skills.

Linear equations in two variables are linear polynomials with two unknowns. They are of the general form ax + by + c = 0, where x and y are the two variables, a and b are non-zero real numbers and c is a constant. The graphical representation of a linear equation in two variables is a straight line.

Linear Equations in Two Variables Questions with Solutions

Below are some practice questions on linear equations in two variables with detailed solutions.

Question 1: Solve for x and y:

\(\begin{array}{l}\frac{1}{2x}-\frac{1}{y}=-1,\:\:\frac{1}{x}+\frac{1}{2y}=8\:\:\:(x\neq0,\;y\neq0)\end{array} \)

Put 1/x = u and 1/y = v. The given equations become

u/2 – v = –1 ⇒ u – 2v = – 2 ….(i)

u + v/2 = 8 ⇒ 2u + v = 16 ….(ii)

Multiplying equation (ii) by 2 on both sides and adding (i) and (ii), we get

(u + 4u) + ( –2v + 2v) = –2 + 32

⇒ u = 6 ⇒ x = ⅙ and y = ¼

Question 2: Solve the system of linear equations 2x + 3y = 17 and 3x – 2y = 6 by the cross multiplication method.

By cross multiplication

\(\begin{array}{l}\frac{x}{\left\{ 3\times (-6)-(-2)\times(-17)\right\}}=\frac{y}{\left\{ -17\times 3-(-6)\times 2 \right\}}=\frac{1}{\left\{2\times (-2)-3 \times3\right\}}\end{array} \)

⇒ x/( –52) = y/( –39) = 1/( – 13)

⇒ x = 52/13 = 4 and y = 39/13 = 3

Hence x = 4 and y = 3 is the solution of given equations.

Question 3: Solve the following system of equations by substitution method:

2x + 3y = 0 and 3x + 4y = 5

Given equations,

2x + 3y = 0 ….(i)

3x + 4y = 5 …..(ii)

From (i) we get, y = – 2x/3, substituting value of y in (ii), we get

3x + 4(–2x/3) = 5

⇒ 9x – 8x = 15

Then y = (–2 × 15)/3 = – 10

Therefore, x = 15 and y = – 10 is solution of given system of equations.

Video Lesson on Consistent and Inconsistent Equations

Question 4: Find the value of k for which the given system of equations has infinitely many solutions: x + (k + 1)y = 5 and (k + 1)x + 9y + (1 – 8k) = 0.

The given equations will have infinitely many solutions if a 1 /a 2 = b 1 /b 2 = c 1 /c 2

Hence, 1/(k + 1) = (k + 1)/9 = – 5/(1 – 8k)

Solving the equations we get k = 2.

Question 5: If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel. Find the value of k.

If the lines are parallel, then they are inconsistent system of equations and a 1 /a 2 = b 1 /b 2 ≠ c 1 /c 2

Now, it should be 3/2 = 2k/5

Then we have 2k/5 = 30/20 = 3/2, which satisfies the condition of inconsistency.

Question 6: Find the value of k for which the system of equations has a non-zero solution

5x + 3y = 0 and 10x + ky = 0

The given equations are homogenous equations, they will have a non-zero solution if a 1 /a 2 = b 1 /b 2

Then, 5/10 = 3/k

⇒ 1/2 = 3/k

Question7: The monthly incomes of A and B are in the ratio 8:7 and their expenditures are in the ratio 19:16. If each saves ₹ 5000 per month, find the monthly income of each.

Let the monthly incomes of A and B be 8x and 7x rupees respectively, and let their monthly expenditure be 19y and 16y rupees respectively.

Monthly savings of A = 8x – 19y = 5000 ….(i)

Monthly savings of B = 7x – 16y = 5000 ….(ii)

Multiplying (i) 16 and (ii) by 19 and subtracting (ii) from (i) we get

(16 × 8x – 19 × 7x) = 5000 (16 – 19)

⇒ 5x = 15000 ⇒ x = 3000

Monthly income of A is (8 × 3000) = ₹24,000

Monthly income of B is (7 × 3000) = ₹21,000

Question 8: The sum of a two-digit number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the original number.

Let the original number be (10x + y)

According to the question,

(10x + y) + (10y + x) = 99

⇒ 11(x + y) = 99

⇒ x + y = 9 ….(i)

And x – y = 3 ….(ii)

Adding equations (i) and (ii), we get,

Hence the required number is 63.

Question 9: A man’s age is three times the sum of the ages of his two sons. After 5 years, his age will be twice the sum of his two son’s age. Find the age of the man.

Let the age of the man be x and the sum of the ages of his two sons be y.

x = 3y ⇒ x – 3y = 0 ….(i)

And (x + 5) = 2(y + 5 + 5)

⇒ x – 2y = 15 ….(ii)

Subtracting equation (i) from (ii) we get

Y = 15 and from (i) x = 45.

The present age of the man is 45 years.

Question 10: A man can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours, Find his speed of rowing in still water. Also, find the speed of the stream.

Let the speed of the man in still water be x km/hr and let the speed of the current be y kn/hr.

Speed in downstream = (x + y) km/hr

Speed in upstream = (x – y) km/hr

But speed in downstream = 20/2 km/hr = 10 km/hr

And speed in upstream = 4/2 km/hr = 2 km/hr

∴ x + y = 10 and x – y = 2

Solving both the equations we get;

x = 6 and y = 4.

Hence, the speed of the man in still water is 6 km/hr and the speed of the current is 4 km/hr.

Question 11: Find the four angles of a cyclic Quadrilateral ABCD in which ∠A = (2x – 1) o , ∠B = (y + 5) o , ∠C = (2y + 15) o , and ∠D = (4x – 7) o .

We know that sum of opposite angles of a cyclic quadrilateral is 180 o

∴ ∠A + ∠C = 180 o and ∠B + ∠C = 180 o

∠A + ∠C = 180 o ⇒ (2x – 1) + (2y + 15) = 180 o

⇒ x + y = 83 ….(i)

∠B + ∠C = 180 o ⇒ (y + 5) + (4x – 7) = 180 o

⇒ 4x + y = 182 …..(ii)

Subtracting (i) from (ii) we get

3x = 182 – 83 ⇒ x = 33

Substituting in (i), we get y = 50

∴ ∠A = 2 × 33 – 1 = 65 o

∠B = 50 + 5 = 55 o

∠C = 2 × 50 + 15 = 115 o

∠D = 4 × 33 – 7 = 125 o .

Question 12: 8 men and 12 boys can finish a piece of work in 5 days, while 6 men and 8 boys can finish it in 7 days. Find time taken by a man and a boy alone to finish the same work.

Let 1 man can finish the work in x days and let 1 boy can finish the work in y days.

1 man’s one day work = 1/x

1 boy’s one day work = 1/y

8 men’s 1 day’s work + 12 boy’s one day’s work = ⅕

⇒ 8/x + 12/y = ⅕

⇒ 8u + 12v = ⅕ ….(i) where u = 1/x and v = 1/y

Similarly, 6u + 8v = 1/7 ….(ii)

On solving (i) and (ii) we get, x = 70 and y = 140

∴ One man alone can finish the work in 70 days and one boy alone can finish the work in 140 days.

Related Articles:

Practice questions:.

1. Five years ago Anna was three times older than Mira and ten years later Anna will be two times older than Mira. What are the present ages of Anna and Mira?

2. The difference of two numbers is 4 and the difference of their reciprocals is 4/21. Find the numbers.

3. Find the value of k for which the system of equations 5x – 3y = 0, and 2x + ky = 0 has a non-zero solution.

4. Find the value of a and b for which each of the following systems of linear equations

(a – 1)x + 3y = 2 and 6x + (1 – 2b)y = 6 has infinite number of solutions.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.20: Word Problems for Linear Equations

• Last updated
• Save as PDF
• Page ID 45640

Word problems are important applications of linear equations. We start with examples of translating an English sentence or phrase into an algebraic expression.

Example 18.1

Translate the phrase into an algebraic expression:

a) Twice a variable is added to 4

Solution: We call the variable \(x .\) Twice the variable is \(2 x .\) Adding \(2 x\) to 4 gives:

\[4 + 2x\nonumber\]

b) Three times a number is subtracted from 7.

Solution: Three times a number is \(3 x .\) We need to subtract \(3 x\) from 7. This means:\

\[7-3 x\nonumber\]

c) 8 less than a number.

Solution: The number is denoted by \(x .8\) less than \(x\) mean, that we need to subtract 8 from it. We get:

\[x-8\nonumber\]

For example, 8 less than 10 is \(10-8=2\).

d) Subtract \(5 p^{2}-7 p+2\) from \(3 p^{2}+4 p\) and simplify.

Solution: We need to calculate \(3 p^{2}+4 p\) minus \(5 p^{2}-7 p+2:\)

\[\left(3 p^{2}+4 p\right)-\left(5 p^{2}-7 p+2\right)\nonumber\]

Simplifying this expression gives:

\[\left(3 p^{2}+4 p\right)-\left(5 p^{2}-7 p+2\right)=3 p^{2}+4 p-5 p^{2}+7 p-2 =-2 p^{2}+11 p-2\nonumber\]

e) The amount of money given by \(x\) dimes and \(y\) quarters.

Solution: Each dime is worth 10 cents, so that this gives a total of \(10 x\) cents. Each quarter is worth 25 cents, so that this gives a total of \(25 y\) cents. Adding the two amounts gives a total of

\[10 x+25 y \text{ cents or } .10x + .25y \text{ dollars}\nonumber\]

Now we deal with word problems that directly describe an equation involving one variable, which we can then solve.

Example 18.2

Solve the following word problems:

a) Five times an unknown number is equal to 60. Find the number.

Solution: We translate the problem to algebra:

\[5x = 60\nonumber\]

We solve this for \(x\) :

\[x=\frac{60}{5}=12\nonumber\]

b) If 5 is subtracted from twice an unknown number, the difference is \(13 .\) Find the number.

Solution: Translating the problem into an algebraic equation gives:

\[2x − 5 = 13\nonumber\]

We solve this for \(x\). First, add 5 to both sides.

\[2x = 13 + 5, \text{ so that } 2x = 18\nonumber\]

Dividing by 2 gives \(x=\frac{18}{2}=9\).

c) A number subtracted from 9 is equal to 2 times the number. Find the number.

Solution: We translate the problem to algebra.

\[9 − x = 2x\nonumber\]

We solve this as follows. First, add \(x\) :

\[9 = 2x + x \text{ so that } 9 = 3x\nonumber\]

Then the answer is \(x=\frac{9}{3}=3\)

d) Multiply an unknown number by five is equal to adding twelve to the unknown number. Find the number.

Solution: We have the equation:

\[5x = x + 12.\nonumber\]

Subtracting \(x\) gives

\[4x = 12.\nonumber\]

Dividing both sides by 4 gives the answer: \(x=3\).

e) Adding nine to a number gives the same result as subtracting seven from three times the number. Find the number.

Solution: Adding 9 to a number is written as \(x+9,\) while subtracting 7 from three times the number is written as \(3 x-7\). We therefore get the equation:

\[x + 9 = 3x − 7.\nonumber\]

We solve for \(x\) by adding 7 on both sides of the equation:

\[x + 16 = 3x.\nonumber\]

Then we subtract \(x:\)

\[16 = 2x.\nonumber\]

After dividing by \(2,\) we obtain the answer \(x=8\)

The following word problems consider real world applications. They require to model a given situation in the form of an equation.

Example 18.3

a) Due to inflation, the price of a loaf of bread has increased by \(5 \%\). How much does the loaf of bread cost now, when its price was \(\$ 2.40\) last year?

Solution: We calculate the price increase as \(5 \% \cdot \$ 2.40 .\) We have

\[5 \% \cdot 2.40=0.05 \cdot 2.40=0.1200=0.12\nonumber\]

We must add the price increase to the old price.

\[2.40+0.12=2.52\nonumber\]

The new price is therefore \(\$ 2.52\).

b) To complete a job, three workers get paid at a rate of \(\$ 12\) per hour. If the total pay for the job was \(\$ 180,\) then how many hours did the three workers spend on the job?

Solution: We denote the number of hours by \(x\). Then the total price is calculated as the price per hour \((\$ 12)\) times the number of workers times the number of hours \((3) .\) We obtain the equation

\[12 \cdot 3 \cdot x=180\nonumber\]

Simplifying this yields

\[36 x=180\nonumber\]

Dividing by 36 gives

\[x=\frac{180}{36}=5\nonumber\]

Therefore, the three workers needed 5 hours for the job.

c) A farmer cuts a 300 foot fence into two pieces of different sizes. The longer piece should be four times as long as the shorter piece. How long are the two pieces?

\[x+4 x=300\nonumber\]

Combining the like terms on the left, we get

\[5 x=300\nonumber\]

Dividing by 5, we obtain that

\[x=\frac{300}{5}=60\nonumber\]

Therefore, the shorter piece has a length of 60 feet, while the longer piece has four times this length, that is \(4 \times 60\) feet \(=240\) feet.

d) If 4 blocks weigh 28 ounces, how many blocks weigh 70 ounces?

Solution: We denote the weight of a block by \(x .\) If 4 blocks weigh \(28,\) then a block weighs \(x=\frac{28}{4}=7\)

How many blocks weigh \(70 ?\) Well, we only need to find \(\frac{70}{7}=10 .\) So, the answer is \(10 .\)

Note You can solve this problem by setting up and solving the fractional equation \(\frac{28}{4}=\frac{70}{x}\). Solving such equations is addressed in chapter 24.

e) If a rectangle has a length that is three more than twice the width and the perimeter is 20 in, what are the dimensions of the rectangle?

Solution: We denote the width by \(x\). Then the length is \(2 x+3\). The perimeter is 20 in on one hand and \(2(\)length\()+2(\)width\()\) on the other. So we have

\[20=2 x+2(2 x+3)\nonumber\]

Distributing and collecting like terms give

\[20=6 x+6\nonumber\]

Subtracting 6 from both sides of the equation and then dividing both sides of the resulting equation by 6 gives:

\[20-6=6 x \Longrightarrow 14=6 x \Longrightarrow x=\frac{14}{6} \text { in }=\frac{7}{3} \text { in }=2 \frac{1}{3} \text { in. }\nonumber\]

f) If a circle has circumference 4in, what is its radius?

Solution: We know that \(C=2 \pi r\) where \(C\) is the circumference and \(r\) is the radius. So in this case

\[4=2 \pi r\nonumber\]

Dividing both sides by \(2 \pi\) gives

\[r=\frac{4}{2 \pi}=\frac{2}{\pi} \text { in } \approx 0.63 \mathrm{in}\nonumber\]

g) The perimeter of an equilateral triangle is 60 meters. How long is each side?

Solution: Let \(x\) equal the side of the triangle. Then the perimeter is, on the one hand, \(60,\) and on other hand \(3 x .\) So \(3 x=60\) and dividing both sides of the equation by 3 gives \(x=20\) meters.

h) If a gardener has \(\$ 600\) to spend on a fence which costs \(\$ 10\) per linear foot and the area to be fenced in is rectangular and should be twice as long as it is wide, what are the dimensions of the largest fenced in area?

Solution: The perimeter of a rectangle is \(P=2 L+2 W\). Let \(x\) be the width of the rectangle. Then the length is \(2 x .\) The perimeter is \(P=2(2 x)+2 x=6 x\). The largest perimeter is \(\$ 600 /(\$ 10 / f t)=60\) ft. So \(60=6 x\) and dividing both sides by 6 gives \(x=60 / 6=10\). So the dimensions are 10 feet by 20 feet.

i) A trapezoid has an area of 20.2 square inches with one base measuring 3.2 in and the height of 4 in. Find the length of the other base.

Solution: Let \(b\) be the length of the unknown base. The area of the trapezoid is on the one hand 20.2 square inches. On the other hand it is \(\frac{1}{2}(3.2+b) \cdot 4=\) \(6.4+2 b .\) So

\[20.2=6.4+2 b\nonumber\]

Multiplying both sides by 10 gives

\[202=64+20 b\nonumber\]

Subtracting 64 from both sides gives

\[b=\frac{138}{20}=\frac{69}{10}=6.9 \text { in }\nonumber\]

and dividing by 20 gives

Exit Problem

Write an equation and solve: A car uses 12 gallons of gas to travel 100 miles. How many gallons would be needed to travel 450 miles?

Word Problems on Simultaneous Linear Equations

Solving the solution of two variables of system equation that leads for the word problems on simultaneous linear equations is the ordered pair (x, y) which satisfies both the linear equations.

Problems of different problems with the help of linear simultaneous equations:

We have already learnt the steps of forming simultaneous equations from mathematical problems and different methods of solving simultaneous equations.

In connection with any problem, when we have to find the values of two unknown quantities, we assume the two unknown quantities as x, y or any two of other algebraic symbols.

Then we form the equation according to the given condition or conditions and solve the two simultaneous equations to find the values of the two unknown quantities. Thus, we can work out the problem.

Worked-out examples for the word problems on simultaneous linear equations: 1. The sum of two number is 14 and their difference is 2. Find the numbers. Solution: Let the two numbers be x and y.

x + y = 14 ………. (i)

x - y = 2 ………. (ii)

Adding equation (i) and (ii), we get 2x = 16

or, 2x/2 = 16/2 or, x = 16/2

or, x = 8 Substituting the value x in equation (i), we get

or, 8 – 8 + y = 14 - 8

or, y = 14 - 8

or, y = 6 Therefore, x = 8 and y = 6

Hence, the two numbers are 6 and 8.

2. In a two digit number. The units digit is thrice the tens digit. If 36 is added to the number, the digits interchange their place. Find the number. Solution:

Let the digit in the units place is x

And the digit in the tens place be y.

Then x = 3y and the number = 10y + x

The number obtained by reversing the digits is 10x + y. If 36 is added to the number, digits interchange their places,

Therefore, we have 10y + x + 36 = 10x + y

or, 10y – y + x + 36 = 10x + y - y

or, 9y + x – 10x + 36 = 10x - 10x

or, 9y - 9x + 36 = 0 or, 9x - 9y = 36

or, 9(x - y) = 36

or, 9(x - y)/9 = 36/9

or, x - y = 4 ………. (i) Substituting the value of x = 3y in equation (i), we get

or, y = 4/2

or, y = 2 Substituting the value of y = 2 in equation (i),we get

or, x = 4 + 2

Therefore, the number becomes 26. 

3.  If 2 is added to the numerator and denominator it becomes 9/10 and if 3 is subtracted from the numerator and denominator it become 4/5. Find the fractions. 

Solution:   Let the fraction be x/y. 

If 2 is added to the numerator and denominator fraction becomes 9/10 so, we have

(x + 2)/(y + 2) = 9/10

or, 10(x + 2) = 9(y + 2) 

or, 10x + 20 = 9y + 18

or, 10x – 9y + 20 = 9y – 9y + 18

or, 10x – 9x + 20 – 20 = 18 – 20 

or, 10x – 9y = -2 ………. (i)  If 3 is subtracted from numerator and denominator the fraction becomes 4/5 so, we have 

(x – 3)/(y – 3) = 4/5

or, 5(x – 3) = 4(y – 3) 

or, 5x – 15 = 4y – 12

or, 5x – 4y – 15 = 4y – 4y – 12 

or, 5x – 4y – 15 + 15 = – 12 + 15

or, 5x – 4y = 3 ………. (ii) 

So, we have 10x – 9y = – 2 ………. (iii) 

and 5x – 4y = 3 ………. (iv)  Multiplying both sided of equation (iv) by 2, we get

10x – 8y = 6 ………. (v) 

Now, solving equation (iii) and (v) , we get

10x – 9y = -2

10x – 8y =  6         - y = - 8

          y = 8 

Substituting the value of y in equation (iv) 

5x – 4 × (8) = 3

5x – 32 = 3

5x – 32 + 32 = 3 + 32

Therefore, fraction becomes 7/8. 4.  If twice the age of son is added to age of father, the sum is 56. But if twice the age of the father is added to the age of son, the sum is 82. Find the ages of father and son.  Solution:  Let father’s age be x years

Son’s ages = y years

Then 2y + x = 56 …………… (i) 

And 2x + y = 82 …………… (ii)  Multiplying equation (i) by 2, (2y + x = 56 …………… × 2)we get

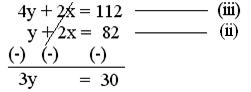
or, 3y/3 = 30/3

or, y = 30/3

or, y = 10 (solution (ii) and (iii) by subtraction) Substituting the value of y in equation (i), we get;

2 × 10 + x = 56

or, 20 + x = 56

or, 20 – 20 + x = 56 – 20

or, x = 56 – 20

5. Two pens and one eraser cost Rs. 35 and 3 pencil and four erasers cost Rs. 65. Find the cost of pencil and eraser separately. Solution: Let the cost of pen = x and the cost of eraser = y

Then 2x + y = 35 ……………(i)

And 3x + 4y = 65 ……………(ii) Multiplying equation (i) by 4,

Subtracting (iii) and (ii), we get;

or, 5x/5 = 75/5

or, x = 75/5

or, x = 15 Substituting the value of x = 15 in equation (i) 2x + y = 35 we get;

or, 2 × 15 + y = 35

or, 30 + y = 35

or, y = 35 – 30

Therefore, the cost of 1 pen is Rs. 15 and the cost of 1 eraser is Rs. 5.

●   Simultaneous Linear Equations

Simultaneous Linear Equations

Comparison Method

Elimination Method

Substitution Method

Cross-Multiplication Method

Solvability of Linear Simultaneous Equations

Pairs of Equations

Practice Test on Word Problems Involving Simultaneous Linear Equations

●   Simultaneous Linear Equations - Worksheets

Worksheet on Simultaneous Linear Equations

Worksheet on Problems on Simultaneous Linear Equations

8th Grade Math Practice   From Word Problems on Simultaneous Linear Equations to HOME PAGE

New! Comments

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer

Apr 09, 24 02:58 PM

Division by Two-Digit Numbers | Knowledge of Estimation | Division

Apr 09, 24 02:51 PM

4th Grade Mental Math on Division | Division Mental Math | Answers

Apr 09, 24 12:53 PM

4th Grade Division Worksheet | Simple Division | Math Division|Answers

Apr 09, 24 01:27 AM

Worksheet on Word Problems on Division | Division Word Problems

Apr 08, 24 02:58 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Become a math whiz with AI Tutoring, Practice Questions & more.

Writing Systems of Linear Equations from Word Problems

As we learn about math, we often ask ourselves, "How is any of this knowledge useful in life? When will I ever need to use algebra?" Here''s the thing: When you know how to "translate" word problems into algebraic equations, you''ll immediately see how useful math really is. With a few simple steps, you can turn real questions about the world around you into equations, allowing you to calculate things that you never thought possible. It''s one of the most interesting things about math -- so let''s get started!

How to tell when a word problem can become a linear equation

• There are different quantities of things, such as a specific number of people, objects, hours, and so on.
• Each quantity has a clear value. Instead of saying, "There are a few boxes," the word problem needs to tell us how many boxes there are. Are there five? Six? Seven?
• We need to know at least some of these values to build our linear equation. The unknowns can become variables, like "x" or "y."

How to turn word problems into linear equations

• Take a second to think about the "problem." What are we trying to find out? What is the "variable" in this word problem? Define all of the words carefully. If we can''t define the words properly, our equation won''t be accurate.
• Turn the word problem into an equation. Plug in all of your known values and use letters like "x" and "y" to represent the unknown variables. Make sure you write out what each variable represents below the equation so you don''t forget.
• Solve the equation. Using our math skills, we can now solve the problem and find the values of our variables. We can use a wide range of strategies to solve the equation, including substitution, elimination, or graphing.

An example of a word problem translated into a linear equation

Now let''s see how this all works with an example. Here''s our word problem: We decided to go to a music concert with all our friends, including 12 children and 3 adults. We paid for everyone''s tickets for a total of $162. Another group of friends paid $122 for 8 children and 3 adults. How much does a child''s ticket cost, and how much does an adult''s ticket cost? 1. Understand the problem We know two values: 12 children and 3 adults cost $162, while 8 children and 3 adults cost $122. What we don''t know is how much an adult''s ticket costs, and how much a child''s ticket costs. Let''s create variables for those unknowns: x = the cost of one child''s ticket y = the cost of one adult''s ticket 2. Translate the problem into an equation We know that 12 children and 3 adults cost $162. Let''s plug in our variables and create an equation based on this: 12x+3y = 162 We can do the same for the other group of concert-goers: 8x+3y = 122 3. Solve the equation, On one weekend they sold a total of 12 adult tickets and 3 child tickets for a total of 162 dollars, and the next weekend they sold 8 adult tickets and 3 child tickets for 122 dollars, find the price for a child''s and adult''s ticket. When we have two very similar equations like this, we can simply subtract them from each other to get the values we need: 12x+3y = 162 8x +3y = 1224x = 40x = 10 Now that we know the value of x, we can use it to find y. 12(10)+3y = 162120+3y = 1623y = 42y = 14 Now we know that a child''s ticket costs $10, while an adult''s ticket costs $14. We can now check our work by plugging our solutions back into our original equations: 12(10)+3(14) = 162 8(10)+3(14) = 122 You can use this strategy to solve all kinds of everyday math problems you encounter in life!

Topics related to the Writing Systems of Linear Equations from Word Problems

Consistent and Dependent Systems

Word Problems

Cramer''s Rule

Flashcards covering the Writing Systems of Linear Equations from Word Problems

Algebra 1 Flashcards

College Algebra Flashcards

Practice tests covering the Writing Systems of Linear Equations from Word Problems

Algebra 1 Diagnostic Tests

College Algebra Diagnostic Tests

Get more help with linear equation word problems

Does your child need a little extra help? Are they craving new challenges? Contact Varsity Tutors today, and we will find them a professional math tutor whose skills match your student''s unique needs. Whether they need more help identifying elements from a word problem to plug into a potential linear equation or they need more challenging problems, a tutor can provide exactly the type of assistance your student needs.

• Contemporary Communication Tutors
• Immunology Tutors
• Honors Brief Calculus Tutors
• Nanoscience Tutors
• Actuarial Exam PA Courses & Classes
• Naturalization Tutors
• Animal Communications Tutors
• Security Management Tutors
• High School Reading Tutors
• CNA - Certified Nursing Assistant Tutors
• Interlinguistics Tutors
• Subtraction Tutors
• CLEP Introductory Business Law Test Prep
• Supply Chain Management Tutors
• Arabic Tutors
• TESOL - Teaching English to Speakers of Other Languages Training
• SAT Subject Test in Japanese with Listening Courses & Classes
• CCNA Collaboration - Cisco Certified Network Associate-Collaboration Test Prep
• NMLS - Nationwide Mortgage Licensing System Test Prep
• Oklahoma Bar Exam Test Prep
• Buffalo Tutoring
• Kansas City Tutoring
• San Diego Tutoring
• Detroit Tutoring
• Denver Tutoring
• San Francisco-Bay Area Tutoring
• New York City Tutoring
• Chicago Tutoring
• Tucson Tutoring
• Dayton Tutoring
• Statistics Tutors in Phoenix
• Spanish Tutors in Chicago
• ACT Tutors in Boston
• ACT Tutors in Chicago
• Physics Tutors in San Diego
• Algebra Tutors in Chicago
• Chemistry Tutors in Dallas Fort Worth
• Spanish Tutors in Seattle
• SSAT Tutors in New York City
• Computer Science Tutors in Philadelphia