word problems solved by elimination method

WORD PROBLEMS USING ELIMINATION METHOD

Problem 1 :

Find the value of two numbers if their sum is 12 and their difference is 4.

Let x and y be the two numbers.

Given : T heir sum is 12.

x + y = 12 ----(1)

Given : T heir difference is 4.

x - y = 4 ----(1)

(1) + (2) :

Divide both sides by 2.

Substitute x = 8 into (1).

Subtract 12 from both sides.

Therefore, the numbers are 8 and 4.

Problem 2 :

Kevin bought pen and pencils in a total of 50. The cost of each pen is $2 and that of a pencil is $1.50. If he had paid a total of $85 for his purchase, find the cost of a pen and a pencil.

Let x and y be the costs of a pen and a pencil respectively.

Given : Kevin bought pen and pencils in a total of 50.

x + y = 50 ----(1)

Given : The cost of each pen is $2, a pencil is  $1.50 and Kevin paid a total of $85 for his purchase.

2x + 1.5y = 85 ----(2)

1.5(1) - (2) :

Divide both sides by 0.5.

Substitute x = 20 into (1).

20 + y = 50

Subtract 20 from both sides.

number of pens = 20

number of pencils = 30

Problem 3 :

The sum of two numbers is 7. The difference between 5 times the larger and 3 times the smaller is equal 11. Find the numbers. 

Let x and y be the two numbers such that x > y.

Given : The sum of two numbers is 7.

x + y = 7 ----(1)

Given : The difference between 5 times the larger and 3 times the smaller is equal 11.

5x - 3y = 11 ----(2)

3(1) + (2) :

Divide both sides by 8.

Substitute x = 4 into (1).

Subtract 3 from both sides.

Therefore, the two numbers are 4 and 3.

Problem 4 :

Chase and Sara went to the candy store. Chase bought 5 pieces of fudge and 3 pieces of bubble gum for a total of $5.70. Sara bought 2 pieces of fudge and 10 pieces of bubble gum for a total of $3.60. Find the cost of 1 piece of fudge and 1 piece of bubble gum?

Let f and g be the costs of 1 piece of fudge and 1 piece of bubble.

From the given information,

5f + 3b = 5.7 ----(1)

2f + 10b = 3.6 ----(2)

2(1) - 5(2) :

Divide both sides by -44.

Substitute x = 0.15 into (2).

 2(0.15) + 10b = 3.6

0.3 + 10b = 3.6

Subtract 0.3 from both sides.

Divide both sides by 10.

cost of 1 piece of fudge = $0.15

cost of 1  piece of bubble gum = $0.33

Problem 5 :

Daily earnings of Oliver and Henry are in the ratio 3 : 4 and their expenditures are in the ratio 5 : 7. If each saves $50 per day, find the daily earnings of each.

From the earnings ratio 3 : 4,

earnings of Oliver = 3x

earnings of Henry = 4x

From the expenditures ratio 5 : 7,

expenditure of Oliver = 5y

expenditure of Henry = 7y

The relationship between income, expenditure and savings :

Income - Expenditure = Savings

Then, we have

3x - 5y = 50 ----(1)

4x - 7y = 50 ----(2)

7(1) - 5(2) :

earnings of Oliver = 3(100) = $300

earnings of Henry = 4(100) = $400

Problem 6 :

The sum of the present ages of a father and his son is 45 years. 10 years hence, the difference between their ages is 25 years. Find the present age of the father and son.

Let f and s be the present ages of father and son.

Given : The sum of the present ages 45.

f + s = 45 ----(1)

Given : 10 years hence, the difference between the ages is 25.

(f + 10) - (s + 10) = 25

f + 10 - s - 10 = 25

f - s = 25 ----(2)

Substitute f = 35 into (1).

 35 + s = 45

Subtract 35 from both sides.

present age of the father = 35 years

present age of the son = 10 years

Problem 7 :

In a three digit number, the middle digit is zero and sum of the other two digits is 9. If 99 is added to it, the digits are reversed. Find the three digit number.

Let x 0 y  be the required three digit number.

x + y = 9 ----(1)

Given : When 99  is added to it, the digits are reversed.

x 0 y + 99 = y 0 x

100(x) + 10(0) + 1(y) + 99 = 100(y) + 10(0) + 1(x)

100x + 0 + y + 99 = 100y + 0 + x

100x + y + 99 = 100y + x

99x - 99y = -99

Divide both sides by 99.

x - y = -1 ----(2)

Substitute x  = 4 into (1).

Subtract 4 from both sides.

x 0 y = 405

Therefore, the three digit number is 405.

Problem 8 :

Two numbers are such that twice the greater number exceeds twice the sm aller one by 18. One-third of the smaller number and one-fifth of the greater number are together 21. Find the two numbers.

Let x  and  y  be the two numbers such that x > y .

Given : Twice the greater number exceeds twice the smaller one by 18.

2x - 2y = 18

x - y = 9 ----(1)

Given : One-third of the smaller number and one-fifth of the greater number are together 21.

5y  + 3x = 315

3x + 5y = 315 ----(2)

5(1) + (2) :

Substitute x  = 45 into (1).

Subtract 45 from both sides.

Therefore, the two numbers are 45 and 36.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

How to Find a Limit Using a Table

Apr 09, 24 08:44 PM

Evaluating Logarithms Worksheet

Apr 09, 24 09:30 AM

Evaluating Logarithmic Expressions Worksheet

Apr 09, 24 02:01 AM

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Use Elimination to Solve a System of Equations: Word Problems

When confronted with a system of equations, numerous methods can guide you toward the solution, each with its unique process and appeal. One such method, termed ‘Elimination,’ provides a structured, systematic approach. This article will detail the elimination method step-by-step, contextualizing it within word problems.

A Step-by-step Guide to Using Elimination to Solve a System of Equations: Word Problems

Elimination, as the name suggests, focuses on eliminating one variable to simplify a system of equations. This method is particularly effective for linear equation systems where addition or subtraction can effectively reduce the system to one equation with one unknown.

Step 1: Decipher the Word Problem

The first step involves translating the narrative problem into mathematical terms . Identify the unknown variables and define them. For example, a problem may involve the cost of apples and bananas. Here, the unknowns are the cost of an apple and a banana.

Step 2: Develop the System of Equations

With the variables identified, the next task is to formulate a system of equations based on the problem’s conditions. Suppose the problem states that three apples and two bananas cost \($13\), and five apples and four bananas cost \($23\), you would get two equations: \(3a+2b=13\) and \(5a+4b=23\).

Step 3: Arrange for Elimination

Before you can eliminate a variable, the equations must be arranged appropriately . You should arrange the equations so that one of the variable’s coefficients in one equation is the opposite of the same variable’s coefficient in the other equation. If such a condition doesn’t exist, you might have to multiply one or both equations by a suitable number.

Step 4: Execute the Elimination

With the equations arranged, it’s time to add or subtract them to eliminate one variable . In our example, if we multiply the first equation by \(2\), we obtain: \(6a+4b=26\) and \(5a+4b=23\). Subtraction of the first from the second equation eliminates \(b\), giving \(-a=-3\).

Step 5: Solve for the Remaining Variable

With one variable eliminated, you’re left with a simple equation to solve. In our case, solving \(-a=-3\) gives the price of an apple.

Step 6: Substitute and Solve for the Second Variable

Substitute the found value into any original equation to solve for the second variable . If the price of an apple is found to be \(3\), substituting this into \(3a+2b=13\) will yield the price of a banana.

Step 7: Verify Your Solution

Always ensure to check the solution by substituting the values back into the original equations. If both equations hold true, you’ve successfully solved the system.

by: Effortless Math Team about 10 months ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• The Best THEA Math Worksheets: FREE & Printable
• SAT Math Level 2 Calculator Tips to Boost Your Score
• Top 5 Best Math YouTube Channels for High School Students
• The Ultimate 7th Grade FSA Math Course (+FREE Worksheets)
• How to Find Domain and Range of a Function?
• Top 10 Algebra 2 Textbooks in 2024 (Expert Recommendations)
• Deciphering Chance: A Comprehensive Guide to Mutually Exclusive Events in Probability
• 7th Grade SBAC Math FREE Sample Practice Questions
• Check Registers: Learn How to Develop the Ability to Organize Transactions
• Using Number Lines to Compare and Order Rational Numbers

What people say about "How to Use Elimination to Solve a System of Equations: Word Problems - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos
• Google Play
• Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Math Worksheets

Just another wordpress site, site navigation.

• Constant of Proportionality Worksheets
• Coordinate Graph Worksheets–Interpreting
• Equivalent Expressions Worksheets–Perimeter
• Equivalent Expressions Worksheets–Word Problems
• Integer Division Worksheets
• Number Line Worksheets–Integers
• Number Line Worksheets–Rational Numbers
• Rational Number Expressions Worksheets
• Tape Diagram Worksheets
• Analyzing Equations Worksheets
• Function Interval Worksheets
• Repeating Decimals Worksheets
• Scientific Notation Worksheets–Multiples
• Simultaneous Linear Equation Worksheets (Part I)
• Simultaneous Linear Equation Worksheets (Part II)
• Systems of Equations (How Many Solutions?)
• Transformation Effects Worksheets
• Transformation Series Worksheets
• Evaluating Expressions Worksheets
• Factoring Polynomials Worksheets
• Graphing Inequalities Worksheets (Single Variable)
• Solving Inequalities Worksheets
• Solving Inequalities with Absolute Value Worksheets
• Order of Operations Worksheets
• Equations & Word Problems (Combining Like Terms)
• Slope of a Line from a Graph–Points Given
• Slope Worksheets (Two Points-No Graph)
• Changing One Equation
• Changing Two Equations

Word Problems

• Multiple Choice Worksheets
• Substitution Worksheets
• Already Graphed
• Graphing Systems of Equations (Slope-Intercept Form)
• Graphing Systems of Equations (Standard Form)
• Trigonometry Worksheets
• Auto-Generated Worksheets
• Interpreting Points on a Graph
• Adding Decimals Worksheets
• Comparing Decimals-Decimal Inequalities
• Decimal Division-Integer Divisors (1 Digit)
• Decimal Division-Integer Divisors (2 Digit)
• Decimal Division-Integer Divisors (3 Digit)
• Decimal Division-Integer Divisors (MIXED Digits)
• Decimal Division-Decimal Divisors (Tenths into Tenths)
• Decimal Division-Decimal Divisors (Tenths into Hundredths)
• Decimal Division-Decimal Divisors (Tenths into Thousandths)
• Decimal Division-Decimal Divisors (Hundredths into Hundredths)
• Decimal Division-Decimal Divisors (Hundredths into Thousandths)
• Decimal Division-Decimal Divisors (Thousandths into Thousandths)
• Decimal Division-MIXED Decimal Divisors
• MIXED Decimal & Integer Divisors (1-Digit)
• MIXED Decimal & Integer Divisors (2-Digits)
• MIXED Decimal & Integer Divisors (3-Digits)
• Adding 1 Zero (Single-Digit Integer Divisor)
• Adding 1 Zero (Two-Digit Integer Divisor)
• Adding 1 Zero (Single-Digit Decimal Divisors)
• Adding 1 Zero (Two-Digit Decimal Divisors)
• Adding 2 Zeros (Single-Digit Integer Divisors)
• Adding 2 Zeros (Two-Digit Integer Divisors)
• Adding 2 Zeros (Decimal Divisors)
• Repeating Decimals (One Digit Patterns)
• Repeating Decimals (Two Digit Patterns)
• Repeating Decimals (Three Digit Patterns)
• Decimal Division Word Problem Worksheets
• Multiplying Decimals Worksheets
• Subtracting Decimals Worksheets
• Writing Decimals as Fractions Worksheets
• Checking Equation Solutions–Distributive Property
• Checking Equation Solutions–Like Terms
• Checking Equation Solutions–Variables on Both Sides
• Checking Two-Step Equation Solutions
• Solving Equations with Like Terms
• Solving Equations with the Distributive Property Worksheets
• Solving Equations with Variables on Both Sides Worksheets
• Solving Equations with Absolute Value Worksheets
• Solving Proportions
• Equations and Word Problems (Two Step Equations)
• Equations and Word Problems (Combining Like Terms) Worksheets
• Adding Fractions Worksheets
• Comparing Fractions Worksheets
• Dividing Fractions Worksheets
• Multiplying Fractions Worksheets
• Proportions & Fractions Worksheets
• Subtracting Fractions Worksheets
• Exterior Angles Worksheets
• Interior Angles Worksheets
• Parallel Lines & Transversals Worksheets
• Areas of Circles Worksheets
• Areas of Parallelograms Worksheets
• Areas of Trapezoids Worksheets
• Areas of Triangles Worksheets
• Radius Given (Using 3.14)
• Diameter Given (Using 3.14)
• Radius or Diameter Given (Using 3.14)
• Radius Given (In Terms of Pi)
• Diameter Given (In Terms of Pi)
• Radius or Diameter Given (In Terms of Pi)
• Volume of a Rectangular Prism
• Volume of a Triangular Prism
• Absolute Value of a Number Worksheets
• Absolute Value Expressions (Simplifying) Worksheets
• Absolute Value Equations Workssheets
• Absolute Value Inequalities Worksheets
• Addition Worksheets
• Division Worksheets
• Multiplication Worksheets
• Percentage Worksheets
• Square Roots
• Subtraction Worksheets
• Mean/Median/Mode/Range Worksheets
• Mean Worksheets
• Median Worksheets
• Graphs and Mean/Median/Mode Worksheets
• Absolute Value–Simplifying Expressions Worksheets
• Absolute Value Equations Worksheets
• Absolute Value Inequality Worksheets
• Probability & Compound Events Worksheets
• Probability & Predictions Worksheets
• Theoretical Probability Worksheets
• Comparing Ratios Word Problem Worksheets
• Comparing Ratios Worksheets
• Part-to-Part Ratio Worksheets
• Part-to-Whole Ratio Worksheets
• Ratio Word Problems (w/Fractions)
• Simplified Ratios Word Problem Worksheets
• Writing Ratios Word Problem Worksheets
• Writing Ratios Word Problems (missing info)
• Writing Ratios Word Problems (w/distractors)
• Writing Ratios Worksheets
• Comparing Unit Rates Worksheets
• Unit Rate Word Problem Worksheets
• Unit Rates & Graphs Worksheets
• Unit Rates & Proportions Worksheets
• Unit Rates & Tables

Looking for Something?

Popular content.

• Simplifying Expressions Worksheets
• Absolute Value Worksheets

Word Problems Worksheet 1 – This 6 problem algebra worksheet will help you practice creating and solving systems of equations to represent real-life situations. You will use the “ elimination ” method to eliminate variables from standard form equations. Word Problems Worksheet 1 RTF Word Problems Worksheet 1 PDF View Answers

Word Problems Worksheet 3 – This 6 problem algebra worksheet will help you practice creating and solving systems of equations to represent real-life situations. Most of the problems involve money, so make sure you’re ready for some decimals. Word Problems Worksheet 3 RTF Word Problems Worksheet 3 PDF View Answers

Word Problems Worksheet 4 – This 6 problem algebra worksheet will help you practice creating and solving systems of equations to represent real-life situations. Most of the problems involve money, and a few distractors are introduced. Word Problems Worksheet 4 RTF Word Problems Worksheet 4 PDF View Answers

Word Problems Worksheet 5 – This 8 problem algebra worksheet features more abstract word problems like “ The sum of x and y is 42.  the difference of x and y is 13.  Find x and y .” There are a few negative integers, so be careful! Word Problems Worksheet 5 RTF Word Problems Worksheet 5 PDF View Answers

Word Problems Worksheet 6 – This 8 problem algebra worksheet features more abstract word problems like “ The sum of  twice a number, x, and twice another number, y, is 118.  The value of y is one less than twice the value of x.  Find x and y. ” One of the problems even has an infinite number of solutions! Word Problems Worksheet 6 RTF Word Problems Worksheet 6 PDF View Answers

These free  systems of equations   worksheets  will help you practice solving real-life systems of equations using the “ elimination ” method.  You will  need to create and solve a system of equations to represent each situation.  The exercises can also be solved using other algebraic methods if you choose.

This is a progressive series that starts simple with problems involving buying movie tickets and collecting for fundraisers.  Eventually the negative numbers , decimals , the  distributive property  and “ the opposite of x ” come into play.

Each worksheet will help students master Common Core skills in the Algebra strand.  They are great for ambitious students in pre-algebra or algebra classes.

These free  elmination  worksheets are printable and available in a variety of formats.  Each sheet includes an example to help you get started.  Of course, answer keys are provided as well.

Philip Teas

There are multiple problems with your worksheets. You have word problems which are unanswerable or answers which make no sense such as fractions of people. Your answer sheets are frequently incorrect. For a quick example: System of Equations- Word Problems #1 – KEY. Question #1 states that there are 9 tickets purchased, the Answer shows a=6 and b=2. 6+2 is 8 not 9. Question 5 on that same worksheet is unanswerable. I’ve found problems on worksheet 1, 2, 5 so far. How can you claim to have the best materials with so many clear problems?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Systems of Linear Equations Word Problems - Practice - Expii

Systems of linear equations word problems - practice, explanations (3).

(Videos) Set up Word Problems Using a System

by mathman1024

This video by mathman1024 works through word problems with systems of equations.

The general guideline to follow when doing these word problems is:

• Define your variables . Since this is a system, there will be two or more variables.
• Write your equations. Again, since this is a system, there will be two or more equations. This is also the tricky part which will be focused on in the videos.
• Solve the system. This can be done using the elimination method , substitution method , or graphing .
• State your answer.

The first problem that he goes over in the video is, " The sum of two numbers is 79, and their difference is 23. What are the two numbers? "

We want to write algebraic expressions for this system.

Step one is defining the variables. The question asks for two numbers so we can see that these are the variables. Let x=one numbery=the other number The first sentence is, " The sum of two numbers is 79. " Since sum means addition , we write, x+y=79 The next part states, " The difference of those two numbers is 23. " Since difference means subtraction, we write, x−y=23 And now we have our system of equations: {x+y=79x−y=23. This can be solved with substitution but you might notice it would be easier with elimination. x+y=79+x−y=232x+0y=1022x=1022x2=1022x=51 Finally, plug this back in to either equation to find the y value. (51)+y=7951−51+y=79−51y=28 The solution to this word problem's system of equations is (51,28).

The next problem is a little trickier. It isn't as obvious how to set up the equations. It says, " A minor league ballpark attracts 88 fans and draws in $553 in revenue from ticket sales. A child's ticket costs $4 and an adult's ticket is $7. How many of each type of ticket were sold? "

First, we define our variables. The problem asks for how many of each type of ticket. Since there are two types of tickets we can write, Let C=# of childrenA=# of adults The first snippet is, " A minor league ballpark attracts 88 fans ". We know there's a total of 88 fans which are made up of children and adults. So we can write, C+A=88 Next we have, " and draws in $553 in revenue from ticket sales. A child's ticket costs $4 and an adult's ticket is $7. " So we have to factor in the money. We see that we get $4 from each child and we get $7 from each adult. Total, we have $553. So we can write, 4C+7A=553 Now we have the system: {C+A=884C+7A=553. This can be solved by either elimination or substitution. For this one, I personally would choose substitution, but either works.

Let's solve the first equation for C. C+A=88C+A−A=88−AC=88−A Plug this back into the other equation to solve for A. 4(88−A)+7A=553352−4A+7A=553352+3A=553352−352+3A=553−3523A=2013A3=2013A=67 Finally, plug this back into either equation to solve for C. C=88−(67)C=21 Our solution is (21,67).

Remember, the best way to double check your answer to either of these example problems is to plug in your solved coordinates back into the original equations.

Related Lessons

As with most word problems, the most effective approach to take is translation. The goal is to take written information and translate into a new language: math equations.

Let's work through an example to see how this translation works.

Image by Clker-Free-Vector-Images via Pixabay ( CC0 )

The key to translating a word problem is to identify the given information. Here's what we know from reading the problem:

• Cupcakes cost $2
• Pies cost $7.50
• William bought 20 items
• Total cost (pies + cupcakes) = $73

We can get two equations from this information.

First, we know that, all together, William bought 20 items. If we say that the number of cupcakes is C and the number of pies is P, we can write the equation:

Systems of Linear Equations: Word Problems

Sometimes, it is helpful to translate a word problem into a system of linear equations and solve the system. After translating words to math, isolate one variable in one equation, then use its corresponding expression to solve for the other variable in the other equation. Finally, solve for the first variable! Here is a graphic with an example.

Image source: By Caroline Kulczycky

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 6

• Age word problem: Imran
• Age word problem: Ben & William
• Age word problem: Arman & Diya
• Age word problems
• System of equations word problem: walk & ride

Systems of equations word problems

• System of equations word problem: no solution
• System of equations word problem: infinite solutions
• Systems of equations word problems (with zero and infinite solutions)
• Systems of equations with elimination: TV & DVD
• Systems of equations with elimination: apples and oranges
• Systems of equations with substitution: coins
• Systems of equations with elimination: coffee and croissants
• Systems of equations: FAQ
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

• Maths Questions

Elimination Method Questions

Elimination method questions and practice questions are provided here for students to understand the concept very well. The elimination method is generally used to solve the system of equations. It means finding the values of variables in the given equation. Students can find a number of elimination method questions to enhance their knowledge and score high in exams. To know more about the elimination method, click here .

Elimination Method Questions with Solutions

1. Solve the equations by elimination method.

5a – b = 11

The above equation can be written as:

3a – b = 5 …(1)

5a – b = 11 …(2)

Using the elimination method, the second term of both equations can be eliminated by subtracting the equations.

3a – b = 5

(-)   (+)   (-)

-2a + 0 = -6

Hence, -2a = -6

Now, substitute a = 3 in equation (1), we get the value of b.

3(3) – b = 5

9 – b = 5

-b = 5 – 9

Therefore, the values of a and b are 3 and 4, respectively.

2. Find the values of a and b from the system of equation 2a + b = -4 and 5a – 3b = 1 using the method of elimination.

Given equations are:

2a + b = -4 …(1)

5a – 3b = 1 …(2)

Now, multiply the equation (1) on both sides by 3, and we get

6a + 3b = -12 …(3)

Now, solve the equation (2) and (3) to get the value of a:

6a + 3b = -12

5a – 3b = 1

11a + 0 = -11

Therefore, 11a = -11

Hence, the value of a is -1.

Now, substitute a = -1 in equation (1),

2(-1) + b = -4

-2 + b = -4

Hence, the values of a and b are -1 and -2, respectively.

3. Solve the following pair of linear equations using the elimination method: a + b = 5, 2a – 3b = 4

a + b = 5 …(1)

2a – 3b = 4 …(2)

Now, multiply both sides of the equation (1) by 2, and we get

2a + 2b = 10 …(3)

Now, solving equation (2) and (3) using elimination method, we get

2a – 3b = 4

2a + 2b = 10

(-)    (-)    (-)

_____________

Hence, the value of b is:

Now, substitute b = 6/5 in equation (1), we get

a + (6/5) = 5

5a + 6 = 25

5a = 25 – 6

Hence, the values of a and b are 19/5 and 6/5, respectively.

4. Solve the following equations using the elimination method: p + q – 40 = 0 and 7p + 3q = 180.

Given pair of linear equations are:

p + q – 40 = 0

It can be written as:

p + q = 40 …(1)

7p + 3q = 180 …(2)

Now, multiply the equation (1) by 7, we get

7p + 7q = 280 …(3)

Now, solve the equations (2) and (3) using elimination method, we get the following:

7p + 3q = 180

7p + 7q = 280

(-)    (-)     (-)

____________

-4q = – 100

q = -100/-4

Now, substitute q = 25 in equation (1), we get

p + 25 = 40

p = 40 – 25

Therefore, p = 15 and q = 25.

5. Using the elimination method, solve the following equations: a/2 + 2/3 b = -1 and a – 1/3b = 3.

a/2 + 2/3 b = -1 …(1)

a – 1/3b = 3 …(2)

Now, multiply equation (1) by 6 and equation (2) by 3, we get;

3a + 4b = -6 …(3)

3a – b = 9 …(4)

Now, solve the equations (3) and (4), we get

3a + 4b = -6

3a – b = 9

(-)  (+)  (-)

0 + 5b = -15

Thus, 5b = -15

Now, substitute b = -3 in equation (4), we get;

3a – (-3) = 9

3a = 9 – 3

Hence, the solution of the given equations a/2 + 2/3 b = -1 and a – 1/3b = 3 are:

a = 2 and b = -3.

Also, read:

• Substitution Method
• Cross Multiplication Method

6. If p = a and q = b are the solutions of the equations p – q = 2 and p + q = 4, then find the values of a and b.

p – q = 2 …(1)

p + q = 4 …(2)

Now, solve the equations (1) and (2)

p – q = 2

Now, substitute p = 3 in equation (1), we get

3 – q = 2

-q = 2 – 3

Hence, q = 1

As given, p = a and q = b,

The values of a and b are 3 and 1, respectively.

7. Determine the values of a and b which satisfies both the equations 47a + 31b = 63 and 31a + 47b = 15.

Given equations:

47a + 31b = 63 …(1)

31a + 47b = 15 …(2)

To solve the equations, multiply equation (1) by 31 and equation (2) by 47.

1457a + 961b = 1953 …(3)

1457a + 2209b = 705 …(4)

1457a + 961b = 1953

1457a + 2209b = 705

(-)        (-)             (-)

___________________

0 – 1248b = 1248

Thus, -1248b = 1248

b = -1248/1248

Now, substitute b = -1 in equation (2), we get

31a + 47(-1) = 15

31a – 47 = 15

31a = 15 + 47

Thus, a = 62/31

Therefore, a = 2 and b = -1.

8. A book shop was selling 3 books and 5 notebooks for Rs. 309 and 6 books and 2 notebooks for Rs. 282 during a closing down deal. What would be the cost of a book and a notebook?

From the given conditions, we can frame 2 equations:

Let’s take book = a and notebook = b.

Condition 1: 3 books and 5 notebooks for Rs. 309

I.e., 3a + 5b = 309 …(1)

Condition 2: 6 books and 2 notebooks for Rs. 282

I.e., 6a + 2b = 282 …(2)

To solve the equations, multiply equation (1) by 2:

6a + 10b = 618 …(3)

Now, solve the equations (2) and (3)

6a + 2b = 282

6a + 10b = 618

(-)    (-)      (-)

0 – 8b = – 336

Hence, -8b = -336

b = -336/-8

Therefore, the cost of a notebook is Rs. 42.

Now, substitute b = 42 in equation (2)

6a + 2(42) = 282

6a +84 = 282

6a = 282 – 84

Therefore, the cost of a book is Rs. 33.

Hence, the cost of a book and a notebook = Rs. 33 + Rs. 42

9. Solve the following system of equations using the elimination method:

3p + 4q = 10 and 2p – 2q = 2.

3p + 4q = 10 …(1)

2p – 2q = 2 …(2)

Now, multiply equation (2) by 2:

4p – 4q = 4 …(3)

Now, solve the equations (1) and (3),

3p + 4q = 10

4p – 4q = 4

7p + 0 = 14

Hence, 7p = 14

Substituting p = 2 in equation (2), we get

2(2) – 2q = 2

4 – 2q = 2

-2q = 2 – 4

Hence, the solutions of the system of equations are p = 2 and q = 1.

10. Find two numbers if the addition of two numbers is 14, and their difference is 2.

Let the two numbers be p and q.

According to the given condition, we can frame the equation as follows:

p + q = 14 …(1)

p – q = 2 …(2)

Now, solve the equations (1) and (2),

2p + 0 = 16

Thus, 2p = 16

Therefore, p = 16/2 = 8

Now, substitute p = 8 in equation (2), we get

8 – q = 2

-q = 2 – 8

Hence, q = 6

Therefore, the two numbers are:

p = 8 and q = 6.

Practice Questions

• Use the elimination method to solve the following system of linear equations: 3a – b – 7, 2a + 5b + 1 = 0.
• Find the value of p and q for the given system of linear equations using the elimination method: 2p + 3q = 11, p + 2q = 7.
• Solve the following system of linear equations by the elimination method: 3a – 5b – 4 = 0 and 9a = 2b + 7.

Explore more Maths-related videos to learn the concepts quickly by downloading BYJU’S – The Learning App.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Solving Systems of Equations Using Elimination

More specific topics in solving systems of equations using elimination.

• Elimination by Addition and Subtraction
• Elimination by Multiplication

Popular Tutorials in Solving Systems of Equations Using Elimination

How Do You Use a System of Linear Equations to Find Coordinates on a Map?

Like riddles? A word problem is just like a riddle! In this word problem, you'll need to find the solution to a system of linear equations solve the riddle and find a location on a map. Check it out!

How Do You Solve a System of Equations Using the Elimination by Addition Method?

There are many different ways to solve a system of linear equations. In this tutorial, you'll see how to solve a system of linear equations by combining the equations together to eliminate one of the variables. Then, see how find the value of that variable and use it to find the value of the other variable. Take a look!

How Do You Solve a System of Equations Using the Elimination by Subtraction Method?

There are many different ways to solve a system of linear equations. In this tutorial, you'll see how to solve such a system by combining the equations together in a way so that one of the variables is eliminated. Then, see how find the value of that variable and use it to find the value of the other variable. Take a look!

How Do You Solve a System of Equations Using the Elimination by Multiplication Method?

What's Another Way of Solving a System of Equations Using the Elimination by Multiplication Method?

There are many different ways to solve a system of linear equations. In this tutorial, you'll see how to solve a system of linear equations by combining the equations together in order to eliminate one of the variables. Then, see how find the value of that variable and use it to find the value of the other variable. Take a look!

How Do You Solve a Word Problem Using the Elimination by Subtraction Method?

Word problems are a great way to see math in action! In this tutorial, you'll see how to write a system of linear equations from the information given in a word problem. Then, you'll see how to solve this system using the elimination method. See this entire process by watching this tutorial!

What Are the Ways You Can Solve a System of Linear Equations?

Knowing the definition of a system of equations is great, but you should also know how to solve them! This tutorial introduces you to the graphing method, substitution method, and elimination method for solving a system of equations. Take a look and learn them all!

Related Topics

Other topics in systems of equations and inequalities :.

• Solving Systems of Equations By Graphing
• Solving Systems of Equations Using Substitution
• Solving Special Systems
• Systems of Inequalities
• Terms of Use

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Solving Systems of Equations Real World Problems

Wow! You have learned many different strategies for solving systems of equations! First we started with Graphing Systems of Equations . Then we moved onto solving systems using the Substitution Method . In our last lesson we used the Linear Combinations or Addition Method to solve systems of equations.

Now we are ready to apply these strategies to solve real world problems! Are you ready? First let's look at some guidelines for solving real world problems and then we'll look at a few examples.

Steps For Solving Real World Problems

• Highlight the important information in the problem that will help write two equations.
• Define your variables
• Write two equations
• Use one of the methods for solving systems of equations to solve.
• Check your answers by substituting your ordered pair into the original equations.
• Answer the questions in the real world problems. Always write your answer in complete sentences!

Ok... let's look at a few examples. Follow along with me. (Having a calculator will make it easier for you to follow along.)

Example 1: Systems Word Problems

You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. You must report the number of hot dogs sold and the number of sodas sold. How many hot dogs were sold and how many sodas were sold?

1.  Let's start by identifying the important information:

• hot dogs cost $1.50
• Sodas cost $0.50
• Made a total of $78.50
• Sold 87 hot dogs and sodas combined

2.  Define your variables.

• Ask yourself, "What am I trying to solve for? What don't I know?

In this problem, I don't know how many hot dogs or sodas were sold. So this is what each variable will stand for. (Usually the question at the end will give you this information).

Let x = the number of hot dogs sold

Let y = the number of sodas sold

3. Write two equations.

One equation will be related to the price and one equation will be related to the quantity (or number) of hot dogs and sodas sold.

1.50x + 0.50y = 78.50    (Equation related to cost)

 x + y = 87   (Equation related to the number sold)

4.  Solve! 

We can choose any method that we like to solve the system of equations. I am going to choose the substitution method since I can easily solve the 2nd equation for y.

5. Think about what this solution means.

x is the number of hot dogs and x = 35. That means that 35 hot dogs were sold.

y is the number of sodas and y = 52. That means that 52 sodas were sold.

6.  Write your answer in a complete sentence.

35 hot dogs were sold and 52 sodas were sold.

7.  Check your work by substituting.

1.50x + 0.50y = 78.50

1.50(35) + 0.50(52) = 78.50

52.50 + 26 = 78.50

35 + 52 = 87

Since both equations check properly, we know that our answers are correct!

That wasn't too bad, was it? The hardest part is writing the equations. From there you already know the strategies for solving. Think carefully about what's happening in the problem when trying to write the two equations.

Example 2: Another Word Problem

You and a friend go to Tacos Galore for lunch. You order three soft tacos and three burritos and your total bill is $11.25. Your friend's bill is $10.00 for four soft tacos and two burritos. How much do soft tacos cost? How much do burritos cost?

• 3 soft tacos + 3 burritos cost $11.25
• 4 soft tacos + 2 burritos cost $10.00

In this problem, I don't know the price of the soft tacos or the price of the burritos.

Let x = the price of 1 soft taco

Let y = the price of 1 burrito

One equation will be related your lunch and one equation will be related to your friend's lunch.

3x + 3y = 11.25  (Equation representing your lunch)

4x + 2y = 10   (Equation representing your friend's lunch)

We can choose any method that we like to solve the system of equations. I am going to choose the combinations method.

5. Think about what the solution means in context of the problem.

x = the price of 1 soft taco and x = 1.25.

That means that 1 soft tacos costs $1.25.

y = the price of 1 burrito and y = 2.5.

That means that 1 burrito costs $2.50.

Yes, I know that word problems can be intimidating, but this is the whole reason why we are learning these skills. You must be able to apply your knowledge!

If you have difficulty with real world problems, you can find more examples and practice problems in the Algebra Class E-course.

Take a look at the questions that other students have submitted:

Problem about the WNBA

Systems problem about ages

Problem about milk consumption in the U.S.

Vans and Buses? How many rode in each?

Telephone Plans problem

Systems problem about hats and scarves

Apples and guavas please!

How much did Alice spend on shoes?

All about stamps

Going to the movies

Small pitchers and large pitchers - how much will they hold?

Chickens and dogs in the farm yard

• System of Equations
• Systems Word Problems

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.3: Solve Systems of Equations by Elimination

• Last updated
• Save as PDF
• Page ID 142811

Learning Objectives

By the end of this section, you will be able to:

• Solve a system of equations by elimination
• Solve applications of systems of equations by elimination
• Choose the most convenient method to solve a system of linear equations

Before you get started, take this readiness quiz.

• Simplify −5(6−3a). If you missed this problem, review Example 1.10.43 .
• Solve the equation \(\frac{1}{3}x+\frac{5}{8}=\frac{31}{24}\). If you missed this problem, review Example 2.5.1 .

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

Solve a System of Equations by Elimination

The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For any expressions a , b , c , and d ,

\[\begin{array}{lc} \text{ if } & a=b \\ \text { and } & c=d \\ \text { then } &a+c =b+d \end{array}\]

To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.

Notice how that works when we add these two equations together:

\[\begin{array}{l} 3x+y=5 \\ \underline{2x-y=0} \\ 5x\quad\quad=5\end{array}\]

The y ’s add to zero and we have one equation with one variable.

Let’s try another one:

\[\left\{\begin{array}{l}{x+4 y=2} \\ {2 x+5 y=-2}\end{array}\right.\]

This time we don’t see a variable that can be immediately eliminated if we add the equations.

But if we multiply the first equation by −2, we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2.

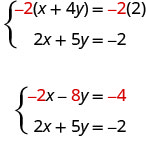
Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.

Add the equations yourself—the result should be −3 y = −6. And that looks easy to solve, doesn’t it? Here is what it would look like.

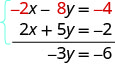
We’ll do one more:

\[\left\{\begin{array}{l}{4 x-3 y=10} \\ {3 x+5 y=-7}\end{array}\right.\]

It doesn’t appear that we can get the coefficients of one variable to be opposites by multiplying one of the equations by a constant, unless we use fractions. So instead, we’ll have to multiply both equations by a constant.

We can make the coefficients of x be opposites if we multiply the first equation by 3 and the second by −4, so we get 12 x and −12 x .

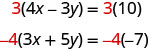
This gives us these two new equations:

\[\left\{\begin{aligned} 12 x-9 y &=30 \\-12 x-20 y &=28 \end{aligned}\right.\]

When we add these equations,

\[ \left\{\begin{array}{r}{12 x-9 y=30} \\ {\underline{-12 x-20 y=28}} \\\end{array}\right.\\\quad\qquad {-29 y=58}\]

the x ’s are eliminated and we just have −29 y = 58.

Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.

Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.

Example \(\PageIndex{1}\): How to Solve a System of Equations by Elimination

Solve the system by elimination. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)

Try It \(\PageIndex{2}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x-3 y=7}\end{array}\right.\)

(2,−1)

Try It \(\PageIndex{3}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{4 x+y=-5} \\ {-2 x-2 y=-2}\end{array}\right.\)

(−2,3)

The steps are listed below for easy reference.

HOW TO SOLVE A SYSTEM OF EQUATIONS BY ELIMINATION.

• Write both equations in standard form. If any coefficients are fractions, clear them.
• Decide which variable you will eliminate.
• Multiply one or both equations so that the coefficients of that variable are opposites.
• Add the equations resulting from Step 2 to eliminate one variable.
• Solve for the remaining variable.
• Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
• Write the solution as an ordered pair.
• Check that the ordered pair is a solution to both original equations.

First we’ll do an example where we can eliminate one variable right away.

Example \(\PageIndex{4}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{x+y=10} \\ {x-y=12}\end{array}\right.\)

Try It \(\PageIndex{5}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{2 x+y=5} \\ {x-y=4}\end{array}\right.\)

(3,−1)

Try It \(\PageIndex{6}\)

Solve the system by elimination.\(\left\{\begin{array}{l}{x+y=3} \\ {-2 x-y=-1}\end{array}\right.\)

(−2,5)

In Example \(\PageIndex{7}\), we will be able to make the coefficients of one variable opposites by multiplying one equation by a constant.

Example \(\PageIndex{7}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{3 x-2 y=-2} \\ {5 x-6 y=10}\end{array}\right.\)

Try It \(\PageIndex{8}\)

Solve the system by elimination.\(\left\{\begin{array}{l}{4 x-3 y=1} \\ {5 x-9 y=-4}\end{array}\right.\)

Try It \(\PageIndex{9}\)

Solve the system by elimination.\(\left\{\begin{array}{l}{3 x+2 y=2} \\ {6 x+5 y=8}\end{array}\right.\)

(−2,4)

Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.

Example \(\PageIndex{10}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{4 x-3 y=9} \\ {7 x+2 y=-6}\end{array}\right.\)

In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by a constant to get the opposites.

Try It \(\PageIndex{11}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.\)

Try It \(\PageIndex{12}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{7 x+8 y=4} \\ {3 x-5 y=27}\end{array}\right.\)

(4,−3)

When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by its LCD.

Example \(\PageIndex{13}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{x+\frac{1}{2} y=6} \\ {\frac{3}{2} x+\frac{2}{3} y=\frac{17}{2}}\end{array}\right.\)

In this example, both equations have fractions. Our first step will be to multiply each equation by its LCD to clear the fractions.

Try It \(\PageIndex{14}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{\frac{1}{3} x-\frac{1}{2} y=1} \\ {\frac{3}{4} x-y=\frac{5}{2}}\end{array}\right.\)

Try It \(\PageIndex{15}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{x+\frac{3}{5} y=-\frac{1}{5}} \\ {-\frac{1}{2} x-\frac{2}{3} y=\frac{5}{6}}\end{array}\right.\)

(1,−2)

In the Solving Systems of Equations by Graphing we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.

Example \(\PageIndex{16}\)

Solve the system by elimination.\(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=3-\frac{3}{4} x}\end{array}\right.\)

\(\begin{array} {ll} & \left\{\begin{aligned} 3 x+4 y &=12 \\ y &=3-\frac{3}{4} x \end{aligned}\right. \\\\\text{Write the second equation in standard form.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {\frac{3}{4} x+y=3}\end{array}\right.\\ \\ \text{Clear the fractions by multiplying thesecond equation by 4.} & \left\{\begin{aligned} 3 x+4 y &=12 \\ 4\left(\frac{3}{4} x+y\right) &=4(3) \end{aligned}\right. \\\\ \text{Simplify.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {3 x+4 y=12}\end{array}\right.\\\\ \text{To eliminate a variable, we multiply thesecond equation by −1.} & \left\{\begin{array}{c}{3 x+4 y=12} \\ \underline{-3 x-4 y=-12} \end{array}\right.\\ &\qquad\qquad\quad 0=0 \\ \text{Simplify and add.} \end{array}\)

This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.

After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.

Try It \(\PageIndex{17}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{5 x-3 y=15} \\ {y=-5+\frac{5}{3} x}\end{array}\right.\)

infinitely many solutions

Try It \(\PageIndex{18}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{x+2 y=6} \\ {y=-\frac{1}{2} x+3}\end{array}\right.\)

Example \(\PageIndex{19}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{-6 x+15 y=10} \\ {2 x-5 y=-5}\end{array}\right.\)

\(\begin{array} {ll} \text{The equations are in standard form.}& \left\{\begin{aligned}-6 x+15 y &=10 \\ 2 x-5 y &=-5 \end{aligned}\right. \\\\ \text{Multiply the second equation by 3 to eliminate a variable.} & \left\{\begin{array}{l}{-6 x+15 y=10} \\ {3(2 x-5 y)=3(-5)}\end{array}\right. \\\\ \text{Simplify and add.} & \left\{\begin{aligned}{-6 x+15 y =10} \\ \underline{6 x-15 y =-15} \end{aligned}\right. \\ & \qquad \qquad \quad0\neq 5 \end{array}\)

This statement is false. The equations are inconsistent and so their graphs would be parallel lines.

The system does not have a solution.

Try It \(\PageIndex{20}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{-3 x+2 y=8} \\ {9 x-6 y=13}\end{array}\right.\)

no solution

Try It \(\PageIndex{21}\)

Solve the system by elimination. \(\left\{\begin{array}{l}{7 x-3 y=-2} \\ {-14 x+6 y=8}\end{array}\right.\)

Solve Applications of Systems of Equations by Elimination

Some applications problems translate directly into equations in standard form, so we will use the elimination method to solve them. As before, we use our Problem Solving Strategy to help us stay focused and organized.

Example \(\PageIndex{22}\)

The sum of two numbers is 39. Their difference is 9. Find the numbers.

\(\begin{array} {ll} \textbf{Step 1. Read}\text{ the problem}& \\ \textbf{Step 2. Identify} \text{ what we are looking for.} & \text{We are looking for two numbers.} \\\textbf{Step 3. Name} \text{ what we are looking for.} & \text{Let n = the first number.} \\ & \text{ m = the second number} \\\textbf{Step 4. Translate} \text{ into a system of equations.}& \\ & \text{The sum of two numbers is 39.} \\ & n+m=39\\ & \text{Their difference is 9.} \\ & n−m=9 \\ \\ \text{The system is:} & \left\{\begin{array}{l}{n+m=39} \\ {n-m=9}\end{array}\right. \\\\ \textbf{Step 5. Solve} \text{ the system of equations. } & \\ \text{To solve the system of equations, use} \\ \text{elimination. The equations are in standard} \\ \text{form and the coefficients of m are} & \\ \text{opposites. Add.} & \left\{\begin{array}{l}{n+m=39} \\ \underline{n-m=9}\end{array}\right. \\ &\quad 2n\qquad=48 \\ \\\text{Solve for n.} & n=24 \\ \\ \text{Substitute n=24 into one of the original} &n+m=39 \\ \text{equations and solve form.} & 24+m=39 \\ & m=15 \\ \textbf{Step 6. Check}\text{ the answer.} & \text{Since 24+15=39 and 24−15=9, the answers check.}\\ \textbf{Step 7. Answer} \text{ the question.} & \text{The numbers are 24 and 15.} \end{array}\)

Try It \(\PageIndex{23}\)

The sum of two numbers is 42. Their difference is 8. Find the numbers.

The numbers are 25 and 17.

Try It \(\PageIndex{24}\)

The sum of two numbers is −15. Their difference is −35. Find the numbers.

The numbers are −25 and 10.

Example \(\PageIndex{25}\)

Joe stops at a burger restaurant every day on his way to work. Monday he had one order of medium fries and two small sodas, which had a total of 620 calories. Tuesday he had two orders of medium fries and one small soda, for a total of 820 calories. How many calories are there in one order of medium fries? How many calories in one small soda?

Try It \(\PageIndex{26}\)

Malik stops at the grocery store to buy a bag of diapers and 2 cans of formula. He spends a total of $37. The next week he stops and buys 2 bags of diapers and 5 cans of formula for a total of $87. How much does a bag of diapers cost? How much is one can of formula?

The bag of diapers costs $11 and the can of formula costs $13.

Try It \(\PageIndex{27}\)

To get her daily intake of fruit for the day, Sasha eats a banana and 8 strawberries on Wednesday for a calorie count of 145. On the following Wednesday, she eats two bananas and 5 strawberries for a total of 235 calories for the fruit. How many calories are there in a banana? How many calories are in a strawberry?

There are 105 calories in a banana and 5 calories in a strawberry.

Choose the Most Convenient Method to Solve a System of Linear Equations

When you will have to solve a system of linear equations in a later math class, you will usually not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

Example \(\PageIndex{28}\)

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

• \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
• \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)

1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)

• Since both equations are in standard form, using elimination will be most convenient.

2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)

Since one equation is already solved for y , using substitution will be most convenient.

Try It \(\PageIndex{29}\)

For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

• \(\left\{\begin{array}{l}{4 x-5 y=-32} \\ {3 x+2 y=-1}\end{array}\right.\)
• \(\left\{\begin{array}{l}{x=2 y-1} \\ {3 x-5 y=-7}\end{array}\right.\)
• Since one equation is already solved for xx, using substitution will be most convenient.

Try It \(\PageIndex{30}\)

• \(\left\{\begin{array}{l}{y=2 x-1} \\ {3 x-4 y=-6}\end{array}\right.\)
• \(\left\{\begin{array}{l}{6 x-2 y=12} \\ {3 x+7 y=-13}\end{array}\right.\)
• Since one equation is already solved for \(y\), using substitution will be most convenient;

Access these online resources for additional instruction and practice with solving systems of linear equations by elimination.

• Instructional Video-Solving Systems of Equations by Elimination
• Instructional Video-Solving by Elimination
• Instructional Video-Solving Systems by Elimination

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 10^{1-x}=10^4
• \sqrt{3+x}=-2
• 6+11x+6x^2+x^3=0
• factor\:x^{2}-5x+6
• simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
• x+2y=2x-5,\:x-y=3

algebra-calculator

word problems

• High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables. In this blog post,...

Please add a message.

Message received. Thanks for the feedback.